Uplift Behavior of Pipelines Buried at Various Depths in Spatially Varying Clayey Seabed
Abstract
:1. Introduction
2. Modeling of Spatially Variable Soil
3. Finite Element Methodology
3.1. Small-Strain Finite Element Analysis Model
3.2. Validation of the Numerical Model
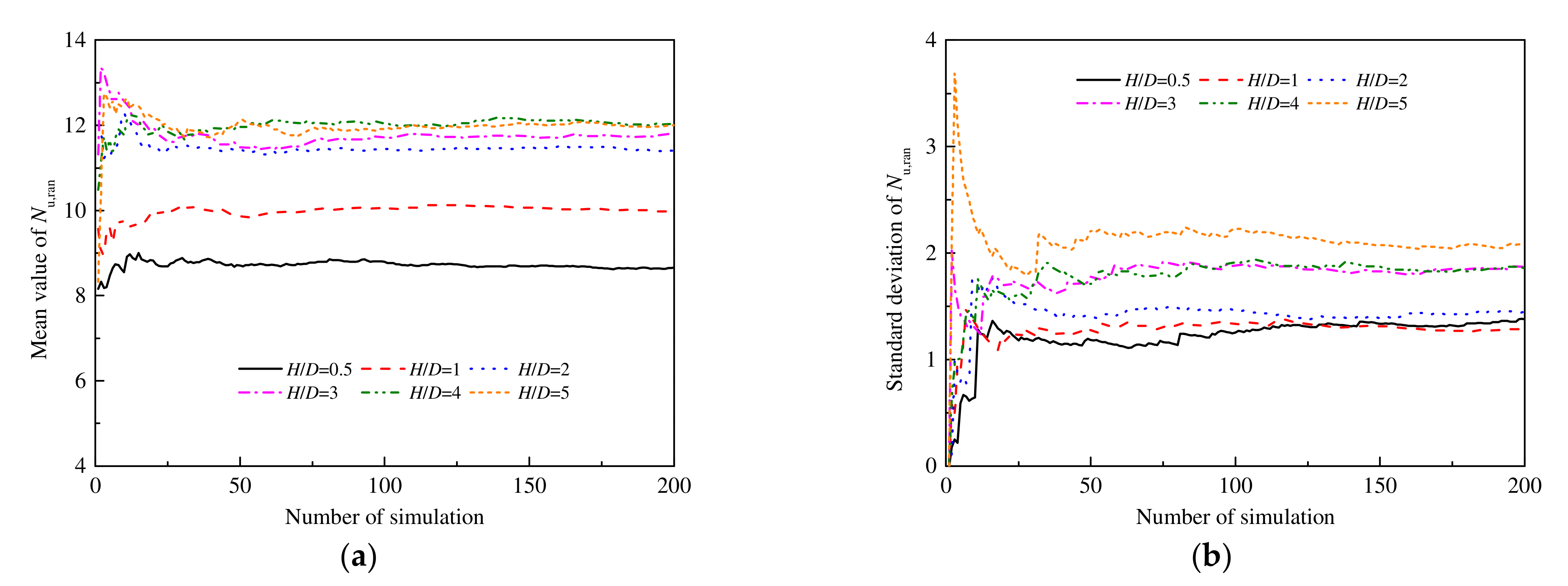
3.3. Random SSFE Analysis
4. Results and Discussions
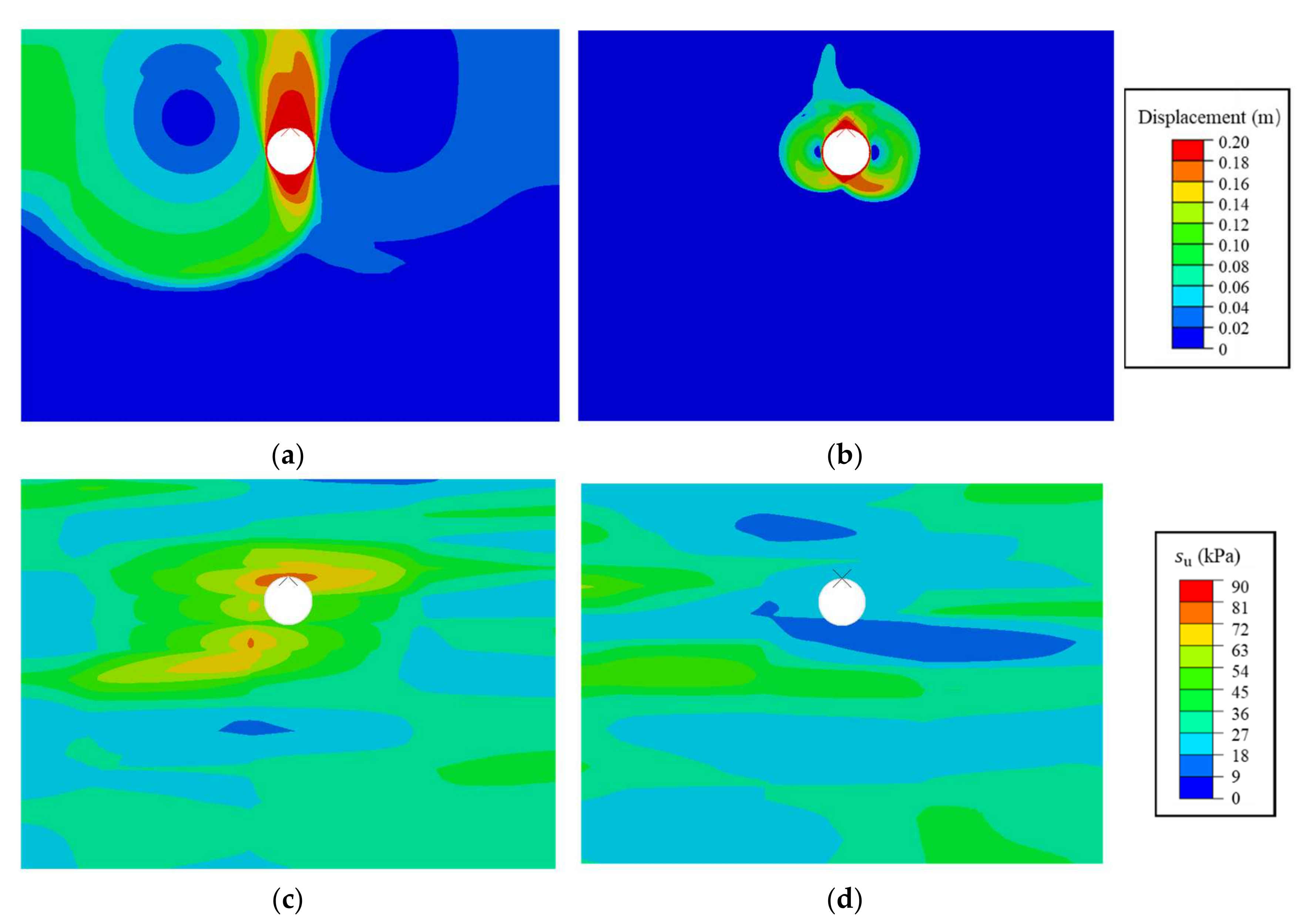
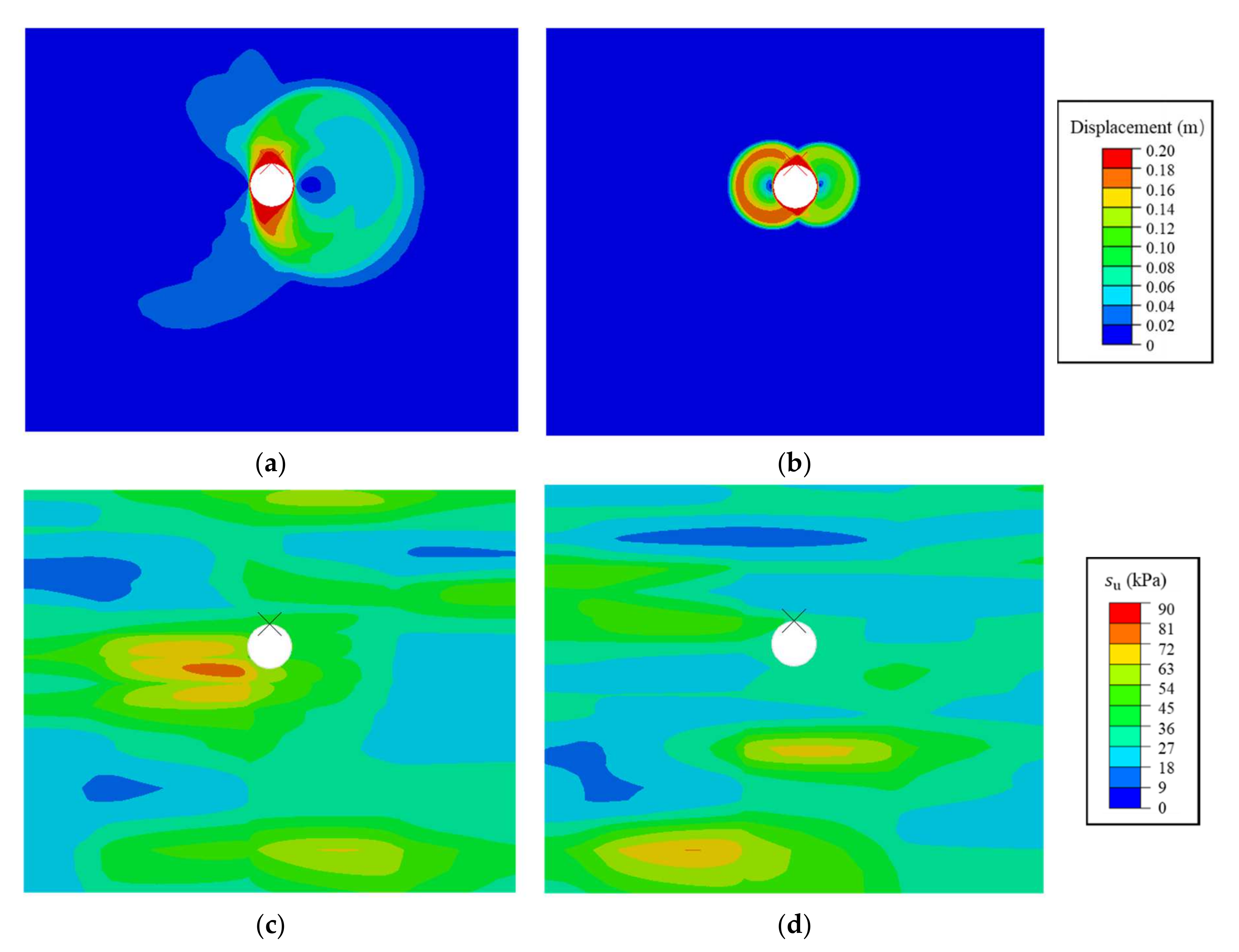
4.1. Failure Mechanism in Deterministic and Random Soil
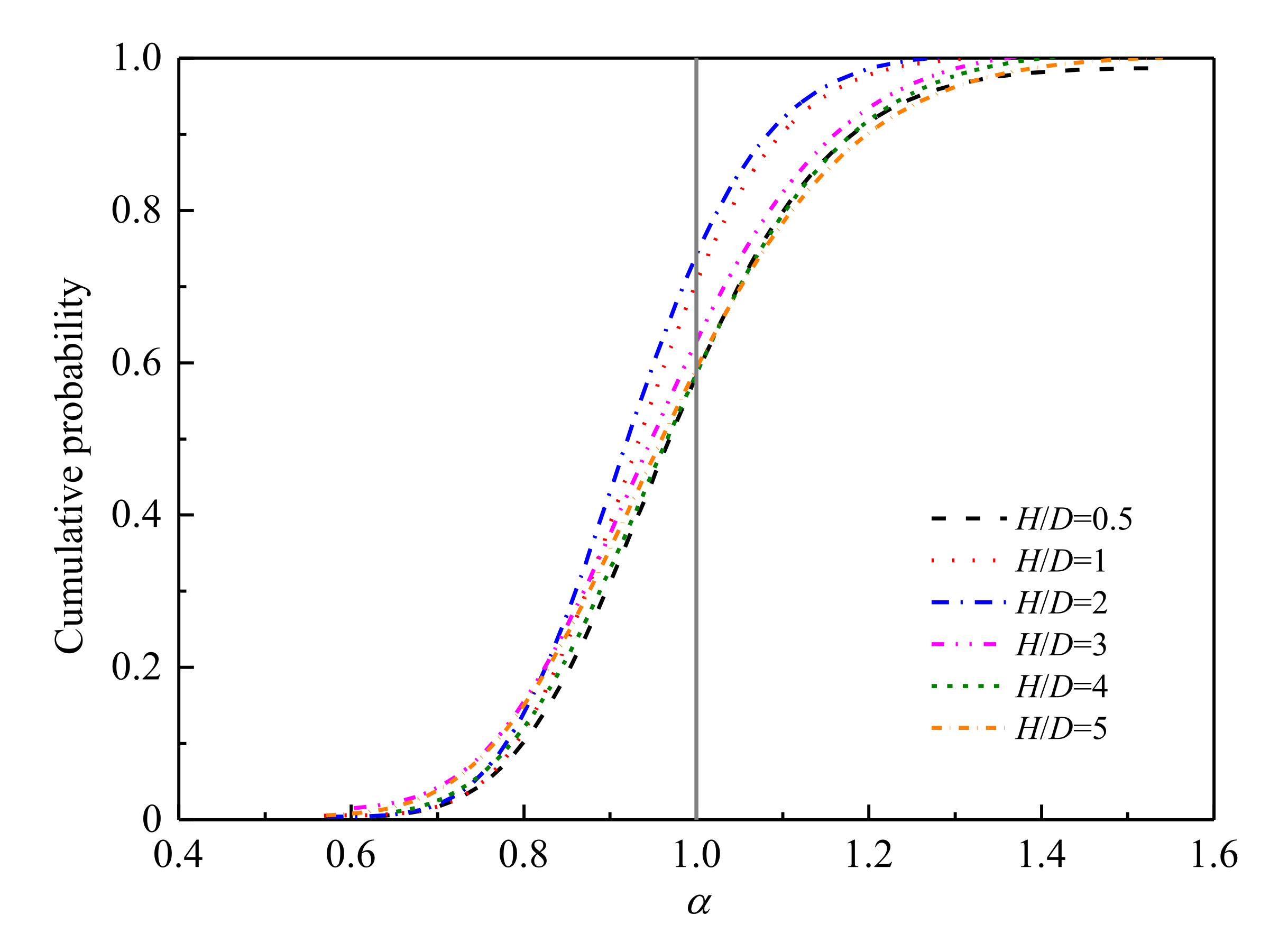
4.2. Uplift Capacity Factors for Pipelines at Various Depths
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sheil, B.B.; Byrne, B.W.; Martin, C.M. Rate effects on the uplift capacity of pipelines embedded in clay: Finite element modelling. Comput. Geotech. 2021, 137, 104155. [Google Scholar] [CrossRef]
- Maitra, S.; Chatterjee, S.; White, D.; Choudhury, D. Uplift resistance of buried pipelines: The contribution of seepage forces. Ocean. Eng. 2022, 250, 111037. [Google Scholar] [CrossRef]
- Seth, D.; Manna, B.; Kumar, P.; Shahu, J.T.; Fazeres-Ferradosa, T.; Taveira-Pinto, F.; Carvalho, H. 2021, Uplift and lateral buckling failure mechanisms of offshore pipes buried in normally consolidated clay. Eng. Fail. Anal. 2022, 121, 105161. [Google Scholar] [CrossRef]
- Kumar, P.; Seth, D.; Manna, B.; Shahu, J.T. Lateral and Uplift Capacity of Pipeline Buried in Seabed of Homogeneous Clay. J. Pipeline Syst. Eng. Pract. 2021, 12, 04021020. [Google Scholar] [CrossRef]
- Maitra, S.; Chatterjee, S.; Choudhury, D. Generalized framework to predict undrained uplift capacity of buried offshore pipelines. Can. Geotech. J. 2016, 53, 1841–1852. [Google Scholar] [CrossRef]
- Chen, R.P.; Zhu, B.; Ni, W.J. Uplift tests on full-scale pipe segment in lumpy soft clay backfill. Can. Geotech. J. 2016, 53, 578–588. [Google Scholar] [CrossRef]
- Martin, C.M.; White, D.J. Limit analysis of the undrained bearing capacity of offshore pipelines. Géotechnique 2012, 62, 847–863. [Google Scholar] [CrossRef]
- Brennan, A.J.; Ghahremani, M.; Brown, M.J. Strength reduction for upheaval buckling of buried pipes in blocky clay backfill. Ocean. Eng. 2017, 130, 210–217. [Google Scholar] [CrossRef] [Green Version]
- Liu, R.; Basu, P.; Xiong, H. Laboratory tests and thermal buckling analysis for pipes buried in Bohai soft clay. Mar. Struct. 2015, 43, 44–60. [Google Scholar] [CrossRef]
- Phoon, K.K.; Kulhawy, F.H. Characterization of geotechnical variability. Can. Geotech. J. 1999, 36, 612–624. [Google Scholar] [CrossRef]
- Phoon, K.K.; Kulhawy, F.H. Evaluation of geotechnical property variability. Can. Geotech. J. 1999, 36, 625–639. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L. Seismic response of pile–raft system embedded in spatially random clay. Géotechnique 2019, 69, 638–645. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Zhang, L.; Zhu, Z.; Hu, J.; Wei, H. Probabilistic stability analyses of undrained slopes by 3D random fields and finite element methods. Geosci. Front. 2018, 9, 1657–1664. [Google Scholar] [CrossRef]
- Liu, Y.; He, L.Q.; Jiang, Y.J.; Sun, M.M.; Chen, E.J.; Lee, F.H. Effect of in situ water content variation on the spatial variation of strength of deep cement-mixed clay. Géotechnique 2019, 69, 391–405. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Jiang, Y.J.; Xiao, H.; Lee, F.H. Determination of representative strength of deep cement-mixed clay from core strength data. Géotechnique 2017, 67, 350–364. [Google Scholar] [CrossRef]
- Liu, Y.; Lee, F.H.; Quek, S.T.; Chen, E.J.; Yi, J.T. Effect of spatial variation of strength and modulus on the lateral compression response of cement-admixed clay slab. Géotechnique 2015, 65, 851–865. [Google Scholar] [CrossRef]
- Chen, X.; Li, D.; Tang, X.; Liu, Y. A three-dimensional large-deformation random finite-element study of landslide runout considering spatially varying soil. Landslides 2021, 18, 3149–3162. [Google Scholar] [CrossRef]
- Chen, X.J.; Fu, Y.; Liu, Y. Random finite element analysis on uplift bearing capacity and failure mechanisms of square plate anchors in spatially variable clay. Eng. Geol. 2022, 304, 106677. [Google Scholar] [CrossRef]
- Charlton, T.S.; Rouainia, M. A probabilistic approach to the ultimate capacity of skirted foundations in spatially variable clay. Struct. Saf. 2017, 65, 126–136. [Google Scholar] [CrossRef] [Green Version]
- Cheng, P.; Liu, Y.; Li, Y.P.; Yi, J.T. A large deformation finite element analysis of uplift behaviour for helical anchor in spatially variable clay. Comput. Geotech. 2022, 141, 104542. [Google Scholar] [CrossRef]
- Luo, W.; Li, J. Effects of installation on combined bearing capacity of a spudcan foundation in spatially variable clay. Appl. Ocean. Res. 2022, 120, 103055. [Google Scholar] [CrossRef]
- Yi, J.T.; Huang, L.Y.; Li, D.Q.; Liu, Y. A large-deformation random finite-element study: Failure mechanism and bearing capacity of spudcan in a spatially varying clayey seabed. Géotechnique 2020, 70, 392–405. [Google Scholar] [CrossRef]
- Charlton, T.S.; Rouainia, M. Probabilistic analysis of the uplift resistance of buried pipelines in clay. Ocean. Eng. 2019, 186, 105891. [Google Scholar] [CrossRef]
- Liu, Y.; Lee, F.H.; Quek, S.T.; Beer, M. Modified linear estimation method for generating multi-dimensional multi-variate Gaussian field in modelling material properties. Probabilistic Eng. Mech. 2014, 38, 42–53. [Google Scholar] [CrossRef]
- Taiebat, H.A.; Carter, J.P. Numerical studies of the bearing capacity of shallow foundations on cohesive soil subjected to combined loading. Géotechnique 2000, 50, 409–418. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Yi, J.; Cheng, P.; Yao, K. Numerical simulation of set-up around shaft of XCC pile in clay. Geomech. Eng. 2020, 21, 489–501. [Google Scholar]
- Peng, Y.; Liu, H.; Li, C.; Ding, X.; Deng, X.; Wang, C. The detailed particle breakage around the pile in coral sand. Acta Geotech. 2021, 16, 1971–1981. [Google Scholar] [CrossRef]
- Yi, J.T.; Liu, F.; Zhang, T.B.; Yao, K.; Zhen, G. A large deformation finite element investigation of pile group installations with consideration of intervening consolidation. Appl. Ocean. Res. 2021, 112, 102698. [Google Scholar] [CrossRef]
- Randolph, M.F.; Houlsby, G.T. The limiting pressure on a circular pile loaded laterally in cohesive soil. Géotechnique 1984, 34, 613–623. [Google Scholar] [CrossRef]
- Li, J.; Tian, Y.; Cassidy, M.J. Failure mechanism and bearing capacity of footings buried at various depths in spatially random soil. J. Geotech. Geoenviron. Eng. 2015, 141, 04014099. [Google Scholar] [CrossRef] [Green Version]
- Cheng, P.; Yi, J.T.; Liu, F.; Dong, J.J. Characterization of Model Uncertainty for the Vertical Pullout Capacity of Helical Anchors in Cohesive Soils. J. Mar. Sci. Eng. 2020, 8, 738. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A. Bearing capacity of spatially random soil: The undrained clay Prandtl problem revisited. Géotechnique 2001, 51, 351–359. [Google Scholar] [CrossRef]
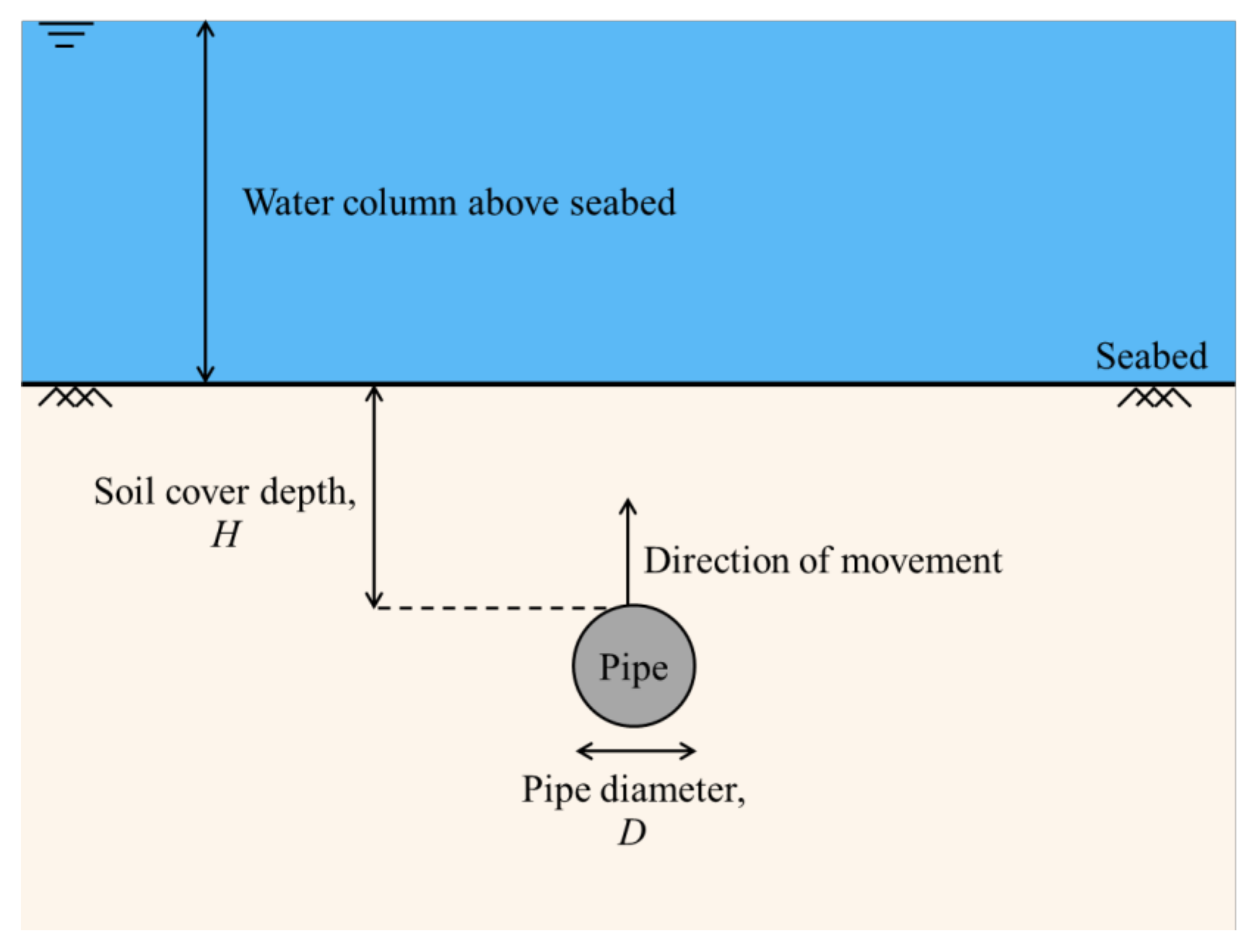
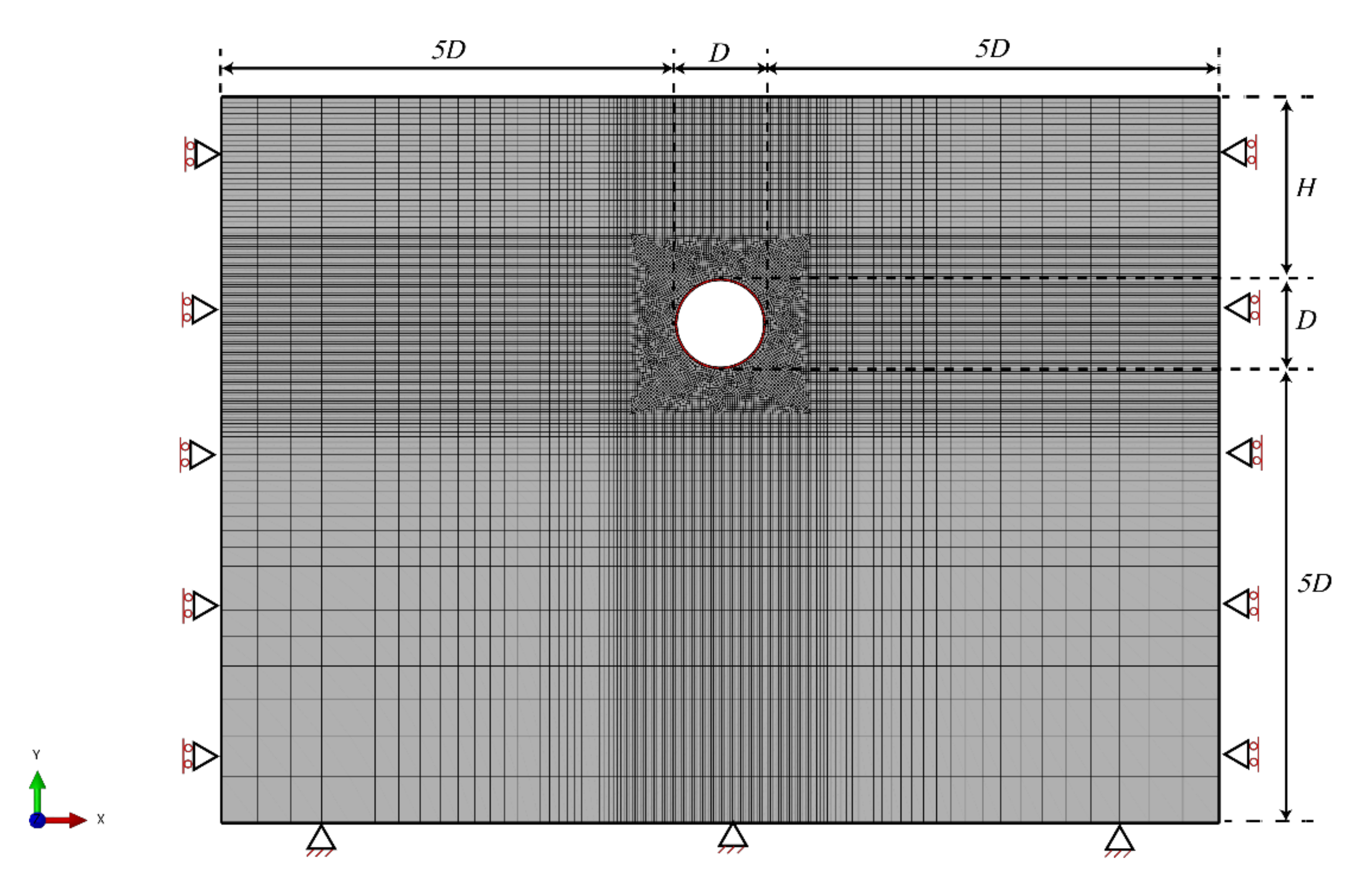
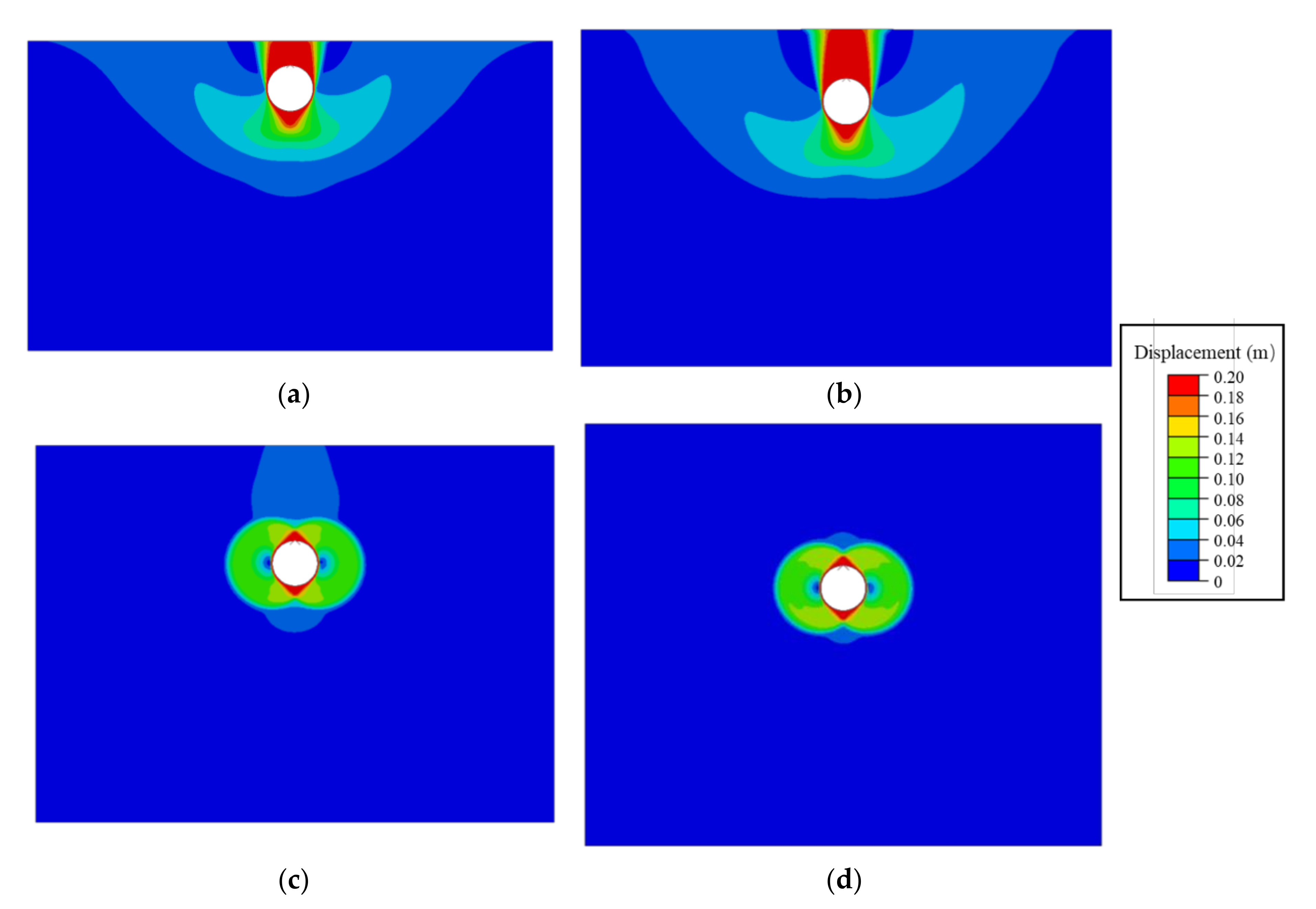

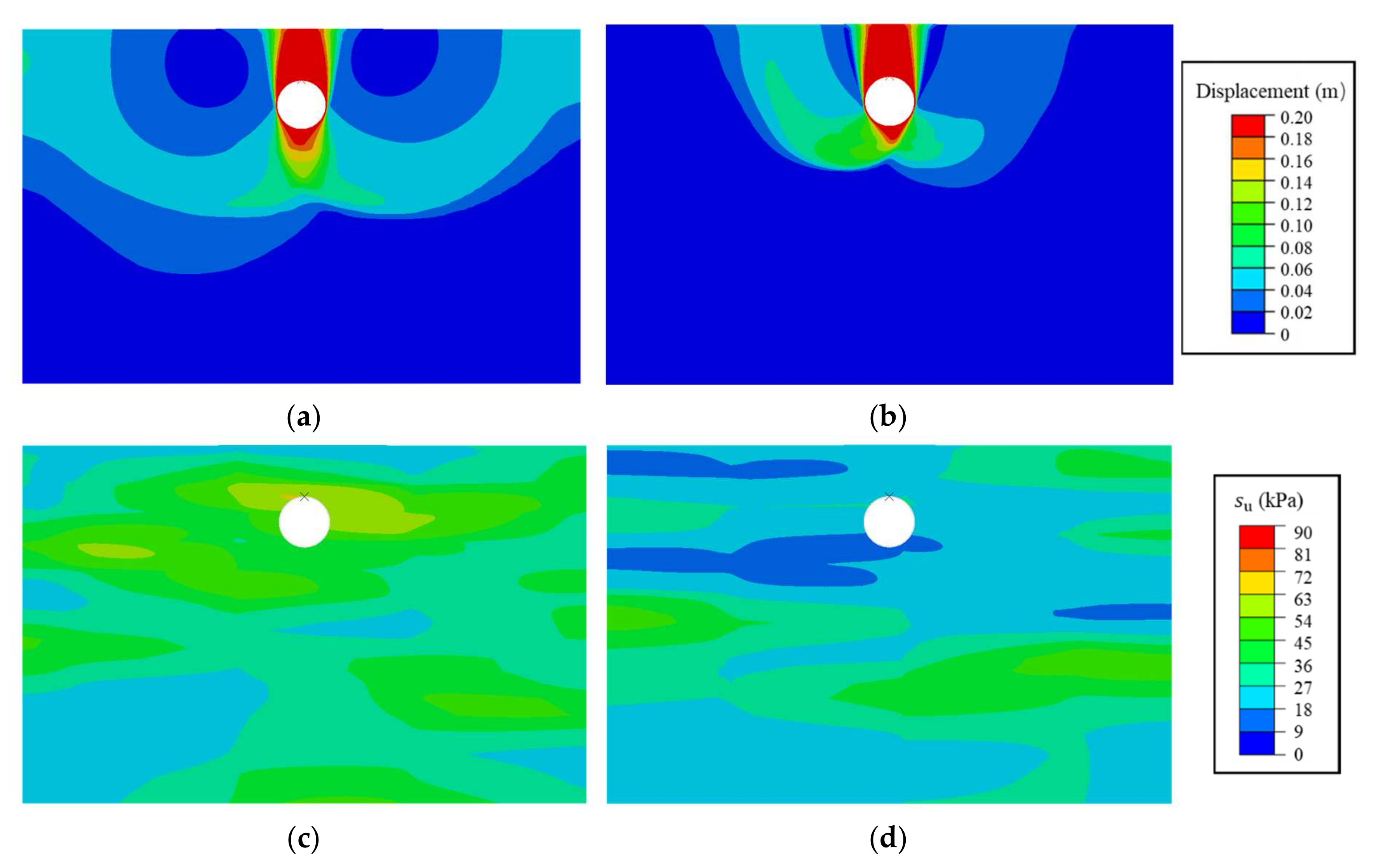


| Parameter | Symbol | Property Value | Units |
|---|---|---|---|
| Pipe diameter | 1 | m | |
| Soil density | 1600 | ||
| Poisson’s ratio | 0.49 | ||
| Undrained shear strength | 30 | ||
| Young’s modulus |
| (Maitra et al. [5]) | ||
|---|---|---|
| 0.5 | 9.02 | 8.98 |
| 1 | 10.47 | 10.59 |
| 2 | 11.98 | 12.11 |
| 3 | 11.98 | 12.11 |
| 4 | 11.98 | 12.11 |
| 5 | 11.98 | 12.11 |
| 6 | 11.98 | 12.11 |
| p-Values | |||
|---|---|---|---|
| 0.5 | 8.65 | 0.13 | 0.88 |
| 1 | 9.96 | 0.15 | 0.61 |
| 2 | 11.21 | 0.16 | 0.72 |
| 3 | 11.77 | 0.16 | 0.92 |
| 4 | 11.77 | 0.16 | 0.86 |
| 5 | 11.77 | 0.17 | 0.83 |
| SF | ||||||
|---|---|---|---|---|---|---|
| 0.5 | 1 | 2 | 3 | 4 | 5 | |
| 1 | 52.95 | 70.45 | 74.49 | 63.87 | 58.97 | 59.29 |
| 1.2 | 13.76 | 19.06 | 21.83 | 22.02 | 17.14 | 20.76 |
| 1.4 | 1.89 | 1.92 | 2.31 | 4.24 | 2.60 | 4.43 |
| 1.6 | 0.17 | 0.09 | 0.12 | 0.54 | 0.25 | 0.67 |
| 1.8 | 0.01 | / | / | 0.05 | 0.02 | 0.08 |
| 2 | / | / | / | / | / | 0.01 |
| Failure Probability (%) | ||||||
|---|---|---|---|---|---|---|
| 0.5 | 1 | 2 | 3 | 4 | 5 | |
| 1 | 1.46 | 1.45 | 1.46 | 1.54 | 1.49 | 1.56 |
| 0.1 | 1.64 | 1.60 | 1.61 | 1.75 | 1.67 | 1.78 |
| 0.01 | 1.77 | 1.70 | 1.71 | 1.89 | 1.81 | 1.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, P.; Guo, J.; Yao, K.; Liu, C.; Liu, X.; Liu, F. Uplift Behavior of Pipelines Buried at Various Depths in Spatially Varying Clayey Seabed. Sustainability 2022, 14, 8139. https://doi.org/10.3390/su14138139
Cheng P, Guo J, Yao K, Liu C, Liu X, Liu F. Uplift Behavior of Pipelines Buried at Various Depths in Spatially Varying Clayey Seabed. Sustainability. 2022; 14(13):8139. https://doi.org/10.3390/su14138139
Chicago/Turabian StyleCheng, Po, Jia Guo, Kai Yao, Chaofan Liu, Xiushui Liu, and Fei Liu. 2022. "Uplift Behavior of Pipelines Buried at Various Depths in Spatially Varying Clayey Seabed" Sustainability 14, no. 13: 8139. https://doi.org/10.3390/su14138139
APA StyleCheng, P., Guo, J., Yao, K., Liu, C., Liu, X., & Liu, F. (2022). Uplift Behavior of Pipelines Buried at Various Depths in Spatially Varying Clayey Seabed. Sustainability, 14(13), 8139. https://doi.org/10.3390/su14138139






