Rebound Effect of China’s Electric Power Demand in the Context of Technological Innovation
Abstract
:1. Introduction
- (1)
- The presentation of a research framework for the electricity power demand rebound effect in three dimensions including generalized technological progress, narrow technological progress, and technical use efficiency.
- (2)
- The comparison of rebound effects between overall energy demand and electricity demand during the New Normal period.
- (3)
- The evaluation of the impact of electricity demand growth on other energy demand under the “electrical energy substitution” strategy.
2. Analytical Framework
2.1. Contribution Rate Measurement of Structural Effect and Technical Effect
- (1)
- Define the ratio of electric power demand intensity and the output value of the three industries using Equation (1).
- (2)
- Calculate the technical and structural effects of electric power demand using Equations (2)–(4).
- (3)
- Calculate the contribution rates of the technical effect and the structural effect using Equations (5) and (6).
2.2. Contribution Rate Measurement of Technological Progress
- (1)
- Calculate the Malmquist Productivity Index using Equation (7).
- (2)
- Decompose the productivity index using Equations (8)–(10).
- (3)
- Calculate the contribution rate of technological progress using Equations (11)–(13).
2.3. Rebound Effect Analysis
2.4. Impact Analysis of Electric Power Demand Changes on Other Energy Demand Based on VAR and IRF
3. Empirical Analysis
3.1. Data Sources and Pre-Processing
3.2. Decomposition Results of Technological Progress and Electric Power Demand Intensity
3.3. Analysis of the Rebound Effect of Electric Power Demand
3.4. Analysis of the Impact of Changes in Electric Power Demand
3.4.1. Unit Root Test and Cointegration Test
3.4.2. Granger Causality Test
3.4.3. Analysis of Impulse Response
4. Discussions and Policy Implications
- (1)
- The generalized rate of technological progress in the electric power industry is increasing gradually. The overall average value for 2012–2016 is 1.6171, which is 0.32 percentage points higher than the average of the previous period. Based on Table 3, the improvement of technical use efficiency as the main factor promoted the increase in the generalized rate of technological progress in the electric power industry.
- (2)
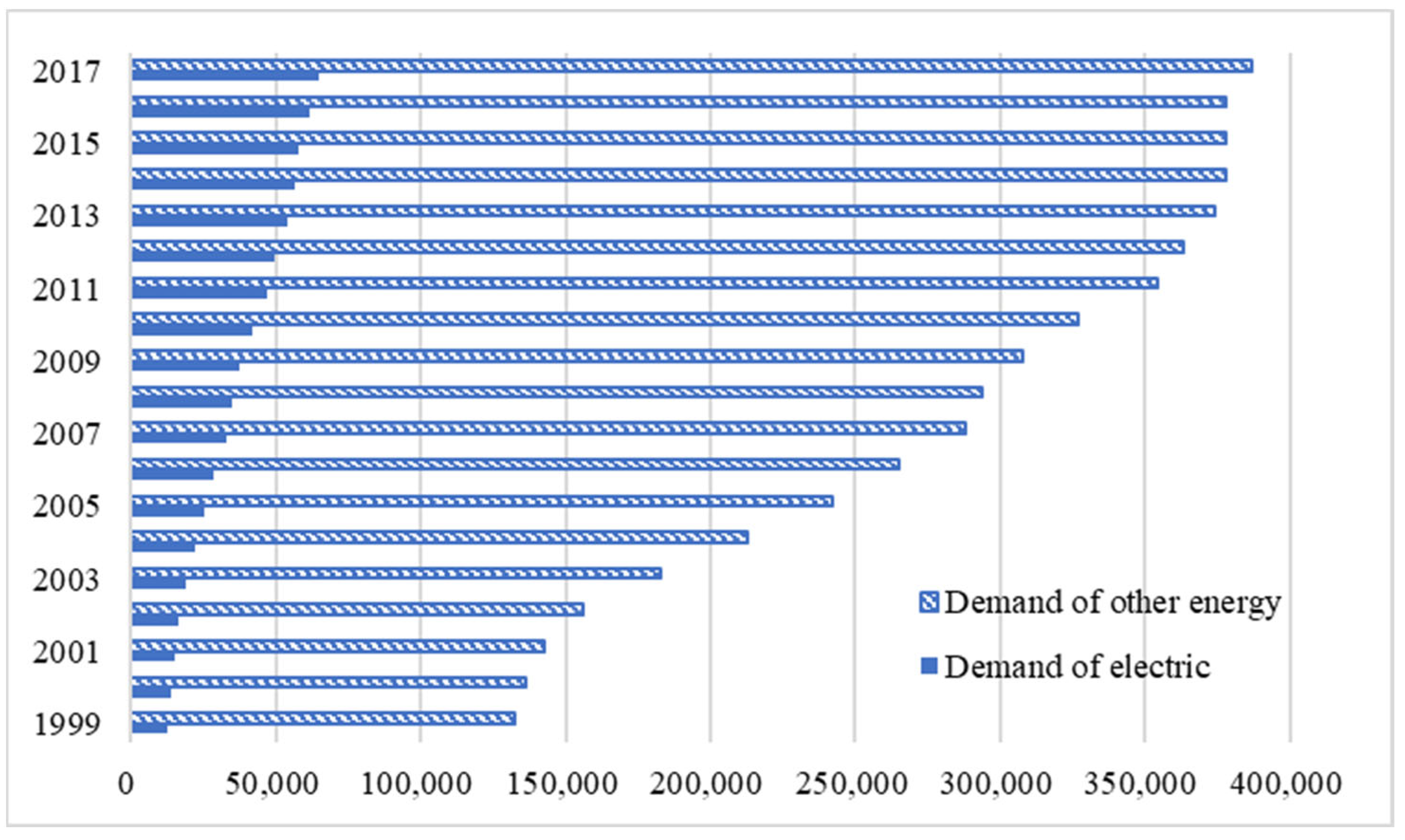
- It can be seen that the rate of decline in electric power demand intensity during the New Normal period slowed down, and with the gradual promotion of the “electrical energy substitution” strategy, the electric power demand shows an upward trend.
- (3)
- Under the condition of generalized technological progress, the improvement of technical use efficiency of electric power instead increases the demand for electric power, resulting in a backfire effect. However, the rebound effect of power energy caused by narrow technological progress mainly presents the characteristics of the partial rebound effect. In addition, compared with the super-saving effect of the overall energy demand, the change in electricity demand shows an opposite trend, and the proportion of electric energy consumption in the terminal energy consumption continues to increase.
- (4)
- The increase in electric power demand will reduce the demand for other energy sources in the medium- and long-term. Furthermore, with the development of the “electrical energy substitution” strategy, the increase in electric power demand will reduce the demand for other energy sources continually.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| TFP | Total Factor Productivity |
| RE | Rebound Effect |
| LMDI | Log Mean Divisia Index |
| DEA | Data Envelopment Analysis |
| VAR | Vector Auto-Regressive |
| IRF | Impulse Response Function |
| GDP | Gross Domestic Product |
| The real GDP growth rate | |
| The electric power demand intensity in period t | |
| The electric power demand in period t | |
| The total output in period t, which is measured by GDP | |
| The electric power demand intensity of the i-th industries in period t | |
| The electric power demand of the i-th industries in period t | |
| The output weight of the i-th industries in period t | |
| The output level of the i-th industries in period t | |
| The rebound effect of electric power demand caused by generalized technological progress in period t | |
| The distance function in period t with the technology in period t | |
| HV | High-voltage |
| The whole change in electric power demand intensity | |
| The change in technical effect | |
| The change in structural effect | |
| The contribution rates of the technical effect | |
| The element input vector in period t | |
| l | The lag order of the endogenous variable |
| Capital stock in period t | |
| Number of laborers in period t | |
| The technical use efficiency in t period | |
| The generalized rate of technological progress in t period | |
| The narrow rate of technological progress in t period | |
| The contribution degrees of generalized rate of technological progress to economic growth | |
| The contribution degrees of narrow rate of technological progress to economic growth | |
| The contribution degrees of technical use efficiency to economic growth | |
| EDi,t | The k-dimensional endogenous variable in t period |
| Al | The corresponding coefficient matrix in lag period l |
| The rebound effect of electric power demand caused by narrow technological progress in period t | |
| The rebound effect of electric power demand caused by technical use efficiency in period t | |
| UHV | The ultra-high voltage |
References
- Wang, Q.; Gao, Z.; Tang, H.; Yuan, X.; Zuo, J. Exploring the Direct Rebound Effect of Energy Consumption: A Case Study. Sustainability 2018, 10, 259. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Zhou, K.L.; Yang, S.L. Regional difference of household electricity consumption: An empirical study of Jiangsu, China. J. Clean. Prod. 2018, 171, 1415–1428. [Google Scholar] [CrossRef]
- Zhou, K.; Yang, S.; Shen, C.; Ding, S.; Sun, C. Energy conservation and emission reduction of China’s electric power industry. Renew. Sustain. Energy Rev. 2015, 45, 10–19. [Google Scholar] [CrossRef]
- Delmastro, C.; Lavagno, E.; Mutani, G. Chinese residential energy demand: Scenarios to 2030 and policies implication. Energy Build. 2015, 89, 49–60. [Google Scholar] [CrossRef]
- Li, X.F.; Cui, G.L. Special report on the achievements realized by researchers of Chinese Academy of Sciences in the field of energy storage technologies. J. Energy Storage 2018, 18, 285–294. [Google Scholar] [CrossRef]
- Sun, X.; Zhou, X.; Chen, Z.; Yang, Y. Environmental efficiency of electric power industry, market segmentation and technological innovation: Empirical evidence from China. Sci. Total Environ. 2020, 706, 135749. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Zhang, N.; Liu, Y. The energy rebound effects across China’s industrial sectors: An output distance function approach. Appl. Energy 2016, 184, 1165–1175. [Google Scholar] [CrossRef]
- Lu, M.L.; Wang, Z.H. Rebound effects for residential electricity use in urban China: An aggregation analysis based E-I-O and scenario simulation. Ann. Oper. Res. 2017, 255, 525–546. [Google Scholar] [CrossRef]
- Safarzadeh, S.; Rasti-Barzoki, M.; Hejazi, S.R. A review of optimal energy policy instruments on industrial energy efficiency programs, rebound effects, and government policies. Energy Policy 2020, 139, 111342. [Google Scholar] [CrossRef]
- Zhang, J.S.; Lawell, C.Y.C.L. The macroeconomic rebound effect in China. Energy Econ. 2017, 67, 202–212. [Google Scholar] [CrossRef]
- Ouyang, X.L.; Gao, B.Y.; Du, K.R.; Du, G. Industrial sectors' energy rebound effect: An empirical study of Yangtze River Delta urban agglomeration. Energy 2018, 145, 408–416. [Google Scholar] [CrossRef]
- Yang, L.; Li, Z. Technology advance and the carbon dioxide emission in China–Empirical research based on the rebound effect. Energy Policy 2017, 101, 150–161. [Google Scholar] [CrossRef]
- He, S.L.; Wang, J.; Zhang, L. Study on the Characteristics of Information Service Industry in Yangtze River Delta. In Proceedings of the International Conference on Advanced Control, Automation and Artificial Intelligence (ACAAI 2018), Shenzhen, China, 21–22 January 2018; Volume 155, pp. 226–230. [Google Scholar]
- Liu, W.S.; Liu, Y.; Lin, B.Q. Empirical analysis on energy rebound effect from the perspective of technological progress-a case study of China's transport sector. J. Clean. Prod. 2018, 205, 1082–1093. [Google Scholar] [CrossRef]
- Ren, W.; Wang, Q.; Ji, J. Research on China's marine economic growth pattern: An empirical analysis of China's eleven coastal regions. Mar. Policy 2018, 87, 158–166. [Google Scholar] [CrossRef]
- Feng, F.; Ye, A.Z. Does the rebound effect increase the total energy consumption in China? J. Quant. Tech. Econ. 2015, 32, 104–119. [Google Scholar]
- Cheng, S.L.; Wu, Y.Y.; Chen, H.; Chen, J.D.; Song, M.L.; Hou, W.X. Determinants of changes in electricity generation intensity among different power sectors. Energy Policy 2019, 130, 389–408. [Google Scholar] [CrossRef]
- Lin, B.Q.; Tan, R.P. Estimating energy conservation potential in China's energy intensive industries with rebound effect. J. Clean. Prod. 2017, 156, 899–910. [Google Scholar] [CrossRef]
- Wang, M.; Feng, C. Technological gap, scale economy, and China's industrial energy demand. J. Clean. Prod. 2019, 236, 117618. [Google Scholar] [CrossRef]
- Lin, B.Q.; Liu, X. Dilemma between economic development and energy conservation: Energy rebound effect in China. Energy 2012, 45, 867–873. [Google Scholar] [CrossRef]
- Dong, M.; Xu, Y.Y. Research on the Measurement and Agglomeration of Energy Rebound Effect in China—Based on the Perspective of Technological Progress Decomposition. J. Guizhou Univ. (Soc. Sci.) 2015, 33, 89–95. [Google Scholar]
- Safarzadeh, S.; Rasti-Barzoki, M.; Hejazi, S.R.; Piran, M.J. A game theoretic approach for the duopoly pricing of energy-efficient appliances regarding innovation protection and social welfare. Energy 2020, 200, 117517. [Google Scholar] [CrossRef]
- Shao, S.; Yang, L.L.; Huang, T. Theoretical Model of Energy Rebound Effect and China Experience. Econ. Res. 2013, 48, 96–109. [Google Scholar]
- Jin, L.; Duan, K.; Tang, X. What Is the Relationship between Technological Innovation and Energy Consumption? Empirical Analysis Based on Provincial Panel Data from China. Sustainability 2018, 10, 145. [Google Scholar] [CrossRef] [Green Version]
- Safarzadeh, S.; Rasti-Barzoki, M. A game theoretic approach for assessing residential energy-efficiency program considering rebound, consumer behavior, and government policies. Appl. Energy 2019, 233, 44–61. [Google Scholar] [CrossRef]
- Du, Q.; Li, Y.; Bai, L.B. The Energy Rebound Effect for the Construction Industry: Empirical Evidence from China. Sustainability 2017, 9, 803. [Google Scholar] [CrossRef] [Green Version]
- Zhou, M.F.; Liu, Y.; Feng, S.H.; Liu, Y.; Lu, Y.Y. Decomposition of rebound effect: An energy-specific, general equilibrium analysis in the context of China. Appl. Energy 2018, 221, 280–298. [Google Scholar] [CrossRef]
- Wang, X.L.; Wen, X.H.; Xie, C.P. An evaluation of technical progress and energy rebound effects in China's iron & steel industry. Energy Policy 2018, 123, 259–265. [Google Scholar] [CrossRef]
- Li, J.L.; Lin, B.Q. Rebound effect by incorporating endogenous energy efficiency: A comparison between heavy industry and light industry. Appl. Energy 2017, 200, 347–357. [Google Scholar] [CrossRef]
- Chen, G.Y.; Lin, B.Q.; Ye, B. Is China's Manufacturing Industry Efficient? Evidence from an Energy-Rebound Effect Perspective. Emerg. Mark. Financ. Trade 2018, 54, 2245–2257. [Google Scholar] [CrossRef]
- Lin, B.Q.; Chen, Y.F.; Zhang, G.L. Technological progress and rebound effect in China's nonferrous metals industry: An empirical study. Energy Policy 2017, 109, 520–529. [Google Scholar] [CrossRef]
- Bataille, C.; Melton, N. Energy efficiency and economic growth: A retrospective CGE analysis for Canada from 2002 to 2012. Energy Econ. 2017, 64, 118–130. [Google Scholar] [CrossRef]
- Deng, C.X.; Li, K.; Peng, C.; Han, F. Analysis of technological progress and input prices on electricity consumption: Evidence from China. J. Clean. Prod. 2018, 196, 1390–1406. [Google Scholar] [CrossRef]
- Alvi, S.; Mahmood, Z.; Nawaz, S.M.N. Dilemma of direct rebound effect and climate change on residential electricity consumption in Pakistan. Energy Rep. 2018, 4, 323–327. [Google Scholar] [CrossRef]
- Su, Y.W. Residential electricity demand in Taiwan: Consumption behavior and rebound effect. Energy Policy 2019, 124, 36–45. [Google Scholar] [CrossRef]
- Yu, B.Y.; Zhang, J.Y.; Fujiwara, A. Evaluating the direct and indirect rebound effects in household energy consumption behavior: A case study of Beijing. Energy Policy 2013, 57, 441–453. [Google Scholar] [CrossRef]
- Amjadi, G.; Lundgren, T.; Persson, L. The Rebound Effect in Swedish Heavy Industry. Energy Econ. 2018, 71, 140–148. [Google Scholar] [CrossRef] [Green Version]
- Safarzadeh, S.; Rasti-Barzoki, M. A duopolistic game for designing a comprehensive energy-efficiency scheme regarding consumer features: Which energy policy is the best? J. Clean. Prod. 2020, 255, 120195. [Google Scholar] [CrossRef]
- Ang, B.W.; Liu, F.L.; Chew, E.P. Perfect decomposition techniques in energy and environmental analysis. Energy Policy 2003, 31, 1561–1566. [Google Scholar] [CrossRef]
- Wang, Z.; Ru, X.J. Research on Influencing Factors of Household Energy Carbon Emission Based on Exponential Decomposition. Eco. Econ. 2015, 31, 51–55. [Google Scholar]
- Färe, R.; Shawna, G.; Mary, N.; Zhang, Z. Productivity Growth, Technical Progress, and Efficiency Change in Industrialized Countries. Am. Econ. Rev. 1994, 84, 66–83. [Google Scholar]
- Caves, D.W.; Christensen, L.R.; Diewert, W.E. The Economic Theory of Index Numbers and the Measurement of Input, Output, and Productivity. Econometrica 1982, 50, 1393–1414. [Google Scholar] [CrossRef]
- Li, Y.; Sun, L.Y.; Feng, T.W.; Zhu, C.Y. How to reduce energy intensity in China: A regional comparison perspective. Energy Policy 2013, 61, 513–522. [Google Scholar] [CrossRef]
- Green, R.; Larsson, K.; Lunina, V.; Nilsson, B. Cross-commodity news transmission and volatility spillovers in the German energy markets. J. Bank Financ. 2018, 95, 231–243. [Google Scholar] [CrossRef] [Green Version]
- Mou, D.G.; Lin, B.Q. Study on the Time-Variable Parameters of the Interaction between Chinese Economic Growth, Power Consumption and Coal Prices. Financ. Res. 2012, 6, 42–53. [Google Scholar]
- Dickey, D.A.; Fuller, W.A. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar] [CrossRef]
- Engle, R.F.; Granger, C.W.J. Co-Integration and error correction: Representation, estimation, and testing. Econometrica 1987, 55, 251–276. [Google Scholar] [CrossRef]
- Granger, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Sun, Y.; Zhou, S.; Shan, Y.G.; Jia, D.X.; Cao, Y. Analysis of Electric Energy Substitution Potential under Multiple Scenarios. Power Syst. Technol. 2017, 41, 118–123. [Google Scholar]
- Liu, P.K.; Tan, Z.F. How to develop distributed generation in China: In the context of the reformation of electric power system. Renew. Sustain. Energy Rev. 2016, 66, 10–26. [Google Scholar] [CrossRef]
- Yang, L.S.; Li, J.L. Rebound effect in China: Evidence from the power generation sector. Renew. Sustain. Energy Rev. 2017, 71, 53–62. [Google Scholar] [CrossRef]
- Fang, D.B.; Dong, W.; Yu, Q. Optimization of China's Energy Consumption Structure under Low Carbon Transformation Trend. Tech. Econ. 2016, 35, 71–79+128. [Google Scholar]







| Definition | Situation | Implication |
|---|---|---|
| Backfire effect | RE > 1 | Electric power efficiency improvement increases electric power demand. |
| Full rebound effect | RE = 1 | Power-saving improvement by electric power efficiency is offset by the rebound amount, and the electric power demand is unchanged. |
| Partial rebound effect | 0 < RE < 1 | Power-saving improvement by electric power efficiency is partially offset by electric power demand, and overall electric power demand is reduced. |
| Zero rebound effect | RE = 0 | Improvement of electric power efficiency only leads to a reduction in electric power demand and does not cause a rebound effect. |
| Super saving effect | RE < 0 | Not only does improvement of electric power efficiency reduce the electric power demand, but also the rebound effect is negative. |
| Ref. | Assumptions | Approach | Results | |||||
|---|---|---|---|---|---|---|---|---|
| RE 1 | PF 2 | SW 3 | SE 4 | EM 5 | DEA | GT 6 | ||
| Lin et al. [20] | √ | √ | √ | partial rebound effect | ||||
| Shao et al. [23] | √ | √ | √ | energy-saving effect | ||||
| Dong et al. [21] | √ | √ | √ | partial rebound effect | ||||
| Bataille et al. [32] | √ | √ | √ | backfire effect | ||||
| Jin et al. [24] | √ | √ | √ | energy-saving effect | ||||
| Wang et al. [28] | √ | √ | √ | partial rebound effect | ||||
| Chen et al. [30] | √ | √ | √ | partial rebound effect | ||||
| Su [35] | √ | √ | √ | backfire effect | ||||
| Safarzadeh et al. [38] | √ | √ | √ | √ | partial rebound effect | |||
| Our work | √ | √ | √ | √ | √ | |||
| Year | M | MTEC | MTC | |||
|---|---|---|---|---|---|---|
| 1999 | 0.9700 | 1.1537 | 0.8407 | −0.0015 | −0.0013 | −0.0002 |
| 2000 | 1.0011 | 1.0802 | 0.9267 | 0.0008 | 0.0003 | 0.0005 |
| 2001 | 1.1157 | 1.1021 | 1.0124 | −0.0009 | −0.0002 | −0.0007 |
| 2002 | 1.2443 | 1.1107 | 1.1203 | −0.0001 | 0.0004 | −0.0005 |
| 2003 | 1.3961 | 1.1088 | 1.2592 | 0.0055 | 0.0034 | 0.0021 |
| 2004 | 1.5165 | 1.0908 | 1.3902 | 0.0004 | 0.0001 | 0.0003 |
| 2005 | 1.5807 | 1.0284 | 1.5370 | −0.0050 | −0.0071 | 0.0021 |
| 2006 | 1.6977 | 1.0000 | 1.6977 | −0.0041 | −0.0051 | 0.0011 |
| 2007 | 0.8411 | 1.0000 | 0.8411 | −0.0060 | −0.0051 | −0.0009 |
| 2008 | 0.9612 | 1.0000 | 0.9612 | −0.0129 | −0.0131 | 0.0002 |
| 2009 | 1.0817 | 1.0000 | 1.0817 | −0.0083 | −0.0072 | −0.0012 |
| 2010 | 1.1872 | 1.0033 | 1.1834 | −0.0002 | −0.0009 | 0.0007 |
| 2011 | 1.3043 | 1.0066 | 1.2958 | −0.0032 | −0.0030 | −0.0001 |
| Mean value (1999–2011) | 1.2229 | 1.0527 | 1.1652 | −0.0027 | −0.0030 | 0.0003 |
| 2012 | 1.4161 | 1.0075 | 1.4056 | −0.0076 | −0.0064 | −0.0012 |
| 2013 | 1.5432 | 1.0334 | 1.4933 | −0.0005 | 0.0009 | −0.0014 |
| 2014 | 1.6342 | 1.0222 | 1.5987 | −0.0050 | −0.0040 | −0.0010 |
| 2015 | 1.7046 | 1.0077 | 1.6916 | −0.0035 | −0.0016 | −0.0019 |
| 2016 | 1.7873 | 1.0000 | 1.7873 | −0.0013 | −0.0002 | −0.0011 |
| Mean value (New Normal) | 1.6171 | 1.0142 | 1.5953 | −0.0036 | −0.0023 | −0.0013 |
| Year | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1999 | −0.3097 | 1.5866 | −1.6444 | 0.8503 | 0.1497 | −1.8947 | 11.4166 | −67.1924 |
| 2000 | 0.0151 | 1.1033 | −1.0084 | 0.3592 | 0.6408 | −0.2191 | −44.4704 | 22.7836 |
| 2001 | 1.3049 | 1.1515 | 0.1399 | 0.1747 | 0.8253 | 18.7958 | 94.9682 | 2.4407 |
| 2002 | 2.4485 | 1.1095 | 1.2057 | −3.7816 | 4.7816 | 328.2446 | −39.3321 | 33.8039 |
| 2003 | 3.3229 | 0.9127 | 2.1745 | 0.6123 | 0.3877 | −8.6067 | −3.8608 | −14.5274 |
| 2004 | 4.6450 | 0.8166 | 3.5092 | 0.2849 | 0.7151 | −212.685 | −131.249 | −224.684 |
| 2005 | 3.8417 | 0.1879 | 3.5526 | 1.4314 | −0.4314 | 15.9402 | 0.5446 | −34.1661 |
| 2006 | 3.9626 | 0.0000 | 3.9626 | 1.2646 | −0.2646 | 20.0256 | 0.0000 | −75.6689 |
| 2007 | −0.8776 | 0.0000 | −0.8776 | 0.8505 | 0.1495 | −3.1033 | 0.0000 | −20.7600 |
| 2008 | −0.1963 | 0.0000 | −0.1963 | 1.0126 | −0.0126 | −0.2596 | 0.0000 | 20.5266 |
| 2009 | 0.4677 | 0.0000 | 0.4677 | 0.8590 | 0.1410 | 0.8064 | 0.0000 | 5.7206 |
| 2010 | 1.1998 | 0.0212 | 1.1755 | 4.4816 | −3.4816 | 78.8303 | 0.3101 | −22.1826 |
| 2011 | 2.2640 | 0.0491 | 2.2007 | 0.9556 | 0.0444 | 9.9181 | 0.2251 | 217.165 |
| Mean value (1999–2011) | 1.6991 | 0.5337 | 1.1278 | 0.7196 | 0.2804 | 18.9071 | −8.5729 | −12.0570 |
| 2012 | 2.6810 | 0.0483 | 2.6133 | 0.8456 | 0.1544 | 4.2279 | 0.0901 | 26.6843 |
| 2013 | 3.8120 | 0.2344 | 3.4618 | −1.6749 | 2.6749 | 60.8699 | −2.2346 | 20.6653 |
| 2014 | 6.6641 | 0.2333 | 6.2911 | 0.7936 | 0.2064 | 10.6656 | 0.4704 | 48.7891 |
| 2015 | 7.1527 | 0.0782 | 7.0207 | 0.4569 | 0.5431 | 11.6348 | 0.2783 | 21.0272 |
| 2016 | 11.1032 | 0.0000 | 11.1032 | 0.1439 | 0.8561 | 49.4105 | 0.0000 | 57.7127 |
| Mean value (New Normal) | 6.2826 | 0.1188 | 6.0980 | 0.1130 | 0.8870 | 27.3617 | −0.2792 | 34.9757 |
| Year | ||||
|---|---|---|---|---|
| Overall energy [21] | 2010 | −0.3900 | 0.2100 | 3.2700 |
| 2011 | −0.1600 | 0.4700 | 2.3900 | |
| 2012 | −0.1400 | 0.3700 | 512.9800 | |
| Mean | −0.2300 | 0.3500 | 172.8800 | |
| Electricity energy | 2010 | 78.8303 | 0.3101 | −22.1826 |
| 2011 | 9.9181 | 0.2251 | 217.1650 | |
| 2012 | 4.2279 | 0.0901 | 26.6843 | |
| Mean | 30.9921 | 0.2084 | 73.8889 |
| Variable | ADF Test | EG Test |
|---|---|---|
| − | ||
| * | ** | |
| ** |
| Null Hypothesis | Chi-sq | df | Prob |
|---|---|---|---|
| is not the Granger reason for | 19.3430 | 4 | 0.0007 |
| is not the Granger reason for | 16.2812 | 4 | 0.0027 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Yang, X.; Ma, Y.; Yu, L. Rebound Effect of China’s Electric Power Demand in the Context of Technological Innovation. Sustainability 2022, 14, 8263. https://doi.org/10.3390/su14148263
Lu Y, Yang X, Ma Y, Yu L. Rebound Effect of China’s Electric Power Demand in the Context of Technological Innovation. Sustainability. 2022; 14(14):8263. https://doi.org/10.3390/su14148263
Chicago/Turabian StyleLu, Yan, Xu Yang, Yixiang Ma, and Lean Yu. 2022. "Rebound Effect of China’s Electric Power Demand in the Context of Technological Innovation" Sustainability 14, no. 14: 8263. https://doi.org/10.3390/su14148263
APA StyleLu, Y., Yang, X., Ma, Y., & Yu, L. (2022). Rebound Effect of China’s Electric Power Demand in the Context of Technological Innovation. Sustainability, 14(14), 8263. https://doi.org/10.3390/su14148263







