Economic Growth, CO2 Emissions Quota and Optimal Allocation under Uncertainty
Abstract
:1. Introduction
1.1. Climate Change Impacts
1.2. Global Warming and Greenhouse Gases
1.3. Motivations
2. Literature Review
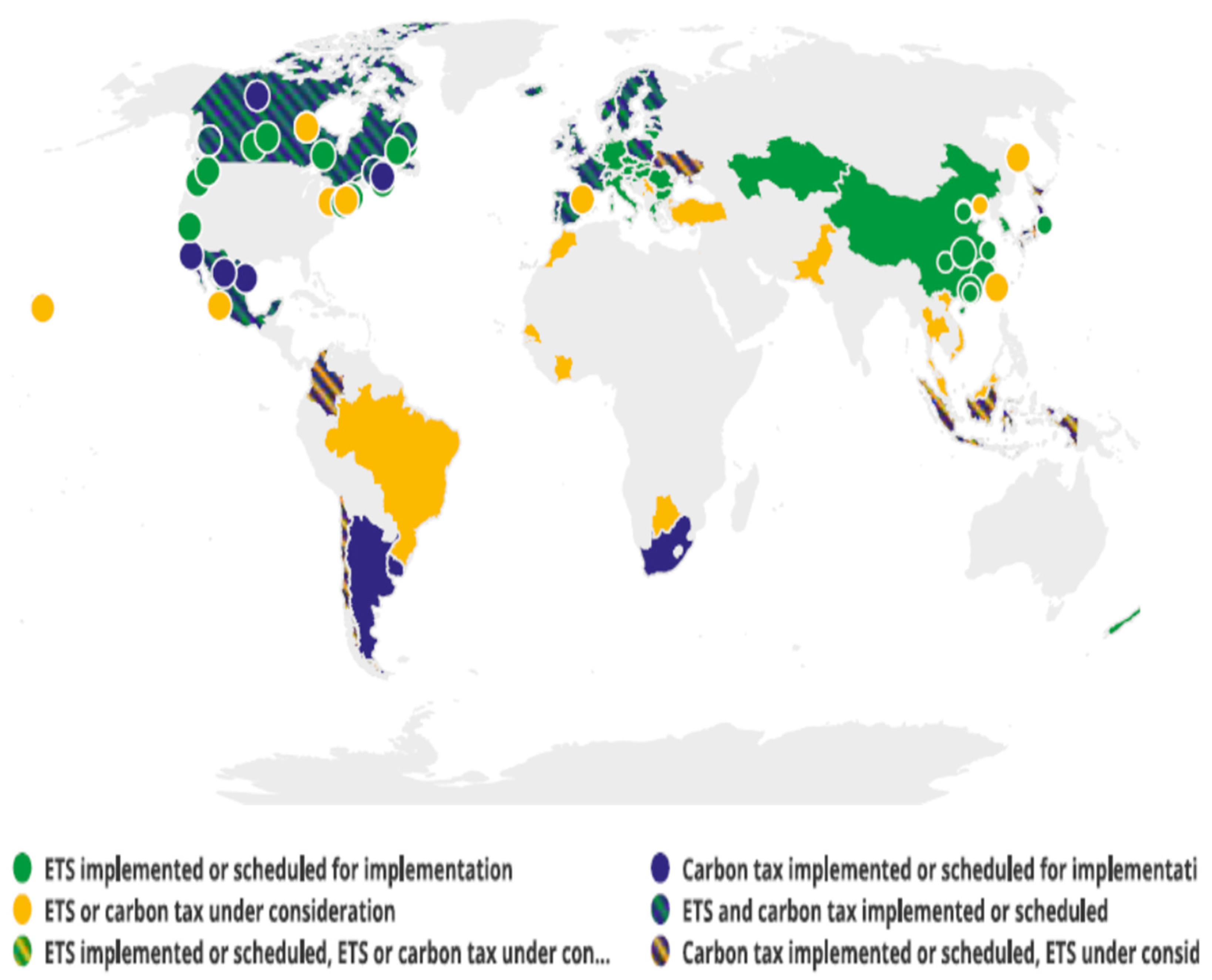
2.1. GHGs and CBAM
2.2. GHGs and Economic Growth
3. The Model
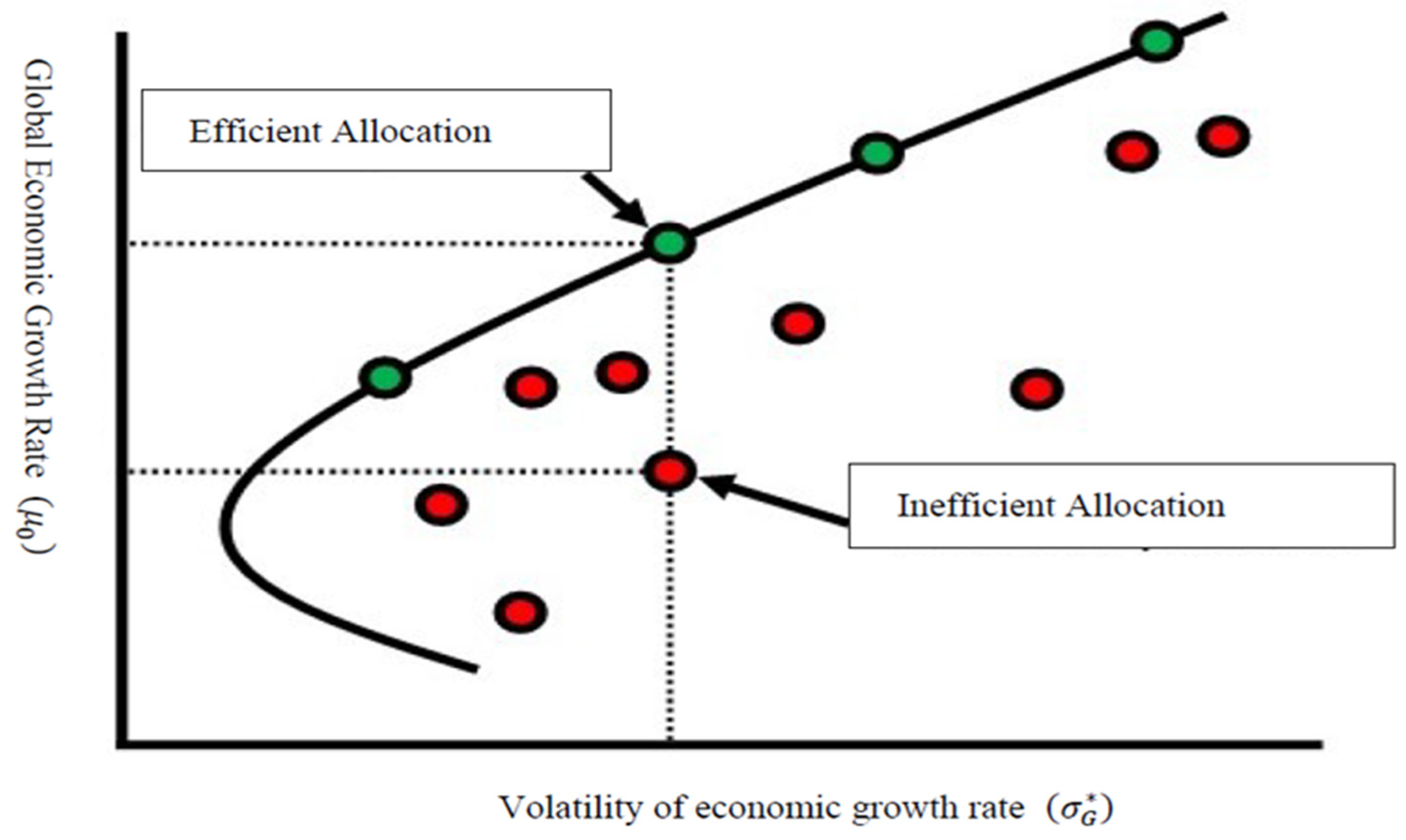
3.1. Optimal Allocation with Economic Growth
3.2. Optimal Allocation with CO2 Emissions
4. Empirical Evidence
4.1. Data
4.2. Test for EKC Hypothesis
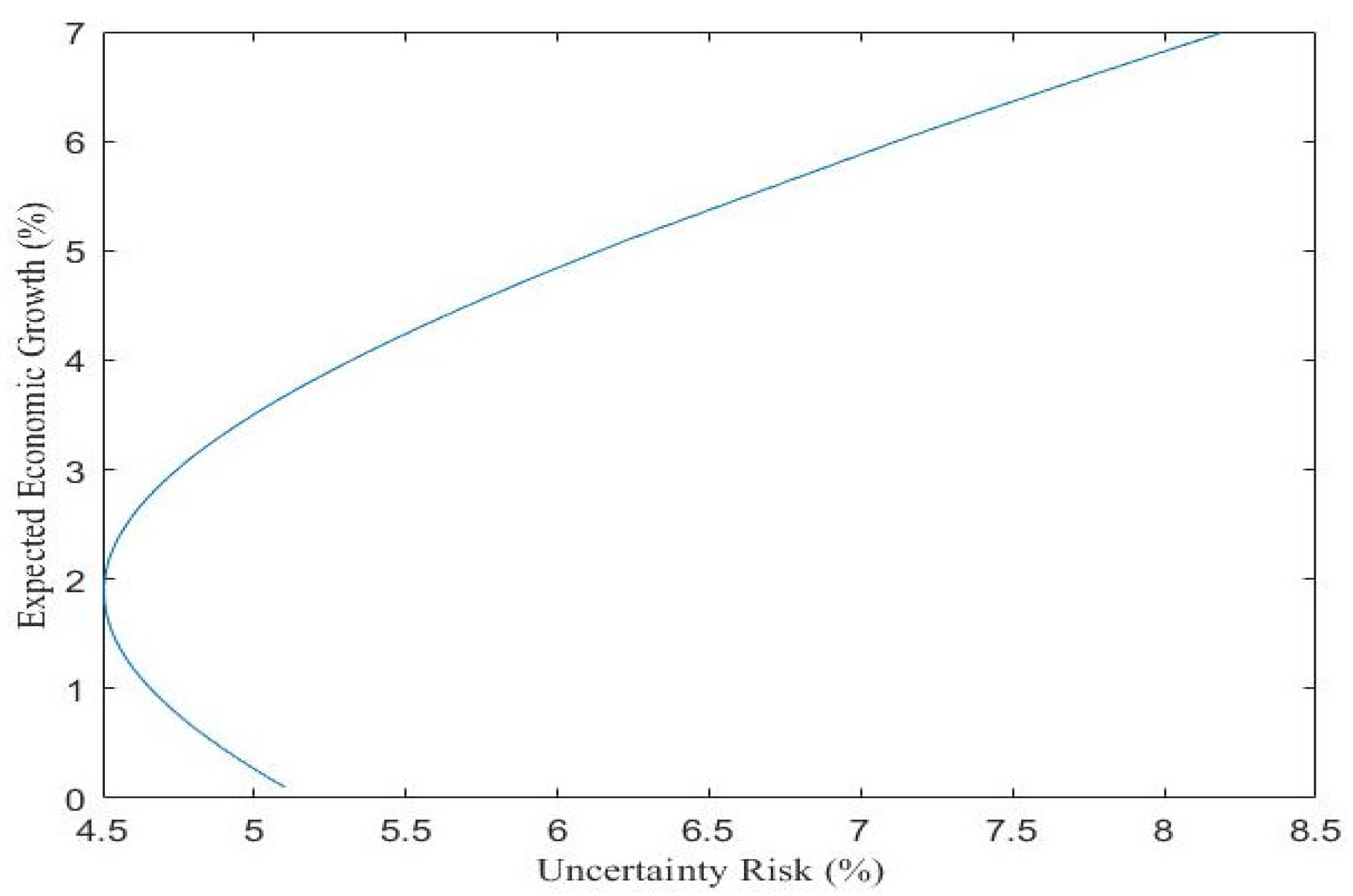
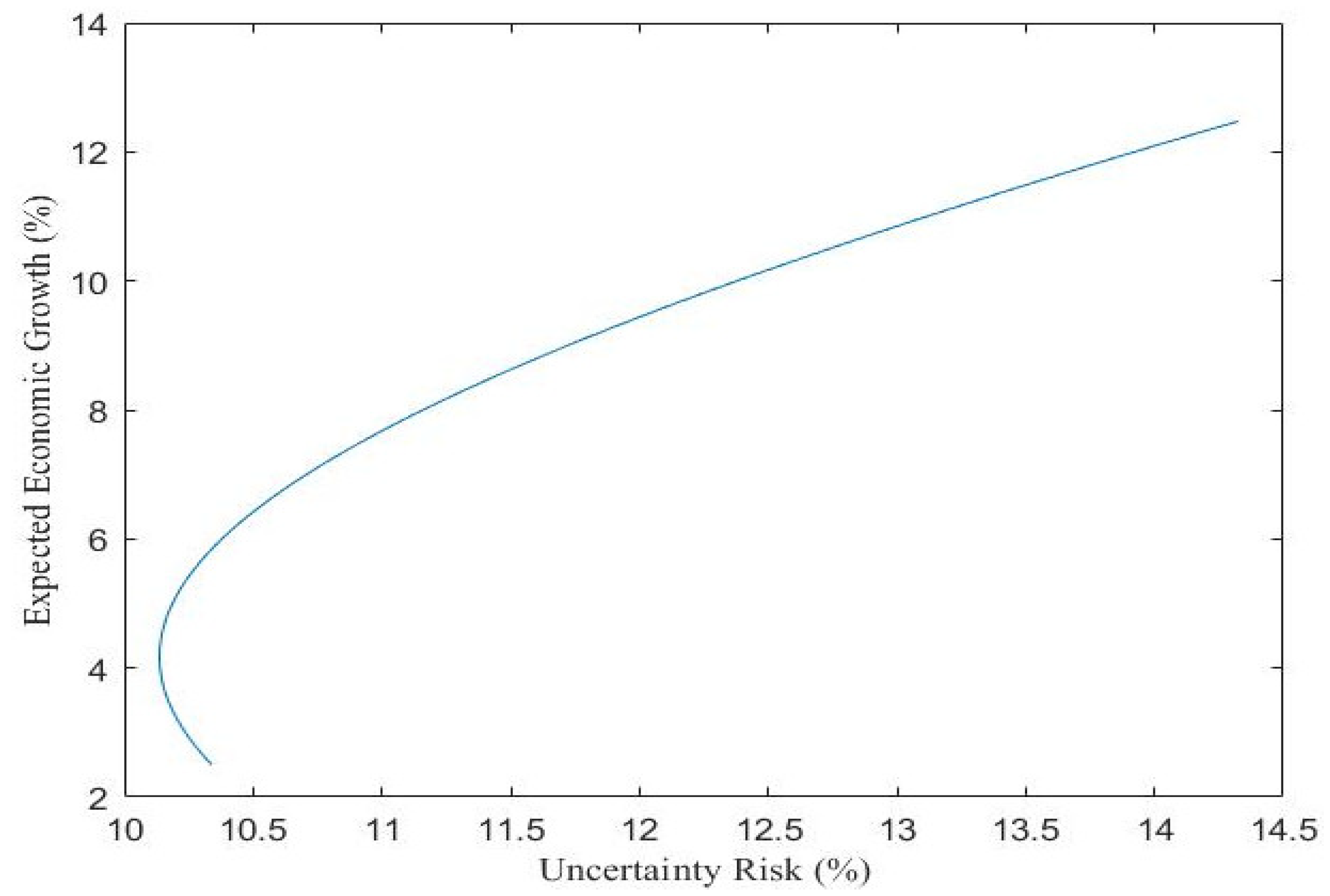
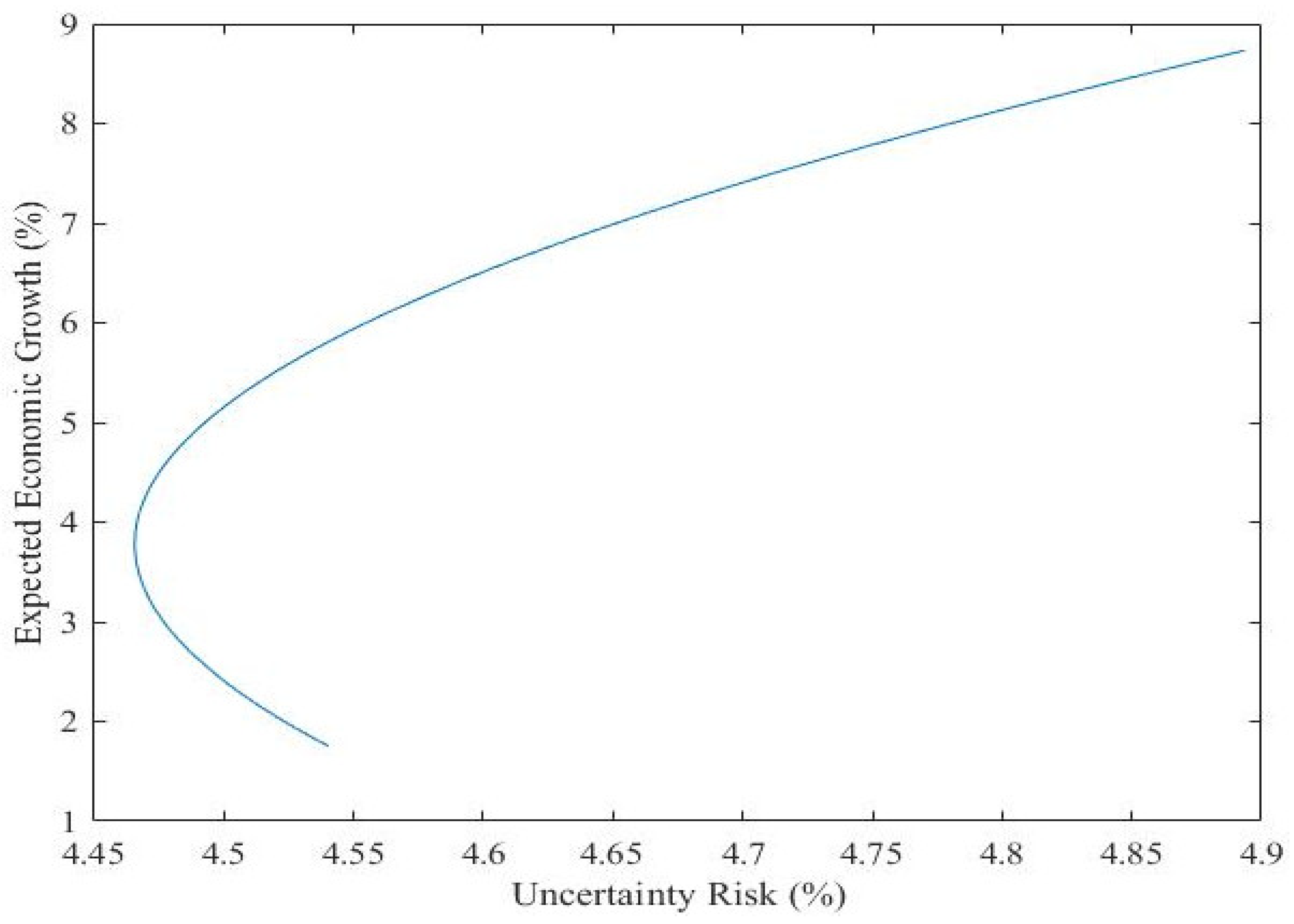
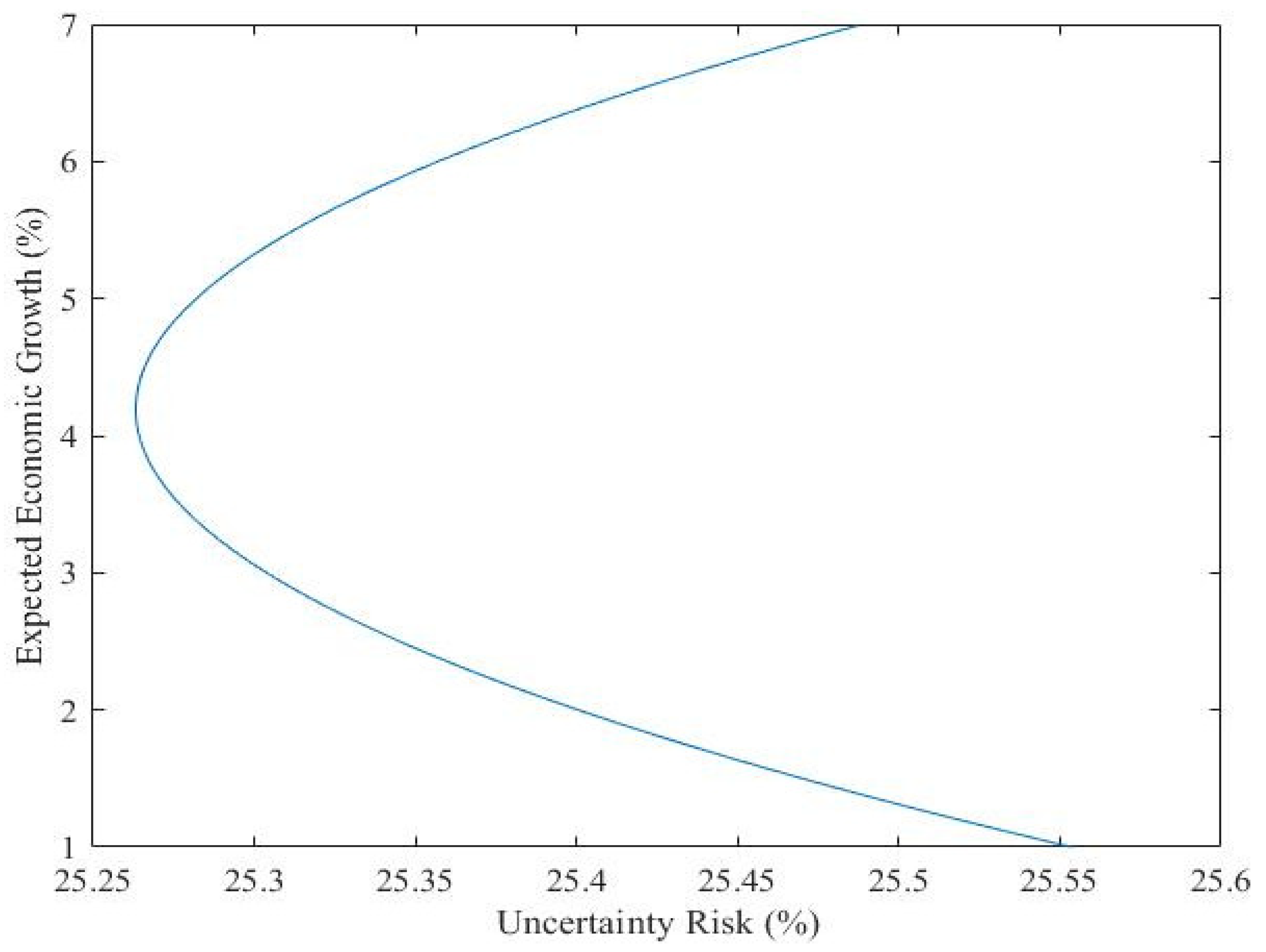
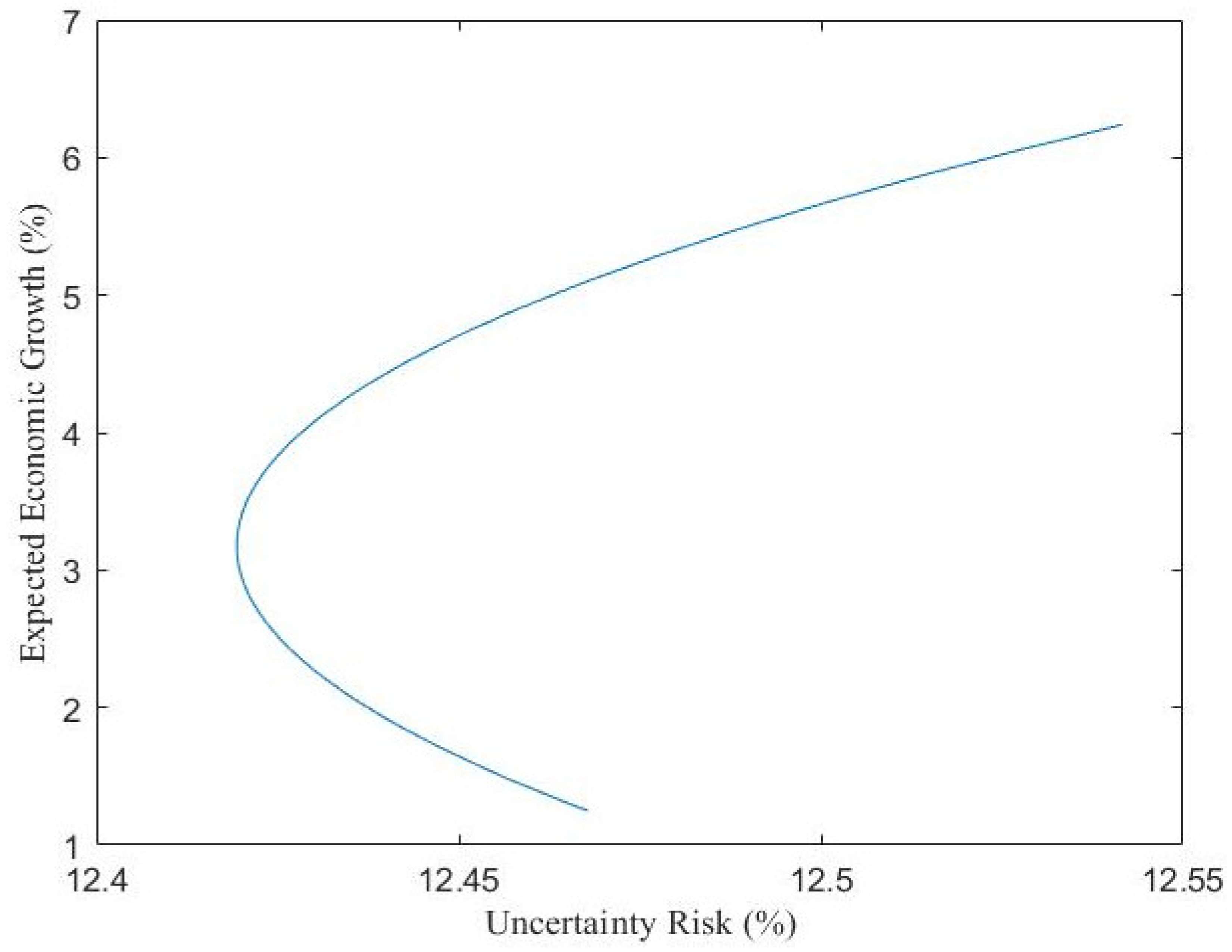
4.3. Computation of Optimal Allocation of CO2 Emission Quota
4.3.1. Continental Economics and CO2 Emissions
4.3.2. Global Economics and CO2 Emissions
5. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guggenheim, P.D.; Al Gore, A.A. An Inconvenient Truth; Paramount Pictures Corporation: Los Angeles, CA, USA, 2006. [Google Scholar]
- TVBS Sisy’s World News Group. ±2 °C—The Truth That Taiwan Must Face; Taiwan, 2010; Available online: https://movie.douban.com/subject/4312211/ (accessed on 16 May 2022).
- Le Quéré, C.; Jackson, R.B.; Jones, M.W.; Smith, A.J.; Abernethy, S.; Andrew, R.M.; De-Gol, A.J.; Willis, D.R.; Shan, Y.L.; Canadell, J.G.; et al. Temporary Reduction in Daily Global CO2 Emissions during the COVID-19 Forced Confinement. Nat. Clim. Change 2020, 10, 647–653. [Google Scholar] [CrossRef]
- Hsiao, C.M. Effects on Second Waves of COVID-19 Epidemics: Social Stringency, Economic Forces, and Public Health. Theor. Econ. Lett. 2022, 12, 278–320. [Google Scholar] [CrossRef]
- Abbass, K.; Qasim, M.Z.; Song, H.M.; Murshed, M.; Mahmood, H.; Younis, I. A Review of the Global Climate Change Impacts, Adaptation, and Sustainable Mitigation Measures. Environ. Sci. Pollut. Res. 2022, 29, 42539–42559. [Google Scholar] [CrossRef] [PubMed]
- Forster, P.; Storelymo, T.; Armour, K.; Collins, W.; Dufresne, J.; Frame, D.; Lunt, D.; Mauritsen, T.; Palmer, M.; Watanabe, M.; et al. Chapter 7: The Earth’s Energy Budget, Climate Feedbacks, and Climate Sensitivity. In Climate Change 2021: The Physical Science Basis; Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2021; Available online: https://www.ipcc.ch/report/ar6/wg1/downloads/report/IPCC_AR6_WGI_FOD_Chapter07.pdf (accessed on 16 May 2022).
- Myhre, G.; Shindell, D.; Bréon, F.M.; Collins, W.; Fuglestvedt, J.; Huang, J.; Koch, D.; Lamarque, J.-F.; Lee, D.; Mendoza, B.; et al. Chapter 8: Anthropogenic and Natural Radiative Forcing. In Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2013; pp. 659–740. Available online: https://archive.ipcc.ch/pdf/assessment-report/ar5/wg1/WG1AR5_Chapter08_FINAL.pdf (accessed on 16 May 2022).
- Golombek, R.; Kittelsen, S.A.C.; Rosendahl, K.E. Price and Welfare Effects of Emission Quota Allocation. Energy Econ. 2013, 36, 568–580. [Google Scholar] [CrossRef] [Green Version]
- Zhou, P.; Zhang, L.; Zhou, D.Q.; Xia, W.J. Modeling Economic Performance of Interprovincial CO2 Emission Reduction Quota Trading in China. Appl. Energy 2013, 112, 1518–1528. [Google Scholar] [CrossRef]
- Wei, Y.M.; Wang, L.; Liao, H.; Wang, K.; Murty, T.; Yan, J.Y. Responsibility Accounting in Carbon Allocation: A Global Perspective. Appl. Energy 2014, 130, 122–133. [Google Scholar] [CrossRef]
- Pan, X.Z.; Teng, F.; Wang, G.H. A Comparison of Carbon Allocation Schemes: On the Equity-Efficiency Tradeoff. Energy 2014, 74, 222–229. [Google Scholar] [CrossRef]
- Pan, X.Z.; Teng, F.; Wang, G.H. Sharing Emission Space at an Equitable Basis: Allocation Scheme based on the Equal Cumulative Emission per Capita Principle. Appl. Energy 2014, 113, 1810–1818. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Wang, A.D.; Da, Y.B. Regional Allocation of Carbon Emission Quotas in China: Evidence from the Shapley Value Method. Energy Policy 2014, 74, 454–464. [Google Scholar] [CrossRef]
- Hao, Y.; Liao, H.; Wei, Y.M. Is China’s Carbon Reduction Target Allocation Reasonable? An Analysis based on Carbon Intensity Convergence. Appl. Energy 2015, 142, 229–239. [Google Scholar] [CrossRef]
- Pang, R.Z.; Deng, Z.Q.; Chiu, Y.H. Pareto Improvement through a Reallocation of Carbon Emission Quotas. Renew. Sustain. Energy Rev. 2015, 50, 419–430. [Google Scholar] [CrossRef]
- Carretero, A.L.; de la Rosa, J.; Sanchez-Rodas, D. Applying Statistical Tools Systematically to Determine Industrial Emission Levels associated with the best Available Techniques. J. Clean. Prod. 2016, 112, 4226–4236. [Google Scholar] [CrossRef]
- Miao, Z.A.; Geng, Y.; Sheng, J.C. Efficient Allocation of CO2 Emissions in China: A Zero Sum Gains Data Envelopment Model. J. Clean. Prod. 2016, 112, 4144–4150. [Google Scholar] [CrossRef]
- Han, R.; Tang, B.J.; Fan, J.L.; Liu, L.C.; Wei, Y.M. Integrated Weighting Approach to Carbon Emission Quotas: An Application Case of Beijing-Tianjin-Hebei Region. J. Clean. Prod. 2016, 131, 448–459. [Google Scholar] [CrossRef]
- Chang, K.; Zhang, C.; Chang, H. Emissions Reduction Allocation and Economic Welfare Estimation through Interregional Emissions Trading in China: Evidence from Efficiency and Equity. Energy 2016, 113, 1125–1135. [Google Scholar] [CrossRef]
- An, Q.X.; Wen, Y.; Xiong, B.B.; Yang, M.; Chen, X.H. Allocation of Carbon Dioxide Emission Permits with the Minimum Cost for Chinese Provinces in Big Data Environment. J. Clean. Prod. 2017, 142, 886–893. [Google Scholar] [CrossRef]
- Zhou, Z.B.; Liu, C.J.; Zeng, X.M.; Jiang, Y.J.; Liu, W.B. Carbon Emission Performance Evaluation and Allocation in Chinese Cities. J. Clean. Prod. 2018, 172, 1254–1272. [Google Scholar] [CrossRef]
- Crémieux, L. What Is at Stake in the “Yellow Jacket” Mobilization. International Viewpoint. 2018. Available online: https://internationalviewpoint.org/IMG/pdf/what-is-at-stake-in-the-yellow-jacket-mobilization_a5802.pdf (accessed on 27 November 2018).
- Markowitz, H. Portfolio Selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Chen, M.H.; Jang, S.C.; Peng, Y.J. Discovering Optimal Tourist Market Mixes. J. Travel Res. 2010, 50, 602–614. [Google Scholar] [CrossRef]
- Hsiao, C.M. Enterprise Risk Management with Foreign Exchange Exposures: Evidence from Taiwan Tourism Industry. Asian Econ. Financ. Rev. 2017, 7, 882–906. [Google Scholar]
- Bashir, M.F.; Ma, B.J.; Shahbaz, M.; Jiao, Z.L. The Nexus between Environmental Tax and Carbon Emissions with the Roles of Environmental Technology and Financial Development. PLoS ONE 2020, 15, e0242412. [Google Scholar] [CrossRef]
- World Bank. State and Trends of Carbon Pricing 2021; World Bank: Washington, DC, USA, 2021; p. 10. [Google Scholar] [CrossRef]
- Grossman, G.M.; Krueger, A.B. Environmental Impacts of a North American Free Trade Agreement. In National Bureau of Economic Research Working Paper, No. 3914; National Bureau of Economic Research: Cambridge, MA, USA, 1991. [Google Scholar]
- Selden, T.M.; Song, D. Environmental Quality and Development: Is there a Kuznets curve for Air Pollution Emissions? J. Environ. Econ. Manag. 1994, 27, 147–162. [Google Scholar] [CrossRef]
- Kuznets, S. Economic Growth and Income Inequality. Am. Econ. Rev. 1955, 45, 1–28. [Google Scholar]
- Stern, D.I.; Common, M.S.; Barbier, E.B. Economic Growth and Environmental Degradation: The Environmental Kuznets Curve and Sustainable Development. World Dev. 1996, 24, 1151–1160. [Google Scholar] [CrossRef]
- Shahbaz, M.; Mutascu, M.; Azim, P. Environmental Kuznets Curve in Romania and the Role of Energy Consumption. Renew. Sustain. Energy Rev. 2013, 18, 165–173. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Li, M.X.; Zhang, M.J.; Khan, H.S.U.; Li, J.Q.; Li, Z.Y.; Sun, H.Z.; Zhu, Y.; Anaba, O.A. A Study on China’s Economic Growth, Green Energy Technology, and Carbon Emissions based on the Kuznets curve (EKC). Environ. Sci. Pollut. Res. 2021, 28, 7200–7211. [Google Scholar] [CrossRef]
- Ahmad, N.; Du, L.S.; Lu, J.Y.; Wang, J.L.; Li, H.Z.; Hashmi, M.Z. Modelling the CO2 Emissions and Economic Growth in Croatia: Is there any Environmental Kuznets Curve? Energy 2017, 123, 164–172. [Google Scholar] [CrossRef]
- Balsalobre-Lorente, D.; Leitão, N.C. The Role of Tourism, Trade, Renewable Energy Use and Carbon Dioxide Emissions on Economic Growth: Evidence of Tourism-led Growth Hypothesis in EU-28. Environ. Sci. Pollut. Res. 2020, 27, 45883–45896. [Google Scholar] [CrossRef]
- Uzar, U.; Eyuboglu, K. The Nexus between Income Inequality and CO2 Emissions in Turkey. J. Clean. Prod. 2019, 227, 149–157. [Google Scholar] [CrossRef]
- Koc, S.; Bulus, G.C. Testing Validity of the EKC Hypothesis in South Korea: Role of Renewable Energy and Trade Openness. Environ. Sci. Pollut. Res. 2020, 27, 29043–29054. [Google Scholar] [CrossRef]
- Salahuddin, M.; Gow, J. Economic Growth, Energy Consumption and CO2 Emissions in Gulf Cooperation Council Countries. Energy 2014, 73, 44–58. [Google Scholar] [CrossRef]
- Lin, B.Q.; Omoju, O.E.; Nwakeze, N.M.; Okonkwo, J.U.; Megbowon, E.T. Is the Environmental Kuznets Curve Hypothesis a Sound Basis for Environmental Policy in Africa? J. Clean. Prod. 2016, 133, 712–724. [Google Scholar] [CrossRef]
- Lu, W.C. Greenhouse Gas Emissions, Energy Consumption and Economic Growth: A Panel Cointegration Analysis for 16 Asian Countries. Int. J. Environ. Res. Public Health 2017, 14, 1436. [Google Scholar] [CrossRef] [Green Version]
- Mensah, I.A.; Sun, M.; Gao, C.X.; Omari-Sasu, A.Y.; Zhu, D.B.; Ampimah, B.C.; Quarcoo, A. Analysis on the Nexus of Economic Growth, Fossil Fuel Energy Consumption, CO2 Emissions and Oil Price in Africa based on a PMG Panel ARDL Approach. J. Clean. Prod. 2019, 228, 161–174. [Google Scholar] [CrossRef]
- Aslan, A.; Altinoz, B.; Özsolak, B. The Nexus between Economic Growth, Tourism Development, Energy Consumption, and CO2 Emissions in Mediterranean Countries. Environ. Sci. Pollut. Res. 2021, 28, 3243–3252. [Google Scholar] [CrossRef] [PubMed]
- Azam, M.; Khan, A.Q.; Abdullah, H.B.; Qureshi, M.E. The Impact of CO2 Emissions on Economic Growth: Evidence from Selected Higher CO2 Emissions Economies. Environ. Sci. Polluti. Res. 2016, 23, 6376–6389. [Google Scholar] [CrossRef] [PubMed]
- Dogru, T.; Bulut, U.; Kocak, E.; Isik, C.; Suess, C.; Sirakaya-Turk, E. The Nexus between Tourism, Economic Growth, Renewable Energy Consumption, and Carbon Dioxide Emissions: Contemporary Evidence from OECD Countries. Environ. Sci. Pollut. Res. 2020, 27, 40930–40948. [Google Scholar] [CrossRef]
- Kongkuah, M.; Yao, H.X.; Fongjong, B.B.; Agyemang, A.O. The Role of CO2 Emissions and Economic Growth in Energy Consumption: Empirical Evidence from Belt and Road and OECD Countries. Environ. Sci. Pollut. Res. 2021, 28, 22488–22509. [Google Scholar] [CrossRef]
- Bekhet, H.A.; Othman, N.S. The Role of Renewable Energy to Validate Dynamic Interaction between CO2 Emissions and GDP toward Sustainable Development in Malaysia. Energy Econ. 2018, 72, 47–61. [Google Scholar] [CrossRef]
- Merton, R. An Analytic Derivation of the Efficient Portfolio Frontier. J. Financ. Quant. Anal. 1972, 7, 1851–1872. [Google Scholar] [CrossRef] [Green Version]
- Jang, S.C.; Chen, M.H. Financial Portfolio Approach to Optimal Tourist Market Mixes. Tour. Manag. 2008, 29, 761–770. [Google Scholar] [CrossRef] [PubMed]


| Rank | Name | Pressure (mbar) | Category (USA) | Year | Damage (Billion USD) | Dead |
|---|---|---|---|---|---|---|
| 1 | Katrina | 920 | 5 | 2005 | 125.0 | 1836 |
| 2 | Harvey | 937 | 4 | 2017 | 125.0 | 107 |
| 3 | Maria | 920 | 5 | 2017 | 91.6 | 3059 |
| 4 | Irma | 914 | 5 | 2017 | 77.6 | 134 |
| 5 | Ida | 929 | 4 | 2021 | 75.3 | 107 |
| 6 | Sandy | 940 | 3 | 2012 | 68.7 | 233 |
| 7 | Ike | 935 | 4 | 2008 | 38.0 | 214 |
| 8 | Andrew | 922 | 5 | 1992 | 27.3 | 65 |
| 9 | Michael | 919 | 5 | 2018 | 25.5 | 74 |
| 10 | Florence | 927 | 4 | 2004 | 24.2 | 54 |
| GHG | Molecular Formula | Emission Sources |
|---|---|---|
| Water vapor | H2O | Boiled water |
| Ozone | O3 | Light causes O2 to act photochemically. |
| Carbon dioxide | CO2 |
|
| Methane | CH4 |
|
| Nitrogen oxides | NO, NO2, N2O, N4O, NO3, N2O3, N2O4, N2O5, N(NO2)3 |
|
| Chlorofluorocarbons | Chlorofluorocarbons (CFCs) Hydrochlorofluorocarbons (HCFCs) Hydrofluorocarbons (HFCs) | Refrigerant escape |
| Perfluorocarbons | CF4, C2F6, SF6, NF3 | Insulator |
| GHG | Lifetime (Years) | Global Warming Potential (GWP) a | ||
|---|---|---|---|---|
| 20 Years | 100 Years | 500 Years | ||
| Carbon dioxide (CO2) | 20~200 | 1 | 1 | 1 |
| Methane (CH4) | 12.4 | 82.5 | 32 | 7.6 |
| Nitrous oxide (N2O) | 109 | 273 | 273 | 130 |
| HFC-134a (CH2FCF) | 14 | 1390 | 1526 | 436 |
| CFC-11 (CCl3F) | 52 | 8321 | 6226 | 2093 |
| CFC-12 (CCl2F2) | 100 | 10,800 | 10,200 | 5200 |
| HCFC-22 (CHClF2) | 12 | 5280 | 1760 | 549 |
| Carbon tetrafluoride (CF4, PFC-14) | 50,000 | 5301 | 7380 | 10,587 |
| HFC-32 (CH2F2) | 5 | 2693 | 771 | 220 |
| Hexafluoroethane (C2F6) | 10,000 | 8210 | 11,100 | 18,200 |
| Nitrogen trifluoride (NF3) | 500 | 12,800 | 19,100 | 20,700 |
| Sulfur hexafluoride (SF6) b | 3200 | 17,500 | 23,500 | 32,600 |
| Reference | Study Area/Period | Interpretations |
|---|---|---|
| Shahbaz et al., (2013) [32] | Romania/1980–2010 | EKC is found both in long- and short-runs in Romania. |
| Salahuddin and Gow (2014) [38] | GCC countries/1980–2012 | No significant relationship is found between economic growth and CO2 emissions. |
| Wang et al., (2016) [10] | China/1990–2012 | Shocks in CO2 emissions has a small effect on energy consumption and GDP. |
| Azam et al., (2016) [43] | USA, China, India, Japan/1971–2013 | Positive relationship between CO2 emissions and GDP in USA, China and Japan |
| Lin et al., (2016) [39] | Five African countries/1980–2011 | There is no evidence of the validity of the hypothesis in Africa |
| Lu (2017) [40] | 16 Asian countries/1990–2012 | In the long run, bidirectional Granger causality between energy consumption, GDP and GHG emissions is established. |
| Ahmad et al., (2017) [34] | Croatia/1992Q1–2011Q1. | Support to EKC for long-run and bidirectional causality for short-run. |
| Bekhet and Othman (2018) [46] | Malaysia/1971–2015 | The inverted N-shaped EKC hypothesis holds in Malaysia and the GDP growth will be a remedy for environmental pollution problems. |
| Uzar and Eyuboglu (2019) [36] | Turkey/1984–2014 | Income inequality has a positive effect on CO2 emissions and the EKC is valid in Turkey. |
| Mensah et al., (2019) [41] | 22 African countries/1990–2015 | A unilateral causality from carbon emissions to economic growth in long-term |
| Koc and Bulus (2020) [37] | South Korea/1971–2017 | An N-shaped relationship has been identified between per capita CO2 emissions and per capita GDP. This indicates that our empirical findings do not support the EKC hypothesis in South Korea. |
| Balsalobre-Lorente, and Leitão (2020) [35] | EU-28/1995–2014 | CO2 emissions are positively correlated with economic growth, showing that growth is directly correlated by climate change and GHG. |
| Bashir et al., (2020) [26] | OECD economies/1995–2015 | Economic growth impedes environmental quality by increasing carbon emissions. |
| Dogru et al., (2020) [44] | OECD | Tourism development has negative and significant effects on CO2 emission in Canada, Czechia, and Türkiye, while it has positive and significant effects on CO2 emission in Italy, Luxembourg, and the Slovak Republic. |
| Kongkuah et al., (2021) [45] | Belt and Road Countries, OECD | Both CO2 emissions and economic growth positively and significantly affect energy consumption. |
| Aslan, Altinoz, and Özsolak (2021) [42] | Mediterranean countries/1995–2014 | Energy consumption supports economic growth at low and medium growth levels. Short-run causality test results illustrated that there is bidirectional causality between GDP and CO2 emission. |
| Sun et al., (2021) [33] | China/1990–2017 | In the long-run, the relationship between economic growth and carbon emissions is inverted U-shaped. |
| Variable | Obs. | Mean | Median | St. Dev. | Min | Max |
|---|---|---|---|---|---|---|
| CO2eton (Mtons) | 1582 | 423.25 | 100.93 | 1124.67 | 1.87 | 9528.20 |
| GDP per capita (1000$) | 1582 | 24.41 | 18.20 | 22.00 | 0.37 | 129.36 |
| Continent | Support to EKC Hypothesis | Reject the EKC Hypothesis |
|---|---|---|
| Europe | Albania (−1.4487 ***) | Cape Verde (0.1149) |
| Austria (−0.4760 ***) | Czech (−0.1615) | |
| Belarus (−1.8549 ***) | Iceland (0.1237) | |
| Belgium (−0.6850 ***) | Moldova (1.8505 ***) | |
| Bulgaria (−1.1135 ***) | Slovakia (−0.1639 **) | |
| Bosnia and Herzegovina (−0.3911 ***) | Ukraine (0.1406) | |
| Croatia (−0.4024 ***) | ||
| Cyprus (−0.4714 ***) | ||
| Denmark (−0.8906 ***) | ||
| Estonia (−2.5935 **) | ||
| Finland (−6750 ***) | ||
| France (−0.8296 ***) | ||
| Germany (−0.8524 ***) | ||
| Greece (−0.7889 ***) | ||
| Hungary (−1.0287 ***) | ||
| Ireland (−0.4113 ***) | ||
| Italy (−0.9941 ***) | ||
| Latvia (−2.6530 ***) | ||
| Lithuania (−1.9727 ***) | ||
| Luxembourg (−0.2095 **) | ||
| Malta (−0.1906 ***) | ||
| Montenegro (−0.3924 ***) | ||
| Netherlands (−0.7989 ***) | ||
| North Macedonia (−0.8944 ***) | ||
| Norway (−0.6379 ***) | ||
| Poland (−0.7666 ***) | ||
| Portugal (−0.3138 ***) | ||
| Romania (−0.5063 ***) | ||
| Russia (−0.9728 ***) | ||
| Serbia (−0.5766 ***) | ||
| Slovenia (−0.2483 ***) | ||
| Spain (−0.9438 ***) | ||
| Sweden (−0.8761 ***) | ||
| Switzerland (−0.4903 ***) | ||
| Turkey (−0.2812 ***) | ||
| United Kingdom (−0.9471 ***) | ||
| Africa | ||
| Algeria (−1.5759 ***) | Angola (2.1134 ***) | |
| Botswana (−0.7280 ***) | Burkina Faso (−7.0044) | |
| Burundi (−10.1060 **) | Chad (1.9051 ***) | |
| Cameroon (−5.7137 ***) | Comoros (1.3505 **) | |
| Cent. African Rep. (−2.9990 ***) | Congo (0.0227) | |
| Dem. Rep. of Congo (−1.8716 ***) | Cote d’Ivoire (−3.9265) | |
| Djibouti (−2.1016 ***) | Equatorial Guinea (0.2423 ***) | |
| Egypt (−0.4208 *) | Ethiopia (0.9081) | |
| Eswatini (−1.0469 ***) | Gambia (0.7366) | |
| Gabon (−3.1903 ***) | Ghana (4.6146 ***) | |
| Guinea (−1.5205 ***) | Guinea-Bissau (0.8004) | |
| Kenya (−0.9679 ***) | Liberia (0.8134 ***) | |
| Lesotho (−6.6436 ***) | Malawi (0.7052 **) | |
| Libya (−0.3754 ***) | Mali (5.7105 ***) | |
| Madagascar (−6.3631 **) | Mauritius (0.1226) | |
| Mauritania (−3.8924 ***) | Mozambique (2.9358 ***) | |
| Morocco (−1.3541 ***) | Namibia (−0.4725) | |
| Niger (−6.2876 ***) | Rwanda (10.9701 ***) | |
| Nigeria (−2.5193 ***) | Senegal (31.5548 *) | |
| Seychelles (−1.3043 ***) | Sierra Leone (1.8441 **) | |
| South Africa (1.7201 ***) | São Tomé and Príncipe (−0.2383) | |
| Tanzania (−1.5524 ***) | Uganda (5.8374 ***) | |
| Togo (−14.5573 ***) | Zambia (0.495) | |
| Tunisia (−0.4595 ***) | ||
| Zimbabwe (−1.7046 *) | ||
| North America | ||
| Canada (−1.1960 ***) | Barbados (0.9096 ***) | |
| Costa Rica (−0.4993 ***) | Haiti (−13.2546) | |
| Cuba (−7.0740 ***) | Jamaica (−0.1269) | |
| Dominica (−0.3737 ***) | Trinidad and Tobago (0.2723) | |
| Dominican Republic (−1.2384 ***) | ||
| El Salvador (−1.8960 ***) | ||
| Guatemala (−4.2802 ***) | ||
| Honduras (−1.3672 ***) | ||
| Mexico (−0.9063 ***) | ||
| Nicaragua (−6.8917 ***) | ||
| Panama (−0.6966 ***) | ||
| Saint Lucia (−0.6775 ***) | ||
| United States (−1.5400 **) | ||
| South America | ||
| Argentina (−1.6496 ***) | ||
| Bolivia (−4.1208 ***) | ||
| Brazil (−0.1704 ***) | ||
| Chile (−0.8802 ***) | ||
| Colombia (−2.2712 ***) | ||
| Ecuador (−0.5463 **) | ||
| Paraguay (−1.0384 ***) | ||
| Peru (−0.8833 ***) | ||
| Venezuela (−1.5521 ***) | ||
| Asia | ||
| Azerbaijan (−0.4356 ***) | Afghanistan (3.1452 ***) | |
| Bahrain (−0.8480 ***) | Armenia (0.5998) | |
| Bangladesh (−1.7524 ***) | Benin (5.5487 ***) | |
| China (−0.8283 ***) | Cambodia (−0.5440) | |
| Hong Kong ((0.3074 ***) | Georgia (0.8713 **) | |
| India (−2.4608 ***) | Iraq (0.8325 **) | |
| Indonesia (−2.2076 ***) | Israel (0.0405) | |
| Iran (−0.6990 ***) | Kazakhstan (−0.2475) | |
| Japan (−0.7631 ***) | Kuwait (0.7893 **) | |
| Jordan (−1.7637 ***) | Kyrgyzstan (1.6259 ***) | |
| Malaysia (−0.6270 ***) | Laos (0.3338 *) | |
| Mongolia (−0.6003 ***) | Lebanon (1.0449 ***) | |
| Myanmar (−0.6113 ***) | Qatar (1.6803 ***) | |
| Nepal (−4.4781 ***) | Sri Lanka (0.0145) | |
| North Korea (−9.0973 ***) | Syria (3.0551 **) | |
| Oman (−0.7282 ***) | Tajikistan (0.8836 ***) | |
| Pakistan (−0.3542 ***) | Turkmenistan (0.2105 ***) | |
| Palestine (−9.4365 *) | Yemen (−1.5609) | |
| Philippines (−2.1951 ***) | Uzbekistan (0.4061) | |
| Saudi Arabia (−1.1383 ***) | United Arab Emirates (8.9096 ***) | |
| Singapore (−0.4399 ***) | ||
| South Korea −0.7387 ***) | ||
| Taiwan (−0.5805 ***) | ||
| Thailand (−0.7234 ***) | ||
| Vietnam (−0.6115 *) | ||
| Oceania | ||
| Australia (−1.4977 ***) | ||
| New Zealand (−0.5440 ***) |
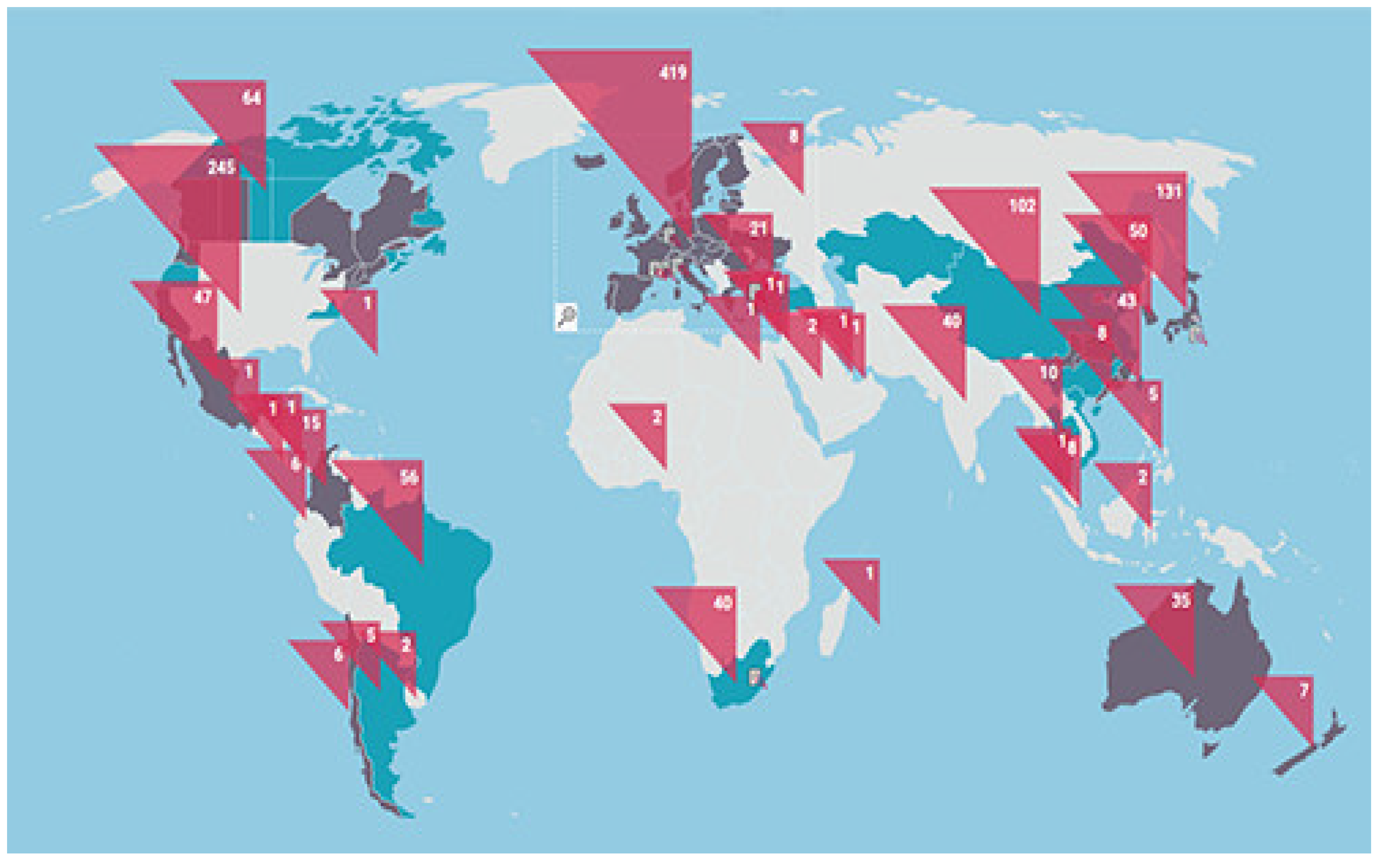
| ISO Code of Country | CO2 Emission Amount in 2020 (MtonCO2e) | Optimal CO2 Emission Quota in 2021 (MtonCO2e) | |
|---|---|---|---|
| European region | |||
| ALB | 4.535 | 4.6028 | 4.6040 |
| AUT | 60.635 | 60.3689 | 60.3706 |
| BEL | 83.749 | 85.0776 | 85.2190 |
| BGR | 37.444 | 37.3882 | 37.3870 |
| BIH | 21.418 | 21.7649 | 21.7655 |
| BLR | 57.445 | 57.7561 | 57.7597 |
| CHE | 32.298 | 31.9855 | 31.9809 |
| CYP | 6.496 | 6.5266 | 6.5277 |
| CZE | 87.975 | 87.1473 | 87.1308 |
| ESP | 208.915 | 207.2991 | 207.2809 |
| EST | 10.452 | 10.1161 | 10.1168 |
| DEU | 644.310 | 636.1301 | 635.5406 |
| DNK | 26.195 | 26.4995 | 26.5038 |
| FIN | 39.288 | 38.6103 | 38.5824 |
| FRA | 276.634 | 271.7850 | 271.7766 |
| GBR | 329.579 | 321.5172 | 321.4169 |
| GRC | 52.235 | 51.2032 | 51.2315 |
| HRV | 16.982 | 16.9874 | 16.9874 |
| HUN | 48.275 | 47.7420 | 47.7310 |
| IRL | 33.349 | 32.9119 | 32.8919 |
| ISL | 2.936 | 2.9774 | 2.9775 |
| ITA | 303.815 | 302.8852 | 302.8285 |
| LTU | 13.799 | 13.8752 | 13.8767 |
| LUX | 8.175 | 8.3003 | 8.2983 |
| LVA | 6.773 | 6.7923 | 6.7926 |
| MDA | 5.147 | 5.2084 | 5.2104 |
| MKD | 7.147 | 6.9914 | 6.9862 |
| MLT | 1.595 | 1.5459 | 1.5427 |
| MNE | 2.310 | 2.3417 | 2.3423 |
| NLD | 138.100 | 137.3132 | 137.3003 |
| NOR | 41.283 | 41.3566 | 41.3579 |
| POL | 299.593 | 299.7536 | 299.7566 |
| PRT | 40.388 | 39.9484 | 39.9286 |
| ROU | 71.475 | 70.9922 | 71.0044 |
| RUS | 1577.136 | 1583.6777 | 1583.8182 |
| SRB | 43.135 | 43.1096 | 43.1091 |
| SVK | 30.730 | 30.4346 | 30.4296 |
| SVN | 12.563 | 12.5463 | 12.5464 |
| SWE | 38.635 | 38.0208 | 37.9904 |
| TUR | 392.794 | 402.0143 | 403.1277 |
| American region | |||
| BRB | 1.087 | 1.0663 | 1.0641 |
| CAN | 535.823 | 536.1096 | 536.1150 |
| CRI | 7.907 | 8.0591 | 8.0617 |
| CUB | 20.152 | 20.2224 | 20.2237 |
| DMA | 0.139 | 0.1456 | 0.1459 |
| DOM | 27.769 | 27.2944 | 27.2812 |
| GTM | 18.938 | 18.3199 | 18.3242 |
| HND | 9.660 | 9.7481 | 9.7499 |
| HTI | 2.920 | 1.8081 | 2.0370 |
| JAM | 7.429 | 7.1724 | 7.1643 |
| LCA | 0.440 | 0.4351 | 0.4350 |
| MEX | 356.968 | 245.7812 | 278.0396 |
| NIC | 5.074 | 5.2303 | 5.2322 |
| PAN | 10.780 | 11.3302 | 11.3460 |
| SLV | 6.124 | 6.1866 | 6.1878 |
| TTO | 35.509 | 36.5395 | 36.5436 |
| USA | 4712.771 | 4672.3139 | 4605.9988 |
| ARG | 156.978 | 161.3801 | 161.6716 |
| BOL | 20.700 | 21.2198 | 21.2328 |
| BRA | 467.384 | 446.0132 | 446.3326 |
| CHL | 81.171 | 84.8071 | 85.0436 |
| COL | 89.105 | 90.4693 | 90.4865 |
| ECU | 30.932 | 32.1550 | 32.3221 |
| PER | 44.706 | 46.9450 | 47.0297 |
| PRY | 7.570 | 7.7630 | 7.7586 |
| VEN | 84.609 | 84.7788 | 85.0845 |
| Oceania region | |||
| AUS | 391.892 | 524.8084 | 514.2120 |
| NZL | 33.475 | 33.4566 | 33.4560 |
| Asian region | |||
| AFG | 12.160 | 13.5445 | 13.4615 |
| ARE | 150.268 | 167.9964 | 165.1578 |
| ARM | 5.890 | 6.7770 | 5.8318 |
| AZE | 37.720 | 34.8413 | 36.4820 |
| BGD | 92.842 | 93.8462 | 93.9066 |
| BHR | 34.960 | 35.4795 | 35.4792 |
| CHN | 10,667.890 | 11,197.6191 | 11,186.7793 |
| HKG | 31.239 | 33.2620 | 33.1307 |
| GEO | 9.968 | 10.0162 | 10.0168 |
| IDN | 589.500 | 598.9654 | 590.7691 |
| IND | 2441.792 | 2517.2714 | 2517.6586 |
| IRN | 745.035 | 776.3739 | 776.3946 |
| IRQ | 210.829 | 219.2870 | 219.0662 |
| ISR | 56.351 | 54.8225 | 54.7648 |
| JOR | 25.487 | 25.5863 | 25.5871 |
| JPN | 1030.775 | 1235.4181 | 1119.6552 |
| KAZ | 291.336 | 301.7645 | 301.7991 |
| KGZ | 11.508 | 10.7879 | 10.9950 |
| KHM | 15.326 | 15.5454 | 15.5486 |
| KOR | 597.605 | 621.4273 | 621.6629 |
| KWT | 88.935 | 102.5310 | 100.3587 |
| LAO | 33.847 | 36.3780 | 36.2851 |
| LBN | 25.969 | 26.5192 | 26.5393 |
| LKA | 21.106 | 31.5918 | 30.3117 |
| MMR | 36.326 | 39.0713 | 39.1506 |
| MNG | 88.442 | 90.3368 | 90.3564 |
| MYS | 272.607 | 310.8236 | 305.0755 |
| NPL | 16.958 | 18.1257 | 18.2163 |
| OMN | 62.163 | 68.3546 | 68.2415 |
| PAK | 234.755 | 330.8475 | 325.9357 |
| PHL | 136.018 | 205.5030 | 188.4140 |
| PRK | 29.311 | 31.5005 | 31.3831 |
| PSE | 2.899 | 3.0471 | 3.0436 |
| QAT | 106.655 | 109.6790 | 107.7144 |
| SAU | 625.508 | 591.3475 | 609.5351 |
| SGP | 45.504 | 42.4464 | 42.3837 |
| SYR | 30.532 | 29.5040 | 29.5009 |
| THA | 257.766 | 282.5505 | 279.5172 |
| TJK | 9.448 | 9.5537 | 9.5556 |
| TKM | 75.338 | 81.2938 | 81.1456 |
| TWN | 273.175 | 377.0800 | 364.9841 |
| UZB | 112.784 | 116.2030 | 116.2643 |
| VNM | 254.303 | 271.4037 | 269.7127 |
| YEM | 9.768 | 9.6506 | 9.6480 |
| African region | |||
| AGO | 22.198 | 23.5458 | 23.5008 |
| BDI | 0.602 | 0.5950 | 0.5956 |
| BEN | 6.703 | 6.8931 | 6.8956 |
| BFA | 3.970 | 2.5417 | 2.8197 |
| BWA | 6.519 | 7.6059 | 7.1416 |
| CAF | 0.188 | 0.4832 | 0.3830 |
| CIV | 10.071 | 8.8744 | 8.8847 |
| CMR | 6.889 | 7.0045 | 6.9824 |
| COD | 2.477 | 2.4377 | 2.4357 |
| COG | 3.117 | 2.8289 | 2.7698 |
| COM | 0.258 | 0.1409 | 0.1268 |
| CPV | 0.550 | 0.5931 | 0.5928 |
| DJI | 0.351 | 0.6326 | 0.5532 |
| DZA | 154.995 | 159.9009 | 160.0371 |
| EGY | 213.457 | 198.6484 | 189.8422 |
| ETH | 14.665 | 14.2352 | 14.2277 |
| GAB | 4.298 | 4.5479 | 4.5413 |
| GHA | 16.001 | 17.1114 | 17.0921 |
| GIN | 3.394 | 3.0935 | 3.0804 |
| GMB | 0.500 | 0.5124 | 0.5128 |
| GNB | 0.287 | 0.3220 | 0.3230 |
| GNQ | 10.265 | 7.0718 | 7.2478 |
| KEN | 16.146 | 14.1335 | 13.2895 |
| LBR | 1.009 | 1.3220 | 1.1334 |
| LBY | 50.721 | 56.3641 | 55.9407 |
| LSO | 2.183 | 2.0025 | 2.0365 |
| MAR | 64.536 | 62.3316 | 62.4447 |
| MDG | 3.680 | 3.8624 | 3.7593 |
| MLI | 3.390 | 3.5199 | 3.5217 |
| MOZ | 6.571 | 3.1883 | 3.7665 |
| MRT | 3.377 | 3.5663 | 3.6931 |
| MUS | 3.979 | 4.5680 | 4.7017 |
| MWI | 1.395 | 1.5412 | 1.3862 |
| NAM | 3.877 | 4.8387 | 4.7688 |
| NER | 1.690 | 2.6664 | 2.4049 |
| NGA | 125.463 | 131.0488 | 131.0921 |
| RWA | 1.033 | 0.4226 | 0.5468 |
| SEN | 10.451 | 10.8063 | 10.8091 |
| SLE | 0.877 | 1.0778 | 1.0768 |
| STP | 0.113 | 0.1346 | 0.1085 |
| SWZ | 0.956 | 1.0630 | 1.0634 |
| SYC | 0.491 | 0.4718 | 0.4700 |
| TCD | 0.912 | 0.9072 | 0.9071 |
| TGO | 2.192 | 2.2348 | 2.2345 |
| TUN | 28.127 | 24.6207 | 24.2436 |
| TZA | 10.939 | 13.0518 | 11.1844 |
| UGA | 4.892 | 4.7703 | 4.7672 |
| ZAF | 451.957 | 465.5652 | 465.6443 |
| ZMB | 6.753 | 8.1071 | 7.8863 |
| ZWE | 10.531 | 10.9705 | 10.9860 |
| Expected growth rate of CO2 emission (%) | 6.0 | 4.0 | |
| Volatility of expected growth rate of CO2 emission (%) | 12.5208 | 8.9529 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsiao, C.-M. Economic Growth, CO2 Emissions Quota and Optimal Allocation under Uncertainty. Sustainability 2022, 14, 8706. https://doi.org/10.3390/su14148706
Hsiao C-M. Economic Growth, CO2 Emissions Quota and Optimal Allocation under Uncertainty. Sustainability. 2022; 14(14):8706. https://doi.org/10.3390/su14148706
Chicago/Turabian StyleHsiao, Chiu-Ming. 2022. "Economic Growth, CO2 Emissions Quota and Optimal Allocation under Uncertainty" Sustainability 14, no. 14: 8706. https://doi.org/10.3390/su14148706
APA StyleHsiao, C. -M. (2022). Economic Growth, CO2 Emissions Quota and Optimal Allocation under Uncertainty. Sustainability, 14(14), 8706. https://doi.org/10.3390/su14148706






