Intelligent Driver Assistance and Energy Management Systems of Hybrid Electric Autonomous Vehicles
Abstract
:1. Introduction
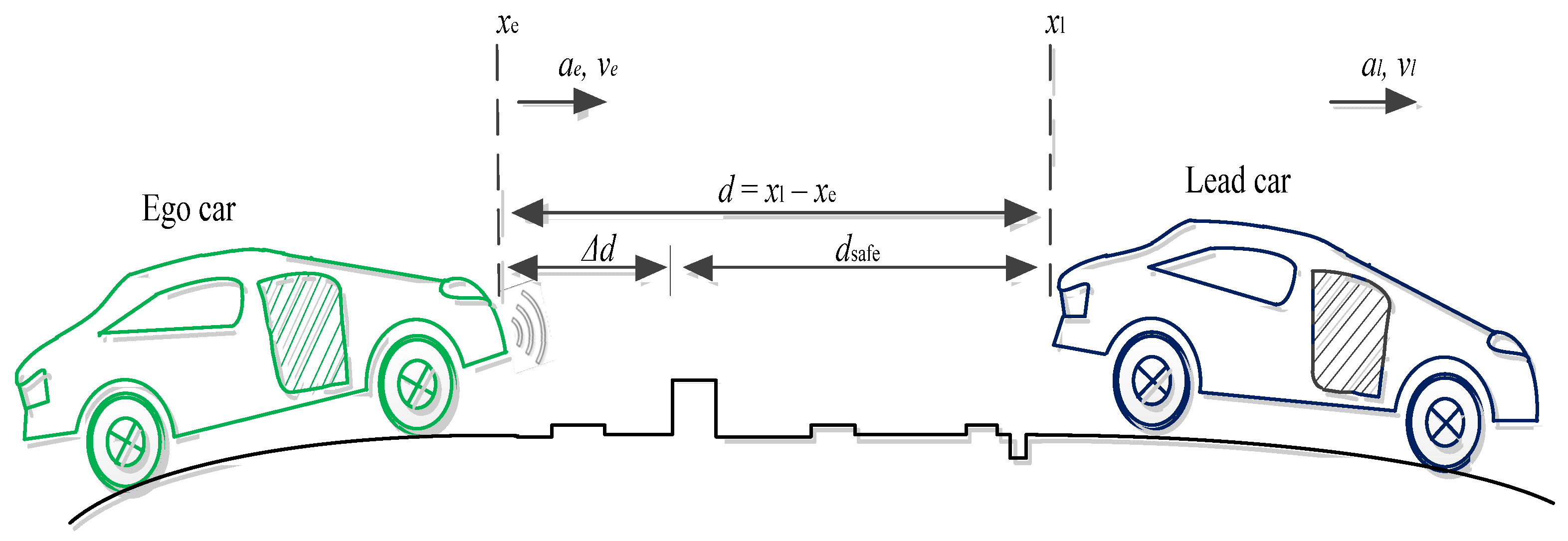
2. Problem Formulation
- The ACC is aimed to maintain a safe car following distance while the ego car follows the speed of the lead car. That means for a small and ;
- The EMS should reduce the energy consumption of the ego car.
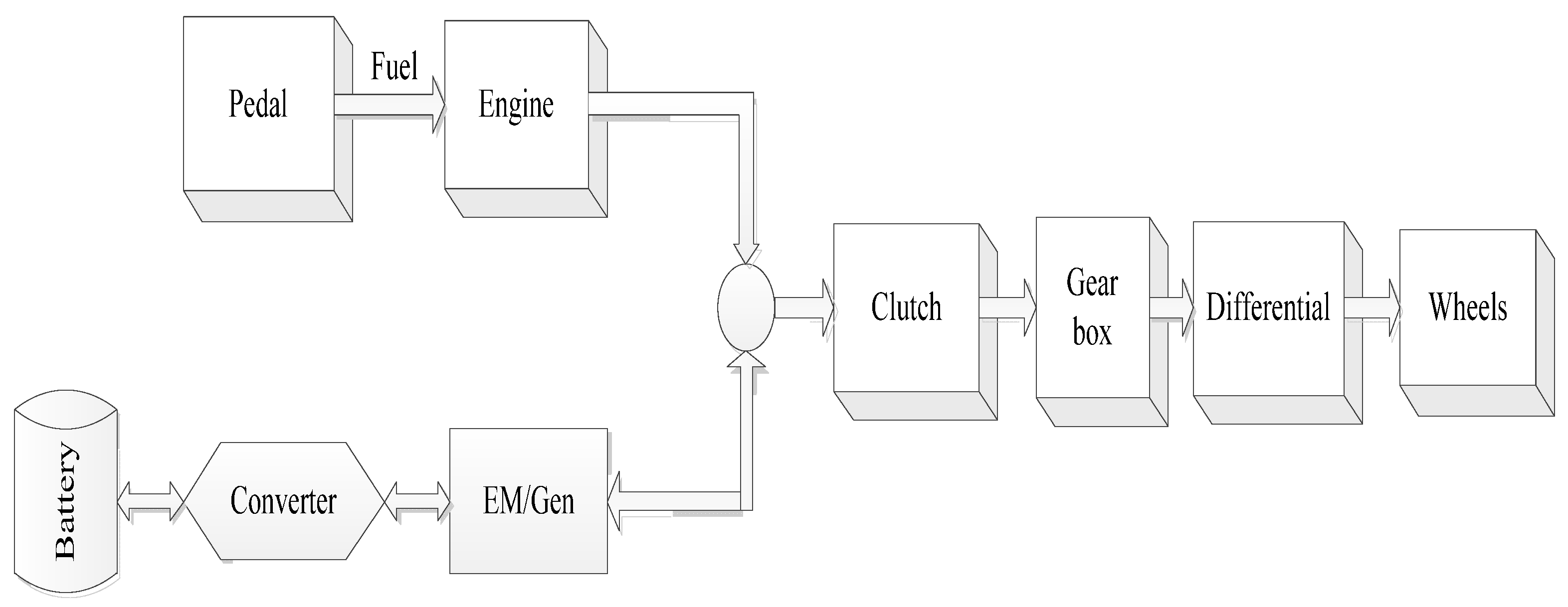
3. Vehicle Configuration and Road Power Demand
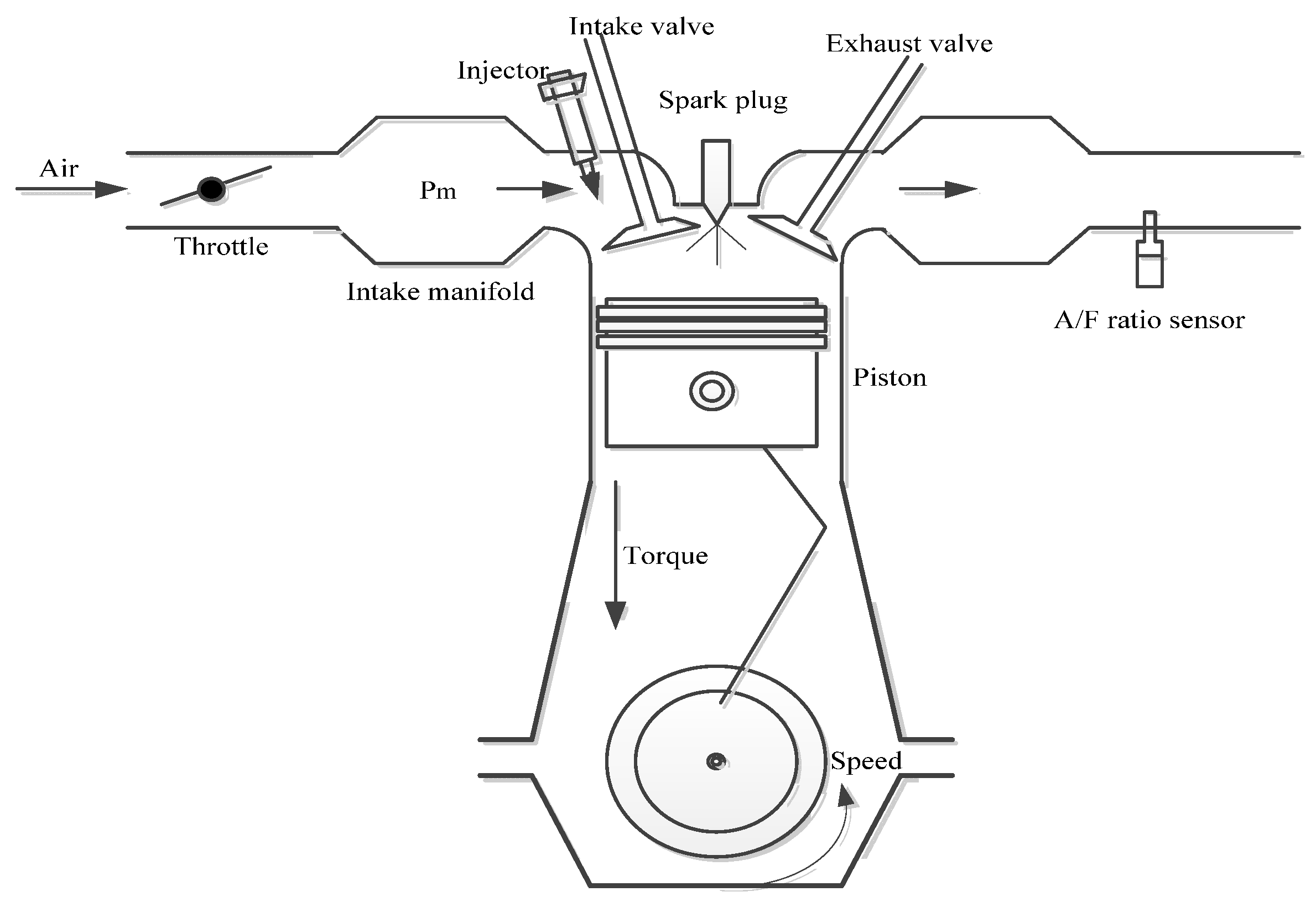
3.1. Internal Combustion Engine
3.2. Electric Motor
3.3. Battery
3.4. Road Power Demand
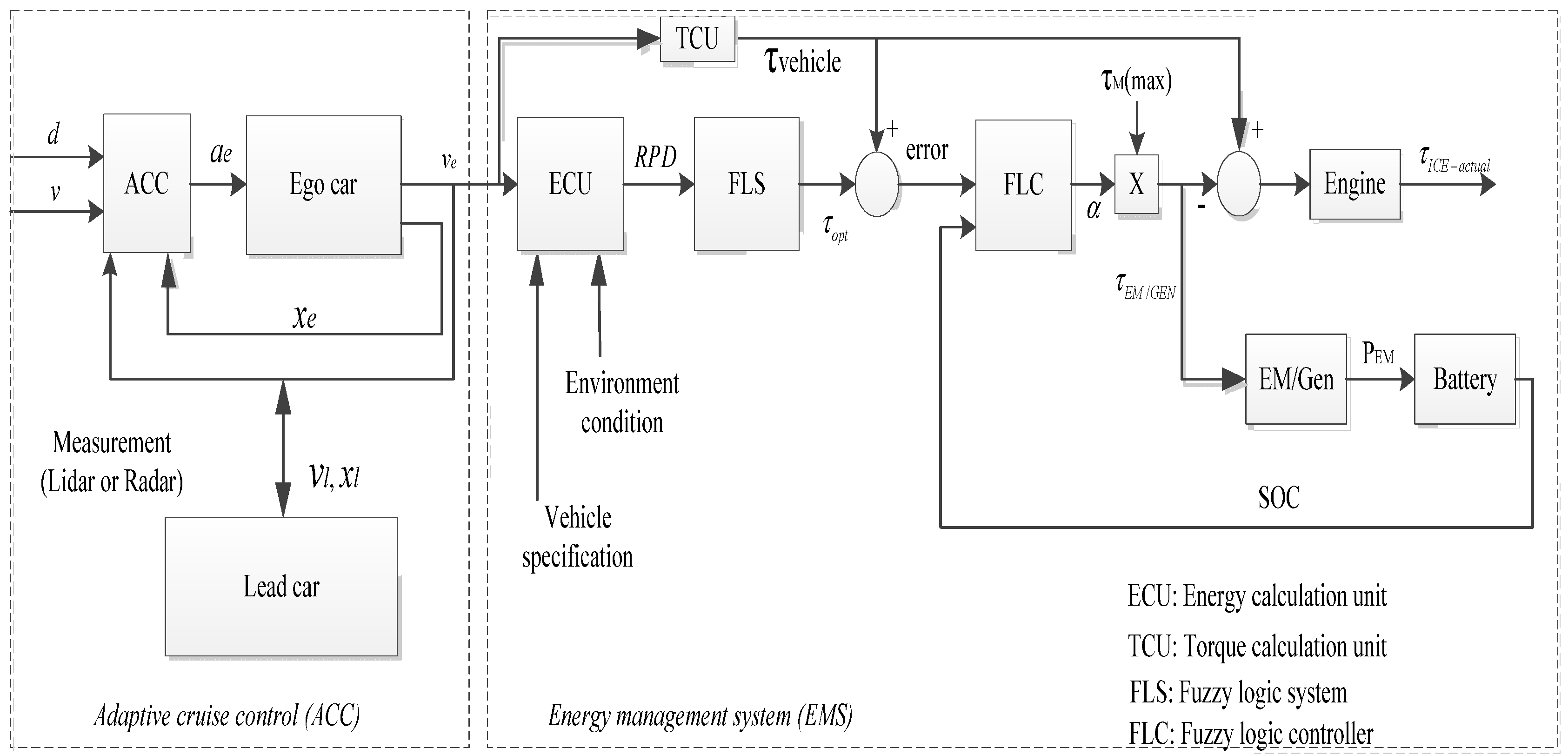
4. Proposed Intelligent Power Driver Assistance System for the Ego Car
4.1. Adaptive Cruise Control
4.1.1. Adaptive Cruise Control Based on Switched MPC
4.1.2. Stability of the Proposed Controller
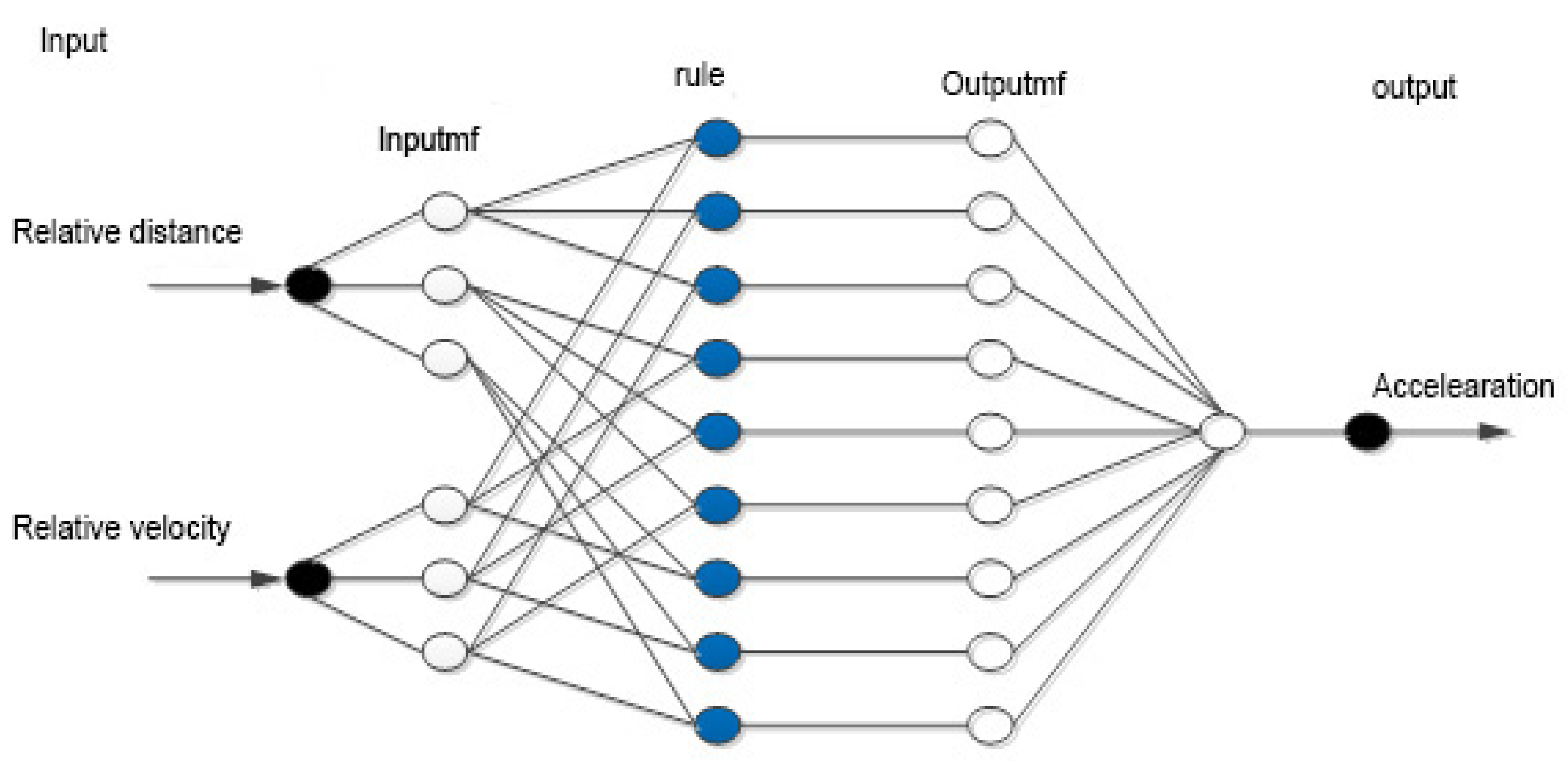
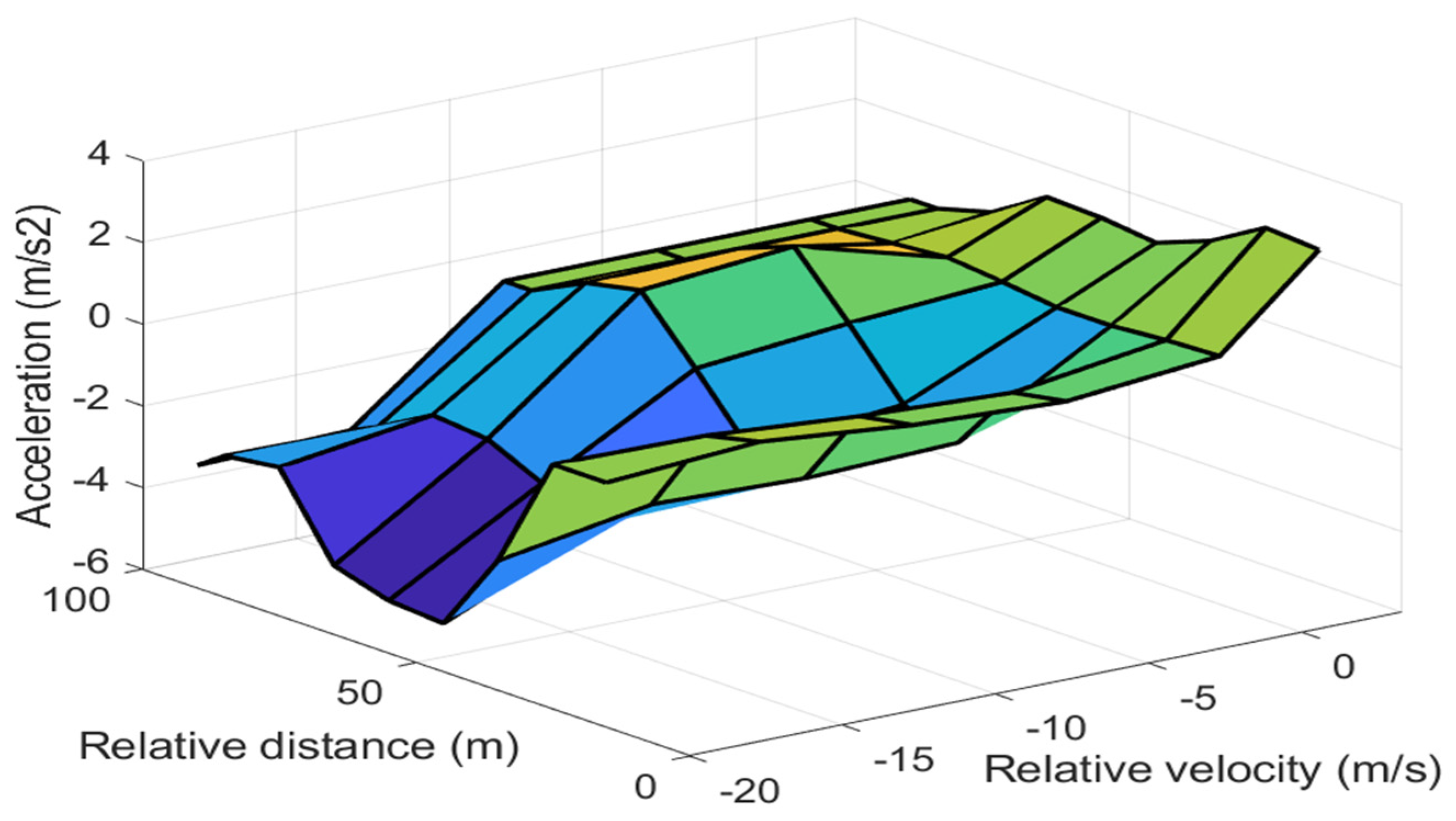
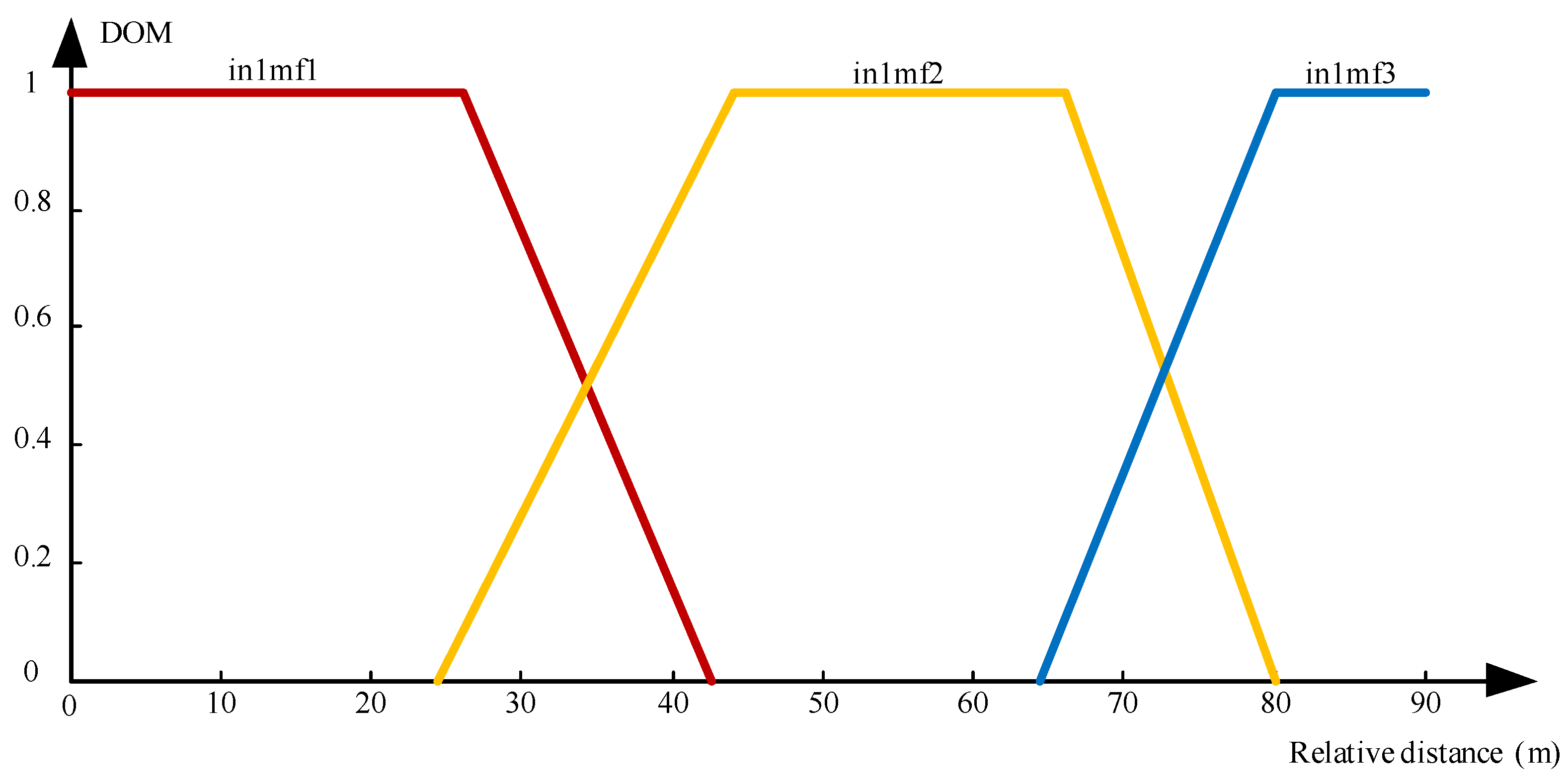
4.1.3. Adaptive Cruise Control Based on NF
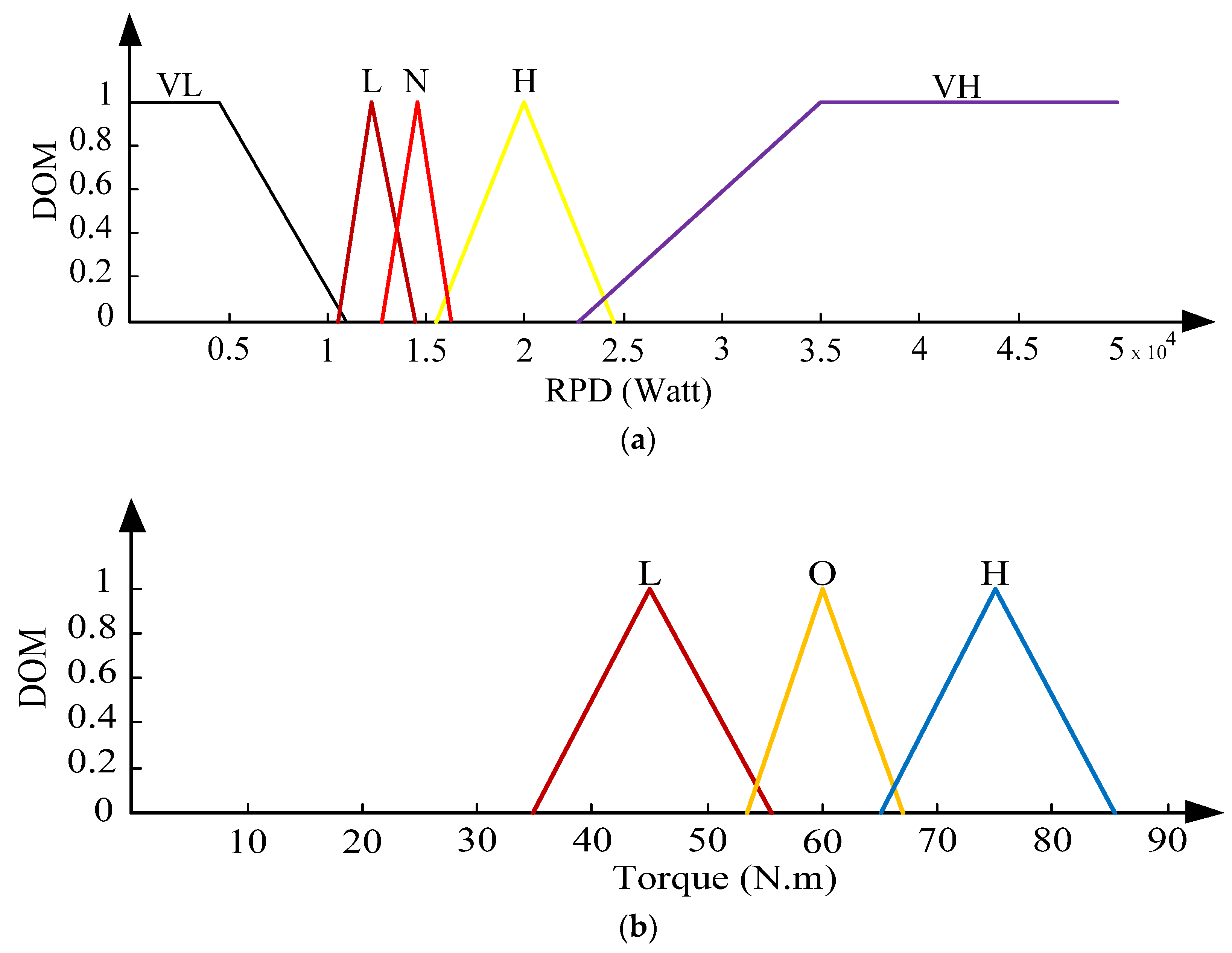
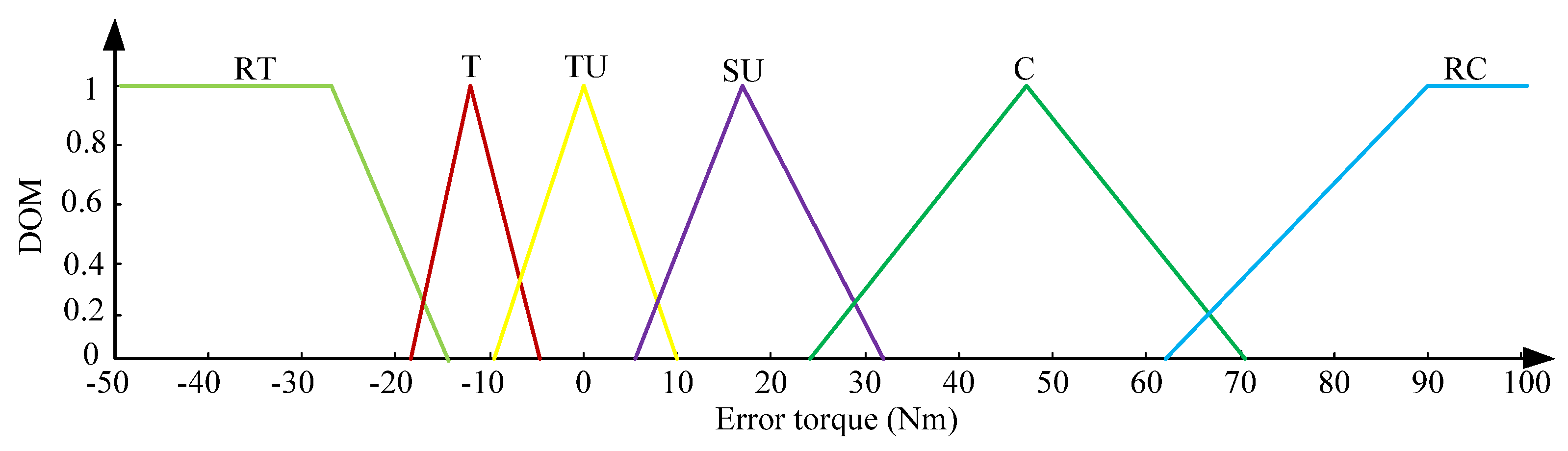
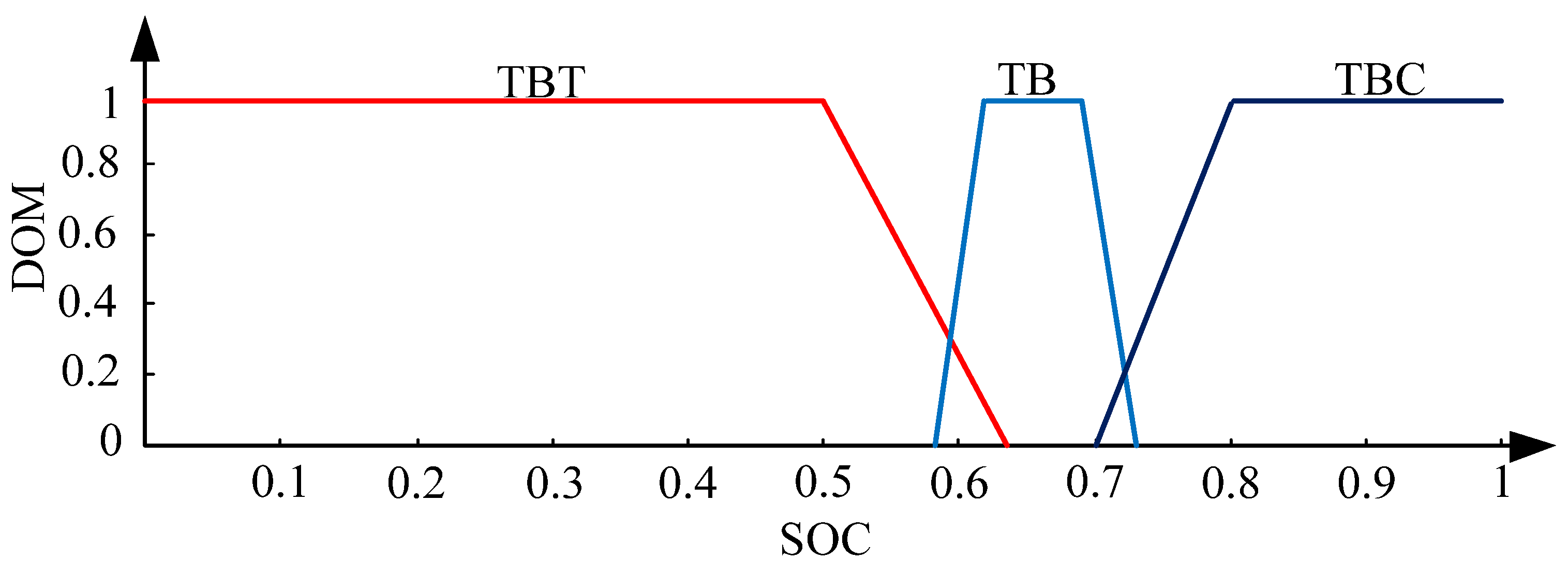
4.2. Energy Management System
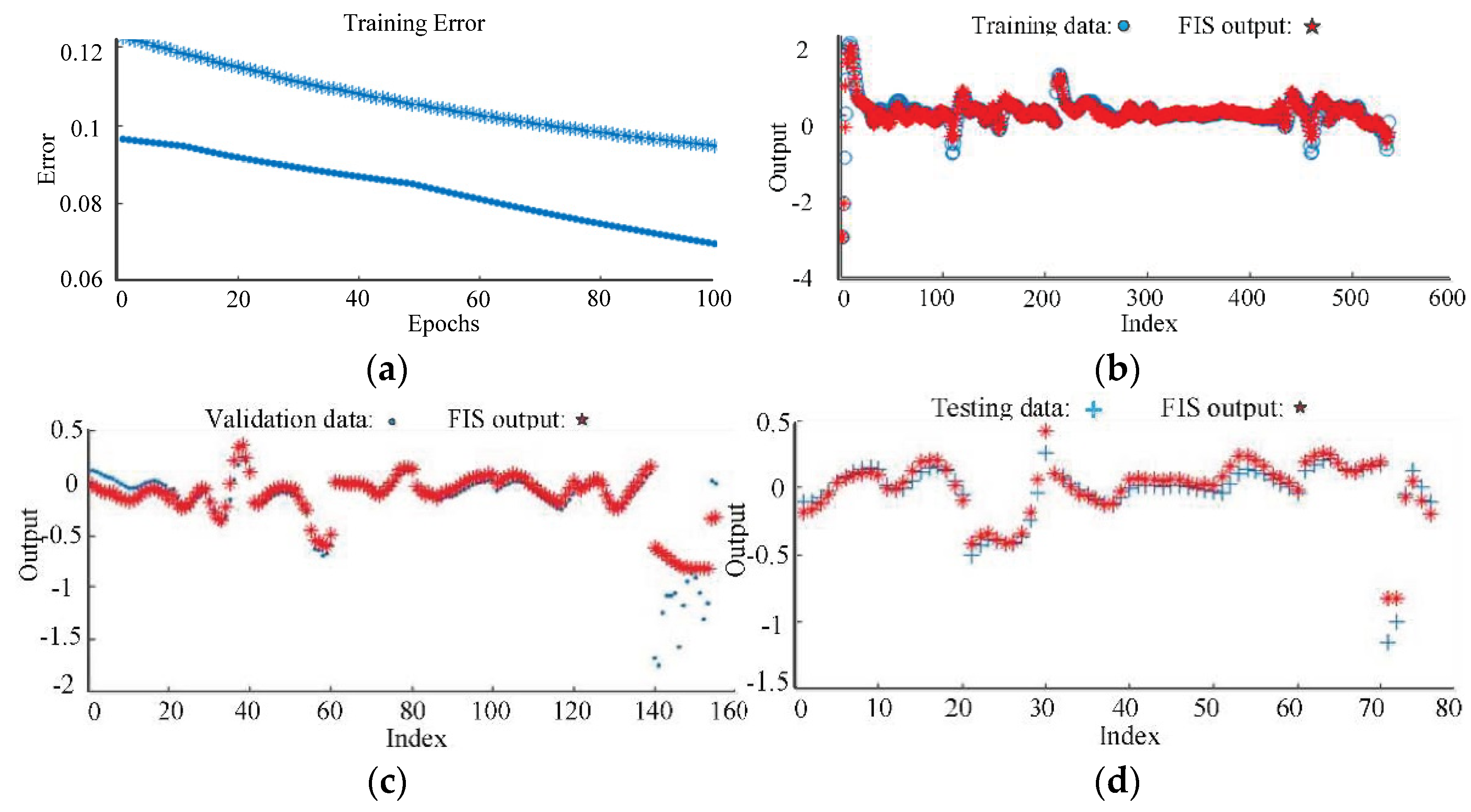
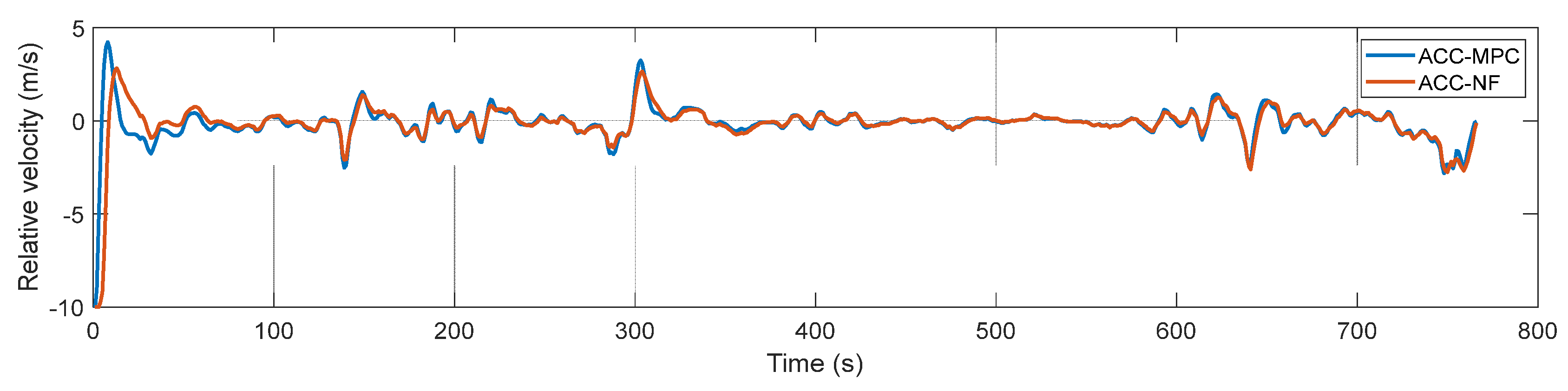
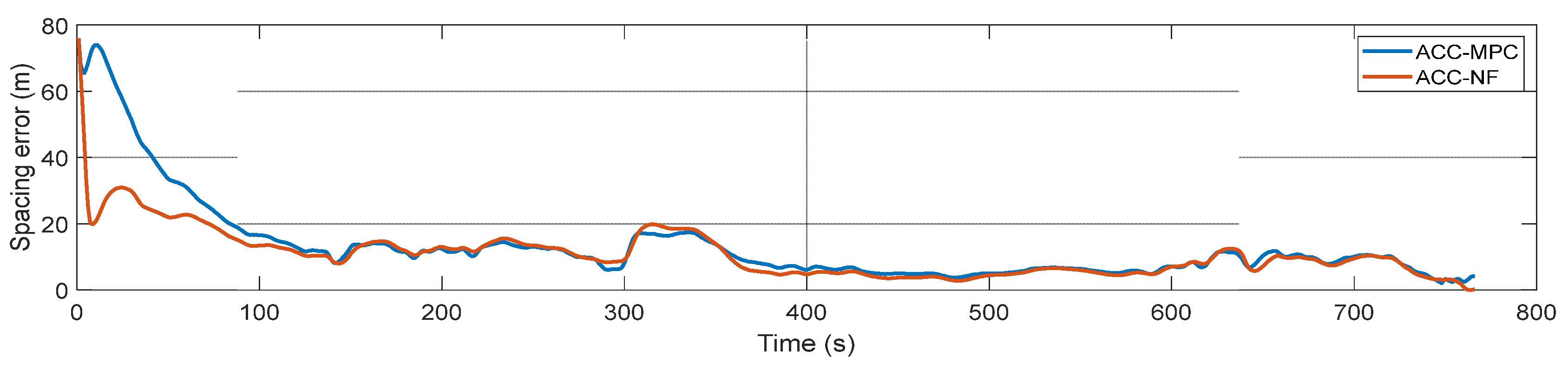
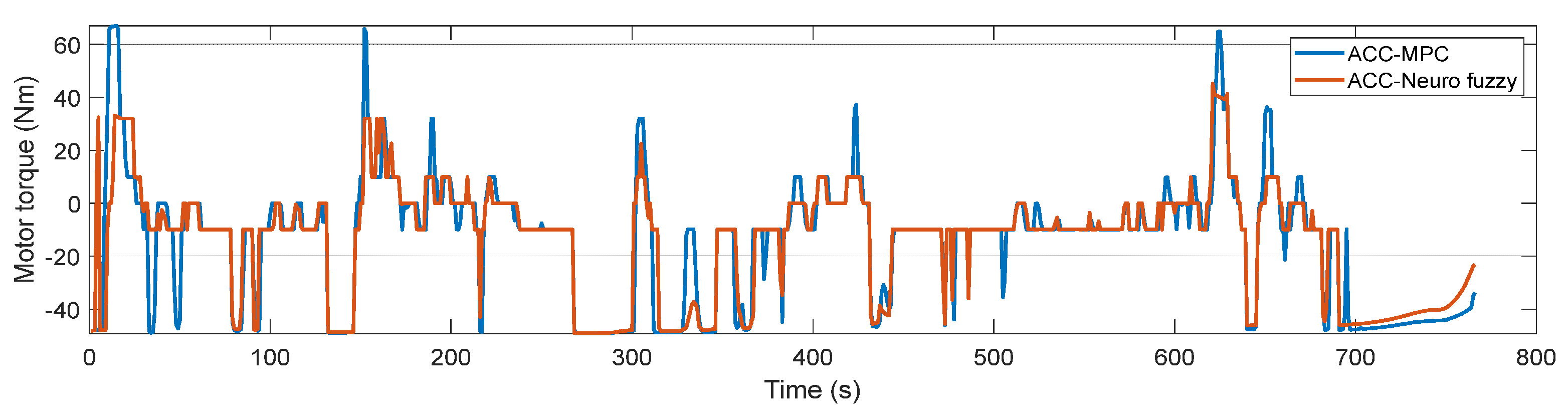
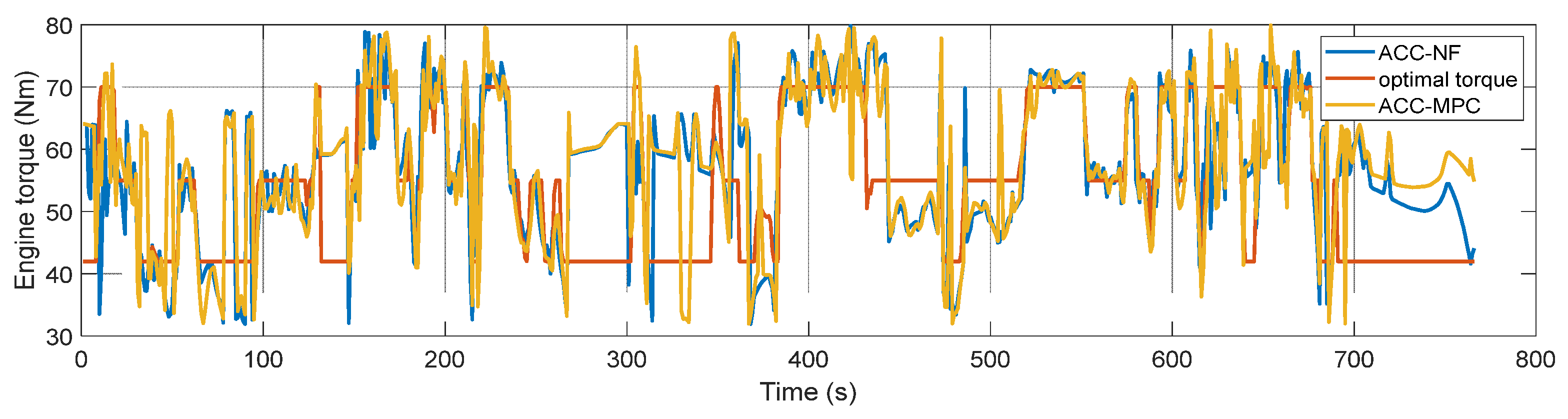
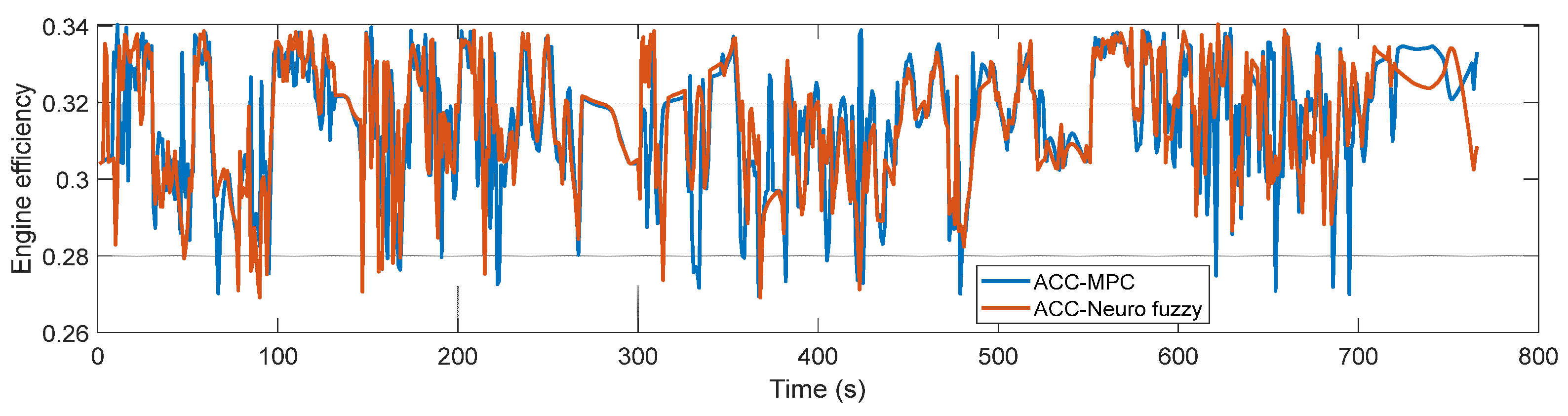
5. Simulation Results and Discussion
5.1. Simulation
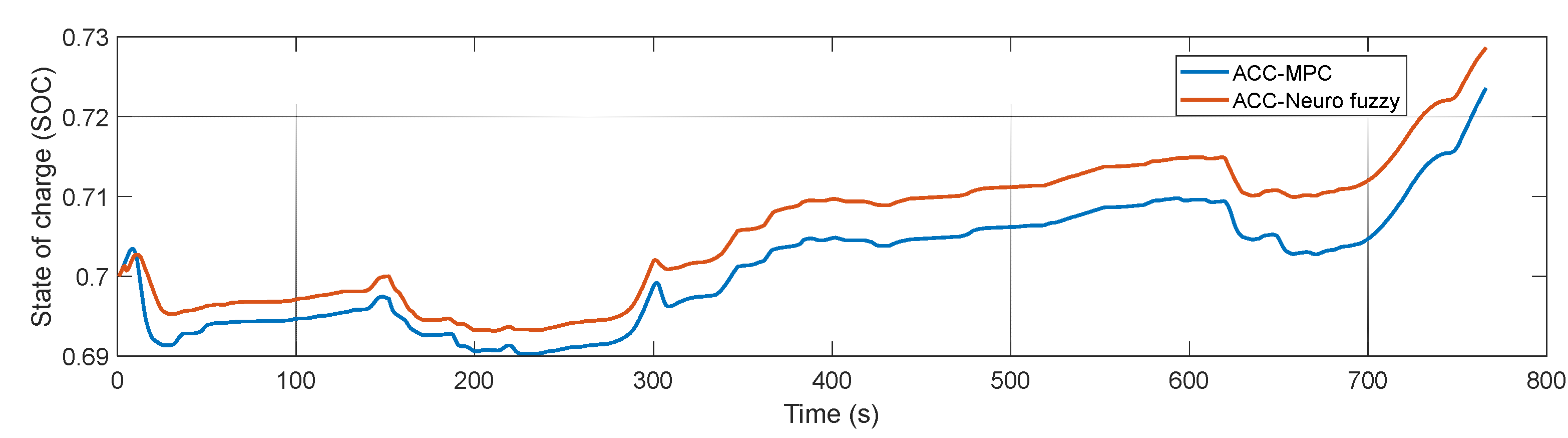
5.2. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Engine torque (N·m) | |
| Engine speed (rpm, rad/s) | |
| Motor torque (N·m) | |
| Motor speed (rpm·rad/s) | |
| Torque of vehicle (N·m) | |
| Road inclination | |
| Air density, (kg/m3) | |
| Mechanical efficiency | |
| Engine efficiency | |
| Mass flow rate fuel consumption, kg/s | |
| Equivalent fuel mass flow rate, kg/s | |
| Power | |
| Combustion energy (kJ/kg) | |
| Drag coefficient | |
| Road friction coefficient | |
| Constant torque | |
| Front surface area, m2 | |
| Function of air to fuel ratio | |
| Air to fuel ratio | |
| Manifold pressure | |
| Battery power (kW) | |
| T | Intake temperature, |
| Temperature of the air in the cabin, | |
| Speed of the vehicle at t (m/s) | |
| Absolute wind speed (m/s) | |
| Manifold volume, m3 | |
| Volumetric displacement of the engine, m3 | |
| SoC | State of Charge |
| MAX | Maximum flow through the throttle |
| HEV | Hybrid Electric Vehicle |
| MPC | Model Predictive Control |
| ACC | Adaptive Cruise Control |
| SMPC | Switching MPC |
| AMPC | Adaptive MPC |
| NF | Neuro Fuzzy |
| ANFIS | Adaptive-Network-based Fuzzy Inference System |
References
- Jazar, R.N.; Dai, L. Nonlinear Approaches in Engineering Applications: Automotive Applications of Engineering Problems; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Marzbani, H.; Khayyam, H.; To, C.N.; Quoc, Đ.V.; Jazar, R.N. Autonomous Vehicles: Autodriver Algorithm and Vehicle Dynamics. IEEE Trans. Veh. Technol. 2019, 68, 3201–3211. [Google Scholar] [CrossRef]
- Lanctot, R. Accelerating the Future: The Economic Impact of the Emerging Passenger Economy; Strategy Analytics: Needham, MA, USA, 2017; Volume 5. [Google Scholar]
- Zöldy, M.; Zsombók, I.J.M.W.C. Modelling fuel consumption and refuelling of autonomous vehicles. MATEC Web Conf. 2018, 235, 37. [Google Scholar] [CrossRef]
- Khayyam, H. Automation, Control and Energy Efficiency in Complex Systems; MDPI Books: Basel, Switzerland, 2020. [Google Scholar]
- Marano, V.; Rizzoni, G.; Tulpule, P.; Gong, Q.; Khayyam, H. Intelligent energy management for plug-in hybrid electric vehicles: The role of ITS infrastructure in vehicle electrification. Oil Gas Sci. Technol. 2012, 67, 575–587. [Google Scholar] [CrossRef] [Green Version]
- Ehsani, M.; Gao, Y.; Longo, S.; Ebrahimi, K. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Khayyam, H.; Kouzani, A.; Nahavandi, S.; Marano, V.; Rizzoni, G. Intelligent energy management in hybrid electric vehicles. In Energy Management; Pérez, F.M., Ed.; IntechOpen: Vienna, Austria, 2010; pp. 147–175. [Google Scholar]
- Milanés, V.; Villagrá, J.; Godoy, J.; González, C. Comparing fuzzy and intelligent PI controllers in stop-and-go manoeuvres. IEEE Trans. Control Syst. Technol. 2011, 20, 770–778. [Google Scholar] [CrossRef] [Green Version]
- Khayyam, H.; Nahavandi, S.; Davis, S. Adaptive cruise control look-ahead system for energy management of vehicles. Expert Syst. Appl. 2012, 39, 3874–3885. [Google Scholar] [CrossRef]
- Liang, Z.; Ren, Z.; Shao, X. Decoupling trajectory tracking for gliding reentry vehicles. IEEE/CAA J. Autom. Sin. 2015, 2, 115–120. [Google Scholar]
- Lin, C.-M.; Chen, C.-H. Car-following control using recurrent cerebellar model articulation controller. IEEE Trans. Veh. Technol. 2007, 56, 3660–3673. [Google Scholar] [CrossRef]
- Bageshwar, V.L.; Garrard, W.L.; Rajamani, R. Model predictive control of transitional maneuvers for adaptive cruise control vehicles. IEEE Trans. Veh. Technol. 2004, 53, 1573–1585. [Google Scholar] [CrossRef]
- Magdici, S.; Althoff, M. Adaptive cruise control with safety guarantees for autonomous vehicles. IFAC-Pap. 2017, 50, 5774–5781. [Google Scholar] [CrossRef]
- Takahama, T.; Akasaka, D. Model Predictive Control Approach to Design Practical Adaptive Cruise Control for Traffic Jam. Int. J. Automot. Eng. 2018, 9, 99–104. [Google Scholar] [CrossRef] [Green Version]
- Jang, J.-S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Khayyam, H.; Fakhrhoseini, S.M.; Church, J.S.; Milani, A.S.; Bab-Hadiashar, A.; Jazar, R.N.; Naebe, M. Predictive modelling and optimization of carbon fiber mechanical properties through high temperature furnace. Appl. Therm. Eng. 2017, 125, 1539–1554. [Google Scholar] [CrossRef]
- Chen, H. Fuel injection control and simulation of efi engine based on anfis. In Proceedings of the 2008 International Conference on Intelligent Computation Technology and Automation (ICICTA), Changsha, China, 20–22 October 2008; pp. 191–194. [Google Scholar]
- Quek, C.; Pasquier, M.; Lim, B. A novel self-organizing fuzzy rule-based system for modelling traffic flow behaviour. Expert Syst. Appl. 2009, 36, 12167–12178. [Google Scholar] [CrossRef]
- Vatankhah, R.; Rahaeifard, M.; Alasty, A. Vibration control of vehicle suspension system using adaptive critic-based neurofuzzy controller. In Proceedings of the 2009 6th International Symposium on Mechatronics and its Applications, Sharjah, United Arab Emirates, 23–26 March 2009; pp. 1–6. [Google Scholar]
- Jinlin, X.; Weigong, Z.; Zongyang, G. Neurofuzzy velocity tracking control with reinforcement learning. In Proceedings of the 2009 9th International Conference on Electronic Measurement & Instruments, Beijing, China, 16–19 August 2009. [Google Scholar]
- Zoldy, M.; Csete, M.S.; Kolozsi, P.P.; Bordas, P.; Torok, A.J.C.S. Cognitive Sustainability. Cogn. Sustain. 2022, 1. [Google Scholar] [CrossRef]
- Barabás, I.; Todoruţ, A.; Cordoş, N.; Molea, A. Current challenges in autonomous driving. IOP Conf. Ser. Mater. Sci. Eng. 2017, 252, 012096. [Google Scholar] [CrossRef]
- Mueller, M.W.; Lee, S.J.; D’Andre, R. Design and Control of Drones. Annu. Rev. Control Robot. Auton. Syst. 2022, 5, 161–177. [Google Scholar] [CrossRef]
- Sajadi-Alamdari, S.A.; Voos, H.; Darouach, M. Ecological advanced driver assistance system for optimal energy management in electric vehicles. IEEE Intell. Transp. Syst. Mag. 2018, 12, 92–109. [Google Scholar] [CrossRef]
- Rajamani, R.; Zhu, C. Semi-autonomous adaptive cruise control systems. IEEE Trans. Veh. Technol. 2002, 51, 1186–1192. [Google Scholar] [CrossRef]
- Cho, D.; Hedrick, J.K. Automotive powertrain modeling for control. J. Dyn. Syst. Meas. Control 1989, 111, 568–576. [Google Scholar] [CrossRef]
- Michael, P.; Anthony, M. Engine Testing Theory and Practice; SAE International: Warrendale, PA, USA, 1999. [Google Scholar]
- Zhang, F.; Xi, J.; Langari, R. An adaptive equivalent consumption minimization strategy for parallel hybrid electric vehicle based on fuzzy pi. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016; pp. 460–465. [Google Scholar]
- Khayyam, H. Stochastic models of road geometry and wind condition for vehicle energy management and control. IEEE Trans. Veh. Technol. 2012, 62, 61–68. [Google Scholar] [CrossRef]
- Moura, S.J.; Callaway, D.S.; Fathy, H.K.; Stein, J.L. Tradeoffs between battery energy capacity and stochastic optimal power management in plug-in hybrid electric vehicles. J. Power Sources 2010, 195, 2979–2988. [Google Scholar] [CrossRef]
- Kim, N.; Lee, D.; Zheng, C.; Shin, C.; Seo, H.; Cha, S. Realization of pmp-based control for hybrid electric vehicles in a backward-looking simulation. Int. J. Automot. Technol. 2014, 15, 625–635. [Google Scholar] [CrossRef]
- Zhang, P. Advanced Industrial Control Technology; William Andrew: Norwich, NY, USA, 2010. [Google Scholar]
- Müller, M.A.; Allgöwer, F. Improving performance in model predictive control: Switching cost functionals under average dwell-time. Automatica 2012, 48, 402–409. [Google Scholar] [CrossRef]
- Müller, M.A.; Martius, P.; Allgöwer, F. Model predictive control of switched nonlinear systems under average dwell-time. J. Process Control 2012, 22, 1702–1710. [Google Scholar] [CrossRef]
- Khayyam, H. Adaptive Intelligent Systems for Energy Management of Vehicles. Ph.D. Thesis, Deakin University, Burwood, Australia, 2010. [Google Scholar]
- Phan, D.; Bab-Hadiashar, A.; Hoseinnezhad, R.; N Jazar, R.; Jamali, A.; Pham, D.B.; Khayyam, H. Neuro-Fuzzy System for Energy Management of Conventional Autonomous Vehicles. Energies 2020, 13, 1745. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, M.; Johnson, K. Feature Engineering and Selection: A Practical Approach for Predictive Models; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Khayyam, H.; Golkarnarenji, G.; Jazar, R.N. Limited data modelling approaches for engineering applications. In Nonlinear Approaches in Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2018; pp. 345–379. [Google Scholar]
- Phan, D.; Bab-Hadiashar, A.; Lai, C.Y.; Crawford, B.; Hoseinnezhad, R.; Jazar, R.N.; Khayyam, H. Intelligent energy management system for conventional autonomous vehicles. Energy 2019, 191, 116476. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M.; Ricker, N.L. Model Predictive Control Toolbox User’s Guide. The Mathworks, 2010. Available online: https://zdocs.pub/doc/model-predictive-control-toolbox-d1m49we9ow10 (accessed on 20 May 2022).
- Phan, D.; Amani, A.M.; Mola, M.; Rezaei, A.A.; Fayyazi, M.; Jalili, M.; Ba Pham, D.; Langari, R.; Khayyam, H.J.S. Cascade adaptive mpc with type 2 fuzzy system for safety and energy management in autonomous vehicles: A sustainable approach for future of transportation. Sustainability 2021, 13, 10113. [Google Scholar] [CrossRef]



| Specification | Parameters | Value |
|---|---|---|
| Road friction coefficient | 0.015 | |
| Gravity acceleration | 9.81 m/s2 | |
| Vehicle velocity | ACC command m/s | |
| Wind velocity | m/s | |
| Mass (vehicle + equivalent rotating parts + passengers) | 1280 kg | |
| Drag coefficient (constant) | 0.335 | |
| Front surface area | 1.9 × (1/cosϕ) | |
| Air density | 1.225 kg/m3 | |
| Combustion energy | qcombustion | 38017 kJ/kg |
| Wheel radius | whr | 0.285 m |
| Differential ratio | dr | 3.21:1 |
| Electric motor/generator | ||
| Maximum current | 480 A | |
| Minimum voltage | 120 V | |
| Max power | 75 kW | |
| Battery pack | ||
| Chemistry | Li-Ion | |
| A cell nominal voltage | 12 V | |
| Nominal capacity | 26.2 Ah | |
| Pack battery power | 4.4 kWh | |
| Temperature | [0 22 40] (0 °C) | |
| Min voltage | 9.5 V | |
| Max voltage | 16.5 V | |
| Condition Number | If Total Required Power | |
|---|---|---|
| 1 | VL | L |
| 2 | L | L |
| 3 | N | O |
| 4 | H | H |
| 5 | VH | H |
| Condition Number | And SoC | Then α | Condition Number | If | And SoC | Then α | |
|---|---|---|---|---|---|---|---|
| 1 | RC | TBT | TO | 10 | TU | TBT | TO |
| 2 | RC | TB | RC | 11 | TU | TB | TO |
| 3 | RC | TBC | RC | 12 | TU | TBC | TO |
| 4 | C | TBT | TO | 13 | T | TBT | T |
| 5 | C | TB | C | 14 | T | TB | T |
| 6 | C | TBC | C | 15 | T | TBC | TO |
| 7 | SU | TBT | TO | 16 | RT | TBT | RT |
| 8 | SU | TB | SU | 17 | RT | TB | RT |
| 9 | SU | TBC | SU | 18 | RT | TBC | TO |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Saadi, Z.; Phan Van, D.; Moradi Amani, A.; Fayyazi, M.; Sadat Sajjadi, S.; Ba Pham, D.; Jazar, R.; Khayyam, H. Intelligent Driver Assistance and Energy Management Systems of Hybrid Electric Autonomous Vehicles. Sustainability 2022, 14, 9378. https://doi.org/10.3390/su14159378
Al-Saadi Z, Phan Van D, Moradi Amani A, Fayyazi M, Sadat Sajjadi S, Ba Pham D, Jazar R, Khayyam H. Intelligent Driver Assistance and Energy Management Systems of Hybrid Electric Autonomous Vehicles. Sustainability. 2022; 14(15):9378. https://doi.org/10.3390/su14159378
Chicago/Turabian StyleAl-Saadi, Ziad, Duong Phan Van, Ali Moradi Amani, Mojgan Fayyazi, Samaneh Sadat Sajjadi, Dinh Ba Pham, Reza Jazar, and Hamid Khayyam. 2022. "Intelligent Driver Assistance and Energy Management Systems of Hybrid Electric Autonomous Vehicles" Sustainability 14, no. 15: 9378. https://doi.org/10.3390/su14159378
APA StyleAl-Saadi, Z., Phan Van, D., Moradi Amani, A., Fayyazi, M., Sadat Sajjadi, S., Ba Pham, D., Jazar, R., & Khayyam, H. (2022). Intelligent Driver Assistance and Energy Management Systems of Hybrid Electric Autonomous Vehicles. Sustainability, 14(15), 9378. https://doi.org/10.3390/su14159378










