Effect of Magnetic Baffles and Magnetic Nanofluid on Thermo-Hydraulic Characteristics of Dimple Mini Channel for Thermal Energy Applications
Abstract
:1. Introduction
2. Computational Methodology
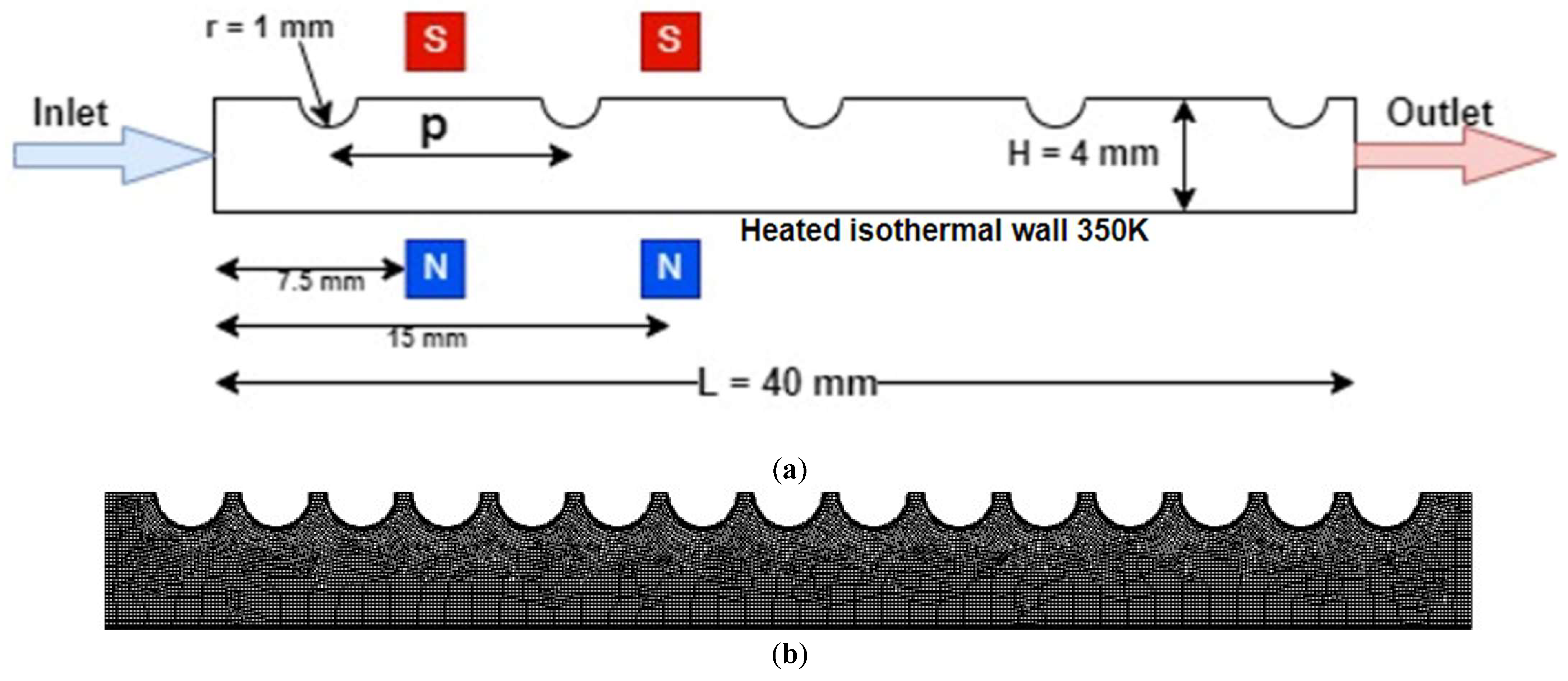
2.1. Geometry and Grid Generation
2.2. Governing Equations
- Continuity equation:
- Momentum equations:
- Energy equation:
2.3. Boundary Conditions
2.4. Thermo-Hydraulic Parameters
2.5. CFD Solver Settings
3. Grid Independence Test and Validation
4. Results and Discussion
4.1. Variation of Nusselt Number with Re
4.2. Variation of Nusselt Number along the Length of the Channel
4.3. Variation of the Pressure Drop across the Channel with Re
4.4. Comparison
5. Conclusions
- The magnetic field is used to create a virtual baffle along with artificial roughness (dimple turbulator) which helps to create turbulence and flow mixing regions, hence increasing the heat transfer;
- The height of the ‘baffle’ is to be varied by varying the magnetic field. Higher Nusselt numbers were obtained when the magnet was placed more downstream as compared to upstream;
- The pressure drop due to the virtual baffle is less than the physical baffle, because of the absence of a horizontal backwards force in the case of the magnetic field;
- There is an increase of 3.53%, 10.77%, and 25.39% in the Nusselt numbers when the magnetic fields of 1200 G, 1500 G, and 2000 G, respectively, are applied at x = 15 mm, as compared to the flow without a magnetic field when the pitch = 10 mm;
- When two sources are placed at x = 7.5 mm and 15 mm, there is an increase of 4.52%, 13.93%, and 33.08% in the Nusselt numbers when the magnetic fields of 1200 G, 1500 G and 2000 G are applied and when the pitch = 10 mm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| B | Magnetic field intensity (Gauss) |
| Cp | Specific heat (J/kg/K) |
| D | Hydraulic diameter (m) |
| Fk | Magnetic body force (N) |
| H | Channel height (m), magnetic field intensity |
| h | Heat transfer coefficient (W/m2 K) |
| k | Boltzmann constant |
| K | Thermal conductivity (W/m−1 K−1) |
| L | 2D channel length (m) |
| M | Magnetization (A m−1) |
| Nu | Nusselt number |
| P | Pressure drop (Pa) |
| q | Heat flux (W/m2) |
| Re | Reynolds number |
| T | Temperature (K) |
| u | Horizontal velocity (m/s) |
| v | Vertical velocity (m/s) |
| V | Velocity (m/s) |
| x, y | Directions |
| Greek Symbols | |
| ϕ | Volume fraction |
| χm | Magnetic susceptibility |
| χo | Differential magnetic Susceptibility (0.06) |
| ρ | Density (kg/m3) |
| μ | Dynamic viscosity (N s/m2) |
| μ0 | Permeability of free space (4π × 10−7 N/A2) |
| β | Fraction of the liquid volume (k−1) |
| τ | Wall shear stress (Pa) |
| δ | Thickness (m) |
| Subscripts | |
| b | Bulk |
| f | Fluid |
| nf | Nanofluid |
| np | Nanoparticle |
| in | Inlet |
| w | Wall |
References
- Bhattacharyya, S.; Vishwakarma, D.K.; Srinivasan, A.; Soni, M.K.; Goel, V.; Sharifpur, M.; Ahmadi, M.H.; Issakhov, A.; Meyer, J. Thermal performance enhancement in heat exchangers using active and passive techniques: A detailed review. J. Therm. Anal. Calorim. 2022, 147, 9229–9281. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Vishwakarma, D.K.; Chakraborty, S.; Roy, R.; Issakhov, A.; Sharifpur, M. Turbulent flow heat transfer through a circular tube with novel hybrid grooved tape inserts: Thermohydraulic analysis and prediction by applying machine learning model. Sustainability 2021, 13, 3068. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Vishwakarma, D.K.; Goel, V.; Chamoli, S.; Issakhov, A.; Meyer, J.P. Thermodynamics and heat transfer study of a circular tube embedded with novel perforated angular-cut alternate segmental baffles. J. Therm. Anal. Calorim. 2021, 145, 1445–1465. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Vishwakarma, D.K.; Soni, M.K. Heat transfer and pressure drop in transitional flow: A short review. In Proceedings of the 3rd International Conference on Advances in Mechanical Engineering and its Interdisciplinary Areas (ICAMEI 2021), Kolaghat, India, 5–7 January 2021; Volume 1080, p. 012050. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Vishwakarma, D.K.; Roy, S.; Biswas, R.; Ardekani, M.M. Applications of heat transfer enhancement techniques: A state-of-the-art review. In Inverse Heat Conduction Heat Exchange; IntechOpen: London, UK, 2020. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Vishwakarma, D.K.; Roy, S.; Dey, K.; Benim, A.C.; Bennacer, R.; Paul, A.R.; Huan, Z. Computational investigation on heat transfer augmentation of a circular tube with novel hybrid ribs. E3S Web Conf. 2021, 321, 04012. [Google Scholar] [CrossRef]
- Kumar, A.; Dey, K.; Bhattacharyya, S.; Paul, A.R.; Benim, A.C.; Vishwakarma, D.K.; Huan, Z. Augmented thermal performance in a non-uniform heat flux circular tube with twisted tape insert using hybrid nanofluid. E3S Web Conf. 2021, 321, 04009. [Google Scholar] [CrossRef]
- Souayeh, B.; Bhattacharyya, S.; Hdhiri, N.; Alam, M.W. Heat and fluid flow analysis and ann-based prediction of a novel spring corrugated tape. Sustainability 2021, 13, 3023. [Google Scholar] [CrossRef]
- Ibrahim, M.; Saeed, T.; Bani, F.R.; Sedeh, S.N.; Chu, Y.M.; Toghraie, D. Two-phase analysis of heat transfer and entropy generation of water-based magnetite nanofluid flow in a circular microtube with twisted porous blocks under a uniform magnetic field. Powder Technol. 2021, 384, 522–541. [Google Scholar] [CrossRef]
- Lee, A.; Jeon, Y.; Chinnasamy, V.; Cho, H. Investigation of forced convective heat transfer with magnetic field effect on water/ethylene glycol-cobalt zinc ferrite nanofluid. Int. Commun. Heat Mass Transf. 2021, 128, 105647. [Google Scholar] [CrossRef]
- Mehryan, S.A.M.; Izadi, M.; Namazian, Z.; Chamkha, A.J. Natural convection of multi-walled carbon nanotube–Fe3O4/water magnetic hybrid nanofluid flowing in porous medium considering the impacts of magnetic field-dependent viscosity. J. Therm. Anal. Calorim. 2019, 138, 1541–1555. [Google Scholar] [CrossRef]
- Niknejadi, M.; Afrand, M.; Karimipour, A.; Shahsavar, A.; Isfahani, A.H.M. An experimental study on the cooling efficiency of magnetite–water nanofluid in a twisted tube exposed to a rotating magnetic field. J. Therm. Anal. Calorim. 2021, 146, 1893–1909. [Google Scholar] [CrossRef]
- Rawa, M.J.H.; Abu-Hamdeh, N.H.; Golmohammadzadeh, A.; Goldanlou, A.S. An investigation on effects of blade angle and magnetic field on flow and heat transfer of non-Newtonian nanofluids: A numerical simulation. Int. Commun. Heat Mass Transf. 2021, 120, 105074. [Google Scholar] [CrossRef]
- Alghamdi, M.; Wakif, A.; Thumma, T.; Khan, U.; Baleanu, D.; Rasool, G. Significance of variability in magnetic field strength and heat source on the radiative-convective motion of sodium alginate-based nanofluid within a Darcy-Brinkman porous structure bounded vertically by an irregular slender surface. Case Stud. Therm. Eng. 2021, 28, 101428. [Google Scholar] [CrossRef]
- Biswas, N.; Mondal, M.K.; Mandal, D.K.; Manna, N.K.; Subba, R.; Gorla, R.; Chamkha, A.J. A narrative loom of hybrid nanofluid-filled wavy walled tilted porous enclosure imposing a partially active magnetic field. Int. J. Mech. Sci. 2021, 271, 107028. [Google Scholar] [CrossRef]
- Bezaatpour, M.; Goharkhah, M. A magnetic vortex generator for simultaneous heat transfer enhancement and pressure drop reduction in a mini channel. Heat Transf. Asian Res. 2020, 49, 1192–1213. [Google Scholar] [CrossRef]
- Bezaatpour, M.; Goharkhah, M. Effect of magnetic field on the hydrodynamic and heat transfer of magnetite ferrofluid flow in a porous fin heat sink. J. Magn. Magn. Mater. 2019, 476, 506–515. [Google Scholar] [CrossRef]
- Karimi, A.; Afghahi, S.S.S.; Shariatmadar, H.; Ashjaee, M. Experimental investigation on thermal conductivity of MFe2O4 (M = Fe and Co) magnetic nanofluids under influence of magnetic field. Thermochim. Acta 2014, 598, 59–67. [Google Scholar] [CrossRef]
- Qi, C.; Tang, J.; Fan, F.; Yan, Y. Effects of magnetic field on thermo-hydraulic behaviors of magnetic nanofluids in CPU cooling system. Appl. Therm. Eng. 2020, 179, 115717. [Google Scholar] [CrossRef]
- Mousavi, S.V.; Sheikholeslami, M.; Goriji Bandpy, M.; Gerdroodbary, M.B. The Influence of magnetic field on heat transfer of magnetic nanofluid in a sinusoidal double pipe heat exchanger. Chem. Eng. Res. Des. 2016, 113, 112–124. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y. Experimental study on enhanced heat transfer and flow performance of magnetic nanofluids under alternating magnetic field. Int. J. Therm. Sci. 2021, 164, 106897. [Google Scholar] [CrossRef]
- Sundar, L.S.; Naik, M.T.; Sharma, K.V.; Singh, M.K.; Reddy, T.C.S. Experimental investigation of forced convection heat transfer and friction factor in a tube with Fe3O4 magnetic nanofluid. Exp. Therm. Fluid Sci. 2012, 37, 65–71. [Google Scholar] [CrossRef]
- Yu, W.; Xie, H.; Chen, L.; Li, Y. Enhancement of thermal conductivity of kerosene-based Fe3O4 nanofluids prepared via phase-transfer method. Colloids Surf. A Physicochem. Eng. Asp. 2010, 355, 109–113. [Google Scholar] [CrossRef]
- Wen, D.; Ding, Y. Experimental investigation into convective heat transfer of nanofluids at the entrance region under laminar flow conditions. Int. J. Heat Mass Transf. 2004, 47, 5181–5188. [Google Scholar] [CrossRef]
- Goharkhah, M.; Ashjaee, M.; Shahabadi, M. Experimental investigation on convective heat transfer and hydrodynamic characteristics of magnetite nanofluid under the influence of an alternating magnetic field. Int. J. Therm. Sci. 2016, 99, 113–124. [Google Scholar] [CrossRef]
- Azizian, R.; Doroodchi, E.; McKrell, T.; Buongiorno, J.; Hu, L.W.; Moghtaderi, B. Effect of magnetic field on laminar convective heat transfer of magnetite nanofluids. Int. J. Heat Mass Transf. 2014, 68, 94–109. [Google Scholar] [CrossRef]
- Li, Q.; Xuan, Y. Experimental investigation on heat transfer characteristics of magnetic fluid flow around a fine wire under the influence of an external magnetic field. Exp. Therm. Fluid Sci. 2009, 33, 591–596. [Google Scholar] [CrossRef]
- Safaei, M.R.; Abdelghany Elkotb, M.; Alsharif, A.M.; Mansir, I.B.; Alamri, S.; Tirth, V.; Goodarzi, M. An innovative design of a high strength and low weight sudden micro expansion by considering a nanofluid: Electronic cooling application. Case Stud. Therm. Eng. 2021, 28, 101637. [Google Scholar] [CrossRef]
- Alrashed, A.A.A.A.; Akbari, O.A.; Heydari, A.; Toghraie, D.; Zarringhalam, M.; Shabani, G.A.S.; Seifi, A.R.; Goodarzi, M. The numerical modeling of water/FMWCNT nanofluid flow and heat transfer in a backward-facing contracting channel. Phys. B Condens. Matter 2018, 537, 176–183. [Google Scholar] [CrossRef]
- Togun, H.; Safaei, M.R.; Sadri, R.; Kazi, S.N.; Badarudin, A.; Hooman, K.; Sadeghinezhad, E. Numerical simulation of laminar to turbulent nanofluid flow and heat transfer over a backward-facing step. Appl. Math. Comput. 2014, 239, 153–170. [Google Scholar] [CrossRef]
- Safaei, M.R.; Togun, H.; Vafai, K.; Kazi, S.N.; Badarudin, A. Investigation of heat transfer enhancement in a forward-facing contracting channel using FMWCNT nanofluids. Numer. Heat Transf. Part A Appl. 2014, 66, 1321–1340. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Chattopadhyay, H.; Haldar, A. Design of twisted tape turbulator at different entrance angle for heat transfer enhancement in a solar heater. Beni-Suef Univ. J. Basic Appl. Sci. 2018, 7, 118–126. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Chattopadhyay, H.; Biswas, R.; Ewim, D.R.E.; Huan, Z. Influence of inlet turbulence intensity on transport phenomenon of modified diamond cylinder: A numerical study. Arab. J. Sci. Eng. 2020, 45, 1051–1058. [Google Scholar] [CrossRef]
- Jin, D.; Quan, S.; Zuo, J.; Xu, S. Numerical investigation of heat transfer enhancement in a solar air heater roughened by multiple V-shaped ribs. Renew. Energy 2019, 134, 78–88. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Abbas, A.K.; Sheriff, J.M. Influence of geometrical parameters and forced convective heat transfer in transversely corrugated circular tubes. Int. Commun. Heat Mass Transf. 2013, 44, 116–126. [Google Scholar] [CrossRef]
- Effatpanah, S.K.; Ahmadi, M.H.; Aungkulanon, P.; Maleki, A.; Sadeghzadeh, M.; Sharifpur, M.; Chen, L. Comparative analysis of five widely-used multi-criteria decision-making methods to evaluate clean energy technologies: A case study. Sustainability 2022, 14, 1403. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Kumar, R.; Assad, M.E.H.; Ngo, P.T.T. Applications of Machine Learning Methods in Modeling Various Types of Heat Pipes: A Review. J. Therm. Anal. Calorim. 2021, 146, 2333–2341. [Google Scholar] [CrossRef]
- Jagtap, H.P.; Bewoor, A.K.; Kumar, R.; Ahmadi, M.H.; El Haj Assad, M.; Sharifpur, M. RAM Analysis and availability optimization of thermal power plant water circulation system using PSO. Energy Rep. 2021, 7, 1133–1153. [Google Scholar] [CrossRef]
- Sabbagh, O.; Fanaei, M.A.; Arjomand, A.; Hossein Ahmadi, M. Multi-objective optimization assessment of a new integrated scheme for co-production of natural gas liquids and liquefied natural gas. Sustain. Energy Technol. Assess. 2021, 47, 101493. [Google Scholar] [CrossRef]
- Zolghadri, A.; Maddah, H.; Ahmadi, M.H.; Sharifpur, M. Predicting parameters of heat transfer in a shell and tube heat exchanger using aluminum oxide nanofluid with artificial neural network (Ann) and self-organizing map (Som). Sustainability 2021, 13, 8824. [Google Scholar] [CrossRef]
- Lohakare, P.; Bewoor, A.; Kumar, R.; Said, N.M.; Sharifpur, M. Benchmark using multi criteria decision making (MCDM) technique to optimally select piston material. Eng. Anal. Bound. Elem. 2022, 142, 52–60. [Google Scholar] [CrossRef]
- Kumar, R.; Nadda, R.; Kumar, S.; Razak, A.; Sharifpur, M.; Aybar, H.S.; Ahamed Saleel, C.; Afzal, A. Influence of artificial roughness parametric variation on thermal performance of solar thermal collector: An experimental study, response surface analysis and ANN modelling. Sustain. Energy Technol. Assess. 2022, 52, 102047. [Google Scholar] [CrossRef]
- Sharma, J.; Soni, S.; Paliwal, P.; Saboor, S.; Chaurasiya, P.K.; Sharifpur, M.; Khalilpoor, N.; Afzal, A. A novel long term solar photovoltaic power forecasting approach using LSTM with Nadam optimizer: A case study of India. Energy Sci. Eng. 2022, 10, 2909–2929. [Google Scholar] [CrossRef]
- Melaibari, A.A.; Khetib, Y.; Alanazi, A.K.; Sajadi, S.M.; Sharifpur, M.; Cheraghian, G. Applying artificial neural network and response surface method to forecast the rheological behavior of hybrid nano-antifreeze containing graphene oxide and copper oxide nanomaterials. Sustainability 2021, 13, 11505. [Google Scholar] [CrossRef]
- KAbu-Nab, A.; Selima, E.S.; Morad, A.M. Theoretical investigation of a single vapor bubble during Al2O3/H2O nanofluids in power-law fluid affected by a variable surface tension. Phys. Scr. 2021, 96, 035222. [Google Scholar] [CrossRef]
- Morad, A.M.; Selima, E.S.; Abu-Nab, A.K. Thermophysical bubble dynamics in N-dimensional Al2O3/H2O nanofluid between two-phase turbulent flow. Case Stud. Therm. Eng. 2021, 28, 101527. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Abraham, J.P.; Cheng, L.; Gorman, J. Introductory chapter: A brief history of and introduction to computational fluid dynamics. In Computational Fluid Dynamics; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Ashjaee, M.; Goharkhah, M.; Khadem, L.A.; Ahmadi, R. Effect of magnetic field on the forced convection heat transfer and pressure drop of a magnetic nanofluid in a miniature heat sink. Heat Mass Transf. 2015, 51, 953–964. [Google Scholar] [CrossRef]



















| Property | Value |
|---|---|
| Diameter | 20 nm |
| Density | |
| Thermal Conductivity | 7 W/m·K |
| Specific Heat | 640 J/Kg·K |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souayeh, B.; Bhattacharyya, S.; Hdhiri, N.; Hammami, F.; Yasin, E.; Raju, S.S.K.; Alam, M.W.; Alsheddi, T.; Al Nuwairan, M. Effect of Magnetic Baffles and Magnetic Nanofluid on Thermo-Hydraulic Characteristics of Dimple Mini Channel for Thermal Energy Applications. Sustainability 2022, 14, 10419. https://doi.org/10.3390/su141610419
Souayeh B, Bhattacharyya S, Hdhiri N, Hammami F, Yasin E, Raju SSK, Alam MW, Alsheddi T, Al Nuwairan M. Effect of Magnetic Baffles and Magnetic Nanofluid on Thermo-Hydraulic Characteristics of Dimple Mini Channel for Thermal Energy Applications. Sustainability. 2022; 14(16):10419. https://doi.org/10.3390/su141610419
Chicago/Turabian StyleSouayeh, Basma, Suvanjan Bhattacharyya, Najib Hdhiri, Fayçal Hammami, Essam Yasin, S. Suresh Kumar Raju, Mir Waqas Alam, Tarfa Alsheddi, and Muneerah Al Nuwairan. 2022. "Effect of Magnetic Baffles and Magnetic Nanofluid on Thermo-Hydraulic Characteristics of Dimple Mini Channel for Thermal Energy Applications" Sustainability 14, no. 16: 10419. https://doi.org/10.3390/su141610419







