Distributed Optimization of Joint Seaport-All-Electric-Ships System under Polymorphic Network
Abstract
:1. Introduction
- (1)
- Considering AESs’ as prosumer, and taking the carbon trading mechanism into account, a joint seaport-AESs power system model is established. The precise mathematical model of power dispatching is established and resolved through fully distributed algorithms.
- (2)
- This paper validates a distributed algorithm based on parameter projection that evades KKT conditions or the Lagrange multiplier operator to slash the difficulty of calculation due to a reduction in variables’ dimensions and applies it to a proposed joint seaport–AES system where AESs’ roles shift to become prosumers.
2. Problem Formulation
2.1. Polymorphic Joint Seaport-AESs System
2.2. Objective Function
- The carbon-trading cost of DG k in MG i:which is adopted in ref. [21] to simplify the analysis, and where is total carbon emission of DG k in MG i, indicates corresponding rated carbon emission share, defined as follow: , where presents the carbon emission intensity.Carbon-trading cost is regarded as an indicator of the expenditure or benefits of the system’s total carbon emissions in the carbon market. Namely, when the system’s carbon emissions quota are greater than its allocations, the excess carbon emissions need to be offset by means of purchasing additional quota; when the system carbon emission is less, the surplus can be sold to the carbon market.
- The cost of MG i for buying power from the neighbor MG j:where is actual power flow from microgrid j to i, and the electricity price of MG i at t time is presented as $/kWh.
- The revenue of MG i for selling power to the neighbor MG j:where is actual power flow to MG j from MG i with $/kWh electricity price of MG i at tth time span.
2.3. Constraints
- Power balance constraint of the integrated seaportAESs’ multiMG system:For each MG (like the seaport or an AES), the power balance constraint will be decomposed as follows:
- Power and ramp rate limit constraints of DG k in MG i:
- Energy constraints of battery energy storage system (BESS) in MG i (the definition of SOC, the definition of BESS capacity, capacity limit constraint, SOC limit constraint and power limit constraint, in order):
- Constraint of power transaction between grids i and j:
3. Distributed Optimization Solution Methodology
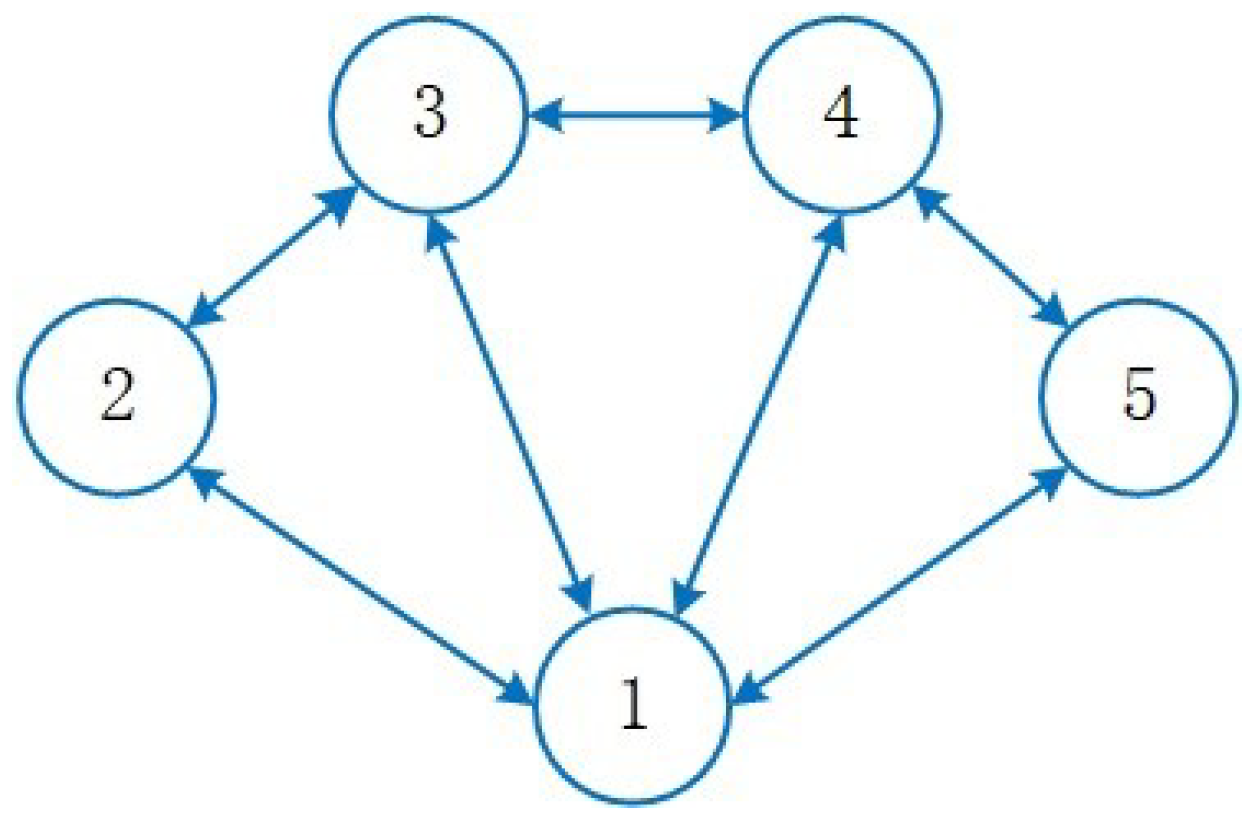
3.1. Graph Theory
3.2. Parameter Projection
3.3. Parameter Projection Distributed Optimization (PPDO)
4. Numerical Results
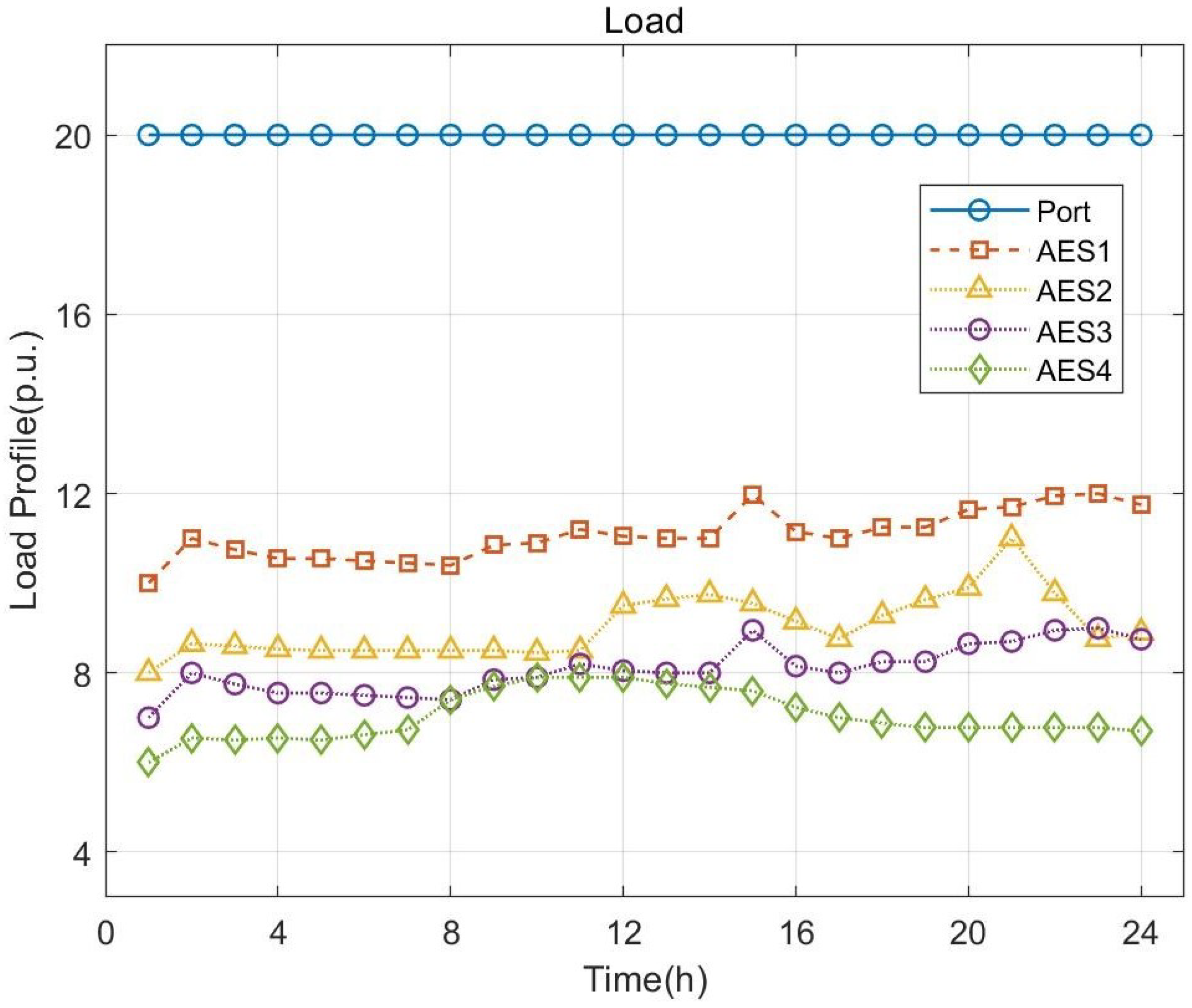
4.1. Text System
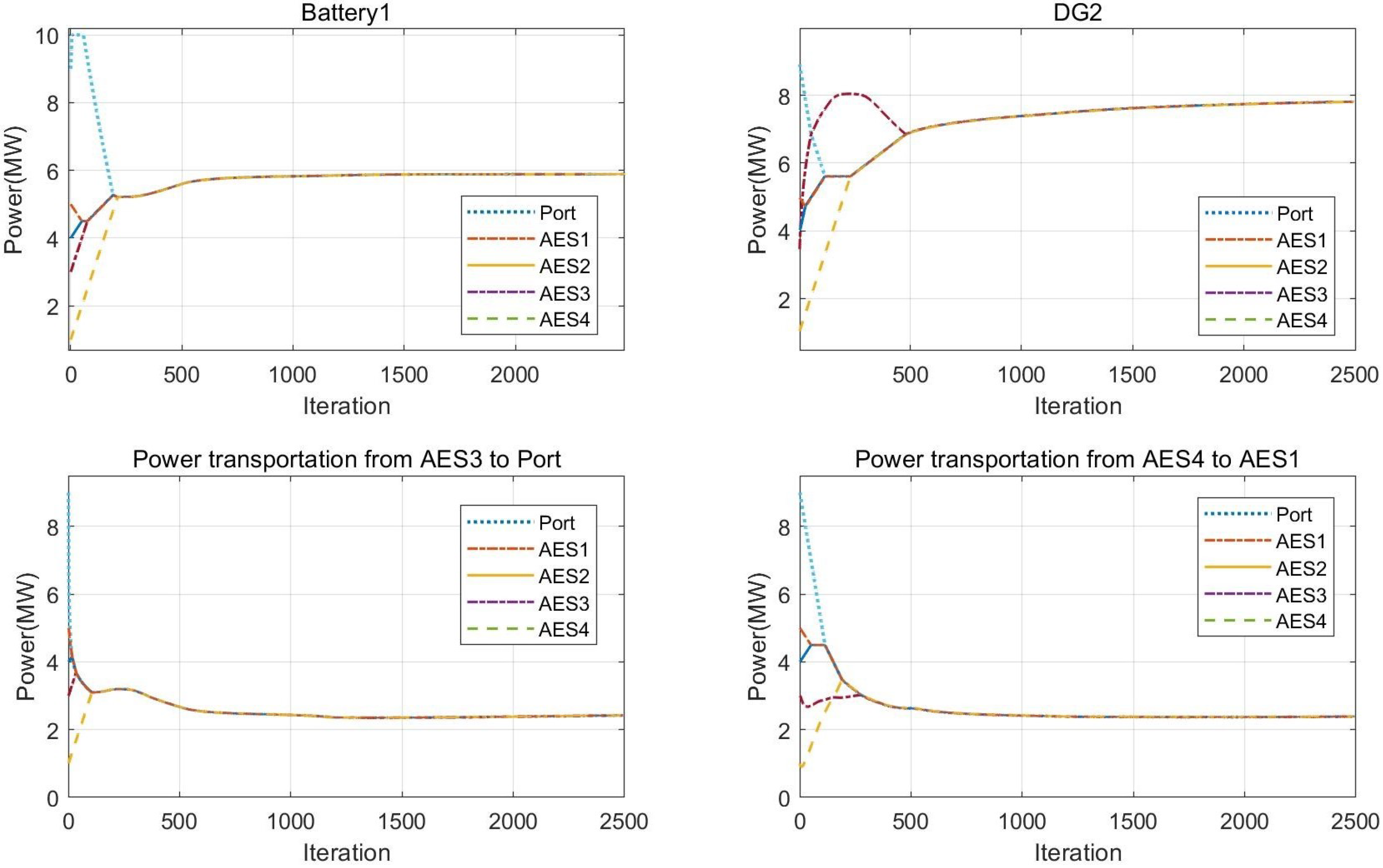
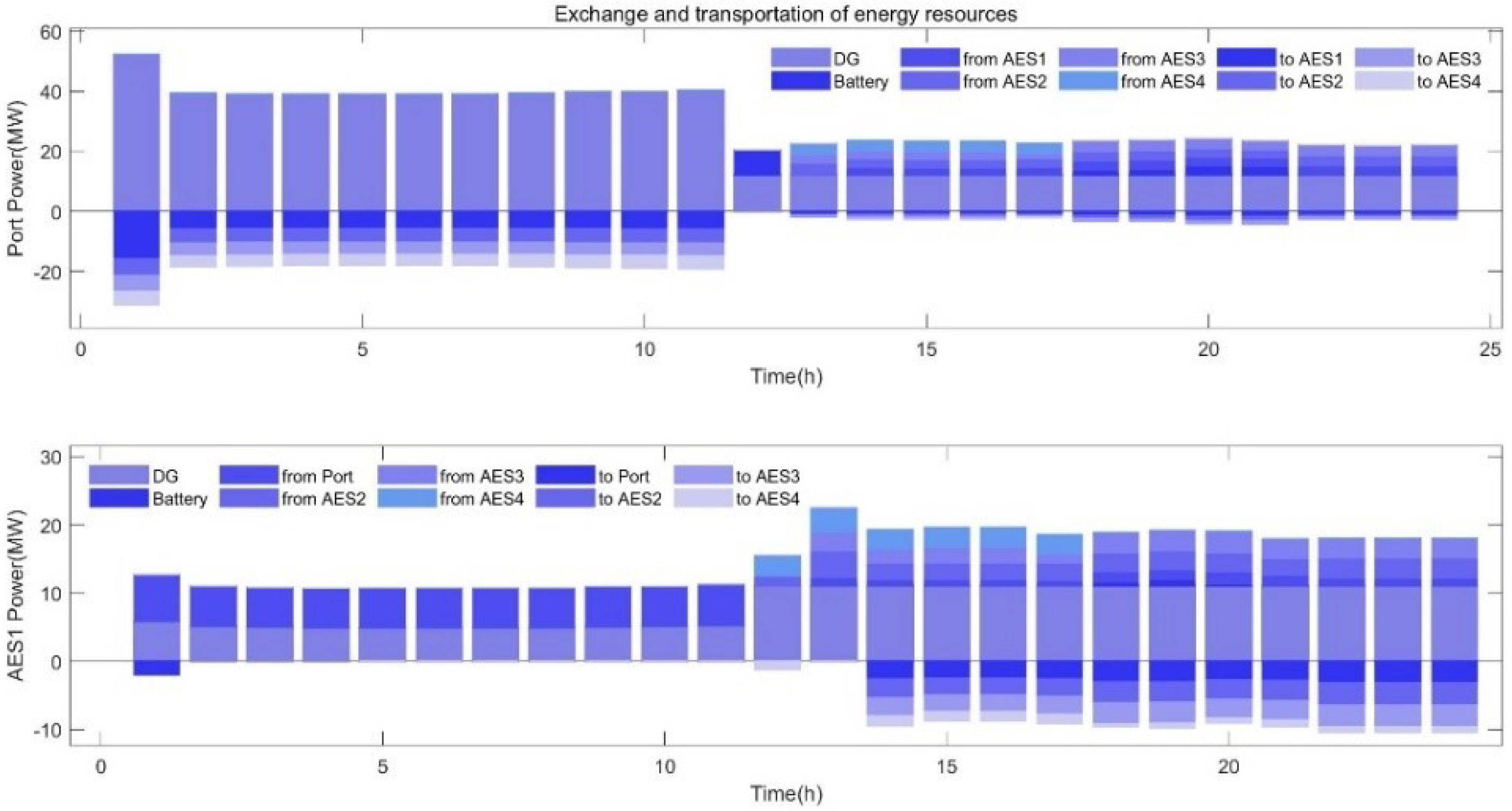
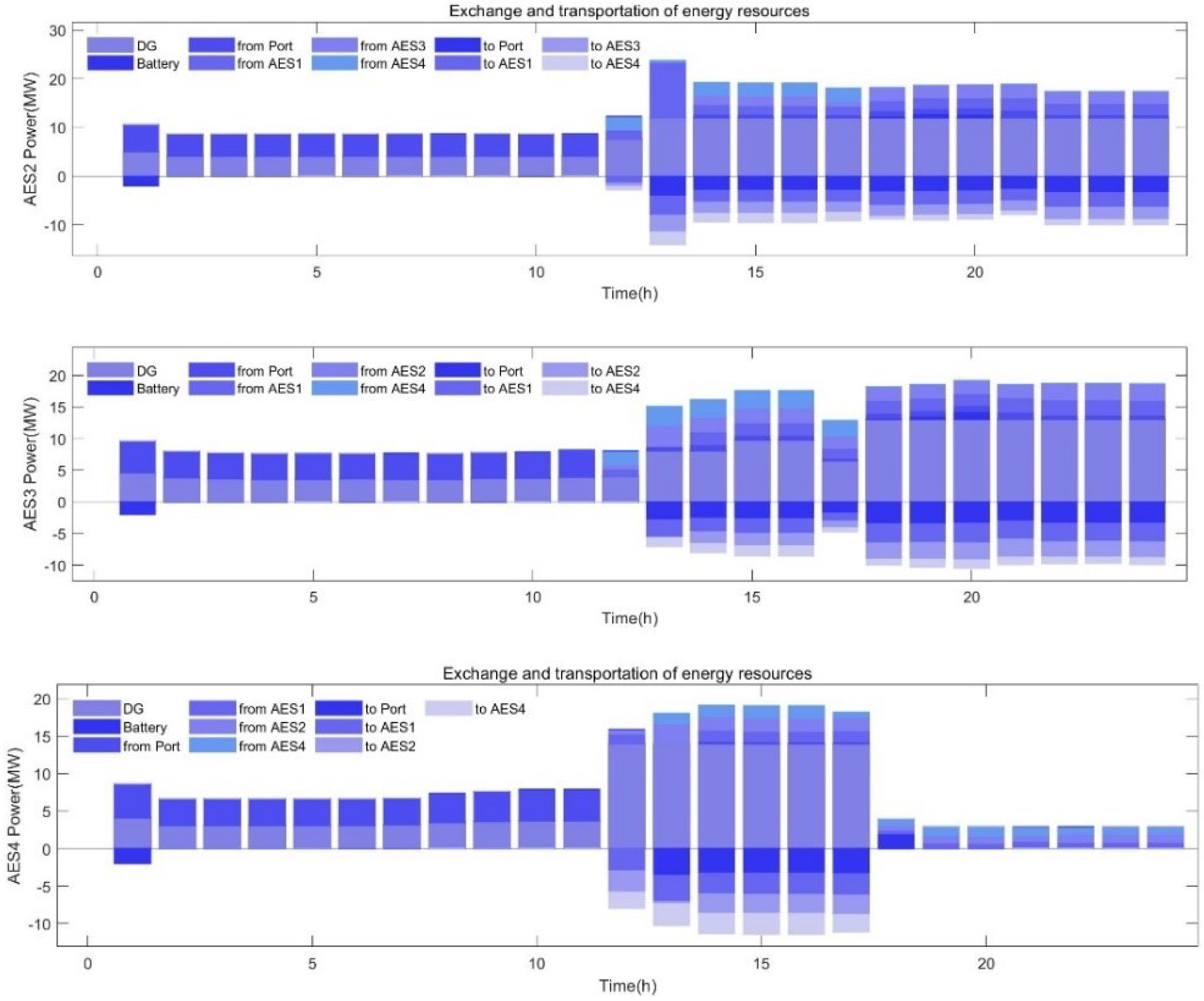
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fourth Greenhouse Gas Study 2020. Available online: https://www.imo.org/en/OurWork/Environment/Pages/Fourth-IMO-Greenhouse-Gas-Study-2020.aspx (accessed on 9 July 2022).
- Gennitsaris, S.G.; Kanellos, F.D. Emission-Aware and Cost-Effective Distributed Demand Response System for Extensively Electrified Large Ports. IEEE Trans. Power Syst. 2020, 34, 4341–4351. [Google Scholar] [CrossRef]
- Kanellos, F.D.; Volanis, E.M.; Hatziargyriou, N.D. Power Management Method for Large Ports with Multi-Agent Systems. IEEE Trans. Veh. Technol. 2019, 10, 1259–1268. [Google Scholar] [CrossRef]
- Iris, Ç.; Siu, J.; Lam, L. Optimal energy management and operations planning in seaports with smart grid while harnessing renewable energy under uncertainty. Omega Int. J. Manag. Sci. 2021, 103, 102445. [Google Scholar] [CrossRef]
- Fang, S.; Xu, Y.; Li, Z.; Zhao, T.; Wang, H. Two-Step Multi-Objective Management of Hybrid Energy Storage System in All-Electric Ship Microgrids. IEEE Trans. Veh. Technol. 2019, 68, 3361–3373. [Google Scholar] [CrossRef]
- Huang, B.; Li, Y.; Zhan, F.; Sun, Q.; Zhang, H. A Distributed Robust Economic Dispatch Strategy for Integrated Energy System Considering Cyber-Attacks. IEEE Trans. Ind. Inform. 2022, 18, 880–890. [Google Scholar] [CrossRef]
- Li, Y.; Gao, D.W.; Gao, W.; Zhang, H.; Zhou, J. Double-Mode Energy Management for Multi-Energy System via Distributed Dynamic Event-Triggered Newton-Raphson Algorithm. IEEE Trans. Smart Grid 2020, 11, 5339–5356. [Google Scholar] [CrossRef]
- Li, Y.; Gao, W.; Huang, S.; Wang, R.; Yan, W.H.; Gevorgian, V.; Gao, W.D. Data-driven Optimal Control Strategy for Virtual Synchronous Generator via Deep Reinforcement Learning Approach. J. Mod. Power Syst. Clean Energy 2021, 9, 919–929. [Google Scholar] [CrossRef]
- Li, X.; Xie, L.; Hong, Y. Distributed Continuous-Time Nonsmooth Convex Optimization With Coupled Inequality Constraints. IEEE Trans. Control Netw. Syst. 2020, 7, 74–84. [Google Scholar] [CrossRef]
- Notarnicola, I.; Notarstefano, G. Constraint-Coupled Distributed Optimization: A Relaxation and Duality Approach. IEEE Trans. Control. Netw. Syst. 2020, 7, 483–492. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, P.; Cortés, J. Network Optimization via Smooth Exact Penalty Functions Enabled by Distributed Gradient Computation. IIEEE Trans. Control Netw. Syst. 2021, 8, 1430–1441. [Google Scholar] [CrossRef]
- Ma, L.; Bian, W. A Novel Multiagent Neurodynamic Approach to Constrained Distributed Convex Optimization. IEEE Trans. Cybern. 2021, 51, 1322–1333. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Huang, K. Innovate the network development paradigm and build a polymorphic networks environment —“Key Technologies of Polymorphic Network Environment”. J. Commum. 2022, 4, 1–2. [Google Scholar]
- Wu, J.; Hu, X. The development paradigm of separation between network technical system and supporting environment. Inf. Commun. Technol. Policies 2021, 8, 1–11. [Google Scholar]
- Zhang, R.; Xiao, G.; Shan, Q.; Zhou, T.; Li, D.; Teng, F. Communication topology reconstruction method for multi-agent cooperative control in polymorphic networks. J. Commum. 2022, 4, 50–59. [Google Scholar]
- Yang, T.; George, J.; Qin, J.; Yi, X.; Wu, J. Distributed least squares solver for network linear equations. Automatica 2020, 113, 108798. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Yu, J.; Deng, X.; Wan, S. FedCPF: An Efficient-Communication Federated Learning Approach for Vehicular Edge Computing in 6G Communication Networks. IEEE Trans. Intell. Transp. 2022, 23, 1616–1629. [Google Scholar] [CrossRef]
- Fang, S.; Wang, Y.; Gou, B.; Xu, Y. Event-Triggered Control of Nonlinear Discrete-Time System with Unknown Dynamics Based on HDP. IEEE Trans. Cybern. 2022, 52, 6046–6058. [Google Scholar]
- Tian, F.; Yu, W.; Fu, J.; Gu, W.; Gu, J. Distributed Optimization of Multiagent Systems Subject to Inequality Constraints. IEEE Trans. Cybern. 2021, 51, 2232–2241. [Google Scholar] [CrossRef]
- Nutkani, I.U.; Loh, P.C.; Wang, P.; Blaabjerg, F. Decentralized Economic Dispatch Scheme with Online Power Reserve for Microgrids. IEEE Trans. Smart Grid 2017, 8, 139–148. [Google Scholar] [CrossRef]
- Chen, H.; Chen, J.; Zhang, Z.; Wang, C.; Wang, J.; Han, H.; Lv, J. Low-carbon economic dispatching of power system considering capture energy consumption of carbon capture power plants with flexible operation mode. Electr. Power Autom. Equip. 2021, 9, 133–139. [Google Scholar]
- Huang, B.; Li, Y.; Zhang, H.; Sun, Q. Distributed optimal co-multi-microgrids energy management for energy internet. IEEE/CAA JAS 2016, 3, 357–364. [Google Scholar]


| Position | |||||
|---|---|---|---|---|---|
| Seaport | 0.5 | 0 | 0 | 0 | 50/12 |
| AES1 | 0.5 | 2 | 2 | 0 | 11 |
| AES2 | 0.5 | 1 | 0.5 | 0 | 12 |
| AES3 | 0.5 | 1 | 0.5 | 0 | 13 |
| AES4 | 0.5 | 3 | 4.5 | 0 | 14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, W.; Shan, Q.; Xiao, G.; Tu, Y.; Liang, Y. Distributed Optimization of Joint Seaport-All-Electric-Ships System under Polymorphic Network. Sustainability 2022, 14, 9914. https://doi.org/10.3390/su14169914
Xia W, Shan Q, Xiao G, Tu Y, Liang Y. Distributed Optimization of Joint Seaport-All-Electric-Ships System under Polymorphic Network. Sustainability. 2022; 14(16):9914. https://doi.org/10.3390/su14169914
Chicago/Turabian StyleXia, Wenjia, Qihe Shan, Geyang Xiao, Yonggang Tu, and Yuan Liang. 2022. "Distributed Optimization of Joint Seaport-All-Electric-Ships System under Polymorphic Network" Sustainability 14, no. 16: 9914. https://doi.org/10.3390/su14169914
APA StyleXia, W., Shan, Q., Xiao, G., Tu, Y., & Liang, Y. (2022). Distributed Optimization of Joint Seaport-All-Electric-Ships System under Polymorphic Network. Sustainability, 14(16), 9914. https://doi.org/10.3390/su14169914






