Experimental Investigation on Bending Behavior of Innovative Poplar LVL Floor Diaphragms
Abstract
:1. Introduction
2. Methods
2.1. Specimen Design
2.2. Test Setup
2.3. Loading Scheme
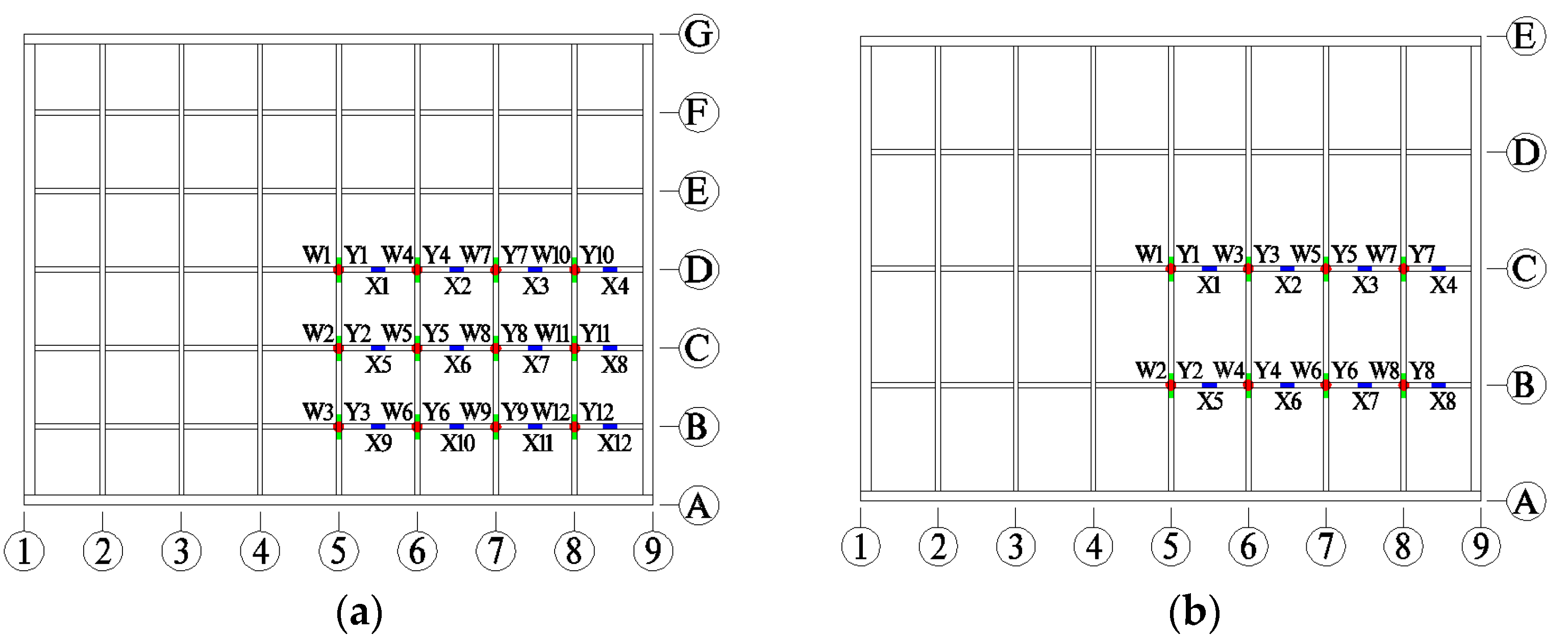
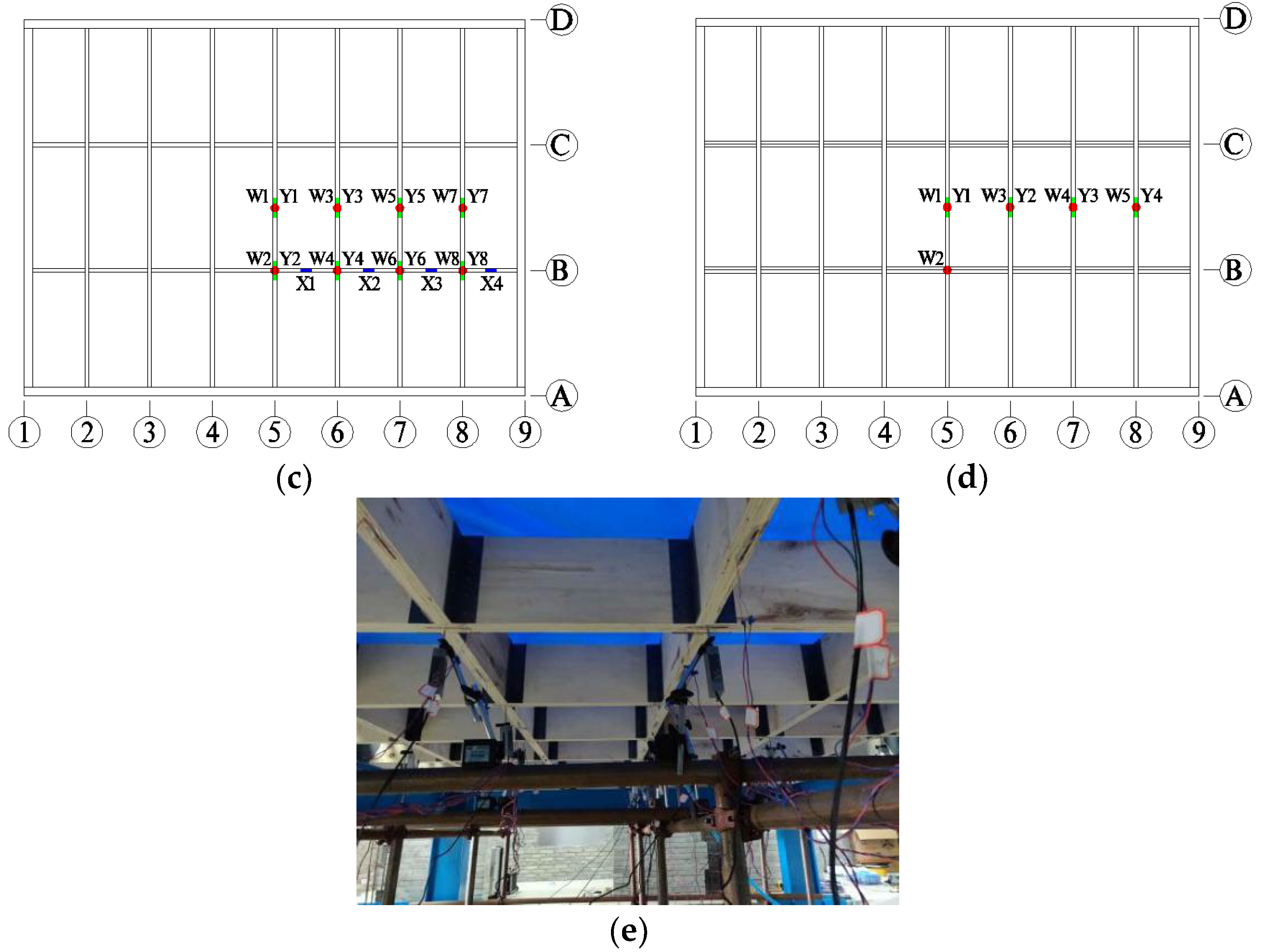
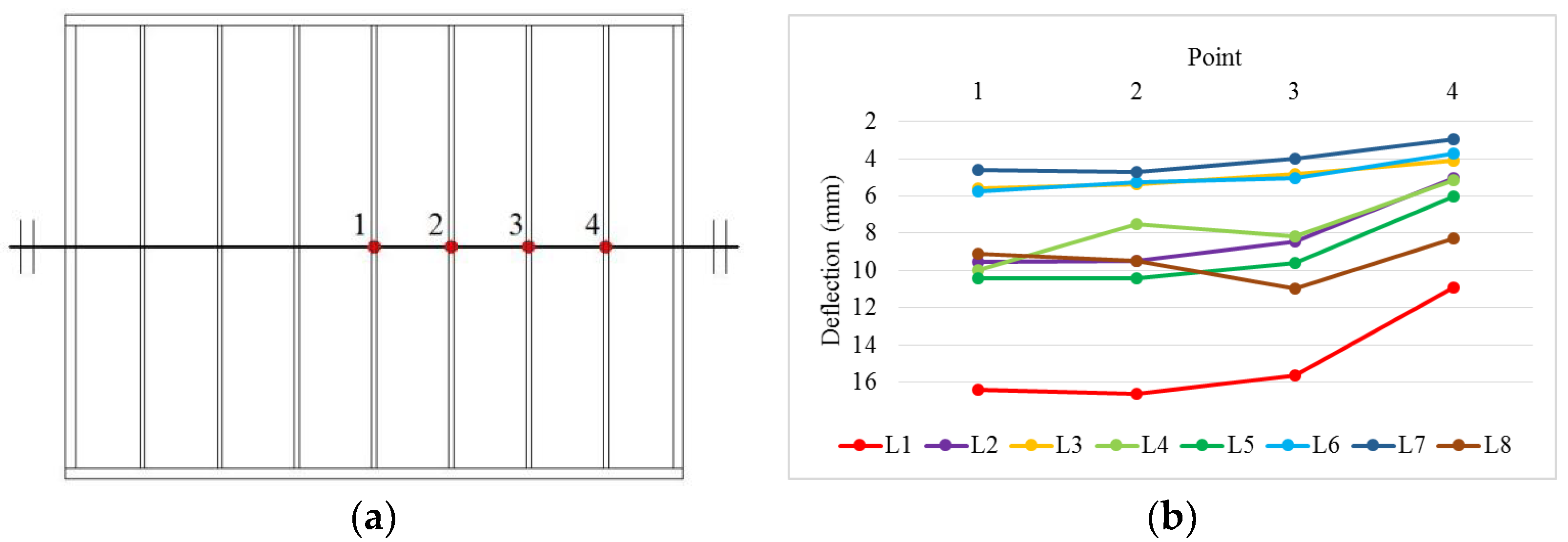
2.4. Measurement Points
3. Test Results
3.1. Testing Phenomena under the Maximum Loading Level
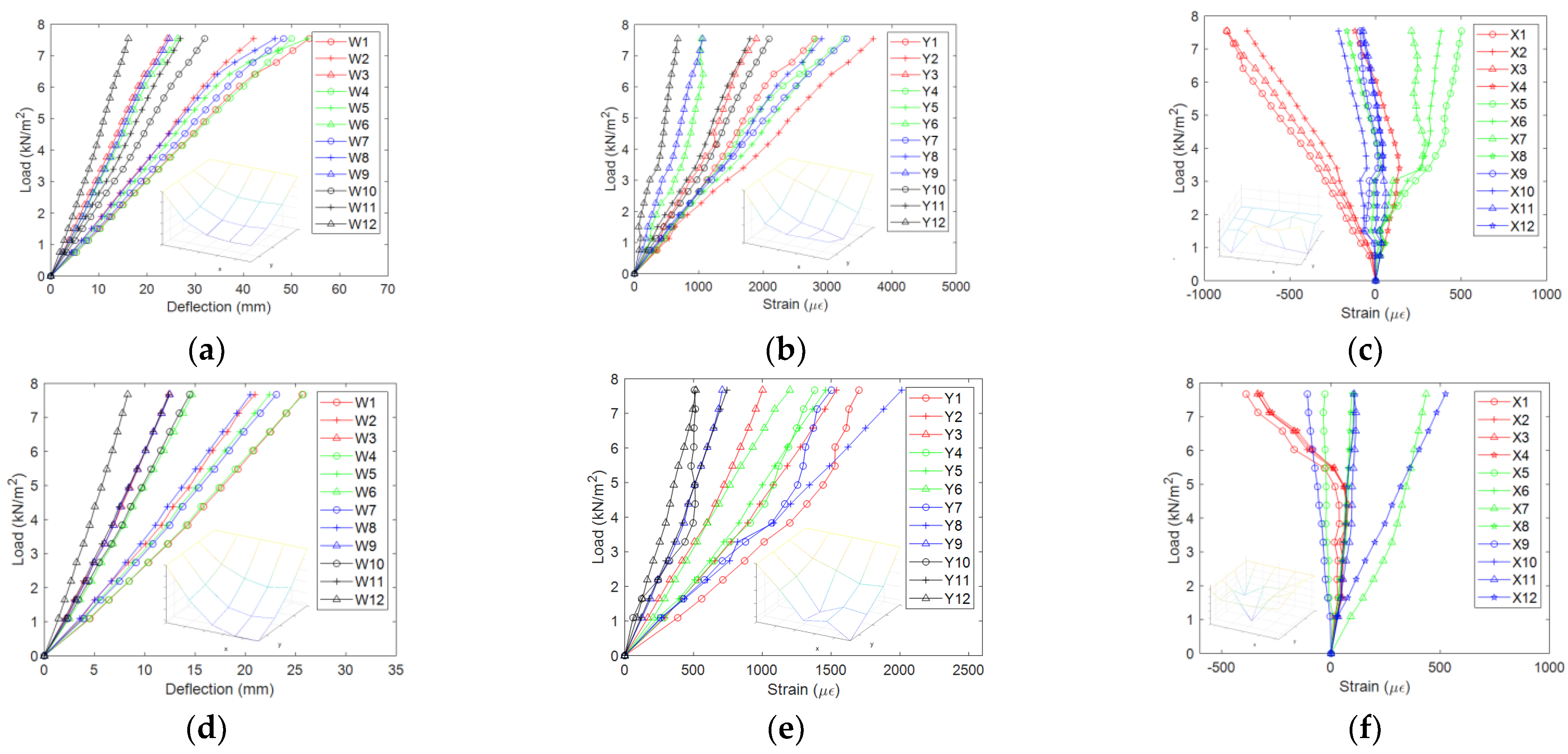
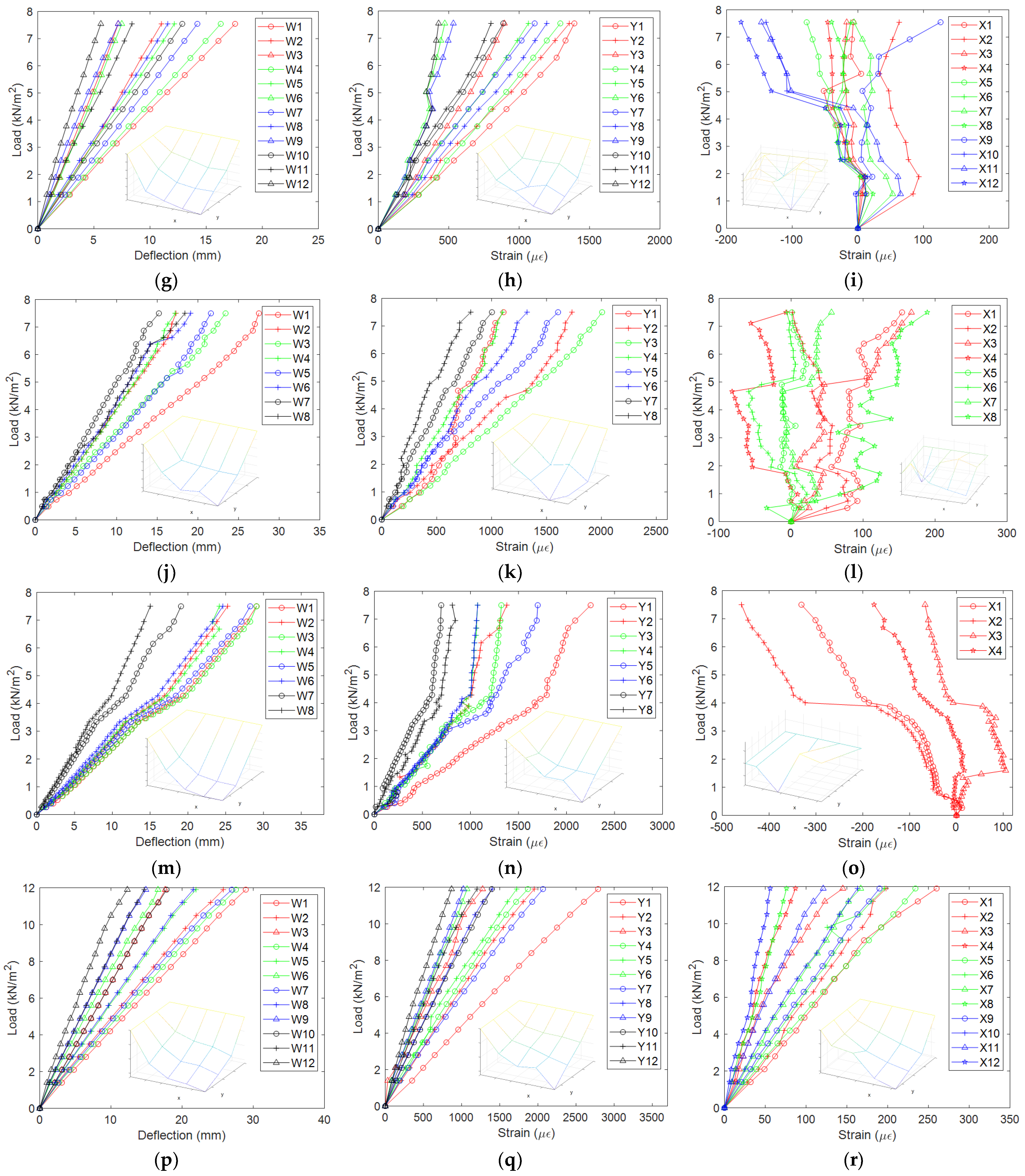
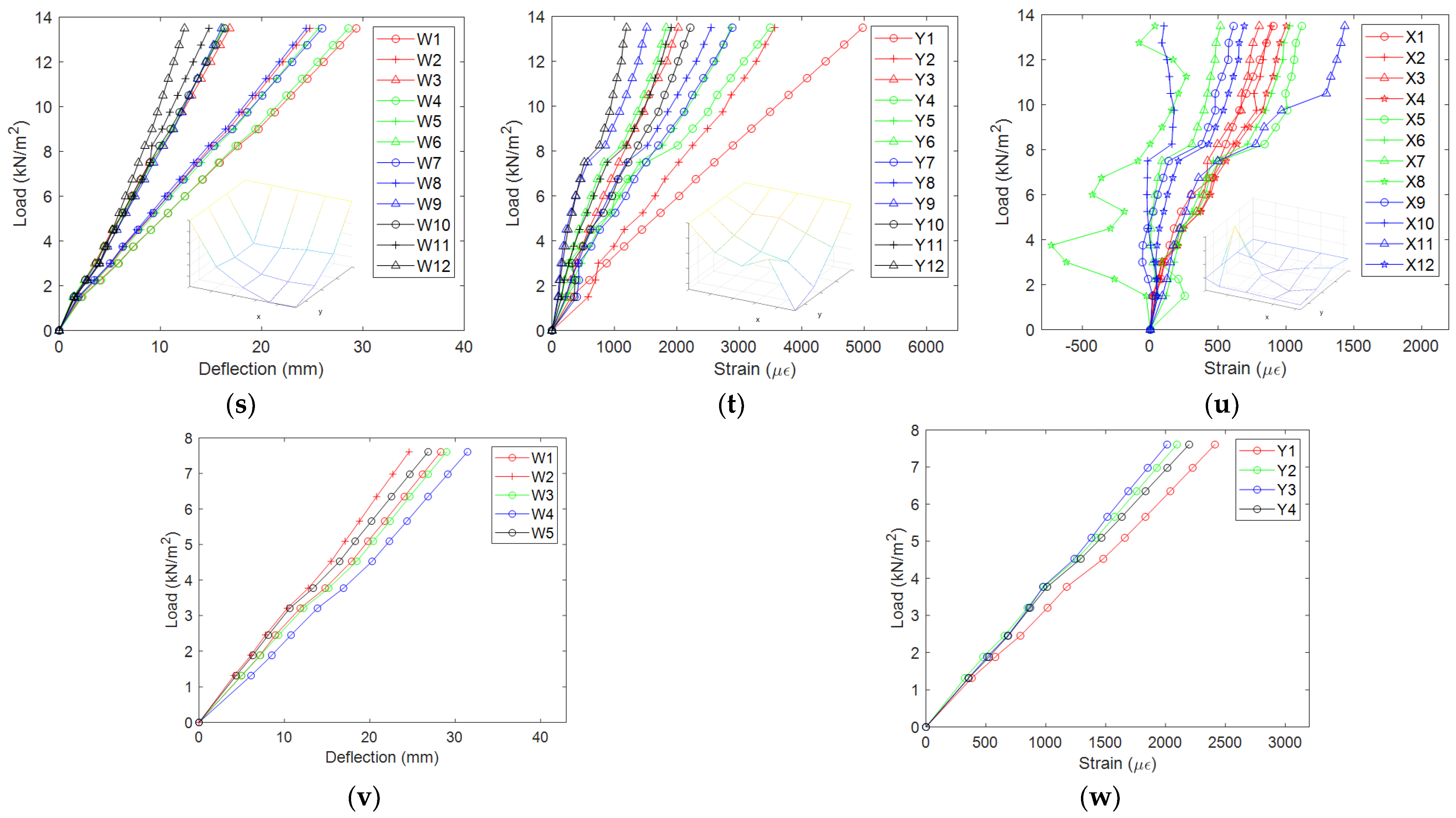
3.2. Load-Deflection and Load-Strain Curves
- Under the service load of 2.5 kN/m2, the distribution of deflection and y-direction strain for the measuring points of 1/4 specimen is much more regular than that of x-direction strain (except for specimen L6), which generally demonstrates the typical shape of a “bowl” for the two-way slab under the action of transverse load. So for this type of floor diaphragm, the stress state of the segmented rib beam is much more complex than that of the full-length rib beam, which can also be reflected by the trend of the curves. Yet, for specimen L6 with only the top panel, due to a stronger integration for the top flange than for the bottom flange of the rib beam, the distribution of x-direction strain (Figure 8r) becomes much more regular.
- Compared with the load-strain curves, the load-deflection curves are generally more “smooth”. This illustrates that for the wood floor, the load-strain curve can reflect some of the local damage phenomena, such as the separation between the beams and the panels, the pulling out of the tapping screw, etc., while some of the local damage doesn’t influence the global trend of the load-deflection curve.
- The load-deflection curves for specimens L1~L4 & L6~L8 are linear before the maximum preset loading level, except that the curves for specimens L1 & L6 emerge unremarkable inflection point at the loading level of 6.5 kN/m2 (Figure 8a) and 10.5 kN/m2 (Figure 8p) respectively, which reflects a slight decrease of the stiffness. The load-deflection curves for L5 show a remarkable decline stage between the loading levels of 3.3 kN/m2 and 4.3 kN/m2 (Figure 8m), then the slope recovers like before. Combined with the load-strain curve (Figure 8n,o), a credible explanation for this phenomenon is that the slope decline is due to the separation between the top edges of the full-length inner beam and the edge beam. In contrast, the slope recovery is due to the restraint for the beams’ lower edge by the segmented rib beam and the edge beam (the slope of the y-direction load-strain curve declines, and the x-direction strain becomes negative); therefore, something such as stiffness hardening happens.
4. General Discussion
4.1. Two-Way Slab Effect of the Floor Diaphragm
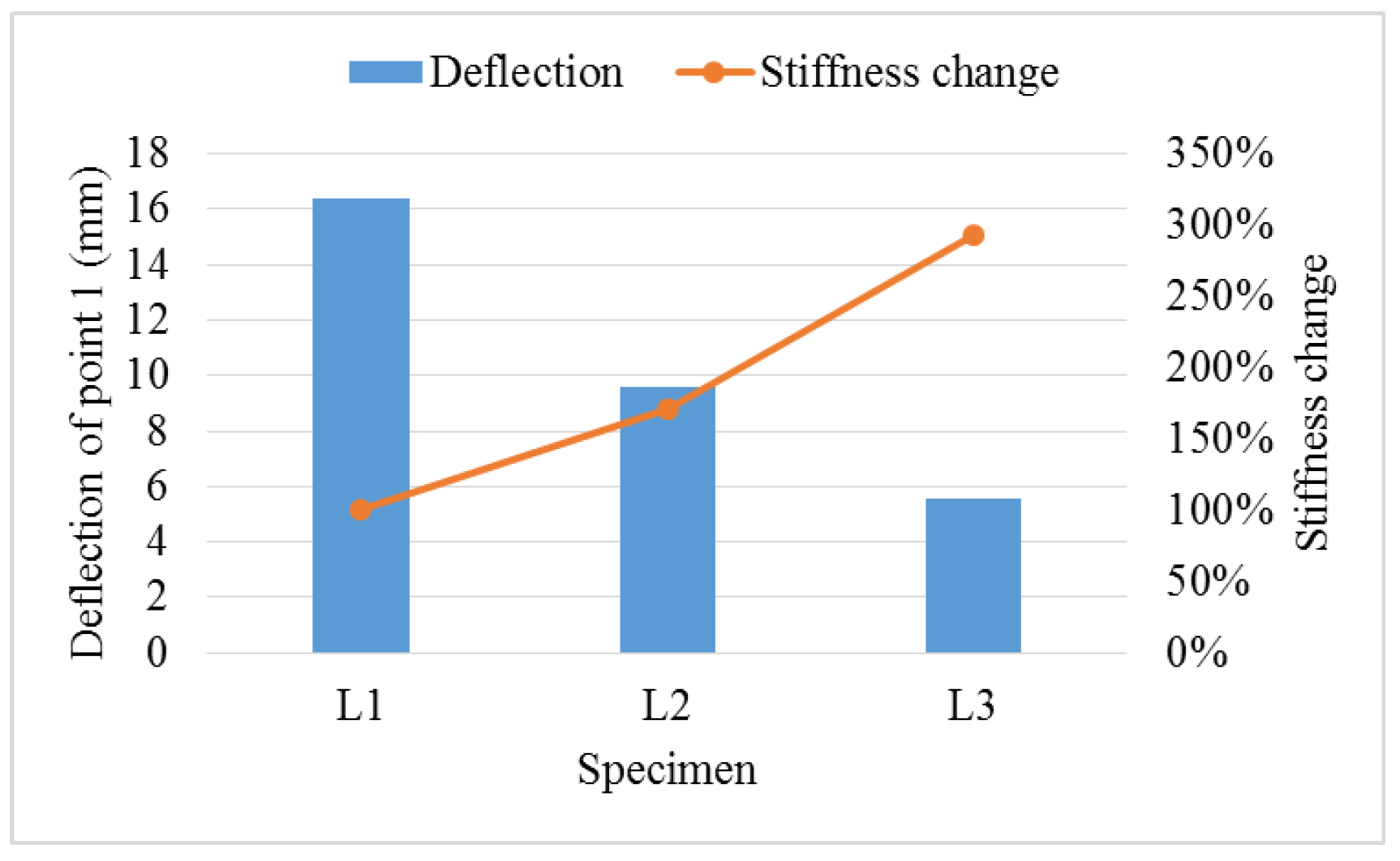
4.2. The Role of Beam Height in Floor Stiffness
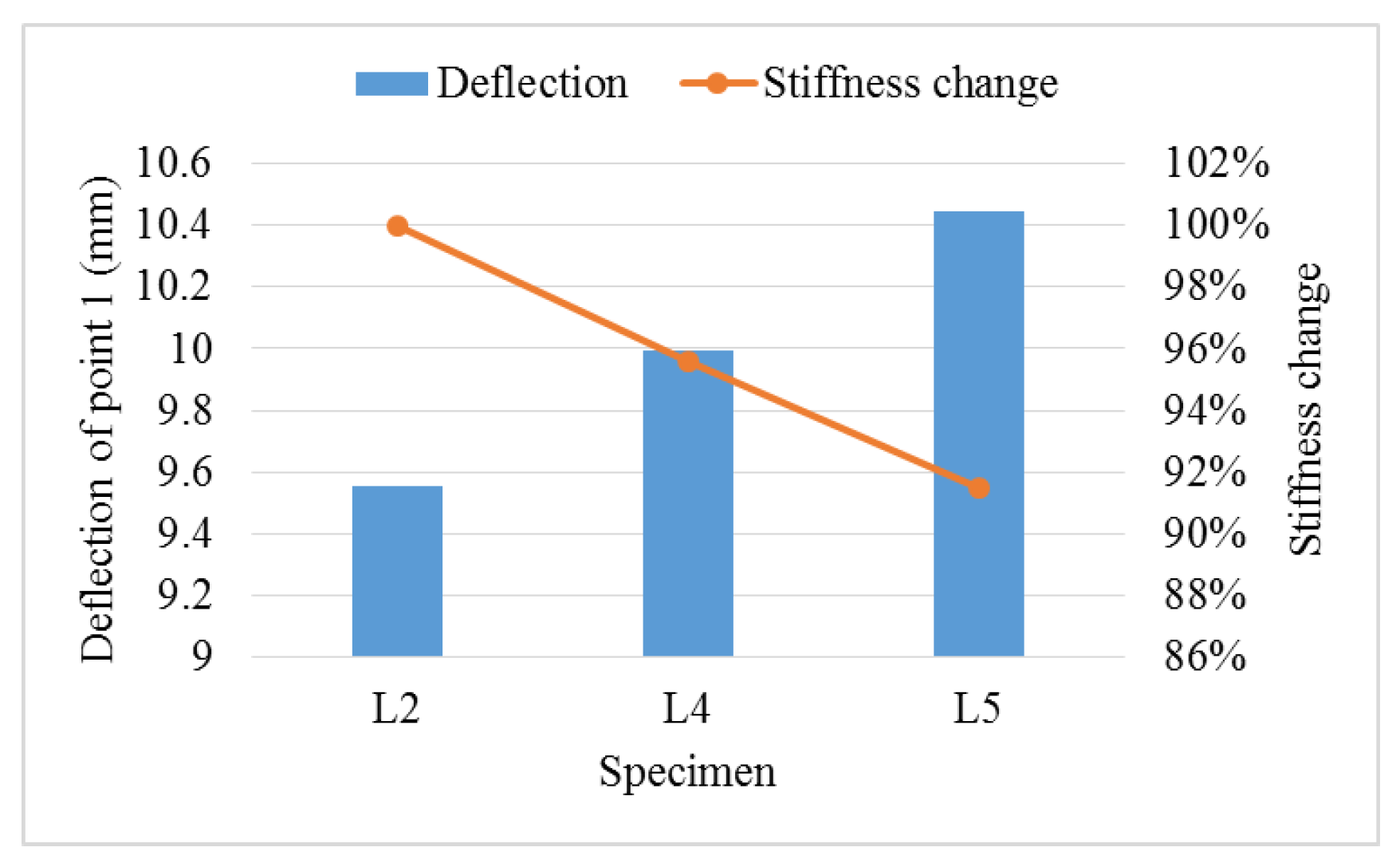
4.3. The Role of Segmented Rib Beam Spacing in Floor Stiffness
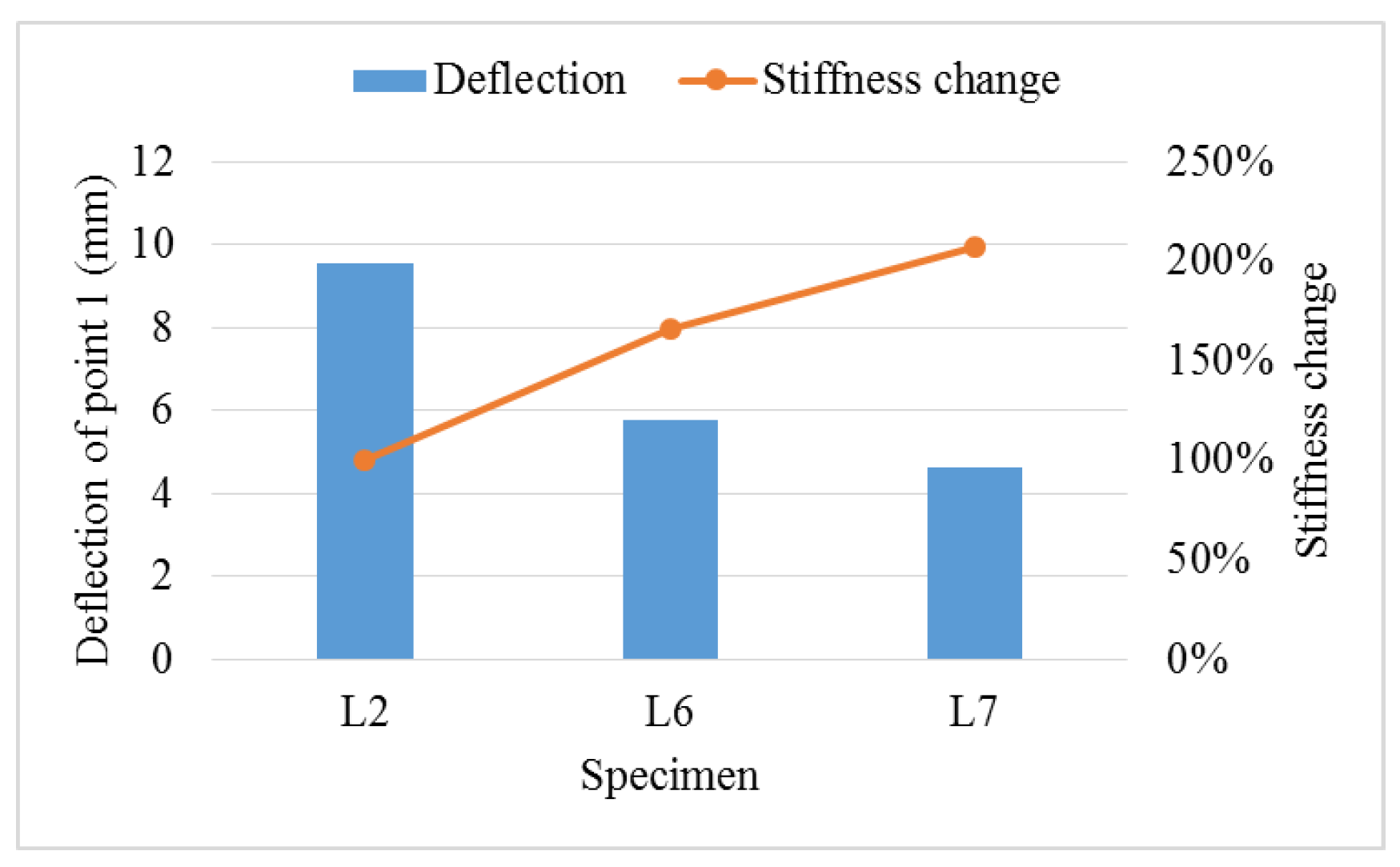
4.4. The Role of Top and Bottom Panels in Floor Stiffness
5. Theoretical Evaluation and Analysis
6. Conclusions
- (1)
- Under the service loading level of 2.5 kN/m2, there was no overall damage to any specimen. Under the preset maximum loading level, which is much greater than the service load, the local damage phenomena are mainly exhibited as a separation between the rib beams, pulling out from the rib beam for the tapping screw, and separation between the top panels and between the bottom panels. This means that for this kind of novel floor, evident phenomena before collapse can ensure the resident’s safety.
- (2)
- Despite some local damage, the global load-deflection curves for the specimens keep linear on the whole before the maximum preset loading level. Under a service load, the distribution of deflection and strain of the full-length rib beam substantially present the characteristic of a two-way slab, while the distribution of strain along the segmented rib beam is much more complex.
- (3)
- As to the transverse stiffness of the novel floor, taking specimen L2 as the reference shows that when the beam height changes from 235 mm to 285 mm, the bending stiffness increases by 71%; when the segmented rib beam spacing changes from 600 mm to 1200 mm, the bending stiffness decreases by 8.5%; and when the top panel is sheathed, the bending stiffness increases by 65.8%. So here, we can conclude that the rib beam height has the most important impact, followed by the top panel, while the role of spacing between the segmented rib beams is not particularly remarkable.
- (4)
- Considering the relatively poor integration of the wood construction, a revised pseudo-plate method based on the rigidity factor is proposed to evaluate the maximum deflection of the novel floor. Compared with the experimental values, the revised method reduces the mean error from 44% to 5%, which results meet well with the testing values.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Hematabadi, H.; Madhoushi, M.; Khazaeyan, A.; Ebrahimi, G.; Hindman, D.; Loferski, J. Bending and shear properties of cross-laminated timber panels made of poplar (Populus alba). Constr. Build. Mater. 2020, 265, 120326. [Google Scholar] [CrossRef]
- Countryman, D. Lateral Tests on Plywood Sheathed Diaphragms. In Laboratory Report, No. 55; Douglas-fir Plywood Association: Tacoma, WA, USA, 1952. [Google Scholar]
- Countryman, D.; Colbenson, P. Horizontal Plywood Diaphragm Tests; Laboratory Report, No. 63; Douglas-fir Plywood Association: Tacoma, WA, USA, 1954. [Google Scholar]
- Tissell, J.R. Horizontal Plywood Diaphragm Tests; Laboratory Report, No. 106; American Plywood Association: Tacoma, WA, USA, 1966. [Google Scholar]
- Corda, D.N. The In-Plane Shear Response of Timber Diaphragms. Master’s Thesis, West Virginia University, Morgantown, WV, USA, 1982. [Google Scholar]
- Zagajeski, S.W.; Halvorsen, G.T.; GangaRao, H.V.S.; Luttrell, L.D.; Jewell, R.B. Theoretical and Experimental Studies on Timber Diaphragms Subject to Earthquake Load; Laboratory Report NSF/CEE-84081; West Virginia University: Morgantown, WV, USA, 1984. [Google Scholar]
- Filiatrault, A.; Fischer, D.; Folz, B.; Uang, C.-M. Experimental parametric study on the in-plane stiffness of wood diaphragms. Can. J. Civ. Eng. 2002, 29, 554–566. [Google Scholar] [CrossRef]
- Xiong, H.B.; Kang, J.H.; Lv, X.L. Bending tests investigation on composite timber beam. J. Tongji Univ. Nat. Sci. 2012, 40, 522–528. [Google Scholar] [CrossRef]
- Awaludin, A.; Firmanti, A.; Muslikh; Theodarmo, H.; Astuti, D. Wood Frame Floor Model of LVL Paraserianthes falcataria. Procedia Eng. 2017, 171, 113–1200. [Google Scholar] [CrossRef]
- Rahman, W.M.N.W.A.; Yunus, N.Y.M.; Khaidzir, M.O.M.; Sani, M.S.H.M. Bending Behaviour of Different Types of Timber I-Joist. KSCE J. Civ. Eng. 2022, 26, 2202–2211. [Google Scholar] [CrossRef]
- Wang, B. Structural Behavior of Two-Way Wood Truss Floors. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2012. (In Chinese). [Google Scholar]
- Yeoh, D.; Fragiacomo, M.; Deam, B. Experimental behaviour of LVL–concrete composite floor beams at strength limit state. Eng. Struct. 2011, 33, 2697–2707. [Google Scholar] [CrossRef]
- Khorsandnia, N.; Valipour, H.R.; Crews, K. Experimental and analytical investigation of short-term behaviour of LVL–concrete composite connections and beams. Constr. Build. Mater. 2012, 37, 229–238. [Google Scholar] [CrossRef]
- Crocetti, R.; Sartori, T.; Tomasi, R. Innovative Timber-Concrete Composite Structures with Prefabricated FRC Slabs. J. Struct. Eng. 2015, 141, 04014224. [Google Scholar] [CrossRef]
- Shi, B.; Zhu, W.; Yang, H.; Liu, W.; Tao, H.; Ling, Z. Experimental and theoretical investigation of prefabricated timber-concrete composite beams with and without prestress. Eng. Struct. 2019, 204, 109901. [Google Scholar] [CrossRef]
- Loss, C.; Piazza, M.; Zandonini, R. Connections for steel–timber hybrid prefabricated buildings. Part I: Experimental tests. Constr. Build. Mater. 2016, 122, 781–795. [Google Scholar] [CrossRef]
- Loss, C.; Davison, B. Innovative composite steel-timber floors with prefabricated modular components. Eng. Struct. 2017, 132, 695–713. [Google Scholar] [CrossRef]
- Loss, C.; Frangi, A. Experimental investigation on in-plane stiffness and strength of innovative steel-timber hybrid floor diaphragms. Eng. Struct. 2017, 138, 229–244. [Google Scholar] [CrossRef]
- Hassanieh, A.; Valipour, H.; Bradford, M. Experimental and numerical investigation of short-term behaviour of CLT-steel composite beams. Eng. Struct. 2017, 144, 43–57. [Google Scholar] [CrossRef]
- Giongo, I.; Schiro, G.; Riccadonna, D. Innovative pre-stressing and cambering of timber-to-timber composite beams. Compos. Struct. 2019, 226, 111195. [Google Scholar] [CrossRef]
- Giongo, I.; Schiro, G.; Walsh, K.; Riccadonna, D. Experimental testing of pre-stressed timber-to-timber composite (TTC) floors. Eng. Struct. 2019, 201, 109808. [Google Scholar] [CrossRef]
- Ghanbari-Ghazijahani, T.; Russo, T.; Valipour, H.R. Lightweight timber I-beams reinforced by composite materials. Compos. Struct. 2019, 233, 111579. [Google Scholar] [CrossRef]
- Chiniforush, A.; Valipour, H.; Ataei, A. Timber-timber composite (TTC) connections and beams: An experimental and numerical study. Constr. Build. Mater. 2021, 303, 124493. [Google Scholar] [CrossRef]
- Hammad, M.; Valipour, H.; Ghanbari-Ghazijahani, T.; Bradford, M. Timber-timber composite (TTC) beams subjected to hogging moment. Constr. Build. Mater. 2022, 321, 126295. [Google Scholar] [CrossRef]
- Shahnewaz; Dickof, C.; Zhou, J.; Tannert, T. Vibration and flexural performance of cross-laminated timber—Glulam composite floors. Compos. Struct. 2022, 292, 115682. [Google Scholar] [CrossRef]
- Ramesh, M.; Rajeshkumar, L.; Sasikala, G.; Balaji, D.; Saravanakumar, A.; Bhuvaneswari, V.; Bhoopathi, R. A Critical Review on Wood-Based Polymer Composites: Processing, Properties, and Prospects. Polymers 2022, 14, 589. [Google Scholar] [CrossRef]
- GB 50005; Standard for Design of Timber Structures. Standardization Administration of China: Beijing, China, 2017. (In Chinese)
- LY/T 1580; Oriented Strand Board. Standardization Administration of China: Beijing, China, 2010. (In Chinese)
- GB 27704; Steel Nails. Standardization Administration of China: Beijing, China, 2011. (In Chinese)
- GB/T 846; Cross-Recessed Countersunk (Flat) Head Tapping Screws. Standardization Administration of China: Beijing, China, 2017. (In Chinese)
- Ding, P. Experimental Study on Flexural Performance of Poplar Laminated Veneer Lumber Box Beam. Master’s Thesis, Yangzhou University, Yangzhou, China, 2018. (In Chinese). [Google Scholar]
- GB/T 50329; Standard for Test Methods of Timber Structures. Standardization Administration of China: Beijing, China, 2012. (In Chinese)
- ASTM E2322-03; Standard Test Method for Conducting Transverse and Concentrated Load Tests on Panels Used in Floor and Roof Construction. ASTM International: West Conshohocken, PA, USA, 2015.
- GB 50009; Load Code for the Design of Building Structures. Standardization Administration of China: Beijing, China, 2012. (In Chinese)
- Liu, Q.; Yang, J.C. The pseudo-plate method for the design of large span rib floor. Build. Sci. 1997, 6, 30–34. (In Chinese) [Google Scholar] [CrossRef]
- GB 50010; Code for Design of Concrete Structures. Standardization Administration of China: Beijing, China, 2015. (In Chinese)
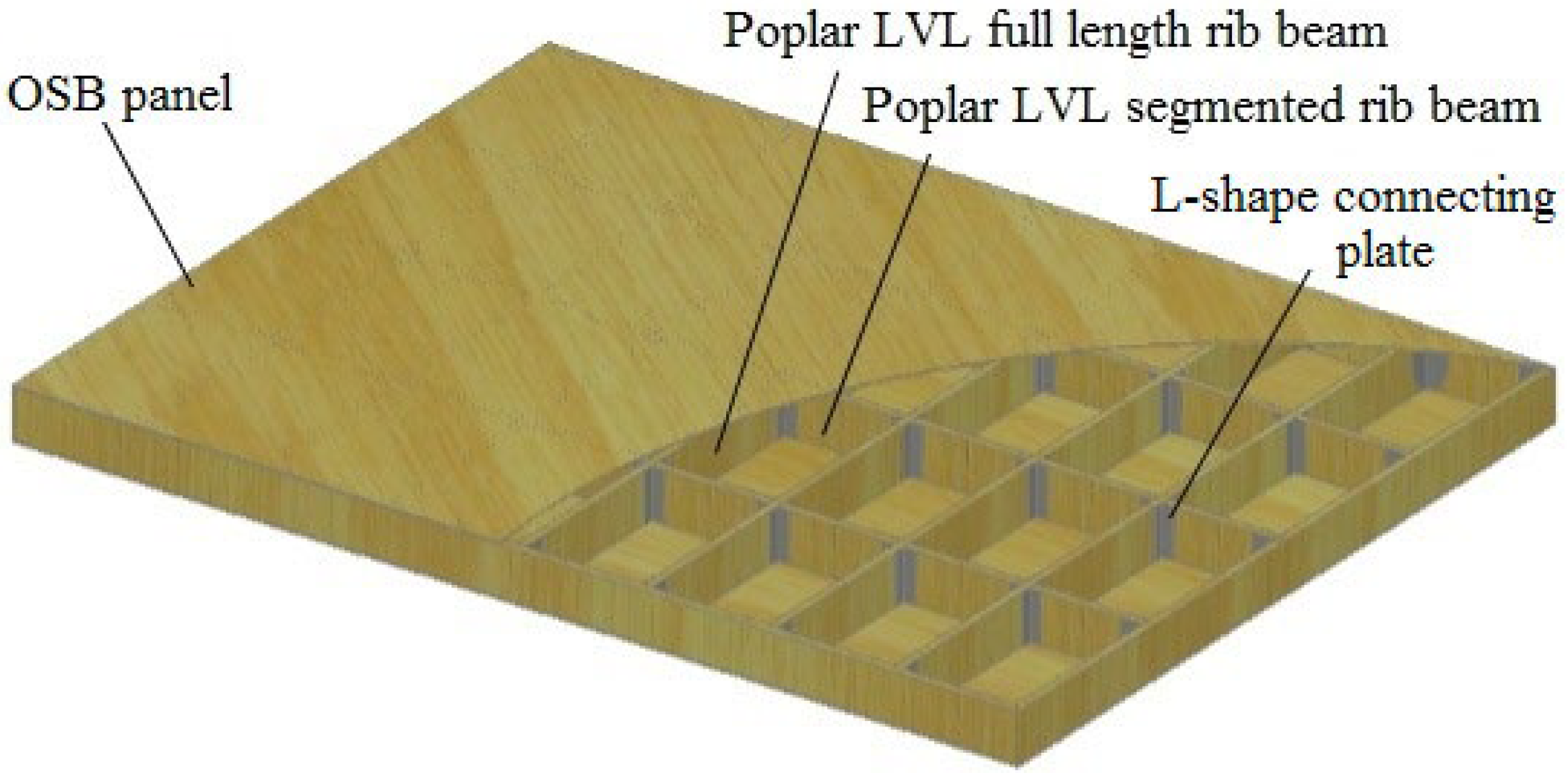
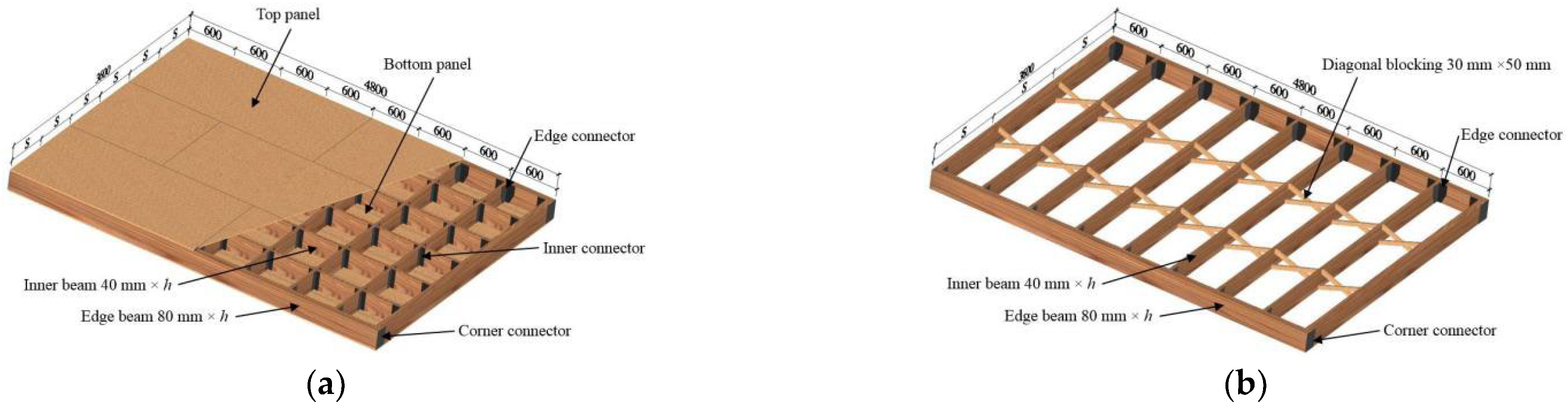
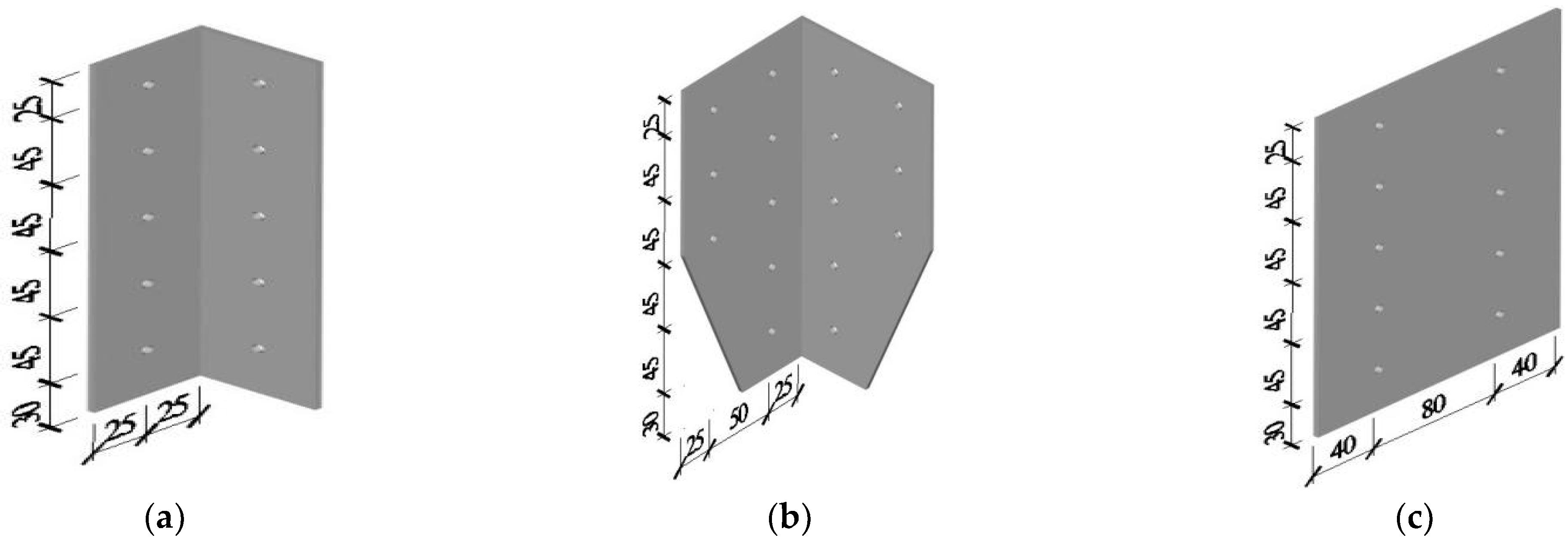




| Specimen | Type | s (mm) | h (mm) | Top Panel | Bottom Panel |
|---|---|---|---|---|---|
| L1 | Two-way | 600 | 185 | None | None |
| L2 | Two-way | 600 | 235 | None | None |
| L3 | Two-way | 600 | 285 | None | None |
| L4 | Two-way | 900 | 235 | None | None |
| L5 | Two-way | 1200 | 235 | None | None |
| L6 | Two-way | 600 | 235 | Yes | None |
| L7 | Two-way | 600 | 235 | Yes | Yes |
| L8 | One-way | 1200 | 235 | None | None |
| Moisture Content (%) | Density (g/cm3) | Tensile Strength Parallel to Grain (MPa) | Compression Strength Parallel to Grain (MPa) | Compression Strength Perpendicular to Grain (MPa) | Bending Strength (MPa) | Flexural Elastic Modulus (MPa) | ||
|---|---|---|---|---|---|---|---|---|
| Adhesive Layer Horizontal | Adhesive Layer Vertical | Adhesive Layer Horizontal | Adhesive Layer Vertical | |||||
| 12.8 | 0.576 | 39.4 | 37.03 | 6.3 | 61.56 | 64.8 | 9877.3 | 10,135.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Wang, C.; Liu, Y.; Ma, H.; Tang, S. Experimental Investigation on Bending Behavior of Innovative Poplar LVL Floor Diaphragms. Sustainability 2022, 14, 10481. https://doi.org/10.3390/su141710481
Sun X, Wang C, Liu Y, Ma H, Tang S. Experimental Investigation on Bending Behavior of Innovative Poplar LVL Floor Diaphragms. Sustainability. 2022; 14(17):10481. https://doi.org/10.3390/su141710481
Chicago/Turabian StyleSun, Xufeng, Changyuan Wang, Yan Liu, Hongwei Ma, and Shukai Tang. 2022. "Experimental Investigation on Bending Behavior of Innovative Poplar LVL Floor Diaphragms" Sustainability 14, no. 17: 10481. https://doi.org/10.3390/su141710481
APA StyleSun, X., Wang, C., Liu, Y., Ma, H., & Tang, S. (2022). Experimental Investigation on Bending Behavior of Innovative Poplar LVL Floor Diaphragms. Sustainability, 14(17), 10481. https://doi.org/10.3390/su141710481






