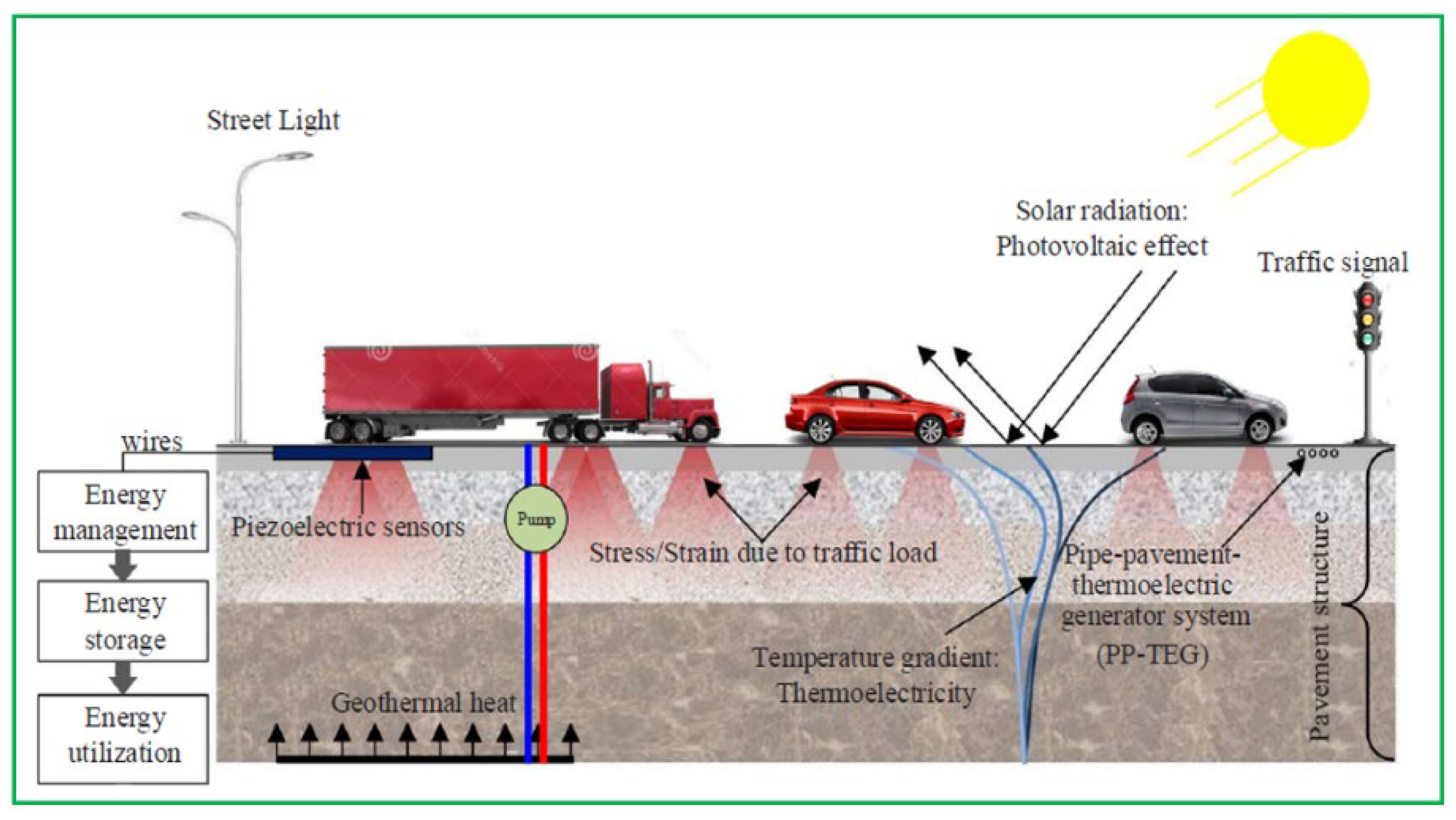
3.1.1. Geothermal Bridge Deck Energy System
Liu et al. [
26,
27] developed a transient heat transfer model of the GRES for bridge deck to assess the influences of climate conditions and flow rate on system performance in Canada.
Figure 4a presents the GRES based on the EP solution.
Figure 4b illustrates the heat transfer mechanism of the bridge deck on the basis of radiation, convection as well as sensible and latent heat.
Table 1 exhibits the energy balance equations.
Figure 5 shows the effects of various influence factors, including snowfall rate, solar radiation, ambient temperature and wind speed, on energy consumption. Results reveal that the increases in snowfall rate and wind speed could give rise to a growth in energy consumption of 35% and 12% whereas the decreases in solar radiation and air temperature could increase energy consumption by 9% and 6.4%, respectively.
As demonstrated in
Figure 6, the heat extraction rate of the GRES in terms of spiral-, W- and U- shapes could be enhanced by 3.4, 2.7 and 2 times, respectively, when the flow rates vary from 0.1 m/s to 4 m/s; this implies that the flow rate has the most vital influence on the heat extraction rate of the spiral shape.
Yu et al. [
28] designed an experimental rig of the GRES to investigate heat transfer characteristic and renovate some existing bridges. The schematic diagrams of the GRES and polyethylene pipe loop are exhibited in
Figure 7. A lab-scale testing is performed to estimate temperature variation of the concrete slab at different locations as presented in
Figure 8; this system consists of 10 polyethylene pipes with a diameter of 13 mm, a water tank and a pump. In the testing, the indoor and water tank temperatures are setup to 4.4 °C and 32.2 °C, respectively.
Figure 9 displays the infrared pictures of the temperature distribution on the slab surface, which could reach an average of 12.8 °C (55 °F); it is indicated that the temperature is higher towards the centre of the concrete slab and progressively reduces outwards. In comparison, the mean temperature at the interface of the geofoam and concrete is 16.1 °C (61 °F). According to
Figure 10, about 60% of the heat is shifted to the slab surface, indicating that around 40% of the heat is missed in the external region of the concrete slab; moreover, the heat transfer efficiency slightly increases by about 1% when the thermal load rises from −1.1 °C (30 °F) to 15.6 °C (60 °F).
Later, Li et al. [
29] built a 3D numerical model of a geothermal bridge deck to evaluate the system performance, and concluded that about 76% of overall supplied heat could be transferred to the top surface of the bridge deck based on different ambient air temperature conditions. In another research, Fabrice et al. [
30] developed a 3D finite element model for de-icing of the bridge to analyze the thermally induced stresses at different seasons.
Figure 11 presents the model mesh and pipe of the monitored location. The total mesh of the model includes 23,760 nodes and 21,060 hexahedral elements, where the initial temperature is set at 11 °C, which is imposed on all faces except the top surface. The results in
Figure 12 indicate that thermal stresses have vital influences on the local and pile temperatures. Most of the stress variation appears at the initial stages of extraction and injection when the maximal temperature gradients occur in the region. Notably, the average overstresses observed are 80 kPa/°C and 90 kPa/°C for cooling and heating seasons, respectively, which are somewhat higher compared to those under the natural recharge state.
In another development, Kong et al. [
31] experimentally tested a GRES for a bridge of 36 m by 26 m dimensions, that has two bicycle and four vehicle lanes. As presented in
Figure 13, the GRES is mounted on the first span slab of the bridge and only half way is covered transversely. The pipe is a polyethylene (PE) tube that has the outer and inner diameters of 16 and 20 mm, which is embedded in the 100 mm thickness of concrete slab. Meanwhile, a thermal water tank is placed between the bridge and EP. The results illustrated in
Figure 14a demonstrate that about 25.7% of the thermal expansion strain is limited via the unheated concrete slab, and the stress through the GRES reaches up to 206 kPa, which is far lower in comparison with the design parameter of the C40 concrete compressive strength of 19.1 MPa, as shown in
Figure 14b.
3.1.2. Geothermal Pavement Energy System
For the road pavement, Mirzanamadi et al. [
32] implemented an experimental testing of the GRES to measure the pavement surface temperature based on Sweden’s weather condition. There is no noticeable infrastructure near the experimental site as displayed in
Figure 15a, and therefore the shading impact of neighbouring infrastructure on the surface of the pavement is ignored; furthermore, the layers of the pavement and relevant parameters are given in
Figure 15b.
Afterwards, Mirzanamadi et al. [
33] built a 3D heat transfer model of the GRES to investigate the unsteady anti-icing method on the basis of the superposition principle. Specifically, the model has a dimension of 1000 × 1000 × 300 mm (L × W × D) with 50 mm depth, a pipe distance of 200 mm is given in
Figure 16a. For the purpose of reducing the computational time, the symmetrical section A-B-C-D-E-F is used to simulate the heat transfer process. According to
Figure 16b, the 3D model is replaced by four 2D vertical cross sections that are serially linked to each other, the initial temperatures of the pavement bottom and top boundaries are set at 0 °C as given in
Figure 17. The basic heat transfer equations are given in
Table 2.
It is found from
Figure 18 that the numerical results are in agreement with the testing data, with a maximum difference of 2.4%. Based on the hybrid 3D model, Mirzanamadi et al. [
34] investigated the system performance for de-icing pavement surface for a 15-year operation period, and found that the maximum value associated with the solar energy harvested is 30 kWh/m
2 in July whereas the minimum value is 0.5 kWh/m
2 in April. Furthermore, the maximum energy demand is 25 kWh/m
2 in December and January, while the mean value of the required energy and the residual number of hours of slippery conditions from October and March are 1.3 kWh/m
2 and 9 h, respectively.
Adl-Zarrabi et al. [
35] developed a 3D COMSOL model of a GRES to study the effect of the pipe position on de-icing performance as presented in
Figure 19. The system involves a surface layer of 150 mm thickness, the base of 250 mm thickness and subbase courses as well as pipes of 1.5mm thickness, which are buried in the concrete slab. The results in
Figure 20a show that the required time for melting the snow on the pavement could be enhanced speedily when the distance between pipes exceeds 200 mm. In other words, the best distance between pipes should be less than 200 mm. Additionally, as depicted in
Figure 20b, there is little effect of the pipe depth on the anti-icing process when its depth is lower than 100 mm.
Xu et al. [
36] setup a numerical model of the GRES to analyse the influences of preheating time and snowfall rate on the snow melting performance at Beijing New Capital International Airport as shown in
Figure 21. The whole area of the experimental site is 90 m
2, with a stainless steel pipe of 32 mm diameter, 0.4 m length and a depth of 0.08 m embedded underground. A geothermal heat pump unit with a rated power of 50 kW is utilized to warm 25% of ethylene glycol solution. The basic equations of water transport, heat transport and error analysis are presented in
Table 3. The results indicate that the percentage of snow-free hours during snowfall at four preheating times is improved ranging from 1.3% to 5.6%. As a result, it is necessary to adjust the snow melting target by the traffic capacity as the design alternatives.
Han and Yu [
37] set up a 3D model of the GRES with EP technology to assess the energy extraction rate and required pile number for three configurations in the USA. As shown in
Figure 22a, the soil domain is defined as a cylinder and has a diameter of 12 m. The Dirichlet boundary condition is used as the borders of the calculation field with the magnitude set to be the undisturbed soil temperature as presented in
Figure 22b.
Additionally, it can be found from
Figure 23 that high soil temperature contributes to extracting energy and producing high-temperature outlet fluid; moreover, the spiral pipe shape (type c) could extract more heat in comparison with U-shape (type a) and W-shape (type b) pipes; this means that the spiral pipe shape is the best choice for the system to improve snow melting performance under the constraint of limited pile length.
In addition, Han and Yu [
38] modified the GRES with EP by integrating a phase change material (PCM) in order to enhance system performance as shown in
Figure 24. The equations of the modified GRES model are given in
Table 4. As shown in
Figure 25, the required numbers of PCM piles for U-, W- and spiral-shape pipes significantly reduce in comparison with those without PCM attached (wt % = 0). The utilization of 3% PCM additive by mass fraction leads to a 25–35% drop in the needed number of piles for the designated cities based on design conditions, and the usage of 12% PCM decreases the pile number by 60–70%; this means that the soil temperature and pipe configuration layout have an influence on the needed number of piles of the modified GRES.
In another study [
39], a finite element GRES model setup to investigate the outlet fluid temperature variation based on USA’s climate condition. As given in
Figure 26, the system includes a heat pump and horizontal pipe loops that are laid under the soil at a depth of 6 m. Results confirm that the outlet fluid temperature could be kept higher than 4 °C when the soil is at full saturation, as indicated in
Figure 27. On the other hand, the outlet fluid temperature could fall to −0.7 °C when the soil is completely dry; this implies that a dry soil is not an ideal medium to embed pipes within the soil layer.
Yang et al. [
40] developed a GRSE model for the underground utility tunnel (UUT) to extract heat from the soil and absorb waste heat within the tunnel. As exhibited in
Figure 28, the UUT is constructed at a depth of 3–6 m under the urban roadway, which is deeper compared with the frozen soil layer. The dimension of the UUT is 3.0 × 2.8 m with 0.3 m of wall thickness. As indicated in
Figure 29, the model results reflect that the outlet fluid temperature dramatically reduces while the maximum temperature difference between inlet and outlet is approximately 1 K when the inlet fluid temperature and flow velocity vary in the ranges of 280.15 K to 278.15 K and 0.1 m/L to 0.5 m/L, respectively; this suggests that the lower inlet water temperature and wind velocity improve the efficiency of heat transfer.
Chiarelli et al. [
41,
42] conducted a novel testing of the GRES called the ground source heat simulator to investigate the impact of the inlet air temperature and wind speed on system performance. As shown in
Figure 30, the dimension of this prototype is 470 × 700 × 180 mm (L × W × H) with a 50 mm thickness of asphalt wearing course and 130 mm of thickness coarse gravel layer; this experiment is carried out at University of Nottingham, UK and divided into two scenarios including air temperature is higher and lower 15 °C of inlet temperature.
Their results reveal from
Figure 31a that the most frequent inlet air temperature appears in the range from 14 °C to 15 °C, while the temperatures between 10 °C and 13 °C are also rather frequent; this is because the system is exposed to the outdoor environment, thereby inlet air temperature could not be maintained as a constant value in a real scenario. According to
Figure 31b, the wind velocity has a negative effect on the pavement surface temperature; this implies that when the wind is existing, the road surface would be cold and less energy is available for extracting.
Mäkiranta and Hiltunen [
43] implemented testing of the GRES to examine the effect of temperature variations at various depths of the soil layer on system energy capturing. As presented in
Figure 32, there are four different pipe depths including two for 10 m depth, one for 5 m depth and two for 3 m depth in Finland. Results conclude that it is able to retain appropriate temperature up to 26 °C at the soil depth of 0.5 m, and there are positive temperature values for at least 9 months per annum; this indicates that the soil layer is suitable for assembling heat collection pipes.
Balbay and Esen [
44,
45] carried out an experimental investigation to explore the feasibility of the GRES utilization to heat roadways for snow melting as shown in
Figure 33. During the testing, the processes of snow melting for bridge and pavement slabs at the initial state (t = 0) and intermediate state (t = 30 min.) are shown in
Figure 34. Results demonstrate that the top surface of the pavement is typically exposed to bigger temperature fluctuation than the bottom surface. Besides, the thermal conductivity of the concrete slab and air convection coefficient have significant influences on the temperature of the pavement surface; this indicates that the higher wind speed, the higher the convection heat coefficient at the surface of the concrete slab, leading to a lower top surface temperature.
Ho et al. [
46] proposed a 3D GRES model to analyze the pavement surface temperature variation. As illustrated in
Figure 35, the GRES includes a closed-loop polyethylene tube that is embedded in the concrete slab, and the initial inlet fluid temperature is set in the range of 60 °C to 82.2 °C for snow and ice melting. As shown in
Figure 36, a high flow rate can warm road surface to a high temperature, and a low fluid flow rate leads to a big temperature reduction.
Tota-Maharaj et al. [
47] designed a GRES experimental rig to evaluate snow removal rates for various mediums. The GRES consists of a geothermal heat pump (GHP) combined with a permeable pavement system (PPS).
Figure 37 despites the interior and exterior views of the testing rig, the interior PPS includes six bins positioned in a temperature-controlled room with an average air temperature of 15 °C, while the exterior part is embedded in the soil where it is subjected to ground temperature and climate conditions. The schematic diagram of the PPS and pavement layers are presented in
Figure 38; it is revealed from
Figure 39 that the mean snow removal rate varies from 80% to 90% for biochemical oxygen demand (BOD), ammonia–nitrogen (NH4) and orthophosphate–phosphorus (PO4). By comparison, the removal rate of suspended solids (SS) is in the range of 40% to 60%.
Zhang et al. [
48] investigated the snow melting performance of a GRES with L-shaped heat pipe system for airfield runways in Beijing and Harbin of China as depicted in
Figure 40; it can be seen from
Figure 41 that the GRES could increase the two city mean airfield runway temperatures of 9.1 °C in 2015, 8.9 °C in 2016 and 9.4 °C in 2017, respectively; this implies that the GRES could work automatically primarily in heating season to enhance the surface temperature adequately to avoid ice accumulation; moreover, it can be found that the surface temperature of airfield-runway is below 0 °C at 68% time of the year in Harbin, whereas it is almost above 0 °C in Beijing for the whole winter period; this means that the geography plays a significant role in the system de-icing performance. As shown in
Figure 42, the system for airfield-runway is applicable in central areas of China whose air temperature exceeds −10 °C, whereas it is inapplicable in north-western and north-eastern areas.
Wang et al. [
49] developed a GRES with super flexible heat pipes (SFHPs) system to investigate the entrainment limit within the pipe and provide the optimal design plan based on the local climate condition. The fabrication and construction of the GRES with SFHPs are shown in
Figure 43. In order to explore the heat transfer mechanism, thermal resistance model and boundary conditions are given in
Figure 44. Simulation results reveal that ammonia is the most suitable thermal fluid for the high entertainment limit, and the system heat output could reach approximately 1.15 kW as illustrated in
Figure 45. Besides, 70 m of SFHP length with Ø32 × 2 mm and 0.2 m distance of condenser horizontal interval are recommended as the optimal choice in the study.
Mauro and Grossman [
50] conducted a dynamic GRES simulation work to decrease the fluctuations of street temperature and avert ice formation. The system includes 12 EPs with a diameter of 150 mm and length of 20 m, and the substrate has a thickness of 20 mm and is placed beneath the street pavement with a thickness of 100 mm; it can be found from
Figure 46 that the minimum street surface temperature varies from 4.6 °C to 6.6 °C in winter, while the maximum temperature changes from 3.8 °C to 7.5 °C in summer.