Hedonic Pricing of Houses in Megacities Pre- and Post-COVID-19: A Case Study of Shanghai, China
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Explanatory Variables
2.3. Research Method
2.3.1. Spatial Autocorrelation
2.3.2. Hot Spot Analysis
2.3.3. Multiscale Geographically Weighted Regression (MGWR)
3. Results and Findings
3.1. Basic Facts
3.2. Spatial Auto-Correlation
3.3. Hot Spot Analysis
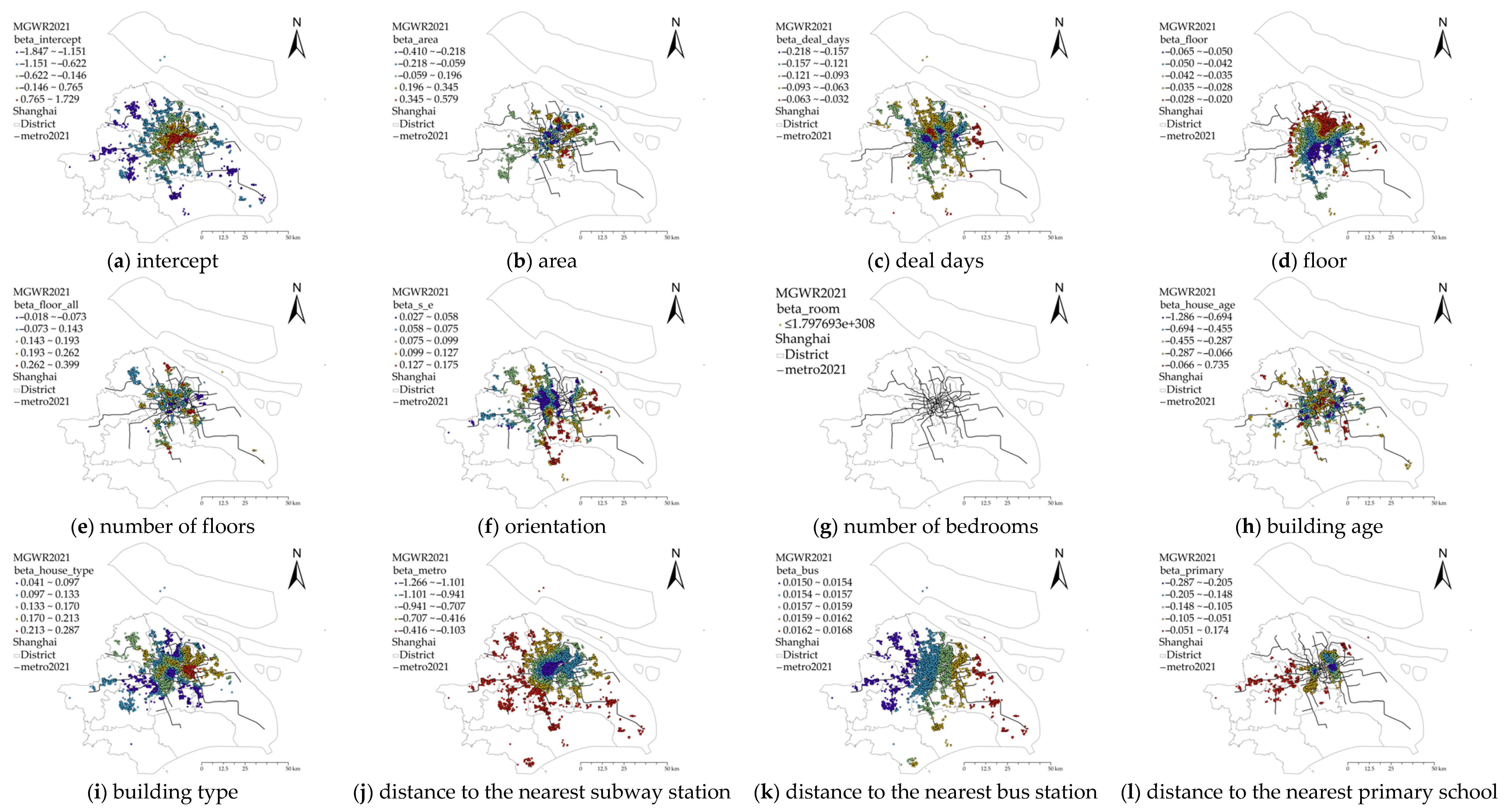
3.4. MGWR
4. Conclusions
4.1. Summary of Results
4.2. Policy Recommendations
4.2.1. Develop Multiple Urban Centers
4.2.2. Build Houses into Consumer’s Preferences in the Post-Epidemic Era
4.2.3. Improve Infrastructure Construction
4.3. Limitations of the Study
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- He, C.; Wang, Z.; Guo, H.; Sheng, H.; Zhou, R.; Yang, Y. Driving Forces Analysis for Residential Housing Price in Beijing. Procedia Environ. Sci. 2010, 2, 925–936. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, R.; Xu, D.; Zhou, W. Spatial and Hedonic Analysis of Housing Prices in Shanghai. Habitat Int. 2017, 67, 69–78. [Google Scholar] [CrossRef]
- Hui, E.C.M.; Yue, S. Housing Price Bubbles in Hong Kong, Beijing and Shanghai: A Comparative Study. J. Real Estate Financ. Econ. 2006, 33, 299–327. [Google Scholar] [CrossRef]
- Li, N.; Li, R.Y.M.; Pu, R. What Is in a Name? A Modern Interpretation from Housing Price in Hong Kong. Pac. Rim Prop. Res. J. 2021, 27, 55–74. [Google Scholar] [CrossRef]
- Piao, Y.; Chen, A.; Shang, Z. Housing Price Prediction Based on CNN. In Proceedings of the 2019 9th International Conference on Information Science and Technology (ICIST), Cairo, Egypt, 24–26 March 2019; IEEE: Hulunbuir, China, 2019; pp. 491–495. [Google Scholar]
- Shanghai Bureau of Statistics. A Review of Shanghai Real Estate Market in 2021. Available online: http://tjj.sh.gov.cn/tjfx/20220129/f49f612d4ec548adbe5db5c91466b324.html (accessed on 29 January 2022).
- Chan, S. Spatial Lock-in: Do Falling House Prices Constrain Residential Mobility? J. Urban Econ. 2001, 49, 567–586. [Google Scholar] [CrossRef]
- Shan, H. Property Taxes and Elderly Mobility. J. Urban Econ. 2010, 67, 194–205. [Google Scholar] [CrossRef]
- Yang, Z.; Pan, Y. Human Capital, Housing Prices, and Regional Economic Development: Will “Vying for Talent” through Policy Succeed? Cities 2020, 98, 102577. [Google Scholar] [CrossRef]
- Can, A. Specification and Estimation of Hedonic Housing Price Models. Reg. Sci. Urban Econ. 1992, 22, 453–474. [Google Scholar] [CrossRef]
- Court, L.M. Entrepreneurial and Consumer Demand Theories for Commodity Spectra: Part I. Econometrica 1941, 9, 135. [Google Scholar] [CrossRef]
- Freeman, A.M. The Hedonic Price Approach to Measuring Demand for Neighborhood Characteristics. In The Economics of Neighborhood; Elsevier: Amsterdam, The Netherlands, 1979; pp. 191–217. ISBN 978-0-12-636250-3. [Google Scholar]
- Rosen, S. Hedonic Prices and Implicit Markets: Product Differentiation in Pure Competition. J. Political Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Tinbergen, J. On the Theory of Income Distribution. Weltwirtschaftliches Arch. 1956, 77, 155–175. [Google Scholar]
- Li, R.; Cheung, K.; Shoaib, M. Walled Buildings, Sustainability, and Housing Prices: An Artificial Neural Network Approach. Sustainability 2018, 10, 1298. [Google Scholar] [CrossRef]
- Wang, R.; Hou, J. Land Finance, Land Attracting Investment and Housing Price Fluctuations in China. Int. Rev. Econ. Financ. 2021, 72, 690–699. [Google Scholar] [CrossRef]
- Harrison, D.; Rubinfeld, D.L. Hedonic Housing Prices and the Demand for Clean Air. J. Environ. Econ. Manag. 1978, 5, 81–102. [Google Scholar] [CrossRef]
- Michaels, R.G.; Smith, V.K. Market Segmentation and Valuing Amenities with Hedonic Models: The Case of Hazardous Waste Sites. J. Urban Econ. 1990, 28, 223–242. [Google Scholar] [CrossRef]
- Straszheim, M.R. Hedonic Estimation of Housing Market Prices: A Further Comment. Rev. Econ. Stat. 1974, 56, 404–406. [Google Scholar] [CrossRef]
- Kain, J.F.; Quigley, J.M. Measuring the Value of Housing Quality. J. Am. Stat. Assoc. 1970, 65, 532–548. [Google Scholar] [CrossRef]
- Sirmans, G.S.; MacDonald, L.; Macpherson, D.A.; Zietz, E.N. The Value of Housing Characteristics: A Meta Analysis. J. Real Estate Financ. Econ. 2006, 33, 215–240. [Google Scholar] [CrossRef]
- Heikkila, E.; Gordon, P.; Kim, J.I.; Peiser, R.B.; Richardson, H.W.; Dale-Johnson, D. What Happened to the CBD-Distance Gradient?: Land Values in a Policentric City. Environ. Plan. A 1989, 21, 221–232. [Google Scholar] [CrossRef]
- Osland, L.; Thorsen, I. Effects on Housing Prices of Urban Attraction and Labor-Market Accessibility. Environ. Plan. A 2008, 40, 2490–2509. [Google Scholar] [CrossRef]
- Richardson, H.W.; Gordon, P.; Jun, M.-J.; Heikkila, E.; Peiser, R.; Dale-Johnson, D. Residential Property Values, the CBD, and Multiple Nodes: Further Analysis. Environ. Plan. A 1990, 22, 829–833. [Google Scholar] [CrossRef]
- Dubin, R.A.; Goodman, A.C. Valuation of Education and Crime Neighborhood Characteristics through Hedonic Housing Prices. Popul. Environ. 1982, 5, 166–181. [Google Scholar] [CrossRef]
- Gibbons, S.; Machin, S. Valuing English Primary Schools. J. Urban Econ. 2003, 53, 197–219. [Google Scholar] [CrossRef]
- Brasington, D.M.; Hite, D. Demand for Environmental Quality: A Spatial Hedonic Analysis. Reg. Sci. Urban Econ. 2005, 35, 57–82. [Google Scholar] [CrossRef]
- Das, R.C.; Chatterjee, T.; Ivaldi, E. Nexus between Housing Price and Magnitude of Pollution: Evidence from the Panel of Some High- and-Low Polluting Cities of the World. Sustainability 2022, 14, 9283. [Google Scholar] [CrossRef]
- Poudyal, N.C.; Hodges, D.G.; Merrett, C.D. A Hedonic Analysis of the Demand for and Benefits of Urban Recreation Parks. Land Use Policy 2009, 26, 975–983. [Google Scholar] [CrossRef]
- Fletcher, M.; Gallimore, P.; Mangan, J. Heteroscedasticity in Hedonic House Price Models. J. Prop. Res. 2000, 17, 93–108. [Google Scholar] [CrossRef]
- Goodman, A.C. Hedonic Prices, Price Indices and Housing Markets. J. Urban Econ. 1978, 5, 471–484. [Google Scholar] [CrossRef]
- Goodman, A.C.; Thibodeau, T.G. Dwelling-Age-Related Heteroskedasticity in Hedonic House Price Equations: An Extension. J. Hous. Res. 1997, 8, 299–317. [Google Scholar]
- Miller, H.J. Tobler’s First Law and Spatial Analysis. Ann. Assoc. Am. Geogr. 2004, 94, 284–289. [Google Scholar] [CrossRef]
- Wong, W.S.D.; Lee, J. Statistical Analysis of Geographic Information with ArcView GIS and ArcGIS; Wiley: Hoboken, NJ, USA, 2005; ISBN 0-471-46899-1. [Google Scholar]
- Cleveland, W.S.; Devlin, S.J. Locally Weighted Regression: An Approach to Regression Analysis by Local Fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
- Wang, C.; Du, S.; Wen, J.; Zhang, M.; Gu, H.; Shi, Y.; Xu, H. Analyzing Explanatory Factors of Urban Pluvial Floods in Shanghai Using Geographically Weighted Regression. Stoch Env. Res Risk Assess 2017, 31, 1777–1790. [Google Scholar] [CrossRef]
- Wheeler, D.C.; Páez, A. Geographically Weighted Regression. In Handbook of Applied Spatial Analysis; Springer: Berlin/Heidelberg, Germany, 2010; pp. 461–486. [Google Scholar]
- Cho, S.; Lambert, D.M.; Kim, S.G.; Jung, S. Extreme Coefficients in Geographically Weighted Regression and Their Effects on Mapping. GIScience Remote Sens. 2009, 46, 273–288. [Google Scholar] [CrossRef]
- Wheeler, D.; Tiefelsdorf, M. Multicollinearity and Correlation among Local Regression Coefficients in Geographically Weighted Regression. J Geogr. Syst 2005, 7, 161–187. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2003; ISBN 0-470-85525-8. [Google Scholar]
- Fotheringham, A.S.; Yang, W.; Kang, W. Multiscale Geographically Weighted Regression (MGWR). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Oshan, T.M.; Smith, J.P.; Fotheringham, A.S. Targeting the Spatial Context of Obesity Determinants via Multiscale Geographically Weighted Regression. Int. J. Health Geogr. 2020, 19, 11. [Google Scholar] [CrossRef]
- Gao, L.; Huang, M.; Zhang, W.; Qiao, L.; Wang, G.; Zhang, X. Comparative Study on Spatial Digital Mapping Methods of Soil Nutrients Based on Different Geospatial Technologies. Sustainability 2021, 13, 3270. [Google Scholar] [CrossRef]
- Shen, T.Y.; Yu, H.C.; Zhou, L.; Gu, H.; He, H. On Hedonic Price of Second-Hand Houses in Beijing Based on Multi-Scale Geographically Weighted Regression: Scale Law of Spatial Heterogeneity. Econ. Geogr. 2020, 40, 75–83. [Google Scholar] [CrossRef]
- Li, S.; Ye, X.; Lee, J.; Gong, J.; Qin, C. Spatiotemporal Analysis of Housing Prices in China: A Big Data Perspective. Appl. Spat. Anal. 2017, 10, 421–433. [Google Scholar] [CrossRef]
- Zheng, S.; Kahn, M.E.; Liu, H. Towards a System of Open Cities in China: Home Prices, FDI Flows and Air Quality in 35 Major Cities. Reg. Sci. Urban Econ. 2010, 40, 1–10. [Google Scholar] [CrossRef]
- Hou, Y. Housing Price Bubbles in Beijing and Shanghai?: A Multi-indicator Analysis. Int. J. Hous. Mark. Anal. 2010, 3, 17–37. [Google Scholar] [CrossRef]
- Li, L.H.; Ge, C.L. Inflation and Housing Market in Shanghai. Prop. Manag. 2008, 26, 273–288. [Google Scholar]
- Liu, C.; Lu, J.; Fu, W.; Zhou, Z. Second-Hand Housing Batch Evaluation Model of Zhengzhou City Based on Big Data and MGWR Model. IFS 2022, 42, 4221–4240. [Google Scholar] [CrossRef]
- Wen, H.; Jin, Y.; Zhang, L. Spatial Heterogeneity in Implicit Housing Prices: Evidence from Hangzhou, China. Int. J. Strateg. Prop. Manag. 2017, 21, 15–28. [Google Scholar] [CrossRef]
- Liu, L.; Yu, H.; Zhao, J.; Wu, H.; Peng, Z.; Wang, R. Multiscale Effects of Multimodal Public Facilities Accessibility on Housing Prices Based on MGWR: A Case Study of Wuhan, China. IJGI 2022, 11, 57. [Google Scholar] [CrossRef]
- Jones, L.; Palumbo, D.; Brown, D. Coronavirus: How the Pandemic Has Changed the World Economy. BBC News 2021. [Google Scholar]
- Pak, A.; Adegboye, O.A.; Adekunle, A.I.; Rahman, K.M.; McBryde, E.S.; Eisen, D.P. Economic Consequences of the COVID-19 Outbreak: The Need for Epidemic Preparedness. Front. Public Health 2020, 8, 241. [Google Scholar] [CrossRef]
- Del Giudice, V.; De Paola, P.; Del Giudice, F.P. COVID-19 Infects Real Estate Markets: Short and Mid-Run Effects on Housing Prices in Campania Region (Italy). Soc. Sci. 2020, 9, 114. [Google Scholar] [CrossRef]
- Li, X.; Zhang, C. Did the COVID-19 Pandemic Crisis Affect Housing Prices Evenly in the U.S.? Sustainability 2021, 13, 12277. [Google Scholar] [CrossRef]
- Qian, X.; Qiu, S.; Zhang, G. The Impact of COVID-19 on Housing Price: Evidence from China. Financ. Res. Lett. 2021, 43, 101944. [Google Scholar] [CrossRef]
- Tanrıvermiş, H. Possible Impacts of COVID-19 Outbreak on Real Estate Sector and Possible Changes to Adopt: A Situation Analysis and General Assessment on Turkish Perspective. J. Urban Manag. 2020, 9, 263–269. [Google Scholar] [CrossRef]
- Zhang, H. Cultural Diversity, Cooperation Spirit and Team Efficiency. Bus. Manag. J. 2022, 44, 108–122. [Google Scholar] [CrossRef]
- Li, H.; Wei, Y.D.; Wu, Y.; Tian, G. Analyzing Housing Prices in Shanghai with Open Data: Amenity, Accessibility and Urban Structure. Cities 2019, 91, 165–179. [Google Scholar] [CrossRef]
- Li, H.; Chen, P.; Grant, R. Built Environment, Special Economic Zone, and Housing Prices in Shenzhen, China. Appl. Geogr. 2021, 129, 102429. [Google Scholar] [CrossRef]
- Yu, H.; Hou, Y. A Tale of Two Districts: The Impact of District Consolidation on Property Values in Shanghai. Reg. Sci. Urban Econ. 2021, 87, 103647. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234. [Google Scholar] [CrossRef]
- Moran, P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17. [Google Scholar] [CrossRef]
- Ord, J.K.; Getis, A. Local Spatial Autocorrelation Statistics: Distributional Issues and an Application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Hui, D.S.; I Azhar, E.; Madani, T.A.; Ntoumi, F.; Kock, R.; Dar, O.; Ippolito, G.; Mchugh, T.D.; Memish, Z.A.; Drosten, C.; et al. The Continuing 2019-NCoV Epidemic Threat of Novel Coronaviruses to Global Health—The Latest 2019 Novel Coronavirus Outbreak in Wuhan, China. Int. J. Infect. Dis. 2020, 91, 264–266. [Google Scholar] [CrossRef]
- Cui, N.; Gu, H.; Shen, T.; Zhou, L.; Cui, D. Research on the Influence of Traffic Spatial Layout on Urban Housing Price—Based on the Analysis of the Correlation between Beijing Road Network Configuration and Housing Price. Price Theory Pract. 2019, 2, 63–66. [Google Scholar] [CrossRef]
- Wang, Y. Study on the Temporal and Spatial Characteristics of Shanghai Residents’ Travel Based on Public Transport Big Data; Shandong Normal University: Jinan, China, 2018. [Google Scholar]


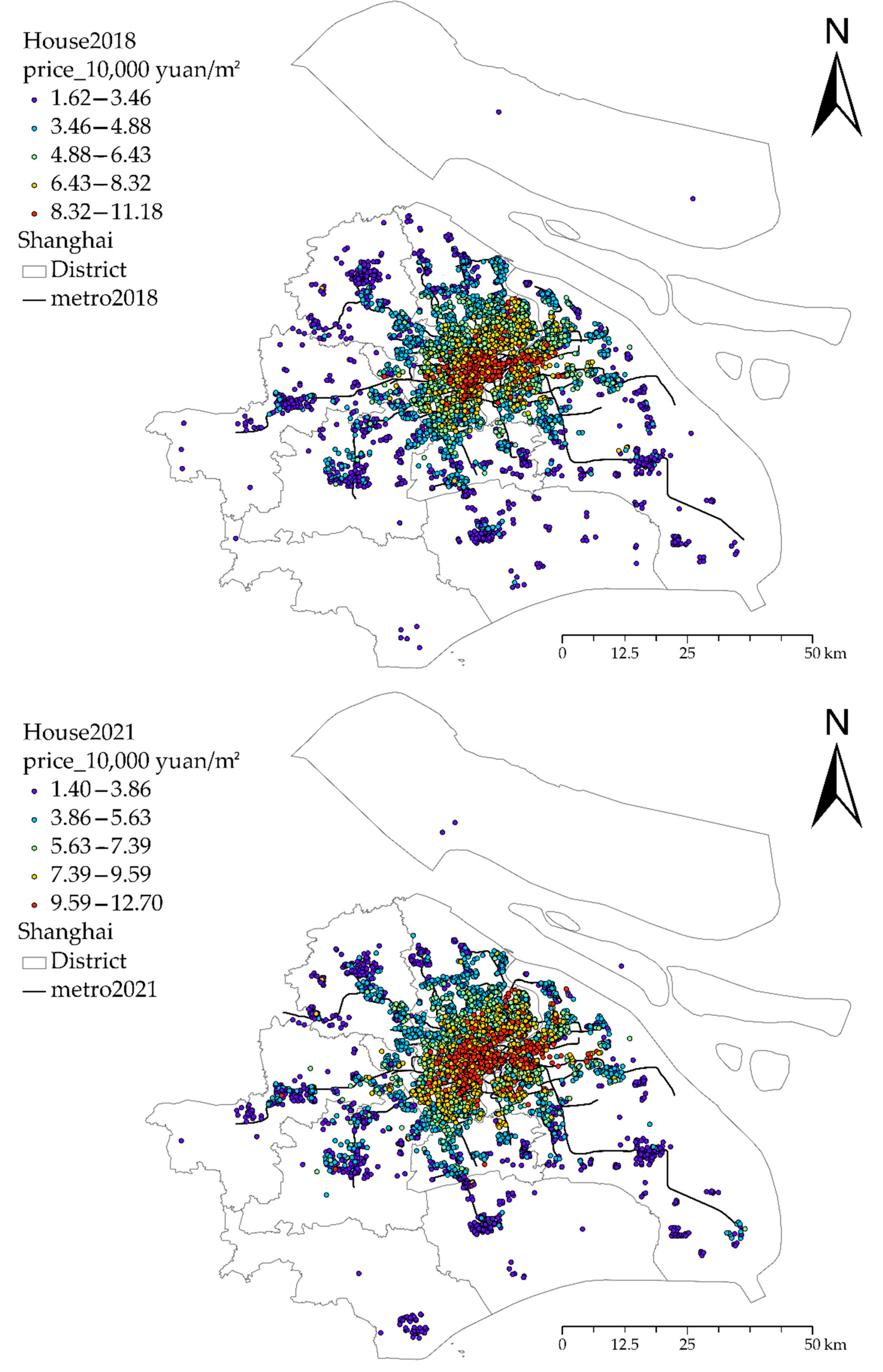

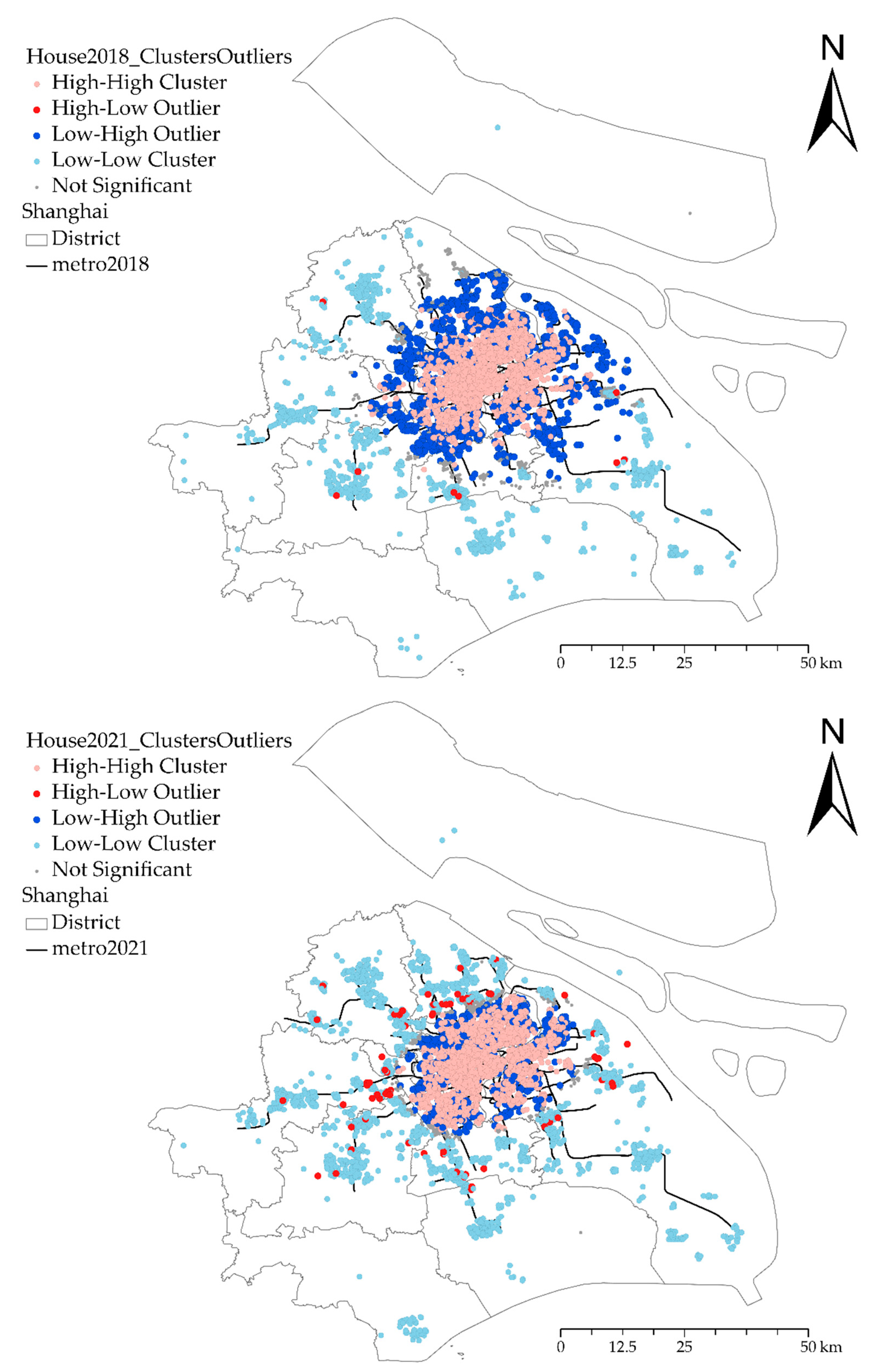

| Variable Types | Variable | Unit | Description |
|---|---|---|---|
| Dependent variable | price | RMB 10,000/m2 | Shanghai’s second-hand housing prices |
| Structural attributes | area | Square meter | Residential(living) area of the house |
| deal_days | Days | Transaction time of the house | |
| floor | Discrete variable | Floor of the house (villa with basement: 1; low floor: 2; middle floor: 3; high floor: 4) | |
| floor_all | Floor | Number of floors of the building (1–56) | |
| s_e | Virtual variable | Orientation of the house (whether the house faces south or east, Yes: 1; No: 0) | |
| room | Room | Number of residential bedrooms (1–9) | |
| house_age | Year | Age of the building (years between deal year and construction year, 0–109) | |
| house_type | Discrete variable | Building type of the building (slab-type apartment building: 1; bungalow: 2; tower-type apartment building: 3; combination: 4) | |
| Locational attributes | metro | Meter | Distance to the nearest subway station |
| bus | Meter | Distance to the nearest bus stop | |
| primary | Meter | Distance to the nearest elementary school | |
| intercept | RMB 10,000 | The intercept term of the model, reflecting the effect of location |
| Variable | Percentage/Mean Value | |
|---|---|---|
| 2018 | 2021 | |
| price | 5.19 | 6.27 |
| area | 74.70 | 87.63 |
| deal_days | 144.02 | 92.55 |
| floor | 3.05 | 3.05 |
| 1: villa with basement | 0.03 | 0.08 |
| 2: low floor | 29.63 | 32.05 |
| 3: middle floor | 35.75 | 30.42 |
| 4: high floor | 34.62 | 37.46 |
| floor_all | 10.21 | 10.70 |
| s_e | ||
| 0 | 3.25 | 4.24 |
| 1 | 96.75 | 95.76 |
| room | 1.80 | 1.82 |
| house_age | 20.10 | 23.13 |
| house_type | ||
| 1: slab-type | 9.32 | 10.63 |
| 2: bungalow | 0.11 | 0.12 |
| 3: tower-type | 0.40 | 1.07 |
| 4: combination | 90.17 | 88.18 |
| metro | 1210.88 | 1182.90 |
| bus | 176.43 | 166.66 |
| primary | 543.89 | 549.68 |
| Variable | 2018 | 2021 |
|---|---|---|
| Moran’s Index | 0.579 | 0.603 |
| Expected Index | −0.005 | −0.005 |
| Variance | 0.000 | 0.000 |
| z-score | 34.043 | 34.019 |
| p-value | 0.000 | 0.000 |
| Index | 2018 | 2021 | ||
|---|---|---|---|---|
| GWR | MGWR | GWR | MGWR | |
| Residual sum of squares | 3808.84 | 800.96 | 4352.27 | 876.55 |
| Log-likelihood: | −6828.94 | −2503.53 | −7582.22 | −2741.19 |
| AICc: | 13,683.94 | 7079.47 | 15,190.50 | 7932.55 |
| Adj. R2 | 0.312 | 0.829 | 0.278 | 0.826 |
| Variable | 2018 | 2021 | ||
|---|---|---|---|---|
| GWR | MGWR | GWR | MGWR | |
| intercept | 398 | 44 | 285 | 43 |
| area | 398 | 77 | 285 | 84 |
| deal_days | 398 | 1756 | 285 | 508 |
| floor | 398 | 4872 | 285 | 2176 |
| floor_all | 398 | 5546 | 285 | 110 |
| s_e | 398 | 5049 | 285 | 601 |
| room | 398 | 1956 | 285 | 6041 |
| house_age | 398 | 46 | 285 | 44 |
| house_type | 398 | 111 | 285 | 484 |
| metro | 398 | 5546 | 285 | 1005 |
| bus | 398 | 1957 | 285 | 6041 |
| primary | 398 | 5546 | 285 | 478 |
| Mean | STD | Min | Median | Max | |
|---|---|---|---|---|---|
| Year 2018 | |||||
| intercept | −0.001 | 0.849 | −1.428 | −0.009 | 2.042 |
| area | 0.067 | 0.163 | −0.738 | 0.065 | 0.571 |
| deal_days | −0.014 | 0.015 | −0.041 | −0.014 | 0.014 |
| floor | −0.031 | 0.004 | −0.038 | −0.032 | −0.016 |
| floor_all | 0.076 | 0.000 | 0.074 | 0.076 | 0.077 |
| s_e | 0.028 | 0.003 | 0.021 | 0.028 | 0.034 |
| room | −0.069 | 0.028 | −0.117 | −0.068 | −0.018 |
| house_age | −0.182 | 0.227 | −1.207 | −0.146 | 0.516 |
| house_type | 0.104 | 0.099 | −0.311 | 0.104 | 0.480 |
| metro | −0.093 | 0.002 | −0.095 | −0.093 | −0.085 |
| bus | 0.017 | 0.011 | −0.009 | 0.019 | 0.040 |
| primary | −0.009 | 0.001 | −0.012 | −0.009 | −0.007 |
| Year 2021 | |||||
| intercept | −0.166 | 0.733 | −1.847 | −0.124 | 1.729 |
| area | 0.039 | 0.166 | −0.410 | 0.031 | 0.579 |
| deal_days | −0.099 | 0.041 | −0.218 | −0.100 | 0.014 |
| floor | −0.035 | 0.013 | −0.065 | −0.037 | 0.000 |
| floor_all | 0.078 | 0.094 | −0.180 | 0.072 | 0.399 |
| s_e | 0.059 | 0.041 | −0.063 | 0.056 | 0.175 |
| room | −0.004 | 0.000 | −0.005 | −0.005 | −0.002 |
| house_age | −0.204 | 0.239 | −1.286 | −0.166 | 0.735 |
| house_type | 0.134 | 0.051 | −0.012 | 0.137 | 0.287 |
| metro | −0.788 | 0.330 | −1.266 | −0.911 | −0.103 |
| bus | 0.016 | 0.000 | 0.015 | 0.016 | 0.017 |
| primary | −0.045 | 0.076 | −0.287 | −0.029 | 0.174 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Luo, Z. Hedonic Pricing of Houses in Megacities Pre- and Post-COVID-19: A Case Study of Shanghai, China. Sustainability 2022, 14, 11021. https://doi.org/10.3390/su141711021
Chen Y, Luo Z. Hedonic Pricing of Houses in Megacities Pre- and Post-COVID-19: A Case Study of Shanghai, China. Sustainability. 2022; 14(17):11021. https://doi.org/10.3390/su141711021
Chicago/Turabian StyleChen, Yujiao, and Zhengbo Luo. 2022. "Hedonic Pricing of Houses in Megacities Pre- and Post-COVID-19: A Case Study of Shanghai, China" Sustainability 14, no. 17: 11021. https://doi.org/10.3390/su141711021
APA StyleChen, Y., & Luo, Z. (2022). Hedonic Pricing of Houses in Megacities Pre- and Post-COVID-19: A Case Study of Shanghai, China. Sustainability, 14(17), 11021. https://doi.org/10.3390/su141711021






