Experimental Investigation of the Mechanical Behavior and Damage Evolution Mechanism of Oil-Impregnated Gypsum Rock
Abstract
:1. Introduction
2. Experimental Pretreatment
2.1. Sample Preparation
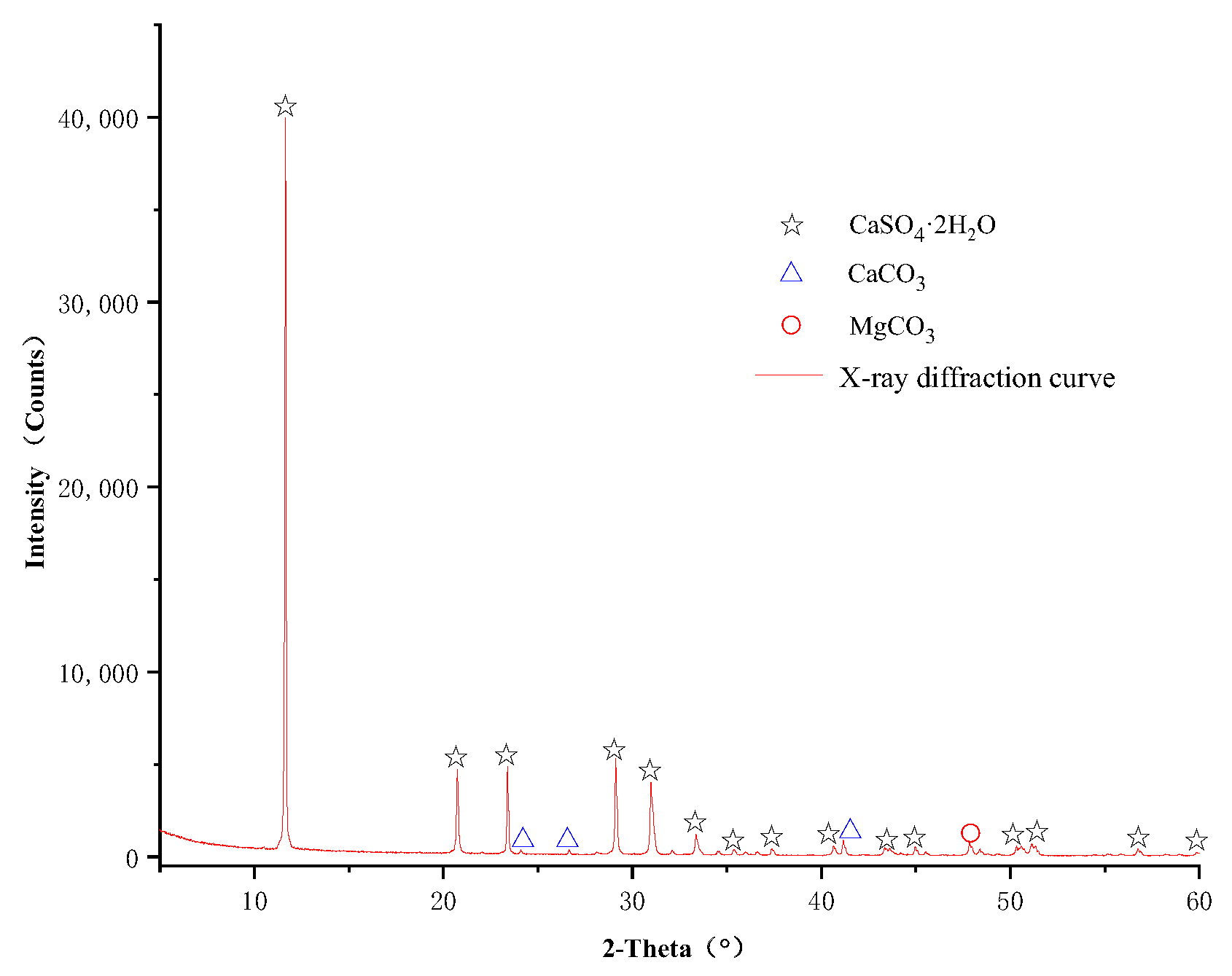
2.2. Rock Composition
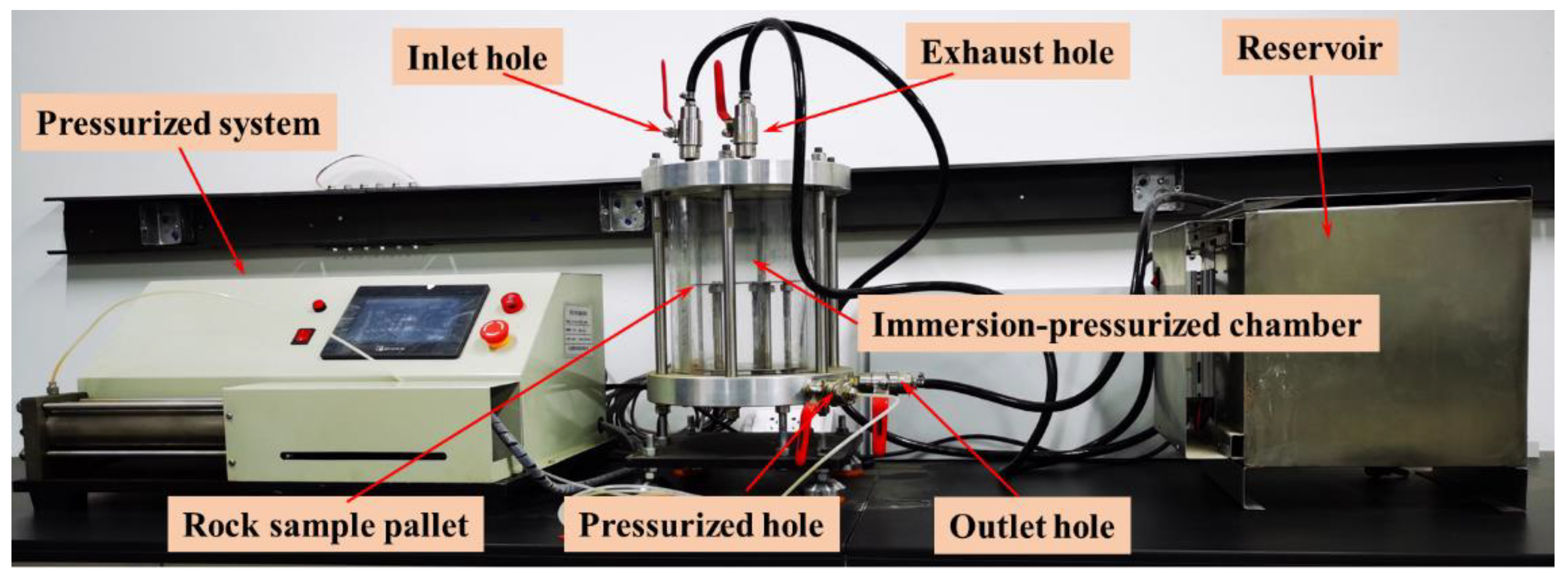
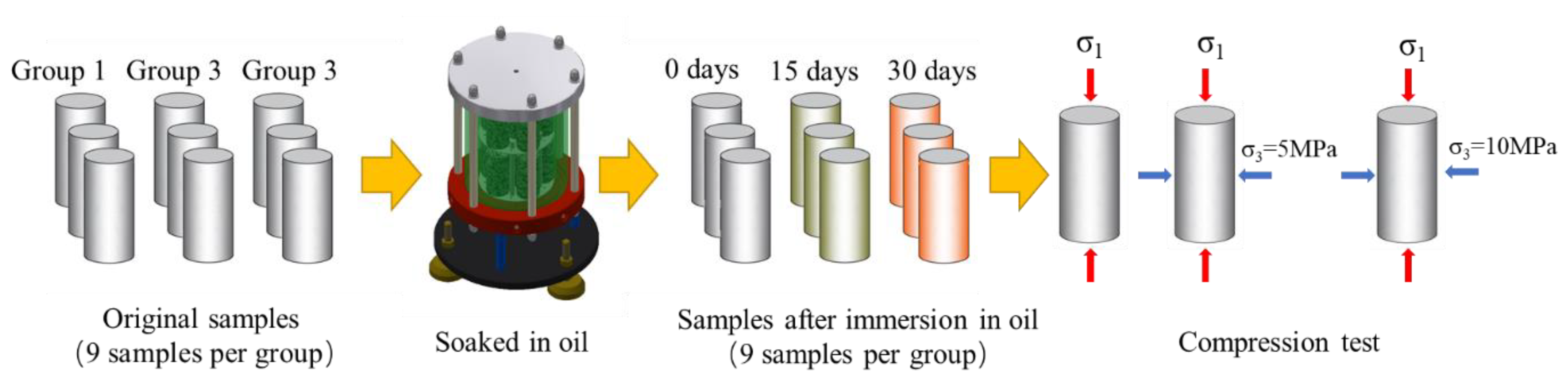
2.3. Preparation of Oil Immersion Samples
2.4. Effects of Oil Immersion on Physical Properties of Gypsum Rock
3. Experimental Process and Result Analysis
3.1. Process of Testing
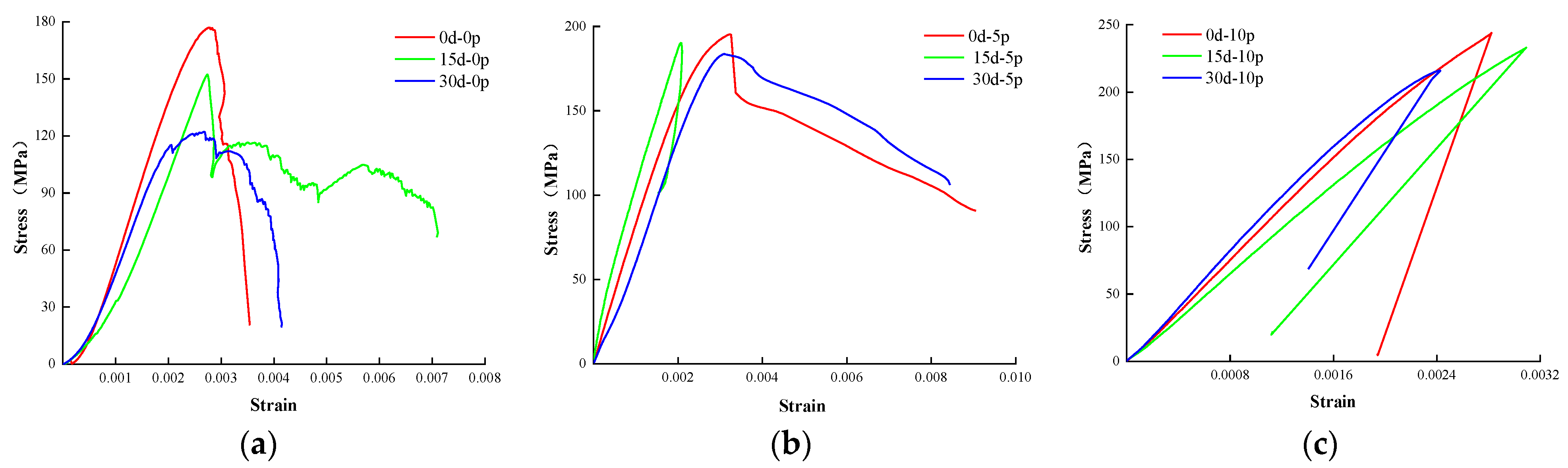
3.2. Analysis of Results
3.3. Law of Mechanical Damage and Deterioration of Oil-Impregnated Gypsum Rock
4. Conclusions
- (1)
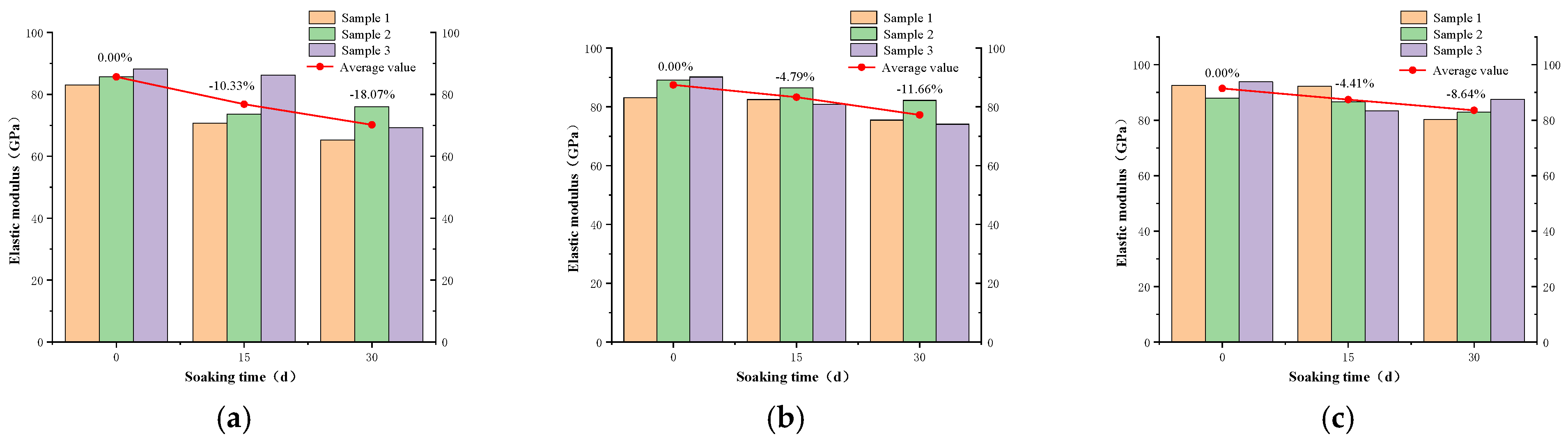
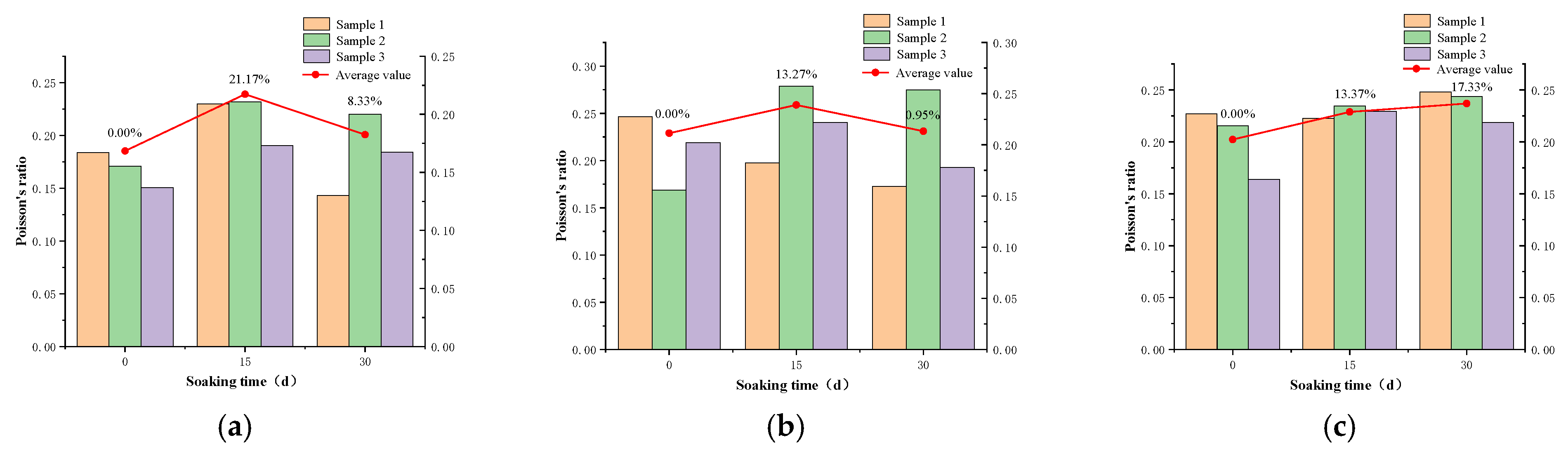
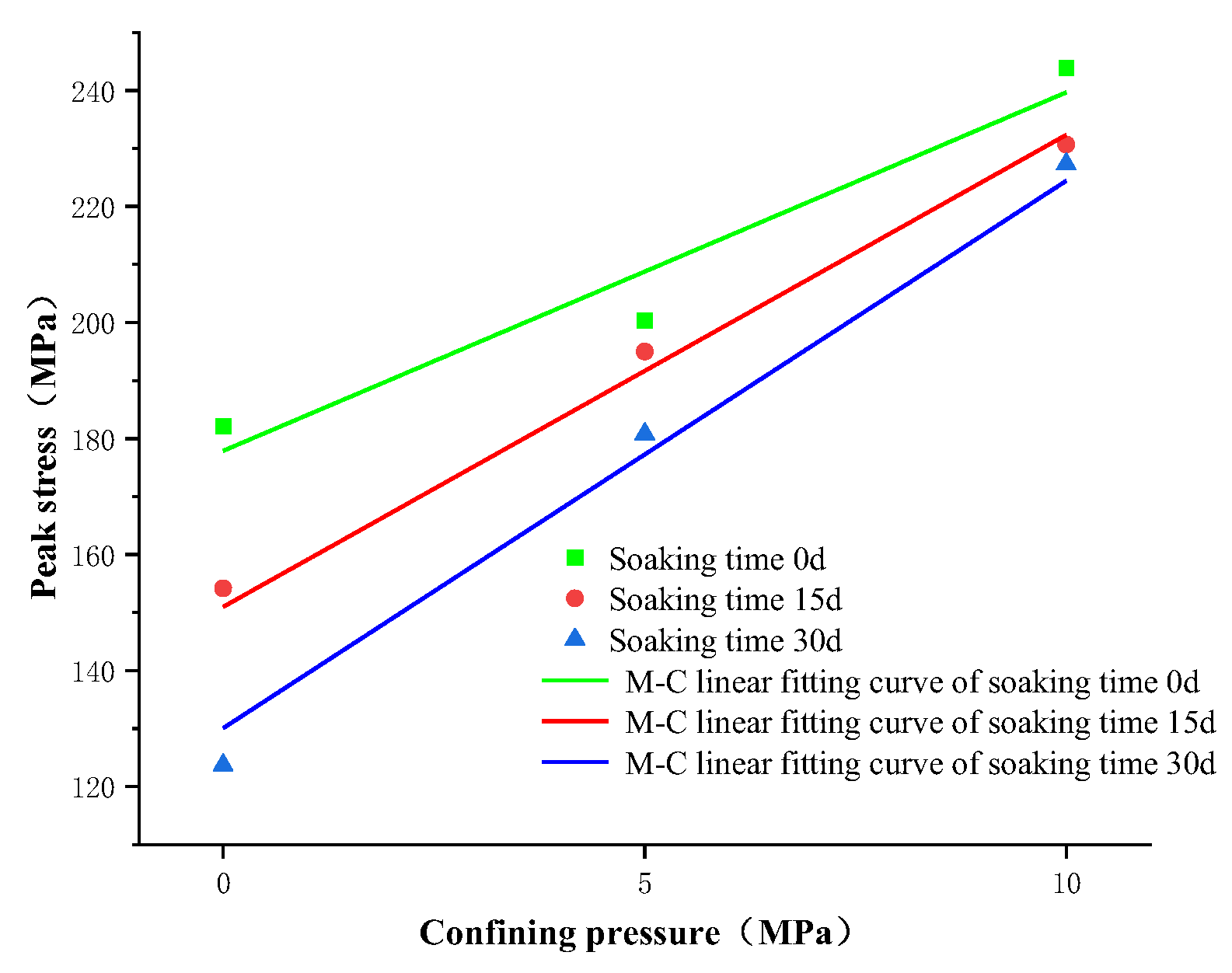
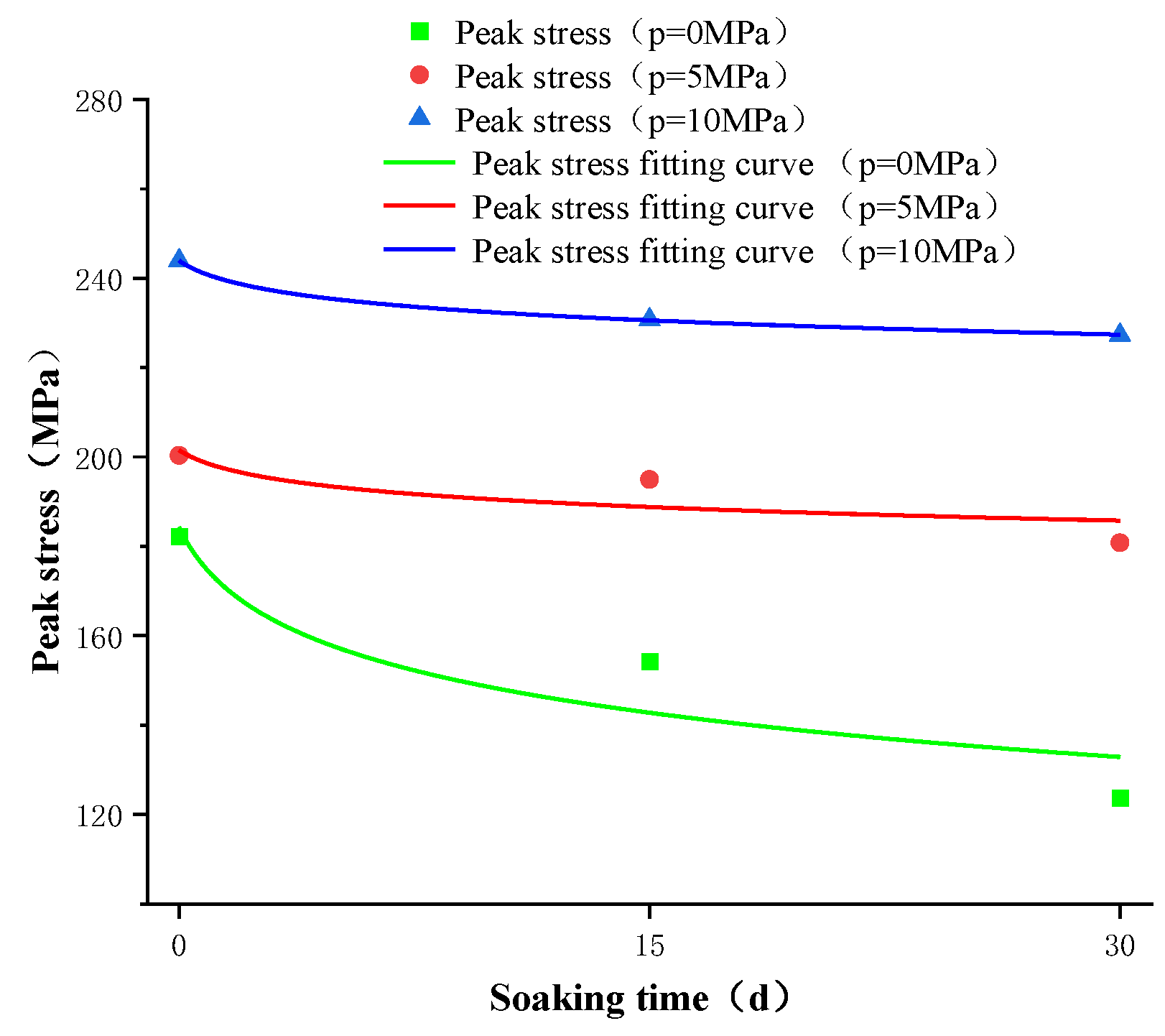
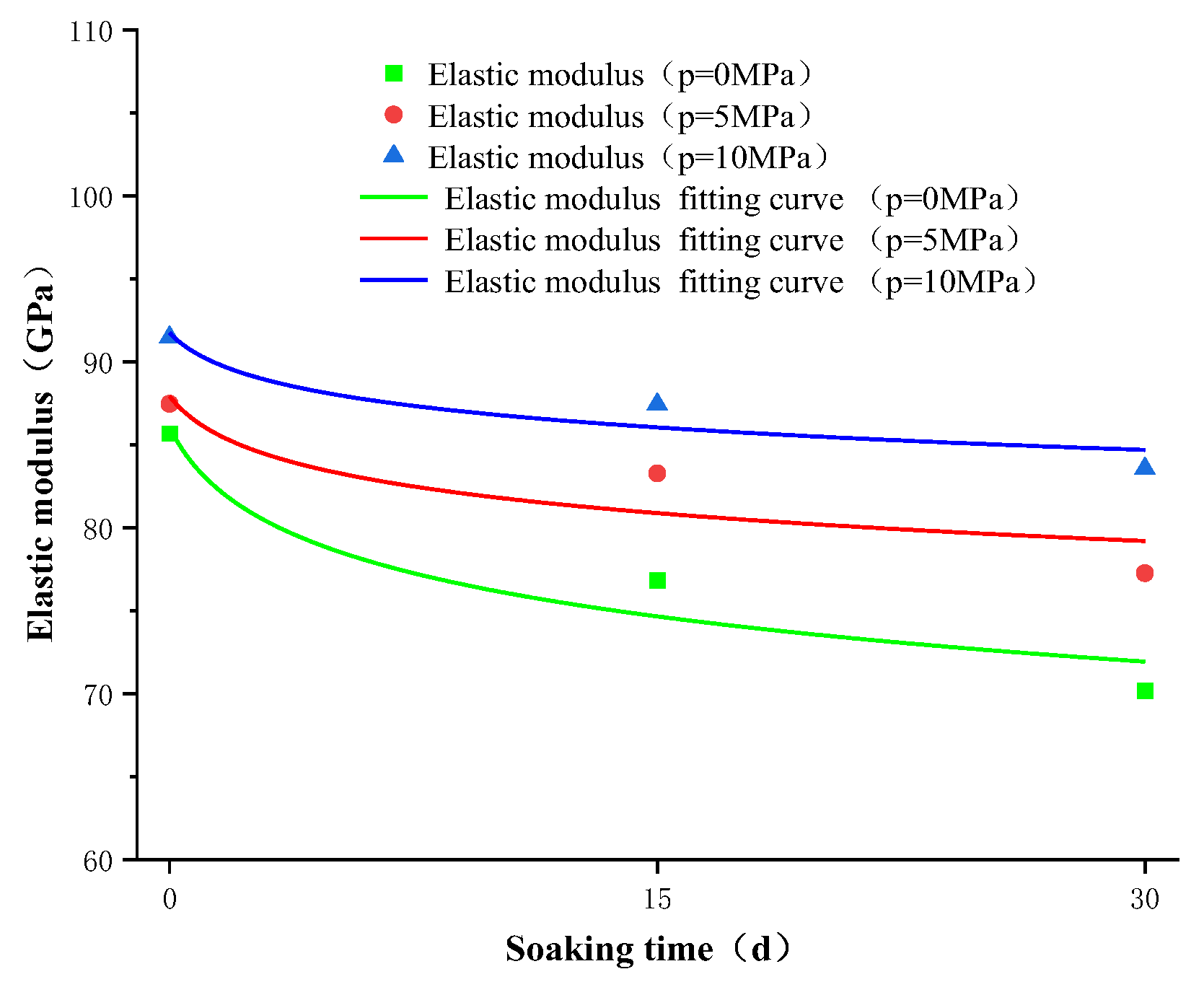
- The effect of different oil immersion times on the mechanical properties of gypsum rock samples was studied. With increasing oil immersion time, the peak stress of gypsum rock tended to decrease. When the confining pressure was higher, the peak stress of the samples with a longer oil immersion time decreased to a lesser extent, indicating that the oil immersion time affected the peak stress of gypsum rock under high confining pressure. The elastic modulus decreased with increasing oil immersion time. When the confining pressure was higher, the elastic modulus of gypsum with a longer oil immersion time decreased to a lesser degree, indicating that the oil immersion time affected the high confining pressure gypsum rock samples. The effect of elastic modulus was also smaller, and the law was shown to be similar to that of peak strength. This indicates that the oil immersion time can soften the gypsum rock to a certain extent, and the high confining pressure makes the gypsum crystals more compact. This causes the oil molecules inside or on the surface of the gypsum to be squeezed out, which reduces the softening effect.
- (2)
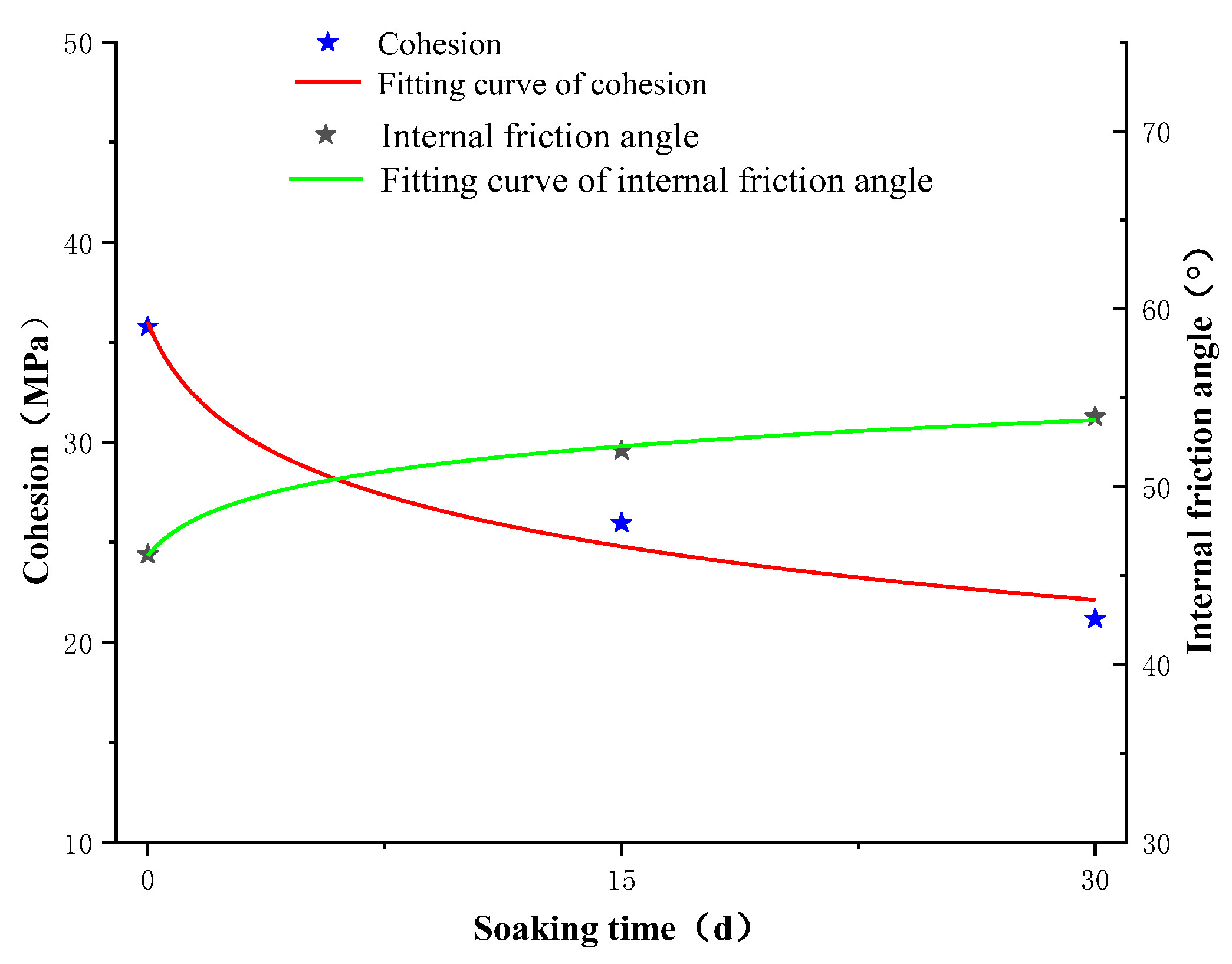
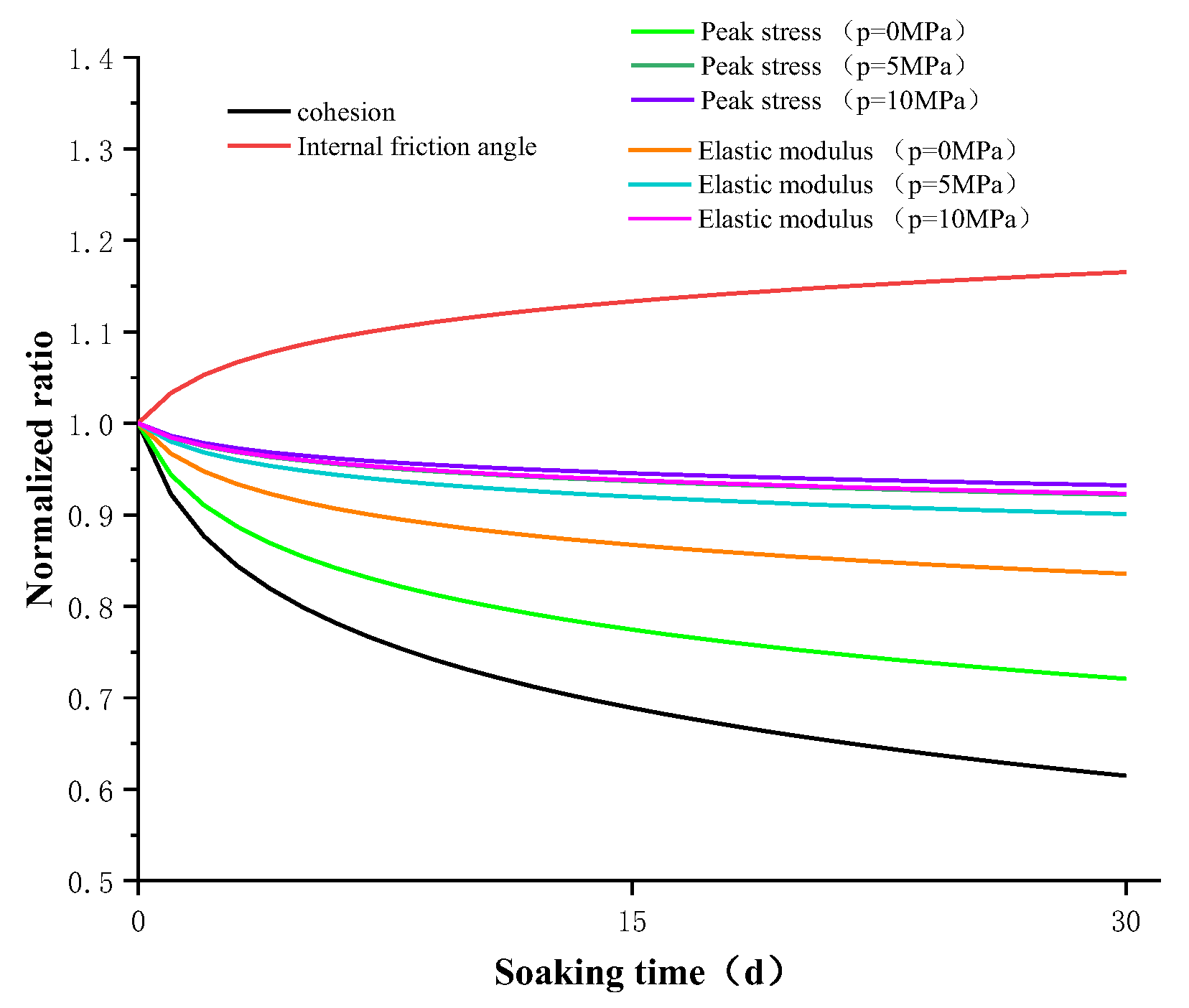
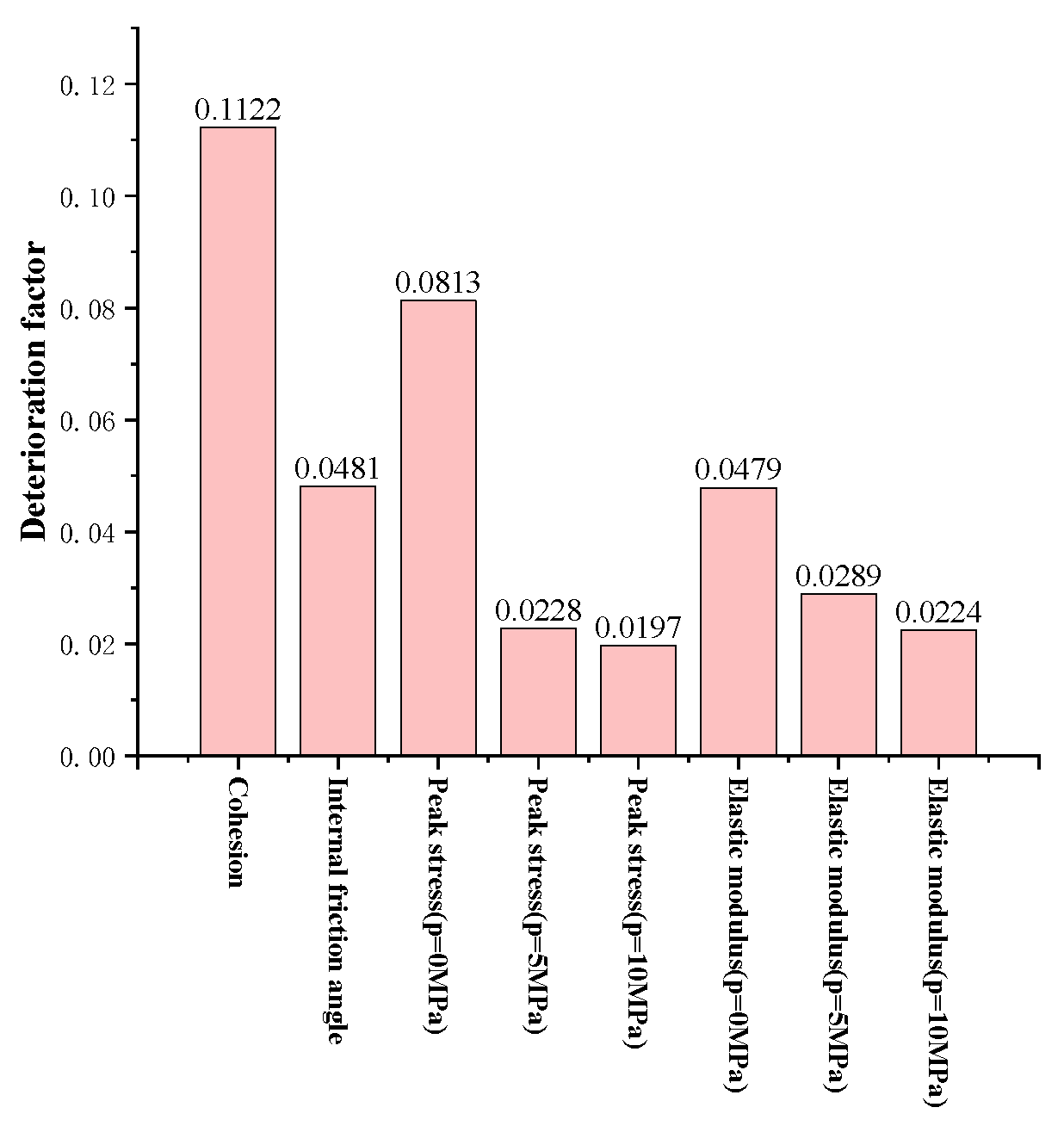
- The damage evolution characteristics of rocks as related to oil immersion time were revealed. Using statistical fitting, the normalized expressions of rock parameters with oil immersion times were established, and the deterioration coefficient was defined to evaluate the influence of oil immersion time on each parameter. The calculation results indicate that, as compared with 0 days of oil immersion, the internal friction angle increased by 12.17% after 15 days of oil immersion, while the internal friction angle increased by 16.81% after 30 days of oil immersion, and the cohesion decreased by 27.45% after 15 days of oil immersion. Moreover, cohesion was reduced by 40.83% after 30 days of oil immersion. In general, except for the internal friction angle, which increased with the increase in oil immersion time, the other parameters exhibited a decreasing trend with the increase in oil immersion time. The effects of oil immersion on the mechanical parameters of gypsum rock differed. Under a confining pressure of 0 MPa, the cohesion force had the greatest influence on the parameters, followed by peak stress, internal friction angle, and elastic modulus. The analysis results under confining pressures of 5 and 10 MPa show that the influence of oil immersion time weakened with the increase in confining pressure, as regards both peak stress and elastic modulus, which further indicates that the high confining pressure state is more effective for crude oil reserves.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, Y.; Li, M.; Xu, X.; Li, X.; Ma, Y.; Ma, Z. Research on Catastrophic Pillar Instability in Room and Pillar Gypsum Mining. Sustainability 2018, 10, 3773. [Google Scholar] [CrossRef]
- Fischer, A.; Hartlieb, P.; Daul, J. Abbauplanung der Schwebenrückgewinnung im Gipsbergbau Preinsfeld. Berg Huettenmaenn Mon. 2020, 165, 270–273. [Google Scholar] [CrossRef]
- Shun, P. Investigation of Instability and Blasting Caving Technology of Composite Support Structure in the Goaf of Gypsum Mine. Geotech. Geol. Eng. 2021, 15, 4377–4391. [Google Scholar] [CrossRef]
- Du, Z.; Liu, Z.; Liu, R.; Wang, S.; Li, F. Influencing Factors for the Instability and Collapse Mode of the Goaf Structure in a Gypsum Mine. Adv. Civ. Eng. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Xie, H.; Zhao, J.W.; Zhou, H.W.; Ren, S.H.; Zhang, R.X. Secondary Utilizations and Perspectives of Mined Underground Space. Tunn. Undergr. Space Technol. 2020, 96, 103129. [Google Scholar] [CrossRef]
- Istvan, J.A.; Evans, L.J.; Weber, J.H.; Devine, C. Rock Mechanics for Gas Storage in Bedded Salt Caverns. Int. J. Rock Mech. Min. Sci. 1997, 34, e1–e142. [Google Scholar] [CrossRef]
- Martinez, J.D. Energy Programs--A Contribution to Knowledge About Salt Domes: ABSTRACT. Bulletin 1986, 70, 227–238. [Google Scholar] [CrossRef]
- Liang, G.; Huang, X.; Peng, X.; Tian, Y.; Yu, Y. Investigation on the Cavity Evolution of Underground Salt Cavern Gas Storages. J. Nat. Gas Sci. Eng. 2016, 33, 118–134. [Google Scholar] [CrossRef]
- Ma, X.; Xu, Z.; Chen, L.; Shi, X. Creep Deformation Analysis of Gas Storage in Salt Caverns. Int. J. Rock Mech. Min. Sci. 2021, 139, 104635. [Google Scholar] [CrossRef]
- Liu, S.; Wang, H.; Du, A.; Zhang, B. Tightness Analysis of Anhydrite Mine-Out Used for Underground Crude Oil Storage Considering Seepage–Stress Coupling: A Case Study. Energies 2022, 15, 2929. [Google Scholar] [CrossRef]
- Wang, T.T.; Ma, H.L.; Shi, X.L.; Yang, C.H.; Zhang, N.; Li, J.L.; Ding, S.L.; Daemen, J.J.K. Salt Cavern Gas Storage in an Ultra-Deep Formation in Hubei, China. Int. J. Rock Mech. Min. Sci. 2018, 102, 57–70. [Google Scholar] [CrossRef]
- Khaledi, K.; Mahmoudi, E.; Datcheva, M.; Schanz, T. Stability and Serviceability of Underground Energy Storage Caverns in Rock Salt Subjected to Mechanical Cyclic Loading. Int. J. Rock Mech. Min. Sci. 2016, 86, 115–131. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, F.; Bai, Q. Underground Space Utilization of Coalmines in China: A Review of Underground Water Reservoir Construction. Tunn. Undergr. Space Technol. 2021, 107, 103657. [Google Scholar] [CrossRef]
- Menéndez, J.; Loredo, J.; Galdo, M.; Fernández-Oro, J.M. Energy Storage in Underground Coal Mines in NW Spain: Assessment of an Underground Lower Water Reservoir and Preliminary Energy Balance. Renew. Energy 2019, 134, 1381–1391. [Google Scholar] [CrossRef]
- Qin, C.; Loth, E. Isothermal Compressed Wind Energy Storage Using Abandoned Oil/Gas Wells or Coal Mines. Appl. Energy 2021, 292, 116867. [Google Scholar] [CrossRef]
- Jiang, D.; Chen, S.; Liu, W.; Ren, Y.; Guo, P.; Li, Z. Underground Hydro-Pumped Energy Storage Using Coal Mine Goafs: System Performance Analysis and a Case Study for China. Front. Earth Sci. 2021, 9, 760464. [Google Scholar] [CrossRef]
- Hangx, S.J.T.; Spiers, C.J.; Peach, C.J. The Effect of Deformation on Permeability Development in Anhydrite and Implications for Caprock Integrity during Geological Storage of CO2: Effect of Deformation on Permeability Development in Anhydrite. Geofluids 2010, 10, 369–387. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, C. Experimental investigation on strength and deformation properties of anhydrite under conventional triaxial compression. Rock Soil Mech. 2010, 31, 1776–1780. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, B.; Wang, L.; Yu, X.; Shi, L.; Fu, D. Experimental Investigation on the Long-Term Interactions of Anhydrite Rock, Crude Oil, and Water in a Mine-out Space for Crude-Oil Storage. Eng. Geol. 2020, 265, 105414. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, B.; Xu, N.; Yu, X. Stability Analysis of Anhydrite Mine-out as an Underground Gas Storage Based on DEM and Similarity Theory: A Case Study. Bull Eng Geol Env. 2022, 81, 99. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, H.; Wang, L.; Mei, G.; Shi, L.; Xu, N.; Li, J. Large-Scale Field Test on Abandoned Deep Anhydrite Mine-out for Reuse as Crude Oil Storage—A Case Study. Eng. Geol. 2020, 267, 105477. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, X.-D.; Zhang, S.-J.; Xie, L.-K. Analysis of Support Requirements for Underground Water-Sealed Oil Storage Cavern in China. Tunn. Undergr. Space Technol. 2018, 71, 36–46. [Google Scholar] [CrossRef]
- Sofianos, A.I. Tunnelling Mohr–Coulomb Strength Parameters for Rock Masses Satisfying the Generalized Hoek–Brown Criterion. Int. J. Rock Mech. Min. Sci. 2003, 40, 435–440. [Google Scholar] [CrossRef]
- Rafiei Renani, H.; Martin, C.D. Slope Stability Analysis Using Equivalent Mohr–Coulomb and Hoek–Brown Criteria. Rock Mech. Rock Eng. 2020, 53, 13–21. [Google Scholar] [CrossRef]
- Lee, Y.-K.; Pietruszczak, S. Limit Equilibrium Analysis Incorporating the Generalized Hoek–Brown Criterion. Rock Mech. Rock Eng. 2021, 54, 4407–4418. [Google Scholar] [CrossRef]
- Lini Dev, K.; Pillai, R.J.; Robinson, R.G. Drained Angle of Internal Friction from Direct Shear and Triaxial Compression Tests. Int. J. Geotech. Eng. 2016, 10, 283–287. [Google Scholar] [CrossRef]
- Wang, S.; Xu, W.; Sun, M.; Wang, W. Experimental Investigation of the Mechanical Properties of Fine-Grained Sandstone in the Triaxial Cyclic Loading Test. Env. Earth Sci. 2019, 78, 416. [Google Scholar] [CrossRef]
- Zha, F.; Huang, K.; Kang, B.; Sun, X.; Su, J.; Li, Y.; Lu, Z. Deterioration Characteristic and Constitutive Model of Red-Bed Argillaceous Siltstone Subjected to Drying-Wetting Cycles. Lithosphere 2022, 2022, 8786210. [Google Scholar] [CrossRef]






| Soaking Time/d | Average Height/mm | Average Diameter/mm | Average Quality/g | Average Density/g cm−3 | ||
|---|---|---|---|---|---|---|
| Before Oil Immersion | After Oil Immersion | Before oil Immersion | After Oil Immersion | |||
| 0 | 100.05 | 50.01 | 563.14 | / | 2.86 | / |
| 15 | 100.05 | 49.96 | 564.75 | 565.36 | 2.88 | 2.88 |
| 30 | 99.99 | 49.97 | 563.88 | 564.26 | 2.88 | 2.88 |
| Soaking Time/d | Average Shear Wave Velocity /m˖s-1 | Average longitudinal Wave Velocity /m s−1 | ||
|---|---|---|---|---|
| Before Oil Immersion | After Oil Immersion | Before Oil Immersion | After Oil Immersion | |
| 0 | 4340 | / | 6651 | / |
| 15 | 4316 | 4420 | 6244 | 6154 |
| 30 | 4303 | 4582 | 6788 | 6779 |
| P/MPa | Soaking Time/d | Peak Stress /MPa | Change/% | Elastic Modulus /GPa | Change/% | Poisson’s Ratio | Change/% |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 182.11 | 0.00% | 85.67 | 0.00% | 0.168 | 0.00% |
| 15 | 154.15 | −15.35% | 76.82 | −10.33% | 0.217 | 21.17% | |
| 30 | 123.67 | −32.09% | 70.19 | −18.07% | 0.182 | 8.33% | |
| 5 | 0 | 200.34 | 0.00% | 87.47 | 0.00% | 0.211 | 0.00% |
| 15 | 194.96 | −2.69% | 83.28 | −4.79% | 0.239 | 13.27% | |
| 30 | 180.79 | −9.76% | 77.27 | −11.66% | 0.213 | 0.95% | |
| 10 | 0 | 243.89 | 0.00% | 91.47 | 0.00% | 0.202 | 0.00% |
| 15 | 230.69 | −5.41% | 87.44 | −4.41% | 0.229 | 13.37% | |
| 30 | 227.30 | −6.80% | 83.57 | −8.64% | 0.237 | 17.33% |
| Soaking Time/d | σ0 | k | R2 | c (MPa) | The Proportion of Change in c | φ (°) | The Proportion of Change in φ |
|---|---|---|---|---|---|---|---|
| 0 | 177.89 | 6.178 | 0.9470 | 35.78 | 0.00% | 46.17 | 0.00% |
| 15 | 150.99 | 8.455 | 0.9876 | 25.96 | −27.45% | 52.04 | 12.17% |
| 30 | 130.08 | 9.435 | 0.9885 | 21.17 | −40.83% | 53.93 | 16.81% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, Y.; Zhang, C.; Ren, G.; Zhang, L. Experimental Investigation of the Mechanical Behavior and Damage Evolution Mechanism of Oil-Impregnated Gypsum Rock. Sustainability 2022, 14, 11172. https://doi.org/10.3390/su141811172
Ge Y, Zhang C, Ren G, Zhang L. Experimental Investigation of the Mechanical Behavior and Damage Evolution Mechanism of Oil-Impregnated Gypsum Rock. Sustainability. 2022; 14(18):11172. https://doi.org/10.3390/su141811172
Chicago/Turabian StyleGe, Yongxiang, Congrui Zhang, Gaofeng Ren, and Luwei Zhang. 2022. "Experimental Investigation of the Mechanical Behavior and Damage Evolution Mechanism of Oil-Impregnated Gypsum Rock" Sustainability 14, no. 18: 11172. https://doi.org/10.3390/su141811172
APA StyleGe, Y., Zhang, C., Ren, G., & Zhang, L. (2022). Experimental Investigation of the Mechanical Behavior and Damage Evolution Mechanism of Oil-Impregnated Gypsum Rock. Sustainability, 14(18), 11172. https://doi.org/10.3390/su141811172






