Design, Modelling and Optimization of a Novel Concentrated Solar Powered (CSP) Flash Desalination System Involving Direct Heating and Pressure Modulation Using Response Surface Methodology (RSM)
Abstract
:1. Introduction
2. Experiments
2.1. Materials and Method
2.2. Experiment Design Using RSM
3. Results and Discussion
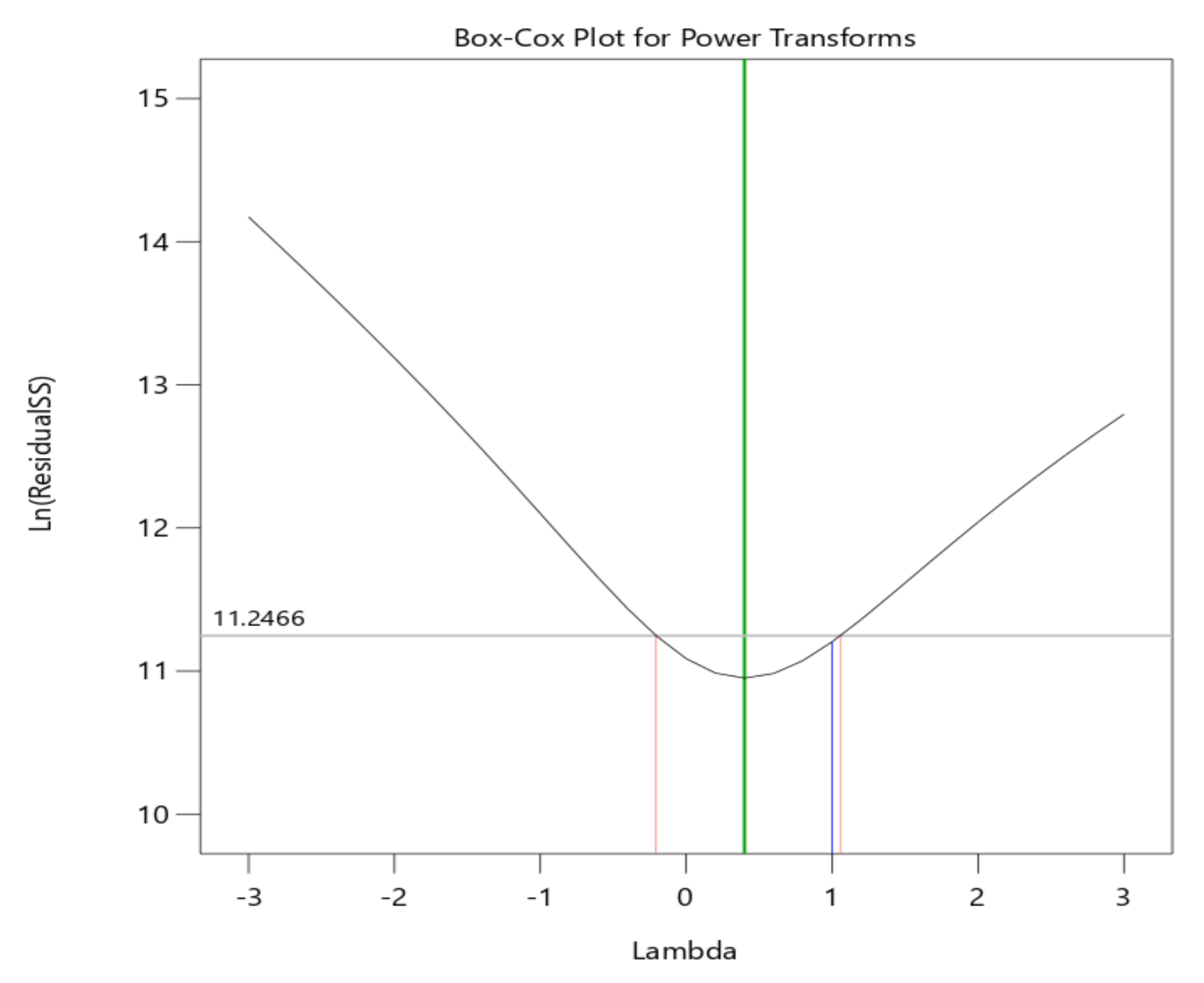
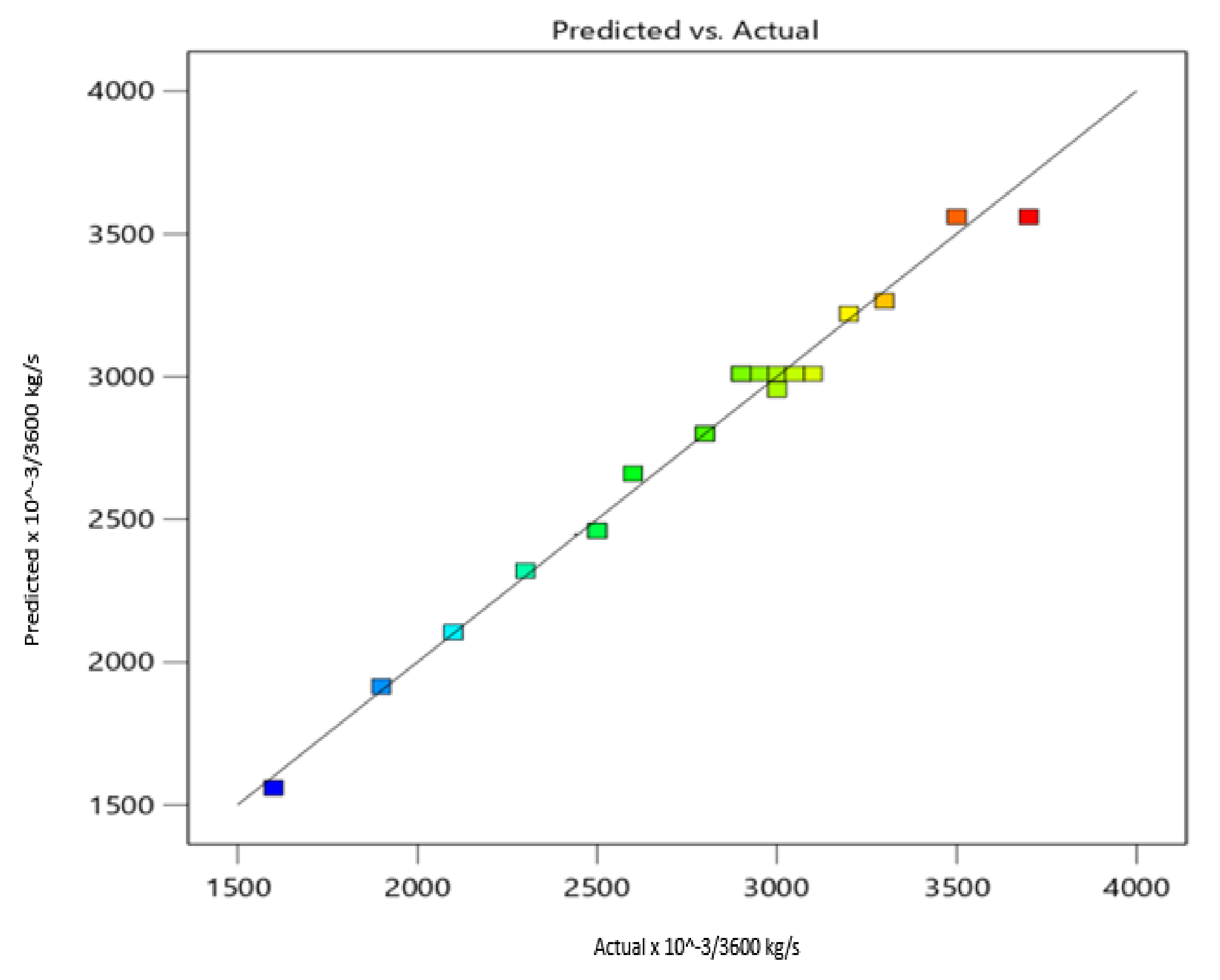
3.1. Model Development for Distillate Production
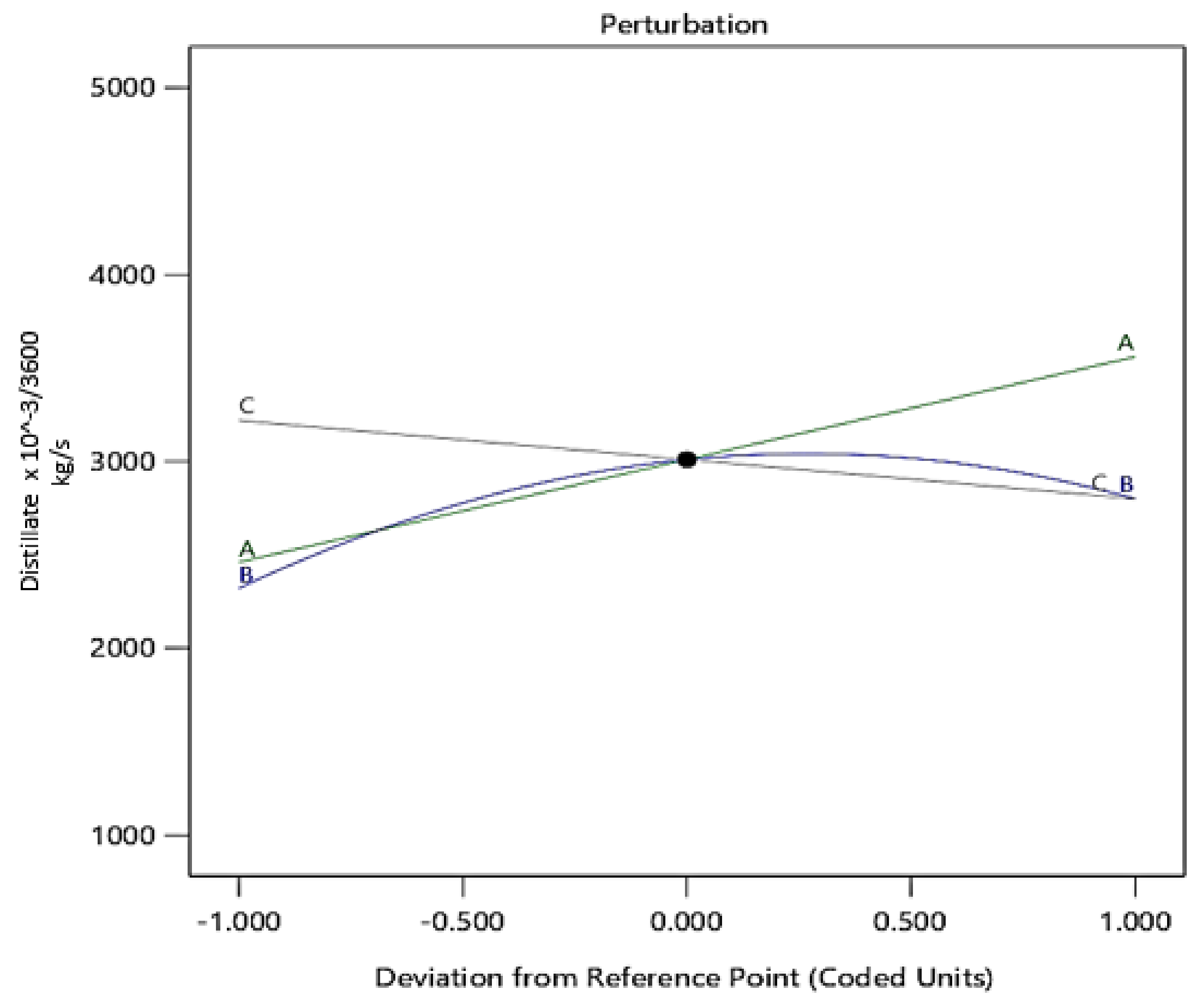
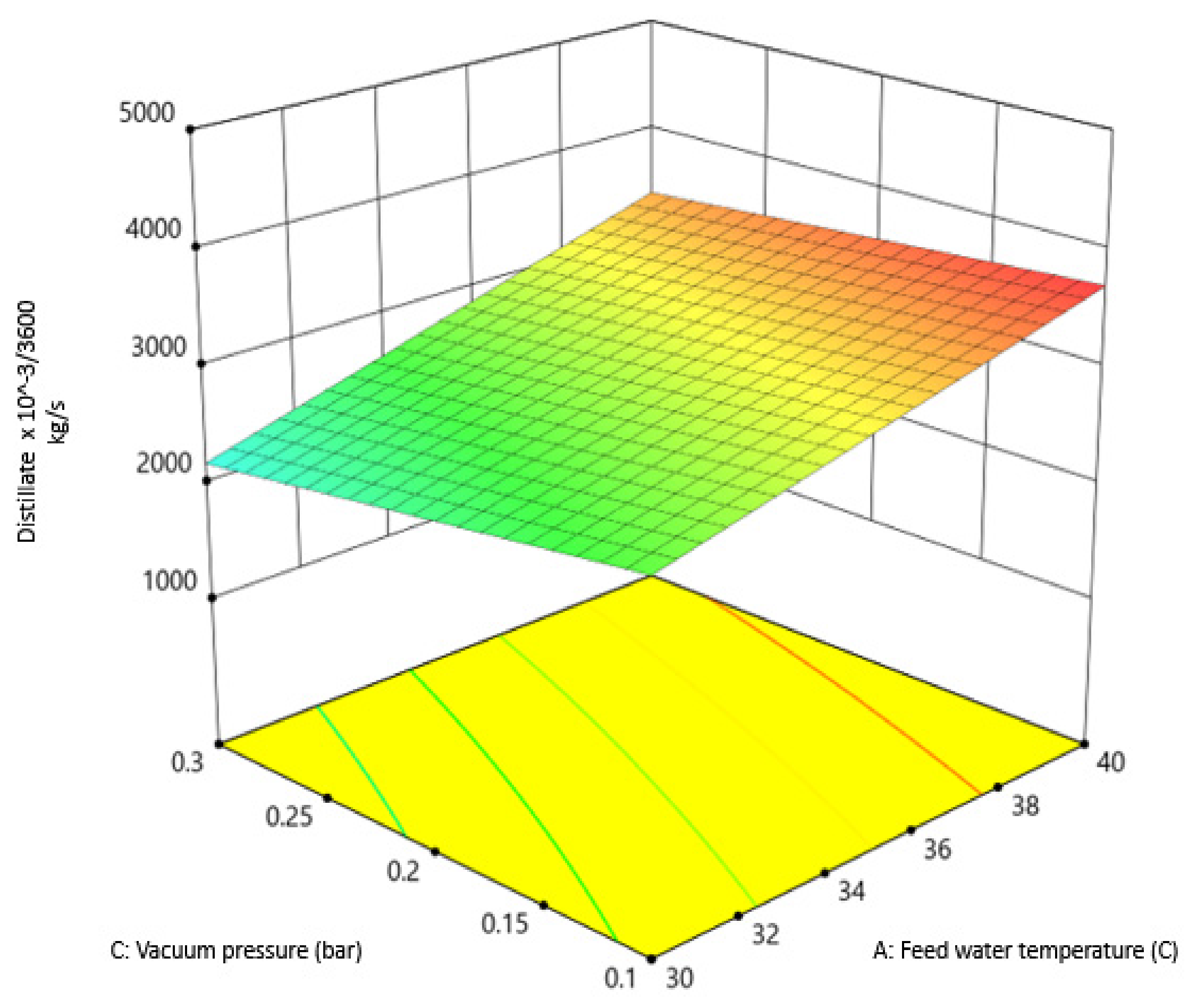
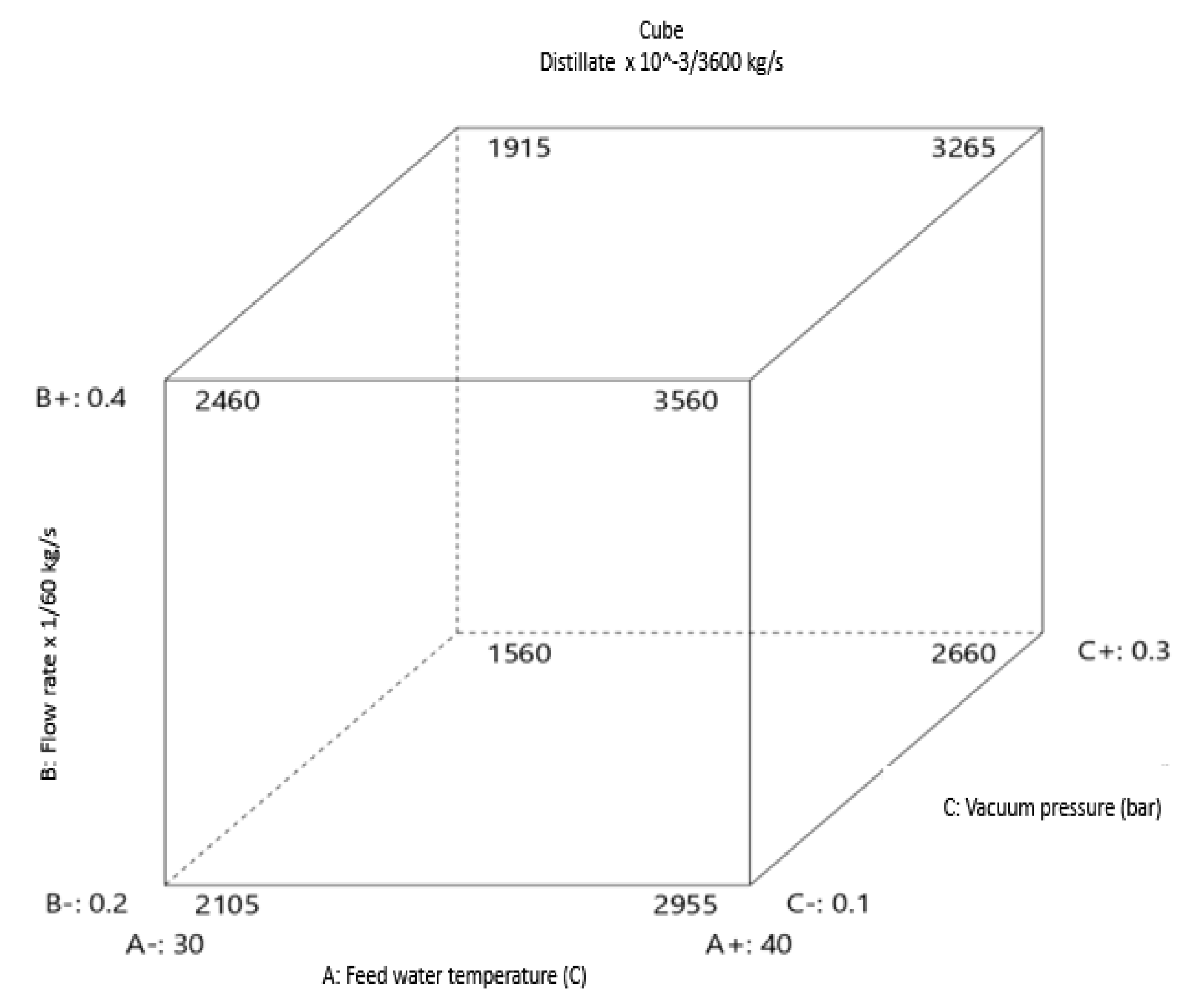
3.2. Effect of Independent Variables on Distillate Production
4. Energy and Exergy Analysis
4.1. Energy Analysis
4.2. Exergy Analysis of Concentrator Plate Heat Exchanger
- Te is environment temperature, K
- Ts is sun temperature, 5800 K
- Tfm is the mean fluid temperature for the heat exchanger
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Risse, B.; Spitzer, D.; Hassler, D.; Schnell, F.; Comet, M.; Pichot, V.; Muhr, H. Continuous formation of submicron energetic particles by the flash-evaporation technique. Chem. Eng. J. 2012, 203, 158–165. [Google Scholar] [CrossRef]
- Lv, H.; Wang, Y.; Wu, L.; Hu, Y. Numerical simulation and optimization of the flash chamber for multi-stage flash seawater desalination. Desalination 2019, 465, 69–78. [Google Scholar] [CrossRef]
- Cheng, W.; Zhang, W.; Cheng, H.; Hu, L. Spray cooling and flash evaporation cooling: The current development and application. Renew. Sustain. Energy Rev. 2016, 55, 614–628. [Google Scholar] [CrossRef]
- Gandhidasan, P. Quick performance prediction of liquid desiccant regeneration in a packed bed. Sol. Energy 2005, 79, 47–55. [Google Scholar] [CrossRef]
- Ezzat, A.W.; Hu, E.; Al-Najjar, H.M.T.; Zhao, Z.; Shu, X. Investigation of steam jet flash evaporation with solar thermal collectors in water desalination systems. Therm. Sci. Eng. Prog. 2020, 20, 100710. [Google Scholar] [CrossRef]
- Chen, L.X.; Hu, P.; Sheng, C.C.; Zhang, N.; Na Xie, M.; Wang, F.X. Thermodynamic analysis of three ejector based organic flash cycles for low grade waste heat recovery. Energy Convers. Manag. 2019, 185, 384–395. [Google Scholar] [CrossRef]
- Lin, S.; Zhao, H.; Zhu, L.; He, T.; Chen, S.; Gao, C.; Zhang, L. Seawater desalination technology and engineering in China: A review. Desalination 2021, 498, 114728. [Google Scholar] [CrossRef]
- Miyatake, O.; Koito, Y.; Tagawa, K.; Maruta, Y. Transient characteristics and performance of a novel desalination system based on heat storage and spray flashing. Desalination 2001, 137, 157–166. [Google Scholar] [CrossRef]
- Lai, X.; Long, R.; Liu, Z.; Liu, W. Solar energy powered high-recovery reverse osmosis for synchronous seawater desalination and energy storage. Energy Convers. Manag. 2021, 228, 113665. [Google Scholar] [CrossRef]
- Ghorbani, B.; Mehrpooya, M.; Dadak, A. Thermo-economic analysis of a solar-driven multi-stage desalination unit equipped with a phase change material storage system to provide heating and fresh water for a residential complex. J. Energy Storage 2020, 30, 101555. [Google Scholar] [CrossRef]
- Gao, W.; Qi, J.; Zhang, J.; Chen, G.; Wu, D. An experimental study on explosive boiling of superheated droplets in vacuum spray flash evaporation. Int. J. Heat Mass Transf. 2019, 144, 118552. [Google Scholar] [CrossRef]
- Ji, C.; Cheng, L.; Wang, N.; Liu, Z. Experimental investigation on high-pressure high-temperature spray flash evaporation and the characteristic Jakob number. Exp. Therm. Fluid Sci. 2019, 102, 94–100. [Google Scholar] [CrossRef]
- Muthunayagam, A.; Ramamurthi, K.; Paden, J. Low temperature flash vaporization for desalination. Desalination 2005, 180, 25–32. [Google Scholar] [CrossRef]
- Ikegami, Y.; Sasaki, H.; Gouda, T.; Uehara, H. Experimental study on a spray flash desalination (influence of the direction of injection). Desalination 2006, 194, 81–89. [Google Scholar] [CrossRef]
- Fathinia, F.; Al-Abdeli, Y.M.; Khiadani, M. Evaporation rates and temperature distributions in fine droplet flash evaporation sprays. Int. J. Therm. Sci. 2019, 145, 106037. [Google Scholar] [CrossRef]
- Peng, Y.; Cheng, W. Experimental investigation on the effect of heat transfer enhancement of vacuum spray flash evaporation cooling using Al2O3–water nanofluid. Energy Procedia 2017, 142, 3766–3773. [Google Scholar] [CrossRef]
- Guo, Y.; Ma, H.; Fu, B.; Ji, Y.; Su, F.; Wilson, C. Heat Transfer Analysis of Flash Evaporation with MEPCM. J. Thermal Sci. Eng. Appl. 2019, 11, 051016. [Google Scholar] [CrossRef]
- Jurkowska, M.; Szczygieł, I. Review on properties of microencapsulated phase change materials slurries (mPCMS). Appl. Therm. Eng. 2016, 98, 365–373. [Google Scholar] [CrossRef]
- Ali, S.; Mustafa, M. Barriers facing Micro-encapsulated Phase Change Materials Slurry (MPCMS) in Photovoltaic Thermal (PV/T) application. Energy Rep. 2020, 6, 565–570. [Google Scholar] [CrossRef]
- Yu, Q.; Romagnoli, A.; Yang, R.; Xie, D.; Liu, C.; Ding, Y.; Li, Y. Numerical study on energy and exergy performances of a microencapsulated phase change material slurry based photovoltaic/thermal module. Energy Convers. Manag. 2019, 183, 708–720. [Google Scholar] [CrossRef]
- Chen, Q.; Xu, G.; Xia, P. The performance of a solar-driven spray flash evaporation desalination system enhanced by microencapsulated phase change material. Case Stud. Therm. Eng. 2021, 27, 101267. [Google Scholar] [CrossRef]
- Moharram, N.A.; Bayoumi, S.; Hanafy, A.A.; El-Maghlany, W.M. Hybrid desalination and power generation plant utilizing multi-stage flash and reverse osmosis driven by parabolic trough collectors. Case Stud. Therm. Eng. 2021, 23, 100807. [Google Scholar] [CrossRef]
- Gnaifaid, H.; Ozcan, H. Multi-objective optimization of a concentrated solar energy driven trigeneration plant with thermal energy storage: A case study for Turkey. Case Stud. Therm. Eng. 2020, 20, 100642. [Google Scholar] [CrossRef]
- Aziz, M.A.; Abdullah, M.; Khor, C.; Azid, I. Optimization of pin through hole connector in thermal fluid–structure interaction analysis of wave soldering process using response surface methodology. Simul. Model. Pract. Theory 2015, 57, 45–57. [Google Scholar] [CrossRef]
- Ishak, M.H.H.; Ismail, F.; Aziz, M.S.A.; Abdullah, M.Z.; Abas, A. Optimization of 3D IC stacking chip on molded encapsulation process: A response surface methodology approach. Int. J. Adv. Manuf. Technol. 2019, 103, 1139–1153. [Google Scholar] [CrossRef]
- Lim, C.H.; Abdullah, M.Z.; Aziz, I.A.; Khor, C.Y.; Aziz, M.S.A. Optimization of flexible printed circuit board’s cooling with air flow and thermal effects using response surface methodology. Microelectron. Int. 2021, 38, 182–205. [Google Scholar] [CrossRef]
- Joy, V.M.; Feroz, S.; Dutta, S. Solar nanophotocatalytic pretreatment of seawater: Process optimization and performance evaluation using response surface methodology and genetic algorithm. Appl. Water Sci. 2021, 11, 18. [Google Scholar] [CrossRef]
- Salih, F.Y.M.; Sakhile, K.; Shaik, F.; Lakkimsetty, N.R. Treatment of petroleum wastewater using synthesised haematite (α-Fe2O3) photocatalyst and optimisation with response surface methodology. Int. J. Environ. Anal. Chem. 2020, 1–20. [Google Scholar] [CrossRef]
- Mohammadi, T.; Safavi, M. Application of Taguchi method in optimization of desalination by vacuum membrane distillation. Desalination 2009, 249, 83–89. [Google Scholar] [CrossRef]
- Alrowais, R.; Qian, C.; Burhan, M.; Ybyraiymkul, D.; Shahzad, M.W.; Ng, K.C. A greener seawater desalination method by direct-contact spray evaporation and condensation (DCSEC): Experiments. Appl. Therm. Eng. 2020, 179, 115629. [Google Scholar] [CrossRef]
- Lovineh, S.; Asghari, M.; Rajaei, B. Numerical simulation and theoretical study on simultaneous effects of operating parameters in vacuum membrane distillation. Desalination 2013, 314, 59–66. [Google Scholar] [CrossRef]
- Malik, A.; Qureshi, S.R.; Abbas, N.; Zaidi, A.A. Energy and exergy analyses of a solar desalination plant for Karachi Pakistan. Sustain. Energy Technol. Assessments 2020, 37, 100596. [Google Scholar] [CrossRef]
- Gomri, R. Energy and exergy analyses of seawater desalination system integrated in a solar heat transformer. Desalination 2009, 249, 188–196. [Google Scholar] [CrossRef]
- Bayu, S.; Yuli, S.I.; Agung, T.W.; Hector, I. Enhancing the performance of floating photo-voltaic system by using thermosiphon cooling method: Numerical and experimental analyses. Int. J. Therm. Sci. 2022, 180, 107727. [Google Scholar]
- Mirmanto; Sayoga, I.M.A.; Wijayanta, A.T.; Sasmito, A.P.; Aziz, M. Enhancement of Continuous-Feed Low-Cost Solar Distiller: Effects of Various Fin Designs. Energy 2021, 14, 4844. [Google Scholar] [CrossRef]



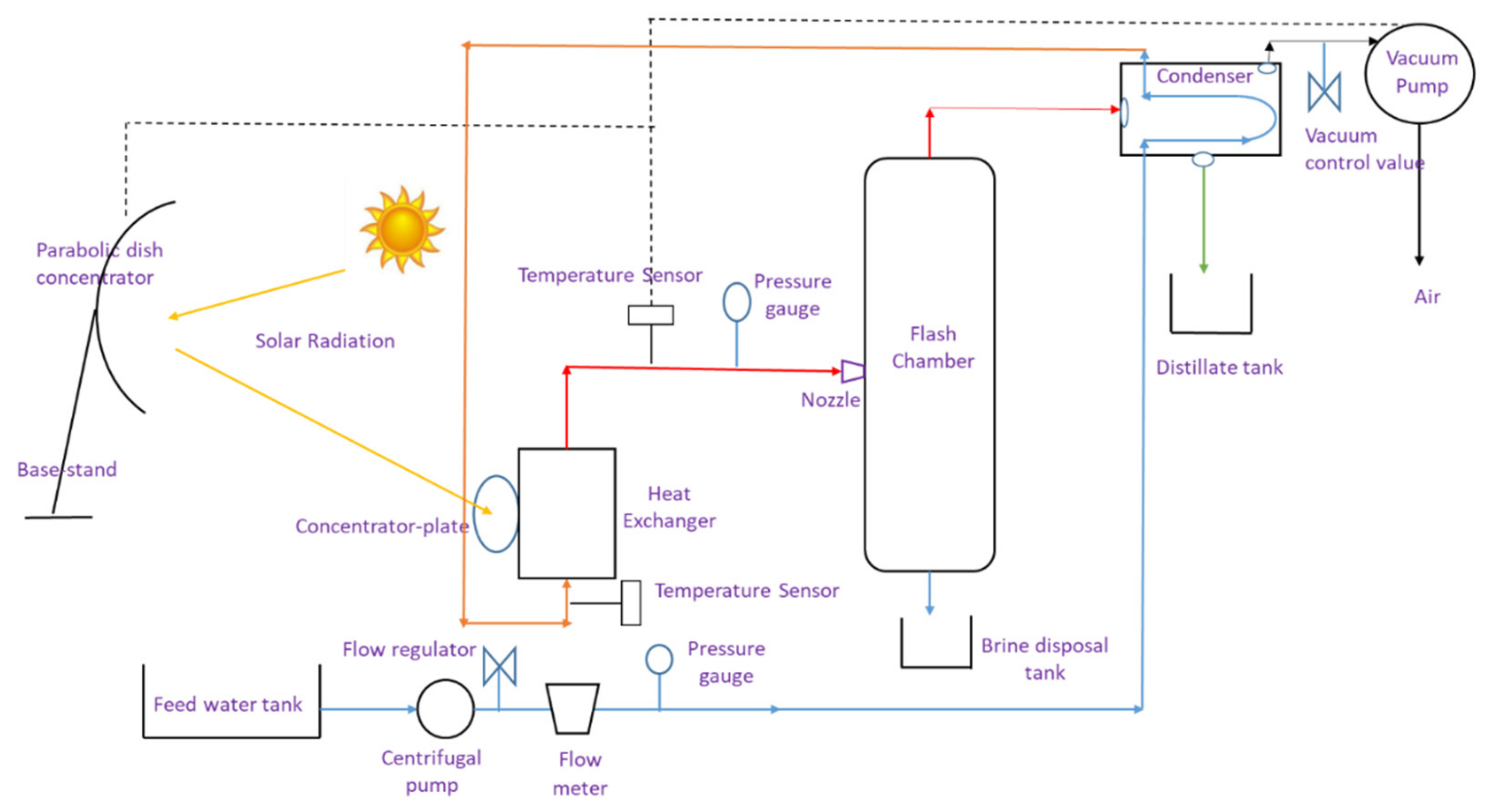

| S. No | Component | Dimensions/Specifications (L = Length, B = Breadth, H = Height) |
|---|---|---|
| 1 | Base board | 1.5 × 0.5 × 1.5 m (L × B × H) |
| 2 | Heat exchanger | 0.05 × 0.05 × 0.1 m (L × B × H) |
| 3 | Flash chamber | 0.1 × 0.1 × 0.2 m (L × B × H) |
| 4 | Condenser | 0.05 × 0.05 × 0.10 m (L × B × H) |
| colo5 | Pipes | 0.006 m |
| 6 | Nozzle | 0.002 m |
| 7 | Water tanks | 0.005 m3 |
| 8 | Water pump | 368 W |
| 9 | Parabolic dish | Radius = 0.28 m, depth = 0.04 m |
| 10 | Copper plate | Diameter = 0.05 m |
| S. No | Parameter | Instrument | Range | Uncertainty |
|---|---|---|---|---|
| 1 | Flow rate | Rotameter | 0.003 to 0.06 kg/s | 1.25% |
| 2 | Temperature | Type-K thermocouple | −50 to 1000 °C | 1.25% |
| Independent Variable | Coded Levels (Range) | ||
|---|---|---|---|
| −1 | 0 | +1 | |
| Flow rate (kg/s) | 0.003 | 0.0045 | 0.006 |
| Feed water temperature (°C) | 30 | 35 | 40 |
| Vacuum pressure (Pa) | 0.1 | 0.2 | 0.3 |
| Run | Independent Variables | Responses | CCD Position | ||
|---|---|---|---|---|---|
| Feed-Water Temperature, A | Flow Rate, B | Vacuum Pressure, C | Distillate Production kg/s | ||
| 1 | 35 | 0.006 | 0.2 | 0.00077 | Axial |
| 2 | 30 | 0.0045 | 0.2 | 0.00069 | Axial |
| 3 | 35 | 0.0045 | 0.2 | 0.00080 | Center |
| 4 | 30 | 0.003 | 0.1 | 0.00058 | Factorial |
| 5 | 35 | 0.0045 | 0.2 | 0.00081 | Center |
| 6 | 30 | 0.006 | 0.3 | 0.00052 | Factorial |
| 7 | 35 | 0.003 | 0.2 | 0.00063 | Axial |
| 8 | 40 | 0.006 | 0.1 | 0.00097 | Factorial |
| 9 | 35 | 0.0045 | 0.2 | 0.00080 | Center |
| 10 | 35 | 0.0045 | 0.3 | 0.00077 | Axial |
| 11 | 35 | 0.0045 | 0.1 | 0.00088 | Axial |
| 12 | 35 | 0.0045 | 0.2 | 0.00086 | Center |
| 13 | 35 | 0.0045 | 0.2 | 0.00083 | Center |
| 14 | 35 | 0.0045 | 0.2 | 0.00084 | Center |
| 15 | 30 | 0.003 | 0.3 | 0.00044 | Factorial |
| 16 | 40 | 0.006 | 0.3 | 0.00091 | Factorial |
| 17 | 40 | 0.005 | 0.2 | 0.001 | Axial |
| 18 | 40 | 0.003 | 0.3 | 0.00072 | Factorial |
| 19 | 40 | 0.003 | 0.1 | 0.00083 | Factorial |
| 20 | 30 | 0.006 | 0.1 | 0.00069 | Factorial |
| Response | Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Remarks |
|---|---|---|---|---|---|---|---|
| Distillate | Model | 5.117 × 106 | 6 | 8.528 × 105 | 150.84 | <0.0001 | SD = 75.19 Mean = 2785 CV = 2.7 R2 = 0.98 R2(adj) = 0.97 R2(pred) = 0.96 AP = 44.95 |
| A: Feed-water temperature | 3.025 × 106 | 1 | 3.025 × 106 | 535.03 | <0.0001 | ||
| B: Flow rate | 5.760 × 105 | 1 | 5.760 × 105 | 101.88 | <0.0001 | ||
| C: Vacuum pressure | 4.410 × 105 | 1 | 4.410 × 105 | 78 | <0.0001 | ||
| AB | 31,250.00 | 1 | 31,250.00 | 5.53 | 0.0352 | ||
| AC | 31,250.00 | 1 | 31,250.00 | 5.53 | 0.0352 | ||
| B² | 6.264 × 105 | 1 | 6.264 × 105 | 108.56 | <0.0001 | ||
| Residual | 73,500 | 13 | 5653.85 | - | - | ||
| Lack of Fit | 40,166.67 | 8 | 5020.83 | 0.7531 | 0.6571 | ||
| Pure Error | 33,333.33 | 5 | 6666.67 | - | - |
| Feed-Water Temperature (°C) | Flow Rate (kg/s) | Vacuum Pressure (Bar) | Distillate Production (kg/s × 10−3/3600) | Desirability | Error % | |
|---|---|---|---|---|---|---|
| Experimental | Predicted | |||||
| 40 | 0.005 | 0.1 | 3700 | 3758 | 0.95 | 1.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, F.; Abdul Aziz, M.S.; Mohd Arif Zainol, M.R.R.; Yee, K.C.; Shaik, F.; Che Halin, D.S.; Mohd Salleh, M.A.A.; Kheimi, M. Design, Modelling and Optimization of a Novel Concentrated Solar Powered (CSP) Flash Desalination System Involving Direct Heating and Pressure Modulation Using Response Surface Methodology (RSM). Sustainability 2022, 14, 11558. https://doi.org/10.3390/su141811558
Ahmed F, Abdul Aziz MS, Mohd Arif Zainol MRR, Yee KC, Shaik F, Che Halin DS, Mohd Salleh MAA, Kheimi M. Design, Modelling and Optimization of a Novel Concentrated Solar Powered (CSP) Flash Desalination System Involving Direct Heating and Pressure Modulation Using Response Surface Methodology (RSM). Sustainability. 2022; 14(18):11558. https://doi.org/10.3390/su141811558
Chicago/Turabian StyleAhmed, Faizan, Mohd Sharizal Abdul Aziz, Mohd Remy Rozainy Mohd Arif Zainol, Khor Chu Yee, Feroz Shaik, Dewi Suriyani Che Halin, Mohd Arif Anuar Mohd Salleh, and Marwan Kheimi. 2022. "Design, Modelling and Optimization of a Novel Concentrated Solar Powered (CSP) Flash Desalination System Involving Direct Heating and Pressure Modulation Using Response Surface Methodology (RSM)" Sustainability 14, no. 18: 11558. https://doi.org/10.3390/su141811558
APA StyleAhmed, F., Abdul Aziz, M. S., Mohd Arif Zainol, M. R. R., Yee, K. C., Shaik, F., Che Halin, D. S., Mohd Salleh, M. A. A., & Kheimi, M. (2022). Design, Modelling and Optimization of a Novel Concentrated Solar Powered (CSP) Flash Desalination System Involving Direct Heating and Pressure Modulation Using Response Surface Methodology (RSM). Sustainability, 14(18), 11558. https://doi.org/10.3390/su141811558







