Optimizing the Sustainable Multimodal Freight Transport and Logistics System Based on the Genetic Algorithm

Abstract

Contrasted with the unimodal road mode, multimodal transport is potentially more feasible as it saves cost and lower environmental effect. This paper investigates freight transport and logistics framework to advance sustainable multimodal freight delivery involving road, rail, and waterway in an inland transportation. We consider a genetic algorithm model comprising time, distance, and CO₂ emissions. The optimal design system is modeled by adapting Genetic Algorithm (GA) and Matlab (R2016a) software to improve the existing transport split modes with high shipment cost. An optimal model is formulated to integrate the existing modes to mitigate the prevailing economic, social, and environmental issues. A case investigation of 10 regional capitals in Ghana where freights are transported to and from the main national port was useful to formulate and model an optimized sustainable multimodal freight transport and logistics system (SMFTLS). The Matlab software was used to solve containerized cargo shipment in the optimal system and compare it with the previous system. It was realized that the total cost savings achieved from the optimized system was USD 97.03 million (i.e., 4.5%) lower than the same cargo quantity shipped with the existing system. This SMFTLS model will assist governments, policy makers and investors in deciding the appropriate transport schemes that would manage their overall effects. The study recommends the development of rail and waterway infrastructures to help build the resilient sustainable system (SMFTLS) to manage the rising freight transport demands and related economic, social, and environmental issues.

1. Introduction

1.1. Background

Around the world. city transport, logistics planners, and policy makers are encouraging the change of cargo conveyance from road to more sustainable modalities, e.g., railway, sea, and waterways [1,2]. For instance, the EU aims at 30% change of long-haul movement (i.e., beyond 300 km) cargo shipping from road to a more sustainable modality by 2030 and another 20% by 2050 [3]. This is due to the challenges from road transport which is mainly used in cargo transport markets over the years [4,5,6,7].

After the Brundtland Commission report in 1987, the concepts of sustainable transport drew the attention of numerous policymakers and academicians involved in urban and municipal planning [8,9]. Since then, the concept has proven to be lasting and attractive, prompting attempts to integrate all technical, social, and economic endeavors, including, transportation, production, and construction industries, due to government laws, customer requests, and the benefits generated from the concept. The policy adoption is recently introduced in the management of logistics and supply chains [10,11]. Sustainable development is described as “Development that fulfills current needs without jeopardizing future generations’ ability to meet theirs” [8,9]. Sustainable supply chain management also refers to the incorporation of environmental challenges into all aspects of the supply chain [12]. The concept of sustainability strives to incorporate environmental protection, social equality, and economic development principles into human activity. Environmental, social, and economic sustainability are thus believed to be the three main pillars of sustainability. Therefore, transporting freight in a sustainable manner, make freight transport and logistics more cost-effective, environmentally friendly, and socially inclusive [13].

Socio-economic, demographic, and environmental issues are thought to influence the long-term viability of transportation and logistics. Sustainable transport and logistics, must be safe, high-quality, and convenient to users. Furthermore, sustainable transport must be environmentally friendly, economically feasible, and contribute to local, national, and worldwide developments. Systems of freight transportation that are environmentally friendly improve the capacity of developing countries to: assess the long-term viability of freight transportation networks; and design and implement dependable, accessible, and inexpensive transportation solutions that promote economic efficiency, connection, and inclusiveness, while minimizing negative externalities [13,14]. Hence, this sustainable and green transport system when established could ensure better quality of life. The investment in managing economic, social and CO₂ emissions helps protect the environment, reduce total transport costs, and ensure sustainability [15] which is the main target of this paper.

Of late, concerns have been shown by trained professionals and specialists on the need to divert their energies towards multimodal transport in light of its connected sustainable benefits. For example, the European Union (EU) has attempted to deal with the negative externalities due to road haulage, for instance, on delays, congestion, and environmental impact from CO₂ emission. These have characterized a couple of targets for a competitive and resource-efficient transport system [16]. One such goal is a modal shift from road transport to more friendly transport modes, such as rail and waterway transport.

Again, Jensen et al. [17] evaluated a discrete freight transport chain choice model for Europe and depicted nine different multi-and single mode chain choices for containerized and non-containerized freights and segregated them into dry bulk, liquid bulk, containers, and general cargos [17]. Their model relied upon disaggregate data at the shipment level by testing a couple of vehicle costs specifications and nesting structures, and compared their elasticity with reference literature. It was revealed that freight models were portrayed by heterogeneity and non-linearity in transport costs, and therefore value of times and non-steady rates of substitution. These factors are significant components worth investigating for the appraisal of transport policies while using the freight transport model.

Comi and Polimeni [18] investigated the usage of short sea shipping services (SSS) as a competitive, sustainable freight transport system prepared for addressing economic, social and environmental needs. They proposed assessment system to evaluate the capacity of SSS and the net benefits derived from lower external costs. Their findings supported the idea of moving freight traffic from the less friendly road mode to more sustainable SSS modes for external benefits [18].

However, the rising in freight transport [19] requires the prerequisite of careful computation of these movements and the inherent cargo flows [20,21]. At the governmental level, the consistent expansion in road transport called for policy making action on the most effective way to upgrade multimodal transport and evaluate the capacity of multimodal mode shifts [22]. Thus, the drive for multimodality and sustainable transport chains are important concepts worthy to pursue both in practice and from a research orientation.

Unfortunately, only a little effort has been put into the development of efficient frameworks to advance the course of alternative modes. A study on freight transportation in Brazil observed the predominance of the road mode. The imbalance in the sector prescribed the need to cultivate useful strategies that could build the reality of alternative modes [23]. It was found that there were relatively few studies exploring firms’ preferences on different attributes of travel modes. It analyzed the travel mode choice decision-making process in the area of Rio de Janeiro and determined shippers’ travel mode choices for freight transport in a Brazilian setting. Discrete choice models were evaluated using state preference data to recognize shippers’ preferences and discussed a couple of potential sustainable systems that could increase the competitiveness of the railway network. The results showed that shippers’ preferences have low sensitivity to changing factors [23].

Economic growth has been linked to the increased use of freight transport. The general society is stressed over surges in turbulence pollution as a result of truck carriers. The global desire to reduce road use has been of grave importance due to associated environmental issues, safety issues, inefficiencies, and the need for cost minimization [24]. As demonstrated by Holguín-Veras, et al. [25], research on freight mode choice, basically probing into road, waterway, and rail transports, are becoming vital in attaining freight transport efficiency.

For instance, in Brazil, freight transport is marked by the progressive usage of the road travel mode [26]. This anomaly in the transport matrix impacts the general expenses charged per ton per kilometer in different travel modes. Thus, a critical objective for the sustainable improvement of the freight transport sector is to promote the substitution of the road mode with different transport mode choices [27].

Accordingly, local market players have begun to transport new cargo types to rail and inland waterways. To augment efficiency, freight is also transported by the use of different cargo types. The cargo types used affect transport, storing, and transshipment costs. Research conducted in Belgium on multimodal freight transport included different generally used cargo types in its assessments to determine the cost-based decision-making in the supply chain. It incorporated different commonly used cargo types into an agent-based freight transport model. The MATSim freight extension is extended by considering the cargo types used and added mode choice to the optimization process. The results showed that the potential for a particular shift varies essentially between the cargo types considered. It was observed that solid bulk, liquid bulk, and containers show the highest shares for rail and inland waterway transport. The sensitivity of the modal split towards changes in the transport costs of road transport contrasts according to the cargo type used. Thus, some cargo types are more favorable for a particular shift than others [28].

In order to estimate impacts, support cost-benefits analyses, and enable project optimization, it is critical to perceive the area of effect of a transport system project. For freight related projects such as ports, state of-the-practice methods to check such areas disregard complex interactions among multimodal supply chains. This can be improved by analyzing the multimodal trips made to and from the workplace. While travel demand models check multimodal trips, they may not consider areas of strength for water and rail, and do not give direct observation. Project-specific data including surveys and local traffic counts can be expensive and more subjective to handle.

Asborno et al. [29] encourages a systematic, objective methods of thinking to identify multimodal freight in a catchment area for a facility from vehicle tracking data and showed its application in a case study involving different freight port terminals. The observed truck global positioning system (GPS) and ocean automatic identification system (AIS) data were subjected to robust processing algorithms to handle noise, cluster stops, assign data points to the network (map-planning), and address spatial and temporary conflation [29].

There exist explicit models of the chaining of activities that lead to freight transport. For example, chains of production activities drive the trade of goods and hence serve as the basis for commodity-based freight models. Chains of truck trips occur in delivery processes, where round trips or tours are designed in a way that vehicles can serve multiple clients and return to their home base. Transport activity chains can relieve cargo delivery by adjusting to freight origins and destinations. Despite the abundance of normative models for optimizing freight operations, descriptive models of most of these chains are scarce and are in the early stages of development [30].

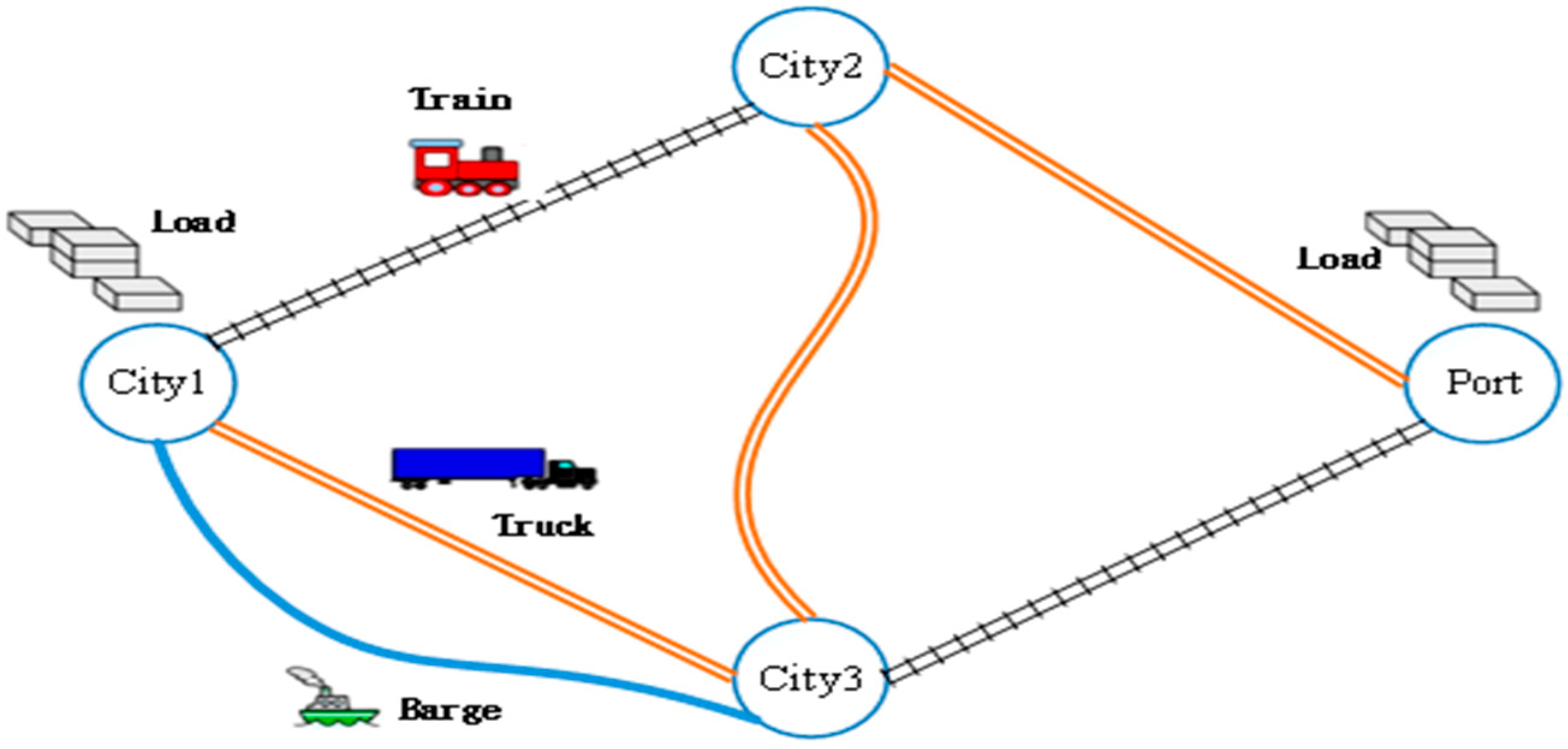
It is against the aforementioned background concerns that informed authors to systematically examine the movements of the inland containerized freight transport system and optimize the multimodal freight transport and logistics system that could enhance overall economic, social, and environmental cost efficiencies using data from the transport and logistics system in a Ghanaian setting.

1.2. Multimodal Choice

Undeniably, multimodal transportation is preferred over single-mode transport because of its flexibility and environmental benefits in terms of sustainable mobility [10,31] The relevance of sea, aviation, and road transportation has been stimulated by global environmental challenges and carbon dioxide mitigation problems, as these modes of transportation play an essential part in lowering carbon footprints [32].

In Ghana, transportation modal choice has been influenced by global logistics firm activities, which account for 20% of overall transportation expenses [7]. Global competition has significantly altered the system in which things are created and moved into world-wide scale [33]. It should be mentioned that transportation has a direct impact on the world supply chain. The primary goal is to convey commodities from origin to destination or point of sale [34]. It helps in identifying key determinants of sustainable transport [35]. Lyson and Gillingham divided traditional or major modern forms of transportation into six categories: water, air, road, sea, rail, and pipeline [36].

Nevertheless, the selection of multimodal transport arose when one mode of freight transportation is not possible for the entire supply chain, originating from various nations, such as the United Kingdom to Ghana, necessitating a collection in order to provide improved service options in satisfying customer requirements [37]. Lyson and Gillingham [36] divided integrated freight transport systems into nine categories: rail–road, rail–water, rail–pipeline, rail–air, road–air, road–pipeline, water–pipeline, water–air, and air–pipeline. However, not all of these systems are practicable, and only a few have acquired widespread recognition in the global transport industry [36].

Rail transport is selected by most Ghanaian organizations having easy access to producers’ premises to move freight to port and, if possible, to the end terminus [10], due to its benefits of less cost and its ability to move large and massive consignments over medium to longer distances. When compared to road freight, rail generates around 10% less carbon dioxide and provides relatively high security in terms of containers and wagons [36]. Hence, this sector needs to be revamped and internationalized.

Furthermore, organizations may choose air freight for urgent shipments and high-value perishable supplies, particularly when patients require medical attention within limited time. Air freight may provide greater market flexibility or marketing benefits, resulting in lower total costs for some high-value light commodities. Marketing benefits may come from a collection of flexibility, speed, and frequency, as well as the benefit of a high-quality environment that results in minimum damage, theft, loss, and protective packaging requirements. All the same, the cost benefits of air freight will be derived from reduced lead times, which will result in lower in-transit inventory, protective packaging, and insurance rates [36,38].

Apparently, the health organizations in Ghana may select sea freight for non-medicine consumables when orders are placed in advance as a cheap cost for economies of scale, which is especially applicable to bulk items with high capacity and large consignments packages for long distances. Unlike air transport, container shipments have a high level of security and are less susceptible to unfavorable weather conditions. Despite these benefits, sea transport has lower speed, unlike air transport, and double handling is common for short sea routes, resulting in product damage and cargo packing on conventional ships, as well as delay issues causing poor and non-regular services [36,38].

1.3. Overview of the Paper

This study fills the above research gap by formulating an optimal sustainable multimodal freight transport and logistics system (SMFTLS) framework to promote feasible freight transport and logistics system which has limited research attention. It considers the cost of distance, time, and CO₂ in the optimization process. To make work simple, we focus on 10 regional capitals in Ghana and their transport networks where road, rail, and waterway are the three main transport modes, dominated by road. A genetic algorithm (GA) mathematical model is developed for this purpose. Matlab R2016a (a mixed integer linear programming solver) was used to solve the final optimization problem.

The paper is further organized as follows; Section 2 describes the SMFTLS model, Section 3 deals with system variables, assumptions, enablers, and constraints, and the modeling of the SMFTLS. Section 4 deals with the model solving the optimal SMFTLS, its analysis, discussion, and presentation with numerical examples. Section 5 presents the GA analyzed results, the suggestions, and insights for the optimal SMFTLS model, and the conclusion furnished in Section 6.

2. Sustainable Multimodal Freight Transport and Logistics System

2.1. Description of the SMFTLS

With a multimodal transport network P, and a collection of modes k, where k denotes the various modes of transportation, such as truck, rail, and barge. In order to describe the SMFTLS, certain fundamental assumptions are made. Considering separate units of freight (cargo) to be conveyed from origin city O to destination port TD, the matter in the network is to assign the demand D to the modes in order to minimize overall generalized cost. To make it easier for comparison with user equilibrium principles, the users are linked to the freight units. We also assume all users to be self-contained, with only one method of transit available. These restrictions may be relaxed in future investigations.

We assume that trip demand is non-stop and that all users will complete their trip regardless of cost. This assumption may be altered by changing the model. For instance, by shifting demand from constant to elastic. The costs are generally determined by the time it takes to arrive at the destination knot (i.e., delays are punished, and early arrival relative to desirable appearance time are also somewhat punished); the distance-related costs, which are determined by travel distance, mode and the number of transport units moved, as well as other antecedents that may boost a particular system [39]. The sustainable multimodal freight transport and logistics system (SMFTLS) is illustrated in Figure 1.

The problem is introduced in Figure 1. Barges, which have a huge vehicle capacity regarding transport units; rail, which has a large vehicle capacity (although lower than barges); and exchanges are the three means of transportation accessible. Only one transport unit can be transported in the latter mode. Loads are transported straight from the city terminal to the port or via multiple city terminals to the port and back. Each of the three modes employs different independent linkages, as shown in Figure 1.

2.2. Description of an Assignment Model

The assignment is made up of user options (which are totally defined by them), mode, and departure time, which are all used in the freight transport system. In most cases, individual users deem to create the decision (i.e., his or her own assignment) that reduces his or her own cost in light of others’ decisions (i.e., their assignment). The equilibrium assignment is a unique and creative assignment that describes an instance where no user has an inducement to vary any aspect of the assignment, such as using a different mode, playing a different role, or leaving at a different time, because each of these options will increase the user’s costs.

Despite its simplicity, it is difficult to model its operational and functionality in order to examine the effects of various measures and actions. Indeed, because of the interaction of different modes, the relative impacts of congestion, economics, and time-related performance are powerfully reliant on the number of active participants and their mode preferences [10]. Different elements influence the result, including user attitudes (time value, flexibility, etc.), trip expenses (length of the travel, extra costs incurred while waiting for the vehicle to be filled up, etc.), and user engagement, notably the regulations implemented to share travel costs.

Our approach only partially addresses the similar problem (i.e., how to best match trips and needs in time and space, what level of similarity for routes is acceptable, etc.) as well as behavioral or organizational problems connected to user perception and desires [40]. The matching problem (in all of its forms) has largely been explored from the perspective of operational research, for example. the ride-sharing matching problem, or matching between a driver and a passenger. Frequently, cross-dock operations are treated as a synchronization or matching challenge, for instance, the construction of a liner network, which entails matching (time-dynamic) demand with a service schedule [41,42]. Despite the fact that a mathematical optimization has been applied in this assignment problem, it is beyond the scope of the current study although a possible future direction.

The circumstances under which users will decide either to travel in a well-established travel medium or do it alone are referred to as behavioral and organizational elements. When it comes to encouraging the adoption of multimodal and intermodal transportation linkages between the freight and logistics industries, this can be a problem [43].

More and more ICT platforms are being established, making it easier to communicate information about transportation wants and the available transportation supply. Transport service providers can use port community systems to incorporate more current information about current unnecessary delays and traffic situations into procedures for a plan in the number of transport vehicles required and crew members available. On paper, such platforms appear to be very promising, they can only be used effectively if a significant number of transport stakeholders are ready to share information. Restrictions include trust, secrecy of information, and justice in cost/benefit sharing. Future research will look into these characteristics of the suggested paradigm [44].

3. The SMFTLS Variables

3.1. Definition of Parameters

The variables and parameters must be used firstly to define the model. A transport demand TD is provided, as is customary in container shipping, and is thought to be separated into a number of generic, interchangeable units. This transportation demand is associated with a single place of origin O and a single point of destination D. In addition, there is no effect of elasticity, implying that all transportation demand must be shifted to the destination. Each mode will cover a specific L of distance, which will be determined by the mode in general.

The origin and destination of all transportation demand are the same. In terms of time, transportation demand is also uniform, with greater demand having a similar time horizon of the earliest achievable departure time, the latest possible departure time, and the optimal arrival time. Applying the technique to a heterogeneous transportation demand will be a fascinating area for future research. We only take into account one connection per mode, therefore the final network will include one link per mode per OD, for a total of three links. For a given mode, all links may be thought of as the collection of multiple homogeneous successive links.

Every mode consists of a set of free-flow travel time (FFTT), which is the shortest possible travel time devoid of congestion effects; and a travel-related price, P, which changes depending on the mode and distance. Whatever elements that influence travel prices, e.g., energy efficiency and technology applied, are beyond the scope of this article and will not be explored in detail here.

In addition, each mode has a vehicle capacity (Cap), which refers to the maximum number of transport demand units that each vehicle may transport. Congestion is generated by varying circumstances, which are functionally defined in the following section which correspond to a major saturation flow for each mode, or maximum number of vehicles which may travel per unit time, and any added criteria that may be required. The main infrastructure capacity of the barge is extraordinarily large, and obtaining saturation flow is extremely challenging.

Expecting costs definition, using the set of parameters are as follows: a value of time (VoT) mechanism to convert a delay into a cost, as well as a share mechanism to split the cost for modes with multiple vehicle capacities. This is determined by a barge and train parameter which specifies whether the cost allotted is equitable to various users (everyone who uses a vehicle pays a fraction of the cost proportional to the vehicle capacity utilized) and whether it favors or disfavors the active roles (which is mostly one per vehicle) may pay more or less than each passive role. This is a measure situation which a strong time responsiveness is required, or in which demand must be adhered to a specific external transportation supply with greater compliance. The final three different cost criteria are applied to assess the cost of early arrival, late arrivals relative to predetermined arrival time, and the cost of waiting for a truck with more than one capacity to be fully loaded and departed.

Other costs elements, such as incentives for specific modes, can also be addressed. These costs can be expressed by a lower cost per km, one-time payments, or a variation in the vehicle loading rate. Trucks will generally have higher prices because the total operational cost can solely be attributed to one distinct transport unit; rail and barge, on the other hand, can reduce costs if fully loaded. Future fees, charges, and money incentives to engage, in addition to the aforementioned fixed expenses, can be represented in such a framework. The parameters used are listed in

Table 1. Used units and reference parameters defined.

Name	Descriptions	Unit(s)
P	Set of the cities
M	Set of the modes
k,l	Mode of the vehicle (truck/train/barge)	Vehicle
i,j	Cities in the transportation network
$d_{ij}$	Distance of city i and city j	Km
$Q_{ij}$	Transportation volume from city i to city j	TEU
$X_{ij}^k$	Transport from city i to city j choose mode k	(0,1)
$Y_i^{kl}$	Transfer from mode k to mode l in city i	(0,1)
$c_k$	Cost per unit load per kilometer per mode k	USD/(km•TEU)
$c_{kl}$	Cost per unit load of transfer from mode k to mode l	USD/TEU
$v_k$	Transportation speed per mode k	km/h
$t_{kl}$	Transfer time per unit from mode k to mode l	Hour
$c_t$	Cost of time per Unit load	USD/h
$C{p}_k$	Vehicle capacity per mode k	Unit/vehicle
$c{o}_k$	Carbon emission per kilometer per mode k	Kg/(km•TEU)
$C_c$	Cost of CO2 emission per Kg	USD/Kg
TD	Total transport demand	TEU

.

3.2. Assumptions

(i) All containers are transported from cities to the port, and no consideration for the inter-city container transportation which does not go to the port. (ii) No separation of the components of the container during the transportation. (iii) Multiple modes are not considered between two cities. (iv) The distance between cities does not change with the mode of transportation.

3.3. Modeling the Sustainable Multimodal Freight Transport and Logistics System(SMFTLS)

The optimization model is described as follows:

$$Min {\displaystyle \sum _{i,j\in P}{\displaystyle \sum _{k,l\in M}\left(c_k\cdot d_{ij}\cdot X_{ij}^k+c_{kl}\cdot Y_i^{k,l}\right)}}\cdot Q_{ij}+{\displaystyle \sum _{i,j\in P}{\displaystyle \sum _{k,l\in M}\left(\frac{d_{ij}}{v_k}\cdot X_{ij}^k+t_{kl}\cdot Y_i^{kl}\right)}}\cdot Q_{ij}\cdot c_t+{\displaystyle \sum _{i,j\in P}{\displaystyle \sum _{k\in M}{d}_{ij}\cdot Q_{ij}\cdot X_{ij}^k\cdot c{o}_k\cdot c_c}}$$

(1)

s.t.

$${\displaystyle \sum _{k\in M}{X}_{ij}^k}=1$$

(2)

$${\displaystyle \sum _{k\in M}{\displaystyle \sum _{l\in M}{Y}_i^{kl}}}\le 1$$

(3)

$$X_{ji}^k\cdot X_{ij}^l=Y_i^{kl}$$

(4)

Formula (1) is the objective function, it consists of three parts: transportation cost, time cost and carbon emission cost.

Formula (2) means only one mode of transport can be used among adjacent cities.

Formula (3) means only one change in transport mode occurs within a city node.

Formula (4) guarantee the continuity of transportation (transport from city j’ to city i in mode k, the transport from city i to city j in mode l, that means transport mode changes from mode k to mode l in city i).

Either $X_{ij}^k=0 \mathrm{or} 1$, if $X_{ij}^k=0$, means in mode k there is no transport from city i to city j; and if $X_{ij}^k=1$, means there is transport from city i to city j in mode k.

In addition, either $Y_i^{kl}=0 \mathrm{or} 1$, if $Y_i^{kl}=0$, means the transport mode does not change in city i; and if $Y_i^{kl}=1$, means the transport mode changes from mode k to mode l in city i.

The simplified map of Ghana connects the immediate neighboring countries and consists of the main freight transportation networks of the various transport modes located in main cities which are illustrations from researcher’s original work. The Ghana map showing the key freight corridors for city freight movements is displayed in Figure 2. It displays the administrative divisions and the existing transportation system networks consisting of air, road, rail, and navigable waterways comprising lakes and rivers.

From the adopted Ghana map in Figure 2, the transport network connecting modes and nodes can be illustrated in simplified networks in the following figures.

Figure 3 shows the transportation network by road connecting the main cities in Ghana.

Figure 4 shows the simplified transportation network, which contains road, rail and waterway, of the main cities in Ghana, showing distances (measured in kilometers) between cities in different modes.

Figure 3. Road transportation network of the main cities in Ghana.

Figure 3. Road transportation network of the main cities in Ghana.

The numbers in the links indicates distances between the cities and they are measured in thousand kilometers (10³ km) for road, rail and waterways as indicated by their respective colors in Figure 4.

Table 2 shows the shortest available road distance (km) between capital cities in Ghana. The “-” means there is no accessible road distance between the two cities. The first three alphabets in the table are used to represent the cities whose names are having more than four letters. All the distances measured were made based on the transport of goods moved from Tema port to other ten regional capital city locations and vice versa as origins and destinations.

The performance validation metrics and variables of the origin port at Tema and the ten (10) destination cities with their abbreviations are as follows; Accra (Acc), Koforidua (Kof), Ho, Cape Coast (Cap), Takoradi (Tak), Kumasi (Kum), Sunyani (Sun), Tamale(Tam), Bolgatanga (Bol), and Wa for the road, rail and waterway distances used in Table 2, Table 3 and Table 4, respectively.

Table 2. Road distance (km) between Ghanaian cities.

Road d(km)	Tema	Acc	Kof	Ho	Cap	Tak	Kum	Sun	Tam	Bol	Wa
Tema	-	27.1	82.7	124.3	158.1	222.1	252.7	361.2	547.9	702.3	684.0
Acc	27.1	-	55.6	-	131.0	195.0	225.6	334.1	576.4	730.8	656.9
Kof	82.7	55.6	-	-	-	-	170.0	278.5	520.8	675.2	301.3
Ho	124.3	-	-	-	-	-	-	-	423.6	578.0	-
Cap	158.1	131.0	-	-	-	64.0	174.5	283.0	525.3	679.7	605.8
Tak	222.1	195.0	-	-	64.0	-	-	-	-	-	-
Kum	252.7	225.6	170.0	-	174.5	-	-	108.5	350.8	505.2	431.3
Sun	361.2	334.1	278.5	-	283.0	-	108.5	-	-	-	322.8
Tam	547.9	576.4	520.8	423.6	523.3	-	-	-	-	154.4	-
Bol	702.3	730.8	675.2	578.0	679.7	350.8	505.2	-	154.4	-	-
Wa	684.0	656.9	301.3	-	605.8	-	431.3	322.8	-	-	-

Table 2. Road distance (km) between Ghanaian cities.

Road d(km)	Tema	Acc	Kof	Ho	Cap	Tak	Kum	Sun	Tam	Bol	Wa
Tema	-	27.1	82.7	124.3	158.1	222.1	252.7	361.2	547.9	702.3	684.0
Acc	27.1	-	55.6	-	131.0	195.0	225.6	334.1	576.4	730.8	656.9
Kof	82.7	55.6	-	-	-	-	170.0	278.5	520.8	675.2	301.3
Ho	124.3	-	-	-	-	-	-	-	423.6	578.0	-
Cap	158.1	131.0	-	-	-	64.0	174.5	283.0	525.3	679.7	605.8
Tak	222.1	195.0	-	-	64.0	-	-	-	-	-	-
Kum	252.7	225.6	170.0	-	174.5	-	-	108.5	350.8	505.2	431.3
Sun	361.2	334.1	278.5	-	283.0	-	108.5	-	-	-	322.8
Tam	547.9	576.4	520.8	423.6	523.3	-	-	-	-	154.4	-
Bol	702.3	730.8	675.2	578.0	679.7	350.8	505.2	-	154.4	-	-
Wa	684.0	656.9	301.3	-	605.8	-	431.3	322.8	-	-	-

Table 3 shows the shortest available railway distance (km) between capital cities in Ghana. The “-” means there is no accessible railway distance between the two cities and also no distance movements are provided within these cities. The entries in the cells are the distances between the respective cities.

Table 3. Railway distance between cities (km).

Railway d(km)	Tema	Acc	Cap	Tak	Kum	Tam
Tema	-	27.1	158.1	222.1	224.8	575.6
Acc	27.1	-	131.0	195.0	197.7	548.5
Cap	158.1	131.0	-	64.0	-	-
Tak	222.1	195.0	64.0	-	194.6	-
Kum	224.8	197.7	-	194.6	-	350.8
Tam	575.6	548.5	-	-	350.8	-

Table 3. Railway distance between cities (km).

Railway d(km)	Tema	Acc	Cap	Tak	Kum	Tam
Tema	-	27.1	158.1	222.1	224.8	575.6
Acc	27.1	-	131.0	195.0	197.7	548.5
Cap	158.1	131.0	-	64.0	-	-
Tak	222.1	195.0	64.0	-	194.6	-
Kum	224.8	197.7	-	194.6	-	350.8
Tam	575.6	548.5	-	-	350.8	-

Table 4 shows the shortest available waterway distance (km) between capital cities in Ghana. The “-” means there is no accessible waterway distance between the two cities.

Table 4. Waterway distance between cities (km).

Waterway d(km)	Ho	Kof	Tam
Ho	-	-	375.4
Kof	-	-	426.2
Tam	375.4	426.2	-

Table 4. Waterway distance between cities (km).

Waterway d(km)	Ho	Kof	Tam
Ho	-	-	375.4
Kof	-	-	426.2
Tam	375.4	426.2	-

The total demand for containerized freight that can be conveyed in the 10 regional capital cities in Ghanaian transport system is 1,006,392 TEUs per year.

Table 5. Transportation volume from city i to Tema port (TEU).

Volume (TEU)	Acc	Kof	Ho	Cap	Tak	Kum	Sun	Tam	Bol	Wa
Cities to Tema port	316,601	38,675	33,318	54,748	106,985	279,432	58,264	55,753	28,127	34,490

shows the maximum transportation volume (capacity) of containerized goods that can be transported from city i to Tema port (TEU).

The optimization modeling also considered some other reference variables in obtaining the optimal results as summarized in

Table 6. Some other reference parameters and values used in the model.

Variables	Description	Value			Unit
$c_k$	Cost per unit load per kilometer per mode k	truck	train	Barge	USD/(km•TEU)
		0.35	0.29	0.23
$c_{kl}$	Cost per unit load of transfer from mode k to mode l	truck ⇄ train	truck ⇄ barge	train ⇄ barge	USD/TEU
		3.2	4.8	6.1
$v_k$	Transportation speed per mode k	truck	train	Barge	km/h
		60	80	40
$t_{kl}$	Transfer time per unit from mode k to mode l	truck ⇄ train	truck ⇄ barge	train ⇄ barge	Min
		10	20	30
$c_t$	Cost of time per unit load	4.60			USD/h
$C{p}_k$	Vehicle capacity per mode k	truck	train	barge	Unit/vehicle
		1	100	200
$S_k$	Saturation flow parameters of mode k	Truck	train	barge	Vehicle/ Day
		500	2	1
$c{o}_k$	Carbon emission per kilometer per mode k	Truck	train	Barge	Kg/(km•TEU)
		1.52	0.32	0.87
$C_c$	Cost of CO2 emission per Kg	0.03			USD/Kg
TD	Total transport demand	1,006,392			TEU

.

4. Model Solving of the Sustainable Multimodal System

4.1. Genetic Algorithms Explained

Genetic algorithms (GA) is an adaptive probability optimization algorithm founded on biologic evolution and genetic mechanism. It was first proposed by Prof. Holland together with his students at the University of Michigan in US. The genetic algorithm is a multi-parameter, multi-group simultaneous optimization algorithm, which is a computer simulation of the natural reproduction behavior of biological organisms. It has good adaptability to the optimization ability of many artificial systems. The basic factors and basic processes of the genetic algorithm are shown in

Table 7. Basic Factors of Genetic Algorithm.

Genetics	Genetic algorithm
Gene	A gene is an element in a string that represents an individual’s characteristics.
Chromosome	Chromosomes are also known as individuals. A certain number of individuals make up a population.
Gene position	A gene position indicates the position of a gene in a string, sometimes referred to as gene location.
Eigenvalues	The Eigenvalue of the gene is consistent with the weight of the binary number
Fitness	The degree to which individuals adapts to the environment

and Figure 5.

The main steps of the genetic algorithm are: randomly generate an initial population; the number of individuals is determined according to the situation of the mode; each individual’s gene is encoded as a labeled chromosome; for each individual population; the individual is calculated by the fitness function; and the fitness degree is judged whether it conforms to the optimization criterion described by the model. If the principle of the optimal solution is met, the individual and the optimal solution it represents are output, and the algorithm ends. If it does not, the population individual is re-selected according to the fitness function.

In the selection process, the probability of the individual with higher fitness being selected is higher, and the probability that the individual with low fitness is selected is low, or can be eliminated. After selecting a new random individual, a new crossover individual is generated according to a certain crossover algorithm and probability. For a new individual, a new variant individual is generated through a certain mutation algorithm and probability. After the individual has been crossed and mutated, the new population is obtained, and the fitness is calculated again. Then, when the optimal individual that meets the optimal principle is obtained, it is regarded as the optimal solution of the problem. Figure 5 represent the GA optimization process.

Figure 5. General genetic algorithm process.

Figure 5. General genetic algorithm process.

The reason for adopting GA optimization over other optimization methods is due to its unique parallelism and probabilistic nature which is convenient for global optimization appropriate for a larger set of solution space, which requires less information, to provide multiple optimal solutions with genetic representations using chromosomes. GA is selected over other optimizers because it has several solutions based on the population size with both exploration and exploitation suitable for multimodal transport solutions.

Genetic algorithm has provided a complete framework when applied to solve complex optimization problems. The only requirement is to design the basic elements of the algorithm for specific problems, including coding method, fitness function, genetic operator, and operating parameters. The optimal model of the problem includes decision variables, constraints, and objective functions. The decision traversal and constraints are used to determine the phenotype of the individual. The coding method is designed to complete the coding and decoding between the individual’s phenotype and genotype. The value of the function converts it into the fitness function applicable to the genetic algorithm. Finally, the genetic operation and the operational parameters are designed according to the coding method and the fitness function.

In this process, it is necessary to observe the genetic evolution process and operation results of the algorithm according to the operation of the algorithm, and change the genetic operation and debugging parameters to improve the efficiency and performance of the algorithm. This section mainly describes how to use genetic algorithm to solve the path planning of multimodal transport. In the process, consideration is given to the problems that are encountered and how to deal with them, and some measures are taken for the operation to improve the efficiency of the algorithm.

4.2. Algorithm Design

When using genetic algorithms to solve the path planning problem of multimodal transport, it is first to solve how to represent the multimodal transport path as a genetic coded string. When designing the coding method, the two points are mainly considered. The chromosome can represent a path containing multiple modes of transportation, and can also easily cross and mutate on the chromosome, and also obey the principle of genetic algorithm coding, as shown in Figure 6.

The coding method adopted in this paper is that the real number coding method, location ID and transport mode code interval coding, the length of the code string is not fixed, and is related to the path node in the path. In this section of the research, similar to the array in the program, the position of the chromosome is marked from 0. Both ends of the head and tail are determined values, indicating the start and end points; the even position gene indicates the location id, and the odd position gene indicates the transport mode code.

The location ID is derived from the network topology of the multimodal transport, using a positive number. In order to distinguish from the location, the code of the transportation mode uses a negative number, and −l, −2, −3, respectively, represent truck, train and barge. As shown in Figure 6, it shows a route from location l to location 9, followed by three locations with locations lD of 6, 5, and 9, with road transport between 1 and 6, rail transport between 6 and 5, rail transport between 5 and 7, and road transport between 7 and 9.

(a)

Selection operator design: This study uses the sorting selection method [45] to select some individuals to inherit into the next generation population:

(i) Calculate the fitness of all individuals in the population. (ii) The fitness is d, N is large, and all individuals in the population are sorted. (iii) The probability of being assigned to the next generation of the population according to the location of the individual in the population.

This study adopts the sorting choice, which takes into account the choice operator and fitness: the commonly used roulette method [46] that is, the proportional selection method, the individual’s selection probability is proportional to its adaptive value. In the early stage of genetic evolution, individual super chromosomes produced too many progeny chromosomes, which have a tendency to control the selection process. In the late stage of genetic evolution, when the population has mostly converged, the individual’s competition is not intense, showing the behavior of random search.

The sorting choice is based on the position of the individual in the sorted population to determine the probability, and such problems do not occur. Sorting selection uses fitness to rank individuals, and is not directly used to calculate the probability that an individual is selected to enter the next generation, and the requirements for fitness are reduced. For the fitness function used in this paper, due to the randomness of the genetic algorithm, the fitness of the new individual will be much larger than the fitness value of the feasible solution. Such individuals should be eliminated without affecting the genetic evolution of the remaining individuals.

• (b) Crossover operator design: In the genetic algorithm, the crossover operator exchanges the partial gene sequences of the two parental chromosomes to generate new progeny chromosomes. The determination of the crossover operator needs to take into account that the excellent gene sequences in the existing chromosomes cannot be excessively destroyed, and can produce better individuals by combination.

In the implementation of genetic algorithm for multimodal transport path planning, a single point crossing is adopted. Selection of intersections: all locations excluding the beginning and the ending. For the code string representing the solution to the problem, the position number starts from 0, and the size indicates the length of the chromosome. It is an odd number, and the position of the intersection is randomly selected in 2, 4, …, size 3. After the intersection is selected, the first half of the A chromosome is combined with the second half of the B chromosome, and the second half of the A chromosome is combined with the first half of the B chromosome, thus generating two new individuals.

• (c) Mutation operator design: this is a genetic operator used to maintain genetic diversity from one generation of a population of GA chromosomes to the next. It is analogous to biological mutation, defined as a small random tweak in the chromosome, to get a new solution. It is used to maintain and introduce diversity in the genetic population which is usually applied with a low probability. It is the part of the GA which is related to the “exploration” of the search space and essential to the convergence of the GA, while crossover is not. Similarly to the crossover operators, we find a combination of these approaches or a problem-specific mutation operator more useful.

As shown in Figure 7, in the process of combination, if the intersection of the A chromosome and the intersection of the B chromosome are exactly the same place, then the direct combination can correctly generate two new paths; otherwise, the new individual needs to be in two. The intersection randomly generates a path connection. After the crossover is completed, the two new individuals need to perform the duplication operation.

The intersection occurs between the paired individuals A and B. First, the intersections of individuals A and B are randomly determined. For the path, the intersection should be the location, not the transport mode. Then determine if the intersections they selected are the same. The process chromosome combinations occurs in the order as shown from A–E in Figure 7.

i.

Fitness function

ii.

We set the objective function to the fitness function

iii.

Genetic algorithm parameters

$$Min {\displaystyle \sum _{i,j\in P}{\displaystyle \sum _{k,l\in M}\left(c_k\cdot d_{ij}\cdot X_{ij}^k+c_{kl}\cdot Y_i^{k,l}\right)}}\cdot Q_{ij}+{\displaystyle \sum _{i,j\in P}{\displaystyle \sum _{k,l\in M}\left(\frac{d_{ij}}{v_k}\cdot X_{ij}^k+t_{kl}\cdot Y_i^{kl}\right)}}\cdot Q_{ij}\cdot c_t$$

(5)

The GA parameters and their values used for the optimization are depicted in Figure 8.

The parameters used for the Genetic algorithm and their values are indicated in

Table 8. The GA parameters and their values used for the optimization.

Parameters	Value
Generation population n	12
Number of generations C	300
Crossover probability	0.8
Mutation probability	0.05

.

5. Presentation of the GA Analysis Results for the SMFTLS

To simplify the calculation of the $+{\displaystyle \sum _{i,j\in P}{\displaystyle \sum _{k\in M}{d}_{ij}\cdot Q_{ij}\cdot X_{ij}^k\cdot c{o}_k\cdot c_c}}$ model, we convert the system’s transportation network map into form as shown in Figure 8. The number in between the cities indicates the distance traveled between the cities in mode k.

Figure 8 indicates the distances connecting the respective cities and the optimized transport networks for road, rail and waterways and measured in kilometers (km).

5.1. Analysis before and after Optimization of Existing Systems

The network traffic graph before optimization is as follows: the number next to the path indicates the amount of traffic between cities in mode k, before the optimization, all transportation is carried out by road. In this case, the total cost of generalized freight transportation of the network is USD 101.59 million.

Table 9. Costs of container transport system before optimization.

Statistics	Value	Unit
Total cost	101,587,161	USD
Cost of transport	75,286,928	USD
Cost of time	16,491,422	USD
Cost of carbon emission	9,808,811	USD
Cost by road	101,587,161	USD
Cost by rail	0	USD
Cost by waterway	0	USD
Total time	3,585,091	Hour
Total carbon emissions	326,960	Ton

shows the costs of container transport system before optimization.

The network traffic graph after optimization is as follows: the number next to the path indicates the amount of traffic between cities in mode k after the optimization, railway and waterway were used in transportation network. In this case, after the optimization process the total cost of generalized freight transportation of the network is USD 97.03 million, 4.5% lower than before optimization. Hence, a cost savings of USD 4.56 million was achieved.

Table 10. Cost of optimized Ghana container transportation system.

Statistics	Value	Unit
Total cost	97,033,053	USD
Cost of transport	72,729,641	USD
Cost of time	16,121,549	USD
Cost of Carbon emission	8,181,862	USD
Cost by road	79,296,290	USD
Cost by rail	13,789,087	USD
Cost by waterway	2,199,082	USD
Total time	3,504,684	Hour
Total carbon emissions	272,728	Ton

shows the cost elements of the optimized container transport and

Table 11. Optimized transportation volume from city i to city j ($Q_{ij}$ ).

Route	Mode	Volume/TEU	Route	Mode	Volume/TEU
Wa-Sun	Road	34,490	Tam-Ho	water	5840
Bol-Tam	Road	28,127	Tam-Ho	road	54,680
Sun-Kum	Road	92,754	Kum-Kof	road	357,586
Tam-Kum	Rail	14,600	Kum-Acc	rail	29,200
Tam-Kof	Water	8760	Kof-Acc	road	405,021
Ho-Tema	Road	93,838	Tak-Cap	road	77,785
Cap-Acc	Road	103,333	Tak-Cap	rail	29,200
Cap-Acc	Rail	116,800	Acc-Tema	road	840,755
Acc-Tema	Rail	53,155

shows the modes, container volumes and transport routes from city i to city j.

5.2. Sensitivity Study of the Optimal SMFTLS

The final assignment equilibrium’s sensitivity to a variety of parameters is then investigated, for example, by comparing the interaction of trains per hour, i.e., the capacity of the infrastructure of the railway link on trains per hour permitted, to the cost per km covered by the barges. A sensitivity study of the optimized system, for example, could ascertain how much rail and barge modes are substitutes for one another, and whether favoring one (via financial inducement or building linkage flow rate) can draw in more users from the different combined modes, or whether it will cause a decline in truck mobility.

The prevalent problem is the high transport cost due to trucks on road, time delays, and CO₂ emissions which need optimization by expanding the saturation flow of railway into the transport system for sustainable means of transport to reduce the total transport cost.

In

Table 12. Influence on freight transport cost by expanding the saturation flow of rail.

Saturation Flow of Rail (per day)	10	20	30	40	50
Total cost (USD)	98,852,443	96,826,573	94,939,070	93,624,508	92,529,720
Transport cost USD	73,602,174	72,706,456	71,852,298	71,205,901	70,695,974
Cost of time USD	16,400,599	16,085,619	15,790,797	15,582,801	15,413,446
Cost of carbon emission (USD)	8,849,670	8,034,497	7,295,974	6,835,805	6,420,299
Cost by road (USD)	87,877,578	77,260,858	67,649,657	61,690,053	56,316,362
Cost by rail (USD)	7,809,019	15,618,039	22,666,746	26,954,331	30,798,884
Cost by waterway (USD)	2,199,082	2,199,082	2,199,082	2,199,082	2,199,082
Total time (h)	3,565,347	3,496,873	3,432,782	3,387,565	3,350,749
Total CO2 emissions (ton)	294,989	267,816	243,199	227,860	214,009

, we realize the influence of cost by expanding the saturation flow of railway. As the saturation flow of railway rises up, the total cost of the system and cost of transport goes down. This has remarkable influence on road transport cost reduction.

As indicated in Figure 9, as the saturation flow of railway rises from 10 to 50, the total cost reduces by 6.39%, and the cost of transport reduce by 3.94%. The cost of time reduces by 6.02%, the cost by road reduces by 35.91%, the cost of carbon emission reduces by 27.45% and these reduce the total transport cost.

6. Conclusions

The researchers went through scientific processes in formulating the optimization model (SMFTLS). The system was described, the network was analyzed, variables were explained, and some basic assumptions made. Afterwards, the genetic algorithm (GA) optimization model was built and the system variables and values determined. The GA was adapted to solve the mathematical optimization model and Matlab R2016a software package was applied. The result indicated a cost savings of USD 4.56 million (i.e., 4.5%) achieved for the total transported containerized cargos, as compared to the existing model. A concern was the existence of fewer trains and barges and their limited infrastructure availability.

Therefore, building more infrastructure for railways and barges to complement the existing road dominant system is recommended, which this SMFTLS shows will inevitably reduce shipments cost. The study optimized the freight transport and logistics system to be sustainable, efficient, and effective by considering transport time, distance (route), and CO₂ emission and proposed pragmatic strategies and policies that could yield institutional changes when implemented.

From the optimization results and sensitivity analysis of the SMFTLS, it can be seen that the current bottlenecks of the Ghana freight transport system are mainly due to the under-developed railway and waterway transport infrastructure systems. This supports the study by Okyere et al. [7] who realized that the influence of cost is affected by expanding the saturation flow of railway and waterway transportation.

As the saturation flow of railway rises up, the total cost of the system and cost of transport goes down, and has remarkable influence on reducing the road transportation cost. As the saturation flow of railway rises from 10 to 50, the total cost reduces by 6.39%, and the cost of transport will reduce by 3.94%, the cost due to time will reduce by 6.02%, the cost caused by road also reduces by 35.91%, and the cost of carbon emission will also reduce by 27.45%, hence, resulting in cost savings on the overall transportation cost.

It was also discovered that Tema container throughput would increase rapidly in the next decade, liberating railway capacity and improving water transport capacity, and reducing the total transportation cost and carbon emission rate of the Ghana multimodal freight transport and logistics management system. This study is in support of Okyere et al. [10] who suggested that a more sustainable and timely research agenda is paramount in order to improve the Ghanaian freight transport system.

This SMFTLS model is relevant to recent technology and has logistics-based applications to help stakeholders and policymakers in their efforts to sustainably manage overall freight transport and logistics costs when considering the economic, social and environmental impacts. In view of the optimal MFTLS, the main suggestions for achieving the construction of Ghana’s future transport and logistics network are:

i.

Improve railway construction nationwide and increase the density of railway container trains to achieve the seamless docking of container water and railway combined transport. For example, the density of railway container trains linking Tema-Accra-Cape Coast-Takoradi and other cities with railways in Ghana, as shown in Figure 8, must be increased. Moreover, the capacity of railway container transport for the multimodal freight transport and logistics system must be increased to meet the container throughput to meet the challenges of the rapidly developing shipment demands in the Ghanaian market.

ii.

Enhance the shipping capacity of the waterway midstream and regional lines to increase the density of container liners. The proportion of water transport in Ghanaian transportation will become larger and larger, with the improvement of the navigation capacity of waterway and the import and export advantages of waterways. Ghana should therefore speed up the construction of waterway shipping to increase the density of container liners, and mobilize the development prospects of container shipping in the feasible regional cities.

iii.

Develop multimodal transport and expand waterway and railway infrastructure to complement the road dominant mode. At present, the composition of railway in the Ghanaian freight transport and logistics system is relatively low and the proportion of railway container transfer is also low. The development of multimodal transport and the expansion of water can effectively reduce the overall average cost of container transportation and reduce the shipment costs and time involved in intermediate links.

Future research on similar work could consider including the accuracy level of the proposed model in graph and compare the model with other methods or models.