Electric Vehicle Charging Station Location-Routing Problem with Time Windows and Resource Sharing
Abstract
:1. Introduction
2. Literature Review
2.1. Electric Vehicle Charging Station Location-Routing Problem
2.2. Electric Vehicle Location-Routing Problem and its Variants
2.3. Transportation Resource Sharing Strategy
2.4. Relevant Solution Methods for Electric Vehicle Location-Routing Problem
3. Problem Statement
4. Related Definitions and Model Formulation
4.1. Assumptions and Definitions
4.2. Model Formulation
5. Solution Methodology
5.1. Customer Clustering
| Algorithm 1. Gaussian Mixture Clustering Algorithm |
| Input: Customer data set, the number of Gaussian mixed clusters k, the number of the maximum iteration t_max |
| Output: Cluster results for each service period |
| 1. // Initial GMM parameters |
| {(wd, μd, Σd)|1< d < k}←GMM (Ci) |
| 2. While t < t_max // Iterated clustering |
| 3. For c = 1: n // Calculate posterior distribution (E-step) |
| 4. Calculate posterior probability of each customer to different depots |
5.
 |
| 6. End for |
| 7. For d = 1 to k // Update parameters (M-step) |
| 8. Calculate the mixing factor, mean vector, and covariance matrix |
9.
 |
| 10. Calculate the gap between the updated parameters and the previous parameters |
| 11. If the gap is small // Check the stop conditions |
| 12. Update parameters (wd, μd, Σd)←(wd’, μd’, Σd’) |
| 13. End if |
| 14. End for |
| 15. For c = 1: n do // Determine clustering |
| 16. Reassign the customer to the depot with the maximum probability |
| 17. End for |
5.2. Improved Non-Dominated Sorting Genetic Algorithm
| Algorithm 2. INSGA-II |
| Input: Cluster results, fitness function, population size (pop_size), maximum iterations (r_max) |
| Output: CS location selection and EV routing plan |
| 1. // Population initialization |
| 2. Generate initial population (Pt) based on sweep algorithm |
| 3. Calculate the angles between customers and origin |
| 4. Obtain initial solutions by sorting the angles |
| 5. Evaluate the fitness function of the initial population |
| 6. While r ≤ r_max |
| 7. For population = 1: pop_size // Genetic operation |
| 8. Execute tournament selection, order crossover, multi-point mutation to generate child population (Qt) |
| 9. End for |
| 10. Combine the parent population (Pt) and child population (Qt) to generate Rt // Elite retention |
| 11. If exist that the battery level of EV is negative while arriving customers // Insertion operation |
| 12. For all routes with negative battery level of EV |
| 13. Perform insertion operation |
| 14. End for |
| 15. End if |
| 16. Repeat // Non-dominated sorting and crowding distance comparison |
| 17. Determine the non-dominated ranking by executing non-dominated sorting |
| 18. Compare the crowding distance of individuals to determine the retention individuals |
| 19. Until the number of individuals reaches the set population size |
| 20. End |
5.2.1. Solution Presentation
5.2.2. Genetic Operation
- (1)
- Tournament selection
- (2)
- Order crossover
- (3)
- Multi-point mutation
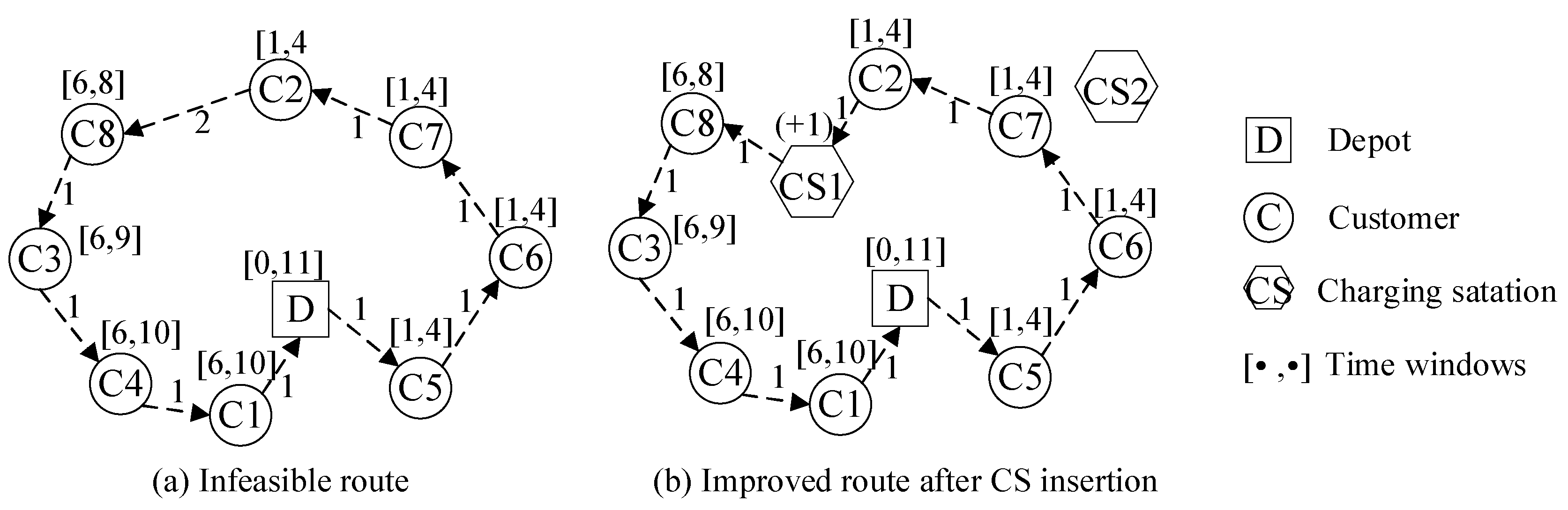
5.2.3. CS Insertion Operation
| Algorithm 3 CS insertion procedure |
| 1. For each infeasible route |
| Repeat |
| 2. Identify the first customer with the negative battery level of the EV |
| 3. Search for all feasible insertion points according to time windows and battery level before the first customer |
| 4. Select a CS from the set of candidate CSs to insert |
| 5. For each candidate CS |
| 6. Calculate the sum of distances from CS to the previous customer and the next customer for each feasible insertion point as the distance increment |
| 7. End for |
| 8. For each feasible insertion point |
| 9. Compare the distance increments between the feasible insertion point and all candidate CSs |
| 10. Select the CS with the minimum distance increment to insert |
| 11. Calculate and compare the delivery cost increment for the CS insertion |
| 12. End for |
| 13. Determine the final insertion point with the minimum delivery cost increment and insert the selected CS for the route |
| 14. Until all of the delivery routes are feasible on the battery level of the EV |
| 15. End for |
5.2.4. Elite Retention Mechanism
5.2.5. Elite Retention Mechanism
6. Computational Experiments
6.1. Algorithm Comparison
6.2. Empirical Study
6.2.1. Data Source
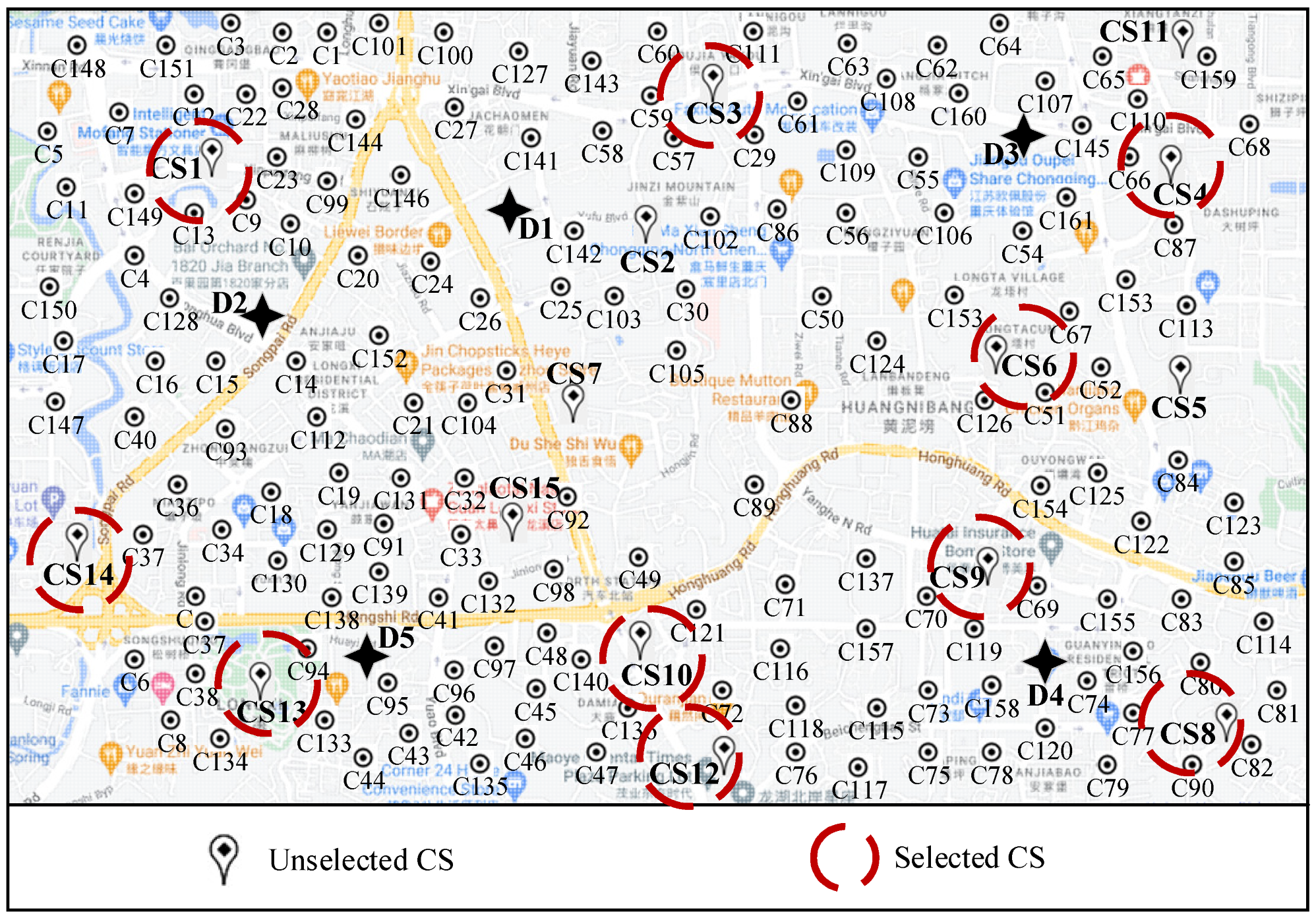
6.2.2. Optimization Results
- (1)
- Customer clustering results
- (2)
- CS location and the routing optimization results
6.2.3. Analysis and Discussion
- (1)
- Comparison of the different service periods
- (2)
- Comparison of different resource sharing strategies
6.3. Management Insights
- (1)
- This study has a significant practical implication for the optimization of logistics networks. The periodic location selections of CSs contribute to promoting delivery efficiency via the reassignment of customers according to their characteristics in different service periods. The optimization of the EV delivery routes greatly alleviates the phenomenon of long-distance transportation and violations of customers’ time windows. The adoption of a transportation resource sharing strategy in a multi-depot multi-period EV distribution network can reduce the number of required EVs, thus facilitating the construction of resource-efficient and environmentally friendly logistics networks.
- (2)
- The proposed solution method in this study to solve the EVCS-LRPTWRS can provide a methodological reference for the research of the EVLRP. The bi-objective nonlinear programming model of the minimum TOC and the minimum number of required EVs balances the operation of the logistics network from two conflicting aspects of economy and efficiency. In addition, the hybrid algorithm, including a customer clustering algorithm and a heuristic algorithm, is developed to solve the EVCS-LRPTWRS. The service periods are divided by customer clustering according to the time window’s characteristics for improving the transportation efficiency. The integration of the CS insertion operation into the heuristic algorithm allows for the reasonable CS location, thus, shortening the delivery distance and saving the operating cost. Therefore, the proposed solution methods contribute to building an economic and sustainable logistics network and promoting the enterprise’s competitiveness.
- (3)
- The optimization of the EV distribution networks plays a great role in alleviating the conflicts between humans and the environment. With the proposal of the dual-carbon goal: carbon peak and carbon neutrality, EVs are widely adopted by enterprises and logistics companies to construct a sustainable logistics distribution network for coping with the increasing competition. Meanwhile, many government departments have enacted a series of policies to promote the popularity and development of EVs to face the two challenges of environmental degradation and energy scarcity. Furthermore, new energy technologies (e.g., vehicle-pile cloud interconnection, wireless charging, and power exchange technology) should be widely promoted to address the technical limitations and practical application constraints of EVs.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, S.Y.; Ning, L.J.; Tong, L.; Shang, P. Integrated electric logistics vehicle recharging station location–routing problem with mixed backhauls and recharging strategies. Transp. Res. Part C Emerg. Technol. 2022, 140, 103605. [Google Scholar] [CrossRef]
- Asadi, S.; Nilashi, M.; Iranmanesh, M.; Ghobakhloo, M.; Samad, S.; Alghamdi, A.; Almulihi, A.; Mohd, S. Drivers and barriers of electric vehicle usage in Malaysia: A DEMATEL approach. Resour. Conserv. Recycl. 2022, 177, 105965. [Google Scholar] [CrossRef]
- Wang, L.; Gao, S.; Wang, K.; Li, T.; Li, L.; Chen, Z.Y. Time-dependent electric vehicle routing problem with time Windows and path flexibility. J. Adv. Transp. 2020, 2020, 3030197. [Google Scholar] [CrossRef]
- Kchaou-Boujelben, M. Charging station location problem: A comprehensive review on models and solution approaches. Transp. Res. Part C Emerg. Technol. 2021, 132, 103376. [Google Scholar] [CrossRef]
- Li, J.Q.; Han, Y.Q.; Duan, P.Y.; Han, Y.Y.; Niu, B.; Li, C.D.; Zheng, Z.X.; Liu, Y.P. Meta-heuristic algorithm for solving vehicle routing problems with time windows and synchronized visit constraints in prefabricated systems. J. Clean. Prod. 2020, 250, 119464. [Google Scholar] [CrossRef]
- Chen, R.; Liu, X.L.; Mia, L.X.; Yang, P. Electric vehicle tour planning considering range anxiety. Sustainability 2020, 9, 3685. [Google Scholar] [CrossRef]
- Schiffer, M.; Walther, G. The electric location routing problem with time windows and partial recharging. Eur. J. Oper. Res. 2017, 260, 995–1013. [Google Scholar] [CrossRef]
- Ran, C.; Zhang, Y.; Yin, Y. Demand response to improve the shared electric vehicle planning: Managerial insights, sustainable benefits. Appl. Energy 2021, 292, 112863. [Google Scholar] [CrossRef]
- Li, J.L.; Liu, Z.B.; Wang, X.F. Public charging station location determination for electric ride-hailing vehicles based on an improved genetic algorithm. Sustain. Cities Soc. 2021, 74, 103182. [Google Scholar] [CrossRef]
- He, P.; Zhang, S.S.; He, C. Impacts of logistics resource sharing on B2C E-commerce companies and customers. Electron. Commer. Res. Appl. 2019, 34, 100820. [Google Scholar] [CrossRef]
- Xu, X.F.; Hao, J.; Zheng, Y. Multi-objective artificial bee colony algorithm for multi-stage resource leveling problem in sharing logistics network. Comput. Ind. Eng. 2020, 142, 106338. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.Y.; Guan, X.Y.; Fan, J.X.; Xu, M.Z.; Wang, H.Z. Two-echelon multi-period location routing problem with shared transportation resource. Knowl. Based Syst. 2021, 226, 107168. [Google Scholar] [CrossRef]
- Wang, Y.; Assogba, K.; Fan, J.X.; Xu, M.Z.; Liu, Y.; Wang, H.Z. Multi-depot green vehicle routing problem with shared transportation resource: Integration of time-dependent speed and piecewise penalty cost. J. Clean. Prod. 2019, 232, 12–29. [Google Scholar] [CrossRef]
- Erdelić, T.; Carić, T. A Survey on the electric vehicle routing problem: Variants and solution approaches. J. Adv. Transp. 2019, 2019, 5075671. [Google Scholar] [CrossRef]
- Ghorbani, E.; Alinaghian, M.; Gharehpetian, G.B.; Mohammadi, S.; Perboli, G. A survey on environmentally friendly vehicle routing problem and a proposal of its classification. Sustainability 2020, 12, 9079. [Google Scholar] [CrossRef]
- Kucukoglu, I.; Dewil, R.; Cattrysse, D. The electric vehicle routing problem and its variations: A literature review. Comput. Ind. Eng. 2021, 161, 107650. [Google Scholar] [CrossRef]
- Dündar, H.; Ömürgönülşen, M.; Soysal, M. A review on sustainable urban vehicle routing. J. Clean. Prod. 2021, 285, 125444. [Google Scholar] [CrossRef]
- Qin, H.; Su, X.X.; Ren, X.; Luo, Z.X. A review on the electric vehicle routing problems: Variants and algorithms. Front. Eng. Manag. 2021, 8, 370–389. [Google Scholar] [CrossRef]
- Xiao, Y.Y.; Zhang, Y.; Kaku, I.; Kang, R.; Pan, X. Electric vehicle routing problem: A systematic review and a new comprehensive model with nonlinear energy recharging and consumption. Renew. Sustain. Energy Rev. 2021, 151, 111567. [Google Scholar] [CrossRef]
- Paz, J.C.; Granada-Echeverri, M.; Escobar, J.W. The multi-depot electric vehicle location routing problem with time windows. Int. J. Ind. Eng. Comput. 2018, 9, 123–136. [Google Scholar] [CrossRef]
- Yang, J.; Sun, H. Battery swap station location-routing problem with capacitated electric vehicles. Comput. Oper. Res. 2015, 55, 217–232. [Google Scholar] [CrossRef]
- Yidiz, B.; Arslan, O.; Karasan, O.E. A branch and price approach for routing and refueling station location model. Eur. J. Oper. Res. 2016, 248, 815–826. [Google Scholar] [CrossRef]
- He, J.; Yang, H.; Tang, T.Q.; Huang, H.J. An optimal charging station location model with the consideration of electric vehicle’s driving range. Transp. Res. Part C Emerg. Technol. 2018, 86, 641–654. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, M.Z.; Zhang, W.Y. A novel location-routing problem in electric vehicle transportation with stochastic demands. J. Clean. Prod. 2019, 221, 567–581. [Google Scholar] [CrossRef]
- Guo, F.; Huang, Z.H.; Huang, W.L. Integrated location and routing planning of electric vehicle service stations based on users’ differentiated perception under a time-sharing leasing mode. J. Clean. Prod. 2020, 277, 123513. [Google Scholar] [CrossRef]
- Calik, H.; Oulamara, A.; Prodhon, C.; Salhi, S. The electric location-routing problem with heterogeneous fleet: Formulation and Benders decomposition approach. Comput. Oper. Res. 2021, 131, 105251. [Google Scholar] [CrossRef]
- Wang, C.L.; Guo, C.C.; Zuo, X.Q. Solving multi-depot electric vehicle scheduling problem by column generation and genetic algorithm. Appl. Soft Comput. 2021, 112, 107774. [Google Scholar] [CrossRef]
- Sadati, M.E.H.; Catay, B. A hybrid variable neighborhood search approach for the multi-depot green vehicle routing problem. Transp. Res. Part E Logist. Transp. Rev. 2021, 149, 102293. [Google Scholar] [CrossRef]
- Lam, E.; Desaulniers, G.; Stuckey, P.J. Branch-and-cut-and-price for the electric vehicle routing problem with time windows, piecewise-linear recharging and capacitated recharging stations. Comput. Oper. Res. 2022, 145, 105870. [Google Scholar] [CrossRef]
- Raeesi, R.; Zografos, K.G. The electric vehicle routing problem with time windows and synchronised mobile battery swapping. Transportation Res. Part B Methodol. 2020, 140, 101–129. [Google Scholar] [CrossRef]
- Li, S.Y.; Huang, Y.X.; Mason, S.J. A multi-period optimization model for the deployment of public electric vehicle charging stations on network. Transp. Res. Part C Emerg. Technol. 2016, 65, 128–143. [Google Scholar] [CrossRef]
- Neves-Moreira, F.; Amorim-Lopes, M.; Amorim, P. The multi-period vehicle routing problem with refueling decisions: Traveling further to decrease fuel cost. Transp. Res. Part E Logist. Transp. Rev. 2017, 133, 101817. [Google Scholar] [CrossRef]
- Lin, B.; Ghaddar, B.; Nathwani, J. Electric vehicle routing with charging/discharging under time-variant electricity prices. Transp. Res. Part C Emerg. Technol. 2021, 130, 103285. [Google Scholar] [CrossRef]
- Brandstätter, G.; Kahr, M.; Leitner, M. Determining optimal locations for charging stations of electric car-sharing systems under stochastic demand. Transp. Res. Part B Methodol. 2017, 104, 17–35. [Google Scholar] [CrossRef]
- Friedrich, M.; Noekel, K. Modeling intermodal networks with public transport and vehicle sharing systems. EURO J. Transp. Logist. 2017, 6, 271–288. [Google Scholar] [CrossRef]
- Almouhanna, A.; Quintero-Araujo, C.L.; Panadero, J.; Juan, A.A.; Khosravi, B.; Ouelhadj, D. The location routing problem using electric vehicles with constrained distance. Comput. Oper. Res. 2020, 115, 104864. [Google Scholar] [CrossRef]
- Jin, F.; Yao, E.; An, K. Analysis of the potential demand for battery electric vehicle sharing: Mode share and spatiotemporal distribution. J. Transp. Geogr. 2020, 82, 102630. [Google Scholar] [CrossRef]
- Chen, Y.R.; Li, D.C.; Zhang, Z.C.; Wahab, M.I.M.; Jiang, Y.S. Solving the battery swap station location-routing problem with a mixed fleet of electric and conventional vehicles using a heuristic branch-and-price algorithm with an adaptive selection scheme. Expert Syst. Appl. 2021, 186, 115683. [Google Scholar] [CrossRef]
- Yang, Y.; He, K.; Wang, Y.P.; Yuan, Z.Z.; Yin, Y.H.; Guo, M.Z. Identification of dynamic traffic crash risk for cross-area freeways based on statistical and machine learning methods. Phys. A Stat. Mech. Its Appl. 2022, 595, 127083. [Google Scholar] [CrossRef]
- Bayliss, C. Machine learning based simulation optimisation for urban routing problems. Appl. Soft Comput. 2021, 105, 107269. [Google Scholar] [CrossRef]
- Yang, Y.; Yuan, Z.Z.; Chen, J.J.; Guo, M.Z. Assessment of osculating value method based on entropy weight to transportation energy conservation and emission reduction. Environ. Eng. Manag. J. 2017, 16, 2413–2423. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, K.; Yuan, Z.Z.; Liu, D. Predicting freeway traffic crash severity using XGBoost-Bayesian network model with consideration of features interaction. J. Adv. Transp. 2022, 2022, 4257865. [Google Scholar] [CrossRef]
- Barco, J.; Guerra, A.; Munoz, L.; Quijano, N. Optimal routing and scheduling of charge for electric vehicles: A case study. Math. Probl. Eng. 2017, 2017, 1–16. [Google Scholar] [CrossRef]
- Kyriakakis, N.A.; Stamadianos, T.; Marinaki, M.; Marinakis, Y. The electric vehicle routing problem with drones: An energy minimization approach for aerial deliveries. Clean. Logist. Supply Chain 2022, 4, 100041. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, L.; Yang, C.; Lan, S.L. Locating electric vehicle charging stations with service capacity using the improved whale optimization algorithm. Adv. Eng. Inform. 2019, 41, 100901. [Google Scholar] [CrossRef]
- Yu, V.F.; Jodiawan, P.; Gunawan, A. An Adaptive Large Neighborhood Search for the green mixed fleet vehicle routing problem with realistic energy consumption and partial recharges. Appl. Soft Comput. 2021, 105, 107251. [Google Scholar] [CrossRef]
- Erdem, M. Optimisation of sustainable urban recycling waste collection and routing with heterogeneous electric vehicles. Sustain. Cities Soc. 2022, 80, 103785. [Google Scholar] [CrossRef]
- Breunig, U.; Baldacci, R.; Hartl, R.F.; Vidal, T. The electric two-echelon vehicle routing problem. Comput. Oper. Res. 2019, 103, 198–210. [Google Scholar] [CrossRef]
- Chakraborty, N.; Mondal, A.; Mondal, S. Intelligent charge scheduling and eco-routing mechanism for electric vehicles: A multi-objective heuristic approach. Sustain. Cities Soc. 2021, 69, 102820. [Google Scholar] [CrossRef]
- Felipe, Á.; Ortuño, M.T.; Righini, G.; Tirado, G. A heuristic approach for the green vehicle routing problem with multiple technologies and partial recharges. Transp. Res. Part E Logist. Transp. Rev. 2014, 71, 111–128. [Google Scholar] [CrossRef]
- Froger, A.; Mendoza, J.E.; Jabali, O.; Laporte, G. Improved formulations and algorithmic components for the electric vehicle routing problem with nonlinear charging functions. Comput. Oper. Res. 2019, 104, 256–294. [Google Scholar] [CrossRef]
- Jie, W.C.; Yang, J.; Zhang, M.; Huang, Y.X. The two-echelon capacitated electric vehicle routing problem with battery swapping stations: Formulation and efficient methodology. Eur. J. Oper. Res. 2019, 272, 879–904. [Google Scholar] [CrossRef]
- Hof, J.; Schneider, M.; Goeke, D. Solving the battery swap station location-routing problem with capacitated electric vehicles using an AVNS algorithm for vehicle-routing problems with intermediate stops. Transportation Res. Part B Methodol. 2017, 97, 102–112. [Google Scholar] [CrossRef]
- Ma, B.S.; Hu, D.W.; Chen, X.Q.; Wang, Y.; Wu, X. The vehicle routing problem with speed optimization for shared autonomous electric vehicles service. Comput. Ind. Eng. 2021, 161, 102214. [Google Scholar] [CrossRef]
- Pelletier, S.; Jabali, O.; Laporte, G. The electric vehicle routing problem with energy consumption uncertainty. Transp. Res. Part B Methodol. 2019, 126, 225–255. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Gao, Z.Y.; Zheng, J.F.; Du, H.M. Charging station location problem of plug-in electric vehicles. J. Transp. Geogr. 2016, 52, 11–22. [Google Scholar] [CrossRef]
- Keskin, M.; Çatay, B. Partial recharge strategies for the electric vehicle routing problem with time windows. Transp. Res. Part C Emerg. Technol. 2016, 65, 111–127. [Google Scholar] [CrossRef]
- Cataldo-Diaz, C.; Linfati, R.; Escobar, J.W. Mathematical model for the electric vehicle routing problem considering the state of charge of the batteries. Sustainability 2022, 3, 1645. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Q.; Guan, X.Y.; Fan, J.X.; Liu, Y.; Wang, H.Z. Collaboration and resource sharing in the multidepot multiperiod vehicle routing problem with pickups and deliveries. Sustainability 2020, 12, 5966. [Google Scholar] [CrossRef]
- Li, J.J.; Fang, Y.H.Q.; Tang, N. A cluster-based optimization framework for vehicle routing problem with workload balance. Comput. Ind. Eng. 2022, 169, 108221. [Google Scholar] [CrossRef]
- Chen, Q.; Pan, X.Y.; Liu, F.; Xiong, Y.; Li, Z.T.; Tang, J.J. Reposition optimization in free-floating bike-sharing system: A case study in Shenzhen City. Phys. A Stat. Mech. Its Appl. 2022, 593, 126925. [Google Scholar] [CrossRef]
- Tang, J.J.; Hu, J.; Hao, W.; Chen, X.Q.; Qi, Y. Markov Chains based route travel time estimation considering link spatio-temporal correlation. Phys. A Stat. Mech. Its Appl. 2020, 545, 123759. [Google Scholar] [CrossRef]
- Liao, W.Z.; Zhang, L.Y.; Wei, Z.Z. Multi-objective green meal delivery routing problem based on a two-stage solution strategy. J. Clean. Prod. 2020, 258, 120627. [Google Scholar] [CrossRef]
- Eydi, A.; Ghasemi-Nezhad, S.A. A bi-objective vehicle routing problem with time windows and multiple demands. Ain Shams Eng. J. 2021, 12, 2617–2630. [Google Scholar] [CrossRef]
- Srivastava, G.; Singh, A.; Mallipeddi, R. NSGA-II with objective-specific variation operators for multiobjective vehicle routing problem with time windows. Exp. Syst. Appl. 2021, 176, 114779. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 5, 8091–8126. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, S.L.; Assogba, K.; Fan, J.X.; Xu, M.Z.; Wang, Y.H. Economic and environmental evaluations in the two-echelon collaborative multiple centers vehicle routing optimization. J. Clean. Prod. 2018, 197, 443–461. [Google Scholar] [CrossRef]
- Li, Q.; Cao, Z.H.; Ding, W.P.; Li, Q. A multi-objective adaptive evolutionary algorithm to extract communities in networks. Swarm Evol. Comput. 2020, 52, 100629. [Google Scholar] [CrossRef]
- Khoo, T.S.; Mohammad, B.B. The parallelization of a two-phase distributed hybrid ruin-and-recreate genetic algorithm for solving multi-objective vehicle routing problem with time windows. Expert Syst. Appl. 2021, 168, 14408. [Google Scholar] [CrossRef]
- Koohestani, B. A crossover operator for improving the efficiency of permutation-based genetic algorithms. Expert Syst. Appl. 2020, 151, 113381. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.W.; Guan, X.Y.; Tang, J.J. Multidepot recycling vehicle routing problem with resource sharing and time window assignment. J. Adv. Transp. 2021, 2021, 2327504. [Google Scholar] [CrossRef]
- Giallanza, A.; Puma, G.L. Fuzzy green vehicle routing problem for designing a three echelons supply chain. J. Clean. Prod. 2020, 259, 120774. [Google Scholar] [CrossRef]
- Martínez-Puras, A.; Pacheco, J. MOAMP-Tabu search and NSGA-II for a real bi-objective scheduling-routing problem. Knowl. Based Syst. 2016, 112, 92–104. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, N.B.; Li, K.L.; Li, M.Q.; Zheng, J.H.; Li, K.Q. An angle dominance criterion for evolutionary many-objective optimization. Inf. Sci. 2020, 509, 376–399. [Google Scholar] [CrossRef]
- Zhang, M.Q.; Wang, L.; Guo, W.A.; Li, W.Z.; Li, D.Y.; Hu, B.; Wu, Q.D. Many-objective evolutionary algorithm based on relative non-dominance matrix. Inf. Sci. 2021, 547, 963–983. [Google Scholar] [CrossRef]
- Ghannadpour, S.F.; Zandiyeh, F. A new game-theoretical multi-objective evolutionary approach for cash-in-transit vehicle routing problem with time windows (A Real life Case). Appl. Soft Comput. 2020, 93, 106378. [Google Scholar] [CrossRef]
- Maiyar, L.M.; Thakkar, J.J. Environmentally conscious logistics planning for food grain industry considering wastages employing multi objective hybrid particle swarm optimization. Transp. Res. Part E Logist. Transp. Rev. 2019, 127, 220–248. [Google Scholar] [CrossRef]
- Li, Y.B.; Soleimani, H.; Zohal, M. An improved ant colony optimization algorithm for the multi-depot green vehicle routing problem with multiple objectives. J. Clean. Prod. 2019, 227, 1161–1172. [Google Scholar] [CrossRef]







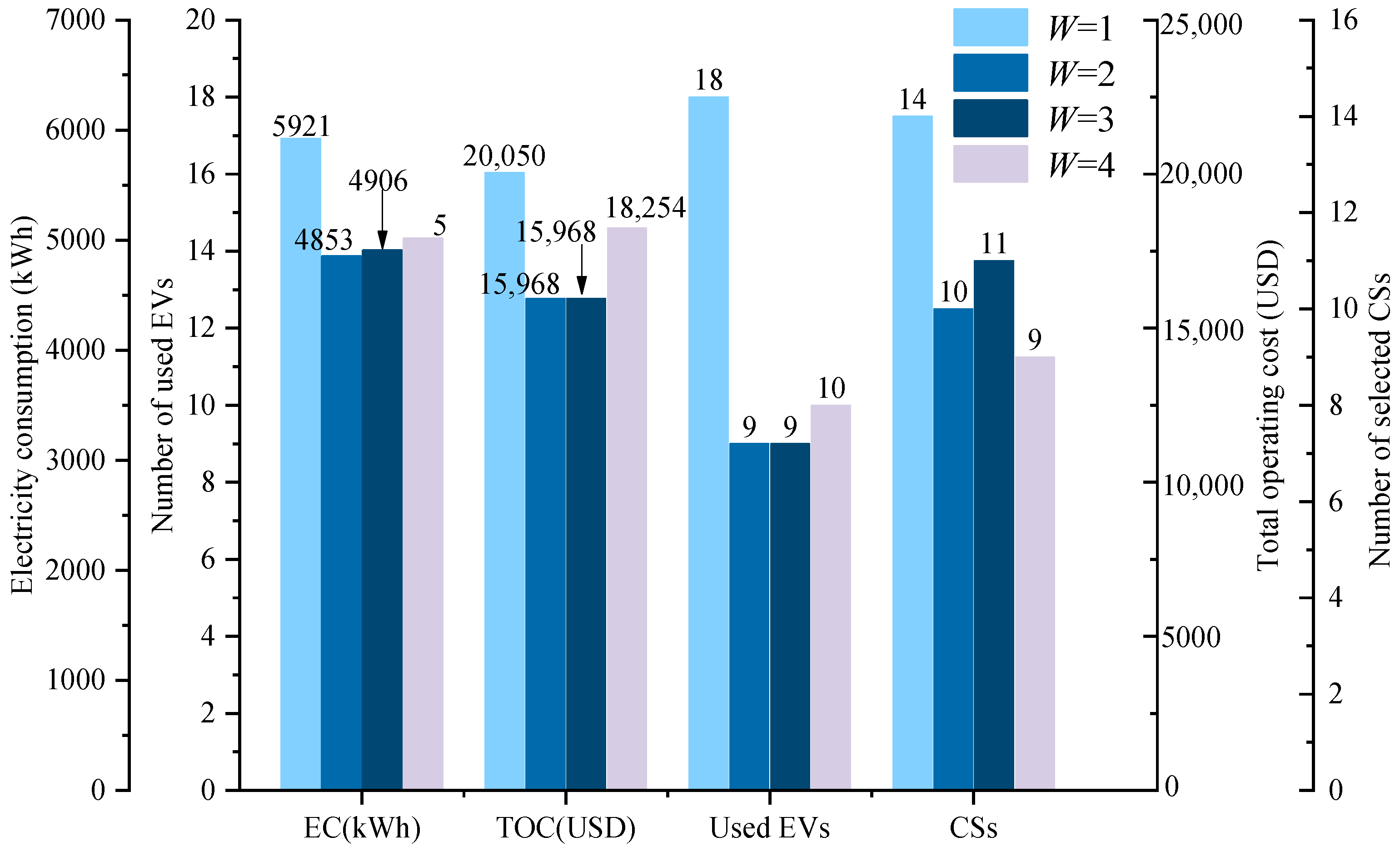
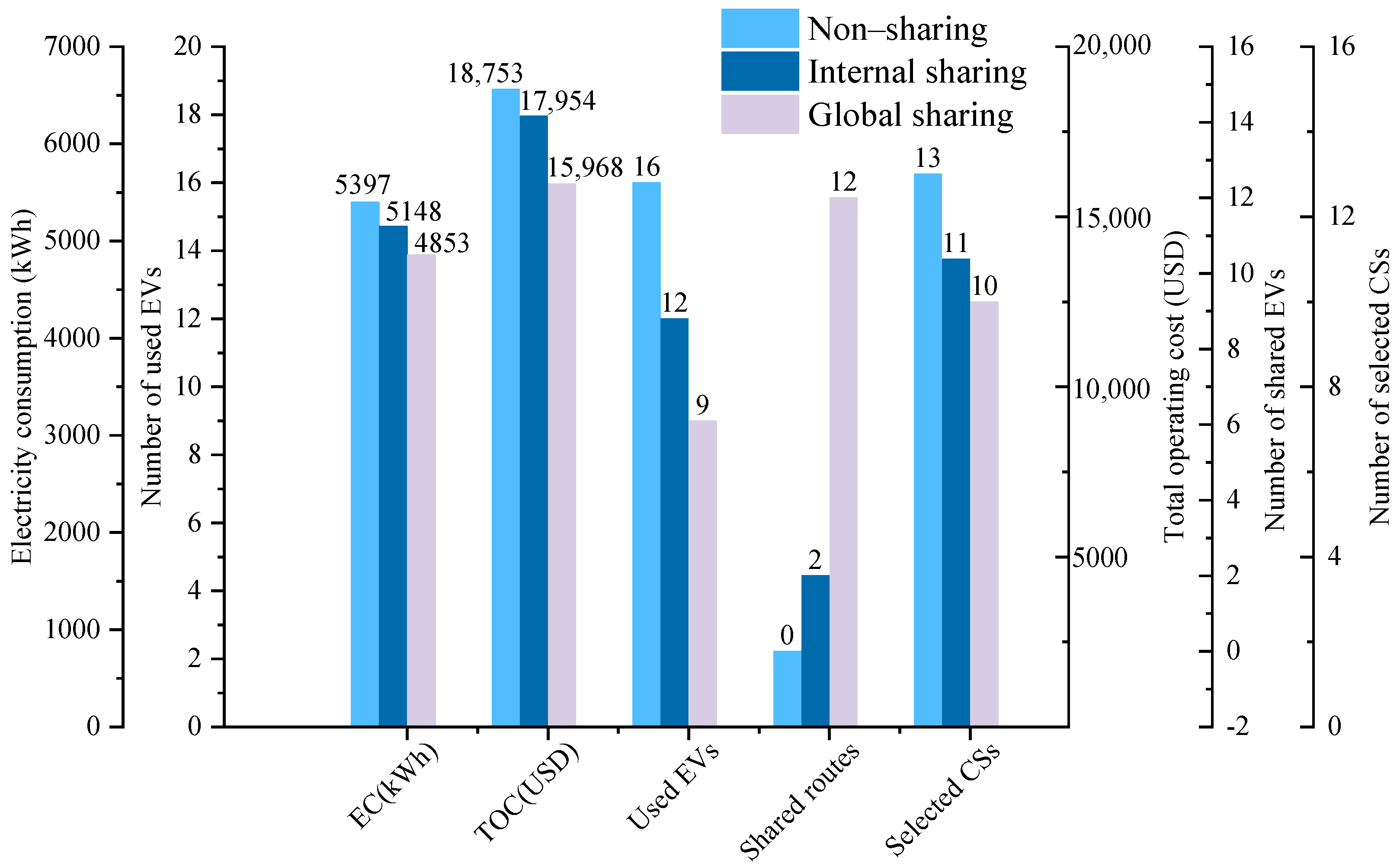
| Abbreviation | Type of Problem | Abbreviation | Solution Method |
|---|---|---|---|
| EVLRPTW | Electric vehicle location-routing problem with time windows | VNS | Variable neighborhood search |
| MDEVLRPTW | Multi-depot electric vehicle location routing problem with time windows | MOPSO | Multi-objective particle swarm optimization |
| EVLRP-BSS | Electric vehicle location-routing problem with a battery swap station | LNS | Large neighborhood search |
| E2EVRP | Two-level electric vehicle routing problem | MOHA | Multi-objective heuristic algorithm |
| GVRP-PR | Green vehicle routing problem with partial charging | CG | Column generation |
| EVRP-BSS | Electric vehicle routing problem with a battery swap station | BP | Biased-randomized |
| EVRPTW | Electric vehicle routing problem with time windows | PSO | Particle swarm optimization |
| References | Type of Problems | Variants | Electric Fleet | Resource Sharing | Solution Method | ||||
|---|---|---|---|---|---|---|---|---|---|
| Multi-Depot | Multi-Echelon | Time Windows | Multi-Period | Homogeneous | Heterogeneous | ||||
| Yang et al. [1] | EVLRP | √ | √ | Lagrange relaxation | |||||
| Schiffer and Walther [7] | EVLRPTW | √ | √ | VNS | |||||
| Wang et al. [12] | MDGVRP | √ | √ | √ | √ | √ | MOPSO | ||
| Paz et al. [20] | MDEVLRPTW | √ | √ | √ | CPLEX | ||||
| Yang and Sun [21] | EVLRP-BSS | √ | ALNS | ||||||
| Zhang et al. [24] | EVLRP-BSS | √ | Hybrid VNS-PSO | ||||||
| Guo et al. [25] | EVLRP | √ | √ | K-shortest ALNS | |||||
| Çalık et al. [26] | EVLRP | √ | √ | Integer programming | |||||
| Brandstätter et al. [34] | CS location problem | √ | Heuristic algorithm | ||||||
| Almouhanna et al. [36] | EVLRP | √ | √ | √ | BR-VNS | ||||
| Breunig et al. [48] | E2EVRP | √ | √ | LNS | |||||
| Chakraborty et al. [49] | EVRP | √ | MOHA | ||||||
| Felipe et al. [50] | GVRP-PR | √ | VNS | ||||||
| Froger et al. [51] | EVRP | √ | √ | Labeling algorithm | |||||
| Jie et al. [52] | EVRP-BSS | √ | √ | CG-ALNS | |||||
| Hof et al. [53] | EVLRP-BSS | √ | √ | AVNS | |||||
| Ma et al. [54] | EVRP | √ | √ | √ | ALNS | ||||
| Pelletier et al. [55] | EVRP | √ | √ | LNS | |||||
| Zhu et al. [56] | CS location problem | √ | Genetic algorithm | ||||||
| Keskin and Çatay [57] | EVRPTW | √ | √ | √ | ALNS | ||||
| This work | EVCS-LRPTW | √ | √ | √ | √ | √ | √ | INSGA-II | |
| Case | Service Period | CTC (USD) | EDC (USD) | EC (kWh) | CC (USD) | Waiting and Delay Times | PC (USD) | TOC (USD) | Number of EVs | Number of ETs | Selected CSs |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial | 1st | 0 | 672 | 224 | 100 | 18 | 270 | 1042 | 6 | 0 | 4 |
| 2nd | 0 | 672 | 224 | 70 | 4 | 60 | 802 | 5 | 0 | 2 | |
| Total | 0 | 1344 | 448 | 170 | 22 | 330 | 1844 | 11 | 0 | 6 | |
| Optimized | 1st | 225 | 456 | 152 | 70 | 1 | 15 | 766 | 3 | 1 | 2 |
| 2nd | 0 | 384 | 128 | 60 | 0 | 0 | 444 | 3 | 0 | 2 | |
| Total | 225 | 840 | 280 | 130 | 1 | 15 | 1210 | 3 | 1 | 3 |
| Sets | Definitions |
|---|---|
| D | Set of depots, D = {1, 2, 3, …, d}, d∈D |
| C | Set of customers, C = {1, 2, 3, …, c}, c∈C |
| R | Set of CSs, R = {1, 2, 3, …, r}, r∈R |
| T | Set of electric trucks for centralized transportation, T = {1, 2, 3, …, t}, t∈T |
| V | Set of EVs for delivery routes, V = {1, 2, 3, …, v}, v∈V |
| W | Set of service periods within one working period, W = {1, 2, 3, …,w}, w∈W |
| , t∈T, w∈W | |
| , v∈V, w∈W | |
| Set of EVs used to serve customers within the wth service period, v∈V, w∈W | |
| , v∈V, w∈W | |
| Parameters | Description |
| fe | Electricity price, (unit: USD/kWh) |
| Fcc | CC of electricity per unit time, (unit: USD/h) |
| FRr | Unit operating cost of CS |
| Charging rate of EV v, v∈V, (unit: kWh/h) | |
| Variable cost coefficient of depot d, d∈D | |
| MNv | Annual maintenance cost of EV v, v∈V |
| K | Number of working periods in one year |
| , w∈W, (unit: kWh) | |
| , w∈W,(unit: kWh) | |
| αv | Arc specific coefficient of EV v, v∈V |
| Arc specific coefficient of ET t, t∈T | |
| Vehicle specific coefficient of ET t, t∈T | |
| βv | Vehicle specific coefficient of EV v, v∈V |
| , w∈W, (unit: m/s) | |
| , w∈W, (unit: m/s) | |
| , w∈W, (unit: kg) | |
| , w∈W, (unit: kg) | |
| ldc | Distance from node d to c, d, c∈R∪D∪C, d ≠ c |
| Ldd’ | Distance from depot d to d’, d, d’∈D, d ≠ d’ |
| QTt | Load capacity of ET t, t∈T |
| QVv | Load capacity of EV v, v∈V |
| Demand quantity of customer c within the wth service period, c∈C, w∈W | |
| Transport quantity from depot d to d’ within the wth service period, d, d’∈D, d ≠ d’, w∈W | |
| Demand quantity of depot d, d∈D | |
| Pe | PC per unit of time of earliness |
| Pl | PC per unit of time of delay |
| Operation time window for depot d within the wth service period, d∈D, w∈W | |
| Service time window for customer c within the wth service period, c∈C, w∈W | |
| , v∈V, w∈W | |
| , w∈W | |
| ,w∈W | |
| , w∈W | |
| , w∈W | |
| , w∈W | |
| Arrival time of EV v at customer c in the nth route within the wth service period, c∈C, v∈V, n∈, w∈W | |
| , w∈W | |
| , w∈W | |
| , w∈W | |
| ,w∈W | |
| , r∈R, d∈C, v∈V,n∈, w∈W | |
| , d, c∈C, d≠ c, v∈V, n∈, w∈W | |
| Amount of electricity remaining when EV v leaves depot or CS r, r∈R∪D, v∈V, n∈, w∈W, (unit: kWh) | |
| , w∈W, (unit: kWh) | |
| Amount of electricity remaining when EV v leaves customer c, c∈C, v∈V, n∈, w∈W, (unit: kWh) | |
| , w∈W, (unit: kWh) | |
| , w∈W, (unit: kWh) | |
| , w∈W, (unit: kWh) | |
| , w∈W, (unit: kWh) | |
| , w∈W, (unit: kWh) | |
| Ev | Battery capacity of EV v, v∈V, (unit: kWh) |
| MM | Extremely large number |
| Number of routes assigned to EV v within the wth service period | |
| Number of customers served by EV v in the nth route within the wth service period | |
| Number of EVs used to serve customers within the wth service period | |
| Decision variable | Description |
| , w∈W | |
| , w∈W | |
| = 0, d, c∈R∪D∪C, d≠ c, v∈V, w∈W | |
| If EV v is selected to serve customers within the wth service period, v∈V, w∈W | |
| = 0, d, d, d’∈D, d≠d’, c∈C, v∈V | |
| = 0, r∈R∪D, v∈V |
| Instances | Datasets | Number of Depots | Number of Customers | Number of CSs | Number of Periods | EV Capacity |
|---|---|---|---|---|---|---|
| 1 | Pr01_15CS_4W | 4 | 48 | 15 | 4 | 200 |
| 2 | Pr02_15CS_4W | 4 | 96 | 15 | 4 | 195 |
| 3 | Pr03_15CS_4W | 4 | 144 | 15 | 4 | 190 |
| 4 | Pr04_15CS_4W | 4 | 192 | 15 | 4 | 185 |
| 5 | Pr05_15CS_4W | 4 | 240 | 15 | 4 | 180 |
| 6 | Pr06_15CS_4W | 4 | 288 | 15 | 4 | 175 |
| 7 | Pr07_20CS_6W | 6 | 72 | 20 | 6 | 200 |
| 8 | Pr08_20CS_6W | 6 | 144 | 20 | 6 | 190 |
| 9 | Pr09_20CS_6W | 6 | 216 | 20 | 6 | 180 |
| 10 | Pr10_20CS_6W | 6 | 288 | 20 | 6 | 170 |
| 11 | Pr11_15CS_4W | 4 | 48 | 15 | 4 | 200 |
| 12 | Pr12_15CS_4W | 4 | 96 | 15 | 4 | 195 |
| 13 | Pr13_15CS_4W | 4 | 144 | 15 | 4 | 190 |
| 14 | Pr14_15CS_4W | 4 | 192 | 15 | 4 | 185 |
| 15 | Pr15_15CS_4W | 4 | 240 | 15 | 4 | 180 |
| 16 | Pr16_15CS_4W | 4 | 288 | 15 | 4 | 175 |
| 17 | Pr17_20CS_6W | 6 | 72 | 20 | 6 | 200 |
| 18 | Pr18_20CS_6W | 6 | 144 | 20 | 6 | 190 |
| 19 | Pr19_20CS_6W | 6 | 216 | 20 | 6 | 180 |
| 20 | Pr20_20CS_6W | 6 | 288 | 20 | 6 | 170 |
| Instance | INSGA-II | MOGA | MOPSO | MOACO | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TOC (USD) | EVs | CSs | TOC (USD) | EVs | CSs | TOC (USD) | EVs | CSs | TOC (USD) | EVs | CSs | |
| 1 | 4953 | 3 | 4 | 5785 | 4 | 7 | 5355 | 4 | 4 | 6075 | 4 | 7 |
| 2 | 9062 | 7 | 6 | 10,051 | 8 | 9 | 9072 | 7 | 7 | 10,141 | 8 | 9 |
| 3 | 12,774 | 10 | 8 | 13,574 | 12 | 10 | 13,061 | 10 | 10 | 13,696 | 12 | 11 |
| 4 | 17,531 | 15 | 11 | 18,357 | 17 | 11 | 17,597 | 15 | 11 | 18,479 | 17 | 12 |
| 5 | 21,796 | 20 | 14 | 22,993 | 20 | 14 | 21,975 | 21 | 16 | 23,218 | 20 | 15 |
| 6 | 25,687 | 23 | 15 | 26,776 | 25 | 15 | 26,560 | 24 | 15 | 26,878 | 26 | 15 |
| 7 | 6931 | 4 | 3 | 8048 | 5 | 4 | 7499 | 4 | 3 | 8162 | 6 | 4 |
| 8 | 13,590 | 6 | 7 | 14,416 | 8 | 10 | 13,595 | 6 | 9 | 14,662 | 8 | 11 |
| 9 | 21,792 | 15 | 9 | 22,849 | 16 | 9 | 22,346 | 16 | 11 | 22,905 | 17 | 10 |
| 10 | 26,795 | 22 | 16 | 27,831 | 24 | 18 | 27,417 | 22 | 18 | 27,939 | 24 | 19 |
| 11 | 5062 | 4 | 4 | 5994 | 4 | 5 | 5598 | 5 | 4 | 6354 | 5 | 6 |
| 12 | 9278 | 7 | 7 | 9855 | 7 | 9 | 9554 | 7 | 7 | 10,101 | 8 | 10 |
| 13 | 12,377 | 11 | 8 | 13,081 | 12 | 8 | 12,548 | 12 | 9 | 13,407 | 12 | 10 |
| 14 | 17,942 | 14 | 11 | 18,614 | 14 | 12 | 18,581 | 14 | 11 | 18,680 | 14 | 13 |
| 15 | 22,188 | 20 | 13 | 23,190 | 20 | 13 | 22,715 | 20 | 15 | 23,555 | 21 | 14 |
| 16 | 25,725 | 22 | 15 | 26,794 | 23 | 16 | 25,726 | 23 | 15 | 26,970 | 24 | 16 |
| 17 | 7274 | 4 | 4 | 8208 | 5 | 5 | 7691 | 4 | 4 | 8269 | 6 | 6 |
| 18 | 13,579 | 7 | 8 | 14,769 | 9 | 10 | 14,076 | 8 | 9 | 14,991 | 9 | 12 |
| 19 | 22,193 | 15 | 10 | 23,308 | 15 | 13 | 22,257 | 15 | 10 | 23,479 | 15 | 14 |
| 20 | 26,841 | 21 | 15 | 27,527 | 21 | 16 | 27,126 | 22 | 16 | 27,628 | 22 | 16 |
| Average | 16,169 | 13 | 9 | 17,101 | 13 | 11 | 16,567 | 13 | 10 | 17,279 | 14 | 12 |
| t-test | −22.75 | −5.41 | −5.15 | −6.41 | −3.94 | −4.56 | −24.71 | −7.63 | −7.76 | |||
| p-value | 1.51 × 10−15 | 1.35 × 10−5 | 2.84 × 10−5 | 1.89 × 10−6 | 4.37 × 10−4 | 3.83 × 10−4 | 3.30 × 10−16 | 1.69 × 10−7 | 1.30 × 10−7 | |||
| Depots | Customers | 1st Period | 2st Period | ||
|---|---|---|---|---|---|
| Number of Services Customers | Time Windows | Number of Services Customers | Time Windows | ||
| D1 | C1-C30 | 17 | [0,10] | 13 | [12,24] |
| D2 | C31-C65 | 19 | [0,10] | 16 | [12,24] |
| D3 | C66-C98 | 15 | [0,10] | 18 | [12,24] |
| D4 | C99-C132 | 20 | [0,10] | 14 | [12,24] |
| D5 | C133-C161 | 13 | [0,10] | 16 | [12,24] |
| Total | 84 | 77 | |||
| Parameter | Description | Value |
|---|---|---|
| fe | Electricity price, (unit: USD/kWh) | 1.8 |
| Fcc | CC of electricity per unit time, (unit: USD/h) | 4.5 |
| FRr | Unit operating cost of CS | 50 |
| δv | Charging rate of EV v, v∈V, (unit: kWh/h) | 25 |
| μd | Variable cost coefficient of depot d, d∈D | 0.4 |
| MNv | Annual maintenance cost of EV v, v∈V | 200 |
| K | Number of working periods in one year | 52 |
| Arc specific coefficient of ET t, t∈T | 0.13 | |
| Vehicle specific coefficient of ET t, t∈T | 0.79 | |
| αv | Arc specific coefficient of EV v, v∈V | 0.11 |
| βv | Vehicle specific coefficient of EV v, v∈V | 0.76 |
| Driving speed of EV v in the nth route within the wth service period, v∈V, n∈, w∈W, (unit: m/s) | 11.11 | |
| Driving speed of EV v in the mth route within the wth service period, t∈T, m∈ w∈W, (unit: m/s) | 11.11 | |
| Weight of EV v in the nth route within the wth service period, v∈V, n∈, w∈W, v∈V, (unit: kg) | 1910 | |
| , w∈W, v∈V, (unit: kg) | 4000 | |
| QTt | Load capacity of ET t, t∈T | 1000 |
| QVv | Load capacity of EV v, v∈V | 600 |
| Pe | PC per unit of time of earliness | 4 |
| Pl | PC per unit of time of delay | 8 |
| Ev | Battery capacity of EV v, v∈V, (unit: kWh) | 48 |
| Depots | 1st | 2nd | CS Location |
|---|---|---|---|
| D1 | CS1 | CS1 | CS1, CS3, CS4 CS6, CS8, CS9, CS10 CS12, CS13, CS14 |
| D2 | CS13, CS14 | CS1, CS14 | |
| D3 | CS3, CS4 | CS3, C6 | |
| D4 | CS6, CS9, CS12 | CS8, CS10 | |
| D5 | CS10, CS13 | CS10 |
| Case | Service Period | EC (kWh) | EDC (USD) | CC (USD) | PC (USD) | CTC (USD) | DOC (USD) | COC (USD) | TOC (USD) | Used EVs | Shared Routes | ETs | Used CSs |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial | 1st | 3569 | 6424 | 197 | 286 | 0 | 500 | 0 | 10,976 | 19 | 0 | 0 | 8 |
| 2nd | 2770 | 4986 | 108 | 154 | 0 | 500 | 0 | 8518 | 13 | 0 | 0 | 7 | |
| Total | 6339 | 11,410 | 305 | 440 | 0 | 1000 | 0 | 19,494 | 32 | 0 | 0 | 15 | |
| Optimized | 1st | 2653 | 4775 | 162 | 107 | 237 | 536 | 300 | 8770 | 9 | 7 | 1 | 9 |
| 2nd | 2178 | 3920 | 83 | 96 | 186 | 513 | 200 | 7176 | 5 | 5 | 1 | 7 | |
| Total | 4853 | 8695 | 245 | 203 | 423 | 1049 | 500 | 15,968 | 9 | 12 | 1 | 10 |
| Depot | EV | Service Period | Route |
|---|---|---|---|
| D1 | EV1 | 1st | C24→C152→C26→C104→C31→C105→C103→C25→C142 |
| EV2 | 1st | C27→C100→C101→C1→C28→C2→C3→C151→C12→CS1→C9→C10→C99→C144→C146 | |
| EV1 | 1st | C58→C59→C143→C141 | |
| EV4 | 2nd | C21→C112→C14→C20→C23→CS1→C22→C127 | |
| D2 | EV3 | 1st | C4→C11→C149→C5→C148→C7 |
| EV4 | 1st | C34→C36→C39→CS13→C38→C8→C6→C37→CS14→C40→C147→C150 | |
| EV5 | 2nd | C15→C93→CS13→C134→CS14→C17→C16→C128→C13 | |
| D3 | EV3 | 1st | C106→C153→C67→C161→C66→C68→CS4→C159→C65→C110→C145 |
| EV7 | 1st | C107→C64→C62→C108→C109→C61→C29→CS3→C30→C102→C60→CS3→C63→C160 | |
| EV8 | 2nd | C54→C87→C113→C53→CS6→C124→C50→C86→CS3→C57→C111→C56→C55 | |
| D4 | EV9 | 1st | C158→C73→C157→C72→C71→C137→C70→CS9→C69→C154→C155→C156→C74 |
| EV8 | 1st | C119→C125→C52→C51→C126→CS6→C88→C89→C121→CS12→C76→C118→C116→C115→C117→C75 | |
| EV1 | 2nd | C120→C77→C79→C90→C82→CS8→C81→C114→C85→C123→C84→C122→C83→C80 | |
| D5 | EV5 | 1st | C43→C44→C42→C135→C136→C140→CS10→C96→C139 |
| EV6 | 1st | C94→C133→C138→CS13→C35→C32→C33→C98→C97→C41→C95 | |
| EV3 | 2nd | C46→C47→C45→C48→CS10→C49→C92→C132→C91→C131→C19→C129→C18→C130 |
| Service Periods | W = 1 | W = 2 | W = 3 | W = 4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EC | TOC (USD) | EVs | CSs | EC | TOC (USD) | EVs | CSs | EC | TOC (USD) | EVs | CSs | EC | TOC (USD) | EVs | CSs | |
| 1st | 5921 | 20,050 | 18 | 14 | 2653 | 8770 | 9 | 9 | 1829 | 6351 | 8 | 11 | 1537 | 5276 | 7 | 7 |
| 2nd | / | / | / | / | 2178 | 7176 | 5 | 7 | 1594 | 5413 | 4 | 6 | 1320 | 4658 | 4 | 6 |
| 3rd | / | / | / | / | / | / | / | / | 1483 | 4974 | 3 | 6 | 1176 | 4366 | 4 | 5 |
| 4th | / | / | / | / | / | / | / | / | / | / | / | / | 980 | 3954 | 3 | 5 |
| Total | 5921 | 20,050 | 18 | 14 | 4853 | 15,968 | 9 | 10 | 4906 | 16,738 | 9 | 11 | 5013 | 18,254 | 10 | 9 |
| Selected CS locations | CS1, CS2, CS3, CS4 CS6, CS7, CS8, CS9, CS10, CS11, CS12, CS13, CS14, CS15 | CS1, CS3, CS4 CS6, CS8, CS9, CS10 CS12, CS13, CS14 | CS1, CS2, CS3, CS4 CS6, CS9, CS10, CS12 CS13, CS14, CS15 | CS1, CS3, CS4 CS6, CS8, CS9, CS10 CS13, CS14 | ||||||||||||
| Case | Service Period | EC (kWh) | TOC (USD) | Used EVs | Shared Routes | Selected CSs |
|---|---|---|---|---|---|---|
| Non-sharing | 1st | 2936 | 9755 | 10 | 0 | 10 |
| 2nd | 2461 | 8998 | 6 | 0 | 7 | |
| Total | 5397 | 18,753 | 16 | 0 | 13 | |
| Internal sharing | 1st | 2722 | 9406 | 10 | 1 | 10 |
| 2nd | 2426 | 8548 | 6 | 1 | 7 | |
| Total | 5148 | 17,954 | 12 | 2 | 11 | |
| Global sharing | 1st | 2653 | 8770 | 9 | 7 | 9 |
| 2nd | 2178 | 7176 | 5 | 5 | 7 | |
| Total | 4853 | 15,968 | 9 | 12 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhou, J.; Sun, Y.; Wang, X.; Zhe, J.; Wang, H. Electric Vehicle Charging Station Location-Routing Problem with Time Windows and Resource Sharing. Sustainability 2022, 14, 11681. https://doi.org/10.3390/su141811681
Wang Y, Zhou J, Sun Y, Wang X, Zhe J, Wang H. Electric Vehicle Charging Station Location-Routing Problem with Time Windows and Resource Sharing. Sustainability. 2022; 14(18):11681. https://doi.org/10.3390/su141811681
Chicago/Turabian StyleWang, Yong, Jingxin Zhou, Yaoyao Sun, Xiuwen Wang, Jiayi Zhe, and Haizhong Wang. 2022. "Electric Vehicle Charging Station Location-Routing Problem with Time Windows and Resource Sharing" Sustainability 14, no. 18: 11681. https://doi.org/10.3390/su141811681






