Experimental Study on Stiffness Degradation of Organic Matter-Disseminated Sand under Cyclic Loading
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation
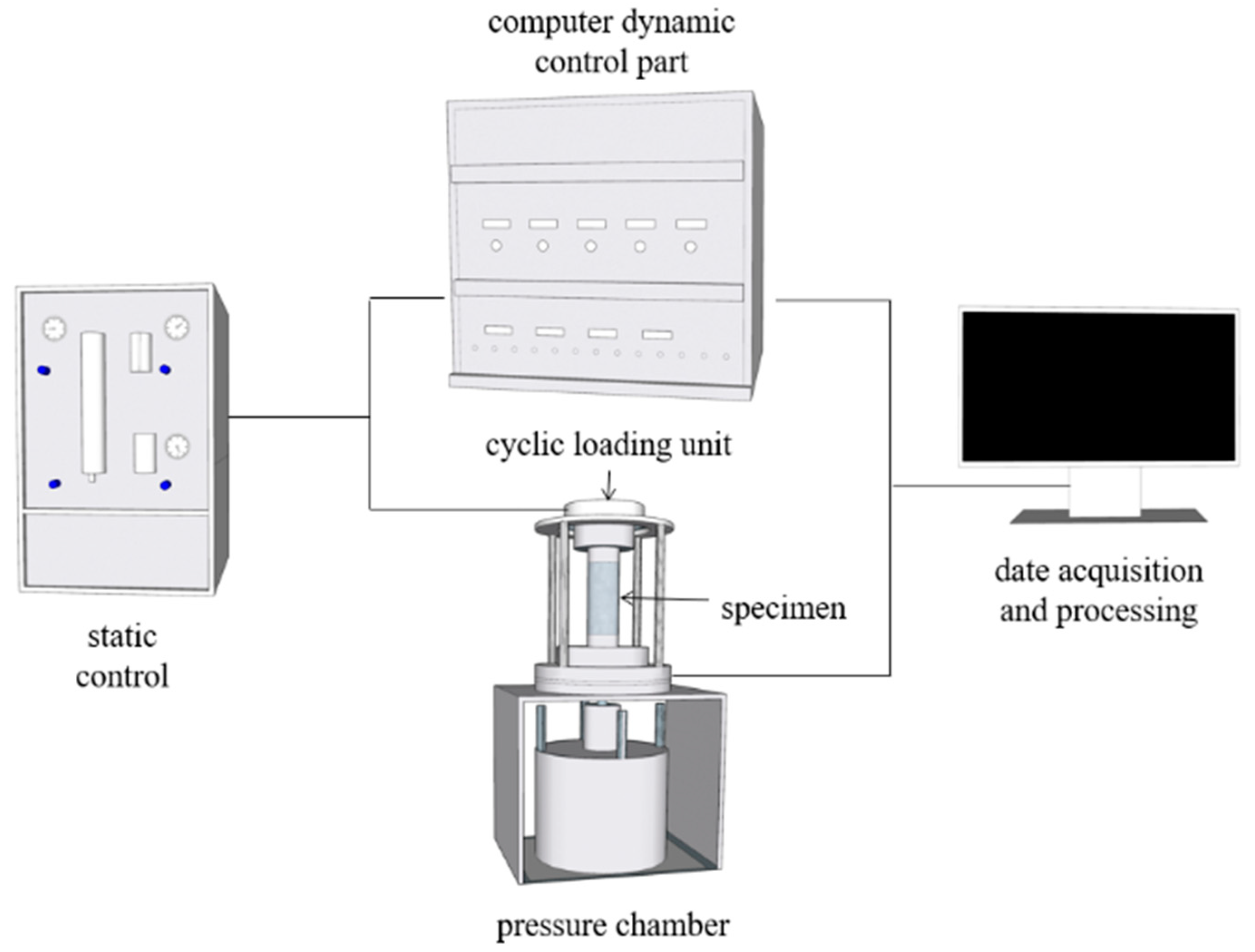
2.3. Scheme of Dynamic Triaxial Test
3. Results
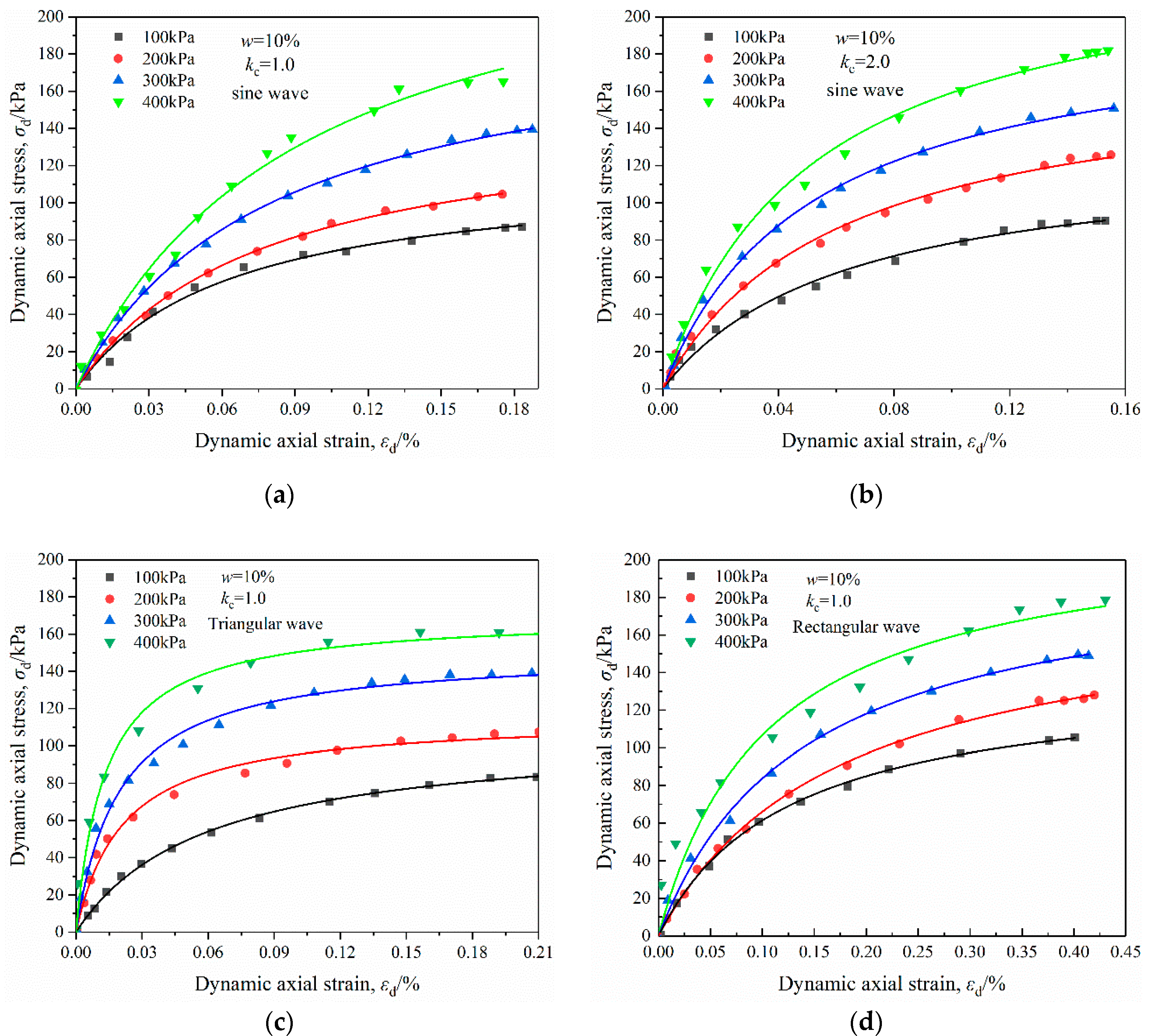
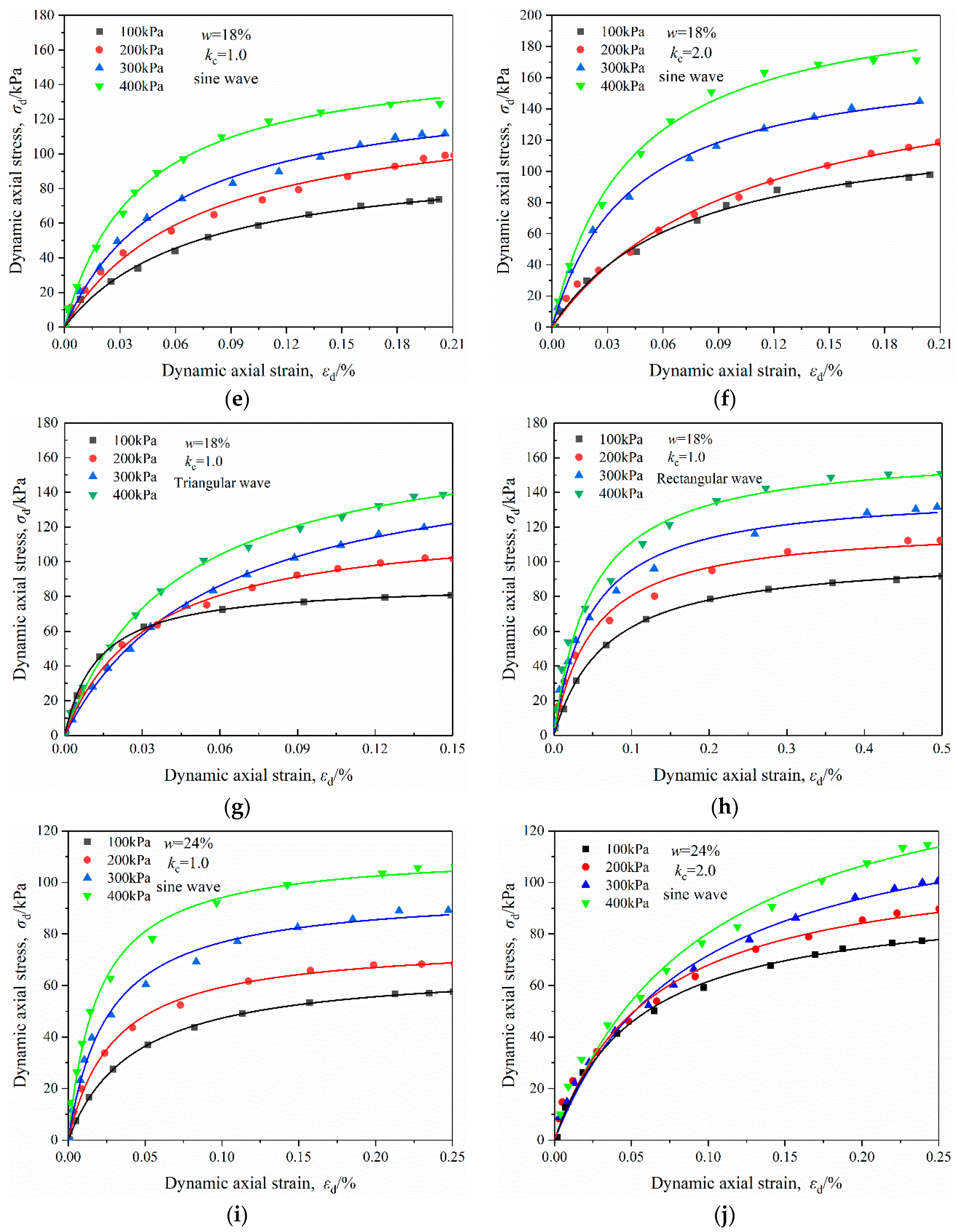
3.1. Skeleton Curve
3.2. Characteristics of Stiffness Degradation
3.2.1. Effects of Vibration Amplitude
3.2.2. Effects of Natural Moisture Content
3.2.3. Effects of Consolidation Ratio
3.2.4. Effects of Wave Form
4. Degradation Model for OMDS
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, J.; Liu, B.Y.; Wang, Z.C.; Zheng, G.; Zhou, H.Z. Dynamic Behavior of Cement-Stabilized Organic-Matter-Disseminated Sand under Cyclic Triaxial Condition. Soil Dyn. Earthq. Eng. 2021, 147, 106777. [Google Scholar] [CrossRef]
- Seed, H.B.; Chan, C.K. Clay strength under earthquake loading conditions. J. Jpn. Soc. Irrig. Drain. Rural Eng. 1966, 92, 53–78. [Google Scholar] [CrossRef]
- Wang, J.-Q.; Chang, Z.-C.; Xue, J.-F.; Lin, Z.-N.; Tang, Y. Experimental Investigation on the Behavior of Gravelly Sand Reinforced with Geogrid under Cyclic Loading. Appl. Sci. 2021, 11, 12152. [Google Scholar] [CrossRef]
- Lei, H.Y.; Li, B.; Lu, H.B.; Ren, Q. Dynamic Deformation Behavior and Cyclic Degradation of Ultrasoft Soil under Cyclic Loading. J. Mater. Civ. Eng. 2016, 28, 04016135. [Google Scholar] [CrossRef]
- Cai, Y.Q.; Wu, T.Y.; Guo, L.; Wang, J. Small Stiffness Degradation and Plastic Strain Accumulation of Clay under Cyclic Load with Principal Stress Rotation and Deviatoric Stress Variation. J. Geotech. Geoenviron. Eng. 2018, 144, 04018021. [Google Scholar] [CrossRef]
- He, S.-H.; Zhang, Q.-F.; Ding, Z.; Xia, T.-D.; Gan, X.-L. Experimental and Estimation Studies of Resilient Modulus of Marine Coral Sand under Cyclic Loading. J. Mar. Sci. Eng. 2020, 8, 287. [Google Scholar] [CrossRef]
- Atkinson, J.H. Non-linear soil stiffness in routine design. Geotechnique 2000, 50, 487–508. [Google Scholar] [CrossRef]
- Liang, F.; Zhang, Z.; Wang, C.; Gu, X.; Lin, Y.; Yang, W. Experimental Study on Stiffness Degradation and Liquefaction Characteristics of Marine Sand in the East Nan-Ao Area in Guangdong Province, China. J. Mar. Sci. Eng. 2021, 9, 638. [Google Scholar] [CrossRef]
- Monismith, C.L.; Ogawa, N.; Freeme, C.R. Permanent Deformation Characteristics of Sub-grade Soils due to Repeated Loading. Transp. Res. Rec. 1975, 537, 1–17. [Google Scholar]
- Li, D.; Selig, E.T. Cumulative Plastic Deformation for Fine-Grained Sub-grade Soils. J. Geotech. Geo-Environ. Eng. 1996, 122, 1006–1013. [Google Scholar] [CrossRef]
- Li, D.; Selig, E.T. Method for Railroad Track Foundation Design. II: Applications. J. Geotech. Geo-Environ. Eng. 1998, 124, 323–329. [Google Scholar] [CrossRef]
- Idriss, I.M.; Dobry, R.; Singh, R.M. Nonlinear behavior of soft clays during cyclic loading. J. Geotech. Eng. ASCE 1978, 104, 1427–1447. [Google Scholar] [CrossRef]
- Yao, M.; Nie, S. A model for calculating deformation of saturated soft clay. J. Hydraul. Eng. 1994, 7, 51–55. (In Chinese) [Google Scholar]
- Chai, J.C.; Miura, N. Traffic-load-induced permanent deformation of road on soft subsoil. J. Geotech. Geoenviron. Eng. 2002, 128, 907–916. [Google Scholar] [CrossRef]
- Parr, G.B. Some Aspects of the Behavior of London Clay under Repeated Loading; University of Nottingham: Nottingham, UK, 1972. [Google Scholar]
- Huurman, M. Development of traffic induced permanent strain in concrete block pavements. Heron 1996, 41, 29–52. [Google Scholar]
- Yasuhara, K.; Hyde, A.F.L.; Toyota, N.; Murakami, S. Cyclic stiffness of plastic silt with an initial drained shear stress. In Pre-failure Deformation of Geomaterials; Thomas Telford Ltd.: London, UK, 1998; pp. 373–382. [Google Scholar]
- Tan, K.; Vucetic, M. Behavior of medium and low plasticity clays under simple shear conditions. In Proceedings of the 4th International Conference on Soil Dynamics and Earthquake Engineering, Mexico City, Mexico, 23–26 October 1989; pp. 131–141. [Google Scholar]
- Wang, J.; Cai, Y.; Xu, C. Experimental study on degradation of stiffness of saturated soft clay under undrained cyclic loading. Rock Soil Mech. 2007, 28, 2138–2144. (In Chinese) [Google Scholar]
- Huang, M.; Li, S. Degradation of stiffness and strength of offshore saturated soft clay under long-term cyclic loading. Chin. J. Geotech. Eng. 2010, 32, 1491–1498. (In Chinese) [Google Scholar]
- Cao, Y.; Kong, L.; Yang, A. Waveform effect of cyclic loading of dynamic character and stiffness degradation characteristics of marine deposited natural soft clay. Chin. J. Geotech. Eng. 2013, 35, 583–589. (In Chinese) [Google Scholar]
- Iraji, A.; Farzaneh, O.; Hosseininia, E.S. A modification to dense sand dynamic simulation capability of Pastor-Zienkiewicz-Chan model. Acta Geotech. 2014, 9, 343–353. [Google Scholar] [CrossRef]
- Hong, Y.; Koo, C.H.; Zhou, C.; Ng, C.W.; Wang, L.Z. Small Strain Path-Dependent Stiffness of Toyoura Sand: Laboratory Measurement and Numerical Implementation. Int. J. Geomech. 2017, 17, 04016036. [Google Scholar] [CrossRef]
- Mei, H.H.; Leng, W.M.; Nie, R.S.; Li, Y.F. Study on dynamic behavior and permanent deformation characteristics of coarse-grained soil. J. Huazhong Univ. Sci. Technol. 2019, 47, 113–119. [Google Scholar]
- Liu, Y.; Zhu, S.Y.; Feng, Y.; Ma, S.K. Research on stiffness softening rules of saturated anisotropic consolidated silty soil under cyclic loading. Highway 2020, 4, 282–288. [Google Scholar]
- Du, J.; Zheng, G.; Liu, B.; Jiang, N.J.; Hu, J. Triaxial behavior of cement-stabilized organic matter–disseminated sand. Acta Geotech. 2021, 16, 211–220. [Google Scholar] [CrossRef]
- Zhang, R.; He, C.; Fei, W.; Gao, M. Effect of consolidation stress ratio on dynamic strength and dynamic pore water pressure of soil. Chin. J. Geotech. Eng. 2006, 28, 101–105. (In Chinese) [Google Scholar]
- Hardin, B.O.; Black, W.L. Closure to vibration modulus of normally consolidated clay: Design equations and curves. J. Soil Mech. Found. Div. ASCE 1969, 95, 1531–1537. [Google Scholar] [CrossRef]
- Wu, Q.; Lu, Q.; Guo, Q.; Zhao, K.; Chen, P.; Chen, G. Experimental Investigation on Small-Strain Stiffness of Marine Silty Sand. J. Mar. Sci. Eng. 2020, 8, 360. [Google Scholar] [CrossRef]
- Liu, J.K.; Cui, Y.H.; Liu, X.; Chang, D. Dynamic characteristics of warm frozen soil under direct shear test-comparison with dynamic triaxial test. Soil Dyn. Earthq. Eng. 2020, 133, 106114. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, J. Experimental and Analytical Study on Residual Stiffness/Strength of CFRP Tendons under Cyclic Loading. Materials 2020, 13, 5653. [Google Scholar] [CrossRef] [PubMed]
- Zhong, H.; Sai, K.V. Normalizing Variation of Stiffness and Shear Strength of Compacted Fine-Grained Soils with Moisture Content. J. Geotech. Geoenviron. Eng. 2017, 143, 04017058. [Google Scholar]
- Huang, J.; Ding, Z.D.; Yuan, T.Y.; Dan, Z.; Li-min, P. Experimental study of dynamic deformation properties of peaty soil under cyclic loading. Rock Soil Mech. 2017, 38, 2551–2558. (In Chinese) [Google Scholar]

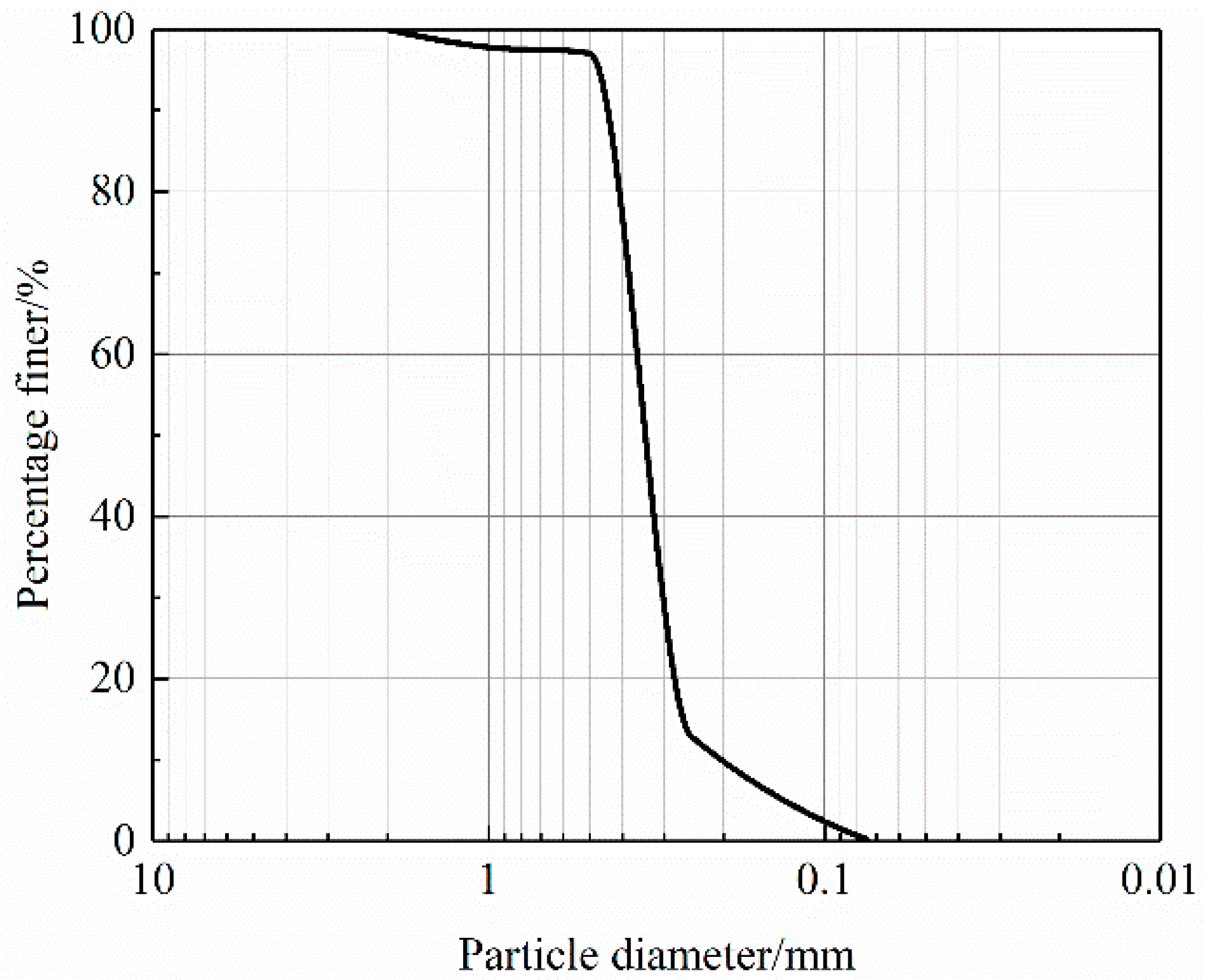




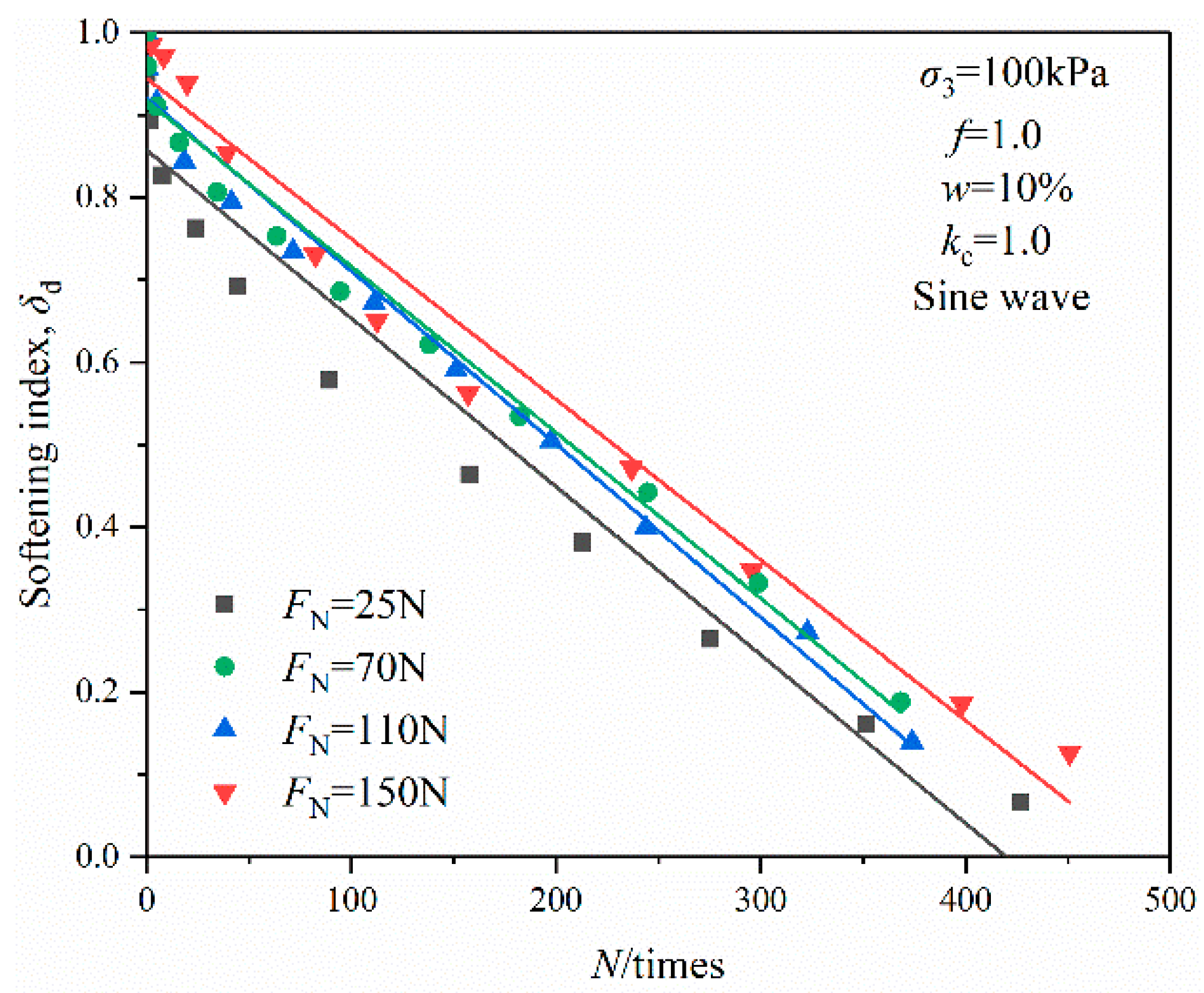

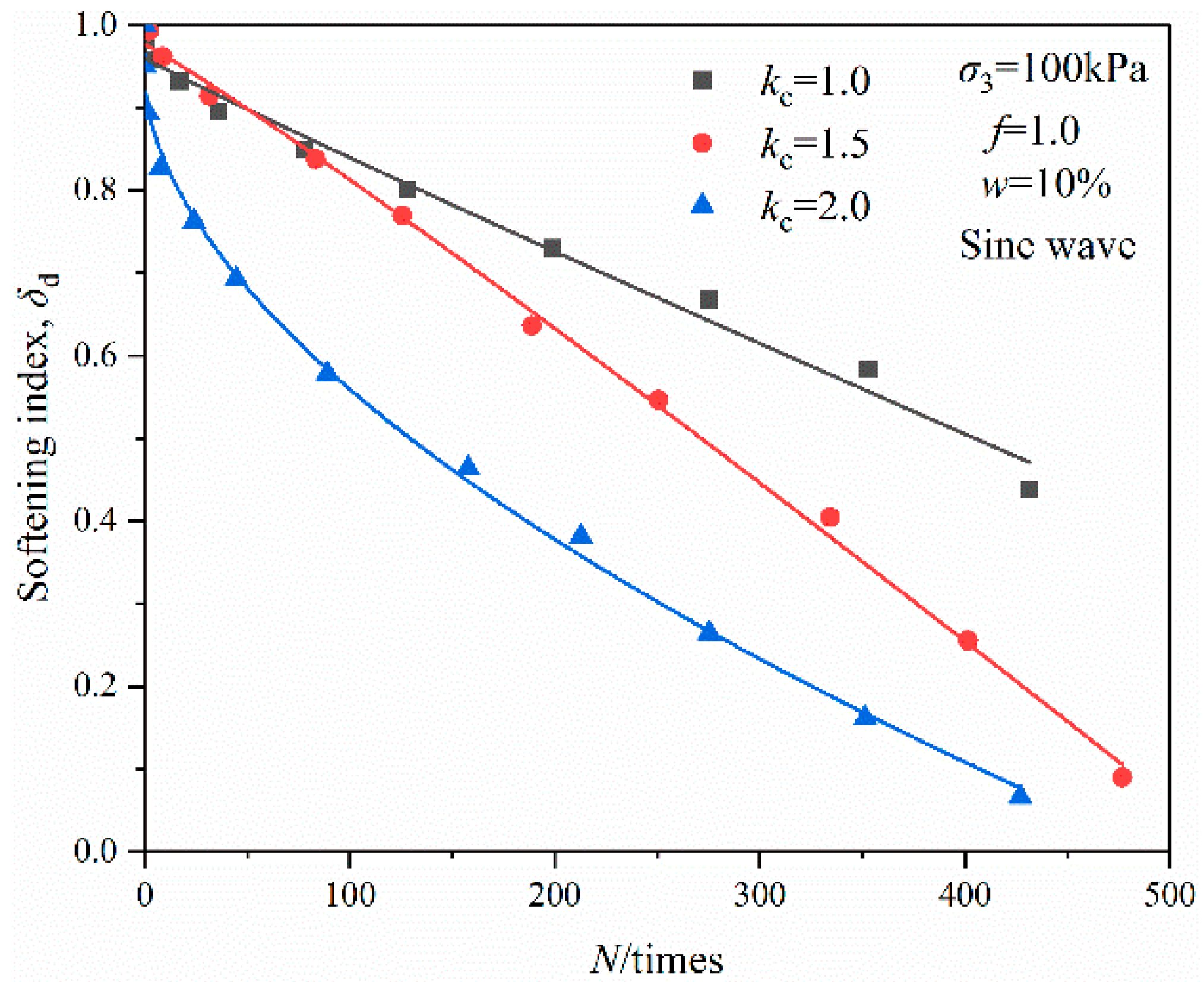
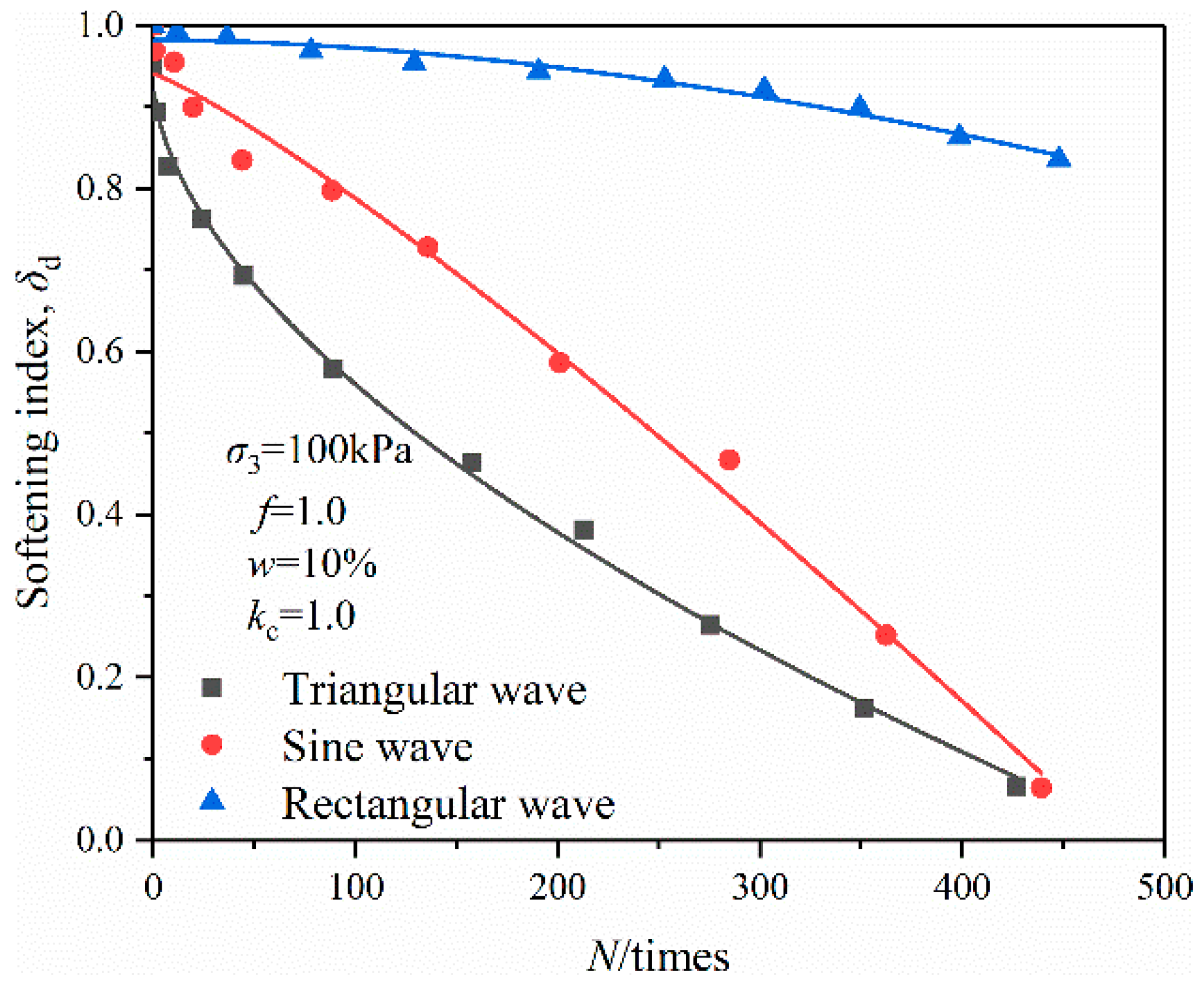


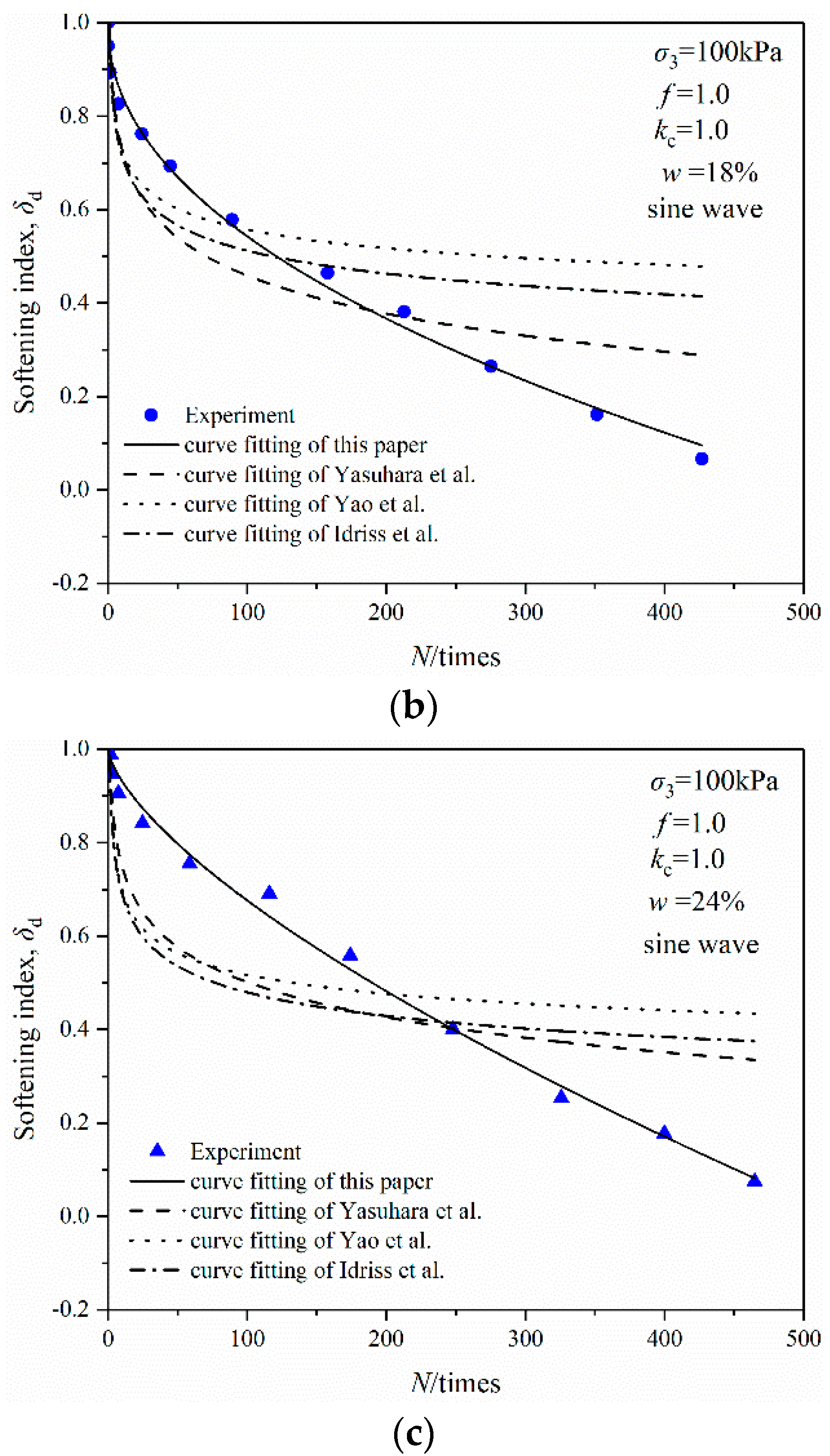
| Organic Content/% | Natural Moisture Content/% | Natural Density/g·cm−3 | Minimum dry Density/g·cm−3 | Maximum Dry Density/g·cm−3 | Specific Gravity |
|---|---|---|---|---|---|
| 5.32 | 12.23 | 1.617 | 1.570 | 1.723 | 2.62 |
| Sample | Consolidation Ratio | Natural Moisture Content/% | Wave Form | Vibrating Load/N |
|---|---|---|---|---|
| OMDS | 1.0 | 10% 18% 24% | sine, triangular, rectangular sine, triangular, rectangular sine, triangular, rectangular | 25, 70, 110, 150 25, 70, 110, 150 25, 70, 110, 150 |
| 1.5 | 10% 18% 24% | sine, triangular, rectangular sine, triangular, rectangular sine, triangular, rectangular | 25, 70, 110, 150 25, 70, 110, 150 25, 70, 110, 150 | |
| 2.0 | 10% 18% 24% | sine, triangular, rectangular sine, triangular, rectangular sine, triangular, rectangular | 25, 70, 110, 150 25, 70, 110, 150 25, 70, 110, 150 |
| Wave Form | Moisture Content/% | Fitting Parameters | ||
|---|---|---|---|---|
| m | n | R2 | ||
| Sine wave | 10 18 24 | −0.01416 −0.05232 −0.09039 | 0.67934 0.47059 0.38753 | 0.87 0.90 0.89 |
| Triangular wave | 10 18 24 | −0.00783 −0.00592 −0.00447 | 1.09822 1.19321 0.8703 | 0.79 0.82 0.85 |
| Rectangular wave | 10 18 24 | −0.00837 −0.00134 −0.00157 | 1.03818 1.02179 1.00179 | 0.79 0.82 0.88 |
| Researcher | Degradation Model | Reference |
|---|---|---|
| Idriss et al. | [12] | |
| Yasuhara et al. | [17] | |
| Yao et al. | [13] | |
| This paper | Present work |
| Sample | Wave Form | Moisture Content (%) | Residual Error Square Sum | |||
|---|---|---|---|---|---|---|
| Idriss Model | Yasuhara Model | Yao Model | This Paper | |||
| OMDS | Sine wave | 10 | 1.198 | 1.058 | 1.279 | 0.016 |
| 18 | 1.472 | 1.239 | 1.617 | 0.007 | ||
| 24 | 1.332 | 1.267 | 1.427 | 0.007 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, J.; Jiang, X.; Liu, B.; Jia, L.; Zhang, Y. Experimental Study on Stiffness Degradation of Organic Matter-Disseminated Sand under Cyclic Loading. Sustainability 2022, 14, 11793. https://doi.org/10.3390/su141811793
Du J, Jiang X, Liu B, Jia L, Zhang Y. Experimental Study on Stiffness Degradation of Organic Matter-Disseminated Sand under Cyclic Loading. Sustainability. 2022; 14(18):11793. https://doi.org/10.3390/su141811793
Chicago/Turabian StyleDu, Juan, Xingfei Jiang, Bingyang Liu, Lin Jia, and Yang Zhang. 2022. "Experimental Study on Stiffness Degradation of Organic Matter-Disseminated Sand under Cyclic Loading" Sustainability 14, no. 18: 11793. https://doi.org/10.3390/su141811793





