Abstract
When exploiting Jurassic-era coal resources in Northwest China, there are risks of water inrush and sand burst disasters from coal seam roofs. To improve the safety of coal mining, it is imperative to accurately and objectively evaluate the water inrush risk of sandstone aquifers from coal seam roofs and to reasonably and effectively prevent and control water disasters. In this paper, the 221 mining area of the Shilawusu Coal Mine was considered. By combining the basic geological condition data, hydrogeological condition data, and drilling data in the area studied, four main control factors, including the equivalent thickness of sandstone, the lithology coefficient of sandstone, the interbedded coefficient of sand and mud, and the core recovery rate, were selected as evaluation indexes for predicting the water inrush risk from the coal seam roof. A hierarchical prediction and discrimination model of water inrush risk based on combination weighting-set pair analysis was established. The combination weighting method, which is based on the sum of squared deviations, was used to optimize the subjective and objective weight values obtained by the improved analytic hierarchy process and entropy weight methods. By applying set pair analysis theory, the comprehensive connection degree was determined using the set pair connection degree function that was constructed with 31 instances of drilling data in the study area. Then, the risk grade of each drilling data instance was evaluated by the confidence criterion of set pair analysis to calculate the water inrush risk evaluation index. Finally, the obtained index was combined with the borehole pumping test data and the discharging test data to partition the water inrush risk from the coal seam roof. The results indicated that most of the 221 mining area is safe, and the small transitional and dangerous areas are only in the central and northern regions. Based on the combination weighting-set pair analysis method, the water inrush risk from the coal seam roofs in the study area was accurately and objectively classified by a discrimination model.
1. Introduction
With the continuous reduction in coal resources in eastern China and the gradual shift of coal mining deployment to the west, the types of mine water disasters have also changed, from Ordovician limestone water inrush in the eastern region to water inrush in the thick sandstone aquifer on the coal seam roof in the western region [1,2,3]. Mine water disasters severely restrict the safety of coal mining processes and pose a great threat to the safety of underground workers [4,5,6]. For example, on 25 April 2016, the roof of the 202 working face in the Zhaojin Coal Mine, Yaozhou District, Tongchuan City, Shanxi Province, had a major water inrush and sand collapse accident, resulting in death. From December 2010 to May 2013, nine roof water inrush accidents occurred in a mine field in the Jiaoping Mining Area, with a water inflow ranging from 249–2000 m3/h; the time interval of each water inrush was approximately 60 days, which posed a serious threat to the safety of the mine [7,8]. Therefore, it is of great significance to objectively and accurately evaluate the water inrush risk of sandstone aquifers in coal seam roofs for the safety of coal mining [9].
Researchers have performed extensive research on assessing the risk of water inrush from coal seam roofs. At present, compared to the geophysical prospecting method and the pumping-and-discharging test method, which have heavy workloads, high costs, and limited control ranges, the multifactor comprehensive analysis method has been preferred by experts and scholars worldwide in the evaluation and prediction of aquifer water abundance in various fields of water disaster prevention and control [10,11,12,13,14,15]. This method considers various influencing factors of aquifer water abundance in geological and hydrogeological data to quantitatively evaluate the aquifer water abundance in the mining area and to establish a prediction model. Wu, Q. et al. [16] predicted the dynamic visualization of water inrush from a coal seam roof using the “three-graph method”. Li, J.Y. et al. [17] applied the entropy weight method to weigh the main control factors, such as the core recovery rate, aquifer thickness, permeability coefficient, fault fractal dimension value, etc., in the study area and then used geographic information science (GIS) to draw the risk zoning map with the use of each indicator. Ji, Y.D. [18] applied the cluster analysis to divide the main control factors into water gushing zones and then graded each water gushing zone by a fuzzy comprehensive evaluation method to obtain the risk evaluation results. Chen, X.F. et al. [19] used the fuzzy set pair analysis method to establish a floor water inrush risk evaluation model for 13 water inrush risk evaluation indexes. Yin, H.Y. et al. [20] used the analytic hierarchy process (AHP) to weigh each influencing factor and superimposed the single-factor thematic map through the information fusion method to obtain the coal seam floor risk zoning map. In addition, some researchers have used methods, such as the “multitype quadruple method” and “TFN” [21,22]. The aforementioned research has made some advancements in the prediction of the water inrush risk from coal seam roofs, but these techniques have their own conditions and limitations of application. At present, the process used by this evaluation method for the prediction of aquifer water abundance is to select various indexes of influencing factors of water abundance and then use AHP, gray theory, principal component analysis, and a BP neural network to obtain the weights that reflect the influence degree of each index [23,24,25,26,27]. Whether the data can be quantitatively fused and processed scientifically in the evaluation process is crucial to the accuracy and reliability of the analysis results. However, at present, few experts and scholars can comprehensively and objectively evaluate the water inrush risk of the aquifer, which impacts the safety of coal seam mining. This paper adopts set pair analysis and a combined weighting method to utilize both the subjective and objective weighting techniques. This feat is accomplished by the improved AHP and entropy weight methods, in order that expert experience and objective data are organically combined, and the water inrush risk of the coal seam roof in the study area is predicted and partitioned. Based on previous studies, this research considered the 221 mining area of the Shilawusu coal mine. On the basis of the analysis of the geological and hydrogeological conditions in the study area, this research group selected four main control factors—the equivalent thickness of sandstone, the lithology coefficient of sandstone, the interbedded coefficient of sand and mud, and the core recovery rate—as the water inrush risk evaluation indexes, and established a combination weighting-set pair analysis model to determine the water inrush risk from the coal seam roofs in the study area.
2. Materials and Methods
2.1. General Situation of Mine
The Shilawusu Coal Mine in the Dongsheng Coalfield is located in the Yijinhuoluo Banner, Erdos City, Inner Mongolia Autonomous Region, which is 87 km away from the Dongsheng District. The mining field is basically a trapezoid, with a width of 7.35 km from north to south, an average length of 9.40 km from east to west, and an area of 70.644 km2 (Figure 1). From the oldest to the newest strata, the strata in the mine field are the Triassic Yanchang Formation (T3y), Jurassic Middle Yan’an Formation (J1–2y), Jurassic Middle Zhiluo Formation (J2z), Jurassic Middle Anding Formation (J2a), Cretaceous Lower Zhidan Group (K1zh), and Quaternary (Q). The coal-bearing strata in the mine field are in the middle of the Jurassic Yan‘an Formation (J1–2y), and the stratum thickness ranges from 280.24~360.59 m, with an average stratum thickness of 312.84 m. The Jurassic Yan’an Formation contains 10~25 coal layers, and the coal seam thickness ranges from 22.78~39.19 m, with an average coal seam thickness of 31.20 m; the coal bearing coefficient is 10.0%. There are 9 minable seams, namely, the 2-1, 2-2upper, 2-2middle, 3-1, 4-1, 4-2middle, 5-1, 5-2, and 6-2 coal seams. The average total thickness of the 9 seams is 28.26 m, and the recoverable coal-bearing coefficient is 9.03%. Two main mining levels are arranged in Shilawusu mine field. In this study area, mining area 221 is the first mining area of the first production level, and now it mainly mines 2-2upper coal seam. The working face adopts a strip layout of alleys and longwall mining along the strike. The caving method is adopted to manage the roof, and the fully mechanized coal mining technology with full height is adopted at one time.
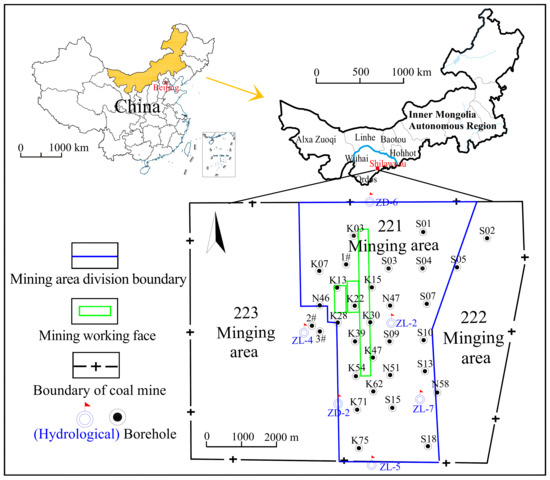
Figure 1.
Map of the research area location and borehole distribution.
The mining field has typical plateau accumulation dune landform features, and the surface vegetation is sparse, which is a desert-semi-desert area. Most of the surface is covered by Quaternary aeolian sand, and some lower Cretaceous strata are exposed locally. The basic structural form of the minefield is a monoclinic structure inclined to the northwest. The dip angle of the coal seam is less than 2, and the formation is slightly wavy. No fault structure and magmatic rock intrusion is found, and the overall structure is simple.
2.2. Determining the Water Inrush Risk Evaluation Index
In this paper, by considering the 2-2upper coal seam in the 221 mining area, the risk of water inrush from the roof of the 2-2upper coal seam is studied. The 2-2upper coal seam thickness is 0.64~7.72 m, with an average coal seam thickness of 5.46 m, making it a medium-thick coal seam. According to the measured data of the water-conducting fracture zone of the coal seam roof, the split-mining ratio of this coal seam is 24.25. Based on calculations, when the 2-2upper coal seam is mined, the water-conducting fracture zone develops to the highest level in the aquifer of the Zhiluo Formation. Therefore, mining fractures will occur that can be used as water-conducting channels between the aquifer of the Zhiluo Formation and the roof of the 2-2upper coal seam [28,29,30]. By combining the geological and hydrogeological conditions and drilling data of the study area with information about the type of water-rich medium, the size of the water-bearing space, and the strength of the hydraulic connection, the four main control factors—the equivalent thickness of sandstone (M), lithology coefficient of sandstone (P), core recovery rate (R), and interbedded coefficient of sand and mud (I)—were selected as the risk evaluation indexes of water inrush from the coal seam roof in the 221 mining area of the Shilawusu Coal Mine [31,32].
2.2.1. Equivalent Thickness of Sandstone (M)
Sandstone thickness is an important index that is used for evaluating the water abundance of underground strata. The greater the sandstone thickness, the stronger the water abundance and the greater the water inrush risk. Since the porosity and permeability of different types of sandstone are different, the thickness of sandstone cannot be obtained by a simple summation of the sandstone in the coal seam roof. By referring to the measurements of porosity and permeability of various types of sandstone in the coal seam roof in the Yingpanhao Mine, Dongsheng Mining Area [33], this research group selected 1, 0.8, and 0.7 as equivalent coefficients for coarse sandstone, medium sandstone, and fine sandstone, respectively. The calculation formula is as follows:
where M is the equivalent thickness of sandstone, m; Mc, Mm, and Mf are the true thicknesses of coarse sandstone, medium sandstone, and fine sandstone, respectively, m; and k is the equivalent coefficient of sandstone thickness conversion, where k1 = 0.8 and k2 = 0.7.
2.2.2. Sandstone Lithology Coefficient (P)
The sandstone lithology coefficient is the ratio of the actual sandstone thickness in the fracture zone of the coal seam roof to the height of the fracture zone. The greater the sandstone lithology coefficient, the greater the proportion of sandstone, the better the water abundance, and the greater the risk of water inrush in the coal seam roof. The calculation formula is as follows:
In this formula, H is the height of the water-conducting fracture zone, m.
2.2.3. Sand-Mud Interbedded Coefficient (I)
Sandstone and mudstone are used as water-bearing and water-resisting layers in underground strata, respectively, and the combined characteristics of sand-mud interbeds directly affect the permeability of the overlying strata on the coal seam roof. The more the layers of sand-mud interbeds, the better the water resistance and the lower the water inrush risk. In this paper, the ratio of the sum of the number of sandstone and mudstone layers in the fracture zone to the height of the fracture zone is defined as the sand-mud interbeded coefficient:
where Z1 is the number of sandstone layers in the fracture zone and Z2 is the number of mudstone layers in the fracture zone.
2.2.4. Core Recovery Rate (R)
The existence of pores and fissures in underground rock strata provides storage space and flow channels for groundwater, and the core recovery rate can directly reflect the integrity of rock formations to evaluate the water abundance of rock strata. The greater the core recovery rate, the higher the formation integrity, the smaller the possibility of pore and fissure formation, and the smaller the risk of water inrush. In this paper, the average core recovery rate of each rock stratum in the fracture zone is as follows:
where Z is the number of rock layers in the fracture zone and Q is the recovery rate of each rock stratum, %.
2.3. Establishment of the Combination Weighting-Set Pair Analysis Prediction Model
2.3.1. Construction of the Set Connection Degree Function
The key to introduce the set pair analysis theory [34] into the risk assessment of water inrush from coal seam roof is by forming a set pair of risk influencing factors and evaluation criteria, and the relationship between them can be divided into two types: Certainty expressed by the same degree and opposition degree and uncertainty expressed by difference degree. Through the quantitative analysis of the similarities, opposites, and differences between them, the quantitative indexes of risk assessment are obtained, and the membership function of the connection degree of each evaluation index and its corresponding grading evaluation standard is constructed [35,36].
The smaller the master control factor, the better the expression, as seen below:
The larger the master control factor, the better the expression, as seen below:
where μmn is the connection degree of the nth evaluation index of sample m; x is the measured value of the sample evaluation index; s1, s2, and s3 are the threshold values of the evaluation standard grades; and I, II, III, and IV are the risk grades. The higher the risk grade, the greater the risk.
2.3.2. Combination Weighting
Subjective weighting attaches importance to expert experience, but insufficient consideration is given to measured data. Objective weighting attaches importance to measured data, but insufficient consideration is given to expert experience. However, the two methods of determining weight can be organically combined to sufficiently consider both expert experience and measured data, thus realizing the accuracy and scientificity of index weight. In this paper, the combination weighting method based on the sum of squared deviations is used to optimize the subjective and objective weights obtained by the improved analytic hierarchy process (IAHP) and entropy weight method.
- Improved Analytic Hierarchy ProcessThe IAHP uses the three-scale method of the optimal transfer matrix to construct the judgment matrix, which not only has good judgment transfer and rationality of scale values, but also avoids the blind and subjective consistency test, greatly improving the accuracy of the judgment results and the objectivity of the evaluation [37]. The weight determination steps are as follows:
- Constructing the Comparison Matrix A
According to the three-scale theory, the importance of the main control factors is compared pairwise, and the comparison matrix is as follows:In this matrix, when aij = 1, i is more important than j; when aij = 0, i and j are equally important; and when aij = −1, j is more important than i.- Calculating the Optimal Transfer Matrix C
where:- Determining the Judgment Matrix D
where:- Weighting the Evaluation Index
According to the judgment matrix D, the weight coefficient of the elements in this level related to some elements of the previous level is obtained using the product square root method. The weight vectors of the n elements in this hierarchy are W = [w1, w2,···,wn]T, and the formula for solving each weight is as follows: - Entropy weight methodThe entropy weight method is an objective method that determines the index weight by quantifying the data information of each unit to be evaluated. The smaller the entropy value of an index, the greater the weight, and vice versa [38]. The weight determination steps are as follows [39]:
- Constructing the Original Data Matrix R
The original data matrix R of m evaluation objects and n evaluation indexes is constructed as follows:- Standardizing the Processing of Original Data
X = (xij)n × m is obtained after standardization of R, where xij is the standard value of the jth evaluation index for the ith evaluation object. The standard values with positive correlation and negative correlation with risk can be calculated by Equations (14) and (15), respectively:- Determining the Entropy of the Evaluation Index
- Weighting the Evaluation Index
- Optimal combination weighting based on the sum of squared deviations
In this paper, the optimal combination weighting method based on the maximum sum of squared deviations is adopted to determine the proportions of the IAHP weight and the entropy weight to maximize the total sum of squared deviations of M evaluation objects [40]. The steps to determine the combination weight are as follows [41]: Let the subjective weight vector be W1 = [w11, w21,···,wn1]T and the objective weight vector be W2 = [w12, w22,···,wn2]T; then, the combined weight vector is as follows:
where and are combination coefficients.
The sum of squared deviations between the ith evaluation object and the other evaluation objects is as follows:
Construct the following objective function as follows:
Let matrix B1 be as follows:
Then, the objective function J(Wz) can be expressed as follows:
According to matrix theory, the optimal solution of Formula (21) is the unitized feature vector corresponding to the maximum eigenvalue of the matrix λmax. The unitized feature vector corresponding to the maximum eigenvalue is θ* = [θ1, θ2]T, which is implemented to obtain the combined weight vector W*z and normalize it as follows:
2.3.3. Calculate the Comprehensive Connection Degree
The expression of the comprehensive connection degree is as follows:
where um is the comprehensive connection degree of the mth sample and Wzj is the combination weight of the jth evaluation index.
2.3.4. Improvement in the Evaluation Criteria
After the comprehensive connection degree of the sample is determined, the risk level can be judged by comparing am, bm, and cm [36].
If max[am, bm, cm] = bm, the water inrush risk level is Grade II.
If max[am, bm, cm] = am and am + bm ≥ 0.7, the water inrush risk level is Grade I; otherwise, it is Grade II.
If max[am, bm, cm] = cm and bm + cm ≥ 0.7, the water inrush risk level is Grade III; otherwise, it is Grade II.
If max[am, bm, cm] = cm and cm ≥ 0.7, the water inrush risk level is Grade IV.
Since the above evaluation criteria cannot compare and analyze the water inrush risk levels of different samples in the same practical applications, the specific steps to improve the criteria are as follows:
- Arrange all the connection data in the same grade in descending order and redefine them as am1, am2, am3, …, amn−1, amt. According to the confidence criterion of set pair analysis, the greater the value of the sample connection degree ami (1 < I < t), the higher its membership degree in the same grade and the lower the water inrush risk.
- Eami is an evaluation index that indicates the water inrush risk. Assuming that ami and Eami are negatively correlated, their relationship can be expressed by establishing a cosine function model:where ami is the comprehensive connection degree of samples in the same grade, 0 < ami < 1, and Eami is the risk evaluation index in the same grade, 0 ≤ Eami ≤ π/2.
- After Eami is standardized in the same grade to obtain the risk evaluation index E*ami in each grade, E*ami is quantified in the grade by Formula (26):where E is the final risk assessment index; E*ami is the standardized evaluation index of each grade; and k is a class constant, k = 1(E*ami∈I), k = 2(E*ami∈II), k = 3 (E*ami∈III), and k = 4 (E*ami∈Ⅳ).
In summary, four levels of the continuously changing water inrush risk evaluation index can be obtained in order that the water inrush risk of all samples can be directly compared according to the risk evaluation index value. The greater the risk assessment index, the greater the risk of water inrush.
2.4. Prediction of Water Inrush Risk of Coal Seam Roof in the 221 Mining Area
2.4.1. Determination of Evaluation Index Partition Threshold
Through the histogram statistical analysis (Figure 2) of the original data of each evaluation index (Table 1) while taking the frequency mutation point as the partition threshold, the classification standards of water inrush risk (Table 2) and spatial variation (Figure 3) corresponding to each evaluation index of the coal seam roof are obtained. The line chart in Figure 2 can clearly reflect the variation and centralized distribution range of each evaluation index in the study area, and classify the water inrush risk reflected by each index into four grades: I, II, III, IV. The zoning threshold is the same as that shown in Table 2.
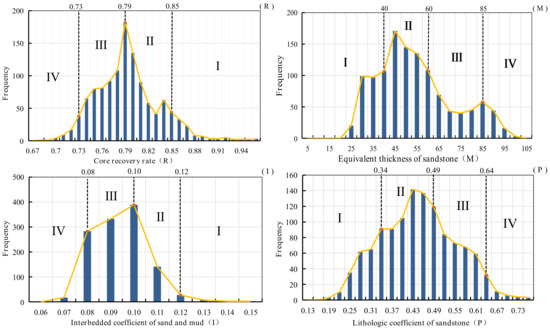
Figure 2.
Frequency distribution histogram of the evaluation index.

Table 1.
Sample data table of the study area.

Table 2.
Classification criteria for risk assessment.
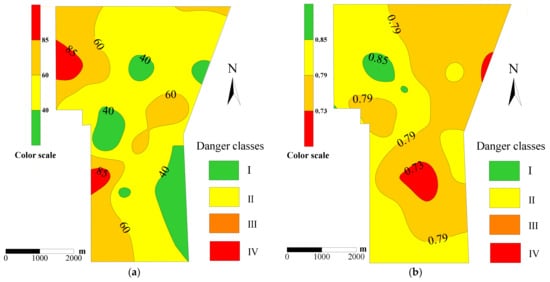
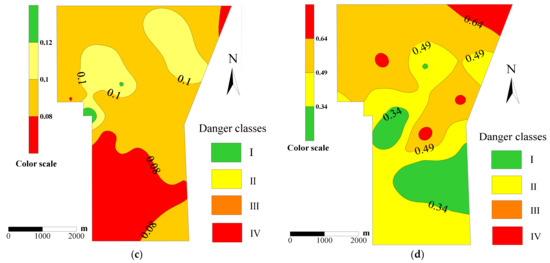
Figure 3.
Spatial changes in risk assessment indicators. (a) Equivalent thickness of sandstone, (b) core recovery rate, (c) interbedded coefficient of sand and mud, (d) lithology coefficient of sandstone.
2.4.2. Calculate the Index Weight
- Improve the analytic hierarchy process and calculate subjective weight
The hierarchical structure model of evaluation indicators in this research area is established, as shown in Figure 4.
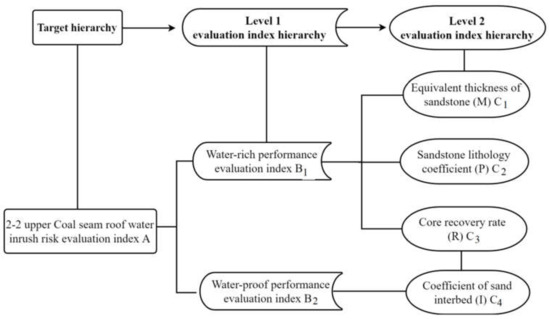
Figure 4.
The hierarchical structure model of roof water inrush risk assessment of the 2-2upper coal seam.
According to the experience of experts, the importance of the first- and second-level evaluation indexes is determined, and the judgment matrix is established. The judgment matrix of the first-level evaluation index is and the weights are WBj = (0.731,0.269). The judgment matrix of the second-level evaluation index is , and . The weights are WCj = (0.563, 0.289, 0.148) and WCj = (1). The linear weighting method is used to multiply the weight value of the first-level index with the weight value of its subordinate second-level index, and the subjective weight value of each main control factor on the water inrush risk of the coal seam roof is obtained, as shown in Table 3.

Table 3.
Weighting of evaluation index combination.
- 2.
- Entropy weight method to calculate the objective weight
The objective weight of each main control factor is calculated by Equations (13)–(18), and the calculation results are shown in Table 3.
- 3.
- Combination weighting
B1 can be found with Equation (21). . Let Q = W1Y1W2, then we obtain . The maximum eigenvalue of matrix Q is 64.5791, and its corresponding unit eigenvector is [0.7147, 0.6994]T. The unit eigenvectors are normalized to obtain the combined weight coefficients of 0.5054 and 0.4946, which help in obtaining the combined weight values (Table 3).
2.4.3. Calculate the Comprehensive Connection Degree and Grade Judgment
According to Equation (24), the comprehensive connection degree of each borehole data point in the study area is obtained, and the water inrush risk level is evaluated according to the confidence criterion of set pair analysis. The results are shown in Table 4.

Table 4.
Comprehensive correlation degree and risk grade evaluation.
3. Results
According to the comprehensive connection degree and risk grade evaluation results, the water inrush risk evaluation indexes (Table 5) of the coal seam roof in the 221 mining area are calculated by Equations (25) and (26), and the water inrush risk zoning map based on the combination weighting-set pair analysis discrimination model is drawn (Figure 5). Combined with the pumping test results of two boreholes in the study area (the unit water inflows of 1# and 3# are q = 0.005421 and q = 0.0741 L/s·m, respectively), the risk evaluation index E [0, 2] is defined as the safe zone; E [2, 3] is defined as the transition zone; and E [3, 4] is defined as the danger zone. According to the danger zoning map, the vast majority of the 221 mining area belongs in the safe zone, and small regions of transition zone and danger zone exist only in the central and northern portions of the mining area.

Table 5.
Results of risk assessment index.
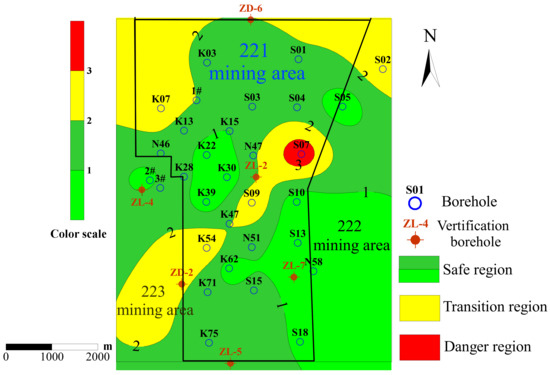
Figure 5.
Partition map of water inrush risk.
4. Discussion
Starting from the research direction of mine water disaster prevention and control, this paper uses set pair analysis and combination weighting method to analyze the drilling data and water pumping and discharging test data in the study area, aiming at establishing the prediction and discrimination model of water inrush risk of coal seam roof. At present, the main idea of the evaluation method for the prediction of aquifer water abundance is to select various indexes of influencing factors of water abundance, and then use AHP, gray theory, principal component analysis, and BP neural network to achieve the weights that reflect the influence degree of each index. Whether the data can be quantitatively fused and processed scientifically in the evaluation process is crucial to the accuracy and reliability of the analysis results. However, at present, few experts and scholars can comprehensively and objectively evaluate the water inrush risk of the aquifer that affects the safe mining of coal seam. This paper adopts set pair analysis and combined weighting method to combine and optimize the subjective and objective weights obtained by IAHP and entropy weight method, in order that the expert experience and objective data are organically combined, and the water inrush risk of the coal seam roof in No. 2-2 of the 221 mining area of Shilawusu Coal Mine is predicted and partitioned, which provides a scientific basis for the prevention and control of water inrush from the mine roof.
The discriminant model has a good application prospect in water inrush risk assessment, but there are few data of drilling water pumping and discharging used to assess the definition index of safety zone, transition zone, and danger zone, thus the accuracy of prediction zoning needs further verification. For this reason, this paper selects six hydrological boreholes in different sub-regions of the working face, and substitutes the borehole data into the aforementioned prediction and discrimination model to verify the final division results of the model. It can be seen from Table 6 that, after calculation, the risk evaluation index E values of six hydrological holes constructed in the later period are basically consistent with the actual hydrological detection results of this hole, thus the prediction results of this model are more accurate.

Table 6.
Risk assessment index results of verification borehole.
5. Conclusions
In this paper, from the perspective of mine water disaster prevention and control, the drilling data and pumping-and-discharging test data in the study area are analyzed by using set pair analysis and combination weighting method. Finally, the prediction and discrimination model of water inrush risk from coal seam roof is established. The main conclusions are as follows:
By considering the characteristics of geological and hydrogeological conditions in the study area, four main control factors—the equivalent thickness of sandstone, lithology coefficient of sandstone, interbedded coefficient of sand and mud, and core recovery rate—are selected to predict the water inrush risk from the coal seam roof.
By combining the water inrush risk discrimination model based on the combination weighting-set pair analysis with the borehole drainage data in the study area, the water inrush risk zoning map of the coal seam roof in the 221 mining area is obtained. The zoning map shows that the majority of the 221 mining area is safe, and only small regions of transition and dangerous zones exist in the central and northern sides of the mining area.
The rationality and accuracy of the above-mentioned model are verified by selecting six hydrological boreholes in different regions of the working face. By substituting the drilling data into the prediction discrimination model, it can be seen that the model can obtain more accurate prediction results.
Author Contributions
Resources, D.X. and H.Z.; investigation, Z.D.; writing—original draft, D.X. and J.H.; supervision, H.Z.; funding acquisition, D.X.; methodology, D.X.; format analysis, T.M. and K.W.; visualization, J.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by the National Natural Science Foundation of China (Grant No. 41702305).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gui, H.R.; Lin, M.L.; Song, X.M. Identification and Application of Roof Bed Separation (Water) in Coal Mines. Mine Water Environ. 2018, 37, 376–384. [Google Scholar] [CrossRef]
- Gui, H.R.; Lin, M.L. Types of water hazards in China coalmines and regional characteristics. Nat. Hazards 2016, 84, 1501–1512. [Google Scholar] [CrossRef]
- Fan, K.F.; Li, W.P.; Wang, Q.Q.; Liu, S.L.; Xue, S.; Xie, C.Y.; Wang, Z.K. Formation mechanism and prediction method of water inrush from separated layers within coal seam mining: A case study in the Shilawusu mining area, China. Eng. Fail. Anal. 2019, 103, 158–172. [Google Scholar] [CrossRef]
- Shi, S.Q.; Wei, J.C.; Yin, H.Y.; Xie, D.L.; Yang, J.H. Forecasting of water abundance of coal roof sandstone aquifer in Jining No. 3 mine. Coal Geol. Explor. 2017, 45, 100–104. [Google Scholar]
- Lin, C.S. Research and application of water control of thick sandstone in coal roof. Coal Geol. Explor. 2019, 47 (Suppl. S1), 81–85. [Google Scholar]
- Liu, J.H.; Zhao, Y.L.; Tan, T.; Zhang, L.Y.; Zhu, S.T.; Xu, F.Y. Evolution and modeling of mine water inflow and hazard characteristics in southern coalfields of China: A case of Meitanba mine. Int. J. Min. Sci. Technol. 2022, 32, 513–524. [Google Scholar] [CrossRef]
- Peng, T.; Feng, X.H.; Long, L.L.; Wang, Y.; Niu, C.; Liu, Y.F. Study on mechanism of water inrush and sand inrush in mining of coal seam with thick overlying bedrock. Coal Sci. Technol. 2019, 47, 260–264. [Google Scholar] [CrossRef]
- Sun, K.; Xia, Y.C.; Li, C.; Chen, J.P.; Fang, G. Risk assessment of water inflow (inrush) from coal seam roof under fully mechanized caving mining. J. Xi’an Univ. Sci. Technol. 2019, 39, 452–460. [Google Scholar] [CrossRef]
- Shi, L.Q.; Qu, X.Y.; Han, J.; Qiu, M.; Gao, W.F.; Qin, D.X.; Liu, H.S. Multi-model fusion for assessing the risk of inrush of limestone karst water through mine floor. J. China Coal Soc. 2019, 44, 2484–2493. [Google Scholar] [CrossRef]
- Lin, C.J.; Zhang, M.; Zhou, Z.Q.; Li, L.P.; Shi, S.Q.; Chen, Y.X.; Dai, W.J. A new quantitative method for risk assessment of water inrush in karst tunnels based on variable weight function and improved cloud model. Tunn. Undergr. Space Technol. 2020, 95, 10313. [Google Scholar] [CrossRef]
- Han, C.H.; Wei, J.C.; Xie, D.L.; Xu, J.G.; Zhang, W.J.; Zhao, Z.C. Water-richness evaluation of sandstone aquifer based on set pair analysis-variable fuzzy set coupling method: A case from Jurassic Zhiluo formation of Jinjiaqu coal mine in Ningdong mining area. J. China Coal Soc. 2020, 45, 2432–2443. [Google Scholar] [CrossRef]
- Yu, H.; Wu, Q.; Zeng, Y.F.; Zheng, L.; Xu, L.L.; Liu, S.Q.; Wang, D. Integrated variable weight model and improved DRASTIC model for groundwater vulnerability assessment in a shallow porous aquifer. J. Hydrol. 2022, 608, 127538. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.C.; Li, L.P.; Peng, L.; Xu, Z.H.; Gao, C.L. Attribute recognition model for risk assessment of water inrush. Bull. Eng. Geol. Environ. 2019, 78, 1057–1071. [Google Scholar] [CrossRef]
- Liu, W.T.; Yu, J.; Shen, J.J.; Zheng, Q.S.; Han, M.K.; Hu, Y.Y.; Meng, X.X. Application of Clustering and Stepwise Discriminant Analysis Based on Hydrochemical Characteristics in Determining the Source of Mine Water Inrush. Geofluids 2021, 2021, 6670645. [Google Scholar] [CrossRef]
- Ding, X.W.; Chong, X.; Bao, Z.F.; Xue, Y.; Zhang, S.H. Fuzzy Comprehensive Assessment Method Based on the Entropy Weight Method and Its Application in the Water Environmental Safety Evaluation of the Heshangshan Drinking Water Source Area, Three Gorges Reservoir Area, China. Water 2017, 9, 329. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, H.; Zhao, Y.W.; Cui, J.Q. Dynamic visualization and prediction for water bursting on coal roof based on “three maps method”. J. China Coal Soc. 2016, 41, 2968–2974. [Google Scholar] [CrossRef]
- Li, J.Y.; Liu, Q.M.; Liu, Y.; Chai, H.C. Risk Assessment of Water Inrush from Coal Seam Roof Based on GIS and Entropy Method. Coal Eng. 2019, 51, 115–119. [Google Scholar]
- Ji, Y.D. The Risk Assessment of Roof Water Inrush based on Cluster Analysis and Fuzzy Comprehensive Evaluation. Min. Saf. Environ. Prot. 2019, 46, 68–72. [Google Scholar]
- Chen, X.F.; Miao, Y.C.; Chen, W.T. Study on evaluation of mine floor water inrush danger based on Fuzzy Set Pair Analysis Method. Coal Sci. Technol. 2019, 47, 218–223. [Google Scholar] [CrossRef]
- Yin, H.Y.; Lefticariu, L.; Wei, J.C.; Xie, D.L.; Xiao, L.L.; Zhang, W.J.; Tong, W.L. Water inrush risk zoning and classification during coal seam mining in the Jiangzhuang coal mine, Shandong province. China Min. Mag. 2015, 24, 149–154. [Google Scholar]
- Li, Y.G.; Li, H.J.; Xia, Y.J.; Liu, H.C.; Han, G. Prediction and evaluation study on coal seam roof water inrush based on multi-type four-double method. Coal Sci. Technol. 2019, 47, 219–228. [Google Scholar] [CrossRef]
- Yin, H.Y.; Shi, Y.L.; Niu, H.G. A GIS-based model of potential groundwater yield zonation for a sandstone aquifer in the Juye Coalfifield, Shangdong, China. J. Hydrol. 2018, 557, 434–447. [Google Scholar] [CrossRef]
- Fan, L.M.; Ma, L.Q.; Yu, Y.H.; Wang, S.K.; Xu, Y.J. Water-conserving mining influencing factors identification and weight determination in northwest China. Int. J. Coal Sci. Technol. 2019, 6, 95–101. [Google Scholar] [CrossRef]
- Onifade, M.; Genc, B. Spontaneous combustion liability of coal and coal-shale: A review of prediction method. Int. J. Coal Sci. Technol. 2019, 6, 151–168. [Google Scholar] [CrossRef]
- Wu, Q.; Jie, S.H.; Pei, Z.J. A new practical methodology of the coal floor water bursting evaluating III: The application of ANN vulnerable index method based on GIS. J. China Coal Soc. 2007, 45, 1301–1306. [Google Scholar]
- Yin, H.Y.; Zhou, X.L.; Lang, N.; Zhang, L.F.; Wang, M.L.; Wu, T.; Li, X. Prediction model and application of GA-BP neural network based on SSA optimization. Geol. Explor. 2021, 49, 175–185. [Google Scholar] [CrossRef]
- Liu, W.T.; Sun, Q.; Xu, B.C. Risk Evaluation of Water Inrush from Coal Seam Floor Based on GIS and Principal Component Analysis-Entropy Weight Method. Min. Res. Dev. 2020, 40, 83–88. [Google Scholar] [CrossRef]
- Li, X.B.; Li, Q.S.; Xu, X.H.; Zhao, Y.Q.; Li, P. Multiple Influence Factor Sensitivity Analysis and Height Prediction of Water-Conducting Fracture Zone. Geofluids 2021, 2021, 8825906. [Google Scholar] [CrossRef]
- Liu, Y.; Yuan, S.C.; Yang, B.B.; Liu, J.W.; Ye, Z.Y. Predicting the height of the water-conducting fractured zone using multiple regression analysis and GIS. Environ. Earth Sci. 2019, 78, 422. [Google Scholar] [CrossRef]
- Chen, J.T.; Zhao, J.H.; Zhang, S.C.; Zhang, Y.; Yang, F.; Li, M. An Experimental and Analytical Research on the Evolution of Mining Cracks in Deep Floor Rock Mass. Pure Appl. Geophys. 2020, 177, 5325–5348. [Google Scholar] [CrossRef]
- Yao, B.H.; Bai, H.B.; Zhang, B.Y. Numerical simulation on the risk of roof water inrush in Wuyang Coal Mine. Int. J. Min. Sci. Technol. 2012, 22, 273–277. [Google Scholar] [CrossRef]
- Meng, Z.P.; Li, G.Q.; Xie, X.T. A geological assessment method of floor water inrush risk and its application. Eng. Geol. 2012, 143–144, 51–60. [Google Scholar] [CrossRef]
- Wu, X. Prediction of Water Abundance of Sandstone Aquifer in 2-2 Coal Seam Roof and Risk Assessment of Water Inrush in 22 Mining Area of Yingpanhao Coal Mine. Shandong Univ. Sci. Technol. 2018. [Google Scholar] [CrossRef]
- Zhao, K.Q. Set Pair Analysis and Its Preliminary Application; Zhejiang Science and Technology Press: Hangzhou, China, 2000. [Google Scholar]
- Wang, T.T.; Jin, D.W.; Liu, J.; Yang, J.; Wang, X.Y.; Zhao, W. Application of dynamic weight-set pair analysis model in mine water inrush discrimination. J. China Coal Soc. 2019, 44, 2840–2850. [Google Scholar] [CrossRef]
- Shi, S.Q.; Wei, J.C.; Xie, D.L.; Yin, H.Y.; Li, L.Y. Prediction analysis model for groundwater potential based on set pair analysis of a confined aquifer overlying a mining area. Arab. J. Geosci. 2019, 12, 115. [Google Scholar] [CrossRef]
- Liu, X.Y.; Jia, Z.X.; Jin, M.J.; Hao, J.N. Routine scheme Comparison of Coal Goaf Expressway Based on Comprehensive Evaluation Method. J. Taiyuan Univ. Sci. Technol. 2019, 40, 395–400. [Google Scholar] [CrossRef]
- Song, X.; Ning, Y.C.; Wang, R.M.; Wang, S.Q. Prediction and Evaluation of Coal Floor Water Inrush Based on Objective Optimization Combination Weighting Model. Saf. Coal Mines. 2019, 50, 138–141+145. [Google Scholar] [CrossRef]
- Hou, E.K.; Ji, Z.C.; Che, X.Y.; Wang, J.W.; Gao, L.J.; Tian, S.X.; Yang, F. Water abundance prediction method of weathered bedrock based on improved AHP and the entropy weight method. J. China Coal Soc. 2019, 44, 3164–3173. [Google Scholar] [CrossRef]
- Yin, X.; Liu, Q.S.; Wang, X.Y. Application of attribute interval recognition model based on optimal combined weighting to prediction of classification of rockburst intensity. J. China Coal Soc. 2020, 45, 3772–3780. [Google Scholar] [CrossRef]
- Deng, H.W.; Wang, P. Evaluation of Regional Water Environmental Carrying Capacity Based on GIS and Sum of Deviation Square Combination Weighting Method. J. Yangtze River Sci. Res. Inst. 2020, 37, 22–28. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).