A Simulation-Based Study of the Influence of Low-Speed Vehicles on Expressway Traffic Safety
Abstract
1. Introduction
2. Literature Review
2.1. Traffic Impact of LSVs
2.2. Study of Traffic Safety on Expressways
2.3. Summary
3. Materials and Methods
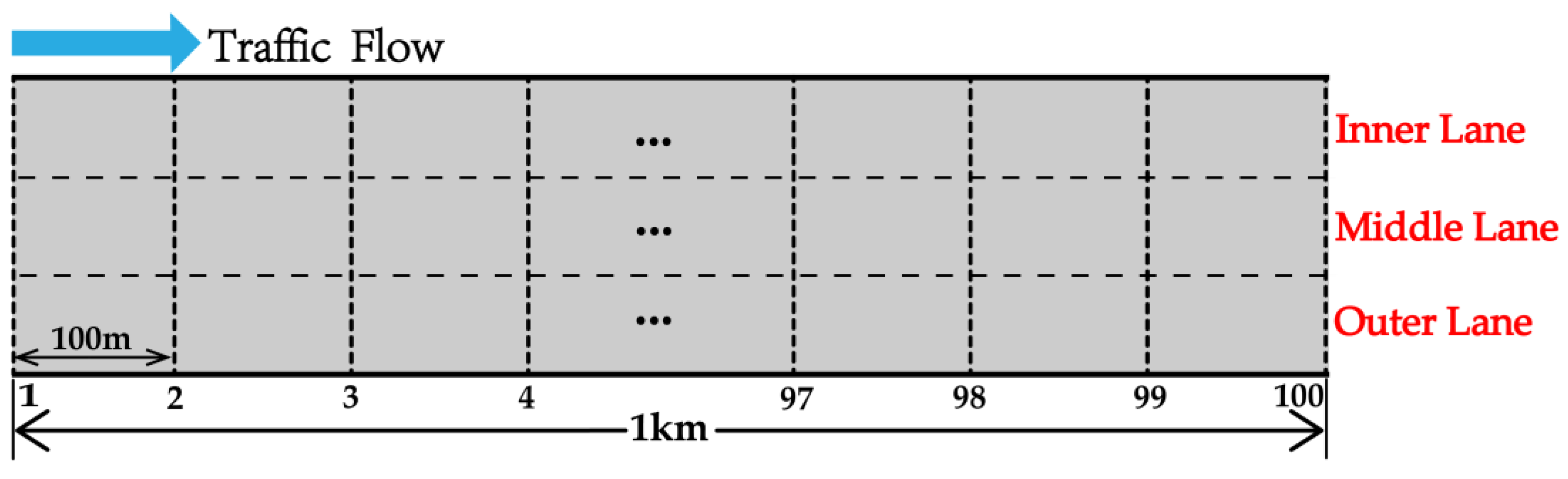
3.1. VISSIM Simulation Model
3.1.1. Parameter Calibration
3.1.2. Parameters Selection
3.1.3. Model Construction
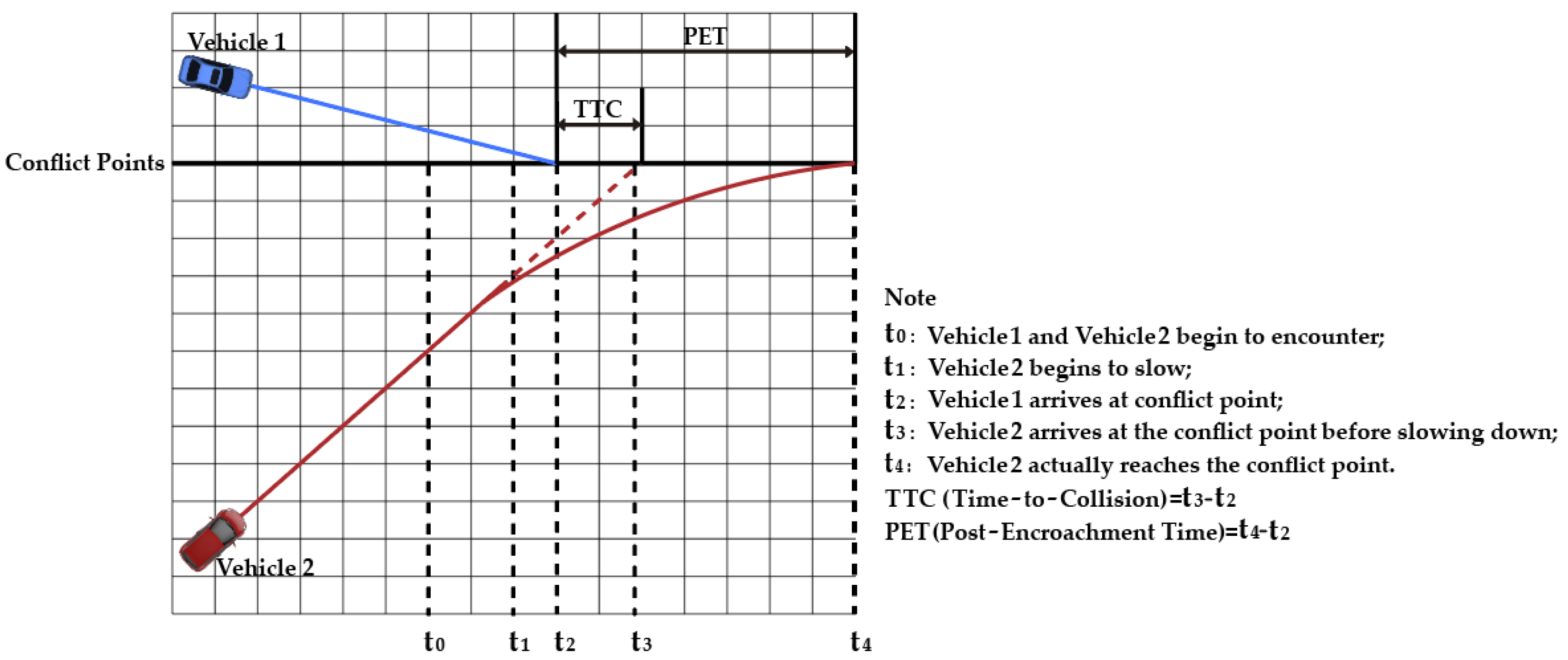
3.2. SSAM-Based Model
- From the initial positions and velocities of Vehicle 1 and Vehicle 2, 100 paths for each vehicle are generated using combinations of acceleration and orientation that are independently generated from two triangular distribution functions;
- All collision points between every pair of projected paths are detected. P(UEA) is the percentage resulting from dividing the number of collision points by the total number of combinations of paths, that is:where represents all collision points between each pair of predicted paths for Vehicle 1 and Vehicle 2. represents the total number of path combinations between Vehicle 1 and Vehicle 2. P(UEA) can not only identify the conflicts that have occurred, but can also show the potential conflicts between vehicles, which has positive implications for traffic safety management and the prevention of traffic accidents.
4. Results
4.1. Vehicle Queuing and Dissipation Characteristics
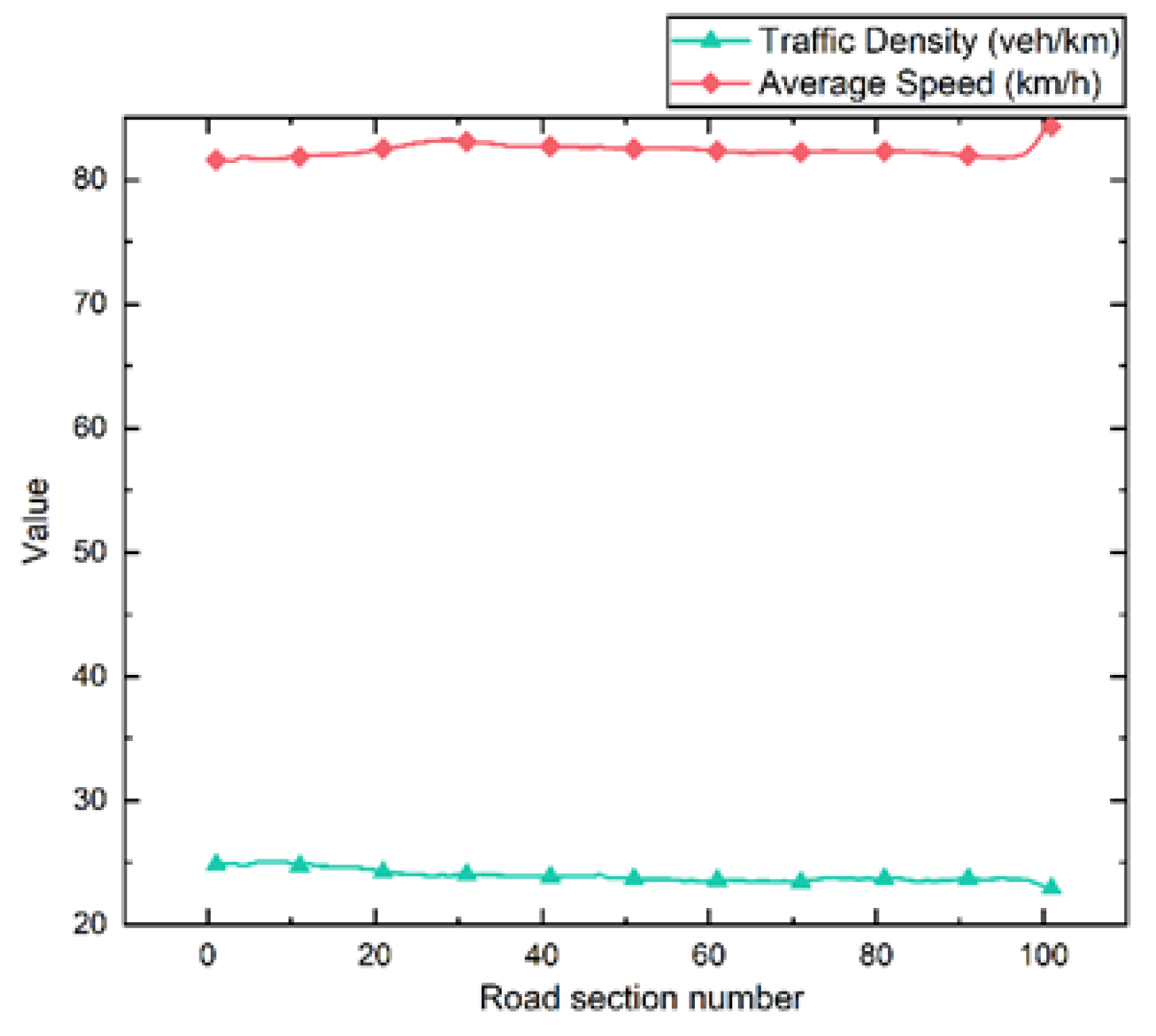
4.1.1. Simulation with No LSVs
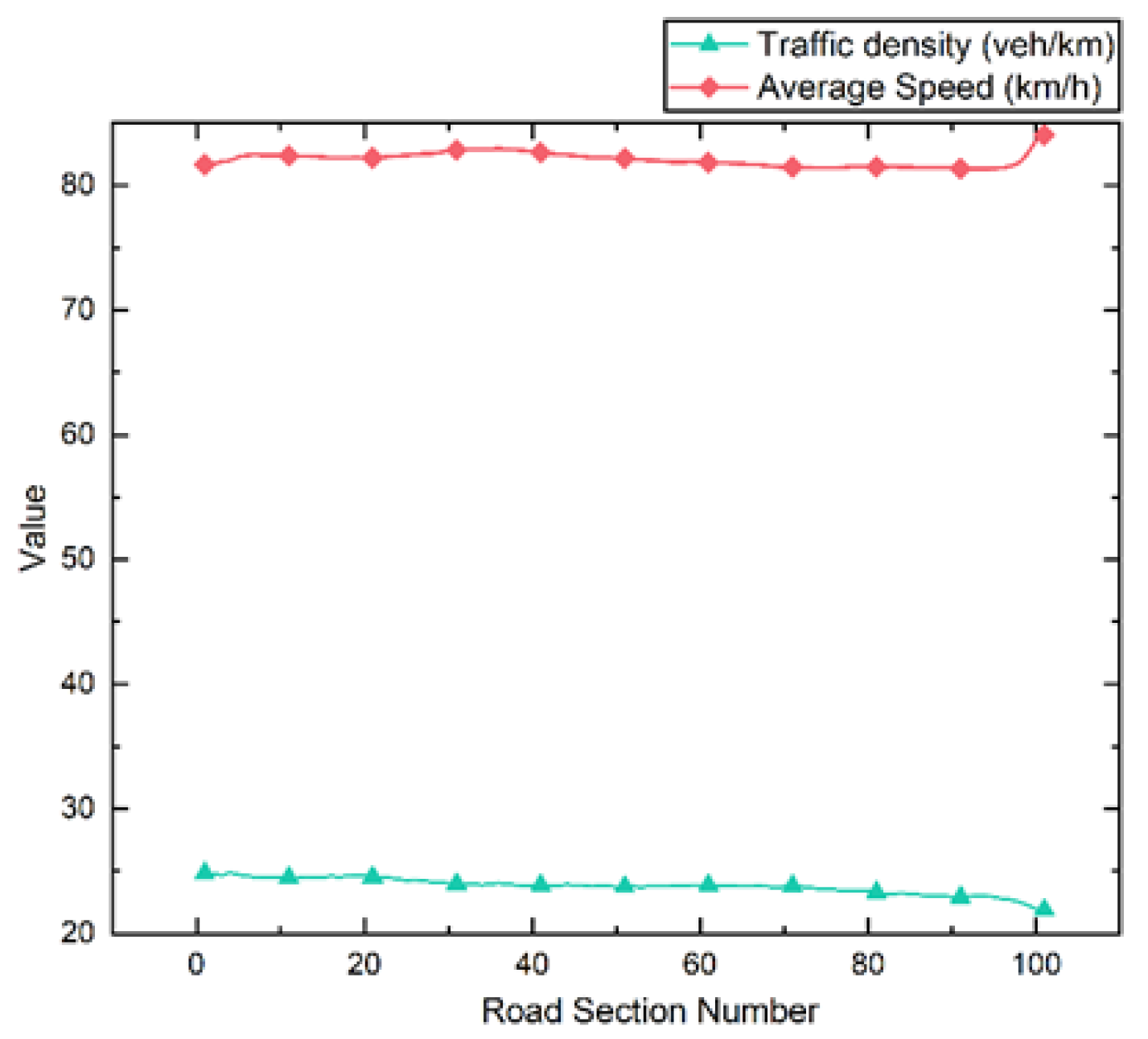
4.1.2. Simulation with LSVs
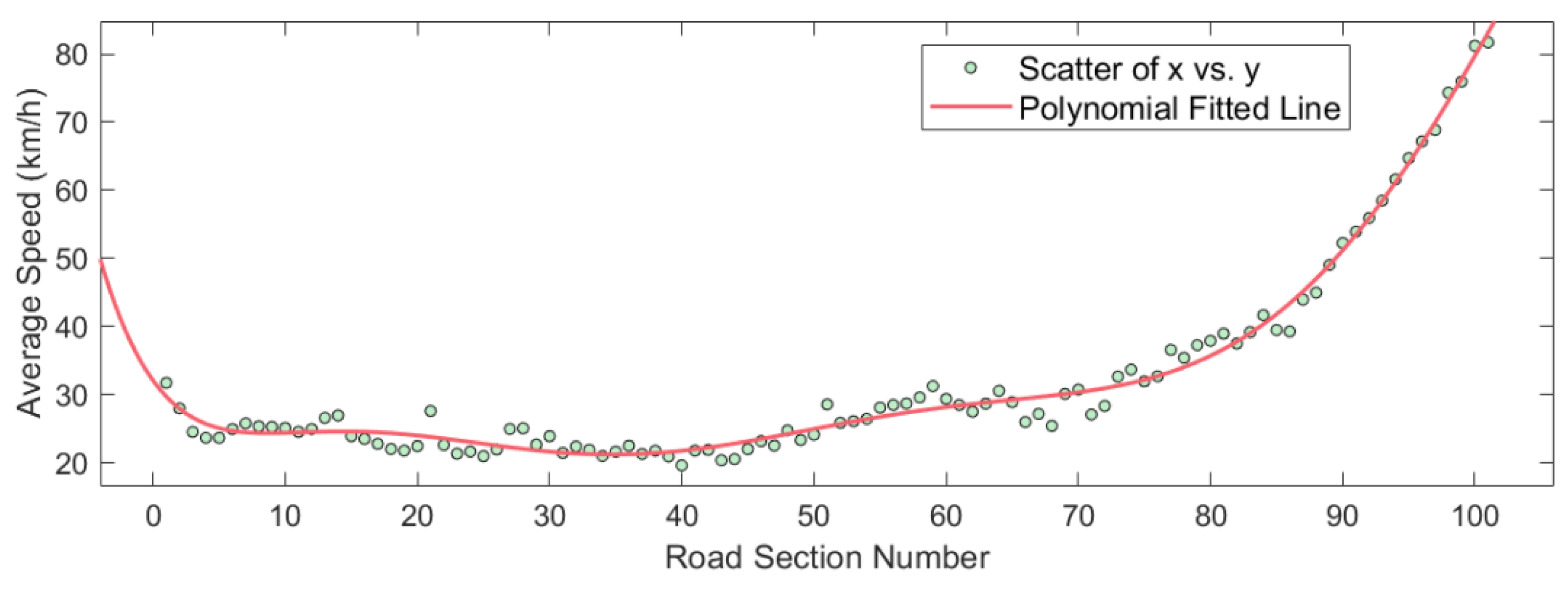
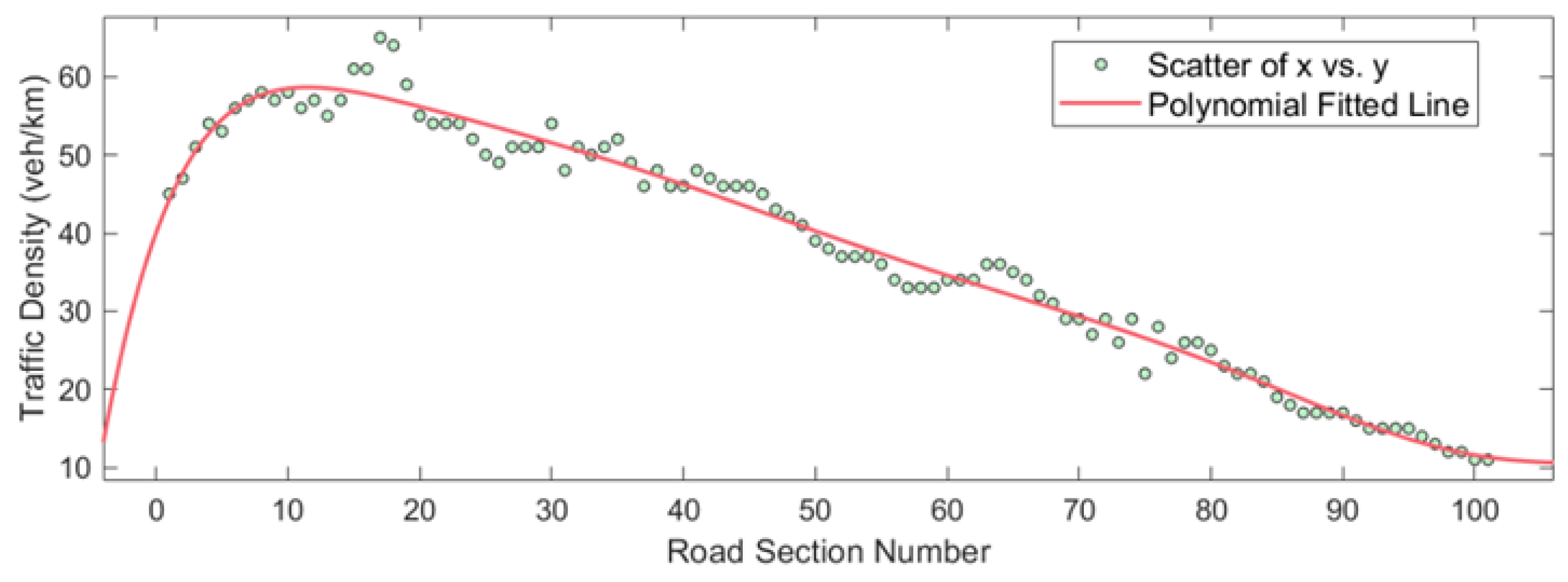
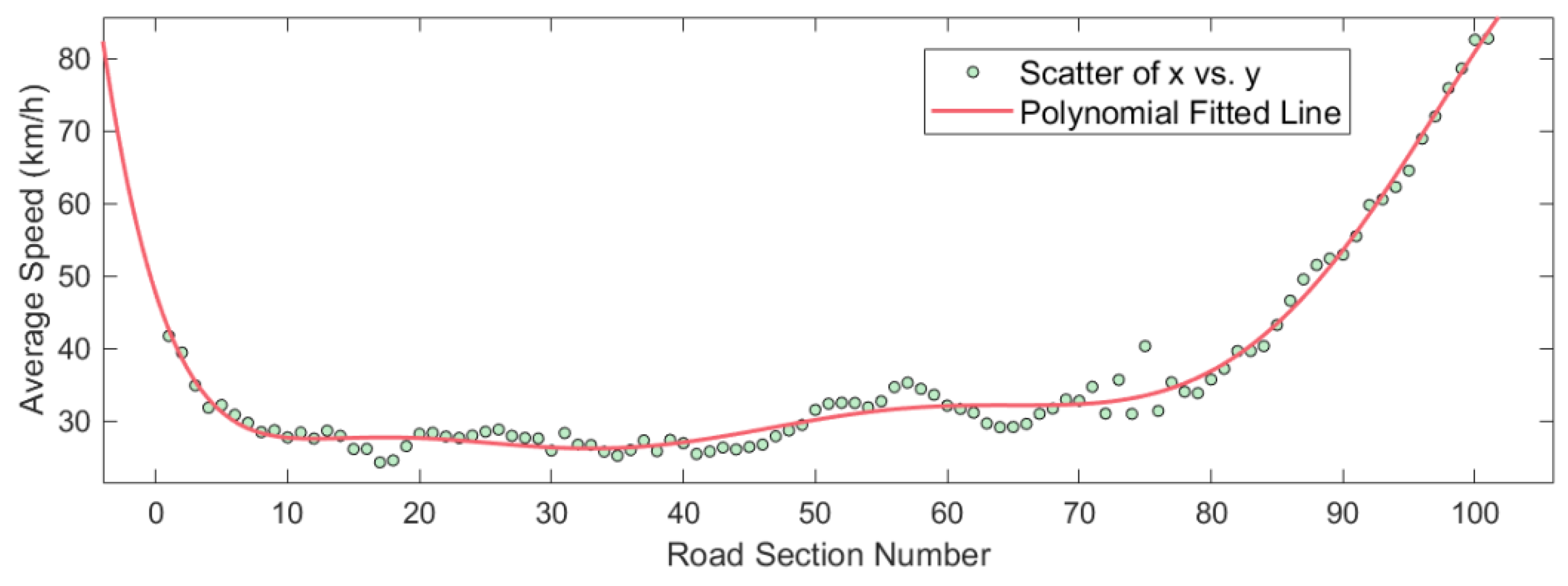
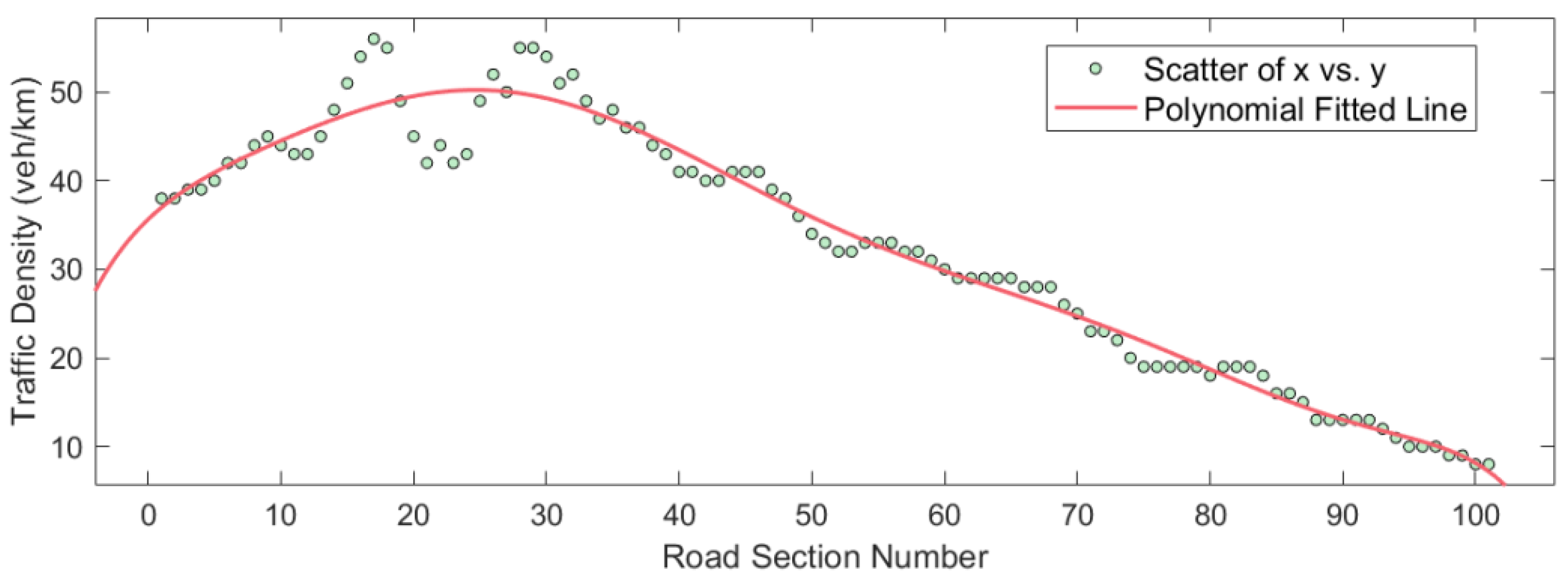
- Compared to a typical driving environment, LSVs will significantly affect road traffic flow due to speed differences with other vehicles. At this time, other vehicles will frequently accelerate, decelerate, or change lanes, causing large fluctuations in the road section’s average traffic density and speed;
- Due to the unique characteristics of LSVs, the vehicles behind them will generate a backlog in a specific area on the road and form a queue, which begins to dissipate when the LSVs gradually move off the expressway.
4.2. Traffic Safety Characteristics Influenced by LSVs on Expressways
5. Discussion
5.1. Theoretical and Practical Applications
5.2. Limitations and Future Research Directions
6. Conclusions
- The evolutionary features of lane traffic density and average speed under different LSV speeds satisfy the octuple polynomial law, reflecting the spatial heterogeneity of vehicle distribution at different LSV driving speeds;
- LSVs with varying speeds have the most significant negative impact on the road section within 400 m of the expressway entrance, and the lower the speed of the LSV, the more substantial the impact produced;
- When an LSV drives in different lanes separately, the inner, middle, and outer lanes have the highest number of total conflicts, rear-end conflicts, and lane-change conflicts, respectively. In addition, vehicles in the outer lane are the most significantly affected by LSVs, while vehicles in the middle lane are the least affected and have the highest traffic efficiency; MaxS and DeltaS for the middle lane are 47.9% and 60.5% higher than those of the outer lane, respectively. Nevertheless, the middle lane has the highest probability of potential traffic conflicts.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gazis, D.C. The moving and ‘phantom’ bottlenecks. Transp. Sci. 1992, 26, 223–229. [Google Scholar] [CrossRef]
- Newell, G.F. A moving bottleneck. Transp. Res. Pt. B-Methodol. 1998, 32, 531–537. [Google Scholar] [CrossRef]
- Wang, C.; Zhong, M.; Zhang, H.; Li, S.Y. Impacts of real-time traffic state on urban expressway crashes by collision and vehicle type. Sustainability 2022, 14, 2238. [Google Scholar] [CrossRef]
- Tian, Y.J.; Xiao, D.L.; Wang, L.; Chen, H. Expressway traffic safety early warning system based on cloud architecture. Comput. Commun. 2021, 171, 140–147. [Google Scholar] [CrossRef]
- Jin, S.; Qu, X.B.; Wang, D.H. Assessment of expressway traffic safety using gaussian mixture model based on time to collision. Int. J. Comput. Intell. Syst. 2011, 4, 1122–1130. [Google Scholar]
- Qu, Q.K.; Chen, F.J.; Zhou, X.J. Road traffic bottleneck analysis for expressway for safety under disaster events using blockchain machine learning. Saf. Sci. 2019, 118, 925–932. [Google Scholar] [CrossRef]
- Shi, Q.; Abdel-Aty, M. Evaluation of the impact of travel time reliability on urban expressway traffic safety. Transp. Res. Record. 2016, 2582, 8–17. [Google Scholar] [CrossRef]
- Sun, J.; Li, T.N.; Li, F.; Chen, F. Analysis of safety factors for urban expressways considering the effect of congestion in Shanghai, China. Accid. Anal. Prev. 2016, 95, 503–511. [Google Scholar] [CrossRef]
- Ma, Y.F.; Meng, H.C.; Chen, S.Y.; Zhao, J.G.; Li, S.; Xiang, Q.J. Predicting traffic conflicts for expressway diverging areas using vehicle trajectory data. J. Transp. Eng. Pt. A-Syst. 2020, 146, 04020003. [Google Scholar] [CrossRef]
- Fadhloun, K.; Rakha, H.; Loulizi, A. Impact of underlying steady-state fundamental diagram on moving bottleneck passing rates using a second-order traffic model. Transp. Lett. 2014, 6, 185–196. [Google Scholar] [CrossRef]
- Hunter-Zaworski, K.M. Impacts of low-speed vehicles on transportation infrastructure and safety. J. Transp. Land Use 2012, 5, 68–76. [Google Scholar] [CrossRef][Green Version]
- Zhang, H.; Li, S.Y.; Wu, C.Z.; Zhang, Q.; Wang, Y.F. Predicting crash frequency for urban expressway considering collision types using real-time traffic data. J. Adv. Transp. 2020, 2020, 1–8. [Google Scholar] [CrossRef]
- Zhao, J.B.; Deng, W. Traffic accidents on expressways: New threat to China. Traffic Inj. Prev. 2012, 13, 230–238. [Google Scholar] [CrossRef]
- Liang, G.H.; Sun, X.J.; Zhang, Y.D.; Chen, M.L.; Zhang, W.T. Identifying expressway accident black spots based on the secondary division of road units. Promet.-Traffic Transp. 2021, 33, 731–743. [Google Scholar] [CrossRef]
- Jia, B.; Jiang, R.; Wu, Q.S.; Hu, M.B. Honk effect in the two-lane cellular automaton model for traffic flow. Physica A. 2005, 348, 544–552. [Google Scholar] [CrossRef]
- Klenov, S.L.; Wegerle, D.; Kerner, B.S.; Schreckenberg, M. Prediction of moving and unexpected motionless bottlenecks based on three-phase traffic theory. Comput. Res. Modeling 2021, 13, 319–363. [Google Scholar] [CrossRef]
- Hu, X.J.; Lin, C.X.; Hao, X.T.; Lu, R.Y.; Liu, T.H. Influence of tidal lane on traffic breakdown and spatiotemporal congested patterns at moving bottleneck in the framework of Kerner’s three-phase traffic theory. Physics A 2021, 584, 126335. [Google Scholar] [CrossRef]
- Wegerle, D.; Kerner, B.S.; Schreckenberg, M.; Klenov, S.L. Prediction of moving bottleneck through the use of probe vehicles: A simulation approach in the framework of three-phase traffic theory. J. Intell. Transport. Syst. 2020, 24, 598–616. [Google Scholar] [CrossRef]
- Kerner, B.S.; Klenov, S.L. A theory of traffic congestion at moving bottlenecks. J. Phys. A Math. Theor. 2010, 43, 425101. [Google Scholar] [CrossRef]
- Lighthill, M.J.; Whitham, J.B. On kinematic waves II. A theory of traffic flow on long crowded roads. Proc. R. Soc. Lond. 1955, 53, 275–354. [Google Scholar]
- Wei, X.Y.; Xu, C.C.; Wang, W.; Yang, M.L.; Ren, X.L. Evaluation of average travel delay caused by moving bottlenecks on highways. PLoS ONE 2017, 12, e0183442. [Google Scholar] [CrossRef] [PubMed]
- Simoni, M.D.; Claudel, C.G. A fast simulation algorithm for multiple moving bottlenecks and applications in urban freight traffic management. Transp. Res. Pt. B-Methodol. 2017, 104, 238–255. [Google Scholar] [CrossRef]
- Daganzo, C.F.; Laval, J.A. Moving bottlenecks: A numerical method that converges in flows. Transp. Res. Pt. B-Methodol. 2005, 39, 855–863. [Google Scholar] [CrossRef]
- Daganzo, C.F.; Laval, J.A. On the numerical treatment of moving bottleneck. Transp. Res. Pt. B-Methodol. 2005, 39, 31–46. [Google Scholar] [CrossRef][Green Version]
- Fang, S.; Ma, J.X. Influence range and traffic risk analysis of moving work zones on urban roads. Sustainability 2021, 13, 4196. [Google Scholar] [CrossRef]
- Gan, X.F.; Weng, J.X.; Zhang, J. Evaluation of travel delay and accident risk at moving work zones. J. Transp. Saf. Secur. 2021, 13, 622–641. [Google Scholar] [CrossRef]
- Yang, Y.; Tian, N.; Wang, Y.P.; Yuan, Z.Z. A Parallel FP-Growth Mining Algorithm with Load Balancing Constraints for Traffic Crash Data. Int. J. Comput. Commun. Control 2022, 17, 4806. [Google Scholar] [CrossRef]
- Yang, Y.; Yuan, Z.Z.; Meng, R. Exploring Traffic Crash Occurrence Mechanism toward Cross-Area Freeways via an Improved Data Mining Approach. J. Transp. Eng. Pt. A-Syst. 2022, 148, 04022052. [Google Scholar] [CrossRef]
- Yang, Y.; He, K.; Wang, Y.P.; Yuan, Z.Z.; Yin, Y.H.; Guo, M.Z. Identification of dynamic traffic crash risk for cross-area freeways based on statistical and machine learning methods. Physica A 2022, 595, 127083. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, K.; Yuan, Z.Z.; Liu, D. Predicting Freeway Traffic Crash Severity Using XGBoost-Bayesian Network Model with Consideration of Features Interaction. J. Adv. Transp. 2022, 2022, 4257865. [Google Scholar] [CrossRef]
- Yao, Z.Z.; Hu, R.; Jiang, Y.S.; Xu, T.R. Stability and safety evaluation of mixed traffic flow with connected automated vehicles on expressways. J. Saf. Res. 2020, 75, 262–274. [Google Scholar] [CrossRef] [PubMed]
- Yu, R.J.; Wang, Y.Y.; Quddus, M.; Li, J.; Wang, X.S.; Tian, Y. Investigating vehicle roadway usage patterns on the Shanghai urban expressway system and their impacts on traffic safety. Int. J. Sustain. Transp. 2021, 15, 217–228. [Google Scholar] [CrossRef]
- Oskarbski, J.; Kaminski, T.; Kyamakya, K.; Chedjou, J.C.; Zarski, K.; Pedzierska, M. Assessment of the Speed Management Impact on Road Traffic Safety on the Sections of Motorways and Expressways Using Simulation Methods. Sensors 2020, 20, 5057. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.F.; Li, X.W.; Yan, Y.; Fu, X.S. Driving Risk Affected Areas and Distribution Function of Sharp Horizontal Curves of Expressway. Discrete Dyn. Nat. Soc. 2015, 2015, 208564. [Google Scholar] [CrossRef]
- Yu, R.J.; Wang, X.S.; Yang, K.; Abdel-Aty, M. A Hybrid Latent Class Analysis Modeling Approach to Analyze Urban Expressway Crash Risk. Accid. Anal. Prev. 2017, 101, 37–43. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Abdel-Aty, M.; Lee, J. Safety analytics for integrating crash frequency and real-time risk modeling for expressways. Accid. Anal. Prev. 2017, 104, 58–64. [Google Scholar] [CrossRef]
- Yang, K.; Wang, X.S.; Yu, R.J. A Bayesian dynamic updating approach for urban expressway real-time crash risk evaluation. Transp. Res. Pt. C-Emerg. Technol. 2013, 51, 252–259. [Google Scholar] [CrossRef]
- Wang, J.H.; Kong, Y.M.; Fu, T. Expressway crash risk prediction using back propagation neural network: A brief investigation on safety resilience. Accid. Anal. Prev. 2019, 124, 180–192. [Google Scholar] [CrossRef]
- Wang, L.N. Real-Time Evaluation Method of Vehicle Conflict Risk on Urban Expressway Based on Smartphone GPS Data. J. Adv. Transp. 2021, 2021, 2407529. [Google Scholar] [CrossRef]
- Charly, A.; Mathew, T.V. Evaluation of driving performance in relation to safety on an expressway using field driving data. Transp. Lett. 2020, 12, 340–348. [Google Scholar] [CrossRef]
- Rahman, M.S.; Abdel-Aty, M. Longitudinal safety evaluation of connected vehicles’ platooning on expressways. Accid. Anal. Prev. 2018, 117, 381–391. [Google Scholar] [CrossRef]
- Qi, W.W.; Wang, Z.X.; Tang, R.R.; Wang, L.H. Driving risk detection model of deceleration zone in expressway based on generalized regression neural network. J. Adv. Transp. 2018, 2018, 8014385. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, B.; Yang, S.X.; Zhang, M.; Gong, Q.L.; Zhang, H. The driving risk analysis and evaluation in rightward zone of expressway reconstruction and extension engineering. J. Adv. Transp. 2020, 2020, 8943463. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, J.Y.; Wang, Y.H.; Wang, W.Y. Drivers’ behavioral responses to driving risk diagnosis and real-time warning information provision on expressways: A smartphone app-based driving experiment. J. Transp. Saf. Secur. 2020, 12, 329–357. [Google Scholar] [CrossRef]
- Balakrishna, R.; Antoniou, C.; Ben-Akiva, M.; Koutsopoulos, H.N.; Wen, Y. Calibration of Microscopic Traffic Simulation Models: Methods and Application. Transp. Res. Rec. 2007, 1999, 198–207. [Google Scholar] [CrossRef]
- Chitturi, M.V.; Benekohal, R.F. Work zone queue length and delay methodology. Transp. Lett. 2010, 2, 273–283. [Google Scholar] [CrossRef]
- Fang, S.; Shen, L.H.; Ma, J.X.; Xu, C.B. Study on the Design of Variable Lane Demarcation in Urban Tunnels. Sustainability 2022, 14, 5682. [Google Scholar] [CrossRef]




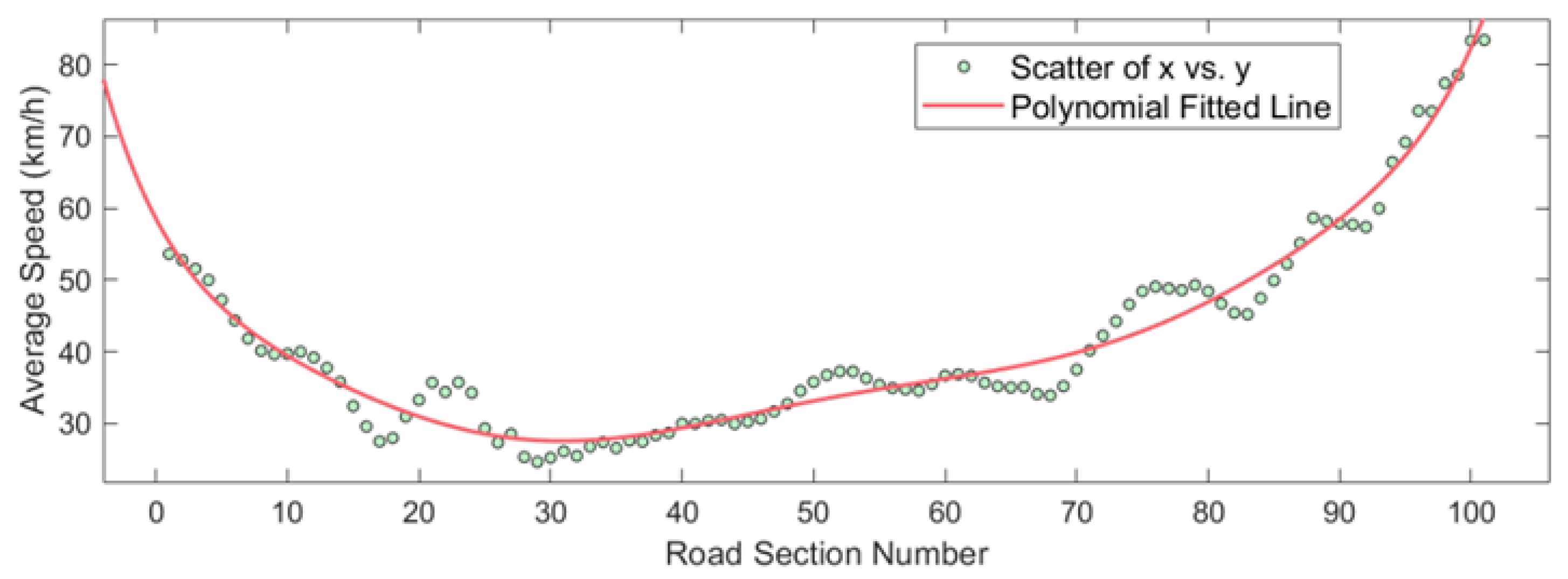
| Speed of LSV | Expressions for Evolutionary Features |
|---|---|
| 10 km/h | |
| 15 km/h | |
| 20 km/h |
| Speed of LSV | Expressions for Evolutionary Features |
|---|---|
| 10 km/h | |
| 15 km/h | |
| 20 km/h |
| Total | Crossing | Rear-End | Lane-Change | |
|---|---|---|---|---|
| Inner Lane | 34 | 0 | 20 | 14 |
| Middle Lane | 28 | 0 | 23 | 5 |
| Outer Lane | 29 | 0 | 14 | 15 |
| Conflict Parameters | Minimum | Maximum | Mean | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Inner | Middle | Outer | Inner | Middle | Outer | Inner | Middle | Outer | |
| TTC | 0.0 | 0.0 | 0.0 | 1.5 | 1.5 | 1.5 | 1.1 | 1.1 | 0.8 |
| PET | 0.0 | 0.0 | 0.0 | 4.6 | 4.2 | 3.6 | 2.1 | 1.9 | 1.5 |
| MaxS | 2.9 | 3.7 | 3.1 | 19.1 | 22.7 | 22.1 | 10.2 | 10.8 | 7.3 |
| MaxD | −7.7 | −7.6 | −8.0 | −1.3 | −1.4 | −1.5 | −5.03 | −4.1 | −5.4 |
| DeltaS | 0.5 | 0.3 | 0.1 | 15.4 | 18.1 | 12.6 | 6.5 | 6.9 | 4.3 |
| P(UEA) | 0.0 | 0.0 | 0.0 | 0.8 | 1.0 | 0.9 | 0.2 | 0.3 | 0.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Ma, J.; Tang, X. A Simulation-Based Study of the Influence of Low-Speed Vehicles on Expressway Traffic Safety. Sustainability 2022, 14, 12165. https://doi.org/10.3390/su141912165
Xu C, Ma J, Tang X. A Simulation-Based Study of the Influence of Low-Speed Vehicles on Expressway Traffic Safety. Sustainability. 2022; 14(19):12165. https://doi.org/10.3390/su141912165
Chicago/Turabian StyleXu, Chubo, Jianxiao Ma, and Xiang Tang. 2022. "A Simulation-Based Study of the Influence of Low-Speed Vehicles on Expressway Traffic Safety" Sustainability 14, no. 19: 12165. https://doi.org/10.3390/su141912165
APA StyleXu, C., Ma, J., & Tang, X. (2022). A Simulation-Based Study of the Influence of Low-Speed Vehicles on Expressway Traffic Safety. Sustainability, 14(19), 12165. https://doi.org/10.3390/su141912165










