Improving Thermoacoustic Low-Temperature Heat Recovery Systems †
Abstract
1. Introduction
2. Materials and Methods
2.1. General Assumptions and Hypothesis
- The TAE works due to the difference in temperature between high- and low-potential energy sources;
- Low-potential sources may have an ambient temperature or lower temperature (cryogenic);
- The energy sources are not connected to the TAE through thermodynamic cycles;
- The energy exchange between the thermoacoustic engine and the energy sources is carried out by means of external systems with intermediate heat carriers;
- The load of the TAE can be electric generators or thermoacoustic machines of reverse action, namely refrigerators.
2.2. Investigation of Energy Exchange Processes in Low-Temperature TAE
- They organize the heat flow between external energy sources with different temperature potentials;
- However, at the same time, these are vital elements of the heat engine, which form a longitudinal temperature gradient in the matrix.
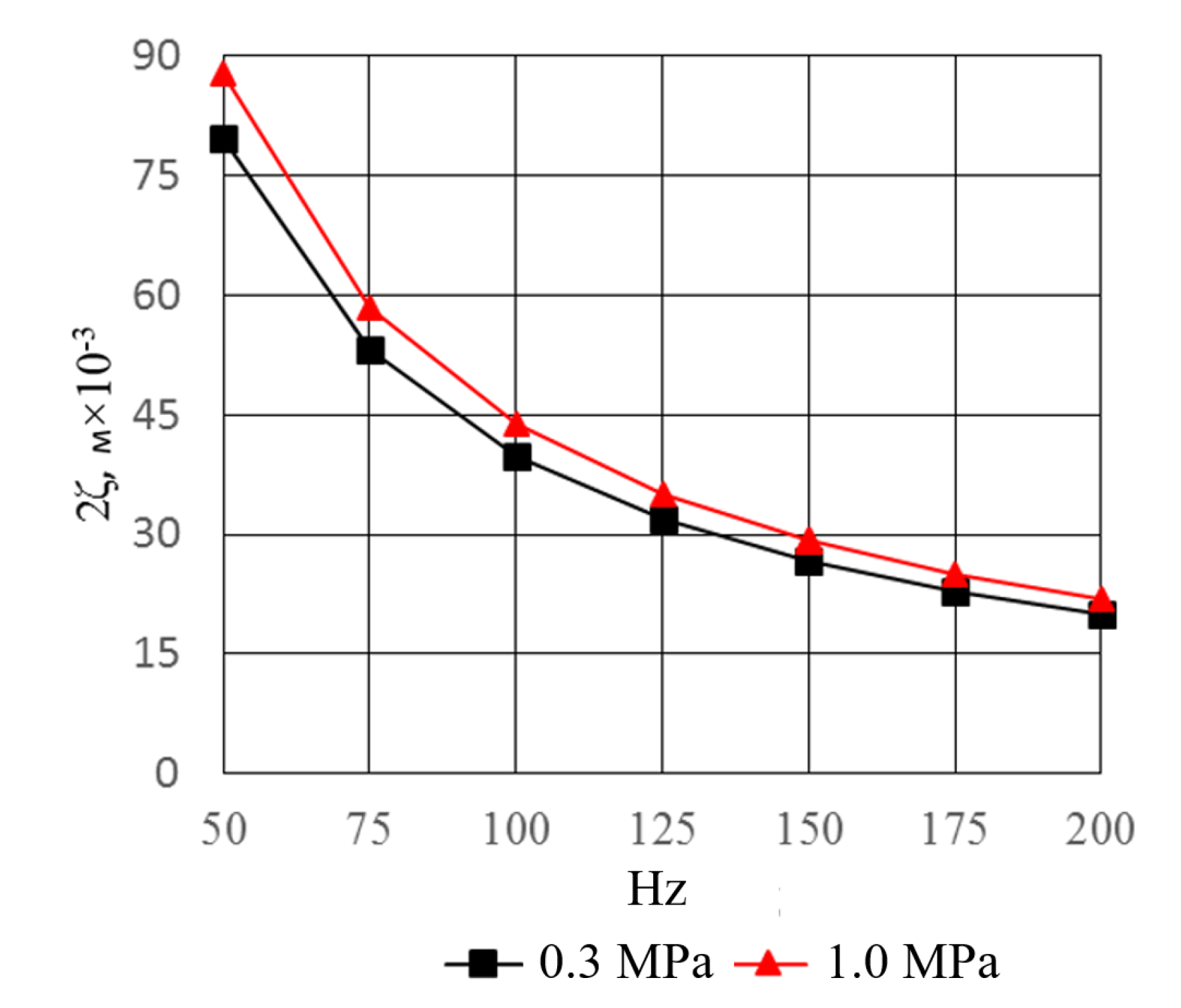
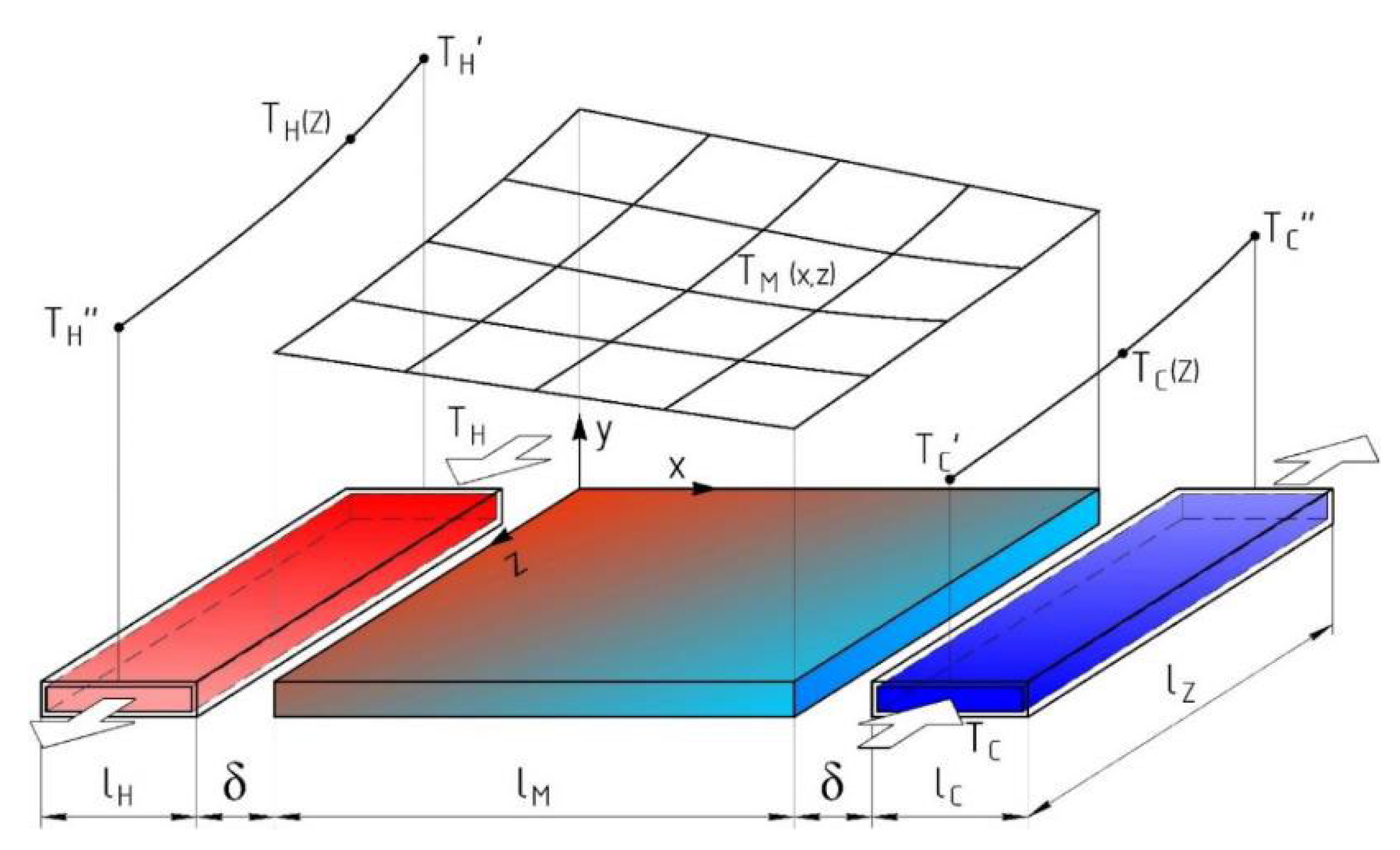
2.3. Analysis of the Influence of Heat Exchanger Surface Temperature Inhomogeneity on Transformation Processes in TAE
- Secondly, the model uses the integral values of heat exchange coefficients, which is quite acceptable for ordinary recuperators, but in TAE heat exchangers, heat exchange is carried out under the conditions of the initial sections, namely hydrodynamic and thermal conditions, which must be taken into account.
- Provided that the TAE operates in the steady state, the distribution of the temperatures in the elements of the heat exchange unit is stabilized and unchanged;
- Regenerative heat exchangers have a tubular-rib structure, and the liquid in the tubes passes through once;
- The intermediate transport coolants, namely thermal oils and water, move in the tubes of the recuperative heat exchangers;
- The distribution of the temperature field in the TAE matrix is determined by the distribution of temperatures over the outer surfaces of the recuperative heat exchangers;
- Taking into account the high thermal conductivity of the material of the heat exchanger tubes, we believe that the surface temperatures of the tubes in each lumbar section are the same and change only along the length of the tube and are equal to the temperatures of the transport coolers;
- Working fluid—gas that makes oscillation movement across the liquid coolant flow;
- The thermal resistance of each of the heat exchangers, heaters, and coolers determines the heat transfer coefficient on the inner surface of the tubes as a value much lower than the heat exchange coefficient from the outside.
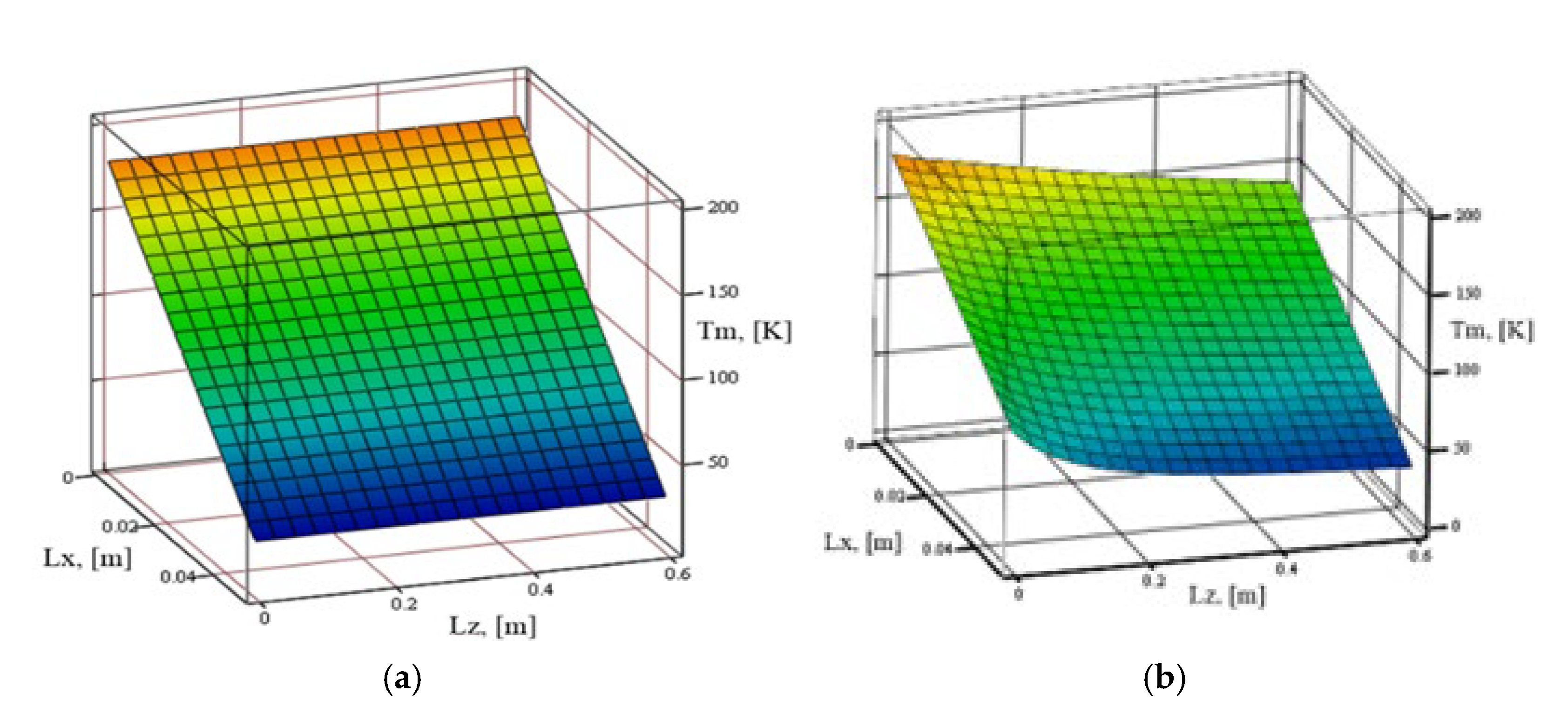
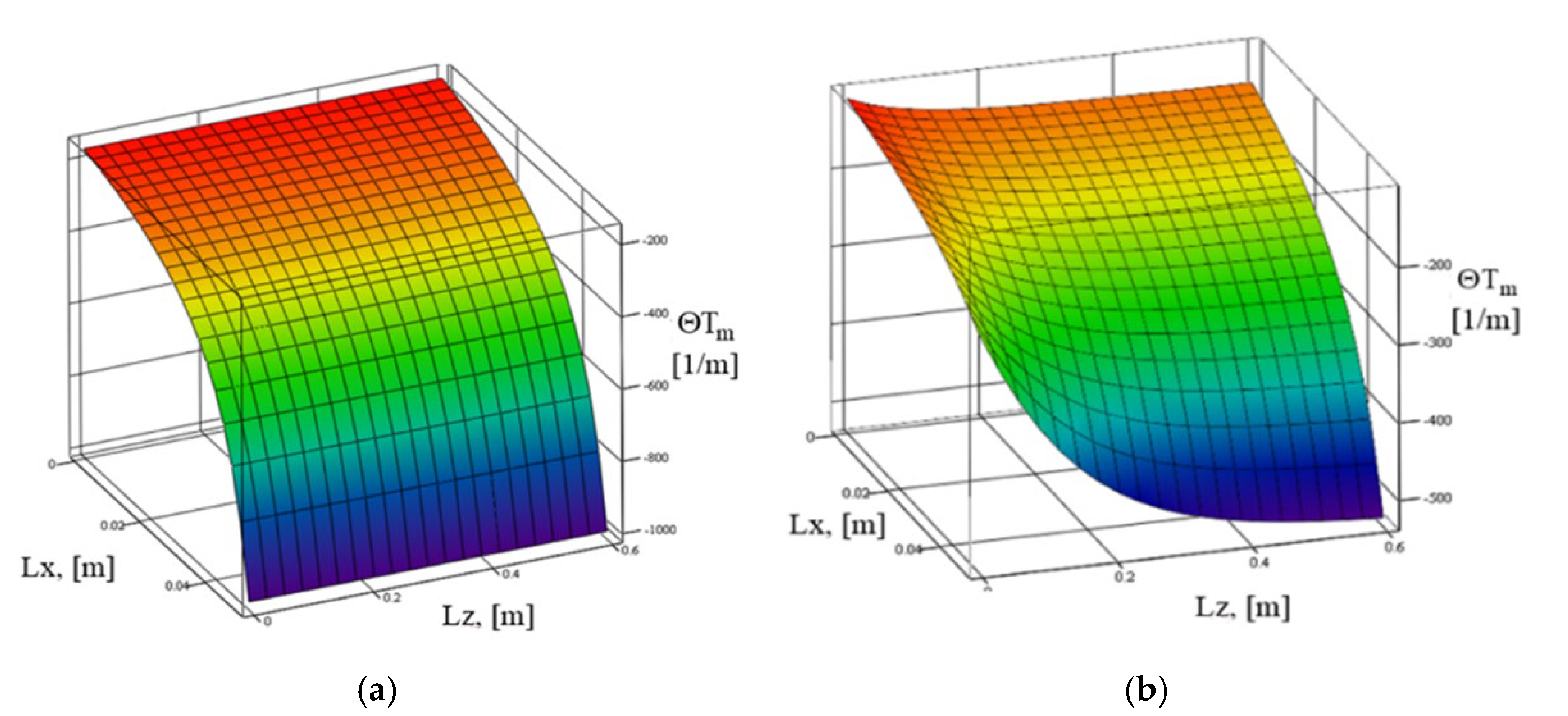
3. Results
4. Discussion
5. Conclusions
- A principal scheme of a power plant with a thermoacoustic energy saving system, desired for the utilization of low-temperature thermal emissions was proposed, the peculiarity of which consisted of the possibility of converting the waste heat of different potentials in the case of using cryogenic fuels;
- A mathematical model of a power plant with a thermoacoustic energy saving system, which allows for the determination of the effectiveness of the use of a thermoacoustic system for different types of power plants, was synthesized;
- The original mathematical model of the energy exchange processes between the elements of the thermoacoustic core, namely the heat exchangers, the matrix, and the working body, was created. The model makes it possible to determine the influence of the inhomogeneity of the temperature field on the surface of heat exchangers and the characteristics of thermoacoustic engines;
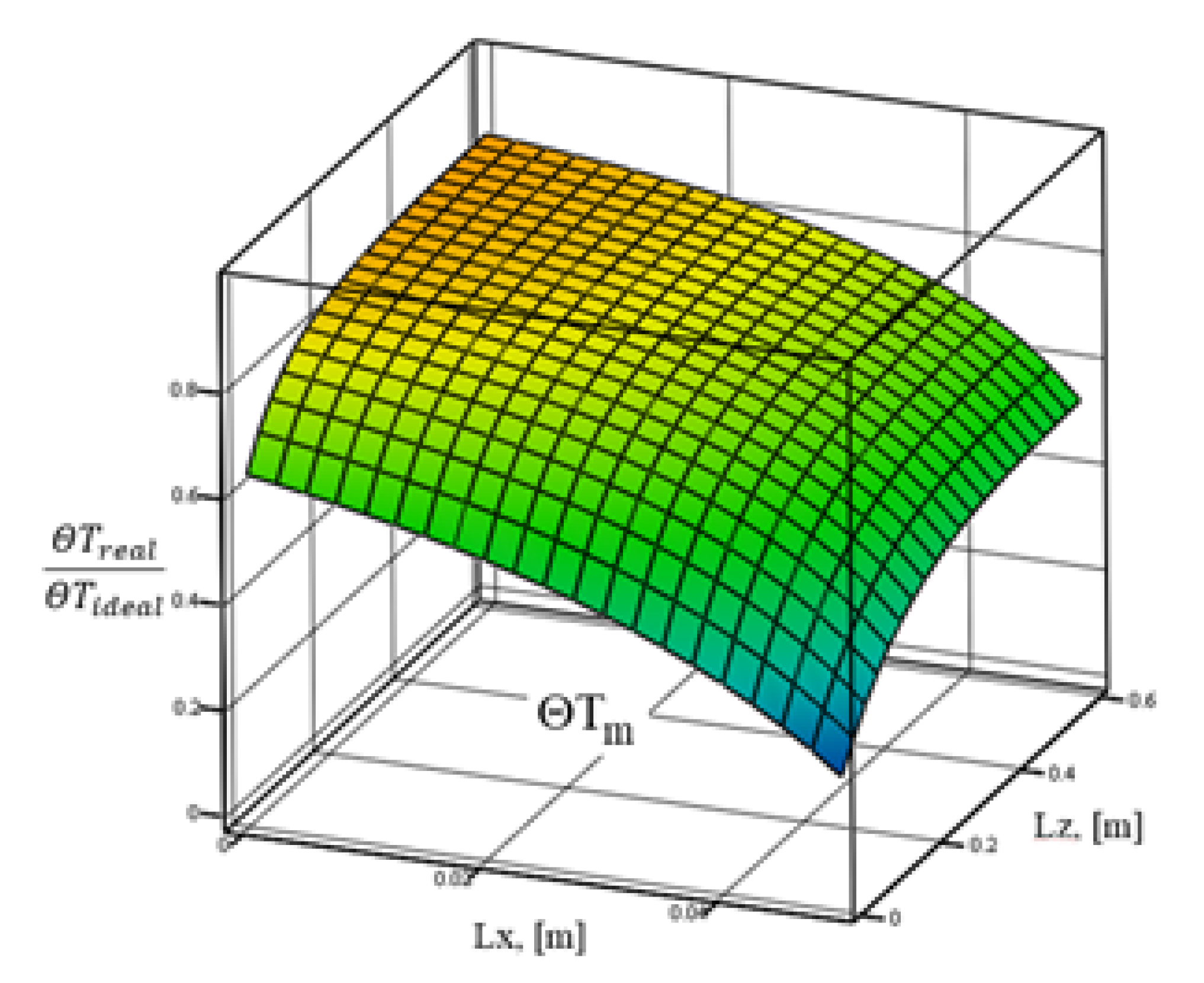
- The application of recuperative heat exchangers with "liquid–gas" types of mechanisms in thermoacoustic systems leads to efficiency losses, associated with both the irreversibility of the heat exchange processes and the formation of temperature heterogeneity in the elements of the thermoacoustic core. It was proved that these losses reduce the potential power of the thermoacoustic installations by 1.1-1.3 times;
- For low-temperature TAEs, it is advisable to apply heat exchangers with high thermal power and even temperatures along the front as evaporators or condensers. It was proved that the recuperative liquid–gas HEX reduces the efficiency of TAEs and their total capacity by 10-35%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Benveniste, H.; Oppenheimer, M.; Fleurbaey, M. Climate change increases resource-constrained international immobility. Nat. Clim. Chang. 2022, 12, 634–641. [Google Scholar] [CrossRef]
- Gambhir, A.; George, M.; McJeon, H.; Arnell, N.W.; Bernie, D.; Mittal, S.; Köberle, A.C.; Lowe, J.; Rogelj, J.; Monteith, S. Near-term transition and longer-term physical climate risks of greenhouse gas emissions pathways. Nat. Clim. Chang. 2022, 12, 88–96. [Google Scholar] [CrossRef]
- Olmer, N.; Comer, B.; Roy, B.; Mao, X.; Rutherford, D. Greenhouse Gas Emissions from Global Shipping, 2013–2015/N; ICCT: Washington, DC, USA, 2017; 38p. [Google Scholar]
- Kornienko, V.; Radchenko, R.; Bohdal, Ł.; Kukiełka, L.; Legutko, S. Investigation of condensing heating surfaces with reduced corrosion of boilers with water-fuel emulsion combustion. In Proceedings of the Integrated Computer Technologies in Mechanical Engineering—2020. ICTM 2020, Kharkov, Ukraine, 29–30 October 2020; Lecture Notes in Networks and, Systems. Nechyporuk, M., Pavlikov, V., Kritskiy, D., Eds.; Springer: Cham, Switzerland, 2021; Volume 188, pp. 300–309. [Google Scholar]
- Kornienko, V.; Radchenko, R.; Radchenko, M.; Radchenko, A.; Pavlenko, A.; Konovalov, D. Cooling cyclic air of marine engine with water-fuel emulsion combustion by exhaust heat recovery chiller. Energies 2022, 15, 248. [Google Scholar] [CrossRef]
- Yang, Z.; Kornienko, V.; Radchenko, M.; Radchenko, A.; Radchenko, R.; Pavlenko, A. Capture of pollutants from exhaust gases by low-temperature heating surfaces. Energies 2022, 15, 120. [Google Scholar] [CrossRef]
- Balcombe, P.; Brierley, J.; Lewis, C.; Skatvedt, L.; Speirs, J.; Hawkes, A.; Staffell, I. How to decarbonize international shipping: Options for fuels, technologies and policies. Energy Convers. Manag. 2019, 182, 72–88. [Google Scholar] [CrossRef]
- Global Marine Technology Trends 2030. Available online: https:eprints.soton.ac.uk/388628/1/GMTT2030.pdf (accessed on 1 June 2019).
- World Energy Balances 2020 (IEA, 2020). Available online: https://www.iea.org/data-and-statistics/data-product/world-energy-balances (accessed on 12 January 2021).
- Thekdi, A.; Nimbalkar, S.; Sundaramoorthy, S.; Armstrong, K.O.; Taylor, A.; Gritton, J.E.; Wenning, T.; Cresko, J. Technology Assessment on Low-Temperature Waste Heat Recovery in Industry; Oak Ridge National Lab.: Oak Ridge, TN, USA, 2021. [Google Scholar] [CrossRef]
- Johnson, I.; Choate, W.T.; Davidson, A. Waste Heat Recovery. Technology and Opportunities in U.S. Industry; CS, Inc.: Laurel, MD, USA, 2008. [Google Scholar] [CrossRef]
- Thekdi, A.; Nimbalkar, S.U. Industrial Waste Heat Recovery—Potential Applications, Available Technologies and Crosscutting R&D Opportunities; Department of Energy′s (DOE): Washington, DC, USA, 2015. [Google Scholar] [CrossRef]
- Radchenko, A.; Scurtu, I.-C.; Radchenko, M.; Forduy, S.; Zubarev, A. Monitoring the efficiency of cooling air at the inlet of gas engine in integrated energy system. Therm. Sci. 2022, 26, 185–194. [Google Scholar] [CrossRef]
- Yari, M.; Mehr, A.; Zare, V.; Mahmoudi, S.; Rosen, M. Exergoeconomic comparison of TC (trilateral Rankine cycle), ORC (organic Rankine cycle) and Kalina cycle using a low grade heat source. Energy 2015, 83, 712–722. [Google Scholar] [CrossRef]
- Radchenko, A.; Radchenko, M.; Mikielewicz, D.; Pavlenko, A.; Radchenko, R.; Forduy, S. Energy saving in trigeneration plant for food industries. Energies 2022, 15, 1163. [Google Scholar] [CrossRef]
- Radchenko, M.; Mikielewicz, D.; Andreev, A.; Vanyeyev, S.; Savenkov, O. Efficient ship engine cyclic air cooling by turboexpander chiller for tropical climatic conditions. In Proceedings of the Integrated Computer Technologies in Mechanical Engineering—2020. ICTM 2020, Kharkov, Ukraine, 29–30 October 2020; Lecture Notes in Networks and, Systems. Nechyporuk, M., Pavlikov, V., Kritskiy, D., Eds.; Springer: Cham, Switzerland, 2021; Volume 188, pp. 498–507. [Google Scholar]
- Singh, D.; Pedersen, E. A review of waste heat recovery technologies for maritime applications. Energy Convers. Manag. 2016, 111, 315–328. [Google Scholar] [CrossRef]
- Yun, E.; Park, H.; Yoon, S.Y.; Kim, K.C. Dual parallel organic Rankine cycle (ORC) system for high efficiency waste heat recovery in marine application. J. Mech. Sci. Technol. 2015, 29, 2509–2515. [Google Scholar] [CrossRef]
- Hoang, A.T. Waste heat recovery from diesel engines based on Organic Rankine Cycle. Appl. Energy 2018, 231, 138–166. [Google Scholar] [CrossRef]
- Kalina, A.I. Combined cycle and waste heat-recovery power-systems based on a novel thermodynamic energy cycle utilizing low-temperature heat for power-generation. Mech. Eng. 1983, 105, 104. [Google Scholar]
- Yang, Z.; Konovalov, D.; Radchenko, M.; Radchenko, R.; Kobalava, H.; Radchenko, A.; Kornienko, V. Analyzing the efficiency of thermopressor application for combustion engine cyclic air cooling. Energies 2022, 15, 2250. [Google Scholar] [CrossRef]
- Radchenko, M.; Radchenko, R.; Kornienko, V.; Pyrysunko, M. Semi-empirical correlations of pollution processes on the condensation surfaces of exhaust gas boilers with water-fuel emulsion Combustion. In Lecture Notes in Mechanical Engineering; Ivanov, V., et al., Eds.; Springer: Cham, Switzerland, 2020; pp. 853–862. [Google Scholar]
- Konovalov, D.; Radchenko, M.; Kobalava, H.; Kornienko, V.; Maksymov, V.; Radchenko, A.; Radchenko, R. Research of characteristics of the flow part of an aerothermopressor for gas turbine intercooling air. Proc. Inst. Mech. Eng. Part A J. Power Energy 2021, 236, 634–646. [Google Scholar] [CrossRef]
- Yang, Z.; Radchenko, M.; Radchenko, A.; Mikielewicz, D.; Radchenko, R. Gas turbine intake air hybrid cooling systems and a new approach to their rational designing. Energies 2022, 15, 1474. [Google Scholar] [CrossRef]
- Rott, N. Thermoacoustics. Adv. Appl. Mech. 1980, 20, 135–175. [Google Scholar]
- Wheatley, J.; Hofler, T.; Swift, G.W.; Migliori, A. Understanding some simple phenomena in thermoacoustics with application to acoustical heat engines. Am. J. Phys. 1985, 2, 147–162. [Google Scholar] [CrossRef]
- Swift, G.W. Thermoacoustics—A Unifying Perspective for Some Engines and Refrigerators; Acoustical Society of America: Melville, NY, USA, 2002. [Google Scholar]
- Tijani, M.E.H.; Spoestra, S. A high performance thermoacoustic engine. J. Appl. Phys. 2011, 110, 093519. [Google Scholar] [CrossRef]
- De Blok, K. Low operating temperature integral thermoacoustic devices for solar cooling and waste heat recovery. In Proceedings of the Acoustic-2008 International Conference, Paris, France, June 30–4 July 2008; pp. 18–24. [Google Scholar]
- Ward, B.; Clark, J.; Swift, G. Design Environment for Low-Amplitude Thermoacoustic Energy Conversion: Users Guide; Los Alamos National Laboratory: Los Alamos, NM, USA, 2012. [Google Scholar]
- Ceperly, P.H. A pistonless Stirling engine—The traveling wave heat engine. J. Acoust. Soc. Am. 1979, 66, 1508–1513. [Google Scholar]
- Backhaus, S.; Swift, G.W. A thermoacoustic-Stirling heat engine: Detailed study. J. Acoust. Soc. Am. 2000, 107, 3148–3166. [Google Scholar] [CrossRef]
- Kondratenko, Y.; Korobko, V.; Korobko, O.; Kondratenko, G.; Kozlov, O. Green-IT Approach to Design and Optimization of Thermoacoustic Waste Heat Utilization Plant Based on Soft Computing. In Green IT Engineering: Components, Networks and Systems Implementation. Studies in Systems, Decision and Control; Kharchenko, V., Kondratenko, Y., Kacprzyk, J., Eds.; Springer: Cham, Switzerland, 2017; Volume 105, pp. 287–311. [Google Scholar] [CrossRef]
- Timmer MA, G.; de Blok, K.; van der Meer, T.H. Review on the conversion of thermoacoustic power into electricity. J. Acoust. Soc. Am. 2018, 143, 841–857. [Google Scholar] [CrossRef] [PubMed]
- De Blok, K. Bi-Directional Turbines for Converting Acoustic Wave Power into Electricity. 2017. Available online: http://www.aster-thermoacoustics.com/wp-content/uploads/2015/01/Bi-directional-turbines-Riga.pdf (accessed on 15 April 2021).
- Kondratenko, Y.; Serbin, S.; Korobko, V.; Korobko, O. Optimisation of Bi-derectional puls turbine for waste heat utilization plant based on green IT paradigm. In Green IT Engineering: Components, Networks and Systems Implementation. Studies in Systems, Decision and Control; Springer: Cham, Switzerland, 2018; Volume 106. [Google Scholar]
- Wakeland, R.S. Heat Exchangers in Oscillating Flow, with Application to Thermoacoustic Devices That Have Neither Stack nor Regenerator. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2003. [Google Scholar]
- Liu, J.; Garrett, S.L. Relationship between Nusselt number and the thermoviscous (Rott) functions. J. Acoust. Soc. Am. 2009, 119, 1457–1461. [Google Scholar] [CrossRef]
- Wu, F.; Wu, C.; Guo, F.; Li, Q.; Chen, L. Optimization of a thermoacoustic engine with a complex heat transfer exponent. Entropy 2003, 5, 444–451. [Google Scholar] [CrossRef]
- Jin Kan, X.; Wu, F.; Chen, L.; Sun, F.; Guo, F. Exergy efficiency optimization of a thermoacoustic engine with a complex heat transfer exponent. Int. J. Sustain. Energy 2010, 29, 220–232. [Google Scholar] [CrossRef]
- Mozurkewich, G. Heat transfer from transverse tubes adjacent to a thermoacoustic stack. J. Acoust. Soc. Am. 1998, 110, 841–847. [Google Scholar] [CrossRef]
- Mozurkewich, G. Time-average temperature distribution in a thermoacoustic stack. J. Acoust. Soc. Am. 1998, 103, 380–388. [Google Scholar]
- Piccolo, A.; Pistone, G. Estimation of heat transfer coefficients in oscillating flows: The thermoacoustic case. Int. J. Heat Mass Transfer. 2006, 49, 1631–1642. [Google Scholar]
- Nsofor, E.C.; Celik, S.; Wang, X. Experimental study on the heat transfer at the heat exchanger of the thermoacoustic refrigerating system. Appl. Therm. Eng. 2007, 27, 2435–2442. [Google Scholar]
- Jaworski, A.J.; Piccolo, A. Heat transfer processes in parallel-plate heat exchangers of thermoacoustic devices—Numerical and experimental approaches. Appl. Therm. Eng. 2012, 42, 145–153. [Google Scholar]
- Jaworski, A. Editorial for Special Issue: “Heat Transfer Processes in Oscillatory Flow Conditions”. Appl. Sci. 2017, 7, 994. [Google Scholar] [CrossRef]
- Herman, C.; Chen, Y. A simplified model of heat transfer in heat exchangers and stack plates of thermoacoustic refrigerators. Heat Mass Transf. 2006, 42, 901–917. [Google Scholar] [CrossRef]
- Paek, I.; Braun, J.E.; Mongeau, L. Heat transfer coefficients of heat exchangers in the thermoacoustic coolers. In Proceedings of the International Congress of Refrigeration, Washington, DC, USA, 17–22 August 2003; pp. 1–8. [Google Scholar]
- Hausen, H. Heat Transfer in Counterflow, Parallel-Flow, and Cross-Flow; McGraw-Hill: New York, NY, USA, 1983; 515p. [Google Scholar]
- Thermo Acoustic Power (TAP) an Industriële Restwarmte naar Elektriciteit SBIR Fase 1 Haalbaarheidsstudie. Available online: https://docplayer.nl/2251837-Thermo-acoustic-power-tap-van-industriele-restwarmte-naar-elektriciteit-sbir-fase-1-haalbaarheidsstudie.html (accessed on 15 April 2021).
- Eindrapportage Fase II Thermo Acoustic Power (TAP) Conversie Industriële Restwarmte naar Elektriciteit. Available online: http://www.aster-thermoacoustics.com/wp-content/uploads/2012/04/Eindrapportage-TAP-SBIR09313.pdf (accessed on 15 April 2021).
- Final Report Summary—THATEA (Thermo Acoustic Technology for Energy Applications). Available online: https://cordis.europa.eu/docs/results/226/226415/final1-final-report.pdf (accessed on 15 April 2021).
- Kuznetsov, V. Justification of efficiency of plain shaped heat exchange surfaces to increase the compactness of power plants. East. -Eur. J. Enterp. Technol. 2020, 6, 17–24. [Google Scholar] [CrossRef]
- Chen, W.H.; Wang, C.M.; Huat Saw, L.; Hoang, A.T.; Bandala, A.A. Performance evaluation and improvement of thermoelectric generators (TEG): Fin installation and compromise optimization. Energy Convers. Manag. 2021, 250, 114858. [Google Scholar] [CrossRef]
- Kruzel, M.; Bohdal, T.; Dutkowski, K.; Radchenko, M. The Effect of Microencapsulated PCM Slurry Coolant on the Efficiency of a Shell and Tube Heat Exchanger. Energies 2022, 15, 5142. [Google Scholar] [CrossRef]
- Radchenko, M.; Radchenko, A.; Radchenko, R.; Kantor, S.; Konovalov, D.; Kornienko, V. Rational loads of turbine inlet air absorption-ejector cooling systems. Proc. Inst. Mech. Eng. Part A J. Power Energy 2022, 236, 450–462. [Google Scholar] [CrossRef]
- Cebeci, T.; Bradshaw, P. Physical and Computational Aspects of Convective Heat Transfer; Springer: Berlin/Heidelberg, Germnay, 1984. [Google Scholar]


| Abbreviature | Element |
|---|---|
| GHG | Greenhouse gas |
| ICE | Internal combustion engine |
| HEX | Heat exchanger |
| SPP | Ship power plants |
| TA | Thermoacoustic |
| TAE | Thermoacoustic engine |
| TAR | Thermoacoustic refrigerator |
| TAHM | Thermoacoustic heat machine |
| TAC | Thermoacoustic core |
| TATG | Thermoacoustic turbo generator |
| LNG | Liquid nutrition gas |
| LNH3 | Liquid ammonium |
| WHRS | Waste heat recovery system |
| Coolant, K | Low-Speed Engine | Medium-Speed Engine | Characteristics |
|---|---|---|---|
| Exhaust gas | 481–530 K | 500–690 | Low temperature |
| Charge air | 400–490 | 380–470 | |
| Jacket cooling | 355–360 | 360–370 | |
| LNG fuel | 111 | Cryogenic | |
| LNH3 fuel | 250 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Korobko, V.; Radchenko, M.; Radchenko, R. Improving Thermoacoustic Low-Temperature Heat Recovery Systems. Sustainability 2022, 14, 12306. https://doi.org/10.3390/su141912306
Yang Z, Korobko V, Radchenko M, Radchenko R. Improving Thermoacoustic Low-Temperature Heat Recovery Systems. Sustainability. 2022; 14(19):12306. https://doi.org/10.3390/su141912306
Chicago/Turabian StyleYang, Zongming, Volodymyr Korobko, Mykola Radchenko, and Roman Radchenko. 2022. "Improving Thermoacoustic Low-Temperature Heat Recovery Systems" Sustainability 14, no. 19: 12306. https://doi.org/10.3390/su141912306
APA StyleYang, Z., Korobko, V., Radchenko, M., & Radchenko, R. (2022). Improving Thermoacoustic Low-Temperature Heat Recovery Systems. Sustainability, 14(19), 12306. https://doi.org/10.3390/su141912306









