Wave Analysis of Thick Rectangular Graphene Sheets: Thickness and Small-Scale Effects on Natural and Bifurcation Frequencies
Abstract
:1. Introduction
2. Materials and Methods
2.1. Governing Equations
2.2. Exact Wave Solution Procedure
2.3. Wave Analysis
2.4. Vibration Analysis via Wave Method
3. Results and Discussion
3.1. Comparison Study
3.2. Frequency Analysis and Benchmark Results
3.3. Wave Analysis
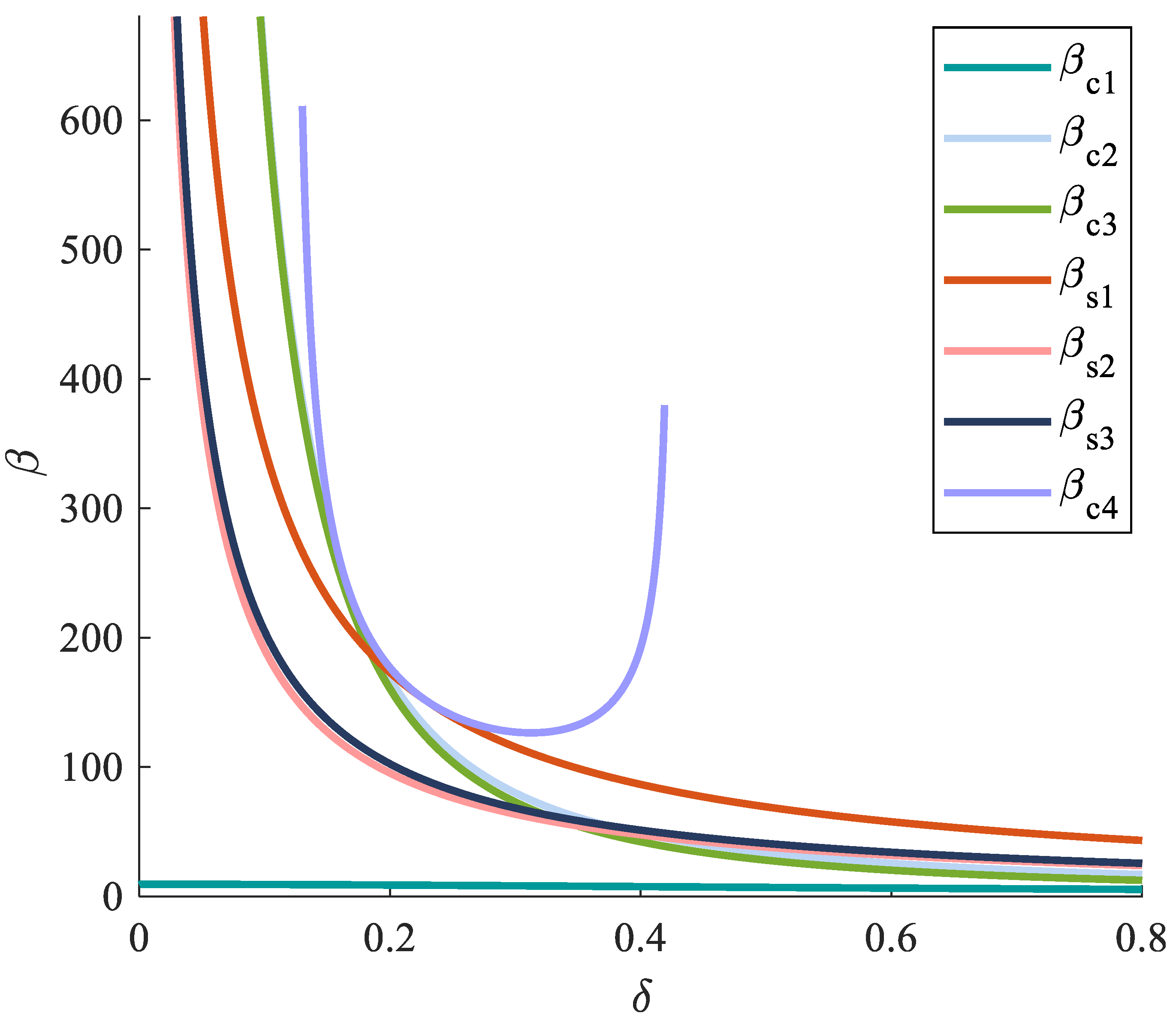
3.3.1. Effect of Nonlocal Parameter on Wave Motion
3.3.2. Effect of Graphene’s Thickness Ratio on Wave Motion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Chen, Z.; Zhang, C.; Wu, Q.; Li, K.; Tan, L. Application of triangular silver nanoplates for colorimetric detection of H2O2. Sens. Actuators B Chem. 2015, 220, 314–317. [Google Scholar] [CrossRef]
- Walkey, C.; Sykes, E.A.; Chan, W.C.W. Application of semiconductor and metal nanostructures in biology and medicine. Hematology 2009, 2009, 701–707. [Google Scholar] [CrossRef] [PubMed]
- La, D.D.; Nguyen, T.A.; Nguyen, T.T.; Ninh, H.D.; Thi, H.P.N.; Nguyen, T.T.; Nguyen, D.A.; Dang, T.D.; Rene, E.R.; Chang, S.W.; et al. Absorption Behavior of Graphene Nanoplates toward Oils and Organic Solvents in Contaminated Water. Sustainability 2019, 11, 7228. [Google Scholar] [CrossRef]
- Lin, S.; Lu, Y.; Xu, J.; Feng, S.; Li, J. High performance graphene/semiconductor van der Waals heterostructure optoelectronic devices. Nano Energy 2017, 40, 122–148. [Google Scholar] [CrossRef]
- Bykkam, S.; Prasad, D.; Maurya, M.; Sadasivuni, K.; Cabibihan, J.-J. Comparison Study of Metal Oxides (CeO2, CuO, SnO2, CdO, ZnO and TiO2) Decked Few Layered Graphene Nanocomposites for Dye-Sensitized Solar Cells. Sustainability 2021, 13, 7685. [Google Scholar] [CrossRef]
- Guo, T.; Fu, H.; Wang, C.; Chen, H.; Chen, Q.; Wang, Q.; Chen, Y.; Li, Z.; Chen, A. Road Performance and Emission Reduction Effect of Graphene/Tourmaline-Composite-Modified Asphalt. Sustainability 2021, 13, 8932. [Google Scholar] [CrossRef]
- Wang, L.; Loh, K.J.; Mousacohen, R.; Chiang, W.-H. Printed Graphene-Based Strain Sensors for Structural Health Monitoring. Asme Conf. Smart Mater. 2017. [Google Scholar] [CrossRef]
- Sankar, V.; Nambi, A.; Bhat, V.N.; Sethy, D.; Balasubramaniam, K.; Das, S.; Guha, M.; Sundara, R. Waterproof Flexible Polymer-Functionalized Graphene-Based Piezoresistive Strain Sensor for Structural Health Monitoring and Wearable Devices. ACS Omega 2020, 5, 12682–12691. [Google Scholar] [CrossRef]
- Morsin, M.; Salleh, M.M.; Umar, A.A.; Sahdan, M.Z. Gold Nanoplates for a Localized Surface Plasmon Resonance-Based Boric Acid Sensor. Sensors 2017, 17, 947. [Google Scholar] [CrossRef]
- Xu, C.; Qu, J.; Rong, D.; Zhou, Z.; Leung, A. Theory and modeling of a novel class of nanoplate-based mass sensors with corner point supports. Thin-Walled Struct. 2021, 159, 107306. [Google Scholar] [CrossRef]
- Acharyya, S.; Manna, B.; Nag, S.; Guha, P.K. WO3 Nanoplates Based Chemiresistive Sensor Device for Selective Detection of 2-Propanol. In Proceedings of the IEEE SENSORS, Montreal, QC, Canada, 27–30 October 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Yang, Z.; Pang, Y.; Han, X.-L.; Yang, Y.; Ling, J.; Jian, M.; Zhang, Y.; Yang, Y.; Ren, T.-L. Graphene Textile Strain Sensor with Negative Resistance Variation for Human Motion Detection. ACS Nano 2018, 12, 9134–9141. [Google Scholar] [CrossRef]
- Trung, T.Q.; Lee, N.-E. Flexible and Stretchable Physical Sensor Integrated Platforms for Wearable Human-Activity Monitoringand Personal Healthcare. Adv. Mater. 2016, 28, 4338–4372. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Jiang, K.; Lou, Z.; Chen, D.; Shen, G. Recent Developments in Graphene-Based Tactile Sensors and E-Skins. Adv. Mater. Technol. 2018, 3, 1700248. [Google Scholar] [CrossRef]
- Liu, T.-C.; Chuang, M.-C.; Chu, C.-Y.; Huang, W.-C.; Lai, H.-Y.; Wang, C.-T.; Chu, W.-L.; Chen, S.-Y.; Chen, Y.-Y. Implantable Graphene-based Neural Electrode Interfaces for Electrophysiology and Neurochemistry in In Vivo Hyperacute Stroke Model. ACS Appl. Mater. Interfaces 2016, 8, 187–196. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Jiang, X.; Zhong, Y.; Zhao, X.; Lin, S.; Li, J.; Li, X.; Xu, J.; Li, Z.; Zhu, H. A Wearable and Highly Sensitive Graphene Strain Sensor for Precise Home-Based Pulse Wave Monitoring. ACS Sens. 2017, 2, 967–974. [Google Scholar] [CrossRef]
- Huang, H.; Su, S.; Wu, N.; Wan, H.; Wan, S.; Bi, H.; Sun, L. Graphene-Based Sensors for Human Health Monitoring. Front. Chem. 2019, 7, 399. [Google Scholar] [CrossRef]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Nazemnezhad, R.; Zare, M.; Hosseini-Hashemi, S. Sandwich plate model of multilayer graphene sheets for considering interlayer shear effect in vibration analysis via molecular dynamics simulations. Appl. Math. Model. 2017, 47, 459–472. [Google Scholar] [CrossRef]
- Legoas, S.B.; Coluci, V.R.; Braga, S.F.; Coura, P.Z.; Dantas, S.O.; Galvão, D.S. Molecular-Dynamics Simulations of Carbon Nanotubes as Gigahertz Oscillators. Phys. Rev. Lett. 2003, 90, 055504. [Google Scholar] [CrossRef] [Green Version]
- John, T.; Thomas, T.; Abel, B.; Wood, B.R.; Chalmers, D.K.; Martin, L.L. How kanamycin A interacts with bacterial and mammalian mimetic membranes. Biochim. Et Biophys. Acta (BBA) Biomembr. 2017, 1859, 2242–2252. [Google Scholar] [CrossRef]
- Fu, T.; Mao, Y.; Tang, Y.; Zhang, Y.; Yuan, W. Effect of nanostructure on rapid boiling of water on a hot copper plate: A molecular dynamics study. Heat Mass Transf. 2016, 52, 1469–1478. [Google Scholar] [CrossRef]
- Sahmani, S.; Fattahi, A.M. Development of efficient size-dependent plate models for axial buckling of single-layered graphene nanosheets using molecular dynamics simulation. Microsyst. Technol. 2017, 24, 1265–1277. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, T.; Chen, C. Effective elastic modulus and atomic stress concentration of single crystal nano-plate with void. Comput. Mater. Sci. 2007, 40, 51–56. [Google Scholar] [CrossRef]
- Sarayi, S.M.M.J.; Faghihi, D.; Waqas, M.; Siddiqui, A.H.; Tutino, V.M. A Hybrid Finite Element and Smoothed-Particle Hydrodynamics Method Can Simulate Peri-Procedural Complications of Thrombectomy. Circulation 2022, 144, A14359. Available online: https://www.ahajournals.org/doi/abs/10.1161/circ.144.suppl_1.14359 (accessed on 24 August 2022).
- Cemal, A. Eringen, Nonlocal Continuum Field Theories; Springer: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Peddieson, J.; Buchanan, G.R.; McNitt, R.P. Application of nonlocal continuum models to nanotechnology. Int. J. Eng. Sci. 2003, 41, 305–312. [Google Scholar] [CrossRef]
- Aydogdu, M. Axial vibration of the nanorods with the nonlocal continuum rod model. Phys. E Low-Dimens. Syst. Nanostructures 2009, 41, 861–864. [Google Scholar] [CrossRef]
- Lei, Z.; Zhang, L.; Liew, K.; Yu, J. Dynamic stability analysis of carbon nanotube-reinforced functionally graded cylindrical panels using the element-free kp-Ritz method. Compos. Struct. 2014, 113, 328–338. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Y.; Liew, K. Vibration analysis of quadrilateral graphene sheets subjected to an in-plane magnetic field based on nonlocal elasticity theory. Compos. Part B Eng. 2017, 118, 96–103. [Google Scholar] [CrossRef]
- Pradhan, S.; Phadikar, J. Nonlocal elasticity theory for vibration of nanoplates. J. Sound Vib. 2009, 325, 206–223. [Google Scholar] [CrossRef]
- Phadikar, J.; Pradhan, S. Variational formulation and finite element analysis for nonlocal elastic nanobeams and nanoplates. Comput. Mater. Sci. 2010, 49, 492–499. [Google Scholar] [CrossRef]
- Aghababaei, R.; Reddy, J. Nonlocal third-order shear deformation plate theory with application to bending and vibration of plates. J. Sound Vib. 2009, 326, 277–289. [Google Scholar] [CrossRef]
- Namin, S.A.; Pilafkan, R. Vibration analysis of defective graphene sheets using nonlocal elasticity theory. Phys. E Low-Dimens. Syst. Nanostructures 2017, 93, 257–264. [Google Scholar] [CrossRef]
- Hashemi, S.H.; Zare, M.; Nazemnezhad, R. An exact analytical approach for free vibration of Mindlin rectangular nano-plates via nonlocal elasticity. Compos. Struct. 2013, 100, 290–299. [Google Scholar] [CrossRef]
- Sarrami-Foroushani, S.; Azhari, M. Nonlocal vibration and buckling analysis of single and multi-layered graphene sheets using finite strip method including van der Waals effects. Phys. E Low-Dimens. Syst. Nanostructures 2014, 57, 83–95. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Kermajani, M.; Nazemnezhad, R. An analytical study on the buckling and free vibration of rectangular nanoplates using nonlocal third-order shear deformation plate theory. Eur. J. Mech. A/Solids 2015, 51, 29–43. [Google Scholar] [CrossRef]
- Patel, P.; Sarayi, S.M.M.J.; Chen, D.; Hammond, A.L.; Damiano, R.J.; Davies, J.M.; Xu, J.; Meng, H. Fast virtual coiling algorithm for intracranial aneurysms using pre-shape path planning. Comput. Biol. Med. 2021, 134, 104496. [Google Scholar] [CrossRef]
- Charvade, A.S.; Sarayi, S.M.M.J. An Analytical Approach for Preliminary Response-Based Design of Semi Rigid Moment Resisting Frames. Prog. Appl. Sci. Eng. 2021, 6. Available online: https://www.crpase.com/viewmore.php?pid=174 (accessed on 24 August 2022).
- Eftekhar, S.; Sarayi, S.M.M.J. An analytical solution for nonlinear dynamics of one kind of scanning probe microscopes. arXiv 2020, arXiv:2009.05600. [Google Scholar]
- Mei, C.; Mace, B.R. Wave Reflection and Transmission in Timoshenko Beams and Wave Analysis of Timoshenko Beam Structures. J. Vib. Acoust. 2004, 127, 382–394. [Google Scholar] [CrossRef]
- Tan, C.; Kang, B. Wave reflection and transmission in an axially strained rotating Timoshenko shaft. J. Sound Vib. 1998, 213, 483–510. [Google Scholar] [CrossRef]
- Lee, S.-K.; Mace, B.; Brennan, M. Wave propagation, reflection and transmission in non-uniform one-dimensional waveguides. J. Sound Vib. 2007, 304, 31–49. [Google Scholar] [CrossRef]
- Mei, C.; Karpenko, Y.; Moody, S.; Allen, D. Analytical approach to free and forced vibrations of axially loaded cracked Timoshenko beams. J. Sound Vib. 2006, 291, 1041–1060. [Google Scholar] [CrossRef]
- Mei, C. In-plane Vibrations of Classical Planar Frame Structures? an Exact Wave-based Analytical Solution. J. Vib. Control 2010, 16, 1265–1285. [Google Scholar] [CrossRef]
- Mei, C. Studying the effects of lumped end mass on vibrations of a Timoshenko beam using a wave-based approach. J. Vib. Control 2012, 18, 733–742. [Google Scholar] [CrossRef]
- Mei, C. Free vibration analysis of classical single-story multi-bay planar frames. J. Vib. Control 2013, 19, 2022–2035. [Google Scholar] [CrossRef]
- Bahrami, M.N.; Arani, M.K.; Saleh, N.R. Modified wave approach for calculation of natural frequencies and mode shapes in arbitrary non-uniform beams. Sci. Iran. 2011, 18, 1088–1094. [Google Scholar] [CrossRef]
- Bahrami, A.; Teimourian, A. Study on vibration, wave reflection and transmission in composite rectangular membranes using wave propagation approach. Meccanica 2017, 1–19. [Google Scholar] [CrossRef]
- Bahrami, A.; Teimourian, A. Nonlocal scale effects on buckling, vibration and wave reflection in nanobeams via wave propagation approach. Compos. Struct. 2015, 123, 1061–1075. [Google Scholar] [CrossRef]
- Bahrami, A. A wave-based computational method for free vibration, wave power transmission and reflection in multi-cracked nanobeams. Compos. Part B Eng. 2017, 120, 168–181. [Google Scholar] [CrossRef]
- Bahrami, A. Free vibration, wave power transmission and reflection in multi-cracked nanorods. Compos. Part B Eng. 2017, 127, 53–62. [Google Scholar] [CrossRef]
- Bahrami, A.; Teimourian, A. Small scale effect on vibration and wave power reflection in circular annular nanoplates. Compos. Part B Eng. 2017, 109, 214–226. [Google Scholar] [CrossRef]
- Sarayi, S.M.M.J.; Bahrami, A.; Bahrami, M.N. Free vibration and wave power reflection in Mindlin rectangular plates via exact wave propagation approach. Compos. Part B Eng. 2018, 144, 195–205. [Google Scholar] [CrossRef]
- Sarayi, S.M.M.J.; Damiano, R.J.; Patel, P.; Dargush, G.; Siddiqui, A.H.; Meng, H. A Nonlinear Mechanics-based Virtual Coiling Method For Intracranial Aneurysm. Summer Biomech. Bioeng. Biotransport Conf. 2020. [Google Scholar] [CrossRef]
- Zitoun, A.; Fakis, D.; Jayasree, N.; Omairey, S.; Oikonomidis, F.; Stoeva, Z.; Kazilas, M. Graphene-based strain sensing in composites for structural and health monitoring applications. SN Appl. Sci. 2022, 4, 1–17. [Google Scholar] [CrossRef]
- Bahrami, A.; Teimourian, A. Study on the effect of s. mall scale on the wave reflection in carbon nanotubes using nonlocal Timoshenko beam theory and wave propagation approach. Compos. B Eng. 2016, 91, 492–504. [Google Scholar] [CrossRef]
- Mindlin, R.D. Influence of Rotatory Inertia and Shear on Flexural Motions of Isotropic, Elastic Plates. J. Appl. Mech. 2021, 18, 31–38. [Google Scholar] [CrossRef]
- Samaei, A.; Abbasion, S.; Mirsayar, M. Buckling analysis of a single-layer graphene sheet embedded in an elastic medium based on nonlocal Mindlin plate theory. Mech. Res. Commun. 2011, 38, 481–485. [Google Scholar] [CrossRef]
| η | References | (m = 1, n = 1) | (m = 2, n = 2) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| τ | τ | |||||||||
| 0 (βL) | 0.2 | 0.4 | 0.6 | 0 (βL) | 0.2 | 0.4 | 0.6 | |||
| SSSS | 1 | Exact sol. [35] | 19.0840 | 0.7475 | 0.4904 | 0.3512 | 79.0219 | 0.4904 | 0.2708 | 0.1843 |
| HSDT [37] | 19.0839 | 0.7477 | 0.4904 | 0.3512 | 79.0219 | 0.4906 | 0.2708 | 0.1844 | ||
| FSDT [31] | 19.0840 | 0.7475 | 0.4904 | 0.3512 | 79.0219 | 0.4904 | 0.2708 | 0.1844 | ||
| CLPT [31] | 19.0840 | 0.7475 | 0.4904 | 0.3512 | 79.0219 | 0.4905 | 0.2707 | 0.1843 | ||
| Present | 19.0840 | 0.7475 | 0.4904 | 0.3512 | 79.0219 | 0.4904 | 0.2708 | 0.1844 | ||
| 0.5 | Exact sol. | 12.0752 | 0.8183 | 0.5799 | 0.4287 | 45.5845 | 0.5799 | 0.3353 | 0.2309 | |
| HSDT | 12.0752 | 0.8183 | 0.5799 | 0.4287 | 45.5845 | 0.5799 | 0.3353 | 0.2309 | ||
| CLPT | 12.0752 | 0.8183 | 0.5799 | 0.4287 | 45.5845 | 0.5799 | 0.3353 | 0.2308 | ||
| Present | 12.0752 | 0.8183 | 0.5799 | 0.4287 | 45.5845 | 0.5799 | 0.3353 | 0.2308 | ||
| SCSC | 1 | Exact sol. | 26.7369 | 0.7319 | 0.4721 | 0.3359 | 79.1951 | 0.4770 | 0.2617 | 0.1778 |
| HSDT [35] | 26.7369 | 0.7213 | 0.4695 | 0.3312 | 79.1953 | 0.4561 | 0.2365 | 0.1569 | ||
| CLPT | 26.7369 | 0.7322 | 0.4703 | 0.3334 | 79.1951 | 0.4596 | 0.2459 | 0.1614 | ||
| Present | 26.7369 | 0.7319 | 0.4721 | 0.3359 | 79.1951 | 0.4816 | 0.2646 | 0.1799 | ||
| 5/3 | Exact sol. | 56.8967 | 0.6080 | 0.3560 | 0.2458 | 143.6230 | 0.3600 | 0.1893 | 0.1274 | |
| Present | 56.8967 | 0.6080 | 0.3560 | 0.2458 | 143.6230 | 0.3693 | 0.1946 | 0.1311 | ||
| 0.5 | Exact sol. | 13.2843 | 0.8140 | 0.5735 | 0.4228 | 47.2245 | 0.5723 | 0.3324 | 0.2262 | |
| CLPT | 13.2843 | 0.8032 | 0.5689 | 0.4124 | 46.6541 | 0.5681 | 0.3311 | 0.2136 | ||
| present | 13.2843 | 0.8140 | 0.5735 | 0.4228 | 47.2245 | 0.5769 | 0.3329 | 0.2291 | ||
| SFSF | 1 | Exact sol. | 9.4458 | 0.8683 | 0.6578 | 0.5019 | 42.8870 | 0.6305 | 0.3745 | 0.2596 |
| Present | 9.4458 | 0.8683 | 0.6578 | 0.5019 | 42.8870 | 0.6324 | 0.3758 | 0.2605 | ||
| 5/3 | Exact sol. | 9.3561 | 0.8759 | 0.6712 | 0.5166 | 51.6274 | 0.6290 | 0.3731 | 0.2586 | |
| Present | 9.3561 | 0.8756 | 0.6712 | 0.5166 | 51.6274 | 0.6283 | 0.3725 | 0.2580 | ||
| SCSS | 1 | Exact sol. | 22.4260 | 0.7374 | 0.4785 | 0.3412 | 74.4019 | 0.4833 | 0.2660 | 0.1809 |
| CLPT | 22.4260 | 0.7364 | 0.4795 | 0.3411 | 74.4019 | 0.4813 | 0.2675 | 0.1795 | ||
| Present | 22.4260 | 0.7374 | 0.4785 | 0.3412 | 74.4019 | 0.4856 | 0.2675 | 0.1820 | ||
| 1.25 | Exact sol. | 29.8086 | 0.6914 | 0.4308 | 0.3030 | 94.0851 | 0.4364 | 0.2357 | 0.1596 | |
| present | 83.7200 | 0.6914 | 0.4308 | 0.3030 | 94.0851 | 0.4398 | 0.2377 | 0.1610 | ||
| SFSS | 1 | Exact sol. | 11.3810 | 0.8548 | 0.6331 | 0.4772 | 53.3852 | 0.5688 | 0.3264 | 0.2243 |
| Present | 11.3810 | 0.8548 | 0.6331 | 0.4772 | 53.3852 | 0.5693 | 0.3268 | 0.2246 | ||
| 1.25 | Exact sol. | 12.2549 | 0.8548 | 0.6330 | 0.4771 | 61.6058 | 0.5454 | 0.3093 | 0.2117 | |
| Present | 12.2549 | 0.8548 | 0.6330 | 0.4771 | 61.6058 | 0.5450 | 0.3091 | 0.2119 | ||
| SCSF | 1 | Exact sol. | 12.2606 | 0.8616 | 0.6458 | 0.4904 | 55.9736 | 0.5666 | 0.3248 | 0.2231 |
| Present | 12.2606 | 0.8616 | 0.6458 | 0.4904 | 55.9735 | 0.5677 | 0.3255 | 0.2236 | ||
| 1.25 | Exact sol. | 13.8996 | 0.8667 | 0.6559 | 0.5014 | 65.9053 | 0.5415 | 0.3062 | 0.2096 | |
| Present | 13.8996 | 0.8667 | 0.6559 | 0.5015 | 65.9053 | 0.5416 | 0.3063 | 0.2097 | ||
| (m = 1, n = 1) | (m = 1, n = 2) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| τ | τ | |||||||||
| δ | 0 | 0.1 | 0.3 | 0.5 | δ | 0 | 0.1 | 0.3 | 0.5 | |
| SFSF | 0.01 | 9.6270 | 0.9611 | 0.7566 | 0.5696 | 0.01 | 16.0971 | 0.9559 | 0.7328 | 0.5408 |
| 0.1 | 9.4458 | 0.9615 | 0.7584 | 0.5717 | 0.1 | 16.0971 | 0.9570 | 0.7376 | 0.5460 | |
| 0.2 | 8.9997 | 0.9614 | 0.7580 | 0.5713 | 0.2 | 14.1341 | 0.9553 | 0.7308 | 0.5385 | |
| SCSC | 0.01 | 28.925 | 0.9055 | 0.5787 | 0.3913 | 0.01 | 69.1986 | 0.8011 | 0.4060 | 0.2574 |
| 0.1 | 26.7369 | 0.9069 | 0.5815 | 0.3936 | 0.1 | 59.4801 | 0.8059 | 0.4110 | 0.2607 | |
| 0.2 | 22.5099 | 0.9093 | 0.5871 | 0.3982 | 0.2 | 45.0569 | 0.8128 | 0.4196 | 0.2668 | |
| SCSF | 0.01 | 12.6728 | 0.9587 | 0.7458 | 0.5568 | 0.01 | 32.9925 | 0.9017 | 0.5676 | 0.3804 |
| 0.1 | 12.2606 | 0.9594 | 0.7487 | 0.5600 | 0.1 | 30.4743 | 0.9018 | 0.5680 | 0.3809 | |
| 0.2 | 11.3931 | 0.9587 | 0.7457 | 0.5564 | 0.2 | 25.8975 | 0.8998 | 0.5640 | 0.3777 | |
| SCSS | 0.01 | 23.6327 | 0.9087 | 0.5864 | 0.3981 | 0.01 | 58.5687 | 0.8092 | 0.4173 | 0.2658 |
| 0.1 | 22.4260 | 0.9094 | 0.5881 | 0.3995 | 0.1 | 52.3247 | 0.8117 | 0.4198 | 0.2675 | |
| 0.2 | 19.7988 | 0.9108 | 0.5914 | 0.4023 | 0.2 | 41.7813 | 0.8154 | 0.4244 | 0.2706 | |
| SFSS | 0.01 | 11.6746 | 0.9564 | 0.7352 | 0.5435 | 0.01 | 27.7042 | 0.9057 | 0.5814 | 0.3953 |
| 0.1 | 11.3810 | 0.9572 | 0.7381 | 0.5466 | 0.1 | 26.1910 | 0.9057 | 0.5816 | 0.3957 | |
| 0.2 | 10.7218 | 0.9570 | 0.7375 | 0.5459 | 0.2 | 23.2429 | 0.9030 | 0.5750 | 0.3898 | |
| SSSS | 0.01 | 19.7322 | 0.9139 | 0.6001 | 0.4105 | 0.01 | 49.3045 | 0.8183 | 0.4287 | 0.2738 |
| 0.1 | 19.0840 | 0.9139 | 0.6001 | 0.4105 | 0.1 | 45.5845 | 0.8183 | 0.4287 | 0.2738 | |
| 0.2 | 17.5055 | 0.9139 | 0.6001 | 0.4105 | 0.2 | 38.3847 | 0.8183 | 0.4287 | 0.2738 | |
| (m = 2, n = 1) | (m = 2, n = 2) | |||||||||
| SFSF | 0.01 | 38.9043 | 0.8580 | 0.4844 | 0.3148 | 0.01 | 46.6393 | 0.8531 | 0.4748 | 0.3072 |
| 0.1 | 36.4246 | 0.8588 | 0.4853 | 0.3154 | 0.1 | 42.8870 | 0.8543 | 0.4765 | 0.3083 | |
| 0.2 | 31.4338 | 0.8574 | 0.4835 | 0.3140 | 0.2 | 36.1646 | 0.8495 | 0.4699 | 0.3033 | |
| SCSC | 0.01 | 54.6743 | 0.8135 | 0.4223 | 0.2691 | 0.01 | 94.3686 | 0.7360 | 0.3401 | 0.2120 |
| 0.1 | 49.2606 | 0.8150 | 0.4240 | 0.2703 | 0.1 | 79.1951 | 0.7404 | 0.3437 | 0.2144 | |
| 0.2 | 40.1384 | 0.8165 | 0.4261 | 0.2718 | 0.2 | 59.1227 | 0.7448 | 0.3480 | 0.2172 | |
| SCSF | 0.01 | 41.6472 | 0.8541 | 0.4774 | 0.3093 | 0.01 | 62.8595 | 0.8093 | 0.4164 | 0.2648 |
| 0.1 | 38.7128 | 0.8550 | 0.4784 | 0.3099 | 0.1 | 55.9735 | 0.8099 | 0.4174 | 0.2655 | |
| 0.2 | 33.0747 | 0.8530 | 0.4757 | 0.3079 | 0.2 | 45.0445 | 0.8068 | 0.4137 | 0.2628 | |
| SCSS | 0.01 | 51.6210 | 0.8156 | 0.4250 | 0.2711 | 0.01 | 85.9792 | 0.7414 | 0.3453 | 0.2155 |
| 0.1 | 47.2245 | 0.8164 | 0.4259 | 0.2718 | 0.1 | 74.4019 | 0.7436 | 0.3472 | 0.2168 | |
| 0.2 | 39.2032 | 0.8172 | 0.4271 | 0.2726 | 0.2 | 57.3380 | 0.7460 | 0.3495 | 0.2183 | |
| SFSS | 0.01 | 41.1469 | 0.8530 | 0.4754 | 0.3077 | 0.01 | 58.9430 | 0.8108 | 0.4441 | 0.2848 |
| 0.1 | 38.3610 | 0.8540 | 0.4764 | 0.3084 | 0.1 | 53.3852 | 0.8111 | 0.4448 | 0.2853 | |
| 0.2 | 32.8922 | 0.8524 | 0.4744 | 0.3069 | 0.2 | 43.8579 | 0.8075 | 0.4428 | 0.2838 | |
| SSSS | 0.01 | 49.3045 | 0.8183 | 0.4287 | 0.2738 | 0.01 | 78.8455 | 0.7475 | 0.3512 | 0.2196 |
| 0.1 | 45.5845 | 0.8183 | 0.4287 | 0.2738 | 0.1 | 70.0219 | 0.7475 | 0.3512 | 0.2196 | |
| 0.2 | 38.3847 | 0.8183 | 0.4287 | 0.2738 | 0.2 | 55.5860 | 0.7475 | 0.3512 | 0.2196 | |
| (m = 1, n = 1) | (m = 1, n = 2) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| τ | τ | |||||||||
| δ | 0 | 0.1 | 0.3 | 0.5 | δ | 0 | 0.1 | 0.3 | 0.5 | |
| SFSF | 0.01 | 9.5078 | 0.9644 | 0.7723 | 0.5892 | 0.01 | 27.3597 | 0.9557 | 0.7323 | 0.5401 |
| 0.1 | 9.3306 | 0.9647 | 0.7737 | 0.5908 | 0.1 | 24.9711 | 0.9552 | 0.7305 | 0.5382 | |
| 0.2 | 8.9007 | 0.9642 | 0.7712 | 0.5878 | 0.2 | 21.3271 | 0.9489 | 0.7060 | 0.5113 | |
| SCSC | 0.01 | 94.9657 | 0.7926 | 0.3957 | 0.2500 | 0.01 | 252.3968 | 0.5813 | 0.2309 | 0.1409 |
| 0.1 | 75.1962 | 0.8009 | 0.4032 | 0.2549 | 0.1 | 166.7806 | 0.5988 | 0.2403 | 0.1467 | |
| 0.2 | 52.1283 | 0.8100 | 0.4149 | 0.2631 | 0.2 | 102.7371 | 0.6141 | 0.2499 | 0.1529 | |
| SCSF | 0.01 | 22.7512 | 0.9692 | 0.8086 | 0.6758 | 0.01 | 99.3823 | 0.7782 | 0.3474 | 0.1914 |
| 0.1 | 21.1870 | 0.9574 | 0.7992 | 0.6753 | 0.1 | 81.0357 | 0.7746 | 0.3509 | 0.1928 | |
| 0.2 | 18.4903 | 0.9592 | 0.7579 | 0.6016 | 0.2 | 57.8767 | 0.7771 | 0.3623 | 0.2102 | |
| SCSS | 0.01 | 69.1986 | 0.8011 | 0.4060 | 0.2573 | 0.01 | 207.3996 | 0.5964 | 0.1894 | 0.1478 |
| 0.1 | 59.4801 | 0.8059 | 0.4110 | 0.2607 | 0.1 | 151.1821 | 0.6054 | 0.2013 | 0.1507 | |
| 0.2 | 45.0569 | 0.8127 | 0.4196 | 0.2668 | 0.2 | 99.7234 | 0.6131 | 0.2507 | 0.1536 | |
| SFSS | 0.01 | 16.0971 | 0.9559 | 0.7328 | 0.5408 | 0.01 | 75.0554 | 0.7998 | 0.4383 | 0.2642 |
| 0.1 | 15.4054 | 0.9570 | 0.7375 | 0.5459 | 0.1 | 66.3720 | 0.7924 | 0.4009 | 0.2567 | |
| 0.2 | 14.1341 | 0.9552 | 0.7307 | 05385 | 0.2 | 52.8012 | 0.7831 | 0.3875 | 0.2459 | |
| SSSS | 0.01 | 49.3045 | 0.8183 | 0.4287 | 0.2737 | 0.01 | 167.2821 | 0.6111 | 0.4287 | 0.1526 |
| 0.1 | 45.5845 | 0.8183 | 0.4287 | 0.2737 | 0.1 | 134.3586 | 0.6111 | 0.4287 | 0.1526 | |
| 0.2 | 38.3847 | 0.8183 | 0.4287 | 0.2737 | 0.2 | 95.8088 | 0.6111 | 0.4287 | 0.1526 | |
| (m = 2, n = 1) | (m = 2, n = 2) | |||||||||
| SFSF | 0.01 | 38.4774 | 0.8669 | 0.5003 | 0.3272 | 0.01 | 64.2036 | 0.8520 | 0.4729 | 0.3057 |
| 0.1 | 35.9987 | 0.8678 | 0.5014 | 0.3281 | 0.1 | 56.5363 | 0.8496 | 0.4694 | 0.3029 | |
| 0.2 | 31.0963 | 0.8645 | 0.4963 | 0.3242 | 0.2 | 45.3418 | 0.8357 | 0.4491 | 0.2879 | |
| SCSC | 0.01 | 115.3920 | 0.7293 | 0.3339 | 0.2078 | 0.01 | 275.2751 | 0.5553 | 0.2167 | 0.1319 |
| 0.1 | 90.0396 | 0.7369 | 0.3400 | 0.2118 | 0.1 | 180.2276 | 0.5707 | 0.22.46 | 0.1369 | |
| 0.2 | 62.9729 | 0.7432 | 0.3463 | 0.2161 | 0.2 | 112.1661 | 0.5815 | 0.2311 | 0.1411 | |
| SCSF | 0.01 | 50.6057 | 0.8599 | 0.4881 | 0.3178 | 0.01 | 131.4853 | 0.7207 | 0.3242 | 0.2007 |
| 0.1 | 45.5725 | 0.8595 | 0.4869 | 0.3168 | 0.1 | 103.5900 | 0.7167 | 0.3215 | 0.1991 | |
| 0.2 | 37.5487 | 0.8512 | 0.4741 | 0.3069 | 0.2 | 73.0862 | 0.7138 | 0.3190 | 0.1976 | |
| SCSS | 0.01 | 94.3686 | 0.7360 | 0.3401 | 0.2119 | 0.01 | 233.3530 | 0.5672 | 0.2239 | 0.1366 |
| 0.1 | 79.1951 | 0.7404 | 0.3437 | 0.2144 | 0.1 | 167.1253 | 0.5753 | 0.2280 | 0.1392 | |
| 0.2 | 59.1227 | 0.7447 | 0.3479 | 0.2172 | 0.2 | 109.7471 | 0.6298 | 0.2312 | 0.1411 | |
| SFSS | 0.01 | 46.6393 | 0.8530 | 0.4748 | 0.3072 | 0.01 | 110.5043 | 0.7309 | 0.4213 | 0.2603 |
| 0.1 | 42.8870 | 0.8543 | 0.4765 | 0.3083 | 0.1 | 92.9718 | 0.7248 | 0.3860 | 0.2379 | |
| 0.2 | 36.1646 | 0.8495 | 0.4698 | 0.3033 | 0.2 | 69.9757 | 0.7156 | 0.3762 | 0.2294 | |
| SSSS | 0.01 | 78.8455 | 0.7475 | 0.3512 | 0.2195 | 0.01 | 196.6991 | 0.5799 | 0.2308 | 0.1409 |
| 0.1 | 70.0219 | 0.7475 | 0.3512 | 0.2196 | 0.1 | 153.5390 | 0.5799 | 0.2308 | 0.1409 | |
| 0.2 | 55.5860 | 0.7475 | 0.3512 | 0.2196 | 0.2 | 106.9195 | 0.5799 | 0.2308 | 0.1409 | |
| (m = 1, n = 2) | (m = 1, n = 1) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| τ | τ | |||||||||
| δ | 0 | 0.1 | 0.3 | 0.5 | δ | 0 | 0.1 | 0.3 | 0.5 | |
| SFSF | 0.01 | 9.7328 | 0.9581 | 0.7432 | 0.5536 | 0.01 | 11.6746 | 0.9564 | 0.7352 | 0.5435 |
| 0.1 | 9.5560 | 0.9584 | 0.7443 | 0.5547 | 0.1 | 11.3811 | 0.9572 | 0.7381 | 0.5466 | |
| 0.2 | 9.1061 | 0.9584 | 0.7444 | 0.5548 | 0.2 | 10.7218 | 0.9570 | 0.7375 | 0.5459 | |
| SCSC | 0.01 | 13.6815 | 0.9417 | 0.6819 | 0.4880 | 0.01 | 23.6327 | 0.9087 | 0.5864 | 0.3981 |
| 0.1 | 13.2843 | 0.9419 | 0.6825 | 0.4886 | 0.1 | 22.4260 | 0.9094 | 0.5881 | 0.3995 | |
| 0.2 | 12.3152 | 0.9423 | 0.6838 | 0.4898 | 0.2 | 19.7988 | 0.9108 | 0.5914 | 0.4023 | |
| SCSF | 0.01 | 10.4206 | 0.9568 | 0.7372 | 0.5463 | 0.01 | 15.7393 | 0.9400 | 0.6757 | 0.4815 |
| 0.1 | 10.2054 | 0.9572 | 0.7387 | 0.5478 | 0.1 | 15.1956 | 0.9406 | 0.6777 | 0.4835 | |
| 0.2 | 9.6782 | 0.9572 | 0.7387 | 0.5477 | 0.2 | 13.9934 | 0.9403 | 0.6771 | 0.4829 | |
| SCSS | 0.01 | 12.9152 | 0.9425 | 0.6847 | 0.4909 | 0.01 | 21.5239 | 0.9111 | 0.5929 | 0.4039 |
| 0.1 | 12.6022 | 0.9426 | 0.6850 | 0.4912 | 0.1 | 20.6396 | 0.9115 | 0.5937 | 0.4046 | |
| 0.2 | 11.8061 | 0.9428 | 0.7053 | 0.4919 | 0.2 | 18.6005 | 0.9122 | 0.6231 | 0.4060 | |
| SFSS | 0.01 | 10.2948 | 0.9564 | 0.7355 | 0.5443 | 0.01 | 14.7549 | 0.9406 | 0.6778 | 0.4836 |
| 0.1 | 10.0929 | 0.9146 | 0.7369 | 0.5456 | 0.1 | 14.3272 | 0.9410 | 0.6794 | 0.4853 | |
| 0.2 | 9.5902 | 0.9569 | 0.7371 | 0.5457 | 0.2 | 13.3463 | 0.9407 | 0.6786 | 0.4845 | |
| SSSS | 0.01 | 12.3343 | 0.9435 | 0.6884 | 0.4948 | 0.01 | 19.7322 | 0.9139 | 0.6001 | 0.4105 |
| 0.1 | 12.0752 | 0.9435 | 0.6884 | 0.4948 | 0.1 | 19.0840 | 0.9139 | 0.6001 | 0.4105 | |
| 0.2 | 11.3961 | 0.9435 | 0.6884 | 0.4948 | 0.2 | 17.5055 | 0.9139 | 0.6001 | 0.4105 | |
| (m = 2, n = 1) | (m = 2, n = 1) | |||||||||
| SFSF | 0.01 | 39.1526 | 0.8528 | 0.4762 | 0.3086 | 0.01 | 41.1469 | 0.8530 | 0.4754 | 0.3077 |
| 0.1 | 36.6824 | 0.8534 | 0.4767 | 0.3089 | 0.1 | 38.3610 | 0.8540 | 0.4764 | 0.3084 | |
| 0.2 | 31.6538 | 0.8528 | 0.4760 | 0.3084 | 0.2 | 32.8922 | 0.8524 | 0.4744 | 0.3069 | |
| SCSC | 0.01 | 42.5528 | 0.8386 | 0.4564 | 0.2941 | 0.01 | 51.6210 | 0.8156 | 0.4250 | 0.2711 |
| 0.1 | 39.6410 | 0.8388 | 0.4567 | 0.2943 | 0.1 | 47.2245 | 0.8164 | 0.4259 | 0.2718 | |
| 0.2 | 33.8397 | 0.8093 | 0.4570 | 0.2946 | 0.2 | 39.2032 | 0.8172 | 0.4271 | 0.2726 | |
| SCSF | 0.01 | 39.7874 | 0.8062 | 0.4740 | 0.3069 | 0.01 | 45.0551 | 0.8379 | 0.4547 | 0.2926 |
| 0.1 | 37.2242 | 0.8524 | 0.4746 | 0.3072 | 0.1 | 41.7409 | 0.8385 | 0.4554 | 0.2931 | |
| 0.2 | 32.0545 | 0.8517 | 0.4737 | 0.3066 | 0.2 | 35.3839 | 0.8375 | 0.4542 | 0.2922 | |
| SCSS | 0.01 | 42.2071 | 0.8389 | 0.4570 | 0.2946 | 0.01 | 50.3833 | 0.8169 | 0.4268 | 0.2724 |
| 0.1 | 39.3897 | 0.8390 | 0.4446 | 0.2947 | 0.1 | 46.3599 | 0.8173 | 0.4272 | 0.2727 | |
| 0.2 | 33.7085 | 0.8116 | 0.4439 | 0.2948 | 0.2 | 38.7801 | 0.8177 | 0.4278 | 0.2732 | |
| SFSS | 0.01 | 39.7326 | 0.8215 | 0.4736 | 0.3065 | 0.01 | 44.4758 | 0.8382 | 0.3613 | 0.2267 |
| 0.1 | 37.1858 | 0.8521 | 0.4741 | 0.3069 | 0.1 | 41.3217 | 0.8386 | 0.3528 | 0.2208 | |
| 0.2 | 32.0309 | 0.8516 | 0.4735 | 0.3051 | 0.2 | 35.1634 | 0.8376 | 0.3979 | 0.2518 | |
| SSSS | 0.01 | 41.9144 | 0.8393 | 0.4576 | 0.2951 | 0.01 | 49.3045 | 0.8183 | 0.4287 | 0.2738 |
| 0.1 | 39.1713 | 0.8393 | 0.4576 | 0.2853 | 0.1 | 45.5845 | 0.8183 | 0.4287 | 0.2738 | |
| 0.2 | 33.5896 | 0.8138 | 0.4576 | 0.2946 | 0.2 | 38.3847 | 0.8183 | 0.4287 | 0.2738 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mousavi Janbeh Sarayi, S.M.; Rajabpoor Alisepahi, A.; Bahrami, A. Wave Analysis of Thick Rectangular Graphene Sheets: Thickness and Small-Scale Effects on Natural and Bifurcation Frequencies. Sustainability 2022, 14, 12329. https://doi.org/10.3390/su141912329
Mousavi Janbeh Sarayi SM, Rajabpoor Alisepahi A, Bahrami A. Wave Analysis of Thick Rectangular Graphene Sheets: Thickness and Small-Scale Effects on Natural and Bifurcation Frequencies. Sustainability. 2022; 14(19):12329. https://doi.org/10.3390/su141912329
Chicago/Turabian StyleMousavi Janbeh Sarayi, Seyyed Mostafa, Amir Rajabpoor Alisepahi, and Arian Bahrami. 2022. "Wave Analysis of Thick Rectangular Graphene Sheets: Thickness and Small-Scale Effects on Natural and Bifurcation Frequencies" Sustainability 14, no. 19: 12329. https://doi.org/10.3390/su141912329






