Protecting Power Transmission Systems against Intelligent Physical Attacks: A Critical Systematic Review

Abstract

Power systems are exposed to various physical threats due to extreme events, technical failures, human errors, and deliberate damage. Physical threats are among the most destructive factors to endanger the power systems security by intelligently targeting power systems components, such as Transmission Lines (TLs), to damage/destroy the facilities or disrupt the power systems operation. The aim of physical attacks in disrupting power systems can be power systems instability, load interruptions, unserved energy costs, repair/displacement costs, and even cascading failures and blackouts. Due to dispersing in large geographical areas, power transmission systems are more exposed to physical threats. Power systems operators, as the system defenders, protect power systems in different stages of a physical attack by minimizing the impacts of such destructive attacks. In this regard, many studies have been conducted in the literature. In this paper, an overview of the previous research studies related to power systems protection against physical attacks is conducted. This paper also outlines the main characteristics, such as physical attack adverse impacts, defending actions, optimization methods, understudied systems, uncertainty considerations, expansion planning, and cascading failures. Furthermore, this paper gives some key findings and recommendations to identify the research gap in the literature.

1. Introduction

Various natural and unnatural factors may threaten power systems and their normal operation. Such factors have natural, technological, and human origins as presented in Figure 1 [1]. However, physical attacks, as a key threat, intelligently target the most critical components of power grids; they are more destructive than other threatening factors [2,3]. Figure 2 shows the potential targets in a physical attack on power systems. As this figure shows, a physical attack may target every component of the system. Among power systems components, power transmission systems are more endangered due to the dispersion of Transmission Lines (TLs) in wide geographical areas [4]. Disruption agents (physical attackers) can identify the critical TLs and target/destroy them with the aim of load interruption, imposing unserved load cost, disrupting power systems operation (e.g., creating cascading failures), imposing repair/replacement cost of targeted elements, etc.

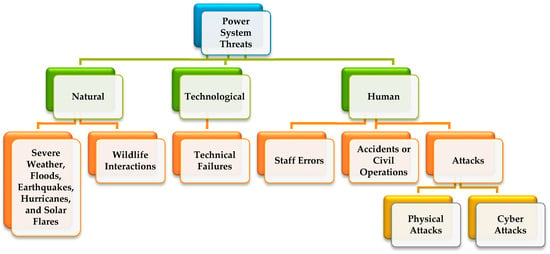
Figure 1. The origins of power systems threats.

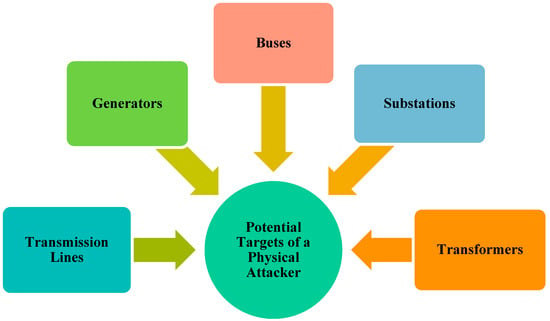
Figure 2. The potential targets of physical attacks on power systems.

On the other hand, power systems operators protect power grids by defending actions before the attack and during the restoration process [5]. For instance, installing Distributed Generation (DG) units and incorporating physical attack impacts on transmission expansion planning problems can be considered as a preventive action before the attack [6]. This is while system reconfiguration and redispatch of energy resources to prevent the loss of loads are required actions during the restoration process and until repair/replacement of targeted TLs [7]. Since power systems cannot be fully protected, the system operators estimate the impacts of physical attacks and minimize them [8]. Vulnerability analysis of power systems is an essential step to counter physical attacks. Vulnerability analysis is estimating the ability of a typical power system to follow up on the changes [9,10].

To mitigate physical attacks and conduct proper actions, estimating the characteristics of potential attacks is important [11]. From a viewpoint, the physical attack may be a single attack [12] or multiple attacks [13]. From another perspective, the attacks may be conducted in one action (during a single time interval) [14] or during a multiple time period [15]. The amount of attack resources (budget) is another factor related to the characteristics of a physical attack [16]. Understanding such characteristics can contribute to mitigating the sabotages of the power system. Different stages of power systems protection against physical attacks are shown in Figure 3.

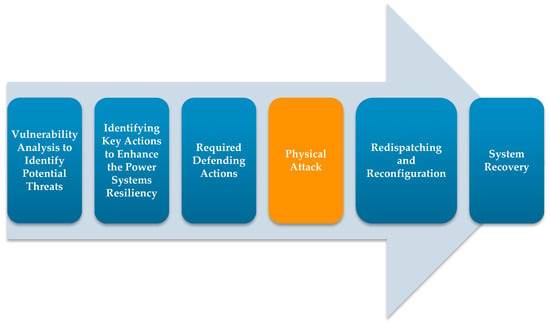
Figure 3. The order of protecting actions against physical attacks on power transmission systems.

The conceptual diagram for power systems protection against physical attacks on power transmission systems is illustrated in Figure 4. According to this figure, the system operator monitors power systems conditions to reduce the loss of loads due to potential physical attacks. The adverse impacts of physical attacks are illustrated in Figure 5 which can be from a loss of load to a blackout.

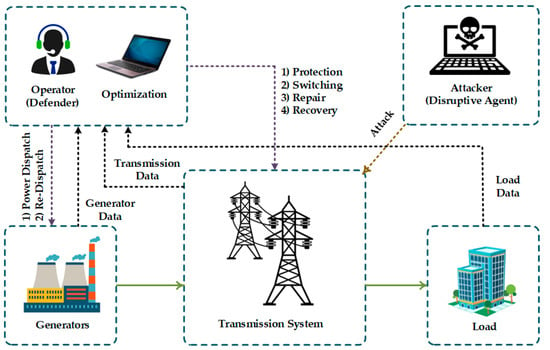
Figure 4. Conceptual diagram for protecting power systems against physical attacks on power transmission systems.

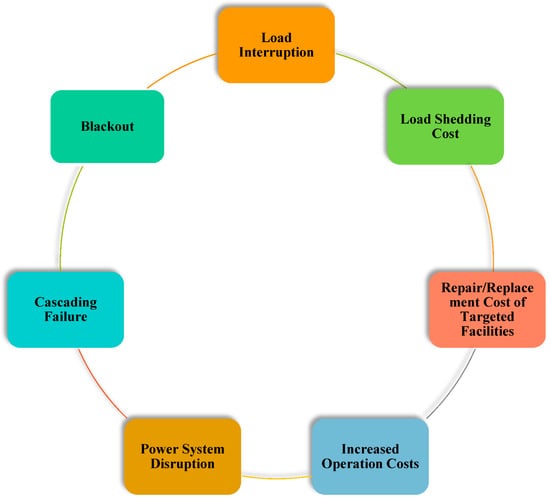
Figure 5. Different implications of physical attacks on power transmission systems.

In the literature, many research studies have been accomplished related to power systems protection against physical attacks on TLs. Various methods have been adopted to mitigate the impacts of physical attacks on power systems. However, research studies have not been limited to test systems. A number of such research studies have focused on the vulnerability of real systems against physical attacks. The North American power transmission grid has been studied in [17] to distinguish its vulnerability against targeting the TLs. A risk-based approach has been proposed to manage the risk associated with the problem. In [18], the possible damages to the North American power grid by multiple attacks on transmission systems with high betweenness and high degree have been highlighted.

This paper deals with the previous research studies in the context of intelligent physical attacks in power systems. The proposed approaches in the literature for power systems protection are categorized and reviewed in detail. The impacts of physical attacks on cascading failures and blackouts, which are critical issues in power systems, are also reviewed. The previous research studies related to the expansion planning of power grids under physical attacks are discussed. In addition, physical attacks in distributed and reconfigurable grids and also the contribution of DG units to enhance the reliability of power systems against physical attacks are discussed. The restoration time of targeted components, as well as the unserved energy cost considered in the literature, are also studied in this paper. The test systems and objective functions and related models considered in the literature are also focused on in this review paper.

The paper is continued as follows. Section 2 discusses the adverse impacts of physical attacks on power systems, including potential load interruptions, the cost of the unserved load, cascading failures, and blackouts. The existing strategies to mitigate physical attacks on power systems are given in Section 3. In this section, probable attack characteristics, uncertainty considerations, power systems restoration after physical attacks, expansion planning, DG units, and reconfigurable systems are outlined as defense strategies against such destructive attacks. Section 4 focuses on defending objective functions against physical attacks on power systems. This section investigates single-objective, multi-objective, competitive, and multi-level optimization models related to power systems protection against physical attacks. Finally, conclusions are provided in Section 5.

2. Adverse Impacts of Physical Attacks on Power Systems

A physical attack on TLs may have different adverse impacts, such as load interruption, imposing unserved energy costs, cascading failures, etc. The system operator should estimate such impacts and optimize the power systems operation based on them. In the following, these adverse impacts are discussed.

2.1. Load Interruptions

The simplest adverse impact of a physical attack on TLs is load interruption. Some research studies [13,19,20,21] have minimized the amount of unserved energy as a single-objective model, whereas some other research studies have considered the unserved load as one of the objectives in a bi-objective [6] or a tri-objective [22] model. In addition, the loss of load in multi-level models has also been accomplished in the literature [23,24]. The methods proposed in the literature to minimize the amount of the unserved load are outlined in Table 1.

Table 1. The approaches used to minimize load interruptions.

References	Methods for Minimzing Load Interruptions
[2]	Lower level of a bi-level optimization model after the attack
[6]	First objective of a bi-objective model of a transmission expansion planning problem
[7]	Lower level of a bi-level optimization model by reconfiguration after the attack
[13,19,20,21]	The objective function was to minimize the amount of total interrupted loads.
[15]	Lower level of a tri-level optimization model during the restoration process
[22]	First objective of a tri-objective model of a transmission expansion planning problem
[23,24]	Upper level of a tri-level model of a transmission expansion planning problem
[25]	First objective of a bi-objective model of a transmission expansion planning problem
[26]	Lower level of a tri-level optimization model during the restoration process
[27]	Upper and lower levels of a tri-level optimization model for before and after the attack
[28]	The first objective of a bi-objective optimization model for a resiliency problem
[29]	The system defender minimizes the load interruption after the attack at the lower level of a tri-level optimization model
[30]	The system defender minimizes the load interruption after the attack at the lower level of a tri-level optimization model
[31]	Lower level of a tri-level optimization model after the attack
[32]	Lower level of a tri-level optimization model after the attack

2.2. Unserved Load Costs

Imposing unserved load costs to power systems is a destructive impact of physical attacks on TLs. In a wide number of research studies, a fixed cost has been considered for lost loads, namely the penalty cost of unserved loads. In this regard, $1000/MWh [33] and $1500/MWh [6,34] have been considered for unmet demands resulting from targeting TLs by physical attacks. The variable cost for the loss of load has been considered in a research study for the value of the lost load, namely $80–120/MWh in [35]. Furthermore, in [36], the unserved load costs for both the power and gas loads have been considered as $1000/MWh and $200/Sm³ (standard cubic metric), respectively. Although, some other research studies [12,14,15,23,24,26,31,37,38] have considered unserved load cost, its value has not been mentioned.

2.3. Cascading Failures

Physical attacks may cause cascading failures in TLs due to the interdependencies in transmission systems [39,40]. In addition, cascading failures are the major reason for blackouts in power systems [41]. In a physical attack, the attacker’s aim may be cascading failures, which is the most destructive result for power systems. The cascading failure impacts due to physical attacks have been studied in a number of previous research studies. In [14,37], a stochastic game model based on game theory has been presented to estimate the cascading failure attacks on transmission systems. The attacker aimed to maximize the unmet load by attacking TLs, whereas the defender aimed to minimize the same objective. A limited number of TLs could be destructed and protected by the attacker and the system defender, respectively. In [13], the cascading failure phenomenon in power systems due to sequential physical attacks on TLs has been studied, in which the aim of the attacker was to maximize the load curtailment. In [42], the vulnerability analysis of smart grids to concurrent physical attacks on transmission systems has been assessed. The multi-attack combinations were discussed from the viewpoint of the loss of generation power and time to reach the steady-state to identify the strongest attack combination (which leads to blackout) An attack combination is a set of TLs, which are concurrently or orderly targeted by the attacker. Furthermore, in [43], a Q-Learning-based approach has been used to evaluate the vulnerability of smart grids to sequential attacks. In this regard, the objective was to identify a minimal attack sequence that causes a critical system failure through cascading outages. The test power systems studied in the previous research studies, from the viewpoint of the cascading failure effect of physical attacks, are listed in Table 2.

Table 2. The detailed highlight of the previous research studies related to occurring the cascading failure phenomenon caused by physical attacks.

References	Studied Cases
[13]	IEEE-39 bus system
[14,37]	IEEE 9-bus system IEEE 30-bus system IEEE 118-bus system
[42]	W&W 6-bus system IEEE 30-bus system
[43]	IEEE 5-bus, IEEE RTS-79, IEEE 300-bus

3. Defending Actions against Physical Attacks

A system operator should overcome the likelihood of physical threat occurrence using the existing methods, such as estimating the characteristics of potential attacks, uncertainty evaluation, restoration of power systems after the attack, considering the impacts of physical attacks on expansion planning problems, installing DG units, and using the line switching to reconfigure them after a physical attack. There are some other approaches to improve the resilience of power systems, such as using the charging capability of electric vehicles in power grids [44,45], timely maintenance of generation units to reduce their failure probability [46], integrating energy systems to increase the energy options [47], demand-side flexibility to supply more important loads during the restoration process [48], and installing energy storage systems to cover critical loads [49]. These existing options are outlined in Figure 6. In the following, such defending actions to overcome the physical attacks are outlined.

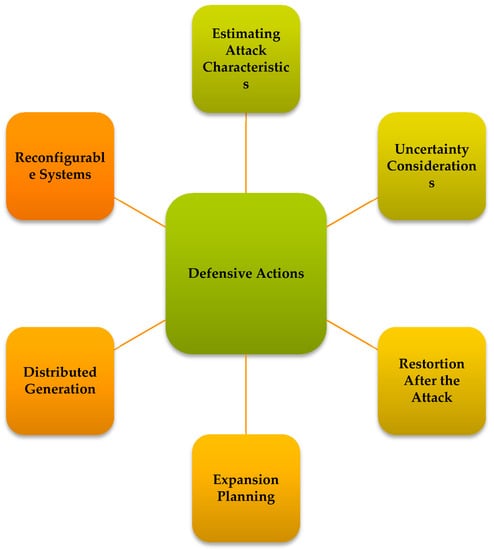
Figure 6. Existing options to protect power transmission systems against physical attacks.

3.1. Detection Methods for Attacks on Power Systems

Different methods have been presented in the literature to detect intentional attacks, including centralized and distributed methods. In centralized detection methods, the collected data from all major components is needed, whereas, in decentralized detection methods, the facilities share information only with their neighbors with physical connections [50]. In [51], a decentralized framework based on the waveform relaxation method has been presented in which power systems were considered as linear time-invariant systems. In this method, detection filters are entirely distributed and only limited knowledge about the system is required. The entire system was sectionalized among dispersed detecting centers, situated at transmission substations. In [52], the main concentration has been on identifying attacks on the Supervisory Control And Data Acquisition (SCADA) system. The proposed framework was based on identifying transient variations in known profiles of probabilistic-dynamical networks with unspecified system conditions. In [53], to overcome the drawback of the existing state estimation method to detect attacks, which was updated minutely, an approach based on the support vector domain has been presented, which was updated secondly. The presented method needed limited information about the characteristics of the attack and was based on dynamic changes of variables to identify affected signals compared to main signals in the normal operating condition. In [54], a bi-level model based on a sensitivity factor of changes in the lines’ flow has been introduced to detect the most damaging and unpredictable attacks. The upper level identified the attack, whereas the lower level determined the optimal alteration in related measurement devices with the lowest budget.

3.2. Estimating Attack Characteristics

To overcome physical attacks, the system operator should estimate the potential attack characteristics such as singularity/multiplicity of physical attacks and multi-period considerations. In the following, these characteristics of physical attacks are discussed.

(a)

Single or Multiple Attacks

The adverse impact of an attack depends on the type of attack from the viewpoint of singularity or multiplicity of such attacks. Table 3 lists the previous research studies based on singularity and multiplicity of physical attacks. As this table shows, various cases exist in the literature from single attack (attack one line) [12,55,56] to multiple attacks on 12 TLs [16,57,58,59]. Some research studies have considered one case for the physical attack, such as 6 lines to be attacked [13,60,61] or 10 lines to be attacked [62], whereas some research studies have considered a range of multiple attacks, such as 5 cases of 1, 2, 3, 4, and 5 lines to be attack [27].

Table 3. Attack types (single or multiple attacks) considered in the previous research studies.

Types of Attack	References
Single attack	[12,55,56]
Multiple attacks	1 and 2 lines [28,35] 1, 2, and 3 lines [30] 1, 2, 3, and 5 lines [23,24] 1–7 lines [27] 1–12 lines [16,57,58,59] 2 lines [14,20,31,37] 2, 3, or 4 lines in each seasonal sample day [6] 2–5 lines [29] 2, 3, 4, and 6 lines [15] 2, 4, and 6 lines [7,63] 2 and 6 lines [33,64] 2, 10, and 28 lines [22] 3 lines [2,32,36,65,66] 3 lines and 5 [42] 4 lines [26,67] 5 lines [21,25] 6 lines [13,60,61] 6, 9, and 15 lines [43] 10 lines [62] 10 and 28 lines [34] 11 lines [38] All lines [19]

(b)

Multi-Period Considerations

Multi-period consideration of power system problems leads to a better analysis of the performance of power systems in different stages of an attack. The system defender should evaluate the system condition and accomplish the required actions in different stages, including pre-attack, intra-attack, and post-attack stages. Despite its importance, few research studies have investigated the multi-period considerations. In some research studies [2,28,30], three time periods have been considered for the physical attack problem when multiple lines were targeted. In [36], four time periods have been considered, in which power and gas lines were considered to be physically attacked. In [43], six, eight, and five time periods for three case studies have been considered and TLs were targeted by the attacker. Twelve time periods during the year have been taken into account in [33], in which the lines were considered to be attacked by the interdiction agent. In [13], fourteen time stages have been considered to study the impact of attacking lines on cascading failure phenomenon. In some other research studies, a 24-h horizon has been considered to analyze the impact of attacking TLs [15,26]. Additionally, in [6], 4 × 24 h (four sample seasonal days) have been considered. The highlights of the above-mentioned research studies are listed in Table 4.

Table 4. The multi-period considerations in the previous research studies related to the understudy context.

References	Number of Time Periods
[2]	3 time periods
[6]	96 time periods (for four seasonal days of the year)
[13]	14 stages
[15]	24 time periods (for hourly periods of the day)
[26]	24 time periods (for hourly periods of the day)
[28]	3 time periods (for base load, peak load, and mean load in a typical day of year)
[30]	3 time periods
[33]	12 time periods (for 12 months of the year)
[36]	4 time periods (each time period was 6 h in a 24-h horizon)
[43]	6, 8, and 5 time period respectively for case studies I, II, and III

3.3. Uncertainty Considerations

A defending problem against physical attacks is associated with different uncertainties. The system operator should estimate the potential physical attacks on the transmission systems by considering uncertainties in the attacker’s actions and system conditions. The existing research studies in the literature have dealt with different uncertainties. Some research studies have considered one type of uncertainty, namely uncertainty in the budget for transmission expansion [6,23,24], defended TLs [20,64], investment cost for energy storage [28], attacker resources [32], attacked TLs [25,34], load demand [43], the total number of TLs to be targeted [57], and the amount of load interruption by the attacker [60].

Several research studies have handled two types of uncertainties, including uncertainty in attack budget and restoration duration [15], uncertainty in defender budget and attacker budget [19,27,36], and uncertainty in the maximum number of TLs to be attacked and maximum number of TLs to be defended [31]. Some other research studies have dealt with three types of uncertainty sources in the physical attack problem in power systems, i.e., uncertainty in the defense budget, defense targets, and investment for DG units allocation [30], uncertainty in location, i.e., bus, of installing control center, the maximum number of TLs to be attacked, and load demand [62], and uncertainty in investment for TL switching, the maximum number of TLs allowed to be switchable, and attack budget [63].

Various types of uncertainties have been taken into consideration in some other research studies [68]. Some studies have dealt with four types of uncertainties, namely uncertainty in the maximum number of TLs that are defended, success probabilities of attacks, defense budget, and load demand [2] and the uncertainty in attack resources, defense resources, cyber-attack resources, and the proportion of post-allocated DG units [29]. In [26], five uncertainty sources, i.e., attack budget, attack time, and maximum number of concurrent attacks (maximum number of TLs to be simultaneously attacked), the total capacity of energy storage to be installed, the maximum number of buses for energy storage installation have been taken into account.

Table 5 lists the highlights of the above-mentioned research studies.

Table 5. The uncertainty considerations in the previous research studies related to physical attacks on power systems.

	Uncertainty Sources
References	Expansion Budget	Defense Targets	Attack Targets	Investment Cost for Energy Storage	Total Capacity of Energy Storage to be Installed	Maximum Number of Buses for Energy Storage Installation	Investment for DG Units Allocation	Load Demand	Attacker Budget (Resources)	Defense Budget (Resources)	Total Number of Lines to be Attacked	Total Number of Lines to be Defended	Level of Load Shed by Attacker	Maximum Number of Lines to be Hidden for Deception	Fortification/Hardening Budget	Restoration Duration	Investment in TLs Switching	Maximum Number of Lines Allowed to be Switchable	Location (Bus) of Control Center	Success Probabilities of Attacks	The Proportion of Post-Allocated DG Units	Attack Time	Maximum Number of Components to be Simultaneously Attacked
[2]								✓		✓		✓								✓
[6,23,24]	✓
[15]									✓							✓
[19,27]									✓						✓
[20,64]		✓
[25,34]			✓
[26]					✓	✓			✓													✓	✓
[28]				✓
[29]									✓	✓											✓
[30]		✓					✓			✓
[31]											✓			✓
[32]									✓
[36]		✓							✓
[43]								✓
[57]											✓
[60]													✓
[62]								✓			✓								✓
[63]									✓								✓	✓

3.4. System Restoration after Physical Attacks

After physical attacks, restoration of the loss of loads is followed by the system operator, especially the load that has a higher load interruption cost, i.e., the value of the lost load. Restoration duration depends on the intensity and location of physical attacks and also the characteristics of the under-attacked power systems. In some research studies, 1 h has been considered for load restoration after a single attack [12] and multiple attacks [20] on TLs. A number of other research studies have considered 2 h for restoring loads after the physical attack [26]. The uncertainty in restoration duration (2, 3, or 4 h) has been considered in [15]. Table 6 highlights the previous research studies from the viewpoint of the restoration duration of loads after the physical attack on the transmission system.

Table 6. Considered restoration duration after the physical attack.

References	Repair Duration
[12,20]	1 h
[26]	2 h
[15]	2, 3, and 4 h
[14,28,37,56,61,64]	Not specified

3.5. Expansion Planning

Expansion planning problems, particularly transmission expansion planning problems, should consider the system’s resilience against different threats, such as physical attacks. The expansion planning of power systems subjected to physical attacks on TLs decreases the system’s vulnerability against such destructive attacks. Some research studies have been accomplished in this context. A bi-objective model has been introduced in [6], in which one objective was energy not supplied, and the other objective was the total annual cost. This cost included the investment cost for new TLs and energy storage, the average cost of unserved loads, and the operation cost of generators and energy storage. In [23,24], a tri-level model for transmission expansion of power systems considering physical attacks on grid lines has been presented. The proposed approach considered the impact of physical attacks on both existing as well as planned TLs for construction. The results showed a significant improvement in the grid vulnerability. In [33], a bi-level model was introduced for generation and transmission expansion planning of power networks considering the level of immunity of TLs against physical attacks. The upper level is related to the attacker with a limited budget to destruct transmission systems to maximize the unserved load, whereas, in the lower level, the operator minimizes the Expected Energy Not Supplied (EENS) and total cost (the total cost included the investment, operation, and EENS costs). In [63], the investment for capacity expansion planning and switch placement are simultaneously optimized to enhance the resilience of reconfigurable power systems against physical attacks. A tri-objective model was introduced, in which the system planner, the attacker, and the operator optimize the total investment, system disruptions, and system performance loss after the attack, respectively.

Additionally, some research studies have incorporated the reinforcement of existing lines in the expansion planning problem. In [22], a tri-objective model has been presented based on expected load shed, expected cost of load shed, and investment cost for TLs and switches. In [25], a bi-objective model based on load shedding minimization (with the importance degree of system loads) as well as investment cost minimization has been introduced under the physical attack consideration with a limited budget of the attacker. Moreover, in [34], a risk-constrained transmission expansion planning problem subjected to the vulnerability aspect of the system against physical attacks on TLs has been introduced. The total costs, including the investment cost and the unserved energy cost, were minimized considering risk management. In Table 7, the previous research studies related to expansion planning of power systems considering system protection against physical attacks are highlighted. As this table shows, sensitivity analysis of investment cost has been accomplished in all the previous research studies.

Table 7. Detailed highlighted of the previous research studies in the context of expansion planning of power systems with physical attack considerations.

References	Generation Expansion	Transmission Expansion	Reinforcing Existing Lines	Switch Installation	Sensitivity Analysis of Investment Cost
[6]		✓			✓
[22]		✓	✓		✓
[23,24]		✓			✓
[25]		✓	✓		✓
[33]	✓	✓			✓
[34]		✓	✓		✓
[63]		✓		✓	✓

3.6. DG Units

Load interruption is another adverse impact of physical attacks. After a physical attack and during the restoration process of unmet loads, DG units, such as renewable energy sources, diesel generators, and energy storage systems, can fully or partially supply the unserved loads. The role/application of DG units in reinforcing power networks against deliberate damages (by enhancing power grids flexibility) has been outlined in the literature. The role of energy storage systems to mitigate the impact of physical attacks has been highlighted in some research studies. A tri-level model was presented in [15], to defend TLs integrated with energy storage systems. The upper level dealt with minimizing the operation costs of generators and energy storage and also the unserved energy cost. The middle level focused on maximizing the unserved energy caused by targeting some TLs from the physical attacker. Finally, the lower level minimizes the unmet energy cost during the restoration process under different restoration duration scenarios. Moreover, in [26], the objective was to determine the optimal sizing of energy storage and improve the system’s resilience against physical attacks on multiple TLs, through a tri-level multi-period model. The impacts of the maximum number of attacked TLs and the maximum number of buses for energy storage installation have been outlined. In [28], investment for energy storage has been focused on using a multi-objective model based on the minimum unserved load and total costs (the total costs included the investment cost for energy storage and production cost of generators) with a sensitivity analysis for the investment cost.

A number of other research studies have focused on using DGs to improve the system’s resilience against physical attacks. In [27], the resilience of reconfigurable diesel-integrated radial distribution systems against physical attacks on TLs through a tri-level model has been improved. On the outer level, the system defender tried to minimize the load shedding by reconfiguration, in the middle level, the attack scenario with the maximum damage was investigated, and on the bottom level, the optimal islanding operation based on the minimum load interruption was investigated. In [29,30], a model has been evaluated for power systems protection against multiple and multi-period physical attacks on TLs during seven time periods after installing diesel generators. The problem was formulated in three levels that were related to the system defender, attacker, and operator. The aims of the levels were allocating a defensive budget on TLs and locating pre-allocated diesel generators, identifying the critical targets based on the maximal unserved demand, and optimal power flow for the healthy part of the power system, respectively. In [36], gas-electric energy systems incorporating the gas storage system were protected against physical attacks on electric and gas lines using a tri-level robust model. The outer level was related to the planner to reinforce the critical components, the middle level dealt with identifying the critical facilities by the attacker, and the bottom level was related to minimizing the total cost including the operation costs and the unserved cost of power and gas loads. Table 8 lists the detailed highlight of the previous research studies.

Table 8. Detailed highlighted of the previous research studies related to the role of DG units in supplying unserved loads after physical attacks.

References	Energy Resources		Energy Storage Systems
	Conventional Generators	Diesel Generator
[6]	✓		✓
[15]	✓		✓
[26]	✓		✓
[27]	✓	✓
[28]	✓		✓
[29]	✓	✓
[30]	✓	✓
[36]	✓		✓

3.7. Reconfigurable Systems

Reconfiguration is an effective way to decrease the unserved energy after a physical attack. Protecting reconfigurable power systems against physical attacks has been investigated in some research studies. In [7], the IEEE RTS system (version 1996) has been considered as a reconfigurable power system subjected to attack on 2, 4, and 6 TLs. A bi-level model was presented to protect the system, in which the attacker tried to impose the maximum loss of load, whereas the system defender tried to retain the load interruption at a minimal level by re-dispatching the resources as well as line switching, i.e., the system reconfiguration. In [27], the resilience of reconfigurable radial distribution systems incorporating diesel generators against physical attacks on TLs has been studied through a tri-level model. The outer level was related to the defender, which minimizes the load interruption by reconfiguration capability of the grid, in the middle level, the attack scenario with the maximum damage was investigated, and in the bottom level, the optimal islanding operation based on the minimal unserved load was searched. IEEE 33-bus and IEEE 94-bus radial distribution systems were tested by attacking 1–5 TLs. Moreover, in [63], a modified version of the IEEE 14-bus system was considered to be planned for transmission expansion and switch installation to enable the reconfigurability of TLs against concurrent physical attacks on six TLs. The sensitivity analysis of the investment cost for TLs and switches was accomplished. Moreover, the uncertainty in attack resources was considered.

4. Objective Functions and Optimization Methods

In the literature, different objective functions have been considered for protecting power systems against physical attacks. Some research studies have introduced single-objective optimization models, such as load interruption [13], cost of unserved loads [37], investment cost for protection power systems’ components [65], and the sum of the operation cost and the cost of the loss of load [38]. A number of other research studies have focused on multi-objective models, including bi-objective [64] and tri-objective [22] models. Different objectives have been considered through multi-objective models in the previous research studies, such as load interruption, unserved load cost, operation cost, investment cost, etc. Multi-level models have been presented in some other research studies including bi-level [58] and multi-level [32] models. Interaction between the system operator and attacker, and the actions of the operator before and after the physical attack have been investigated by bi-level models, whereas tri-level models were introduced to model the interaction among the system planner, attacker, and system operator. Table 9 categorizes the previous research studies from the viewpoint of the objective function.

Table 9. The categorization of the previous research studies from the objective function point of view.

Types of Objective Functions	References
Single-Objective Models	[12,13,19,20,21,37,38,42,43,55,65,66]
Multiple Objectives Models	Bi-objective [6,25,28,34] Tri-objective [22]
Competitive Models (Competitive between the operator and attacker)	[14,16,56,60,63,64,67]
Multiple level	Bi-level [2,7,33,35,57,58,62] Tri-level [15,23,24,26,27,29,30,31,32,36,59,61]

4.1. Single-Objective Models

Some research studies have investigated the physical attack problem with the aim of minimum unserved load for attacking lines [13,19,20,21]. The unserved load cost was the objective of some other research studies to protect power systems against attacking lines [12,37]. In [38], the sum of operation cost and the cost of the loss of load has been considered as the objective function [38]. The investment cost for protection was considered in [65] for TLs protection. The vulnerability of the power network in the case of physical attacks on transmission systems has been investigated in a wide number of research studies [42,43,55,66]. Detailed highlights of the above-mentioned references, which have adopted a single-objective model are presented in Table 10. As this table shows, the optimization models have been solved by optimization algorithms, such as game theory [12,20], Column-and-constrains generation (C&CG) algorithm [21], greedy algorithm [38], or software tools, such as GAMS software [66], MATLAB toolboxes [13,37], Python [19], cascading failure simulators [42,43], and CPLEX Optimization Studio [65]. Most of these research studies have adopted IEEE RTS and IEEE 30-bus test systems for numerical simulation.

Table 10. The detailed highlight of the previous research studies with single-objective optimization.

References	Objective Functions	Defender Budget	Attacker Budget	Optimization Methods	Test Systems
[12]	Minimum expected unserved load cost caused by attacking the critical TL	Protection budget, recovery budget	1 TL was targeted	A game framework	A 5-bus system, IEEE 300-bus system
[13]	Maximum load curtailment by the attacker (physical and load redistribution attack)	Without defense	6 TLs were attacked in every stage	Gurobi solver under YALMIP toolbox of MATLAB (The DC optimal power flow was solved by Matpower6.0)	IEEE 39-bus system
[19]	Minimum total load curtailment	Prevent the load interruption from exceeding a certain threshold	Non-limited	CPLEX solver under Python	IEEE 14-bus System, IEEE RTS 96, IEEE 30-bus system
[20]	Minimizing the maximum expected unserved energy	Defense resource	Maximum 2 targets were targeted	A game theory framework	A 5-bus system, IEEE RTS 96
[21]	Minimum expected load interruption	2 lines were defended	5 lines were targeted as the worst-case attack	C&CG algorithm	IEEE RTS 96
[37]	Maximum total load curtailment cost	Without defense	2 TLs were targeted	MATPOWER toolbox under MATLAB	IEEE 9-bus system, IEEE 30-bus system, IEEE 118-bus system
[38]	Minimum combined cost of generation and unserved loads	15 TLs were hardened	11 TLs were attacked	Greedy algorithm	IEEE RTS 96, IEEE Two Area RTS-96
[42]	Identification of the attack combination with the strongest damage	Without defense	Maximum 3 and 5 TLs were targeted, (respectively for test systems I and II)	DCSIMSEP cascading failure simulator	W&W 6-bus system, IEEE 30-bus system
[43]	Identifying of the minimal attack sequence that caused cascading outages	Without defense	6, 9, and 15 TLs were required for blackout (respectively for case studies I, II, and III)	A cascading failure simulator	IEEE 5-bus system, IEEE RTS 79, IEEE 300-bus system
[55]	Identifying the most vulnerable TL	Without defense	Only 1 TL was targeted	The graph-theoretical (topological) network analysis	IEEE RTS 96
[65]	Minimum investment costs for increasing reliable protections of TLs	Investment based on load shed threshold	Maximum 3 lines were targeted	CPLEX Optimization Studio	IEEE 24-bus system, IEEE 57-bus system
[66]	Maximizing the system risk from the viewpoint of attacker	Without defense	Maximum 3 lines were targeted	CPLEX solver under GAMS	A 6-bus system, IEEE RTS 96

4.2. Multi-Objective Models

Considering more than one objective function can lead to a better system optimization against physical attacks. A number of research studies have introduced bi-objective models to mitigate the implications of physical attacks on TLs [6,25,28,34]. Tri-objective models have been employed in [22] to defend power systems against such attacks. Table 11 lists the detailed highlights of the previous research studies, which have adopted multi-objective models for power systems protection against physical attacks. These optimization models were solved using GAMS software [6,25,28,34] and branch-and-cut software [22].

Table 11. Detailed highlights of the previous research studies with multi-objective optimization.

References	Objective Functions	Defender Budget	Attacker Budget	Methods for Multi-Objective Optimization	Optimization Methods	Test Systems
[6]	(1) Minimum weighted average energy not supplied (2) Minimum total annual investment for new TLs and energy storage systems + cost of unserved loads + operation costs of energy storage systems and generators	Expansion budget for transmission and energy storage (i.e., 6 M$)	Maximum 2, 3, or 4 TLs were attacked in each sample seasonal day	Weighted sum	CPLEX solver under GAMS	IEEE 30-bus system
[22]	(1) Minimum expected loss of load (2) Minimum expected cost of load shed (3) Minimum investment cost	Transmission expansion planning budget	2, 10, and 28 TLs were attacked	Weighted sum	Branch-and-cut software	Two Area IEEE RTS-96
[25]	(1) Minimum load shed associated with each attack plan with its degree of importance (2) Minimum investment cost	Transmission expansion planning budget	Maximum 5 TLs were attacked	Weighted parameter	CPLEX solver under GAMS	The Garver’s six-node test system
[28]	(1) Minimum unserved load (2) Minimum total cost (investment cost for energy storage and production cost of generators)	Investment for energy storage (i.e., 12 M$)	1 or 2 TLs were attacked	Weighted sum	CPLEX solver under GAMS	A 5-bus system
[34]	(1) Minimum risk of vulnerability of the transmission network against physical attacks (2) Minimum investment cost and the cost of nodal weighted average unserved demand	Transmission expansion planning budget	Maximum 10 TLs were targeted	Weighted sum	CPLEX solver under GAMS	The Two Area IEEE RTS-96

4.3. Competitive Models

Competitive models for simulating the competitiveness between the system operator and physical attacker have been focused on in some research studies. In such models, the system operator predicts the behavior of the attacker in targeting TLs. These optimization models were solved using optimization methods, including genetic algorithm [16], game theory [64], Markov decision processes [56] and Spectral graph theory [67], and software tools, including GAMS software [60], MATPOWER toolbox [14], and CPLEX Optimization Studio [63]. Table 12 lists the detailed highlights of these research studies.

Table 12. Detailed highlights of the previous research studies with competitive optimization models.

References	Objective Functions	Defender Budget	Attacker Budget	Methods for Multi-Objective Optimization	Optimization Methods	Test Systems
[14]	Attacker *: Maximum total unserved load cost Operator: Minimum total unserved load cost	1 TL was defended	2 TL was attacked	A zero-sum stochastic game	MATPOWER toolbox	IEEE 9-bus system, IEEE 30-bus system, IEEE 118 bus system
[16]	Attacker: maximum total lost load for a given number of simultaneously destroyed TLs Defender: minimum load interruption under the combination of destroyed TLs (by lines’ switching plan)	Lines’ switching plan	Maximum 12 TLs were targeted	A proposed approach based on genetic algorithm	Genetic algorithm	IEEE RTS 96
[56]	Attacker: maximum unserved load by targeting TLs (even a damaged TL to increase the probability of recovery in a time period Defender: reinforcing healthy TLs and repairing damaged TLs	1 TL was defended	1 TL was attacked	Zero-sum Markov games	Markov decision processes	A 5-bus system, WECC 9-bus system, IEEE 14-bus system
[60]	Attacker: minimum total number of TLs that must be destroyed in order to cause a minimum load interruption level Defender: minimum system load interruption by corrective actions	Redispatch of resources to minimize the lost load	A Specified loss of load level	Karush–Kuhn–Tucker optimality conditions	CPLEX solver under GAMS	A 5-bus system, IEEE RTS 96
[67]	Attacker: minimum attack cost of the maximum damage (finding a small group of TLs that could cause a severe blackout) Defender: minimum total unserved load	Without defense	4 TLs were targeted	Zero-sum game theory	Spectral graph theory	IEEE 30-bus system
[63]	Network planner: minimum total investment cost and operation cost before a physical attack Attacker: maximum system disruptions (i.e., unserved load) System operator: re-dispatching resources through healthy TLs to minimize unserved load after the attack	Investment budget on transmission expansion and switching	Maximum 6 TLs were targeted	Karush-Kuhn-Tucker optimality conditions and C&CG algorithm	CPLEX Optimization Studio	A modified version of IEEE 14-bus system
[64]	Attacker: maximum unserved demand Defender: minimum total unserved load	2–6 units as defense resources	2–6 TLs were attacked	Game theory	Game theory	A 5-bus system

* The bold words show the agent of each objective.

4.4. Multi-Level Models

Some research studies have introduced multi-level models for power systems protection against deliberate outages of TLs caused by an attacker. Bi-level models were presented for interaction between attacker and defender/operator, whereas tri-level models were introduced for interactions among planner, attacker, and operator. In some research studies, bi-level models have been introduced to mitigate the implications of physical attacks on TLs [2,7,33,35,57,58,62]. Tri-level model have been focused on some other research studies for attacking TLs [15,23,24,26,27,29,30,31,32,59,61] and electric and gas lines [36]. Table 13 and Table 14 outline the previous research studies, which have, respectively, adopted bi-level and tri-level models to mitigate the impacts of physical attacks on power systems. As this table shows, these optimization models have been solved by optimization methods, including genetic algorithm [7] and C&CG method [26], and software tools, such as MATLAB toolbox [2,31] and GAMS software [33,57].

Table 13. Detailed highlights of the previous research studies with bi-level optimization models.

References	Objective Functions	Defender Budget	Attacker Budget	Methods for Multi-Level Optimization	Optimization Methods	Test Systems
[2]	Upper level (Attacker) *: identify the critical TLs Lower level (Operator): minimizing the maximum lost load caused by a set of attacks	Maximum 0–9 (Case I) and 1–6 (Case II) TLs in each time period/dimension	Maximum 2–7 (Case I) and 7 (Case II) TLs in each time period	C&CG method	CPLEX solver under MATLAM toolbox	IEEE RTS 79, IEEE 118-bus system
[7]	Upper level (Attacker): conducting the greatest load interruption Lower level (Defender): minimum unserved load by reconfiguration (line switching) and redispatch of available resources	✕	2, 4, and 6 TLs were attacked	Not specified	Genetic algorithm	IEEE RTS 96
[33]	Upper level (Attacker): maximum lost load Lower level (system operator): multi-objective 1: minimum EENS 2: minimum investment cost + operation cost + EENS cost	Generation and transmission expansion budget	2 and 6 TLs were targeted	Weighted sum	CPLEX solver under GAMS	IEEE RTS 96
[35]	Upper level (Attacker): identifying the minimum total number of attacked TLs to cause the damage effect greater than a specified value LS Lower level (Control center): minimum operation cost plus load interruption penalty	Retain the damage effect cost ($/h) in a minimum level i.e., 78,000 $/h (16,539.2$ defense budget was required)	140 units of disruptive cost (1 or 2 TLs were sufficient for damage cost of 78,000 $/h)	Primal-dual interior-point method	Primal-dual interior-point method	IEEE 5-bus system
[57]	Upper level (disruptive agent): maximum load shed for a given number of simultaneously destroyed TLs Lower level (system operator): minimum load interruption under the destroyed TLs	✕	Maximum 12 TLs could be targeted	Benders decomposition	CPLEX solver under GAMS	IEEE RTS 96
[58]	Upper level (Attacker): minimum load interruption Lower-level (system operator): maximum unserved load	✕	Attack budget indexes 5, 12, 6, and 2 (respectively for case studies I, II, III, and IV)	C&CG algorithm	CPLEX Optimization Studio	A 7-bus system, IEEE RTS-96 system, IEEE Three-Area RTS-96 system, IEEE 118-Bus system
[62]	Upper level (attacker): maximum total load interruption Lower level (defender): minimum load shedding + change in the production of generation units	✕	Maximum 10 TLs could be attacked	Karush–Kuhn–Tucker optimality conditions and duality theory	Upper level: The Genetic algorithm Lower level: CPLEX solver under GAMS	IEEE RTS 96

* The bold statements show the agent and layer of each objective.

Table 14. Detailed highlights of the previous research studies with tri-level optimization models.

References	Objective Functions	Defender Budget	Attacker Budget	Methods for Multi-Level Optimization	Optimization Methods	Test Systems
[15]	Upper level (operator before the attack) *: minimum generation fuel cost, energy storage operating cost, and unserved load cost Middle level (disruptive agent): maximum unserved energy Lower level (operator following the attack): minimum unserved energy during the restoration process	✕	Maximum number of concurrent attacks (2, 3, and 4 TLs were attacked)	A duality theorem together with C&CG method	CPLEX solver under GAMS	The WSCC 9-bus system, IEEE 57-bus system
[23,24]	Upper level (network planner): Multi-objective (1) minimum vulnerability of the system (load shed amount) (2) minimum TL construction cost and operation cost (unserved load cost and operating cost of generators) Middle level (disruptive agents): Multi-objective (1) maximum network vulnerability (load interruption)(2) maximum network operation cost Lower level (system operator): minimizing the same objective of attacker	Case I: 60 M$ Case II: 100 M$	Case 1: All TLs could be attacked Case II: maximum 3 TLs could be attacked	Primal-dual transformation	CPLEX solver under GAMS	The Garver network, A modified version of IEEE 30-bus network
[26]	Upper level (system defender): minimum system operation cost, installation cost of energy storage, and lost load cost caused by physical attacks Middle level (Attacker): maximum lost load during restoration process Lower level (Operator): minimum lost load during restoration process	Maximum number of buses for energy storage installation (5 buses)	Maximum number of concurrent attacks (2, 3, and 4 TLs were attacked)	A duality theorem	C&CG method	IEEE 57-bus systems.
[27]	Upper level (system defender): minimum load interruption by reconfiguration Middle level (Attacker): finding the attack scenario with maximum load interruption Lower level (Operator): finding the optimal islanding operation to maintain the minimal load interruption	0–4 and 2–4 TLs were defended (respectively for cases I and II)	1–5 and 3–7 TLs were attacked (respectively for cases I and II)	C&CG method	A proposed algorithm	IEEE-33-bus distribution system, 94-bus distribution system of Taiwan Power Company
[29]	Upper level (system defender): Investment for TLs and DG units Middle level (Attacker): identifying a set of attacked lines with the highest load interruption Lower level (Operator): redispatch of resources and the placement of post-allocated DG units on the healthy part of microgrid with the aim of minimum lost interruption	Maximum 2–5 TLs were defended	Maximum 2–5 TLs were targeted	Karush-Kuhn-Tucker optimality conditions and Nested C&CG method	YALMIP toolbox of MATLAB (CPLEX solver)	IEEE 14-bus distribution system, IEE RTS 79
[30]	Top level (defender): Protecting TLs and allocating DG units before identifying the attack Middle level (attacker): maximum unserved load by disconnecting a set of TLs Bottom level (operator): minimum unserved load by redispatch of resources	Maximum 4 TLs were defended with the defending budgets (TLs budget: 0–6 unit DG: 0–8 units)	3–5 units of attack budget	Customized C&CG technique	CPLEX solver under MATLAB toolbox	IEEE 30-bus distribution system
[31]	Upper level (Defender): minimum power imbalance caused by the most destructive action of attacker Middle level (Attacker): maximum level of system power imbalance Lower level (Defender): minimum unserved energy after deception and attack	3 TLs are protected	2 TLs were targeted	A master-subproblem solution framework using C&CG strategy	CPLEX solver under the YALMIP toolbox of MATLAB	A 6-bus system, IEEE 57-bus system
[32]	Upper level (security personnel): minimum unserved load considering the optimal attack strategy made by the intelligent attackers Middle level: (Attacker): maximum damage (i.e., load interruption) Lower level (operator): minimum unserved load	Maximum 2 and 3 TLs were defended (respectively for case study I and II)	Maximum 3 TLs were targeted	C&CG algorithm	CPLEX solver under MATLAB toolbox	IEEE RTS 79, IEEE 57-bus system
[36]	Upper level (system defender): reinforcing the vulnerable TLs and increasing the system resilience Middle level (attacker): identifying the most threatening attack on the coupled physical infrastructures Lower level (operator): minimum total cost (including unserved power and gas costs and operational costs	Maximum 3 TLs were defensed	Maximum 3 TLs were attacked	Nested C&CG algorithm	YALMIP toolbox of MATLAB	A hybrid 6-bus power system with 7-node gas system
[59]	Upper level (defender): allocating defensive resources to protect TLs before the attack Middle level (attacker): maximum unserved load by disconnecting a set of TLs Lower level (operator): reacts to disruption redispatch of resources	Budget of protecting TLs (4 lines)	Budget of attacking TLs (1–12 lines)	C&CG algorithm	CPLEX solver under GAMS	IEEE RTS 96
[61]	Lower level (defender based on the in-danger elements): minimum load interruption Middle level (attacker based on the defender strategy): maximum load interruption and the recovery time by allocating attack resources Upper level (defender based on the attacked TLs): minimum unserved load through allocating defense resources	Maximum 6 TLs were defended	Maximum 6 TLs were attacked	Dynamic game theory	Lower level: sequential quadratic programming Middle level: sequential quadratic programming Upper level: particle swarm optimization algorithm	A 5-bus system, IEEE 39-bus system

* The bold statements show the agent and layer of each objective.

5. Conclusions

This paper reviews the previous research studies related to existing strategies for protecting power systems against physical attacks on power Transmission Lines (TLs). In this regard, defensive approaches and technologies to overcome the deliberate and destructive actions of attackers were outlined. The adverse impacts of physical attacks, such as causing load interruption, imposing unserved load costs, repair or replacement costs of targeted facilities, and cascading failures (to increase the load interruption or blackout), were discussed. The defensive actions, such as reconfiguration of power TLs, installing energy storage systems and DG units, system restoration after the attack, and defensive-based expansion planning, were outlined. The objective functions, optimization methods, understudied systems, etc., were also reviewed in this paper. The existing gaps in the literature are highlighted as follows:

• The role of different players in a defensive plan against physical attacks has not been well-discussed. Each defensive plan includes several players, such as the system planner, system operator, disruptive agent, customers, policy-maker, power grid, etc.
• Dynamic aspects of power systems, when TLs are targeted by physical attacks, have not been studied.
• The cost of the unserved load has not been well-focused on in the literature of the understudied context.
• Few research studies have considered a practical multi-period time horizon. Most of them have been focused on a single time interval. Multi-period time horizons should be more studied in future research studies.
• Multi-objective models mainly include bi-objective models, whereas, in practical problems, more than two objectives may be needed to be taken into account.
• Considerations of distributed energy resources only have included diesel generators, whereas renewable energy sources will be the main distributed energy systems in the near future.

The above-mentioned gaps are needed to be focused on in future research studies. In future studies, protection strategies against physical attacks on the other components of power systems, including generation units, buses, substations, transformers, circuit breakers, protective devices, etc., will be discussed. Moreover, technical details of security constraints considered in the literature will be reviewed.