To Share or Not to Share? The Optimal Technology Investment in a Virtual Product Supply Chain
Abstract
:1. Introduction
2. Literature Review
2.1. Virtual Products
2.2. Information Asymmetry
2.3. Information Sharing with Signaling
2.4. Agency Pricing Model
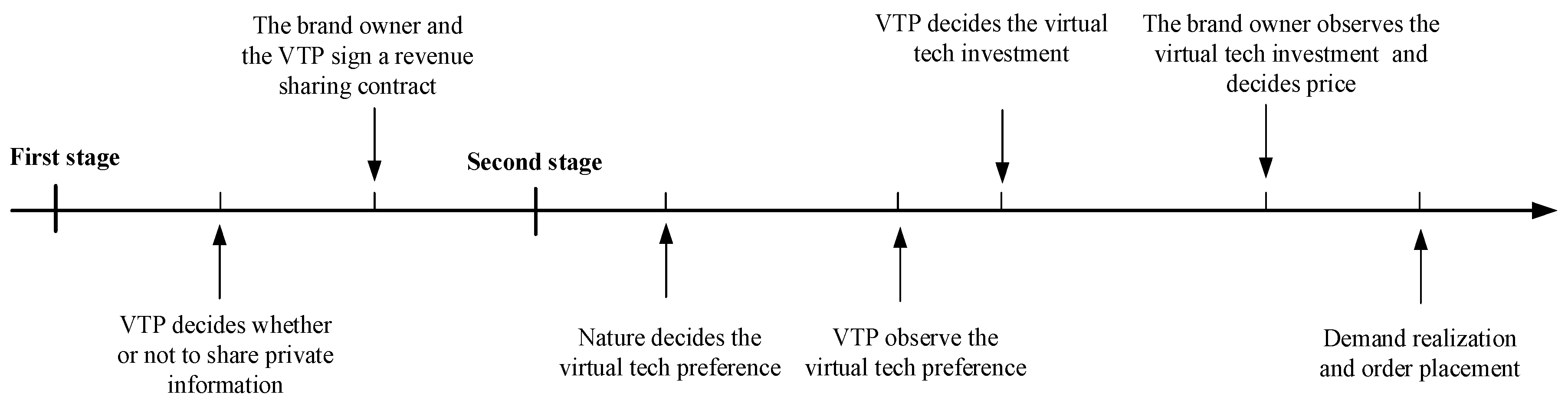
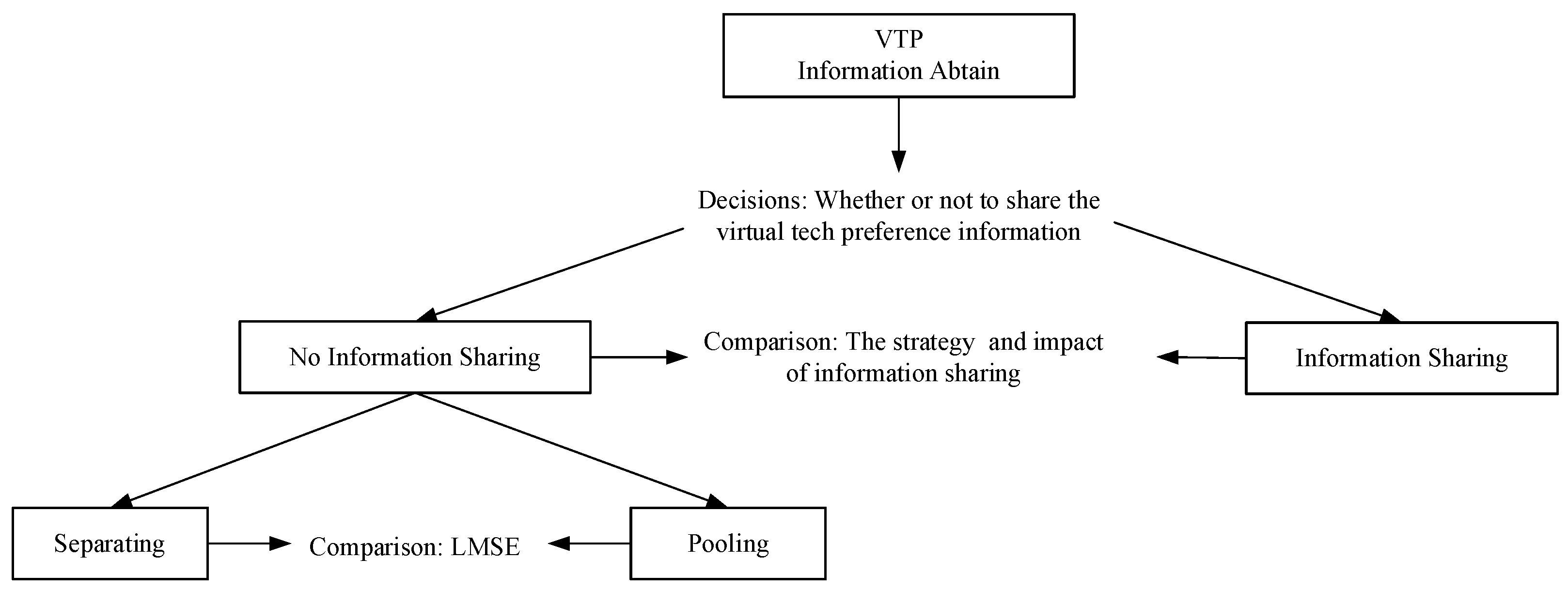
3. Model
4. No Information Sharing
4.1. Separating Equilibrium
- (i)
- The optimal virtual technology investment is;.
- (ii)
- The optimal price is ;.
- (iii)
- The VTP’s and the brand owner’s ex ante expected profit arewhere ,
- (i)
- The virtual technology investmentis decreasing in.
- (ii)
- The retail price of virtual technology product p is decreasing in.
- (iii)
- The degree of upward distortion of virtual investments in h-type platformis decreasing in.
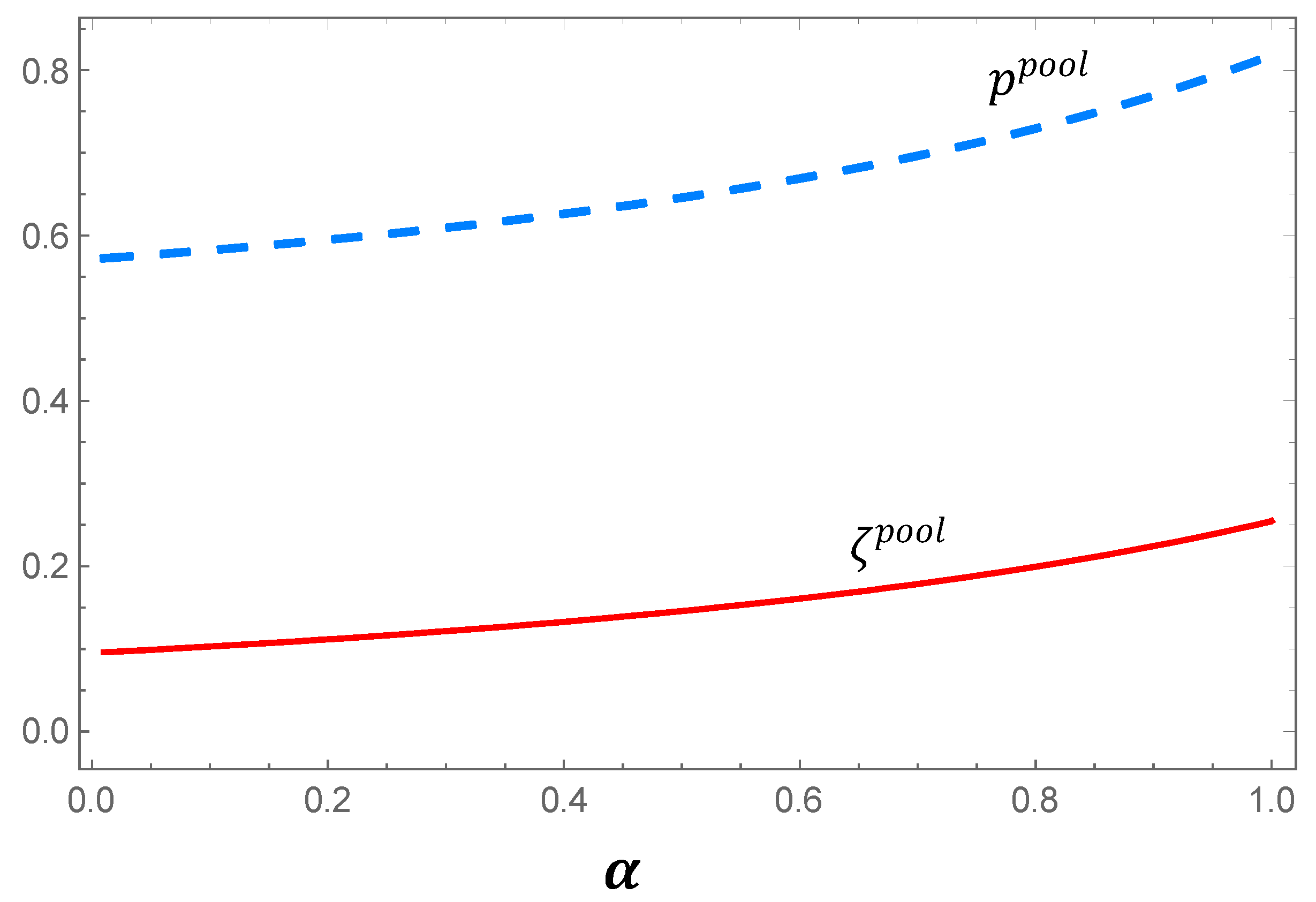
4.2. Pooling Equilibrium
- (i)
- The optimal virtual technology investment is.
- (ii)
- The optimal price is.
- (iii)
- The VTP’s and the brand owner’s ex ante expected profit are
- (i)
- The virtual technology investmentis increasing inand.
- (ii)
- The retail price of virtual technology product p is increasing inand
4.3. The LMSE Equilibrium
- (i)
- if , then the VTP will pool investment at , and the retail price is
- (ii)
- if , then the VTP will separate his investment, and the investment and the retail price are
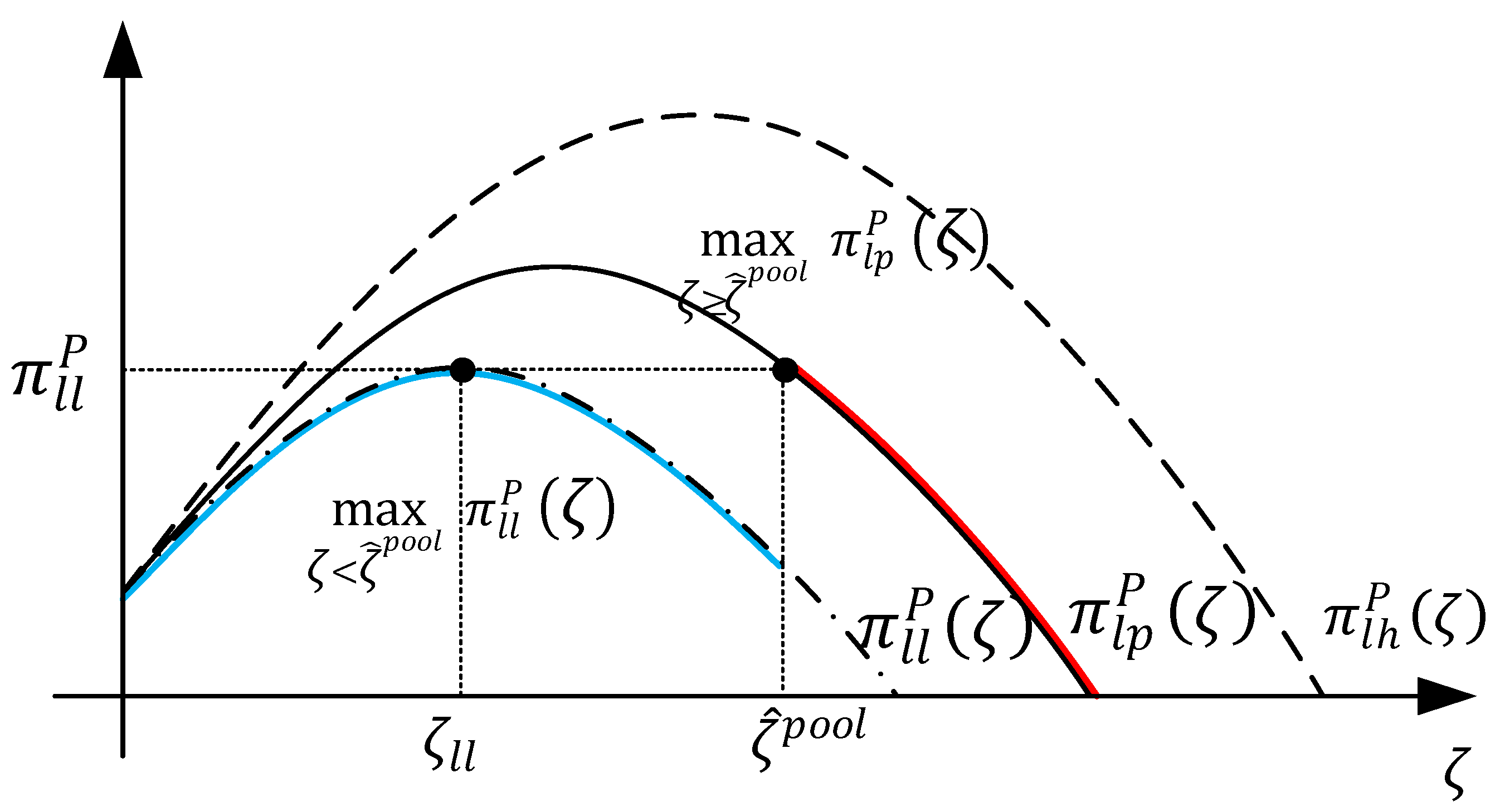
5. Information Sharing
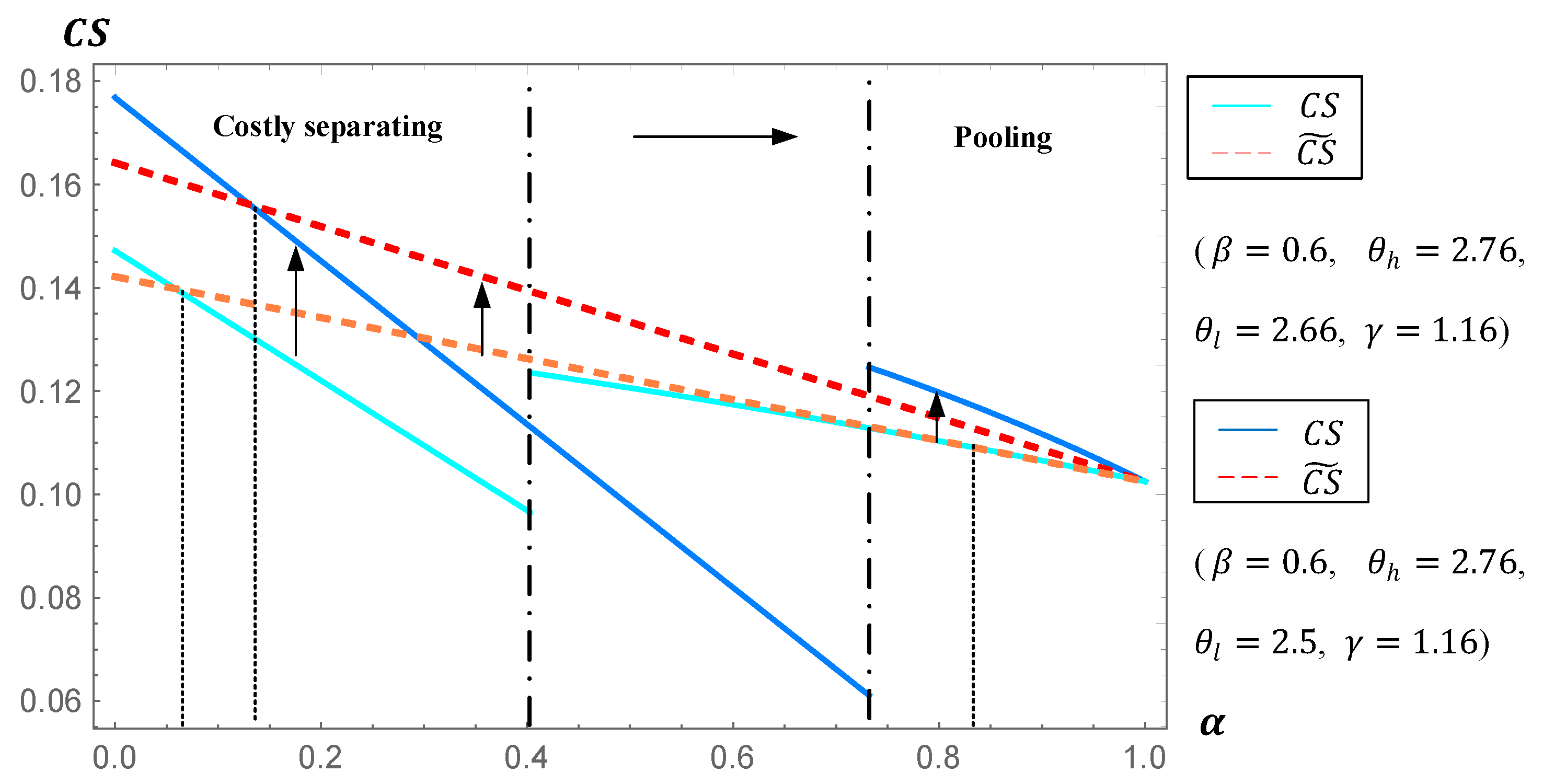
6. Results and Insights
7. Conclusions
- What will be the virtual technology platform’s optimal signaling strategy if it chooses not to share information?
- 2.
- Does a virtual technology platform have an incentive to share its superior preference information with the upstream brand owner?
- 3.
- When can information sharing be a win–win strategy for both the brand owner and the virtual technology platform? How is consumer surplus affected?
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Abbreviations | Description |
|---|---|
| The brand owner | |
| The virtual technology platform | |
| The separating equilibrium case | |
| The pooling equilibrium case | |
| Variables | Description |
| The retail price determined by the brand owner | |
| The virtual technology investment decided by the virtual technology platform | |
| Parameters | Description |
| The scale coefficient the unit cost | |
| Revenue-sharing proportion | |
| The probability of high value virtual technology preference | |
| Preference variability | |
| Functions | Description |
| consumer utility | |
| Market demand | |
| The brand owner’s market demand | |
| The virtual technology platform’s market demand | |
| The brand owner’ profit in the information sharing scenario | |
| The virtual technology platform’ profit in the information sharing scenario | |
| The consumer surplus |


- (i)
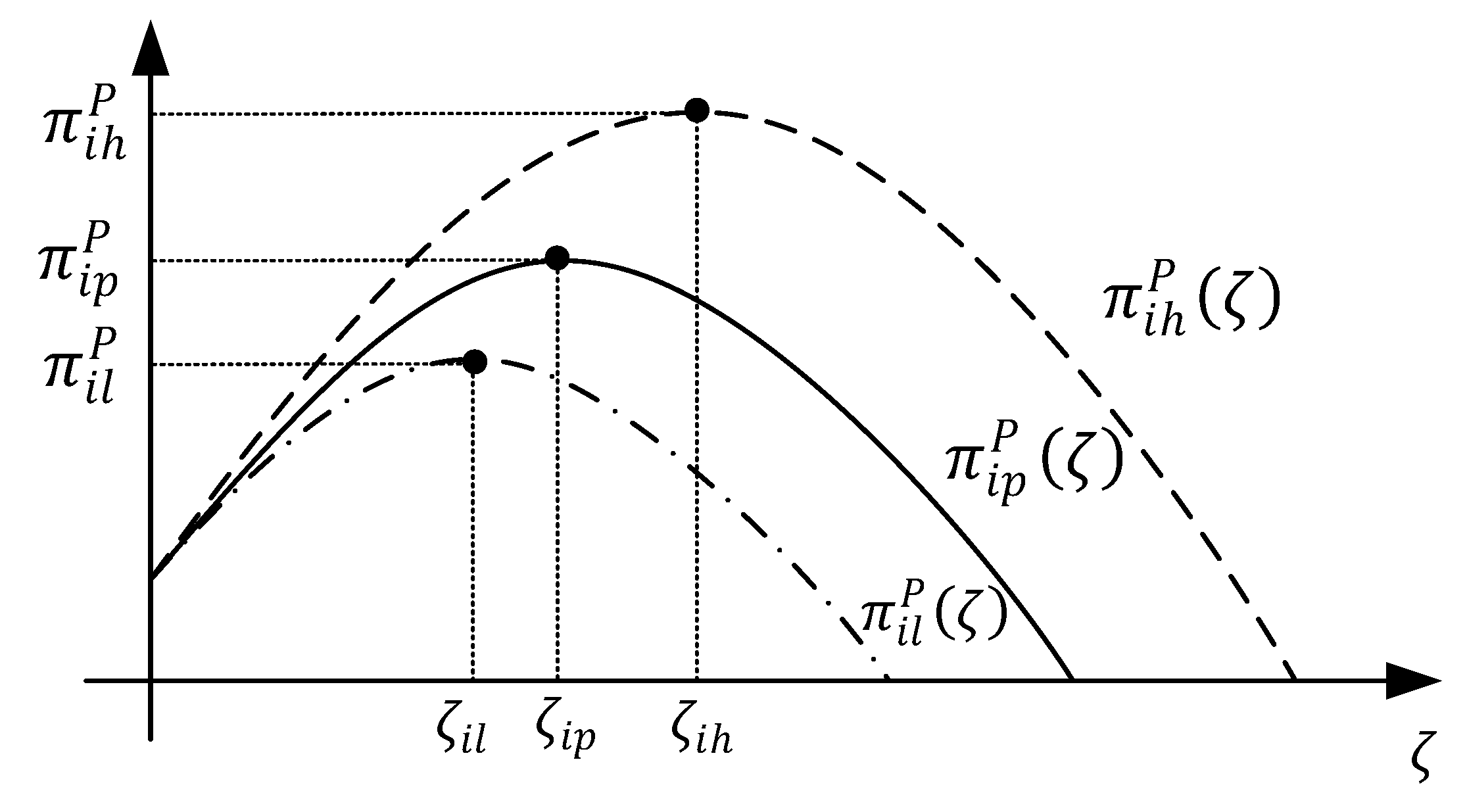
- If , i.e., , then reaches its global maximum value for , i.e., . Condition (A2) is obviously satisfied in this scenario. The illustration is shown in the following figure. Therefore, it is most beneficial for the VTP to set , and then allow _.
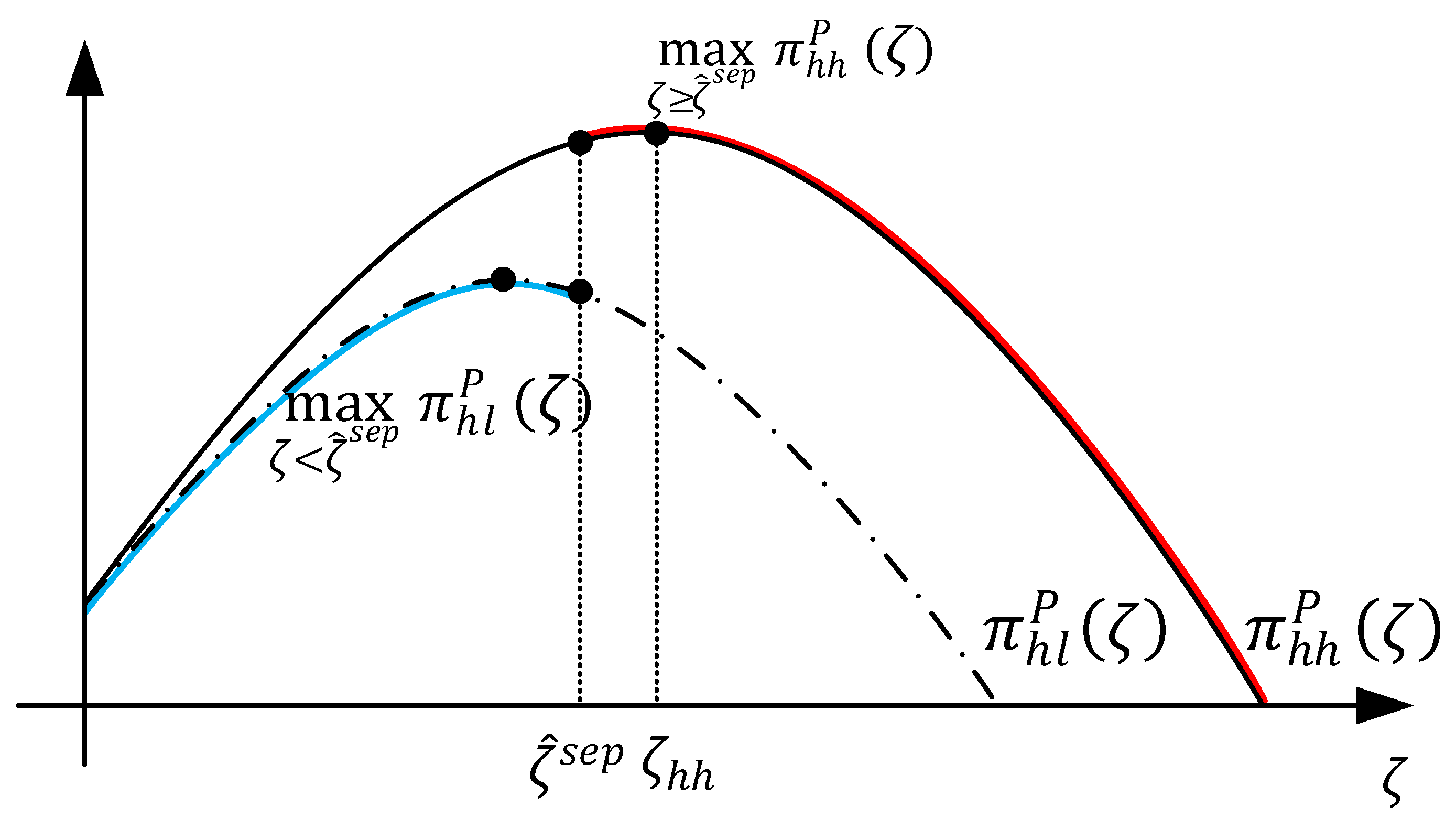
- (i)
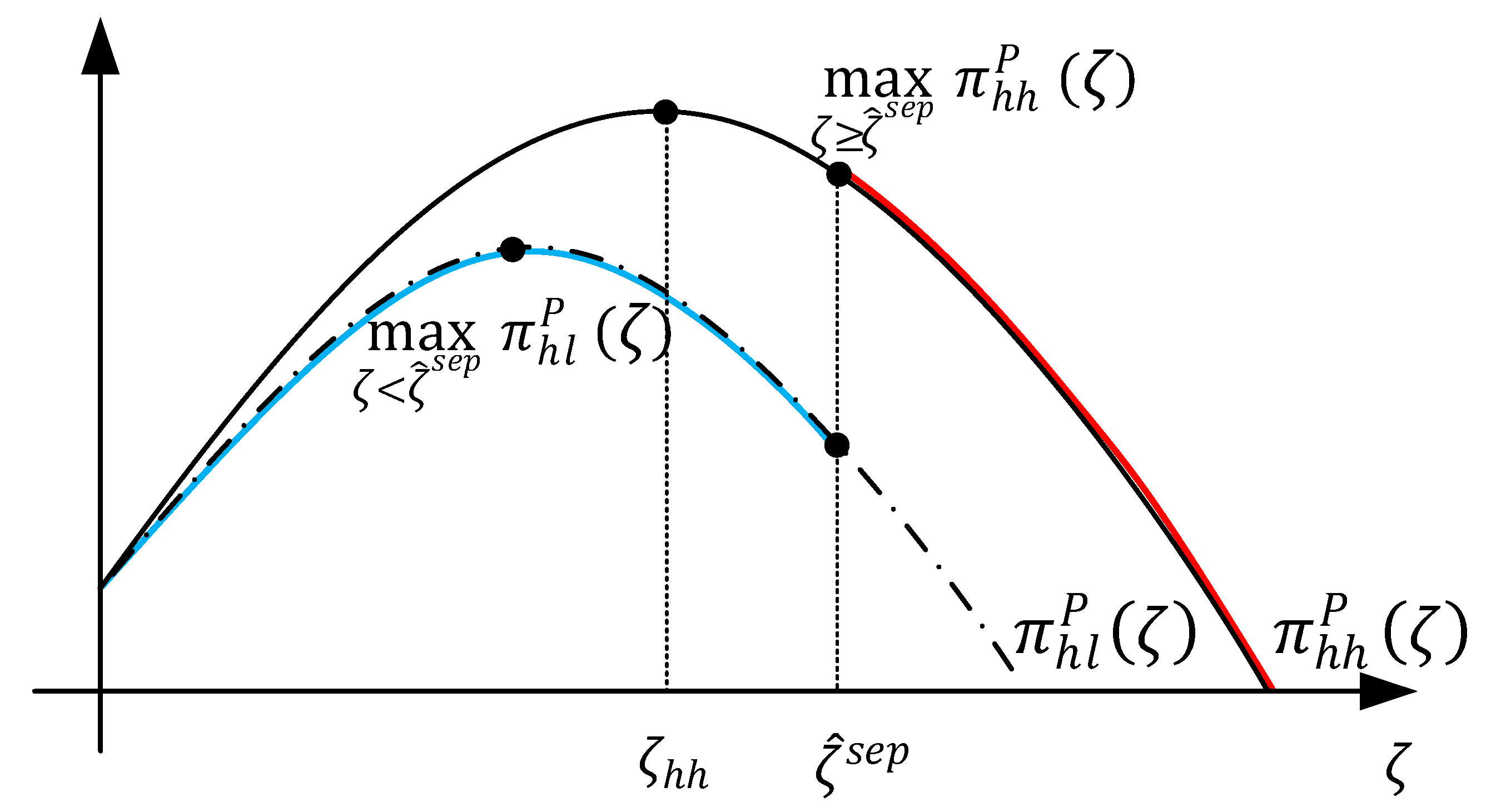
- The blue line indicates that when , the profit of the platform is . The red line represents that when , the profit of the platform is .If , i.e., , then decreases for , and thus . Condition (A2) is more likely to be satisfied with a smaller in this scenario. Then, we can set , and let to obtain the most profitable equilibrium result for the VTP.

References
- Tan, Y. Implications of blockchain-powered marketplace of preowned virtual goods. Prod Oper Manag. 2022, 13657. [Google Scholar] [CrossRef]
- Avinadav, T.; Chernonog, T.; Ben-Zvi, T. The effect of information superiority on a supply chain of virtual products. Int. J. Prod. Econ. 2019, 216, 384–397. [Google Scholar] [CrossRef]
- Kumar, S.; Sethi, S.P. Dynamic pricing and advertising for web content providers. Eur. J. Oper. Res. 2009, 197, 924–944. [Google Scholar] [CrossRef]
- Lu, Q.; Shi, V.; Huang, J. Who benefit from agency model: A strategic analysis of pricing models in distribution channels of physical books and e-books. Eur. J. Oper. Res. 2018, 264, 1074–1091. [Google Scholar] [CrossRef]
- Avinadav, T.; Chernonog, T.; Perlman, Y. The effect of risk sensitivity on a supply chain of mobile applications under a consignment contract with revenue sharing and quality investment. Int. J. Prod. Econ. 2015, 168, 31–40. [Google Scholar] [CrossRef]
- Chernonog, T. Strategic information sharing in online retailing under a consignment contract with revenue sharing. Ann. Oper. Res. 2020, 300, 621–641. [Google Scholar] [CrossRef]
- Avinadav, T.; Chernonog, T.; Khmelnitsky, E. Revenue-sharing between developers of virtual products and platform distributors. Eur. J. Oper. Res. 2021, 290, 927–945. [Google Scholar] [CrossRef]
- Avinadav, T.; Chernonog, T.; Meilijson, I.; Perlman, Y. A consignment contract with revenue sharing between an app developer and a distribution platform. Int. J. Prod. Econ. 2022, 243, 108322. [Google Scholar] [CrossRef]
- Guo, H.; Hao, L.; Mukhopadhyay, T.; Sun, D. Selling Virtual Currency in Digital Games: Implications for Gameplay and Social Welfare. Inf. Syst. Res. 2019, 30, 430–446. [Google Scholar] [CrossRef] [Green Version]
- Royo-Vela, M.; Leszczyński, G.; Velasquez-Serrano, M. Sustainable Value Co-Production and Co-Creation in Virtual Reality: An Exploratory Research on Business-to-Business Interactions. Sustainability 2022, 14, 7754. [Google Scholar] [CrossRef]
- Balasubramanian, S.; Bhattacharya, S.; Krishnan, V.V. Pricing Information Goods: A Strategic Analysis of the Selling and Pay-per-Use Mechanisms. Mark. Sci. 2015, 34, 218–234. [Google Scholar] [CrossRef] [Green Version]
- Sundararajan, A. Nonlinear Pricing of Information Goods. Manag. Sci. 2004, 50, 1660–1673. [Google Scholar] [CrossRef] [Green Version]
- Qu, J.; Meng, C.; Hu, B. Pricing and quality decisions in virtual product supply chains with information sharing. J. Oper. Res. Soc. 2022, 1–17. [Google Scholar] [CrossRef]
- Huang, K.W.; Sundararajan, A. Pricing digital goods: Discontinuous costs and shared infrastructure. Inf. Syst. Res. 2011, 22, 721–738. [Google Scholar] [CrossRef] [Green Version]
- Chernonog, T.; Avinadav, T. Pricing and advertising in a supply chain of perishable products under asymmetric information. Int. J. Prod. Econ. 2019, 209, 249–264. [Google Scholar] [CrossRef]
- Chernonog, T.; Avinadav, T.; Ben-Zvi, T. How to set price and quality in a supply chain of virtual products under bi-criteria and risk consideration. Int. J. Prod. Econ. 2019, 209, 156–163. [Google Scholar] [CrossRef]
- Lariviere, M.A.; Padmanabhan, V. Slotting Allowances and New Product Introductions. Mark. Sci. 1997, 16, 112–128. [Google Scholar] [CrossRef]
- Guo, L.; Iyer, G. Information Acquisition and Sharing in a Vertical Relationship. Mark. Sci. 2010, 29, 483–506. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B.; Tian, L.; Xu, Y.; Zhang, F. To Share or Not to Share: Demand Forecast Sharing in a Distribution Channel. Mark. Sci. 2016, 35, 800–809. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Chen, J. Coordination of information sharing in a supply chain. Int. J. Prod. Econ. 2013, 143, 178–187. [Google Scholar] [CrossRef]
- Shi, C.; Geng, W. To introduce a store brand or not: Roles of market information in supply chains. Transp. Res. E-Log 2021, 150, 102334. [Google Scholar] [CrossRef]
- Guan, X.; Chen, Y.J. The Interplay between Information Acquisition and Quality Disclosure. Prod. Oper. Manag. 2017, 26, 389–408. [Google Scholar] [CrossRef]
- Vosooghidizaji, M.; Taghipour, A.; Canel-Depitre, B. Coordinating corporate social responsibility in a two-level supply chain under bilateral information asymmetry. J. Clean. Prod. 2022, 364, 132627. [Google Scholar] [CrossRef]
- Xu, J.; Wang, P.; Xu, Q. Impact of Information Asymmetry on the Operation of Green Closed-Loop Supply Chain under Government Regulation. Sustainability 2022, 14, 7999. [Google Scholar] [CrossRef]
- Jiang, B.; Jerath, K.; Srinivasan, K. Firm Strategies in the “Mid Tail” of Platform-Based Retailing. Mark. Sci. 2011, 30, 757–775. [Google Scholar] [CrossRef] [Green Version]
- Stock, A.; Balachander, S. The making of a “hot product”: A signaling explanation of marketers’ scarcity strategy. Manag. Sci. 2005, 51, 1181–1192. [Google Scholar] [CrossRef]
- Jiang, B.; Ni, J.; Srinivasan, K. Signaling through pricing by service providers with social preferences. Mark. Sci. 2014, 33, 641–654. [Google Scholar] [CrossRef] [Green Version]
- Jiang, B.; Yang, B. Quality and Pricing Decisions in a Market with Consumer Information Sharing. Manag. Sci. 2019, 65, 272–285. [Google Scholar] [CrossRef]
- Li, Q.; Ding, H.; Shi, T.; Tang., Y. To share or not to share: The optimal advertising effort with asymmetric advertising effectiveness. Ann. Oper. Res. 2020, 1–28. [Google Scholar] [CrossRef]
- Niu, W.; Xia, J.; Shen, H. Decarbonizing investment in a supply chain with information asymmetry under innovation uncertainty. Ann. Oper. Res. 2022, 1–33. [Google Scholar] [CrossRef]
- Xu, M.; Ma, S.; Wang, G. Differential Game Model of Information Sharing among Supply Chain Finance Based on Blockchain Technology. Sustainability 2022, 14, 7139. [Google Scholar] [CrossRef]
- Tan, Y.; Carrillo, J.E. Strategic Analysis of the Agency Model for Digital Goods. Prod. Oper. Manag. 2016, 26, 724–741. [Google Scholar] [CrossRef]
- Hao, L.; Guo, H.; Easley, R.F. A mobile platform’s in-app advertising contract under agency pricing for app sales. Prod. Oper. Manag. 2017, 26, 189–202. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, N.; Ji, X. Reselling or agency selling? The strategic role of live streaming commerce in distribution contract selection. Electron. Commer. Res. 2022, 1–34. [Google Scholar] [CrossRef]
- Bart, N.; Chernonog, T.; Avinadav, T. Revenue sharing contracts in a supply chain: A literature review. IFAC-Pap. OnLine 2019, 52, 1578–1583. [Google Scholar] [CrossRef]
- Li, G.; Tian, L.; Zheng, H. Information sharing in an online marketplace with co-opetitive sellers. Prod. Oper. Manag. 2021, 30, 3713–3734. [Google Scholar] [CrossRef]
- Huang, J.; Leng, M.; Parlar, M. Demand functions in decision modeling: A comprehensive survey and research directions. Decis. Sci. 2013, 44, 557–609. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Li, S.; Zhang, S.; Dai, R. Manufacturer encroachment with quality decision under asymmetric demand information. Eur. J. Oper. Res. 2019, 273, 217–236. [Google Scholar] [CrossRef]
- Guo, X.; Jiang, B. Signaling through price and quality to consumers with fairness concerns. J. Mark. Res. 2016, 53, 988–1000. [Google Scholar] [CrossRef] [Green Version]
- Mailath, G.J.; Okuno-Fujiwara, M.; Postlewaite, A. Belief-based refinements in signalling games. J. Econ. Theory 1993, 60, 241–276. [Google Scholar] [CrossRef]
- Li, Z.; Li, B.; Lan, Y. Contract design on digital platform for the risk-averse retailer with moral hazard: Wholesale price vs two-part tariff. Kybernetes 2017. [Google Scholar] [CrossRef]
- Li, L. Information sharing in a supply chain with horizontal competition. Manag. Sci. 2002, 48, 1196–1212. [Google Scholar] [CrossRef]
- Gal-Or, E.; Geylani, T.; Dukes, A.J. Information sharing in a channel with partially informed retailers. Mark. Sci. 2008, 27, 642–658. [Google Scholar] [CrossRef]





| Brand | Virtual Technology Platform | Virtual Products | Practices |
|---|---|---|---|
| Gucci | Roblox | Bags, Clothes | Gucci and Roblox collaborate to launch the Gucci Garden Archetypes virtual exhibition. |
| Balenciaga | Fortnite | Clothes | Balenciaga cooperates with Fortnite to launch a variety of designs, with virtual clothing and physical products available for purchase. |
| Forever 21 | Roblox | Clothes | Forever 21 built a virtual store on Roblox. |
| Vans | Roblox | Sneakers | Vans launched a skateboard-themed virtual amusement park on Roblox. |
| Nars | Zepeto | Cosmetics | Nars launched a virtual store on Zepeto, selling new makeup products, virtual clothing, and various accessories. |
| Stella Artois | ZED RUN | Game Props | Stella Artois issued a limited number of NFTs and designed a series of breed horses, themed skins, and 3D tracks. |
| Virtual Product | Agency Pricing | Information Asymmetry | Information Sharing | Signaling | |
|---|---|---|---|---|---|
| [27] | √ | √ | |||
| [6] | √ | √ | √ | ||
| [20] | √ | √ | √ | ||
| [19] | √ | √ | √ | ||
| [36] | √ | √ | √ | ||
| [29] | √ | √ | √ | ||
| [24] | √ | √ | √ | ||
| [11] | √ | √ | |||
| [1] | √ | √ | |||
| [8] | √ | √ | √ | ||
| [7] | √ | √ | √ | ||
| [13] | √ | √ | √ | ||
| Our paper | √ | √ | √ | √ | √ |
| Equilibrium | |||
|---|---|---|---|
| Costless separating | |||
| Costly separating and | |||
| Pooling and |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Shen, B.; Cao, Y. To Share or Not to Share? The Optimal Technology Investment in a Virtual Product Supply Chain. Sustainability 2022, 14, 12858. https://doi.org/10.3390/su141912858
Fang Y, Shen B, Cao Y. To Share or Not to Share? The Optimal Technology Investment in a Virtual Product Supply Chain. Sustainability. 2022; 14(19):12858. https://doi.org/10.3390/su141912858
Chicago/Turabian StyleFang, Yuan, Bin Shen, and Yifan Cao. 2022. "To Share or Not to Share? The Optimal Technology Investment in a Virtual Product Supply Chain" Sustainability 14, no. 19: 12858. https://doi.org/10.3390/su141912858
APA StyleFang, Y., Shen, B., & Cao, Y. (2022). To Share or Not to Share? The Optimal Technology Investment in a Virtual Product Supply Chain. Sustainability, 14(19), 12858. https://doi.org/10.3390/su141912858






