Experimental Investigation on Vibration Control of a Suspended Particle-Tuned Liquid Damper
Abstract
:1. Introduction
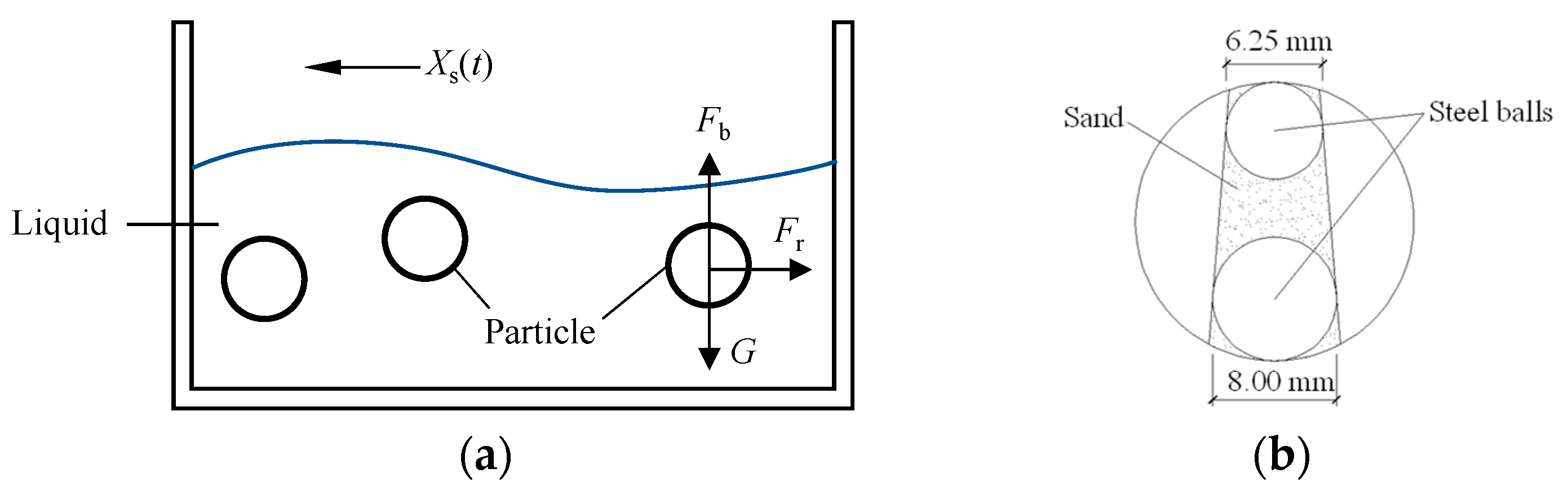
2. Configuration of SPTLD and Experimental Setup
2.1. Configuration of SPTLD
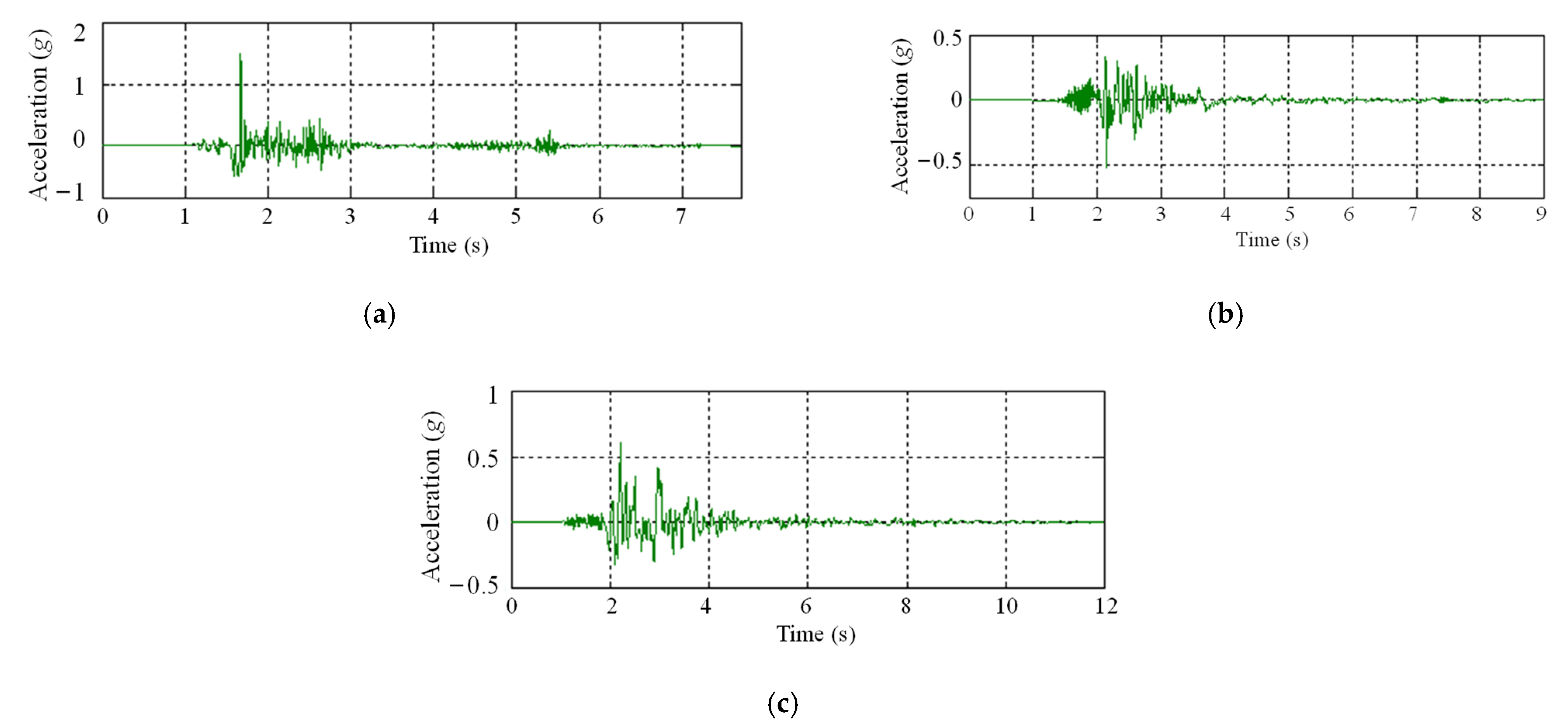
2.2. Experimental Setup
3. Test Results and Discussion
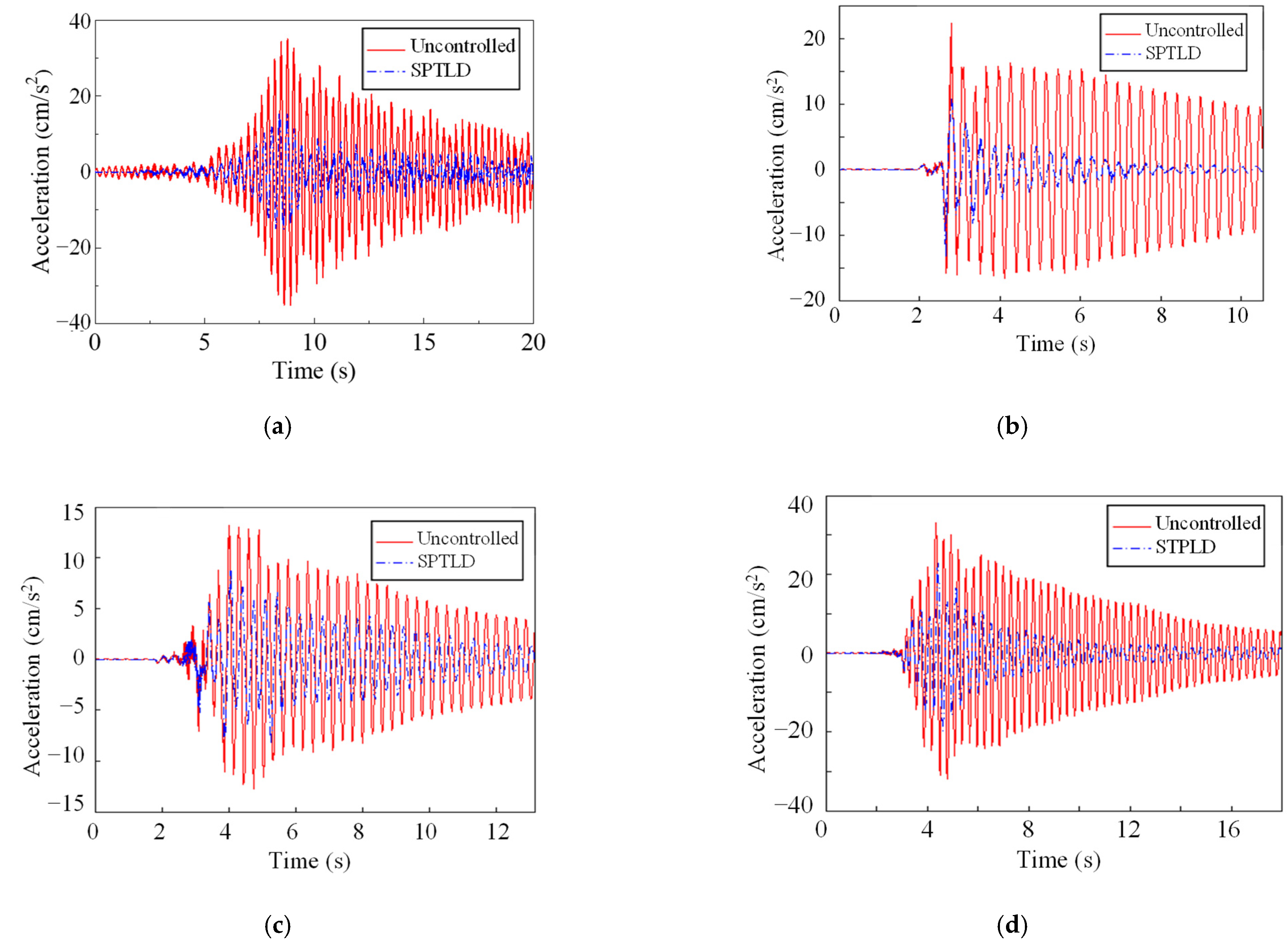
3.1. Control Effectiveness of SPTLD
3.2. Parametric Analysis
3.2.1. Particle Numbers
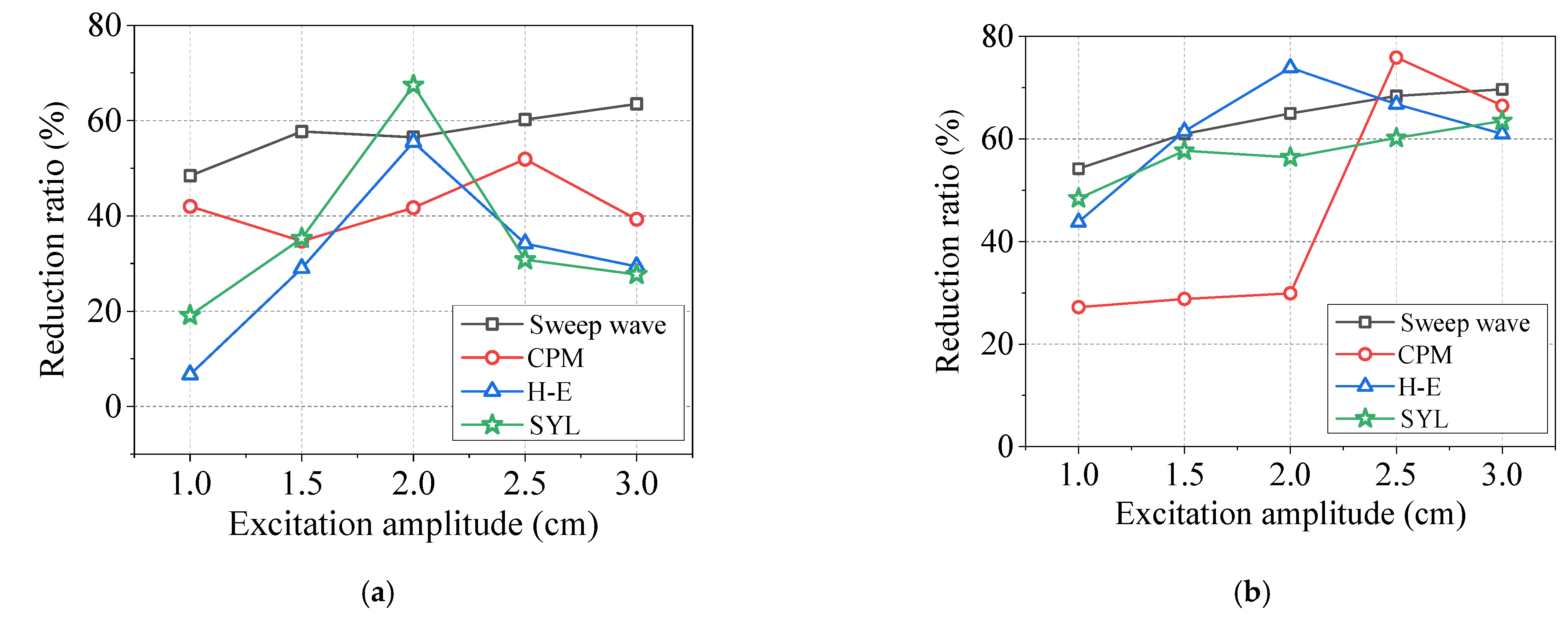
3.2.2. Excitations with Various Amplitudes
3.2.3. Suspended vs. Floating Particles
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, X. Retrofitting Design of Building Structures, 1st ed.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Alajarmeh, O.; Zeng, X.; Aravinthan, T.; Shelley, T.; Alhawamdeh, M.; Mohammed, A.; Nicol, L.; Vedernikov, A.; Safonov, A.; Schubel, P. Compressive behaviour of hollow box pultruded FRP columns with continuous-wound fibres. Thin-Walled Struct. 2021, 168, 108300. [Google Scholar] [CrossRef]
- Vedernikov, A.; Minchenkov, K.; Gusev, S.; Sulimov, A.; Zhou, P.; Li, C.; Xian, G.; Akhatov, I.; Safonov, A. Effects of the Pre-Consolidated Materials Manufacturing Method on the Mechanical Properties of Pultruded Thermoplastic Composites. Polymers 2022, 14, 2246. [Google Scholar] [CrossRef]
- Vedernikov, A.; Tucci, F.; Safonov, A.; Carlone, P.; Gusev, S.; Akhatov, I. Investigation on the Shape Distortions of Pultruded Profiles at Different Pulling Speed. Procedia Manuf. 2020, 47, 1–5. [Google Scholar] [CrossRef]
- Thenozhi, S.; Yu, W. Advances in modeling and vibration control of building structures. Annu. Rev. Control 2013, 37, 346–364. [Google Scholar] [CrossRef]
- El-Khoury, O.; Adeli, H. Recent Advances on Vibration Control of Structures Under Dynamic Loading. Arch. Comput. Methods Eng. 2013, 20, 353–360. [Google Scholar] [CrossRef]
- Konar, T.; Ghosh, A.D. Flow Damping Devices in Tuned Liquid Damper for Structural Vibration Control: A Review. Arch. Comput. Methods Eng. 2021, 28, 2195–2207. [Google Scholar] [CrossRef]
- Tamura, Y.; Fujii, K.; Ohtsuki, T.; Wakahara, T.; Kohsaka, R. Effectiveness of tuned liquid dampers under wind excitation. Eng. Struct. 1995, 17, 609–621. [Google Scholar] [CrossRef]
- Zhang, X.T.; Zhang, R.C.; Xu, Y.L. Analysis on control of flow-induced vibration by tuned liquid damper with crossed tube-like containers. J. Wind Eng. Ind. Aerodyn. 1993, 50, 351–360. [Google Scholar] [CrossRef]
- Zahrai, S.M.; Abbasi, S.; Samali, B.; Vrcelj, Z. Experimental investigation of utilizing TLD with baffles in a scaled down 5-story benchmark building. J. Fluids Struct. 2012, 28, 194–210. [Google Scholar] [CrossRef]
- Fujino, Y.; Sun, L.; Pacheco Benito, M.; Chaiseri, P. Tuned Liquid Damper (TLD) for Suppressing Horizontal Motion of Structures. J. Eng. Mech. 1992, 118, 2017–2030. [Google Scholar] [CrossRef]
- Fu, B.; Jiang, H.; Wu, T. Comparative studies of vibration control effects between structures with particle dampers and tuned liquid dampers using substructure shake table testing methods. Soil Dyn. Earthq. Eng. 2019, 121, 421–435. [Google Scholar] [CrossRef]
- Lu, Z.; Li, K.; Zhou, Y. Comparative Studies on Structures with a Tuned Mass Damper and a Particle Damper. J. Aerosp. Eng. 2018, 31, 04018090. [Google Scholar] [CrossRef]
- Papalou, A.; Strepelias, E. Effectiveness of particle dampers in reducing monuments’ response under dynamic loads. Mech. Adv. Mater. Struct. 2016, 23, 128–135. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, R.; Lu, Z. A particle inerter system for structural seismic response mitigation. J. Frankl. Inst.-Eng. Appl. Math. 2019, 356, 7669–7688. [Google Scholar] [CrossRef]
- Li, S.; Tang, J. On Vibration Suppression and Energy Dissipation Using Tuned Mass Particle Damper. J. Vib. Acoust. 2016, 139, 011008. [Google Scholar] [CrossRef] [Green Version]
- Lu, Z.; Wang, D.; Zhou, Y. Experimental parametric study on wind-induced vibration control of particle tuned mass damper on a benchmark high-rise building. Struct. Des. Tall Spec. Build. 2017, 26, e1359. [Google Scholar] [CrossRef]
- Lu, Z.; Li, K.; Ouyang, Y.; Shan, J. Performance-based optimal design of tuned impact damper for seismically excited nonlinear building, Eng. Struct. 2018, 160, 314–327. [Google Scholar]
- Yan, W.; Xu, W.; Wang, J.; Chen, Y. Experimental Research on the Effects of a Tuned Particle Damper on a Viaduct System under Seismic Loads. J. Bridge Eng. 2014, 19, 04013004. [Google Scholar] [CrossRef]
- Yao, B.; Chen, Q.; Xiang, H.Y.; Gao, X. Experimental and theoretical investigation on dynamic properties of tuned particle damper. Int. J. Mech. Sci. 2014, 80, 122–130. [Google Scholar] [CrossRef]
- Dai, K.; Wang, J.; Mao, R.; Lu, Z.; Chen, S.-E. Experimental investigation on dynamic characterization and seismic control performance of a TLPD system. Struct. Des. Tall Spec. Build. 2017, 26, e1350. [Google Scholar] [CrossRef]
- Ren, H.; Fan, Q.; Lu, Z. Shaking Table Test and Parameter Analysis on Vibration Control of a New Damping System (PDAL). Buildings 2022, 12, 896. [Google Scholar] [CrossRef]
- Shad, H.; Adnan Azlan, B.; Vafaei, M.; Behbahani Hamid, P.; Oladimeji Abdulkareem, M. Experimental study on TLDs equipped with an upper mounted baffle. Smart Struct. Syst. 2018, 21, 37–51. [Google Scholar]



| Case | Acceleration Response (μg) | Reduction Ratio (%) | ||
|---|---|---|---|---|
| Peak | RMS | ηp | ηr | |
| Uncontrolled | 795.3 | 422.5 | / | / |
| TLD | 606.7 | 306.2 | 23.7 | 27.5 |
| SPTLD | 583.0 | 262.4 | 26.7 | 37.9 |
| Number of Particles | μp (%) | Acceleration Response without Control (μg) | Acceleration Response under SPTLD (μg) | Reduction Ratio (%) | |||
|---|---|---|---|---|---|---|---|
| Peak | RMS | Peak | RMS | ηp | ηr | ||
| 1 | 0.91 | 795.3 | 422.5 | 664.3 | 351.4 | 16.5 | 16.8 |
| 2 | 1.82 | 586.1 | 250.7 | 26.3 | 40.7 | ||
| 3 | 2.73 | 583.0 | 262.4 | 26.7 | 37.9 | ||
| 4 | 3.64 | 620.2 | 264.2 | 22.0 | 37.5 | ||
| 5 | 4.55 | 646.4 | 287.4 | 18.7 | 32.0 | ||
| 6 | 5.46 | 653.8 | 300.6 | 17.8 | 28.9 | ||
| 7 | 6.37 | 668.0 | 321.8 | 16.0 | 23.8 | ||
| 8 | 7.28 | 678.6 | 323.1 | 14.7 | 23.5 | ||
| Reduction Ratio (%) | Sweep Wave | CPM Wave | H-E Wave | SYL Wave | |||||
|---|---|---|---|---|---|---|---|---|---|
| Amplitude of the Excitation (cm) | ηp | ηr | ηp | ηr | ηp | ηr | ηp | ηr | |
| 1.0 | 48.4 | 54.2 | 42.0 | 27.2 | 6.7 | 43.8 | 19.1 | 48.4 | |
| 1.5 | 57.7 | 60.9 | 34.7 | 28.8 | 29.0 | 61.5 | 35.3 | 57.7 | |
| 2.0 | 56.5 | 65.0 | 41.7 | 29.9 | 55.5 | 73.9 | 67.4 | 56.4 | |
| 2.5 | 60.2 | 68.4 | 51.9 | 75.9 | 34.2 | 66.8 | 30.8 | 60.2 | |
| 3.0 | 63.5 | 69.7 | 39.3 | 66.5 | 29.4 | 61.0 | 27.7 | 63.5 | |
| Wave | Excitation Amplitude (cm) | Damper | Acceleration Response under SPTLD (μg) | Reduction Ratio (%) | ||
|---|---|---|---|---|---|---|
| Peak | RMS | ηp | ηr | |||
| Harmonic excitation | 1.7 | FPTLD-12 | 589.5 | 266.4 | 25.9 | 36.9 |
| SPTLD-2 | 586.1 | 250.7 | 26.3 | 40.7 | ||
| Sweep wave | 2.0 | FPTLD-12 | 2058.5 | 487.6 | 41.2 | 49.7 |
| SPTLD-2 | 1597.1 | 349.7 | 54.3 | 63.9 | ||
| CPM wave | 2.0 | FPTLD-12 | 2009.3 | 915.6 | 43.3 | 32.5 |
| SPTLD-2 | 1941.9 | 891.3 | 45.2 | 34.3 | ||
| H-E wave | 2.0 | FPTLD-12 | 673.1 | 156.4 | 47.8 | 72.1 |
| SPTLD-2 | 661.9 | 137.9 | 48.7 | 75.4 | ||
| SYL wave | 2.0 | FPTLD-12 | 591.4 | 162.8 | 65.8 | 59.1 |
| SPTLD-2 | 571.2 | 141.9 | 66.9 | 64.3 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Zhou, M.; Ren, H. Experimental Investigation on Vibration Control of a Suspended Particle-Tuned Liquid Damper. Sustainability 2022, 14, 13085. https://doi.org/10.3390/su142013085
Lu Z, Zhou M, Ren H. Experimental Investigation on Vibration Control of a Suspended Particle-Tuned Liquid Damper. Sustainability. 2022; 14(20):13085. https://doi.org/10.3390/su142013085
Chicago/Turabian StyleLu, Zheng, Mengyao Zhou, and Hongmei Ren. 2022. "Experimental Investigation on Vibration Control of a Suspended Particle-Tuned Liquid Damper" Sustainability 14, no. 20: 13085. https://doi.org/10.3390/su142013085
APA StyleLu, Z., Zhou, M., & Ren, H. (2022). Experimental Investigation on Vibration Control of a Suspended Particle-Tuned Liquid Damper. Sustainability, 14(20), 13085. https://doi.org/10.3390/su142013085






