Thermodynamic Analysis of a New Combined Cooling and Power System Coupled by the Kalina Cycle and Ammonia–Water Absorption Refrigeration Cycle
Abstract
1. Introduction
2. System Description
3. Mathematical Modeling
- (1)
- All flows in the equipment reach a steady state;
- (2)
- There is no heat transfer between the equipment and the environment; that is, the heat loss of the equipment is neglected;
- (3)
- The pressure dropping in the heat exchangers and pipelines are neglected;
- (4)
- The two streams of working fluids at the outlet of the separator are saturated ammonia-rich vapor and saturated ammonia-poor solution, respectively;
- (5)
- The two streams of working fluids at the outlet of the rectification column are saturated pure ammonia vapor and saturated ammonia-weak solution, respectively;
- (6)
- In the condenser, the hot fluid is cooled to saturated liquid state by the cold fluid;
- (7)
- In the evaporator, the cold fluid absorbs heat and evaporates to saturated vapor state;
- (8)
- The processes of fluids throttled by the valves are isenthalpic;
- (9)
- The pump and the turbine are given a specific isentropic efficiency, respectively.
3.1. Mathematical Model of System Equipment
3.2. Performance Indicator of System
4. Results and Discussion
4.1. Calculation Results of System Design Conditions
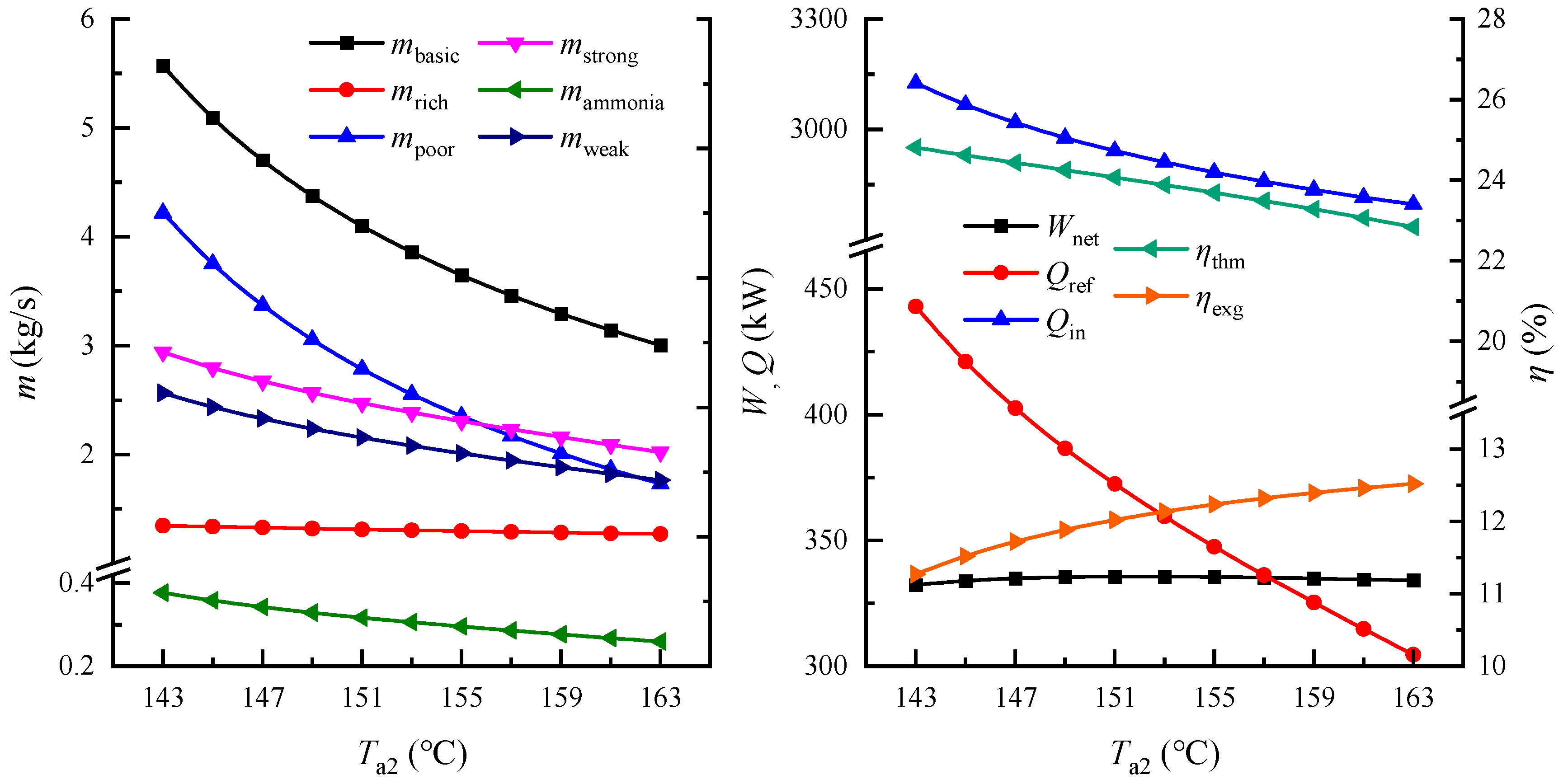
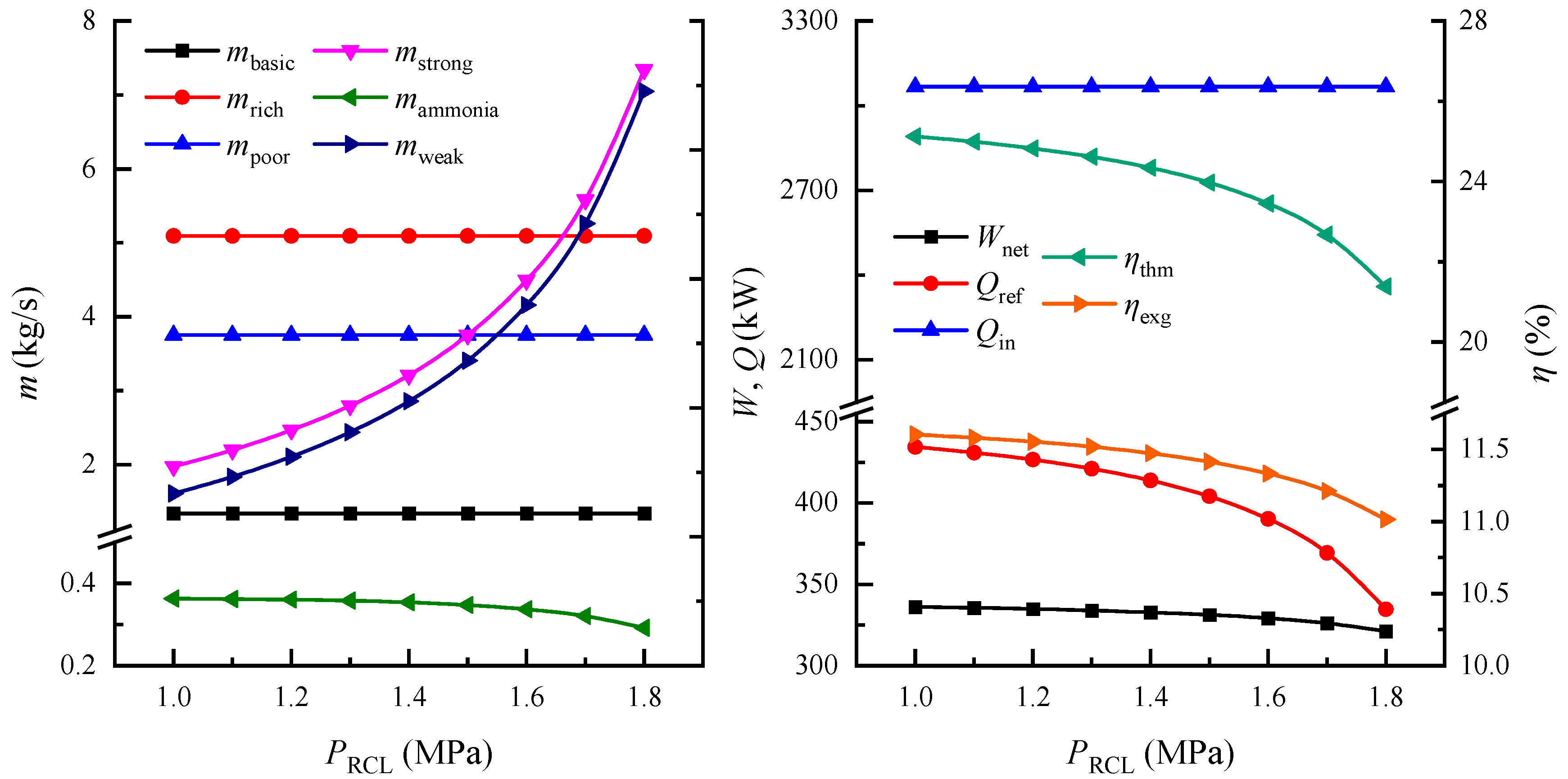
4.2. Thermodynamic Parameter Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| exg: exergy | |
| e: Specific exergy(kW·kg−1) | g: waste gas |
| h: Specific enthalpy (kJ·kg−1) | in: input |
| m: Mass flux (kg·s−1) | net: net value |
| P: Pressure (kPa) | p-I: pump-I |
| Q: Quantity of heat flow (kW) | p-Ⅱ: pump-Ⅱ |
| s: Specific entropy (kJ· kg−1 K−1) | poor: ammonia-poor solution |
| T: Temperature (°C) | RCL: rectification column |
| W: Power input/output (kW) | ref: refrigeration |
| X: Ammonia concentration (%) | rich: ammonia-rich vapor |
| Greek symbol | s: isentropic |
| η: Efficiency | strong: ammonia-strong solution |
| Subscript | tb: turbine |
| ammo: pure ammonia | thm: thermal |
| basic: ammonia–water basic solution | weak: ammonia-weak solution |
| c: cooling water | 0: environmental state |
| EVP: evaporation | g1-g3,a1-a12,b1-b12,c1-c6,d1-d2: state point |
References
- Du, Y.; Han, P.; Qiang, X.; Hao, M.; Long, Y.; Zhao, P.; Dai, Y. Off-design performance analysis of a combined cooling and power system driven by low-grade heat source. Energy Convers. Manag. 2018, 159, 327–341. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Zhao, P.; Dai, Y. Thermodynamic analysis of a new combined cooling and power system using ammonia–water mixture. Energy Convers. Manag. 2016, 117, 335–342. [Google Scholar] [CrossRef]
- Cao, L.; Wang, J.; Chen, L.; Lou, J.; Wang, J.; Dai, Y. Thermoeconomic Analysis and Multi-Objective Optimization of a Combined Cooling and Power System Using Ammonia-Water Mixture: Case Study. J. Energy Eng. 2018, 144, 05018001. [Google Scholar] [CrossRef]
- Hua, J.; Chen, Y.; Wang, Y.; Roskilly, A.P. Thermodynamic analysis of ammonia–water power/chilling cogeneration cycle with low-grade waste heat. Appl. Therm. Eng. 2014, 64, 483–490. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, Y.; Wu, J.; Zhu, Z. Thermodynamic analysis on a modified Kalina cycle with parallel cogeneration of power and refrigeration. Energy Convers. Manag. 2018, 163, 1–12. [Google Scholar] [CrossRef]
- Shankar, R.; Srinivas, T. Coupled cycle with Kalina cycle system and vapor absorption refrigeration. Proc. Inst. Mech. Eng. Part A J. Power Energy 2014, 228, 953–964. [Google Scholar] [CrossRef]
- Shankar, R.; Srinivas, T. Performance investigation of Kalina cooling cogeneration cycles. Int. J. Refrig. 2018, 86, 163–185. [Google Scholar] [CrossRef]
- Shankar, R.; Rivera, W. Investigation of new cooling cogeneration cycle using NH3H2O mixture. Int. J. Refrig. 2020, 114, 88–97. [Google Scholar] [CrossRef]
- Qu, W.; Hong, H.; Su, B.; Tang, S.; Jin, H. A concentrating photovoltaic/Kalina cycle coupled with absorption chiller. Appl. Energy 2018, 224, 481–493. [Google Scholar] [CrossRef]
- Cao, L.; Lou, J.; Wang, J.; Dai, Y. Exergy analysis and optimization of a combined cooling and power system driven by geothermal energy for ice-making and hydrogen production. Energy Convers. Manag. 2018, 174, 886–896. [Google Scholar] [CrossRef]
- Feng, C.; Yu, Z.; Liang, W.; Wang, D. Energetic, exergetic and economic analysis and multi-objective optimization of two novel ammonia-water absorption combined power and cooling cycles driven by low-grade heat sources. Energy Convers. Manag. 2021, 248, 114781. [Google Scholar] [CrossRef]
- Rashidi, J.; Ifaei, P.; Esfahani, I.J.; Ataei, A.; Yoo, C.K. Thermodynamic and economic studies of two new high efficient power-cooling cogeneration systems based on Kalina and absorption refrigeration cycles. Energy Convers. Manag. 2016, 127, 170–186. [Google Scholar] [CrossRef]
- Higa, M.; Yamamoto, E.Y.; Oliveira, J.C.D.d.; Conceição, W.A.S. Evaluation of the integration of an ammonia-water power cycle in an absorption refrigeration system of an industrial plant. Energy Convers. Manag. 2018, 178, 265–276. [Google Scholar] [CrossRef]
- Nedaei, N.; Hamrang, F.; Farshi, L.G. Design and 3E analysis of a hybrid power plant integrated with a single-effect absorption chiller driven by a heliostat field: A case study for Doha, Qatar. Energy 2022, 239, 122415. [Google Scholar] [CrossRef]
- Cao, L.; Wang, J.; Wang, H.; Zhao, P.; Dai, Y. Thermodynamic analysis of a Kalina-based combined cooling and power cycle driven by low-grade heat source. Appl. Therm. Eng. 2017, 111, 8–19. [Google Scholar] [CrossRef]
- Kim, K.H. Thermodynamic Analysis of Kalina Based Power and Cooling Cogeneration Cycle Employed Once Through Configuration. Energies 2019, 12, 1536. [Google Scholar] [CrossRef]
- Dhahad, H.A.; Hussen, H.M.; Nguyen, P.T.; Ghaebi, H.; Ashraf, M.A. Thermodynamic and thermoeconomic analysis of innovative integration of Kalina and absorption refrigeration cycles for simultaneously cooling and power generation. Energy Convers. Manag. 2020, 203, 112241. [Google Scholar] [CrossRef]
- Abam, F.I.; Briggs, T.A.; Diemuodeke, O.E.; Ekwe, E.B.; Ujoatuonu, K.N.; Isaac, J.; Ndukwu, M.C. Thermodynamic and economic analysis of a Kalina system with integrated lithium-bromide-absorption cycle for power and cooling production. Energy Rep. 2020, 6, 1992–2005. [Google Scholar] [CrossRef]
- Ouyang, T.; Wang, Z.; Wang, G.; Zhao, Z.; Xie, S.; Li, X. Advanced thermo-economic scheme and multi-objective optimization for exploiting the waste heat potentiality of marine natural gas engine. Energy 2021, 236, 121440. [Google Scholar] [CrossRef]
- Yadav, S.K.; Singh, O. Parametric study of solid oxide fuel cell based novel power and desalination system. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 3785–3802. [Google Scholar] [CrossRef]
- Almatrafi, E.; Khaliq, A.; Alquthami, T. Thermodynamic investigation of a novel cooling-power cogeneration system driven by solar energy. Int. J. Refrig. 2022, 138, 244–258. [Google Scholar] [CrossRef]
- Yu, Z.; Han, J.; Liu, H.; Zhao, H. Theoretical study on a novel ammonia–water cogeneration system with adjustable cooling to power ratios. Appl. Energy 2014, 122, 53–61. [Google Scholar] [CrossRef]
- Kumar, G.P.; Saravanan, R.; Coronas, A. Experimental studies on combined cooling and power system driven by low-grade heat sources. Energy 2017, 128, 801–812. [Google Scholar] [CrossRef]
- Mahmoudi, S.M.S.; Kordlar, M.A. A new flexible geothermal based cogeneration system producing power and refrigeration. Renew. Energy 2018, 123, 499–512. [Google Scholar] [CrossRef]
- Kordlar, M.A.; Mahmoudi, S.M.S.; Talati, F.; Yari, M.; Mosaffa, A.H. A new flexible geothermal based cogeneration system producing power and refrigeration, part two: The influence of ambient temperature. Renew. Energy 2019, 134, 875–887. [Google Scholar] [CrossRef]
- Pacheco-Reyes, A.; Rivera, W. Thermodynamic cycles for the simultaneous production of power and cooling: A comprehensive review. Int. J. Energy Res. 2021, 45, 12500–12535. [Google Scholar] [CrossRef]
- Jing, X.; Zheng, D. Effect of cycle coupling-configuration on energy cascade utilization for a new power and cooling cogeneration cycle. Energy Convers. Manag. 2014, 78, 58–64. [Google Scholar] [CrossRef]
- Shokati, N.; Ranjbar, F.; Yari, M. A comprehensive exergoeconomic analysis of absorption power and cooling cogeneration cycles based on Kalina, part 1: Simulation. Energy Convers. Manag. 2018, 158, 437–459. [Google Scholar] [CrossRef]
- Shokati, N.; Ranjbar, F.; Yari, M. A comprehensive exergoeconomic analysis of absorption power and cooling cogeneration cycles based on Kalina, Part 2: Parametric study and optimization. Energy Convers. Manag. 2018, 161, 74–103. [Google Scholar] [CrossRef]
- Patil, R.S.; Bhagwat, S.S. Thermodynamic analysis and optimisation of double effect absorption type combined power and cooling cycle using LiBr-water as working fluid. Int. J. Exergy 2021, 34, 159–178. [Google Scholar] [CrossRef]
- Kalan, A.S.; Ghiasirad, H.; Saray, R.K.; Mirmasoumi, S. Thermo-economic evaluation and multi-objective optimization of a waste heat driven combined cooling and power system based on a modified Kalina cycle. Energy Convers. Manag. 2021, 247, 114723. [Google Scholar] [CrossRef]
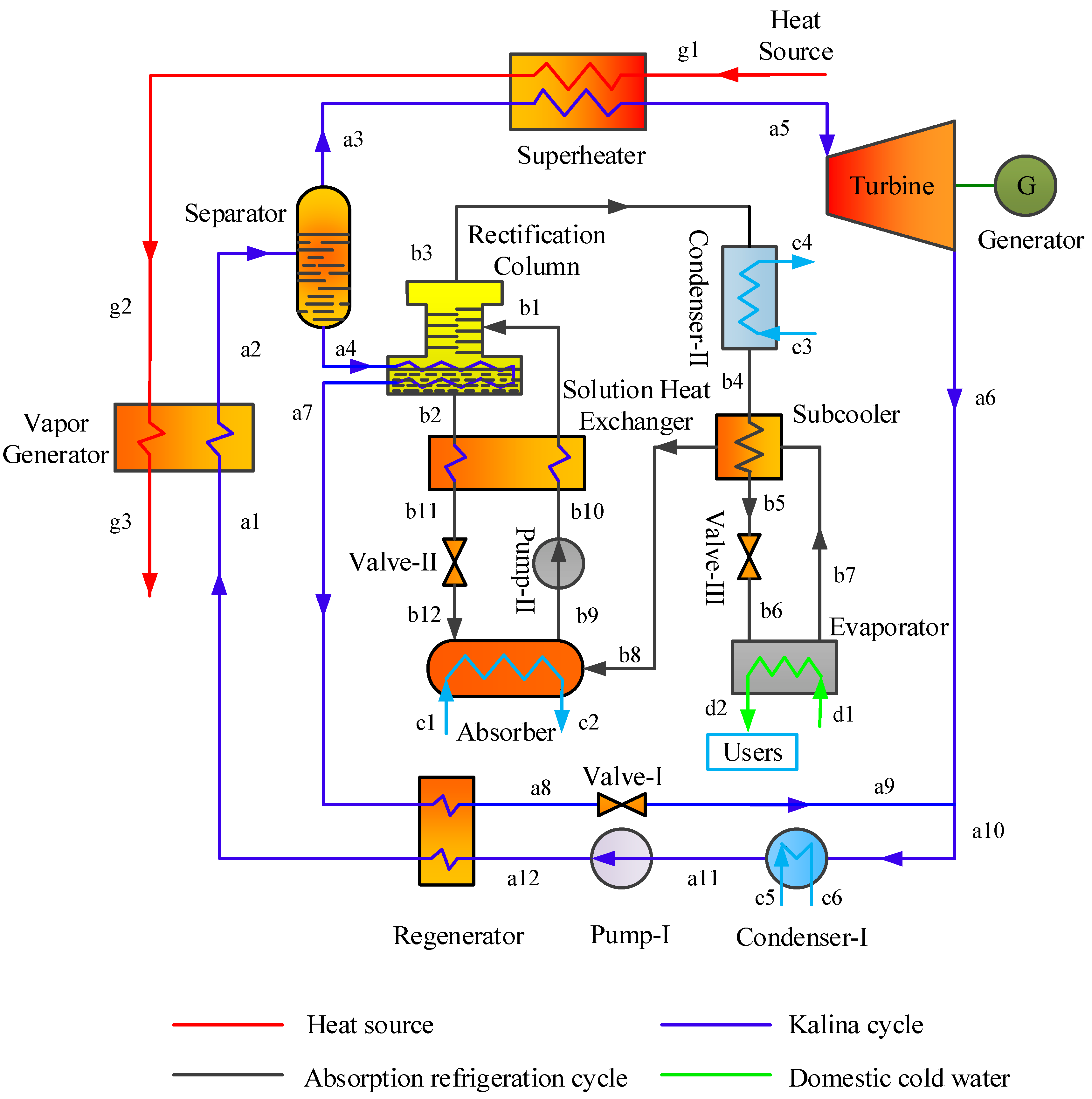




| Component | Exergy Equation (kW) |
|---|---|
| Vapor generator | Ivg = Eg2 − Eg3 + Ea1 − Ea2 |
| Separator | Isep = Ea2 − Ea3 − Ea4 |
| Superheater | Isup = Eg1 − Eg2 + Ea3 − Ea5 |
| Turbine | Itb = Ea5 − Ea6 − Wtb |
| Regenerator | Ireg = Ea12-Ea1 + Ea7-Ea8 |
| Rectification column | Ircl = Ea4 − Ea7 + Eb1 − Eb2 − Eb3 |
| Absorber | Iabs = Eb8 + Eb12 − Eb9 + Ec1 − Ec2 |
| Solution heat exchanger | Ishe = Eb2 − Eb11 + Eb10 − Eb1 |
| Subcooler | Isub = Eb4 − Eb5 + Eb7 − Eb8 |
| Evaporator | Ievp = Eb6 − Eb7 + Ed1 − Ed2 |
| Condenser-I | Icnd-I = Ea10 − Ea11 + Ec5 − Ec6 |
| Condenser-Ⅱ | Icnd-Ⅱ = Eb3 − Eb4 + Ec3 − Ec4 |
| Pump-I | Ip-I = Ea11 − Ea12 |
| Pump-Ⅱ | Ip-I = Eb9-Eb10 + Wp-Ⅱ |
| Valve-I | Iv-I = Ea8 − Ea9 |
| Valve-Ⅱ | Iv-Ⅱ = Eb11 − Eb12 |
| Valve-Ⅲ | Iv-Ⅲ = Eb5 − Eb6 |
| Initial Parameters | Value |
|---|---|
| Ambient temperature Tamb/°C | 20 |
| Ambient pressure Pamb/kPa | 101.3 |
| Heat source temperature Tg/°C | 200 |
| Heat source pressure Pg/kPa | 140 |
| Mass flow rate of heat source mg/kg·s−1 | 30 |
| Cold refrigerant water temperature mc/°C | 5 |
| Ammonia mass fraction of basic solution Xbasic/% | 60 |
| Ammonia mass fraction of ammonia-strong solution Xstrong/% | 40 |
| Turbine isentropic efficiency ηtb/% | 80 |
| Pump isentropic efficiency ηp/% | 70 |
| Turbine inlet pressure Pa5/kPa | 5000 |
| Turbine outlet pressure Pa6/kPa | 600 |
| Heat exchanger minimum terminal temperature difference ∆Tmin/°C | 5 |
| Working Fluid | State | T/°C | P/kPa | h/ kJ·kg−1 | s/ kJ·kg−1·K−1 | Quality | X/% | m/ kg·s−1 |
|---|---|---|---|---|---|---|---|---|
| waste gas | g1 | 200.00 | 140 | 475.84 | 7.24 | / | / | 30.00 |
| waste gas | g2 | 193.56 | 140 | 469.24 | 7.22 | / | / | 30.00 |
| waste gas | g3 | 99.56 | 140 | 373.60 | 6.99 | / | / | 30.00 |
| ammonia–water basic solution | a1 | 84.95 | 5000 | 386.06 | 1.95 | 0 | 60.00 | 5.09 |
| ammonia–water basic solution | a2 | 145.00 | 5000 | 949.57 | 3.38 | 0.26 | 60.00 | 5.09 |
| ammonia-rich vapor | a3 | 145.00 | 5000 | 1857.83 | 5.75 | 1 | 93.49 | 1.34 |
| ammonia-poor solution | a4 | 145.00 | 5000 | 625.61 | 2.53 | 0 | 48.05 | 3.75 |
| ammonia-rich vapor | a5 | 190.00 | 5000 | 2005.63 | 6.09 | 1 | 93.49 | 1.34 |
| ammonia-rich vapor | a6 | 72.19 | 600 | 1722.79 | 6.29 | 0.95 | 93.49 | 1.34 |
| ammonia-poor solution | a7 | 115.00 | 5000 | 466.57 | 2.13 | 0 | 48.05 | 3.75 |
| ammonia-poor solution | a8 | 41.03 | 5000 | 93.53 | 1.07 | 0 | 48.05 | 3.75 |
| ammonia-poor solution | a9 | 41.66 | 600 | 93.53 | 1.08 | 0.25 | 60.00 | 3.75 |
| ammonia–water basic solution | a10 | 47.38 | 600 | 521.87 | 2.46 | 0 | 60.00 | 5.09 |
| ammonia–water basic solution | a11 | 30.11 | 600 | 103.14 | 1.11 | 0 | 60.00 | 5.09 |
| ammonia–water basic solution | a12 | 31.03 | 5000 | 111.10 | 1.12 | 0 | 48.05 | 5.09 |
| ammonia-strong solution | b1 | 91.85 | 1300 | 340.30 | 1.76 | 0.02 | 40.00 | 2.80 |
| ammonia-weak solution | b2 | 110.00 | 1300 | 395.27 | 1.83 | 0 | 31.19 | 2.44 |
| pure ammonia | b3 | 33.68 | 1300 | 1632.74 | 5.70 | 1 | 100.00 | 0.36 |
| pure ammonia | b4 | 33.68 | 1300 | 503.98 | 2.02 | 0 | 100.00 | 0.36 |
| pure ammonia | b5 | 18.12 | 1300 | 429.52 | 1.77 | 0 | 100.00 | 0.36 |
| pure ammonia | b6 | −1.88 | 400 | 429.52 | 1.79 | 0.07 | 100.00 | 0.36 |
| pure ammonia | b7 | −1.88 | 400 | 1605.15 | 6.12 | 1 | 100.00 | 0.36 |
| pure ammonia | b8 | 28.68 | 400 | 1679.60 | 6.38 | 1 | 100.00 | 0.36 |
| ammonia-strong solution | b9 | 46.39 | 400 | 91.44 | 1.04 | 0 | 40.00 | 2.80 |
| ammonia-strong solution | b10 | 46.56 | 1300 | 92.93 | 1.05 | 0 | 40.00 | 2.80 |
| ammonia-weak solution | b11 | 51.56 | 1300 | 111.56 | 1.03 | 0 | 31.19 | 2.44 |
| ammonia-weak solution | b12 | 51.69 | 400 | 111.56 | 1.03 | 0 | 31.19 | 2.44 |
| cooling water | c1 | 20.00 | 101.3 | 84.01 | 0.30 | / | / | 18.47 |
| cooling water | c2 | 28.00 | 101.3 | 117.46 | 0.41 | / | / | 18.47 |
| cooling water | c3 | 20.00 | 101.3 | 84.01 | 0.30 | / | / | 12.08 |
| cooling water | c4 | 28.00 | 101.3 | 117.46 | 0.41 | / | / | 12.08 |
| cooling water | c5 | 20.00 | 101.3 | 84.01 | 0.30 | / | / | 63.73 |
| cooling water | c6 | 28.00 | 101.3 | 117.46 | 0.41 | / | / | 63.73 |
| refrigerant water | d1 | 20.00 | 101.3 | 84.01 | 0.30 | / | / | 6.70 |
| refrigerant water | d2 | 5.00 | 101.3 | 21.12 | 0.08 | / | / | 6.70 |
| Term | Value | Unit |
|---|---|---|
| Power output of turbine | 378.65 | kW |
| Power consumption of pump | 44.70 | kW |
| Net power output of the system | 333.94 | kW |
| Refrigeration output | 421.07 | kW |
| System energy input | 3067.24 | kW |
| Refrigeration exergy | 11.16 | kW |
| System exergy input | 2996.05 | kW |
| Thermal efficiency | 24.62 | % |
| Exergy efficiency | 11.52 | % |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wang, J.; Liu, Z.; Chen, H.; Liu, X. Thermodynamic Analysis of a New Combined Cooling and Power System Coupled by the Kalina Cycle and Ammonia–Water Absorption Refrigeration Cycle. Sustainability 2022, 14, 13260. https://doi.org/10.3390/su142013260
Wang H, Wang J, Liu Z, Chen H, Liu X. Thermodynamic Analysis of a New Combined Cooling and Power System Coupled by the Kalina Cycle and Ammonia–Water Absorption Refrigeration Cycle. Sustainability. 2022; 14(20):13260. https://doi.org/10.3390/su142013260
Chicago/Turabian StyleWang, Haojin, Jianyong Wang, Zhuan Liu, Haifeng Chen, and Xiaoqin Liu. 2022. "Thermodynamic Analysis of a New Combined Cooling and Power System Coupled by the Kalina Cycle and Ammonia–Water Absorption Refrigeration Cycle" Sustainability 14, no. 20: 13260. https://doi.org/10.3390/su142013260
APA StyleWang, H., Wang, J., Liu, Z., Chen, H., & Liu, X. (2022). Thermodynamic Analysis of a New Combined Cooling and Power System Coupled by the Kalina Cycle and Ammonia–Water Absorption Refrigeration Cycle. Sustainability, 14(20), 13260. https://doi.org/10.3390/su142013260







