Mechanical Mechanism and Shaping Effect of Tunnel Blasting Construction in Rock with Weak Interlayer
Abstract
1. Introduction
2. Data and Method
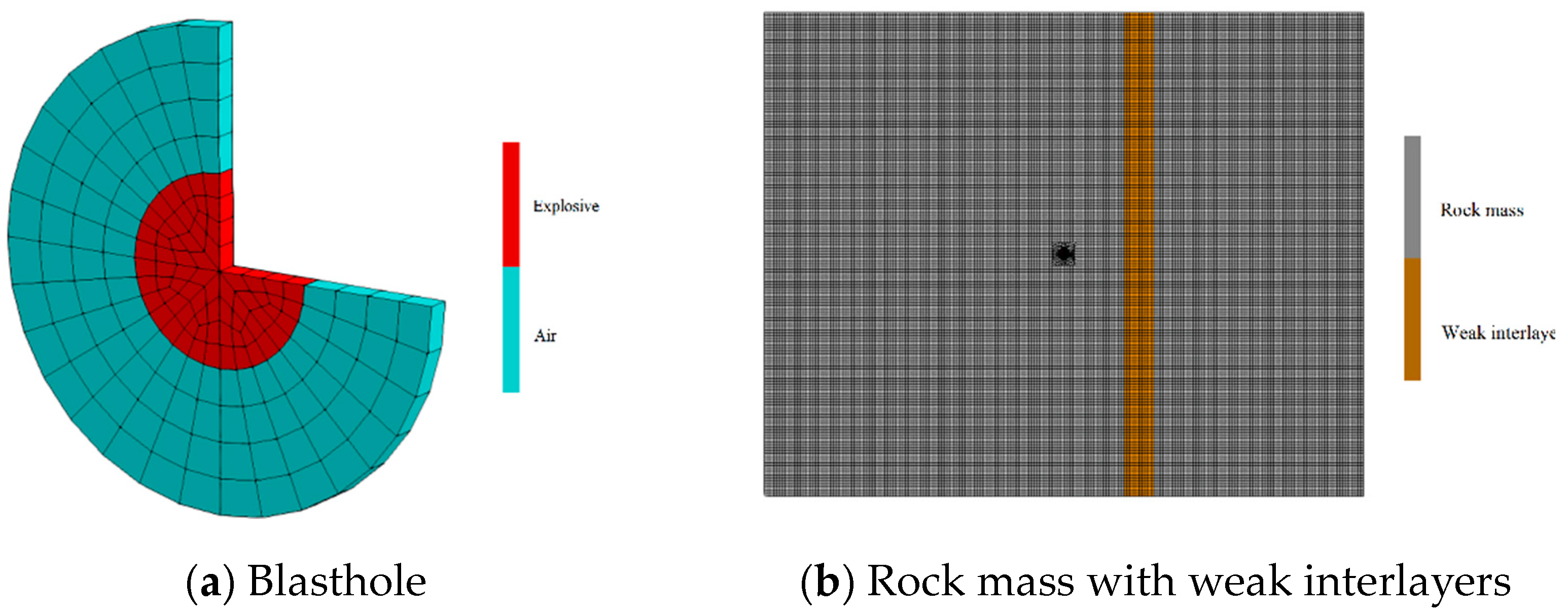
2.1. Numerical Modeling and Material Parameters
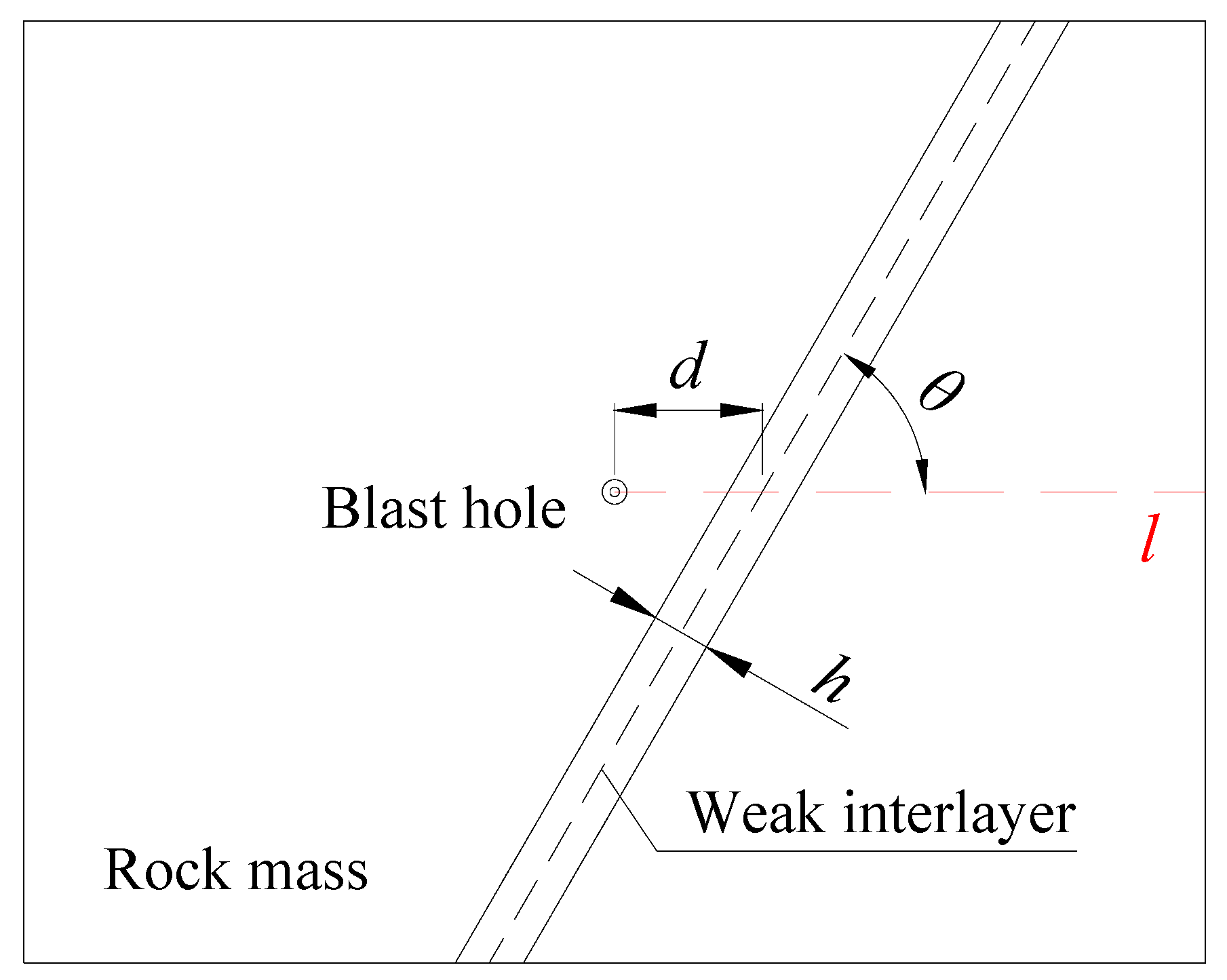
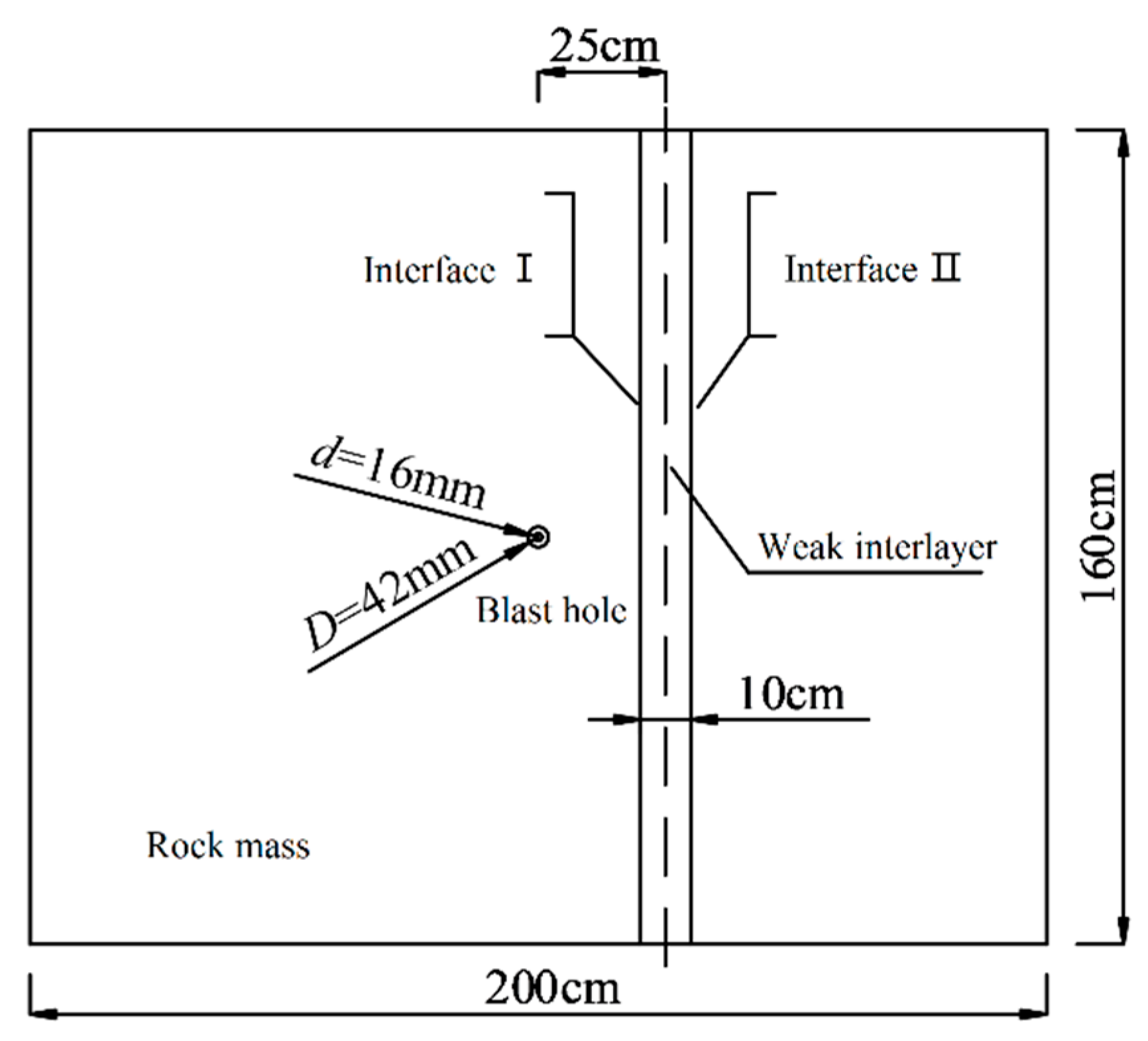
2.2. Modeling of Blasting Stress Wave Propagation with Weak Interlayer
2.3. Modeling of Tunnel Blasting Shaping Effect with Weak Interlayer
3. Result and Analysis
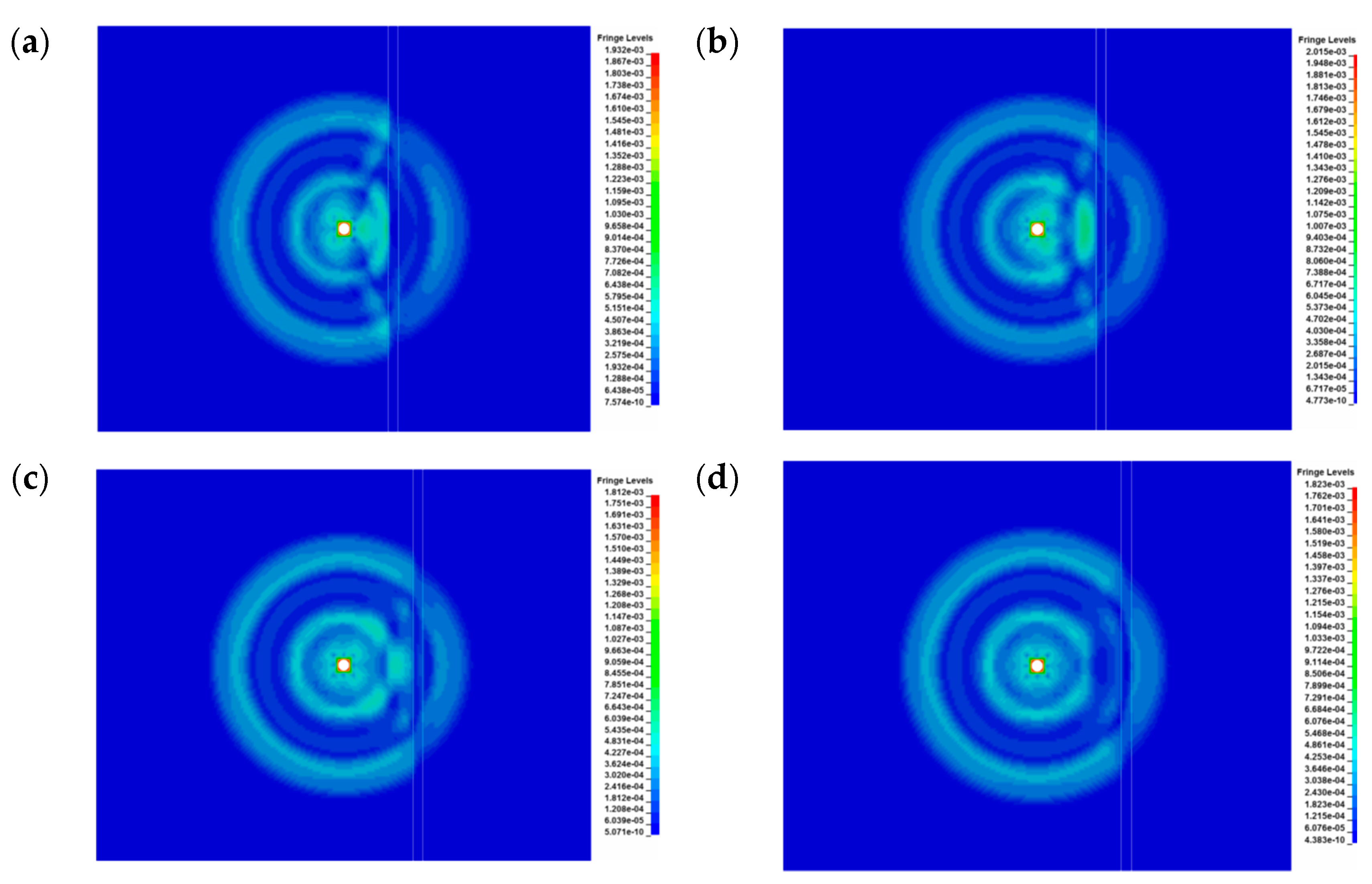
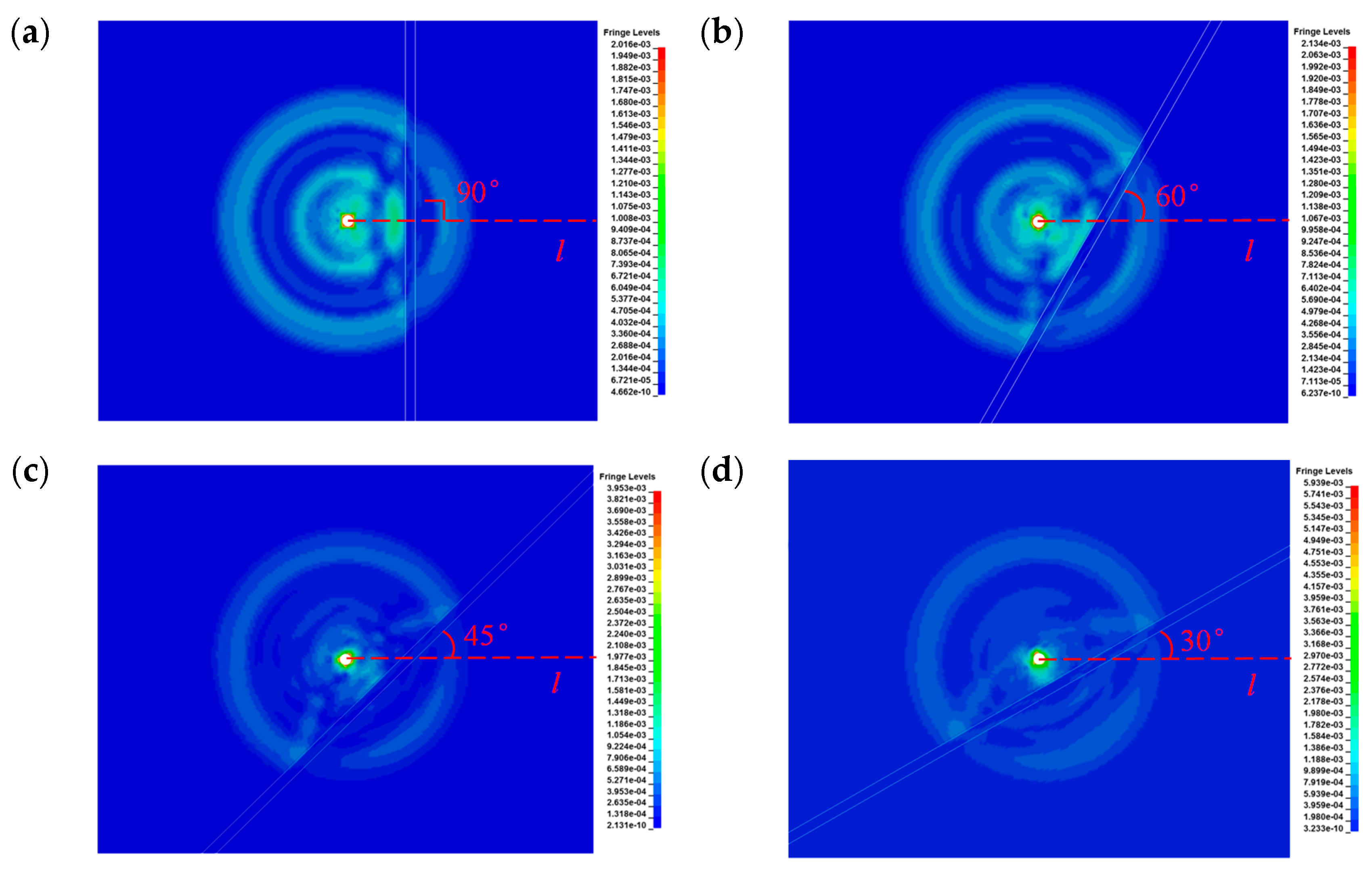
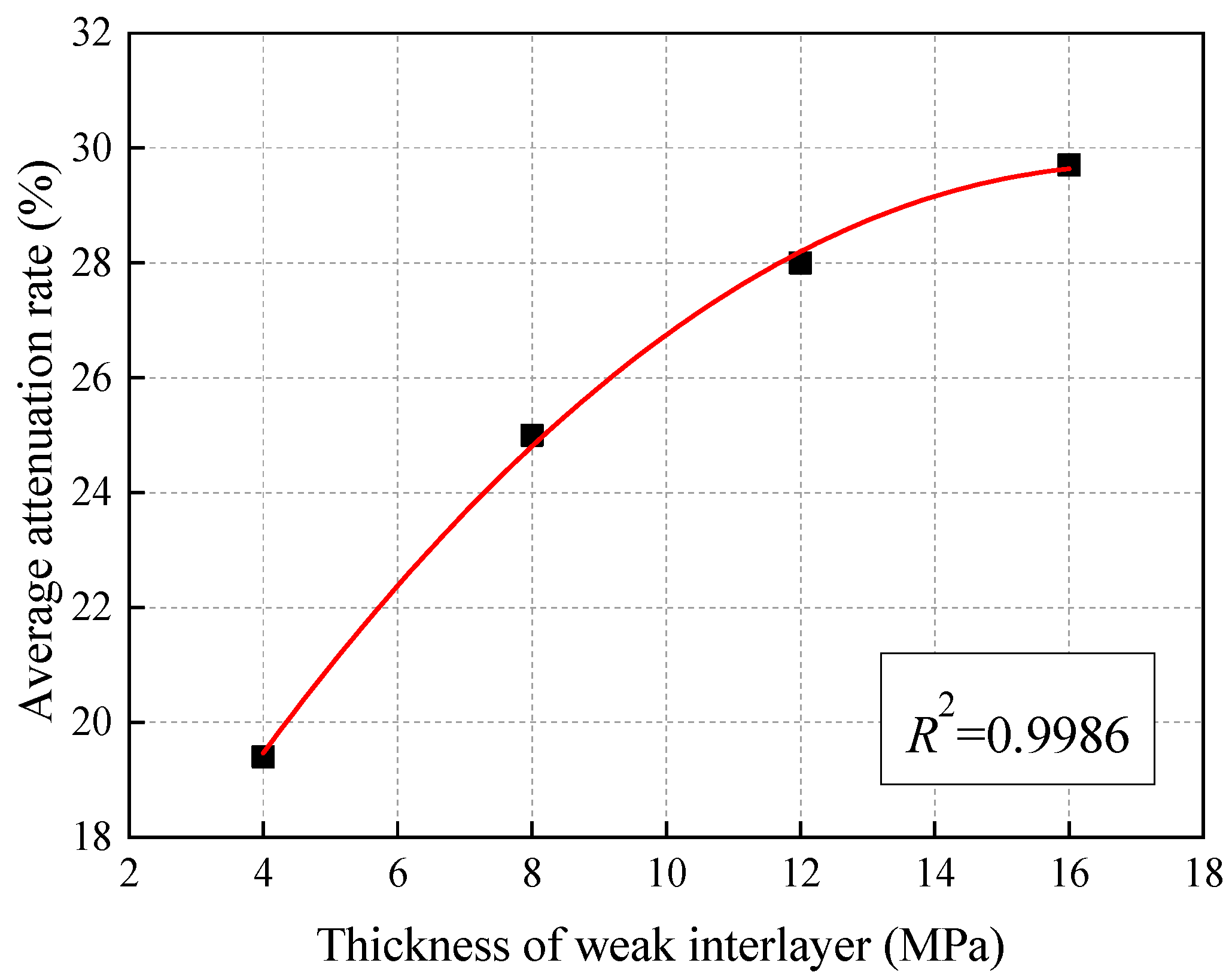
3.1. Blasting Stress Wave Propagation
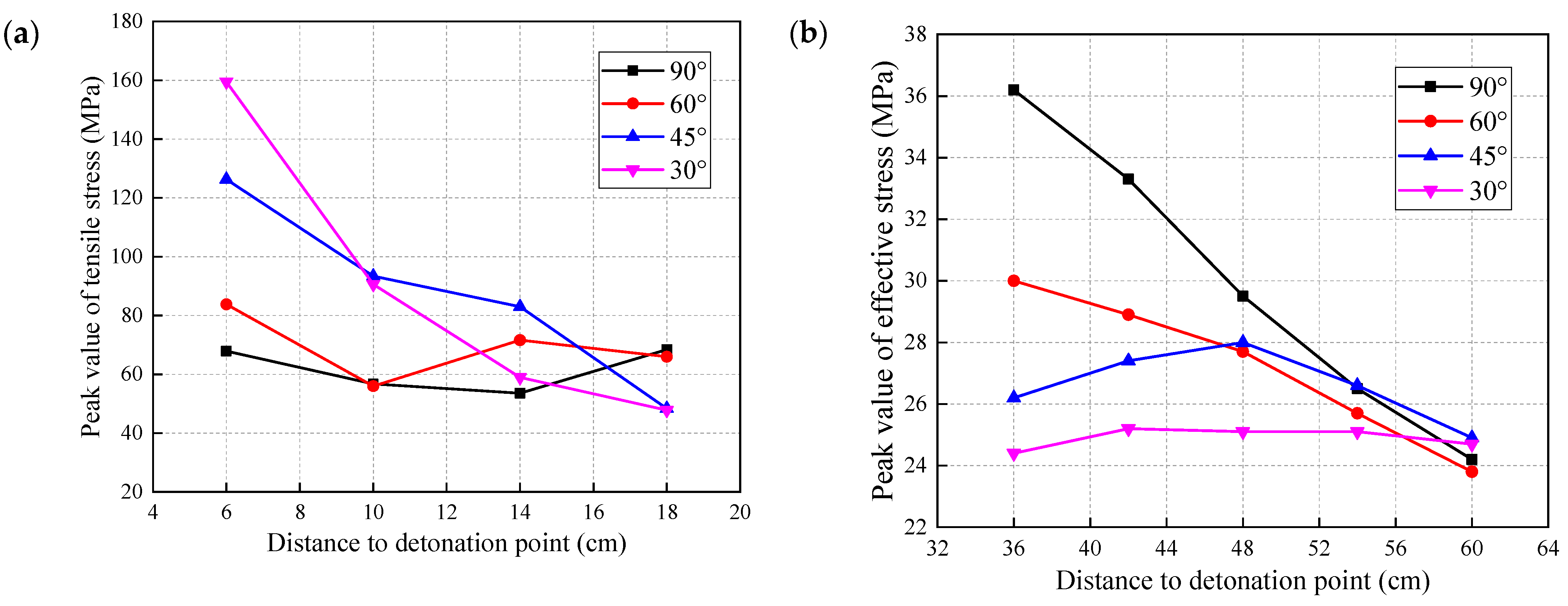
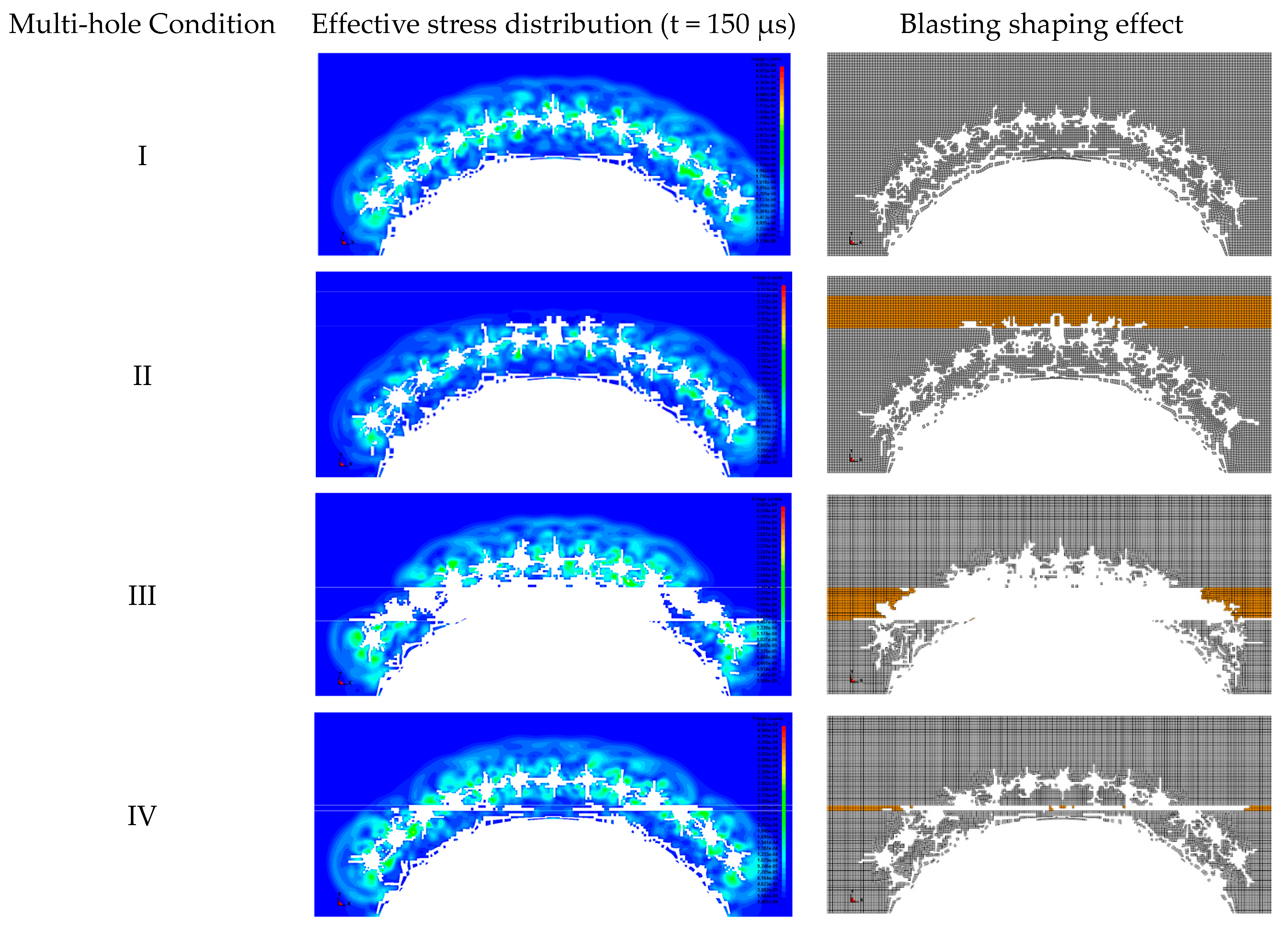
3.1.1. Effective Stress Distribution
3.1.2. Peak Tensile Stress
3.1.3. The Blasting Failure Mode
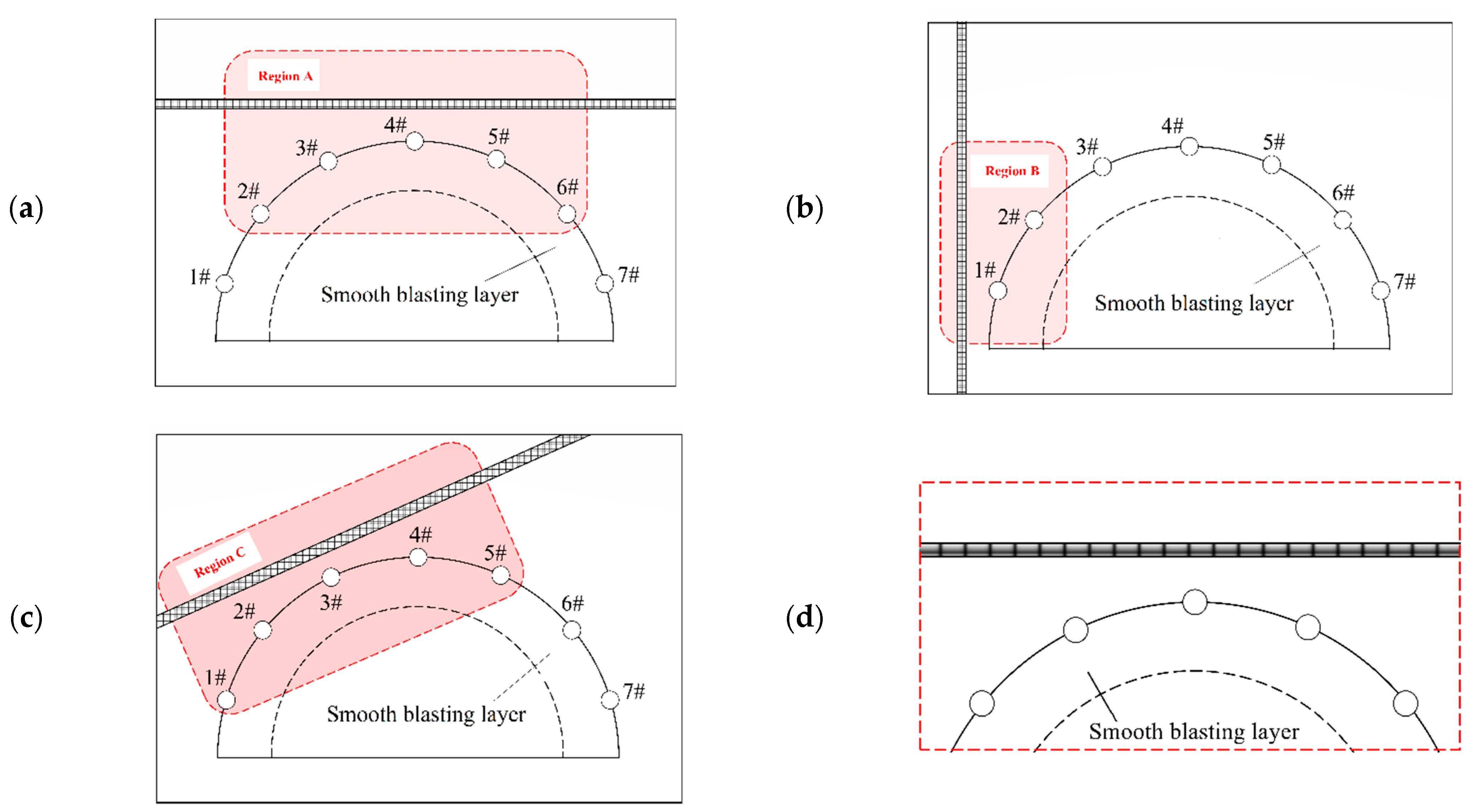
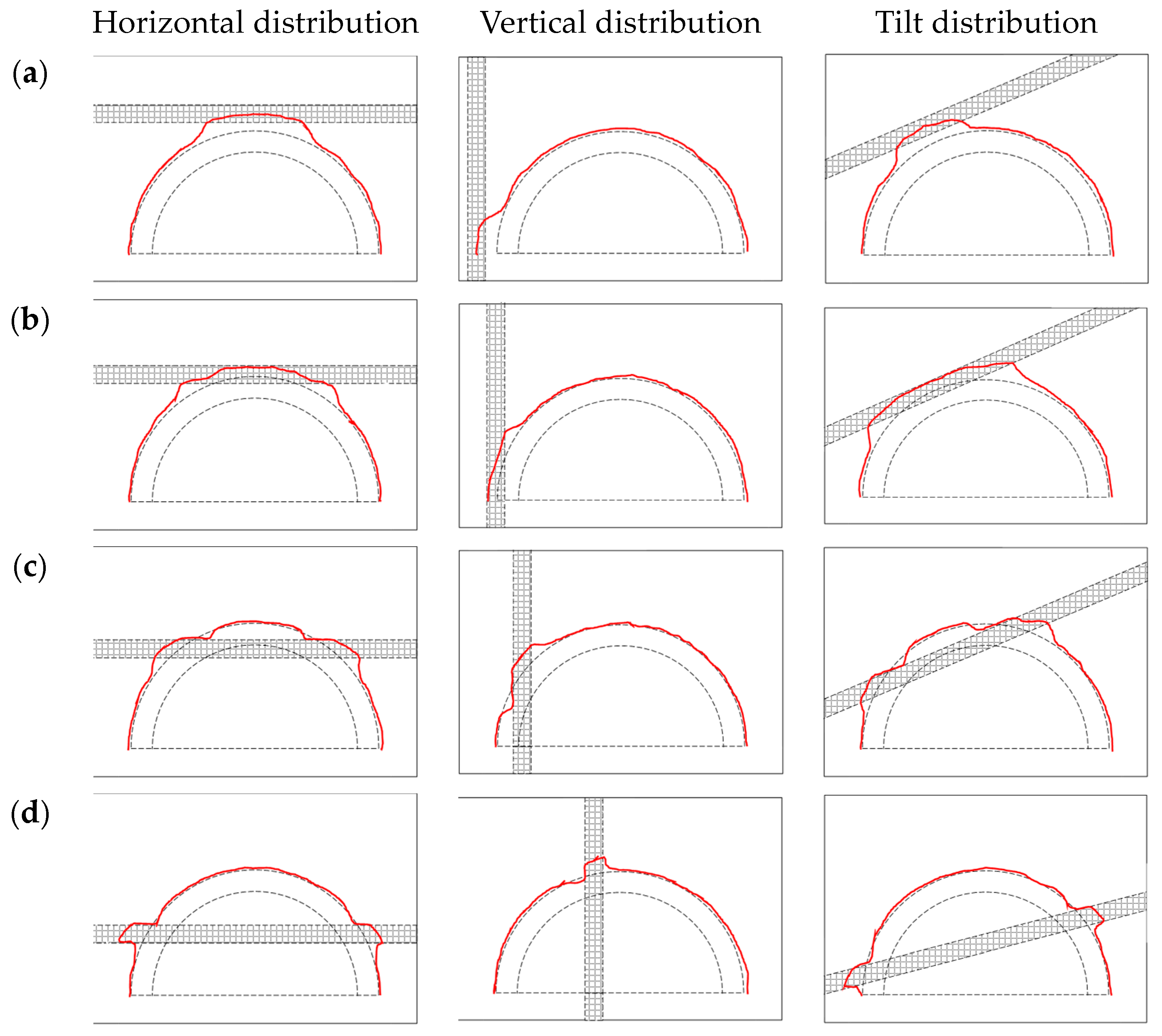
3.2. Tunnel Blasting Shaping Effect
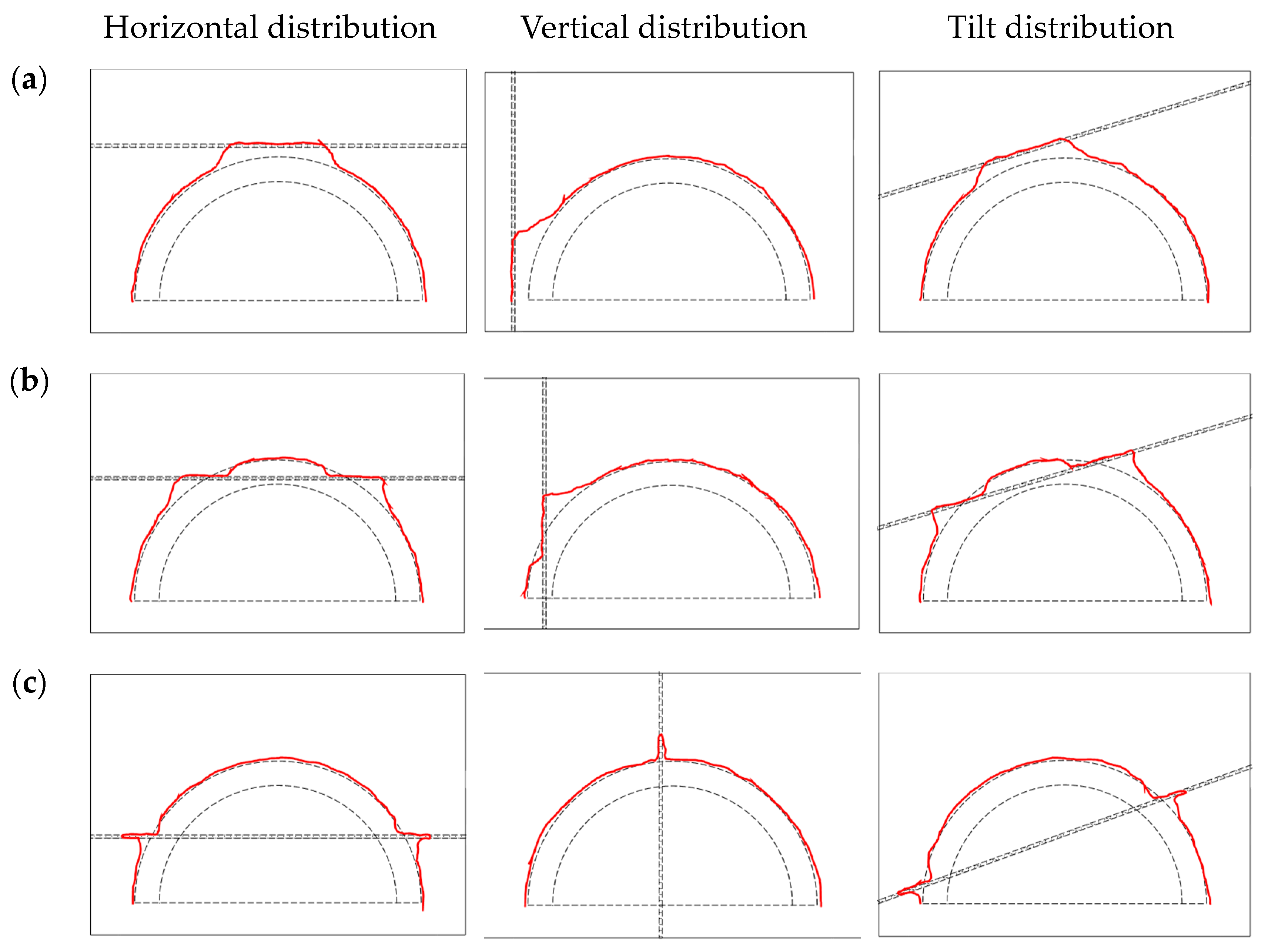
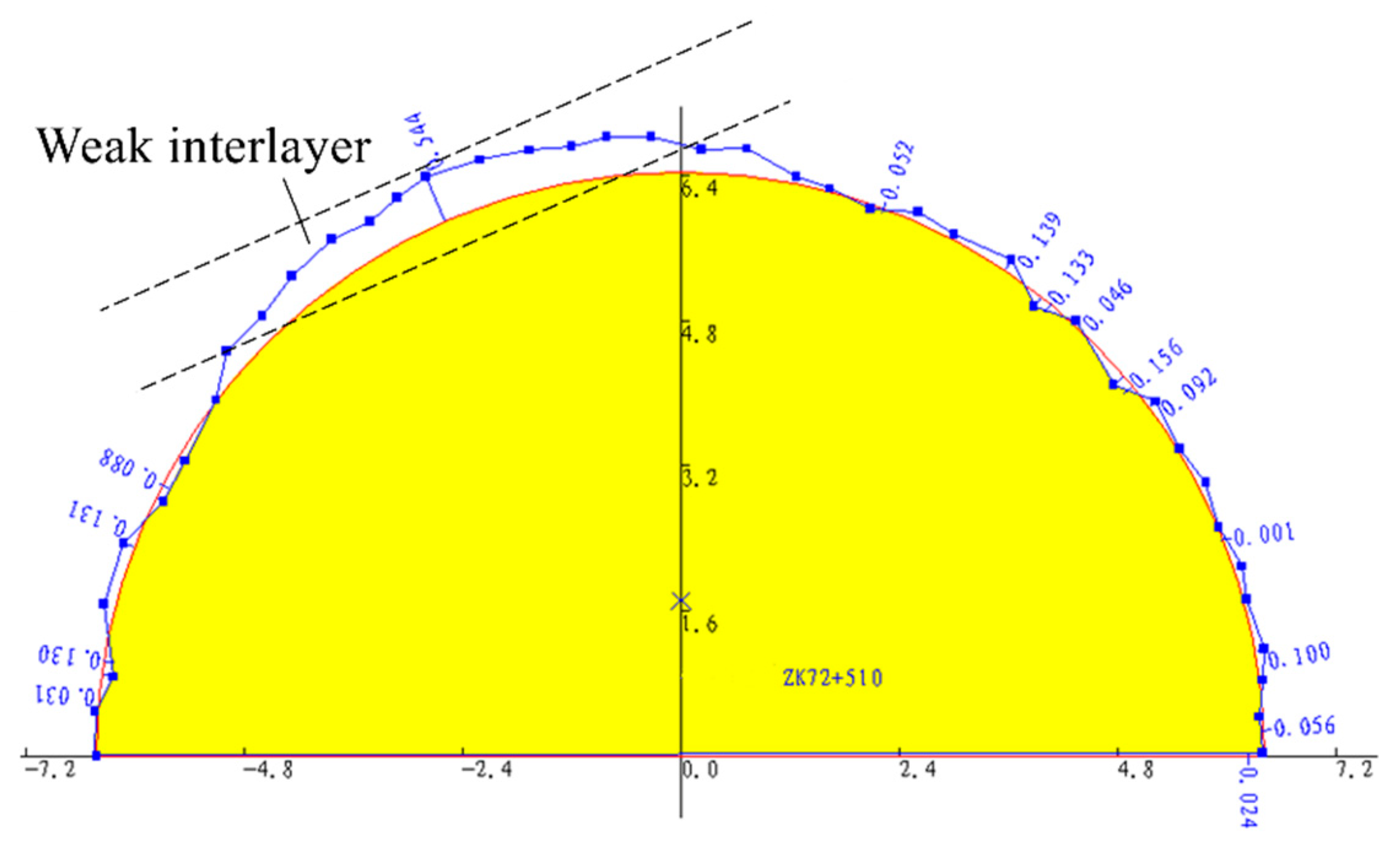
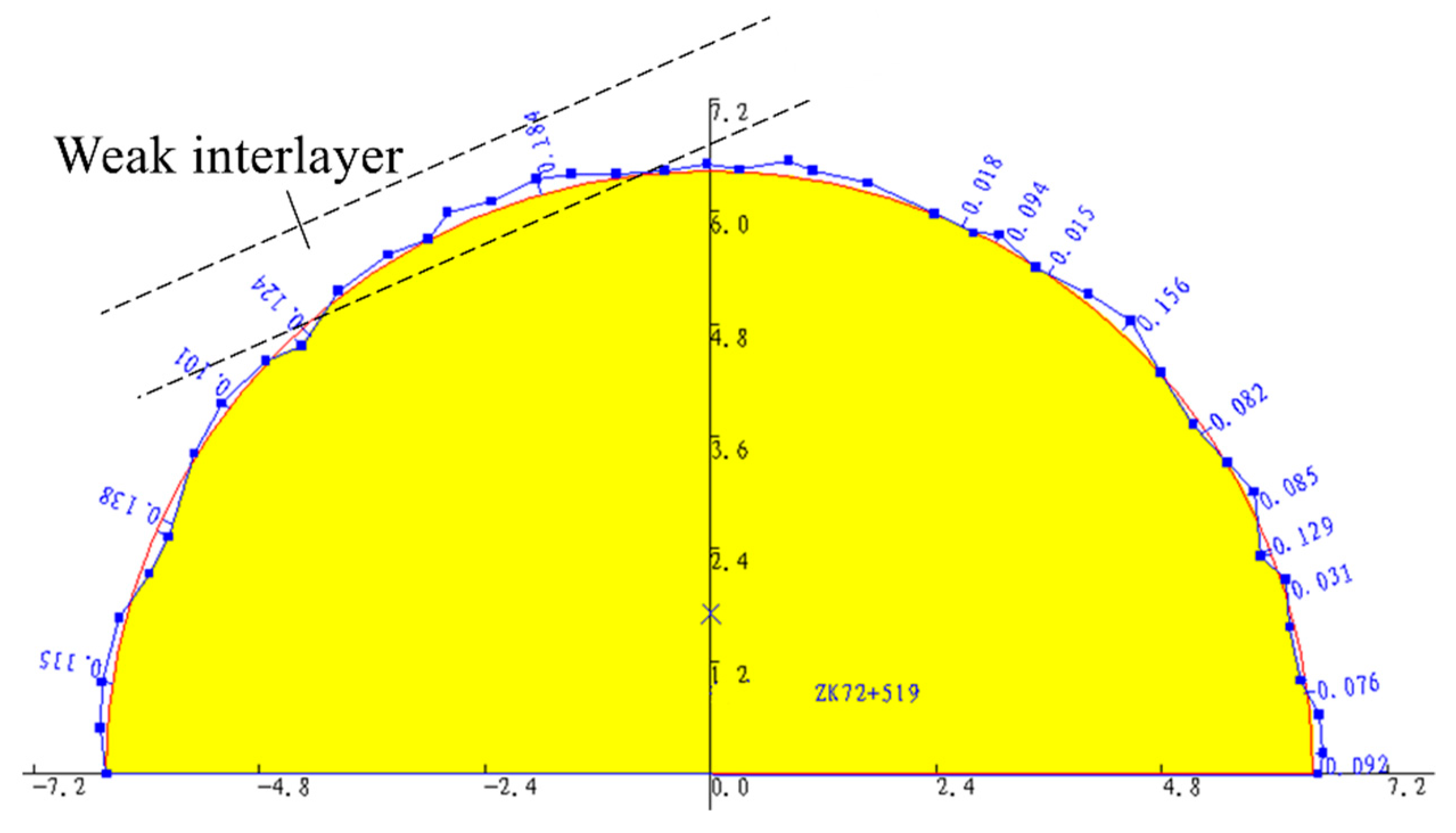
3.3. Devation of the Tunnel Blasting Shaping Outline
3.4. Application of the Tunnel Blasting Shaping Outline
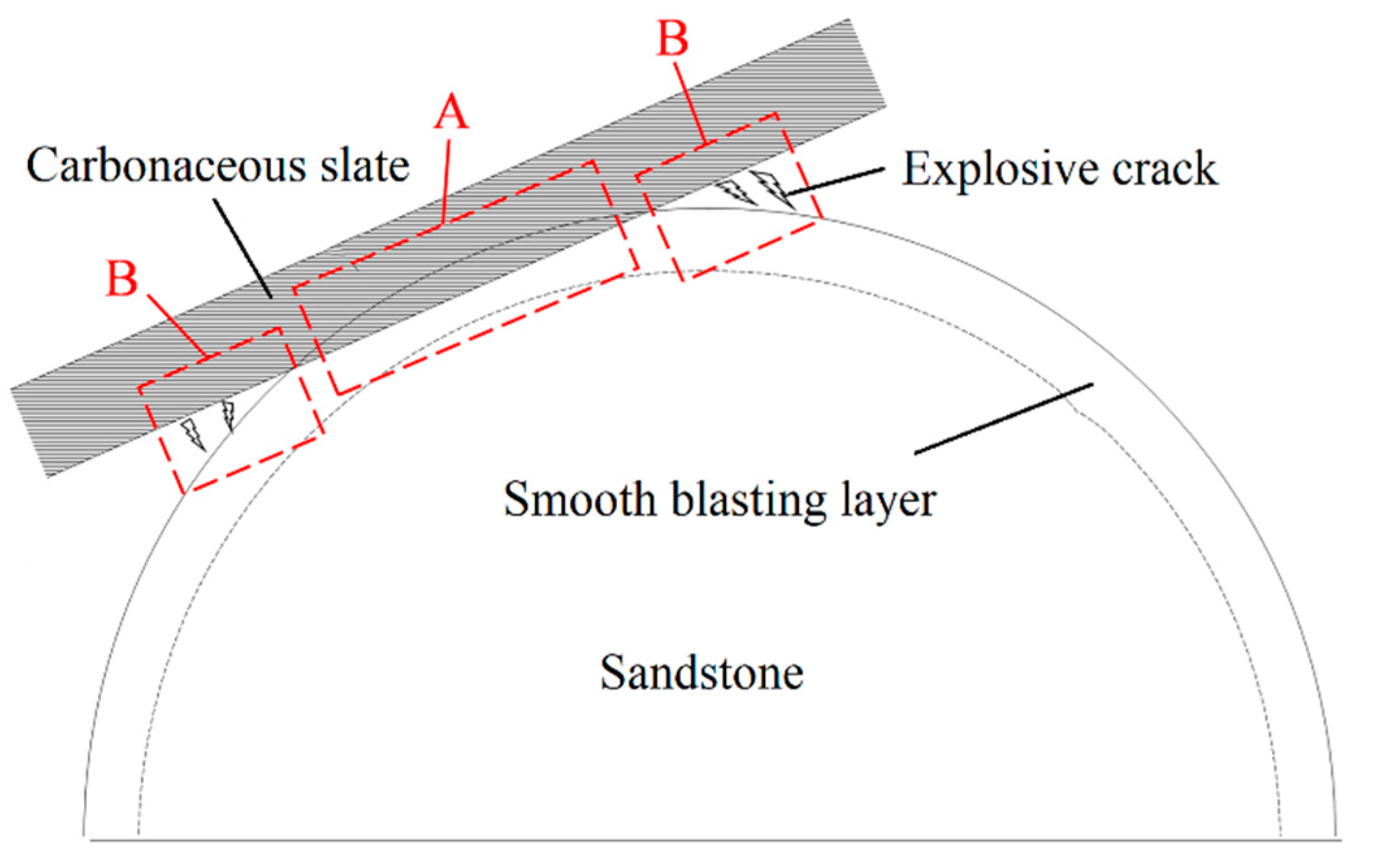
3.4.1. Overbreak Mechanism
3.4.2. Control Measures
3.4.3. Control Effect
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mansurov, V.A. Prediction of rockbursts by analysis of induced seismicity data. Int. J. Rock Mech. Min. 2001, 6, 893–901. [Google Scholar] [CrossRef]
- Pantelidis, L. Rock slope stability assessment through rock mass classification systems. Int. J. Rock Mech. Min. 2009, 46, 315–325. [Google Scholar] [CrossRef]
- Yl, A.; Zyy, B.; Xiang, W.C.; Lh, D. A systematic 3D simulation method for geomaterials with block inclusions from image recognition to fracturing modelling. Theor. Appl. Fract. Mech. 2020, 117, 103194. [Google Scholar]
- Yla, B.; Xiang, W.B.; Jm, C.; Lh, D. A systematic framework for the 3D finite-discrete modelling of binary mixtures considering irregular block shapes and cohesive block-matrix interfaces. Powder. Technol. 2021, 398, 117070. [Google Scholar]
- Yla, B.; Xiang, W.B.; Jm, C.; Lh, D. A finite-discrete element based appoach for modelling the hydraulic fracturing of rocks with irregular inclusions. Eng. Fract. Mech. 2021, 261, 108209. [Google Scholar]
- Fan, L.F.; Ma, G.W.; Li, J.C. Nonlinear viscoelastic medium equivalence for stress wave propagation in a jointed rock mass. Int. J. Rock Mech. Min. 2012, 50, 11–18. [Google Scholar] [CrossRef]
- Zhang, W.; Kong, X.; Qu, Y.; Zhao, Q. Numerical Simulation of Cracked Reinforced Concrete Slabs Subjected to Blast Loading. Civ. Eng. J. 2018, 4, 320–333. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, X.; Zhang, Z.; Luo, L.; Sun, W. Displacement and Deformation of the First Tunnel Lining during the Second Tunnel Construction. Civ. Eng. J. 2019, 5, 332–339. [Google Scholar] [CrossRef]
- Lei, M.; Liu, J.; Lin, Y.; Shi, C.; Liu, C.; Saksala, T. Deformation Characteristics and Influence Factors of a Shallow Tunnel Excavated in Soft Clay with High Plasticity. Adv. Civ. Eng. 2019, 2019, 7483628. [Google Scholar] [CrossRef]
- Lei, M.; Liu, L.; Shi, C.; Tan, Y.; Wang, W. A novel tunnel-lining crack recognition system based on digital image technology. Tunn. Undergr. Space Technol. 2020, 108, 103724. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, D.; Fang, Q.; Dui, G.; Tai, Q.; Sun, F. Analysis of the interaction between tunnel support and surrounding rock considering pre-reinforcement. Tunn. Undergr. Space Technol. 2021, 115, 104074. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, D.; Li, A.; Lu, S.; Tai, Q.; Chu, Z. Model test and numerical analysis for the face failure mechanism of large cross-section tunnels under different ground conditions. Tunn. Undergr. Space Technol. 2022, 130, 104735. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, D.; Fang, Q.; Dui, G.; Chu, Z. Analytical solutions for deep tunnels in strain-softening rocks modeled by different elastic strain definitions with the unified strength theory. Sci. China Technol. Sci. 2021, 115, 104074. [Google Scholar] [CrossRef]
- Haskell, N.A. The dispersion of surface waves on multilayered media. AGU 1953, 73, 17–34. [Google Scholar] [CrossRef]
- Kausel, E.; Ro Sset, J.M. Stiffness matrices for layered soils. B Seism. Soc. Am. 1981, 71, 1743–1761. [Google Scholar] [CrossRef]
- Xu, H.; Chen, D.; Yang, X.; Liang, B. Propagation Characteristics of Plane Sh Wave Passing through Elastic Interlining in Elastic Medium. J. Rock Mech. Geotech. Eng. 2003, 22, 304–308. [Google Scholar]
- Fan, L.M.; Li, N. Transmission Model of Weak Intercalation and Its Vibration Isolation Properties. J. Rock Mech. Geotech. 2005, 24, 2456–2462. [Google Scholar]
- Perino, A.; Zhu, J.B.; Li, J.C.; Barla, G.; Zhao, J. Theoretical Methods for Wave Propagation across Jointed Rock Masses. Rock Mech. Rock Eng. 2010, 43, 799–809. [Google Scholar] [CrossRef]
- Shi-Li, H.U.; Wang, X.G.; Wang, G.S. Waveform change rule of wavelet propagation across soft interlayer. Prog. Geophys. 2015, 8, 5413–5421. [Google Scholar]
- Lei, M.F.; Zhou, B.C.; Lin, Y.X.; Chen, F.D.; Shi, C.H.; Peng, L.M. Model test to investigate reasonable reactive artificial boundary in shaking table test with a rigid container. J. Cent. South Univ. 2020, 27, 210–220. [Google Scholar] [CrossRef]
- Son, M.; Adedokun, S. Earth pressure on a retaining structure in layered and jointed rock masses. KSCE J. Civ. Eng. 2017, 21, 1147–1153. [Google Scholar] [CrossRef]
- Yang, T.H.; Shi, W.H.; Wang, P.T.; Liu, H.L.; Li, Y. Numerical simulation on slope stability analysis considering anisotropic properties of layered fractured rocks: A case study. Arab. J. Geosci. 2014, 8, 5413–5421. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, Y.; Cheng, W.; Feng, X. Stability Analysis and Exploration of Failure Law of Jointed Rock Tunnel—Seminor on Tunnel Stability Analysis. Chin. J. Undergr. Space Eng. 2011, 7, 649–656. [Google Scholar]
- Huang, F.; Zhu, H.; Xu, Q.; Cai, Y.; Zhuang, X. the effect of weak interlayer on the failure pattern of rock mass around tunnel-scaled model tests and numerical analysis. Tunn. Undergr. Space Technol. 2013, 35, 207–218. [Google Scholar] [CrossRef]
- Panthee, S.; PKSingh; Kainthola, A. TNSingh Control of rock joint parameters on deformation of tunnel opening. J. Rock Mech. Geotech. Eng. 2016, 8, 489–498. [Google Scholar] [CrossRef]
- Zhao, J.-S.; Feng, X.-T.; Jiang, Q.; Zhou, Y.-Y. Microseismicity monitoring and failure mechanism analysis of rock masses with weak interlayer zone in underground intersecting chambers: A case study from the Baihetan Hydropower Station, China. Eng. Geol. 2018, 245, 44–60. [Google Scholar] [CrossRef]
- Zhang, N.; Zhu, X.; Ren, Y. Analysis and Study on Crack Characteristics of Highway Tunnel Lining. Civ. Eng. J. 2019, 5, 1119–1123. [Google Scholar] [CrossRef]
- Bu, L.; Yang, Z.J.; Wei, X.D.; Ji-Zhong, L.U.; Xu-Dong, F.U. Failure modes and constitutive model for weak interlayer of dam foundation with different inclination angles. Geotech. Eng. 2019, 159, 105222. [Google Scholar] [CrossRef]
- Liu, X.; Han, Y.; Li, D.; Tu, Y.; Deng, Z.; Yu, C.; Wu, X. Anti-pull mechanisms and weak interlayer parameter sensitivity analysis of tunnel-type anchorages in soft rock with underlying weak interlayers. Eng. Geol. 2019, 253, 123–136. [Google Scholar] [CrossRef]
- Huang, L.; Ma, J.; Lei, M.; Liu, L.; Lin, Y.; Zhang, Z. Soil-water inrush induced shield tunnel lining damage and its stabilization: A case study. Tunn. Undergr. Space Technol. 2020, 97, 103290–103291. [Google Scholar] [CrossRef]
- Liu, Y.P.; Gong, M.; Huang, G.H. Numerical analysis method for optimizing charging structure of deep-hole blasting and its application. Rock Soil Mech. 2012, 33, 1883–1888. [Google Scholar]
- Yang, R.; Bawden, W.F.; Katsabanis, P.D. A new constitutive model for blast damage. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1996, 33, 245–254. [Google Scholar] [CrossRef]
- Xia, X.; Hai-Bo, L.I.; Jun-Ru, L.I.; Xiao, K.Q.; Tang, H.; Guo-Wei, M.A. Numerical simulation of blast-induced cracks in rock. Rock Soil Mech. 2006, 27, 1987–1991. [Google Scholar]
- Wang, Y.; Ye, H.W.; Li, Y.Z. Numerical simulation on jointed and fractured rock blasting. Blasting 2012, 29, 20–22. [Google Scholar]
- Soutis, C.; Mohamed, G.; Hodzic, A. Modelling the structural response of GLARE panels to blast load. Compos. Struct. 2011, 94, 267–276. [Google Scholar] [CrossRef]
- Tian, Z.N.; Zhang, L.W. Numerical analysis of blast wave propagation in rock mass containing weak interlayer. Shenyang Gongye Daxue Xuebao 2010, 32, 349–354. [Google Scholar]
- Ji, L.; Zhou, C.; Lu, S.; Jiang, N.; Gutierrez, M. Numerical Studies on the Cumulative Damage Effects and Safety Criterion of a Large Cross-section Tunnel Induced by Single and Multiple Full-Scale Blasting. Rock Mech. Rock Eng. 2021, 54, 6393–6411. [Google Scholar] [CrossRef]
- Liu, G.W.; Song, D.Q.; Chen, Z.; Yang, J.W. Dynamic Response Characteristics and Failure Mechanism of Coal Slopes with Weak Intercalated Layers under Blasting Loads. Adv. Civ. Eng. 2020, 2020, 1–18. [Google Scholar] [CrossRef]
- Jianguang, L.I.; Wang, Y. Analysis for failure modes and interfacial stress of rock mass with horizontal weak interlayer. J. Liaoning Tech. Univ. Nat. Sci. 2015, 3, 710–715. [Google Scholar]
- Yu, J.X.; Zhi, X.; Cai, S.J. Propagation of explosion stress wave in weak interlayer. In Proceedings of the 7th National Academic Conference on Safety Protection of Engineering Structures, Nigibo, China, 27–19 July 2009; pp. 121–125. [Google Scholar]







| Parameters | Sandstone | Carbonaceous Slate |
|---|---|---|
| Density ρ/kg·m−3 | 2600 | 2200 |
| Elastic modulus E/GPa | 37.5 | 10 |
| Poisson ratio μ | 0.27 | 0.31 |
| Tensile Strength σt/MPa | 5 | 2 |
| Plastic modulus EP/GPa | 0.0375 | 0.01 |
| Hardening parameters β | 0.6 | 0.6 |
| Strain rate parameter C/S−1 | 2.63 | 2.63 |
| Strain rate parameter P | 3.96 | 3.96 |
| Ρ/kg·m−3 | D/m·s−1 | A/GPa | B/GPa | R1 | R2 | ω | E0/GPa |
|---|---|---|---|---|---|---|---|
| 1000 | 3400 | 229 | 0.55 | 6.5 | 1.0 | 0.35 | 3.51 |
| ρ/kg·m−3 | C0 | C1 | C2 | C3 | C4 | C5 | C6 | E0/GPa |
|---|---|---|---|---|---|---|---|---|
| 1.29 | 0 | 0 | 0 | 0 | 0.4 | 0.4 | 0 | 0.025 |
| Factors | Arrangement of Measuring Points | Single-Hole Conditions | |||
|---|---|---|---|---|---|
| I | II | III | IV | ||
| Thickness h/cm | 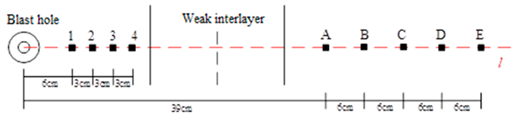 | 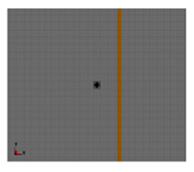 | 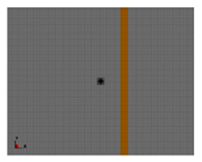 |  |  |
| D = 25 cm, θ = 90° | 4 | 8 | 12 | 16 | |
| Distance d/cm |  |  |  |  |  |
| Θ = 90°, h = 4 cm | 20 | 25 | 30 | 35 | |
| Angle θ/° |  |  |  | 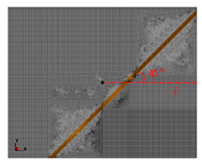 |  |
| H = 4 cm, d = 25 cm | 90 | 60 | 45 | 30 | |
| Multi-Hole Condition | Geometric Position | Concept Model | Numerical Model |
|---|---|---|---|
| I | No weak interlayer exists | 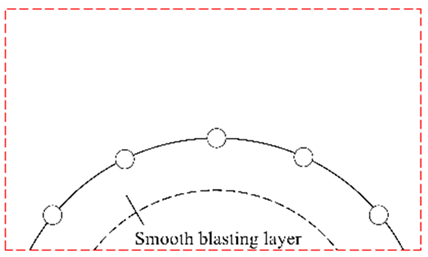 | 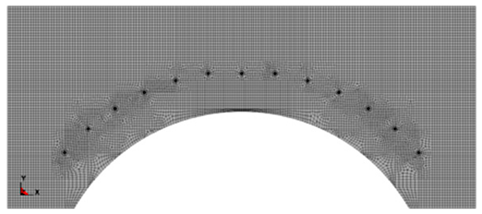 |
| II | Thick interlayer outside the tunnel excavation outline | 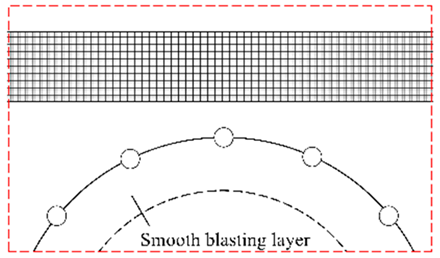 | 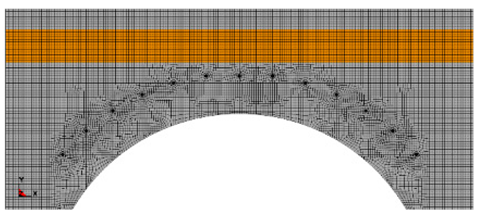 |
| III | Thick interlayer intersects with the inner contour of smooth blasting layer | 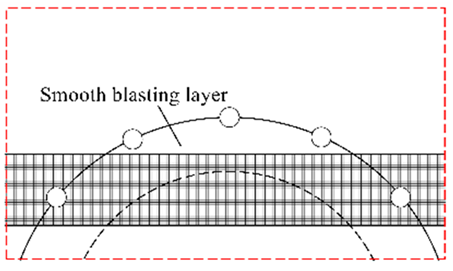 | 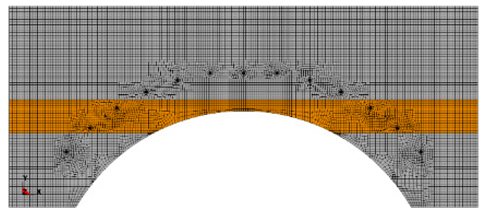 |
| IV | Thin interlayer intersects with the outer contour of smooth blasting layer | 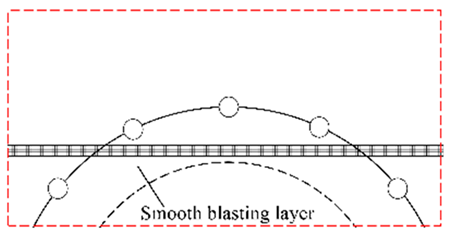 | 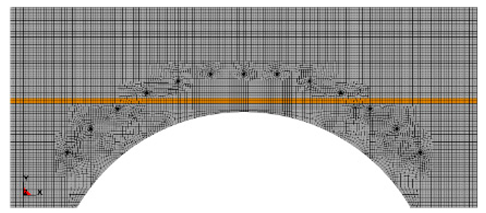 |
| Stage | Statistical Length/m | The Excavation Effect | |||
|---|---|---|---|---|---|
| Average Linear Overbreak/cm | Blast Hole Residue Rate/% | Underbreak Probability/% | Contour Rock Situation | ||
| Prophase | 8 | 16.4 | 19 | 33 | Difficult in forming arched contours; Rock block loose and dropped heavily. |
| Test | 24 | 6.1 | 46 | 12 | Meeting contour design requirements; No rock block dropping phenomenon. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, M.; He, R.; Liu, L.; Sun, N.; Qin, G.; Zhang, Y. Mechanical Mechanism and Shaping Effect of Tunnel Blasting Construction in Rock with Weak Interlayer. Sustainability 2022, 14, 13278. https://doi.org/10.3390/su142013278
Lei M, He R, Liu L, Sun N, Qin G, Zhang Y. Mechanical Mechanism and Shaping Effect of Tunnel Blasting Construction in Rock with Weak Interlayer. Sustainability. 2022; 14(20):13278. https://doi.org/10.3390/su142013278
Chicago/Turabian StyleLei, Mingfeng, Rui He, Linghui Liu, Ningxin Sun, Guifang Qin, and Yunliang Zhang. 2022. "Mechanical Mechanism and Shaping Effect of Tunnel Blasting Construction in Rock with Weak Interlayer" Sustainability 14, no. 20: 13278. https://doi.org/10.3390/su142013278
APA StyleLei, M., He, R., Liu, L., Sun, N., Qin, G., & Zhang, Y. (2022). Mechanical Mechanism and Shaping Effect of Tunnel Blasting Construction in Rock with Weak Interlayer. Sustainability, 14(20), 13278. https://doi.org/10.3390/su142013278






