A Torque-Compensated Fault-Tolerant Control Method for Electric Vehicle Traction Motor with Short-Circuit Fault
Abstract
1. Introduction
2. Topologies of the DT-PMSTM System
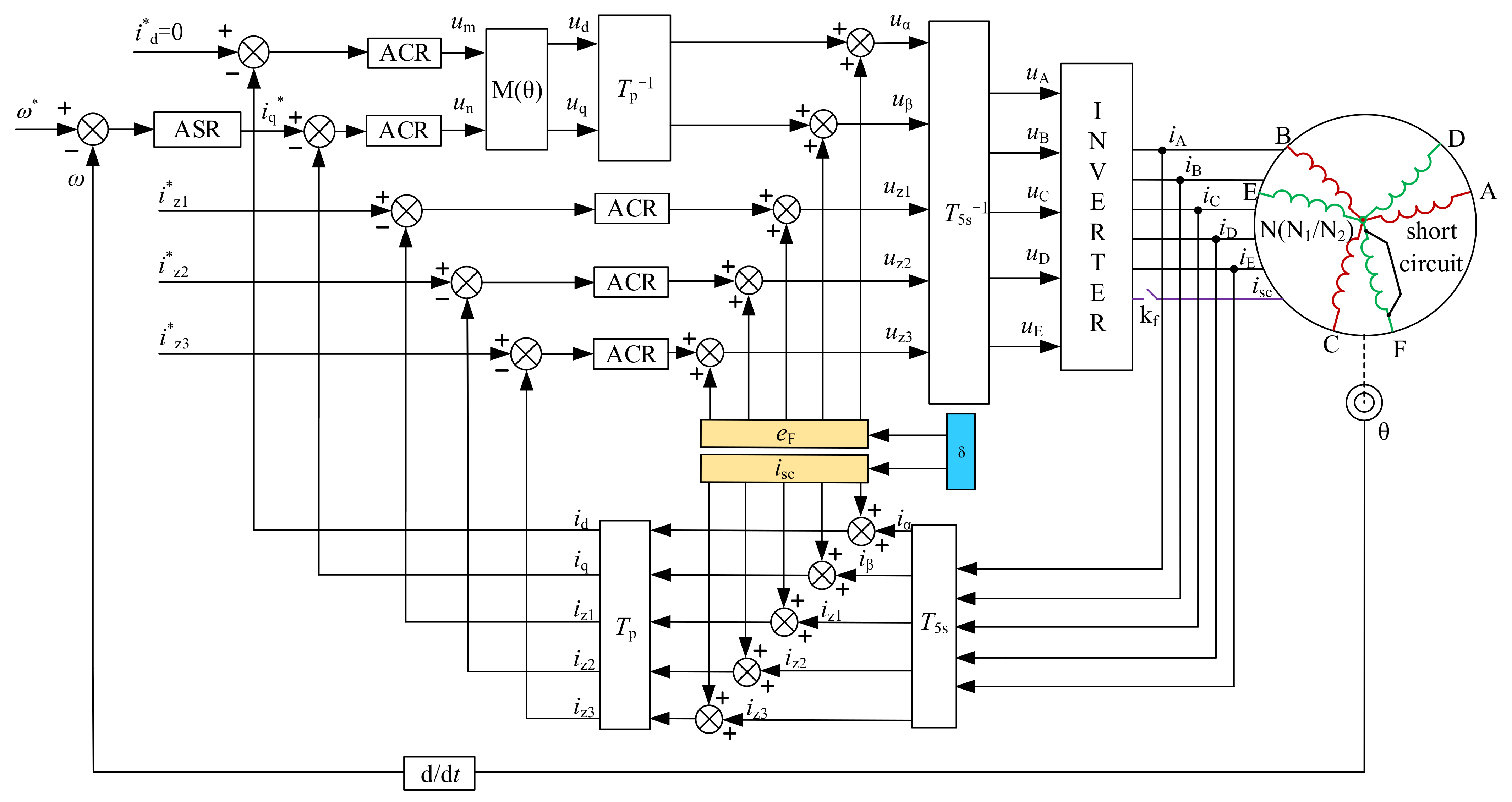
3. Short-Circuit Fault-Tolerant Control of DT-PMSTM
3.1. Reduced Dimensional Mathematical Model for Torque Compensation
3.2. Compensation Voltage Allocation Coefficient Calculation of the Topology with the Isolated Neutral Point
3.3. Compensation Voltage Allocation Coefficient Calculation of the Topology with the Connected Neutral Point
3.4. Short-Circuit Fault-Tolerant Control Strategy of the DT-PMSTM
4. Simulation Validation
4.1. Short-Circuit Fault Current Analysis of the Topology with the Isolated Neutral Point
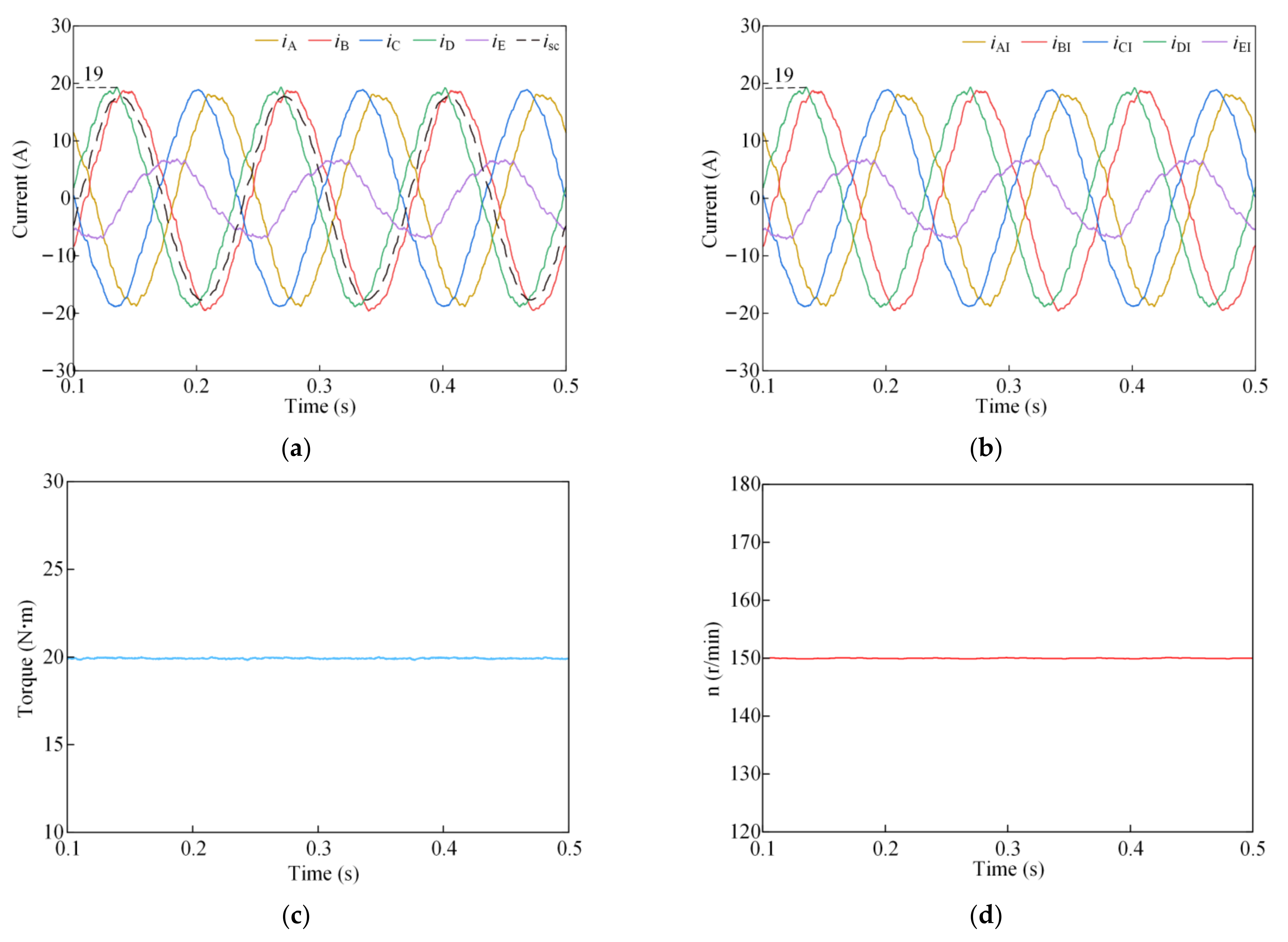
4.2. Short-Circuit Fault-Tolerant Control of the System with the Isolated Neutral Point
4.3. Short-Circuit Fault-Tolerant Control of the System with the Connected Neutral Point
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| DT-PMSTM | Dual three-phase permanent magnet synchronous traction motor. |
| T51s, 52s | The orthogonal order-reduced transformation matrixes. |
| Tp | The park transformation matrix. |
| Nip | The effective number of turns in each phase of the stator winding. |
| kwi | The stator winding factor. |
| isc | Short-circuit current. |
| i’A, B, C, D, E, F | Compensation current for each phase. |
| iA,B, C, D, E, F | Winding phase currents. |
| iAI,BI, CI, DI, EI, FI | Inverter output phase currents. |
| R | Stator resistance. |
| eA,B,C,D,E,F | The phase back electromotive forces. |
| Lls,ms | Self-inductance and mutual inductance of the stator windings. |
| δ1,2 | Allocation coefficients of the compensation voltages in α-β coordinate. |
| ΨF | The magnetic flux linkage of the phase-F stator winding. |
| Fl | The permanent magnet flux linkage. |
| ω | The electric angular velocity. |
| n | Rotor speed. |
References
- Li, Z.; Khajepour, A.; Song, J. A comprehensive review of the key technologies for pure electric vehicles. Energy 2019, 182, 824–839. [Google Scholar] [CrossRef]
- Sun, T.; Wang, J. Extension of Virtual-Signal-Injection-Based MTPA Control for Interior Permanent-Magnet Synchronous Machine Drives Into the Field-Weakening Region. IEEE Trans. Ind. Electron. 2015, 62, 6809–6817. [Google Scholar] [CrossRef]
- Zhao, W.; Zheng, J.; Wang, J.; Liu, G.; Zhao, J.; Fang, Z. Design and Analysis of a Linear Permanent-Magnet Vernier Machine With Improved Force Density. IEEE Trans. Ind. Electron. 2016, 63, 2072–2082. [Google Scholar] [CrossRef]
- Mohammadpour, A.; Parsa, L. Global Fault-Tolerant Control Technique for Multiphase Permanent-Magnet Machines. IEEE Trans. Ind. Appl. 2015, 51, 178–186. [Google Scholar] [CrossRef]
- Immovilli, F.; Bianchini, C.; Lorenzani, E.; Bellini, A.; Fornasiero, E. Evaluation of Combined Reference Frame Transformation for Interturn Fault Detection in Permanent-Magnet Multiphase Machines. IEEE Trans. Ind. Electron. 2015, 62, 1912–1920. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, C. Elimination of Harmonic Currents Using a Reference Voltage Vector Based-Model Predictive Control for a Six-Phase PMSM Motor. IEEE Trans. Power Electron. 2019, 34, 6960–6972. [Google Scholar] [CrossRef]
- Arafat, A.K.M.; Choi, S. Optimal Phase Advance Under Fault-Tolerant Control of a Five-Phase Permanent Magnet Assisted Synchronous Reluctance Motor. IEEE Trans. Ind. Electron. 2018, 65, 2915–2924. [Google Scholar] [CrossRef]
- Che, H.S.; Duran, M.J.; Levi, E.; Jones, M.; Hew, W.-P.; Rahim, N.A. Postfault Operation of an Asymmetrical Six-Phase Induction Machine With Single and Two Isolated Neutral Points. IEEE Trans. Power Electron. 2014, 29, 5406–5416. [Google Scholar] [CrossRef]
- Dwari, S.; Parsa, L. An Optimal Control Technique for Multiphase PM Machines Under Open-Circuit Faults. IEEE Trans. Ind. Electron. 2008, 55, 1988–1995. [Google Scholar] [CrossRef]
- Feng, G.; Lai, C.; Li, W.; Han, Y.; Kar, N.C. Computation-Efficient Solution to Open-Phase Fault Tolerant Control of Dual Three-Phase Interior PMSMs With Maximized Torque and Minimized Ripple. IEEE Trans. Power Electron. 2021, 36, 4488–4499. [Google Scholar] [CrossRef]
- Feng, G.; Lai, C.; Peng, W.; Kar, N.C. Decoupled Design of Fault-Tolerant Control for Dual-Three-Phase IPMSM With Improved Memory Efficiency and Reduced Current RMS. IEEE Trans. Transp. Electrif. 2022, 8, 1144–1154. [Google Scholar] [CrossRef]
- Xue, C.; Song, W.; Wu, X.; Feng, X. A Constant Switching Frequency Finite-Control-Set Predictive Current Control Scheme of a Five-Phase Inverter With Duty-Ratio Optimization. IEEE Trans. Power Electron. 2018, 33, 3583–3594. [Google Scholar] [CrossRef]
- Xiong, C.; Xu, H.; Guan, T.; Zhou, P. A Constant Switching Frequency Multiple-Vector-Based Model Predictive Current Control of Five-Phase PMSM With Nonsinusoidal Back EMF. IEEE Trans. Ind. Electron. 2020, 67, 1695–1707. [Google Scholar] [CrossRef]
- Gonzalez-Prieto, I.; Duran, M.J.; Aciego, J.J.; Martin, C.; Barrero, F. Model Predictive Control of Six-Phase Induction Motor Drives Using Virtual Voltage Vectors. IEEE Trans. Ind. Electron. 2018, 65, 27–37. [Google Scholar] [CrossRef]
- Tao, T.; Zhao, W.; Du, Y.; Cheng, Y.; Zhu, J. Simplified Fault-Tolerant Model Predictive Control for a Five-Phase Permanent-Magnet Motor With Reduced Computation Burden. IEEE Trans. Power Electron. 2020, 35, 3850–3858. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, C. Multi-Vector-Based Model Predictive Torque Control for a Six-Phase PMSM Motor With Fixed Switching Frequency. IEEE Trans. Energy Convers. 2019, 34, 1369–1379. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Z.; Xu, Z.; Wang, W.; Wang, B.; Zou, Z. Deadbeat Predictive Current Control-Based Fault-Tolerant Scheme for Dual Three-Phase PMSM Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1591–1604. [Google Scholar] [CrossRef]
- Sen, B.; Wang, J. Stationary Frame Fault Tolerant Current Control of Poly-phase Permanent Magnet Machines under Open-Circuit and Short-Circuit Faults. IEEE Trans. Power Electron. 2015, 31, 4684–4696. [Google Scholar] [CrossRef]
- AbdulRahman, A.; Galassini, A.; Degano, M.; Buticchi, G.; Cristian Pesce, G.; Gerada, C.; Bozhko, S.; Almurib, H.A.F. Open and Short Circuit Post-Fault Control Strategies for Multi-Three-Phase Interior Permanent Magnet Machines. IEEE Trans. Energy Convers. 2022, 37, 163–174. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, G.; Zhao, W.; Yu, X.; Gao, M. Dynamic Performance Improvement of Five-Phase Permanent-Magnet Motor With Short-Circuit Fault. IEEE Trans. Ind. Electron. 2018, 65, 145–155. [Google Scholar] [CrossRef]









| Parameter | Value |
|---|---|
| Number of pole pairs | 3 |
| Stator resistance (R, Ω) | 0.8 |
| Stator winding self-inductance (Lls, mH) | 1.46 |
| Stator winding mutual inductance (Lms, mH) | 1.06 |
| Fundamental flux linkage of the rotor permanent magnet pole (Fl, Wb) | 0.30 |
| Rotational inertia (kg·m2) | 0.015 |
| Rated torque (N·m) | 30 |
| Parameter | Short-Circuit Fault without Fault-Tolerant Control | Fault-Tolerant Control of the System with the Isolated Neutral Point | Fault-Tolerant Control of the System with the Connected Neutral Point |
|---|---|---|---|
| The amplitude of phase-A current (IA, A) | 7.5 | 7.8 | 18.0 |
| The amplitude of phase-B current (IB, A) | 7.5 | 23.5 | 19.0 |
| The amplitude of phase-C current (IC, A) | 7.5 | 23.5 | 19.0 |
| The amplitude of phase-D current (ID, A) | 29.5 | 6.5 | 18.7 |
| The amplitude of phase-E current (IE, A) | 29.8 | 6.5 | 6.5 |
| The amplitude of short-circuit phase current (ISC, A) | 17.9 | 17.9 | 17.9 |
| The amplitude of inverter phase-A output current (IAI, A) | 7.5 | 7.8 | 18.0 |
| The amplitude of inverter phase-B output current (IBI, A) | 7.5 | 23.5 | 19.0 |
| The amplitude of inverter phase-C output current (ICI, A) | 7.5 | 23.5 | 19.0 |
| The amplitude of inverter phase-D output current (IDI, A) | 29.5 | 6.5 | 18.7 |
| The amplitude of inverter phase-E output current (IEI, A) | 29.8 | 6.5 | 6.5 |
| The amplitude of inverter phase-F output current (IFI, A) | 57.1 | 0 | 0 |
| Total copper loss (W) | 898.9 | 628.1 | 703.3 |
| Winding current maximum reduction percentage (%) | / | 21.14 | 36.24 |
| Inverter current maximum reduction percentage (%) | / | 58.84 | 66.73 |
| Winding copper loss maximum reduction percentage (%) | / | 30.13 | 21.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, F.; Yao, F.; Li, Z. A Torque-Compensated Fault-Tolerant Control Method for Electric Vehicle Traction Motor with Short-Circuit Fault. Sustainability 2022, 14, 13853. https://doi.org/10.3390/su142113853
Hou F, Yao F, Li Z. A Torque-Compensated Fault-Tolerant Control Method for Electric Vehicle Traction Motor with Short-Circuit Fault. Sustainability. 2022; 14(21):13853. https://doi.org/10.3390/su142113853
Chicago/Turabian StyleHou, Feiyu, Fei Yao, and Zheng Li. 2022. "A Torque-Compensated Fault-Tolerant Control Method for Electric Vehicle Traction Motor with Short-Circuit Fault" Sustainability 14, no. 21: 13853. https://doi.org/10.3390/su142113853
APA StyleHou, F., Yao, F., & Li, Z. (2022). A Torque-Compensated Fault-Tolerant Control Method for Electric Vehicle Traction Motor with Short-Circuit Fault. Sustainability, 14(21), 13853. https://doi.org/10.3390/su142113853






