Spatial Heterogeneity of the Recovery of Road Traffic Volume from the Impact of COVID-19: Evidence from China

Abstract

The impact of COVID-19 on traffic volume makes it essential to study the spatial heterogeneity and impact mechanisms of the recovery of road traffic volume to promote the sustainability of related industries. As the research method, this study used a principal component analysis to evaluate the recovery of road traffic volume in China quantitatively, and further conducted an empirical study using a spatial autocorrelation index and a dynamic spatial panel model. The results show that income has a negative impact on the recovery of road traffic volume, while climate suitability has a positive impact. Economic development and COVID-19 can play moderating and mediating effects, respectively. From the aspect of spatial heterogeneity, the recovery of road traffic volume has a positive spatial spillover effect on the surrounding provinces, while the spread of COVID-19 has a negative short-term indirect spatial spillover effect. Corresponding practical insights are provided for the stakeholders based on the above findings. The results of this study will contribute to the development of effective policies to facilitate the recovery of road traffic volume from the impact of COVID-19 and the revitalization of the transportation industry.

1. Introduction

In early 2020, the COVID-19 pandemic spread rapidly, causing a widespread public health crisis [1]. Major countries and regions worldwide adopted non-pharmaceutical interventions as one of the main strategies to contain the pandemic [2]. These measures negatively affected the transport sector, with traffic in the United Kingdom down by over 60% and traffic in Europe falling by 70% [3]. The combined output of the passenger traffic sector in China dropped by 11.44% [4], while intercity traffic fell by 51.35% [5].

Several studies have reported a causal relationship between the lockdown measures imposed against COVID-19 and the decline in road traffic volume [6]. For example, Aloi et al. confirmed the negative impact of lockdown and quarantine measures on road traffic volume based on recorded data from traffic control cameras and environmental sensors [7]. A similar finding was verified in a series of empirical studies in regions such as China [8], Portugal [9], and Canada [10]. From another perspective, the impact of lockdown measures can also be found in the air [11] and railway [12] traffic volume and has negatively affected the revitalization of the transportation industry.

In addition to the lockdown measures, the negative impact of pandemics on traffic volume can be found in terms of tourist psychology [13] and the quality of road service [14]. Specifically, the perceived threat of COVID-19 can reduce people’s subjective willingness to travel across regions [15]. The impact of this mechanism may be influenced by individual attitudes toward the pandemic and previous experience with infection [16]. Furthermore, according to Luan et al., the COVID-19 pandemic could not only change people’s travel patterns, but also significantly affect their willingness to purchase traffic tools and may lead to a decrease in traffic volume [17].

Because of the strong relationship between traffic volume and economic development [18], the recovery of traffic volume from the impact of COVID-19 has an essential role in promoting economic recovery [19]. Therefore, a feasible way to recover traffic volume has been the focus of recent academic discussions. Several empirical studies have shed some light on the effects of COVID-19 on air [20] and urban public [21] transport volume and have further discussed practical measures to promote recovery. A basic consensus among the studies is that there is a significant change in traffic behavior, which can be manifested as decision preferences [22] or traffic modes [23], potentially leading to a decrease in the efficiency of traditional traffic management methods [24]. For example, Cruz et al. suggest that traffic companies should adjust their operational strategies promptly to cope with the negative impact of COVID-19 [25]. Similar findings have been identified in France [26] and Greece [27].

The above studies reflect the broad concern of scholars regarding the pandemic crisis. However, few studies have taken quantitative approaches to the spatial heterogeneity of the recovery of road traffic volume, which is of essential academic and practical significance in promoting the sustainability of related industries. Specifically, the research question in this paper is whether there are factors that can influence the recovery of road traffic volume from the impact of COVID-19. Further, if there are factors that can have an impact, whether this impact is influenced by mediating or moderating effects of other factors or whether it is spatially heterogeneous. To investigate these questions, based on provincial spatial panel data in mainland China, we test the spatial spillover effect of the recovery of road traffic volume from the impact of COVID-19 using a dynamic spatial panel model. Furthermore, we investigate the mechanisms and the robustness of the findings under different spatial weight matrices. Compared with existing studies, the contributions of this paper are as follows:

(1)

A quantitative evaluation method of the recovery of road traffic volume based on a principal component analysis is proposed.

(2)

The above quantitative evaluation methods and dynamic spatial panel models are applied to test the spatial heterogeneity of the recovery of road traffic volume in China.

(3)

The mechanism of the above spatial heterogeneity is discovered through the mediating effect test and the decomposition of the spatial–temporal effect.

The remaining sections of this paper are organized as follows. Section 2 reviews the relevant literature and presents the research hypotheses. Section 3 reports the methodology used for the study and the construction of variables. Section 4 reports the process and results of the empirical study. Section 5 discusses the findings of the empirical study, makes policy recommendations, and compares the results with existing studies. Section 6 summarizes the conclusions of this paper and presents further research perspectives.

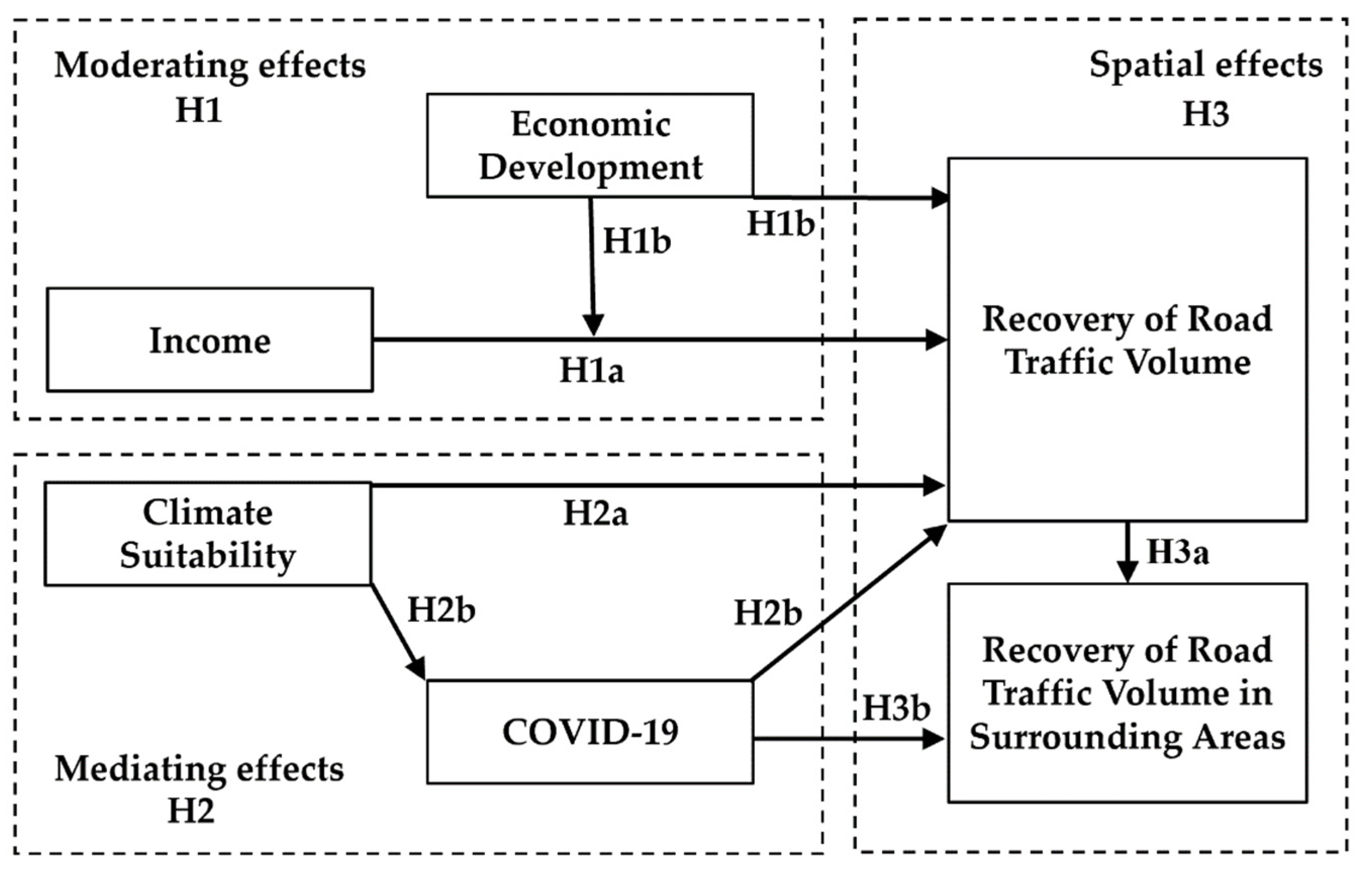
2. Literature Review and Hypotheses

2.1. Income and Economic Development

As an essential part of the transport industry, road traffic has long been one of the major modes of transport [28]. It has better destination accessibility than other modes of transport, such as rail or air [29]. Since the 1980s, the analysis of factors influencing road traffic volume has gradually attracted more and more attention. For example, Gu et al. used the Bayesian combination model [30], the neural network model [31], and other algorithms to test the possible effect of factors such as economic development on road traffic volume. In general, areas with higher income and economic development have higher road traffic volume, a phenomenon supported by studies from the United States [32] and Greece [33].

The above studies illustrate the impact of income and economic development on road traffic volume. However, two issues remain for further empirical study. First, according to Valdes et al., the share of non-essential traffic demand, such as tourism, in overall traffic demand is higher in areas with higher income [34]. This non-essential traffic demand is more negatively affected by COVID-19 than the essential traffic demand, such as seasonal population movement, making it more difficult to recover to the same level as the pre-pandemic level [35]. Therefore, the recovery of road traffic volume in areas with higher income may be relatively low. Meanwhile, economic development can generally lead to a rise in income [36], potentially having a moderating effect in the latter’s mechanism on road traffic volume. Based on this, the following hypotheses are proposed:

Hypothesis 1a (H1a).

Income has a negative effect on the recovery of road traffic volume.

Hypothesis 1b (H1b).

Economic development has a moderating effect in the mechanism of income on the recovery of road traffic volume.

2.2. COVID-19 and Climate Suitability

Since the rapid spread of COVID-19, many scholars have studied the adverse impact of the pandemic on road traffic volume. According to a study by Macioszek et al. based on remote sensing video, the pandemic had a widespread negative impact on traffic volume and led to changes in the characteristics of the temporal distribution of road traffic volume [37]. Many studies point to the lockdown measures [11] and changes in tourist psychology [38] as the main reasons for the negative impact of the pandemic on traffic volume. Specifically, due to the concern of potential travelers about the infection, road traffic volume tended to decrease with the increase of confirmed COVID-19 cases [19]. Several studies have confirmed the existence of this adverse effect in regions such as China [8], the United States [39], and Korea [40].

Furthermore, climate suitability has also been widely considered to affect road traffic volume. Excessively cold weather can lead to a decrease in the travel intentions of potential travelers and, in turn, have a negative impact on road traffic volume, a phenomenon that has been observed in the United States [41] and Canada [42]. In addition to temperature, several studies have pointed out that rainfall [43], floods [44], and other weather events [45] may also have a significant impact on road traffic volume. In particular, according to Bi et al., the effect of climate suitability on road traffic volume varies with urban spatial layout and geographical conditions [46], which suggests the importance of further research using spatial panel models.

From another point of view, there is a strong link between climatic suitability and COVID-19, whereby climatic factors can determine the transmission characteristics of the pandemic. Several empirical studies based in Australia [47], the United States [48], and other regions have demonstrated the impact of climatic factors in the epidemiological process of COVID-19 and confirmed that COVID-19 is more transmissible in areas at higher latitudes with lower temperatures [49]. Climatic suitability can have both a direct effect on road traffic volume and an indirect influence on the ability of COVID-19 to spread. Therefore, COVID-19 may be an essential part of the mechanism of climate suitability on road traffic volume and may play a mediating effect. Based on this, the following hypotheses are proposed:

Hypothesis 2a (H2a).

Climate suitability has a positive effect on the recovery of road traffic volume.

Hypothesis 2b (H2b).

COVID-19 has a mediating effect in the mechanism of climate suitability on the recovery of road traffic volume.

2.3. Spatial Spillover Effect

According to Tobler’s first law of geography, there is a specific spatial correlation between any two subjects, and this correlation always strengthens as the distance between the subjects decreases [50]. Therefore, when considering econometric models, ignoring the spatial factor will lead to biased estimation results, a phenomenon known as the spatial effect [51]. Since the 1990s, the spatial effect has been increasingly used in traffic research. Many scholars support the existence of spatial effects when considering the factors influencing road traffic volume [52]. Specifically, this can be reflected in the spatial correlation of road traffic volume within cities [53] and the spatial spillover effect across cities and provinces [54]. The spatial effect may also be present in the processes of the recovery of road traffic volume from the impact of COVID-19.

In addition to the direct spatial spillover effect generated by road traffic volume, other factors may also spatially affect road traffic volume in the surrounding area. This mechanism is known as the indirect spatial spillover effect [55]. Zhang et al. showed that COVID-19 could significantly affect the economic development of the surrounding area through the indirect spatial spillover effect [56]. From the perspective of travelers’ psychology, when the spread of COVID-19 occurs in the surrounding area, potential travelers may cancel their travel plans to avoid the risk of contracting the disease [57]. Therefore, the indirect spatial spillover effect of COVID-19 may affect the recovery of road traffic volume in the surrounding province. Based on this, the following hypotheses are proposed:

Hypothesis 3a (H3a).

The recovery of road traffic volume has a positive direct spatial spillover effect on the surrounding province.

Hypothesis 3b (H3b).

COVID-19 has a negative indirect spatial spillover effect on the recovery of road traffic volume in the surrounding province.

Figure 1 shows the research hypotheses and model framework of this study. Among them, H1a represents the effect of income on the recovery of road traffic volume, and H1b represents the moderating effect of economic development on this mechanism, which together constitute the first part of the hypotheses of this study. Similarly, H2a represents the effect of climate suitability on the recovery of road traffic volume, and H2b represents the mediating effect of COVID-19, which together constitute the second part of the hypotheses. In the third part of the hypotheses, H3a represents the direct spatial spillover effect of local traffic volume on the surrounding region, and H3b represents the indirect spatial spillover effect of COVID-19. The hypotheses of each part are distinguished using dashed lines.

3. Methods and Data

The Data Flow Chart for this study is shown in Figure 2, where we describe all the methodological steps. In the remainder of this section, we detail each method’s specifics and the data’s processing.

3.1. Principal Component Analysis

Representative indicators such as road passenger turnover and transportation volume can be used to evaluate road traffic volume [58]. In line with Yang et al., to comprehensively reflect the actual situation of each relevant indicator, this paper adopts a principal component analysis (PCA) to reduce the dimensionality of the above indicators [59]. PCA aims to reflect the typical characteristics of the data with as little information as possible. It has the advantages of high information retention and can effectively avoid the problem of multicollinearity [60]. Suppose there are R samples and B indicators, represented by vectors as P = ($P_1$, $P_2$, …, $P_{\mathrm{B}}$), where $P_{\mathrm{B}}$ = ($p_{1b}$, $p_{2b}$, …, $p_{RB}{)}^t$, $p_{rb}$ represents the observation of the rth sample (r = 1, 2, …, R) on the bth (b = 1, 2, …, B) index. At this point, the cth principal component can be expressed as follows:

$${\mathit{Z}}_c={\displaystyle \sum }_{b=1}^B{a}_{bc}{X}_b$$

(1)

In Equation (1), $Z_c$ is the value of the cth principal component and $a_{bc}$ is the loading of the bth index in the cth principal component.

3.2. Spatial Autocorrelation

To study the spatial heterogeneity of road traffic volume, we should first test whether there is significant spatial autocorrelation. In this paper, we adopt Moran’s I to evaluate the spatial autocorrelation [61], which can be expressed as follows:

$$I_t=\frac{N}{S_0}\times \frac{{{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{j=1}^N{\mathit{W}}_{ij} \left(M_{it} - \overline{M_t}\right)\left(M_{jt} - \overline{M_t}\right)}{{{\displaystyle \sum }}_{i=1}^N{\left(M_{it} - \overline{M_t}\right)}^2}$$

(2)

In Equation (2), $I_t$ is Moran’s I in period t; N is the number of study areas. $M_{it}$ and $M_{jt}$ are the study data of areas i and j in period t. $\overline{M_t}$ is the mean of the study data in period t. $S_0$ is the sum of all elements in the spatial weight matrix. $W_{ij}$ is the spatial weight matrix. The range of Moran’s I is [−1, 1]. When Moran’s I is significantly not equal to 0, it can be considered that there is spatial autocorrelation; when it is greater than 0, there is positive spatial autocorrelation, and when the opposite is the case, there is negative spatial autocorrelation. We mainly consider the distance weight matrix ${\mathit{W}}_{ij}^D$ [62] and the economic distance weight matrix ${\mathit{W}}_{ij}^E$ [63], which are calculated as follows.

$${\mathit{W}}_{ij}^D=\{\begin{array}{c}\frac{1}{D_{ij}^2}, \mathrm{when} i \ne j \\ 0, \mathrm{when} i=j \end{array}$$

(3)

$${\mathit{W}}_{ij}^E=\{\begin{array}{c}\frac{1}{\left|{GDP}_i{ - \mathit{GDP}}_j\right|{\times D}_{ij}}, \mathrm{when} i \ne j \\ 0, \mathrm{when} i=j \end{array}$$

(4)

In Equations (3) and (4), $D_{\mathit{ij}}$ is the Euclidean distance between area i and area j. ${\mathit{GDP}}_i$ and ${\mathit{GDP}}_j$ are the regional GDP per capita in area i and area j.

3.3. Spatial Panel Model

The spatial panel model can be used to identify and deal with the interaction effect between spatial data. The main principle is to incorporate the spatial distribution characteristics of the panel data into the econometric model and to achieve an unbiased estimation of the spatial heterogeneity of the data and its influencing factors [64]. The general nested spatial model can be represented as follows.

$$\{\begin{array}{c}{\mathit{Y}}_t{=\rho \mathit{WY}}_t{+\mathbf{\beta }\mathbf{X}}_t{+\theta \mathit{WX}}_t{+\mathbf{\mu }+\mathit{u}}_t\\ {\mathit{u}}_t{=\mathsf{\lambda }\mathit{Wu}}_t{+\mathbf{\epsilon }}_t \end{array}$$

(5)

In Equation (5), ${\mathit{Y}}_t$ is a vector of the explained variable of order N × 1 in period t (t = 1, 2, 3,…, T), where N is the number of spatial areas in the sample; $\mathit{W}$ is a spatial weight matrix; ρ and $\theta$ are spatial autoregressive coefficients of explained variable and explanatory variables; ${\mathit{WY}}_t$ is the direct spatial spillover effect of the explained variables; ${\mathit{X}}_t$ is the explanatory variables matrix of order N × K, where K is the number of explanatory variables; β is a vector of the coefficient to be estimated of order K × 1, indicating the degree of impact of the explanatory variables on the explained variable; ${\mathit{WX}}_t$ is the indirect spatial spillover effect of the explanatory variables; $\mathbf{\mu }$ is the fixed effect; ${\mathit{u}}_t$ is a vector of interference of order N × 1; $\lambda$ is the autoregressive coefficient of the spatial error; ${\mathit{Wu}}_t$ is the spatial spillover effect of the interference; and ${\mathbf{\epsilon }}_t$ is the regression error.

When θ = 0 and λ = 0, the model is called the spatial lag model (SLM); when θ = 0 and ρ = 0, the model is called the spatial error model (SEM); and when λ = 0, the model is called the spatial Durbin model (SDM). Each of the above models is based on different assumptions and has a different scope of application and study significance [65]. Therefore, the models will be further tested and selected according to the data characteristics. Based on the above GNS model and referring to the studies of Akter et al. in the field of road traffic volume using spatial panel models [45], the econometric model constructed in this study is shown as follows:

$$Y_{\mathit{it}}=\rho {\displaystyle \sum }_{j=1}^N{\mathit{W}}_{\mathit{ij}}{Y}_{\mathit{jt}}{+\beta \mathit{X}}_{\mathit{it}}+\theta {\displaystyle \sum }_{j=1}^N{\mathit{W}}_{\mathit{ij}}{\mathit{X}}_{\mathit{jt}}{+\mu }_{\mathit{it}}{+\epsilon }_{\mathit{it}}$$

(6)

$$Y_{\mathit{it}}=\rho {\displaystyle \sum }_{j=1}^N{\mathit{W}}_{\mathit{ij}}{Y}_{\mathit{jt}}+\gamma {\displaystyle \sum }_{j=1}^N{\mathit{W}}_{\mathit{ij}}{Y}_{\mathit{jt}-1}{+\beta \mathit{X}}_{\mathit{it}}+\theta {\displaystyle \sum }_{j=1}^N{\mathit{W}}_{\mathit{ij}}{\mathit{X}}_{\mathit{jt}}{+\mu }_{\mathit{it}}{+\epsilon }_{\mathit{it}}$$

(7)

In Equation (6), i and j are different areas; t is different times; W is the spatial weight matrix; Y is the explained variable; X is the explanatory and control variables; ρ and $\theta$ are the spatial autoregressive coefficients; μ is the fixed effect; and ε is the regression error. In line with the study of Yang et al. [66], the dynamic spatial panel model is shown in Equation (7) by adding the time lag term.

3.4. Variables and Data Source

3.4.1. Explained Variable

The process of constructing the explained variable in this study is as follows:

$${\mathit{PRR}}_{\mathit{it}}=\frac{{\mathit{PN}}_{\mathit{it}}}{{\mathit{PP}}_{\mathit{it}}}$$

(8)

$${\mathit{TRR}}_{\mathit{it}}=\frac{{\mathit{TN}}_{\mathit{it}}}{{\mathit{TP}}_{\mathit{it}}}$$

(9)

In Equations (8) and (9), ${\mathit{PN}}_{\mathit{it}}$ and ${\mathit{TN}}_{\mathit{it}}$ are road passenger transportation volume and road passenger turnover volume in month t of the year 2021 in province i, respectively; ${\mathit{PP}}_{\mathit{it}}$ and ${\mathit{TP}}_{\mathit{it}}$ are average values of road passenger transportation volume and road passenger turnover volume in month t of the five years before the COVID-19 outbreak (2015 to 2019) in province i, respectively; ${\mathit{PRR}}_{\mathit{it}}$ and ${\mathit{TRR}}_{\mathit{it}}$ are the recovery rate of road passenger transportation volume and road passenger turnover volume in month t of 2021 in province i, respectively. To avoid the influence of multicollinearity, PCA is applied to ${\mathit{PRR}}_{\mathit{it}}$ and ${\mathit{TRR}}_{\mathit{it}}$ dimensionality reduction by province [67].

According to Alemzero et al., Bartlett’s test can be used to test the correlation between variables and to determine whether the variables are independent of each other. Bartlett’s test should be performed first before performing PCA. If the results reject the null hypothesis significantly, then the results of PCA are acceptable [68]. The critical values of Bartlett’s test are given by χ² distribution approximation. Therefore, we performed Bartlett’s test and PCA using Stata 17, and the results are shown in

Table 1. Results of Bartlett’s test and PCA.

Serial Number	Province	Bartlett’s Test	Variance Proportion	Loading 1$\left({\mathit{a}}_{1\mathit{i}}\right)$	Loading 2$\left({\mathit{a}}_{2\mathit{i}}\right)$
1	Beijing	22.091 ***	0.976	0.639	0.769
2	Tianjin	26.698 ***	0.985	0.642	0.766
3	Hebei	16.029 ***	0.971	0.413	0.911
4	Shanxi (1)	21.867 ***	0.981	0.481	0.877
5	Neimenggu	23.930 ***	0.981	0.607	0.794
6	Liaoning	16.339 ***	0.954	0.648	0.761
7	Jilin	30.306 ***	0.992	0.504	0.864
8	Heilongjiang	10.447 ***	0.910	0.646	0.764
9	Shanghai	0.231 ***	0.992	0.678	0.735
10	Jiangsu	20.740 ***	0.976	0.533	0.846
11	Zhejiang	5.421 **	0.844	0.560	0.829
12	Anhui	12.547 ***	0.928	0.690	0.724
13	Fujian	20.639 ***	0.981	0.450	0.893
14	Jiangxi	4.483 **	0.828	0.525	0.851
15	Shandong	18.344 ***	0.965	0.600	0.800
16	Henan	19.752 ***	0.968	0.693	0.720
17	Hubei	14.287 ***	0.956	0.477	0.879
18	Hunan	22.824 ***	0.977	0.657	0.754
19	Guangdong	17.447 ***	0.959	0.663	0.748
20	Guangxi	7.612 ***	0.902	0.460	0.888
21	Hainan	28.674 ***	0.991	0.468	0.884
22	Chongqing	10.260 ***	0.908	0.653	0.757
23	Sichuan	24.980 ***	0.988	0.452	0.892
24	Guizhou	18.830 ***	0.979	0.405	0.914
25	Yunnan	17.805 ***	0.976	0.419	0.908
26	Xizang	12.497 ***	0.971	0.311	0.950
27	Shanxi (2)	17.249 ***	0.986	0.292	0.956
28	Gansu	22.188 ***	0.976	0.662	0.750
29	Qinghai	10.139 ***	0.971	0.256	0.967
30	Ningxia	10.833 ***	0.924	0.546	0.838
31	Xinjiang	17.166 ***	0.959	0.637	0.771

** and *** denote significance at the 5%, and 1% levels.

.

As the Bartlett test results have strong significance and the variance proportion is higher than 85% in most provinces, the PCA results have solid statistical significance and empirical value. As a result, we can obtain the recovery index ${\mathit{Recovery}}_{\mathit{it}}$ of road traffic volume in period t and province i as follows:

$${\mathit{Recovery}}_{\mathit{it}}{=\mathit{PRR}}_{\mathit{it}}{ \times a}_{1i}{+\mathit{TRR}}_{\mathit{it} }{\times a}_{2i}$$

(10)

In Equation (10), $a_{1i}$ and $a_{2i}$ are the PCA loadings of ${\mathit{PRR}}_{\mathit{it}}$ and ${\mathit{TRR}}_{\mathit{it}}$ in the ith province. ${\mathit{Recovery}}_{\mathit{it}}$ is the explained variable in the spatial panel model. Figure 3 shows the recovery index of road traffic volume for March, June, September, and December of 2021 to demonstrate the four quarters. Among them, we label the province serial numbers consistent with Table 1. It can be visualized that the provinces with higher recovery indices and those with lower indices tend to be adjacent, so we perform further analysis to investigate its spatial heterogeneity.

3.4.2. Explanatory and Control Variables

We take the per capita disposable income, per capita gross domestic product, temperature and humidity index (THI), and the number of confirmed COVID-19 cases as the explanatory variables. All of the above variables are widely considered suitable explanatory variables for studying income and economic development [69], climate suitability [70], and the spread of COVID-19 [71]. The Chow-Lin frequency transformation method is applied to convert some quarterly data into monthly data. This method has a good conversion effect and is widely used in social science research [72].

Some studies have also pointed out that air quality [73] and season [74] may impact road traffic volume. Therefore, these two factors are added to the model as control variables to avoid endogeneity problems caused by omitted variables. The air quality indicator is the air quality index (AQI). According to the existing air pollution classification standards in China, the monthly average value of AQI in most provinces falls in the same interval, which cannot reflect the control effect. Therefore, Jenks natural breaks is adopted to categorize AQI [75]. As a result, AQI = 1 represents the best air quality, and AQI = 5 represents the worst. For the seasonal index, in line with Liu et al., the season is assigned a value of 1 for the period from June to August and 0 for the rest of the year [76]. The above variables constitute the balanced panel data used for the empirical study. The time series length is 12, representing January to December of 2021, and the cross-section is 31, representing all 31 provinces in mainland China.

Table 2. Description and statistics of variables.

Category	Variable	Description	Source	Expected Effect	Mean	Median	Min	Max	SD
Explained Variable	Recovery	Recovery index of road traffic volume	Ministry of Transport of the People’s Republic of China and authors computation	/	54.031	50.392	15.288	129.056	19.277
Explanatory Variables	THI	THI index	National Meteorological Administration of the People’s Republic of China	+	57.946	59.220	11.363	81.532	15.362
	Income	Disposable income per capita	National Bureau of Statistics of the People’s Republic of China	−	2914.489	2557.016	1447.334	7182.954	1175.549
	Economic	GDP per capita	National Bureau of Statistics of the People’s Republic of China	−	6636.535	5666.043	2830.190	16,542.862	2956.007
	COVID-19 Cases	Number of confirmed cases of COVID-19	National Health Commission of the People’s Republic of China	−	40.987	6	0	1514	121.636
Control Variables	AQI	Level of air pollution	National Meteorological Administration of the People’s Republic of China and authors computation	/	2.543	2	1	5	1.104
	Season	Seasonal index	Authors computation	/	0.250	0	0	1	0.434

shows the description and statistics of the variables.

4. Results

4.1. Spatial Autocorrelation Index

Table 3. Spatial autocorrelation index.

Month	Moran’s I	Z-Value	p-Value	Spatial Pattern
January	−0.112	−0.580	0.562	Random
February	0.326	2.678	0.007	Positive
March	0.126	1.216	0.224	Random
April	0.225	1.992	0.046	Positive
May	0.119	1.129	0.259	Random
June	0.270	2.241	0.025	Positive
July	0.300	1.511	0.012	Positive
August	0.544	4.622	0.000	Positive
September	0.443	3.740	0.000	Positive
October	0.333	2.724	0.006	Positive
November	0.406	3.333	0.001	Positive
December	0.331	2.752	0.006	Positive

shows the results of Moran’s I and the corresponding two-tailed test for recovery from January to December 2021. On the whole, Moran’s I has values in the range of −0.112 to 0.544 and is significant at the 1% confidence level in most periods. It is positive except for January, indicating that the recovery of road traffic volume in mainland China shows a significant positive spatial autocorrelation. Provinces with better and worse recovery tend to be spatially adjacent.

The results of Moran’s I suggest a spatial autocorrelation in the recovery of road traffic volume during the pandemic, indicating that it is scientific and necessary to consider the spatial effect in further empirical studies.

4.2. Tests of Spatial Panel Models

To further test the spatial heterogeneity of the recovery of road traffic volume and its mechanism, we use spatial panel models for the empirical analysis. Each continuous-type variable is log-transformed to clarify the economic significance of the results. Furthermore, based on the distance weight matrix and economic distance weight matrix, the Lagrange multiplier (LM) test, Wald test, likelihood ratio (LR) test, and Hausman test are adopted to screen the spatial panel model [77].

Table 4. Tests of spatial panel models.

Tests	Distance Weight Matrix	Economic-Distance Weight Matrix
LM spatial lag	49.752 ***	18.782 ***
Robust LM spatial lag	36.218 ***	44.302 ***
LM spatial error	28.911 ***	8.136 ***
Robust LM spatial error	15.377 ***	33.656 ***
Wald spatial lag	11.837	15.448
Wald spatial error	17.145 *	18.487 **
LR spatial lag	11.731	15.198
LR spatial error	17.327 *	18.096 *
Hausman for SLM	151.71 ***	46.95 ***
Hausman for SDM	76.53 ***	108.49 ***

*, **, and *** denote significance at the 10%, 5%, and 1% levels.

shows the results.

As Table 4 shows, the study data passed the LM test and robust LM test with high significance, indicating that the ordinary least squares estimate for the study data is biased and that the spatial lag effect and spatial error effect exist simultaneously [78]. The results of the Wald test and LR test are generally consistent, both of which can significantly reject the possibility of degenerating SDM into SEM but cannot reject the possibility of degenerating SDM into SLM. Therefore, we combine the log-likelihood, the Akaike information criterion (AIC), and the Bayesian information criterion (BIC) to make a comprehensive judgment on the validity of SLM and SDM [79]. Meanwhile, the Hausman test for both SLM and SDM can reject the null hypothesis at the 1% significance level. Therefore, the fixed-effect model is chosen for further research [80]. The results tested based on the economic-distance weight matrix are generally consistent with the distance weight matrix, thereby verifying the robustness of the above results.

4.3. Dynamic Spatial Panel Model

Table 5. Empirical results of spatial panel models.

Variables	SLM		SDM		Dynamic SLM		Dynamic SDM
	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6	Model 7	Model 8
COVID-19 Cases	–0.018 ** (–2.289)	–0.016 ** (–2.010)	–0.018 ** (–2.207)	–0.015 * (–1.867)	–0.019 ** (–2.383)	–0.018 ** (–2.144)	–0.018 ** (–2.222)	–0.016 * (–1.941)
THI	0.128 ** (2.561)	0.119 ** (2.322)	0.179 ** (2.564)	0.159 ** (2.255)	0.138 *** (2.722)	0.127 ** (2.455)	0.185 *** (2.647)	0.162 ** (2.303)
Income	–0.396 *** (–4.955)	–5.000 ** (–2.375)	–0.322 *** (–3.621)	–5.110 ** (–2.373)	–0.377 *** (–4.659)	–4.970 ** (–2.361)	–0.314 *** (–3.522)	–5.076 ** (–2.357)
Economic	n.a.	–4.170 ** (–2.181)	n.a.	–4.285 ** (–2.203)	n.a.	–4.145 ** (–2.168)	n.a.	–4.248 ** (–2.183)
Income × Economic	n.a.	0.536 ** (2.188)	n.a.	0.561 ** (2.244)	n.a.	0.535 ** (2.183)	n.a.	0.557 ** (2.227)
AQI = 2	0.072 ** (2.145)	0.070 ** (2.082)	0.087 ** (2.470)	0.088 ** (2.514)	0.072 ** (2.137)	0.070 ** (2.091)	0.089 ** (2.511)	0.090 ** (2.550)
AQI = 3	0.132 *** (3.043)	0.130 *** (2.964)	0.141 *** (2.878)	0.140 *** (2.839)	0.126 *** (2.887)	0.125 *** (2.841)	0.140 *** (2.874)	0.141 *** (2.865)
AQI = 4	0.168 *** (3.115)	0.166 *** (3.045)	0.163 *** (2.623)	0.159 ** (2.557)	0.152 *** (2.781)	0.151 *** (2.747)	0.160 *** (2.581)	0.159 ** (2.560)
AQI = 5	0.249 *** (3.667)	0.241 *** (3.516)	0.244 *** (3.043)	0.231 *** (2.878)	0.221 *** (3.148)	0.215 *** (3.044)	0.239 *** (2.987)	0.231 *** (2.875)
Season	–0.039 (–1.459)	–0.036 (–1.358)	–0.073 (–1.507)	–0.071 (–1.469)	–0.056 * (–1.920)	–0.053 * (–1.824)	–0.077 (–1.593)	–0.073 (–1.507)
W × COVID-19 cases	n.a.	n.a.	–0.029 (–1.118)	–0.018 (–0.584)	n.a.	n.a.	–0.037 (–1.366)	–0.027 (–0.835)
W × THI	n.a.	n.a.	–0.276 (–1.639)	–0.299 * (–1.715)	n.a.	n.a.	–0.287 * (–1.704)	–0.307 * (–1.759)
W × Income	n.a.	n.a.	–0.548* (–1.946)	–11.215 (–1.476)	n.a.	n.a.	–0.495 * (–1.746)	–9.604 (–1.224)
W × Economic	n.a.	n.a.	n.a.	–9.701 (–1.430)	n.a.	n.a.	n.a.	–8.255 (–1.178)
W × Income × Economic	n.a.	n.a.	n.a.	1.192 (1.396)	n.a.	n.a.	n.a.	1.017 (1.156)
W × AQI2	n.a.	n.a.	–0.377 * (–1.661)	–0.460 ** (–2.029)	n.a.	n.a.	–0.369 (–1.627)	–0.447 ** (–1.968)
W × AQI3	n.a.	n.a.	–0.324 (–1.282)	–0.454 * (–1.776)	n.a.	n.a.	–0.354 (–1.396)	–0.459 * (–1.799)
W×AQI4	n.a.	n.a.	–0.338 (–1.312)	–0.459 * (–1.768)	n.a.	n.a.	–0.388 (–1.491)	–0.478 * (–1.834)
W × AQI5	n.a.	n.a.	–0.366 (–1.332)	–0.499 * (–1.793)	n.a.	n.a.	–0.441 (–1.576)	–0.531 * (–1.890)
W × Season	n.a.	n.a.	0.082 (0.831)	0.071 (0.726)	n.a.	n.a.	0.062 (0.625)	0.060 (0.608)
W × Recoveryit	0.771 *** (11.027)	0.777 *** (11.256)	0.749 *** (9.563)	0.751 *** (9.620)	0.765 *** (10.711)	0.771 *** (10.913)	0.753 *** (9.579)	0.752 *** (9.604)
W × Recovery it–1	n.a.	n.a.	n.a.	n.a.	0.148 (1.468)	0.149 (1.484)	0.149 (1.310)	0.099 (0.814)
${\mathrm{R}}^2$	0.240	0.245	0.249	0.270	0.235	0.239	0.249	0.268
Log-likelihood	114.086	116.465	118.267	122.330	114.590	116.973	118.604	122.397
AIC	–208.171	–208.929	–200.533	–200.660	–207.179	–207.946	–199.207	–198.794
BIC	–168.982	–161.903	–129.993	–114.444	–164.072	–157.001	–124.748	–108.660

*, **, and *** denote significance at the 10%, 5%, and 1% levels.

shows the results of the empirical analysis of static and dynamic spatial panel models based on the distance weight matrix. Among them, Model 1 to Model 4 use the static models set in Equation (6); Model 5 to Model 8 use the dynamic models set in Equation (7). Specifically, Model 1 and Model 2 use the static SLM, Model 3 and Model 4 use the static SDM, Model 5 and Model 6 use the dynamic SLM, and Model 7 and Model 8 use the dynamic SDM.

The explained variable in each model is the recovery index of road traffic volume, while the explanatory variables are not exactly the same. To test the moderating effect, the variable Economic representing economic development and the interaction term Income × Economic are added to Model 2, Model 4, Model 6, and Model 8, and the other models represent the results without considering the moderating effect. In addition, AQI has five categorical intervals, so we represent it with four dummy variables to avoid multicollinearity. We add AQI = 2, AQI = 3, AQI = 4, AQI = 5, and Season as control variables to the model to control the effects of air quality and season on road traffic volume. We report the interaction terms of the spatial weight matrix and the explanatory variables, which can respond to the spatial spillover effects of the explanatory variables.

Comparing the performance of SLM and SDM on log-likelihood, AIC, BIC, and other indicators, it can be seen that the fitting effect of SLM is better than that of SDM. Therefore, further analysis will be mainly based on the results of SLM. In Model 1, the coefficient of income is significantly negative, indicating that it has a significant negative impact on the recovery of road traffic volume, and hypothesis H1a is supported.

In Model 2, the coefficients of Income and Economic are found to be negative. The coefficient of the interaction term is significantly positive, indicating that economic development and income have a significant negative impact on the recovery of road traffic volume, and economic development can play a positive moderating effect, and hypothesis H1b is supported. Additionally, in Model 3 and Model 4, which are based on SDM, the coefficients of the main explanatory variables are generally consistent with other models, indicating that the above results are robust.

The empirical results of each explanatory variable in Model 5 to Model 8 are generally consistent with those of the static spatial panel, proving that the spatial panel models are less affected by endogeneity. W × Recovery_it, representing spatial effect, is significantly positive in Model 1 to Model 8, indicating that the recovery of road traffic volume will be affected by the positive spatial spillover effect of the current situation in the surrounding provinces. Therefore, hypothesis H3a is supported.

4.4. Robustness Tests

The distance weight matrix is replaced with the economic distance weight matrix for robustness testing.

Table 6. Robustness and endogeneity tests.

Variables	SLM		SDM		Dynamic SLM		Dynamic SDM
	Model 9	Model 10	Model 11	Model 12	Model 13	Model 14	Model 15	Model 16
COVID-19 Cases	–0.021 ** (–2.412)	–0.021 ** (–2.318)	–0.020 ** (–2.334)	–0.022 ** (–2.407)	–0.021 ** (–2.451)	–0.022 ** (–2.401)	−0.020 ** (−2.341)	−0.022 ** (−2.440)
THI	0.197 *** (3.602)	0.184 *** (3.265)	0.213 *** (3.695)	0.190 *** (3.183)	0.205 *** (3.724)	0.190 *** (3.368)	0.212 *** (3.678)	0.188 *** (3.142)
Income	–0.498 *** (–5.609)	–4.545 * (–1.927)	–0.426 *** (–4.643)	–4.373 * (–1.860)	–0.490 *** (–5.514)	–4.606 * (–1.956)	−0.426 *** (−4.642)	−4.397 * (−1.870)
Economic	n.a.	–3.611 * (–1.686)	n.a.	–3.505 (–1.642)	n.a.	–3.658 * (–1.710)	n.a.	−3.522 * (−1.650)
Income × Economic	n.a.	0.471 * (1.715)	n.a.	0.457 * (1.672)	n.a.	0.479 * (1.746)	n.a.	0.459 * (1.681)
AQI = 2	0.074 ** (1.976)	0.075 ** (1.978)	0.074 * (1.957)	0.073 * (1.928)	0.073 * (1.955)	0.074 ** (1.972)	0.074 * (1.957)	0.073 * (1.927)
AQI = 3	0.156 *** (3.205)	0.158 *** (3.217)	0.146 *** (2.972)	0.145 *** (2.935)	0.149 *** (3.054)	0.152 *** (3.089)	0.146 *** (2.978)	0.146 *** (2.937)
AQI = 4	0.219 *** (3.647)	0.222 *** (3.662)	0.192 *** (3.050)	0.192 *** (3.033)	0.206 *** (3.380)	0.209 *** (3.415)	0.192 *** (3.056)	0.192 *** (3.035)
AQI = 5	0.338 *** (4.484)	0.338 *** (4.432)	0.294 *** (3.797)	0.289 *** (3.677)	0.317 *** (4.124)	0.317 *** (4.093)	0.295 *** (3.802)	0.289 *** (3.679)
Season	−0.054 * (−1.830)	−0.050 * (−1.680)	−0.049 (−1.422)	−0.042 (−1.205)	−0.063 ** (−2.067)	−0.059 * (−1.927)	−0.049 (−1.418)	−0.042 (−1.204)
W × COVID-19 Cases	n.a.	n.a.	–0.079 (–1.106)	–0.081 (–1.092)	n.a.	n.a.	−0.088 (−1.115)	−0.101 (−1.204)
W × THI	n.a.	n.a.	–0.272 (–0.585)	–0.176 (–0.377)	n.a.	n.a.	−0.263 (−0.564)	−0.156 (−0.333)
W × Income	n.a.	n.a.	–3.094 ** (–2.310)	50.928 (0.861)	n.a.	n.a.	−3.017 ** (−2.205)	52.267 (0.883)
W × Economic	n.a.	n.a.	n.a.	49.643 (0.909)	n.a.	n.a.	n.a.	50.794 (0.930)
W × Income × Economic	n.a.	n.a.	n.a.	–6.266 (–0.911)	n.a.	n.a.	n.a.	−6.400 (−0.930)
W × AQI2	n.a.	n.a.	−1.662 (−1.167)	−1.174 (−0.772)	n.a.	n.a.	−1.665 (−1.169)	−1.183 (−0.775)
W × AQI3	n.a.	n.a.	−1.519 (−1.049)	−1.059 (−0.682)	n.a.	n.a.	−1.512 (−1.044)	−1.064 (−0.684)
W × AQI4	n.a.	n.a.	−0.876 (−0.608)	−0.391 (−0.248)	n.a.	n.a.	−0.846 (−0.582)	−0.387 (−0.246)
W × AQI5	n.a.	n.a.	−0.775 (−0.514)	−0.221 (−0.134)	n.a.	n.a.	−0.708 (−0.454)	−0.200 (−0.119)
W × Season	n.a.	n.a.	−0.222 (−0.913)	−0.246 (−1.011)	n.a.	n.a.	−0.212 (−0.833)	−0.242 (−0.950)
W × Recoveryit	0.815 *** (3.287)	0.824 *** (3.341)	0.602 ** (2.146)	0.627 ** (2.244)	0.810 *** (3.229)	0.820 *** (3.284)	0.609 ** (2.168)	0.642 ** (2.297)
W × Recoveryit–1	n.a.	n.a.	n.a.	n.a.	0.415 (1.340)	0.451 (1.456)	0.116 (0.267)	0.224 (0.506)
${\mathrm{R}}^2$	0.226	0.232	0.247	0.254	0.227	0.233	0.246	0.252

*, **, and *** denote significance at the 10%, 5%, and 1% levels.

shows the results.

Comparative analysis of Table 5 and Table 6 shows that the empirical results of the models constructed with different spatial weight matrices do not differ significantly, indicating that the effect of explanatory variables on the recovery is robust. In Model 10 and Model 12, the coefficient of the interaction term is significantly positive, consistent with the results before replacing the spatial weight matrix, thereby verifying the robustness of the moderating effect.

4.5. Mediating Effect and Spatial Effect Decomposition

In line with Jin et al. [81], a stepwise method is used to test the mediating effect based on the dynamic SLM to test hypotheses H2a and H2b.

Table 7. Results of the mediating effect tests.

Variables	Distance Weight Matrix				Economic-Distance Weight Matrix
	Model 17	Model 18	Model 19	Model 8	Model 20	Model 21	Model 22	Model 16
COVID-19 Cases	n.a.	–0.023 *** (–2.953)	n.a.	–0.018 ** (–2.144)	n.a.	–0.031 *** (–3.526)	n.a.	–0.022 ** (–2.401)
THI	0.158 *** (3.185)	n.a.	–1.672 *** (–5.063)	0.127 ** (2.455)	0.230 *** (4.254)	n.a.	–1.926 *** (–6.307)	0.190 *** (3.368)
Income	–5.361 ** (–2.544)	–5.399 ** (–2.560)	20.853 (1.579)	–4.970 ** (–2.361)	–5.067 ** (–2.142)	–5.217 ** (–2.190)	21.656 (1.620)	–4.606 * (–1.956)
Economic	–4.567 ** (–2.390)	–4.418 ** (–2.303)	22.136 * (1.847)	–4.145 ** (–2.168)	–4.159 * (–1.939)	–4.028 * (–1.859)	23.439 * (1.933)	–3.658 * (–1.710)
Income × Economic	0.580 ** (2.366)	0.576 ** (2.345)	–2.431 (–1.582)	0.535 ** (2.183)	0.533 * (1.935)	0.536 * (1.933)	–2.536 (–1.630)	0.479 * (1.746)
AQI = 2	0.068 ** (2.011)	0.065 * (1.917)	0.137 (0.648)	0.070 ** (2.091)	0.071 * (1.881)	0.066 * (1.727)	0.136 (0.640)	0.074 ** (1.972)
AQI = 3	0.124 *** (2.794)	0.111 ** (2.526)	0.149 (0.540)	0.125 *** (2.841)	0.150 *** (3.030)	0.131 *** (2.638)	0.127 (0.456)	0.152 *** (3.089)
AQI = 4	0.159 *** (2.887)	0.121 ** (2.244)	−0.305 (−0.896)	0.151 *** (2.747)	0.219 *** (3.557)	0.163 *** (2.688)	−0.318 (−0.922)	0.209 *** (3.415)
AQI = 5	0.221 *** (3.121)	0.161 ** (2.386)	−0.146 (−0.340)	0.215 *** (3.044)	0.324 *** (4.148)	0.233 *** (3.133)	−0.134 (−0.309)	0.317 *** (4.093)
Season	−0.060 ** (−2.079)	−0.013 (−0.537)	0.499 *** (2.975)	−0.053 * (−1.824)	−0.070 ** (−2.324)	−0.001 (−0.035)	0.586 *** (3.520)	−0.059 * (−1.927)
W × Recoveryit	0.778 *** (11.152)	0.791 *** (11.677)	n.a.	0.771 *** (10.913)	0.820 *** (3.279)	0.845 *** (3.408)	n.a.	0.820 *** (3.284)
W × Recoveryit–1	0.126 (1.255)	0.123 (1.222)	n.a.	0.149 (1.484)	0.405 (1.298)	0.367 (1.172)	n.a.	0.451 (1.456)
W × COVID-19 Casesit	n.a.	n.a.	0.270 ** (2.328)	n.a.	n.a.	n.a.	0.139 (0.502)	n.a.
W × COVID-19 Casesit–1	n.a.	n.a.	0.038 (0.251)	n.a.	n.a.	n.a.	–0.538 (–1.434)	n.a.
${\mathrm{R}}^2$	0.224	0.236	0.202	0.239	0.220	0.210	0.187	0.233

*, **, and *** denote significance at the 10%, 5%, and 1% levels.

shows the results. Model 17 and Model 18 test the direct effect of COVID-19 Cases and THI on recovery, and the results show that they have significant negative and positive effects, respectively. Model 19 tests the indirect effect of THI on COVID-19 cases, and the results are significantly negative, indicating that COVID-19 has more potent propagation in wet and cold weather. Model 8 tests the total effect of COVID-19 cases and THI on recovery, and the results show that the regression coefficients are significant. The above models constitute a complete test path for the mediating effect, indicating that the spread of COVID-19 can have a significant mediating effect in the mechanism of THI acting on recovery. Therefore, hypotheses H2a and H2b are supported.

In Model 16 and Model 20 to Model 22, we replace the distance weight matrix with the economic distance weight matrix and repeat the above mediating effect test. The results are generally consistent, which illustrates the robustness of the above results.

The spatial–temporal effect decomposition of the dynamic SLM is adopted.

Table 8. Results of spatial–temporal effect decomposition.

Effects	Variables	Distance Weight Matrix				Economic-Distance Weight Matrix
		Model 5		Model 6		Model 13		Model 14
		Short Term	Long Term	Short Term	Long Term	Short Term	Long Term	Short Term	Long Term
Direct effect	COVID-9 Cases	–0.021 ** (–2.518)	–0.023 * (–1.922)	–0.020 ** (–2.252)	–0.022 * (–1.898)	–0.022 *** (–2.583)	–0.023 ** (–2.518)	–0.023 ** (–2.520)	–0.024 ** (–2.376)
	THI	0.155 *** (2.984)	0.172 ** (2.401)	0.143 *** (2.696)	0.160 ** (2.068)	0.213 *** (3.996)	0.221 *** (3.658)	0.198 *** (3.634)	0.206 *** (3.457)
	Income	–0.407 *** (–4.655)	–0.461 *** (–2.722)	–5.422 ** (–2.379)	–6.123 * (–1.781)	–0.495 *** (–5.502)	–0.514 *** (–4.603)	–4.676 ** (–1.982)	–4.882 * (–1.909)
	Economic	n.a.	n.a.	–4.524 ** (–2.187)	–5.112 * (–1.674)	n.a.	n.a.	–3.714 * (–1.735)	–3.879 * (–1.685)
	Income × Economic	n.a.	n.a.	0.584 ** (2.202)	0.660 * (1.686)	n.a.	n.a.	0.486 * (1.772)	0.508 * (1.717)
Indirect effect	COVID-19 Cases	–0.016 ** (–2.081)	–0.035 (–0.624)	–0.016 * (–1.729)	–0.033 (–0.737)	–0.002 * (–1.674)	–0.003 (–0.965)	–0.002 (–1.562)	–0.004 (–0.748)
	THI	0.119 ** (2.424)	0.245 (0.722)	0.115 ** (2.184)	0.235 (0.639)	0.018 * (1.939)	0.035 (0.894)	0.017 ** (2.078)	0.034 (1.106)
	Income	–0.317 *** (–2.876)	–0.696 (–0.725)	–4.420 * (–1.812)	–9.380 (–0.591)	–0.040 ** (–2.149)	–0.080 (–0.873)	–0.403 (–1.476)	–0.828 (–0.835)
	Economic	n.a.	n.a.	–3.693 * (–1.711)	–7.857 (–0.574)	n.a.	n.a.	–0.320 (–1.357)	–0.660 (–0.808)
	Income × Economic	n.a.	n.a.	0.477 * (1.717)	1.014 (0.578)	n.a.	n.a.	0.042 (1.374)	0.086 (0.804)
Total effect	COVID-19 Cases	–0.036 ** (–2.413)	–0.058 (–0.880)	–0.036 ** (–2.079)	–0.055 (–1.011)	–0.024 ** (–2.570)	–0.026 ** (–2.284)	–0.025 ** (–2.488)	–0.027 ** (–1.999)
	THI	0.273 *** (2.882)	0.417 (1.052)	0.258 *** (2.588)	0.395 (0.915)	0.231 *** (3.926)	0.256 *** (2.866)	0.215 *** (3.613)	0.240 *** (2.952)
	Income	–0.724 *** (–3.984)	–1.157 (–1.039)	–9.842 ** (–2.182)	–15.502 (–0.823)	–0.535 *** (–5.395)	–0.594 *** (–3.190)	–5.079 ** (–1.974)	–5.711 * (–1.736)
	Economic	n.a.	n.a.	–8.217 ** (–2.024)	–12.969 (–0.795)	n.a.	n.a.	–4.034 * (–1.730)	–4.538 (–1.560)
	Income × Economic	n.a.	n.a.	1.061 ** (2.035)	1.674 (0.801)	n.a.	n.a.	0.528 * (1.766)	0.594 (1.583)

*, **, and *** denote significance at the 10%, 5%, and 1% levels.

shows the results. Among them, Model 5 and Model 6 represent the decomposition results of the spatial–temporal effect before and after considering the moderating effect. In the short term, COVID-19 cases had a significant direct, indirect, and total effect on the surrounding provinces; the regression coefficients are all less than 0. The above results indicate that COVID-19 not only has a significant negative impact on recovery in the local province but also has a particular negative spatial spillover effect on the surrounding provinces. Therefore, hypothesis H3b is supported.

5. Discussion

5.1. Discussion of the Empirical Results

From a temporal perspective, Moran’s I fluctuates between −0.112 and 0.326 from January to May, with an insignificant trend and small absolute value, indicating that the spatial autocorrelation of recovery is relatively weak. Moran’s I reaches a peak of 0.544 in August and maintains a high level of 0.331 to 0.443 after August, indicating that the spatial autocorrelation of road traffic volume in summer is the strongest, and the spatial autocorrelation is stronger overall in the second half of the year than in the first half.

As Model 5 to Model 8 show, compared with the traditional static spatial panel model, the dynamic spatial panel model can effectively test and avoid the endogeneity problem of the model [82]. Income and economic development have a significant adverse effect on the recovery of road traffic volume, and the level of economic development has a significant positive moderating effect on the mechanism of income. The above results confirm the mutual impact between the surrounding province in the recovery of road traffic volume, indicating that the provinces should actively collaborate to jointly promote the recovery of road traffic volume and the recovery of related industries.

In Models 13 to 16, we construct a dynamic spatial panel model based on the economic distances weight matrix. Its main empirical results are generally consistent with the static spatial panel model. In addition, W × Recovery_it is significantly positive in Model 9 to Model 16, indicating a significant spatial spillover effect of recovery in both the distance weight matrix and economic distance weight matrix. The above results further validate the robustness of the above empirical findings and avoid the interference of endogeneity [83].

The result of the mediating effect test indicates that the spread of COVID-19 is more potent in provinces with lower temperature and humidity indices, factors that can negatively impact the recovery of road traffic volume. In line with Jankelova et al., the Sobel test is used to further test the mediating effect [84]. The Z-value statistic is 2.28, corresponding to a p-value of 0.023, which verifies the significance of the above mediating effect. Furthermore, by replacing the distance weight matrix with the economic distance weight matrix, the robustness of the above empirical results is supported in this paper.

In the long term, the indirect effect of COVID-19 cases is not significant, indicating that the spatial spillover effect of COVID-19 on recovery in the surrounding provinces will gradually disappear in the long term. This is because China’s non-pharmaceutical interventions for COVID-19 will be dynamically adjusted as the outbreak progresses, whereby its negative impact on the recovery of road traffic volume in the surrounding provinces will gradually diminish after the pandemic. Model 13 and Model 14 reflect the decomposition results of the spatial effect after replacing the distance weight matrix with the economic distance weight matrix, and it can be found that coefficients of explanatory variables are generally unaffected, verifying the robustness of the above empirical results.

5.2. Policy Recommendations

Considering that factors such as the spread of COVID-19, income, and climate suitability all significantly affect the recovery of road traffic volume, the government should formulate policy measures that meet real needs according to the time and place. For example, when the temperature and humidity indices are low, consideration can be given to increasing policy support for traffic and other related industries to promote the recovery of road traffic volume [85]. At the same time, because the recovery of road traffic volume has a positive spatial spillover effect, the government should minimize traffic closures in the surrounding province to achieve the overall recovery of the traffic volume.

The recovery of road traffic volume is poor in most provinces and fluctuates with the spread of COVID-19. Therefore, traffic companies and other related companies should adjust their risk response strategies and be prepared to face the pressure of the pandemic in the long term [86] and consider the changes in travelers’ behavior [87]. Additionally, traffic companies should focus on further market development in provinces with relatively low income and economic development levels. This is because such provinces have better recovery of road traffic volume.

Due to the negative impact and indirect spatial spillover effect of COVID-19 on traffic volume, communities, residents, and other stakeholders should take measures to avoid the spread of COVID-19, such as maintaining social distance [88]. If the spread of a new pandemic begins, the recovery gains already achieved may be lost, and the development of the surrounding provinces may also be adversely affected.

5.3. Comparison with Existing Studies

As we mentioned above, studying road traffic volume from the impact of COVID-19 is one of the current hot topics of scientific research. Existing studies have mainly discussed the mechanisms of COVID-19 effects on road traffic volume. For example, the number of COVID-19 cases [37] and lockdown measures [7] lead to a decrease in road traffic volume, which is consistent with the above findings. Therefore, the results of this study fit well with the existing literature, and the research hypotheses are supported.

Furthermore, there are some unique findings in this study. According to a series of existing studies, high-income provinces have higher road traffic volume [89]. However, when we study the recovery index of road traffic volume, the opposite is found, with higher-income provinces having a lower recovery index. This is because the current lockdown measures are mainly for non-essential traffic [90], while it occupies a higher proportion of the total traffic in high-income provinces [34]. As a result, it is more difficult for high-income provinces to recover road traffic volume to pre-pandemic levels. This makes it necessary for the government to consider different policies in different provinces to facilitate the recovery of road traffic volume.

From another perspective, by constructing dynamic spatial panel models, we also found the short-term indirect spatial spillover effect of COVID-19. In other words, local COVID-19 cases lead to a short-term decrease in the recovery of road traffic volume in surrounding provinces. This result has not been reported in the existing literature and has important implications for the transportation industry with the impact of COVID-19. According to the above results, there is a need for solidarity and collaboration among surrounding provinces to take measures to overcome the threat of the pandemic together; otherwise, they will be negatively affected by each other.

6. Conclusions

Based on the spatial panel data of all 31 provinces in mainland China in 2021, this paper uses PCA to evaluate the recovery of road traffic volume under the impact of the pandemic. It investigates the spatial heterogeneity of the recovery of road traffic volume and its mechanism by using the spatial autocorrelation index and dynamic spatial panel model, with the following main findings.

The recovery of road traffic volume in China shows a strong positive spatial autocorrelation in general [91]. It is relatively weak between January and May and strong between June and December, indicating that the spatial autocorrelation of the recovery of road traffic volume shows a trend from weak to strong. Road traffic volume in provinces with better income and economic development is slower to recover to pre-pandemic levels. This is because non-essential traffic demand accounts for a higher proportion of total traffic demand [34], and this non-essential traffic demand is more negatively affected by the pandemic than essential traffic demand [35]. From the other point of view, climate suitability can affect the recovery of road traffic volume both indirectly through COVID-19 and directly. This indicates that a warm and humid climate is not conducive to the spread of COVID-19 compared to a cold climate [49] and to the recovery of road traffic volume [92].

Furthermore, in terms of spatial heterogeneity, the recovery of road traffic volume has a positive spatial spillover effect, which can be manifested as a mutual impact between surrounding provinces. At the same time, COVID-19 can have a negative indirect spatial spillover effect in the short term. For example, the spread of the pandemic in one province may have a short-term negative impact on the recovery of road traffic volume in the surrounding provinces [93]. Therefore, the government and other stakeholders should take measures to reduce the spread of COVID-19 to facilitate the recovery of road traffic volume in the local and surrounding provinces.

There are some limitations to our research. First, as COVID-19 continues to spread globally, there is an opportunity to make new findings if further empirical analysis is conducted based on the latest situation of the pandemic and the recovery of traffic volume. Second, we mainly use the distance weight matrix and the economic distance weight matrix, in addition to a variety of spatial weight matrices with different economic significance, for further selection and study [94]. Considering the negative impact of COVID-19, further research on the recovery of traffic would provide vital assistance to stakeholders.