A Time-Space Network-Based Optimization Method for Scheduling Depot Drivers
Abstract
:1. Introduction
2. Literature Review
3. Problem Description
- Task: A task represents an operation a driver may execute, such as signing in, signing out, and driving trains. Tasks can be divided into three categories: (i) driving tasks, which are indicated in the EMU train shunting schedule, such as, shunting an EMU from one track to another, and driving trains at cleaning tracks; (ii) shift tasks which include sign-in and sign-out operations; and (iii) walking and waiting tasks. Practically, the required time for driving tasks is fixed, while the timings for shift tasks is uncertain. Moreover, the numbers and the required time of walking and waiting tasks need to be determined when making solutions.
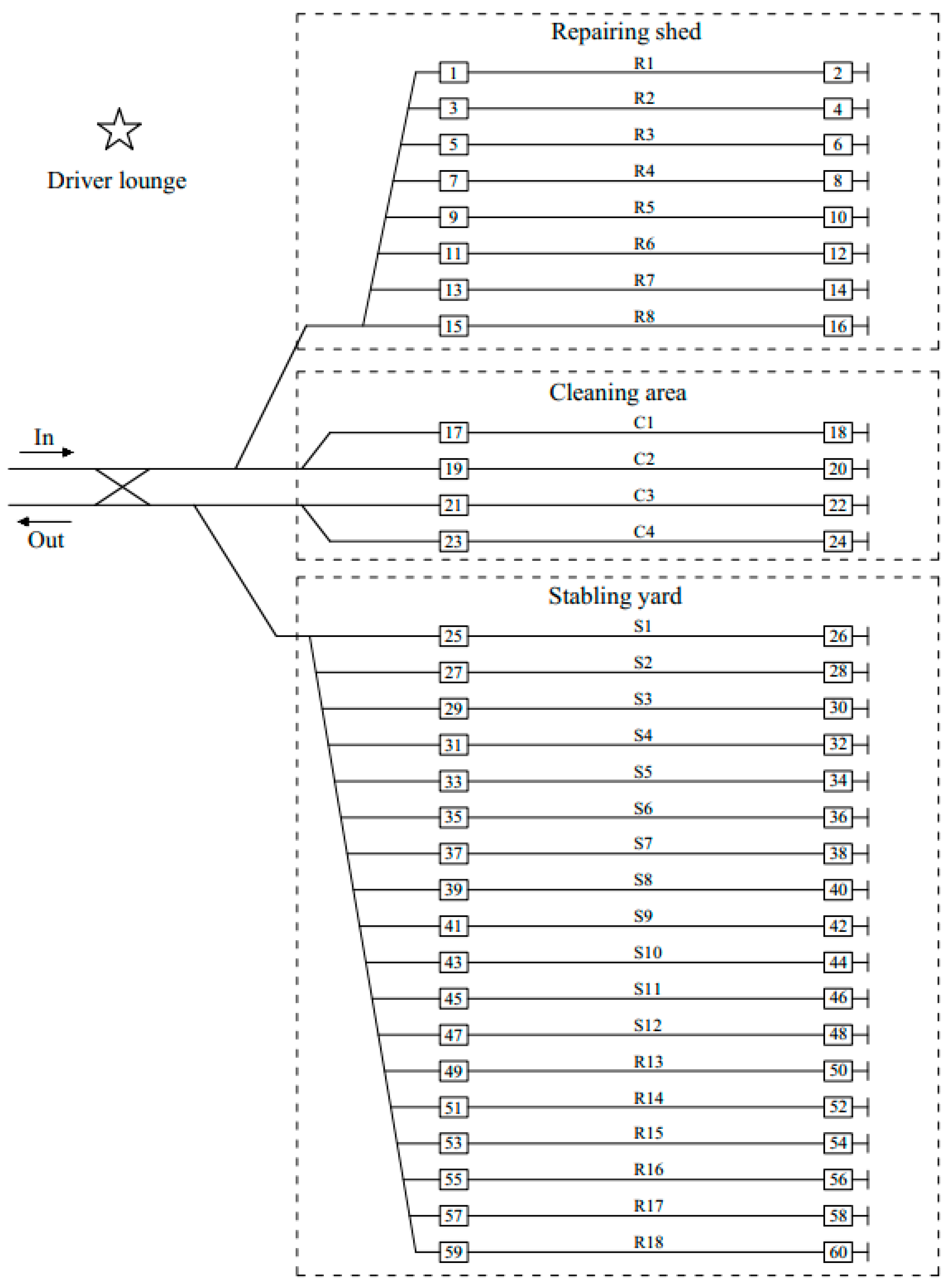
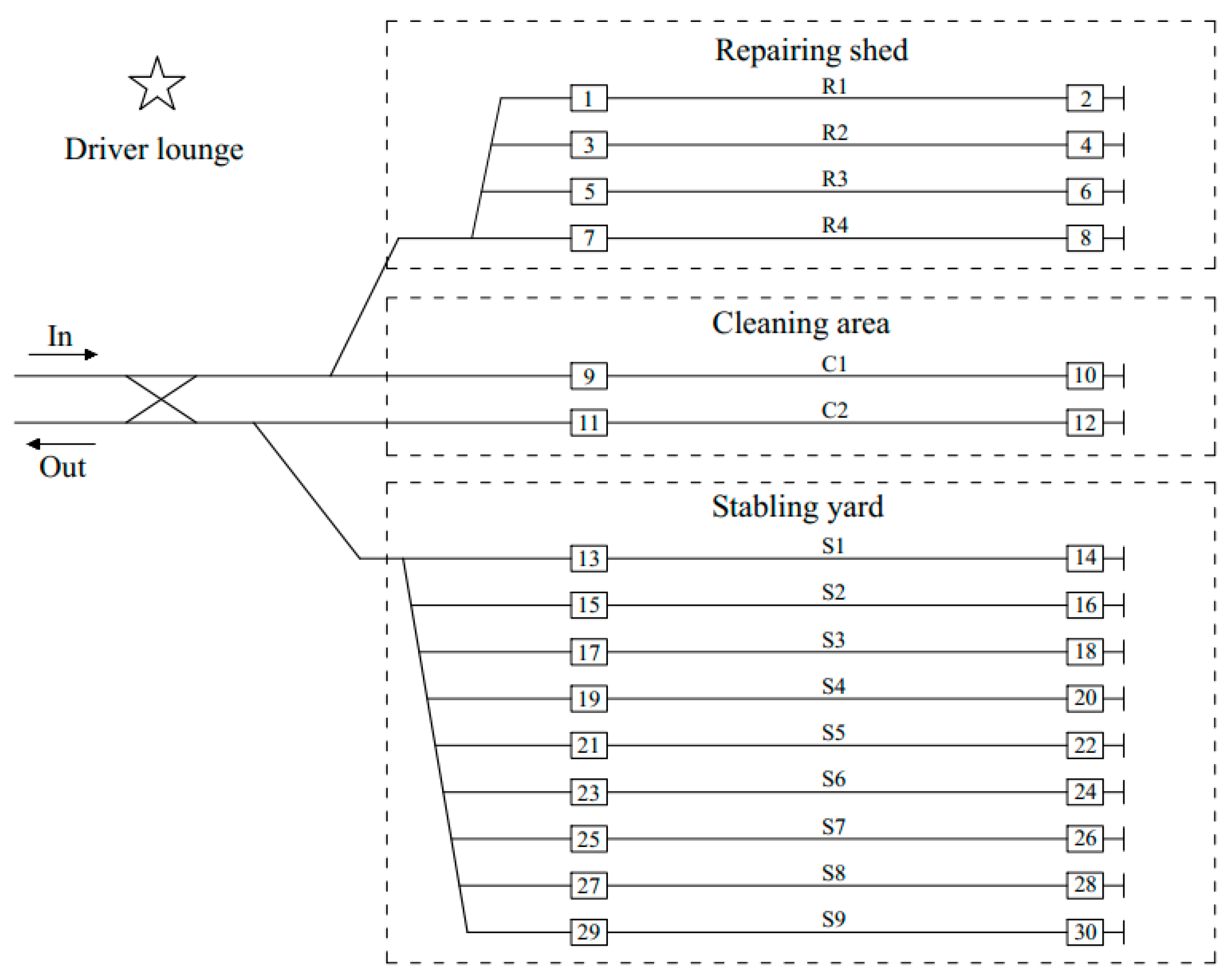
- Shunting schedule: A shunting schedule determines the arrival and departure time of each train at each repairing track (optional), cleaning track, and shunting track it may traverse in the depot, such that certain operational requirements, such as track capacity, minimum headway constraints, and required maintenance procedures, etc., are taken into consideration. The shunting schedule is determined in the shunting schedule planning phase, which is used as input data for the problem studied in this paper.
- Duty: A duty is a chain of tasks that can be assigned to at most one depot driver. A feasible duty must satisfy various labor laws and legislation.
- All trains considered in the paper are homogenous and can be moved bidirectionally on tracks.
- All drivers considered in the paper are homogenous and able to drive all trains.
- All repairing, cleaning, and stabling tracks are first-in-last-out tracks.
- Drivers are smart, they would find the shortest path to reposition themselves between two points.
3.1. Input Data
3.1.1. Depot Data
3.1.2. Task Data
3.1.3. Driver Data
3.2. Objective and Constraints
- Driving task assignment constraints: Each driving task can be executed by a driver at most once.
- Sign-in constraints: If a driver is on-duty, he/she must sign in at the specific time points in in the driver lounge and finally signs out in the driver lounge.
- Walking time constraints: The time interval between executing two consecutive driving tasks for the same driver should be no less than the walking time for the driver to walk from the proceeding task’s destination working point to the succeeding task’s origin working point.
- Maximum working time constraints: For each driver , the maximum duration of duty cannot exceed a fixed value .
4. Time-Space Network Formulation
4.1. Time-Space Network Construction
- Starting arcs: For working point , i.e., the driver lounge, and each time instant , there exists a starting arc . A driver traverses this arc represents that this driver signs in for the duty during the planning horizon, where a fixed cost of is incurred when driver is on-duty.
- Ending arcs: For working point , i.e., the driver lounge, and each time instant , there exists an ending arc . For each driver . This arc allows drivers to complete its operation at time t.
- Transfer arcs: There are transfer arcs in network G which represents the situation where a driver has finished dwelling at a working point and is about to leave current working point. There are two types of transfer arcs depending on what the next operation the driver will do. The first type of transfer arc is for the situation where the driver will walk to leave current point. For each working point and time instant , there is a transfer arc of this type. For each . The second type of transfer arc is for the situation where the driver will execute a driving task. For each working point and time instant , there is a transfer arc of this type if there exists one driving task r such that and . For each .
- Walking arcs: For each and time instants , there is a walking arc if there exists at least one driver such that equals to the round walking time of . For each . This arc allows driver k to walk from working point i to working point j.
- Waiting arcs: For each working point and time instant , there exists a waiting arc . For each . This arc allows a driver to wait at working point i when he/she is not working.
- Driving arcs: For each pair of working points and , and time instants , there is a driving arc if there exists at least one driving task r such that and . For each if task r is a shunting task, and if task r is a driving task at a cleaning track. This arc allows driver k to shunt a train from one track to another or drive a train at a cleaning track. The cost coefficient includes not only the operating cost but also a cost reduction of since task r would not be canceled if task r is executed by driver k.
- Dummy arcs: For the working point that related to the driver lounge, there is a dummy arc . A driver k traverses the dummy arc means the driver has no work to do during the planning horizon, we have .
4.2. Constraints
- Driving task operation requirements: For each , the driving task r is executed at most once if it is uncanceled. Therefore, for each , we impose the constraint that the depot driver s flow in the arc subset is at most one.
- Maximum duty time requirements: For each , the duty time cannot exceed the maximum allowed working time for drivers during the planning horizon if the driver is on duty. For each arc , we denote an arc subset as follows:in case of , andin case of , where is the time component of vertex . For convenience, denote and . For each , if driver k traverses arc , then this driver must traverse an arc in arc in exactly once.
4.3. Time-Space Network Formulation
5. Lagrangian Relaxation Heuristic
5.1. Lagrangian Relaxation
5.2. Upper Bound Heuristic
- Exchange operator: Given two drivers’ duties, choose one task in each duty of the drivers, and exchange the task with the subsequent tasks of the two duties. The procedure of this move is illustrated in Figure 3. The original duty 1 contains task A, B, and C sequentially, and the original duty 2 contains task D, E, and F sequentially, see Figure 3a. When conducting the “exchange” move, we exchange the tasks after task A in duty 1 and the tasks after task D in duty 2. After the “exchange” operator, duty 1 will contain task A, E, and F sequentially; duty 2 will contain task D, B, and C sequentially, see Figure 3b.
- Insert operator: Given two drivers’ duties, choose one task and delete it in one of the duties; insert the task into an appropriate position in the other duty. The procedure of this move is shown in Figure 4. The original duty 1 contains task A, B, and C sequentially; the original duty 2 contains task D and E sequentially. When conducting the “insert” move, we delete task B in duty 1 and insert it into an appropriate position in duty 2 (such as between task D and task E in duty 2). After the “insert” operator, duty 1 will contain task A and C sequentially; duty 2 will contain task D, B, and E sequentially.
- Swap operator: Given two drivers’ duties, choose one task and delete it in one of the duties; insert the task into an appropriate position in the other duty. The procedure of this move is illustrated in Figure 5. The original duty 1 contains task A, B and C sequentially; the original duty 2 contains task D and E sequentially. When conduct the “swap” move, we delete task B in duty 1 and insert it into an appropriate position in duty 2 (such as between task D and task E in duty 2), delete task E in duty 2 and insert it into an appropriate position in duty 1 (such as between task A and task C in duty 1). After the “swap” operator, duty 1 will contain task A, E and C sequentially; duty 2 will contain task D, B and F sequentially.
| Algorithm 1 Pseudocode for the local search: local_search() |
| Input: An initial solution , move operators set let denote the neighborhood of solution with move operator 1: 2:while do 3: for all do 4: 5: if is better than then 6: 7: 8: break 9: |
| Output: |
| Algorithm 2 Framework of the upper bound heuristic |
| Input: Driver set , tasks set , the probability of local search 1:use the greedy heuristic ub_greedy () to obtain solution 2:randomly generate from (0,1) 3:if then 4: |
| Output: |
5.3. Subgradient Optimization Procedure
6. Computational Study
6.1. Generation of Test Instances
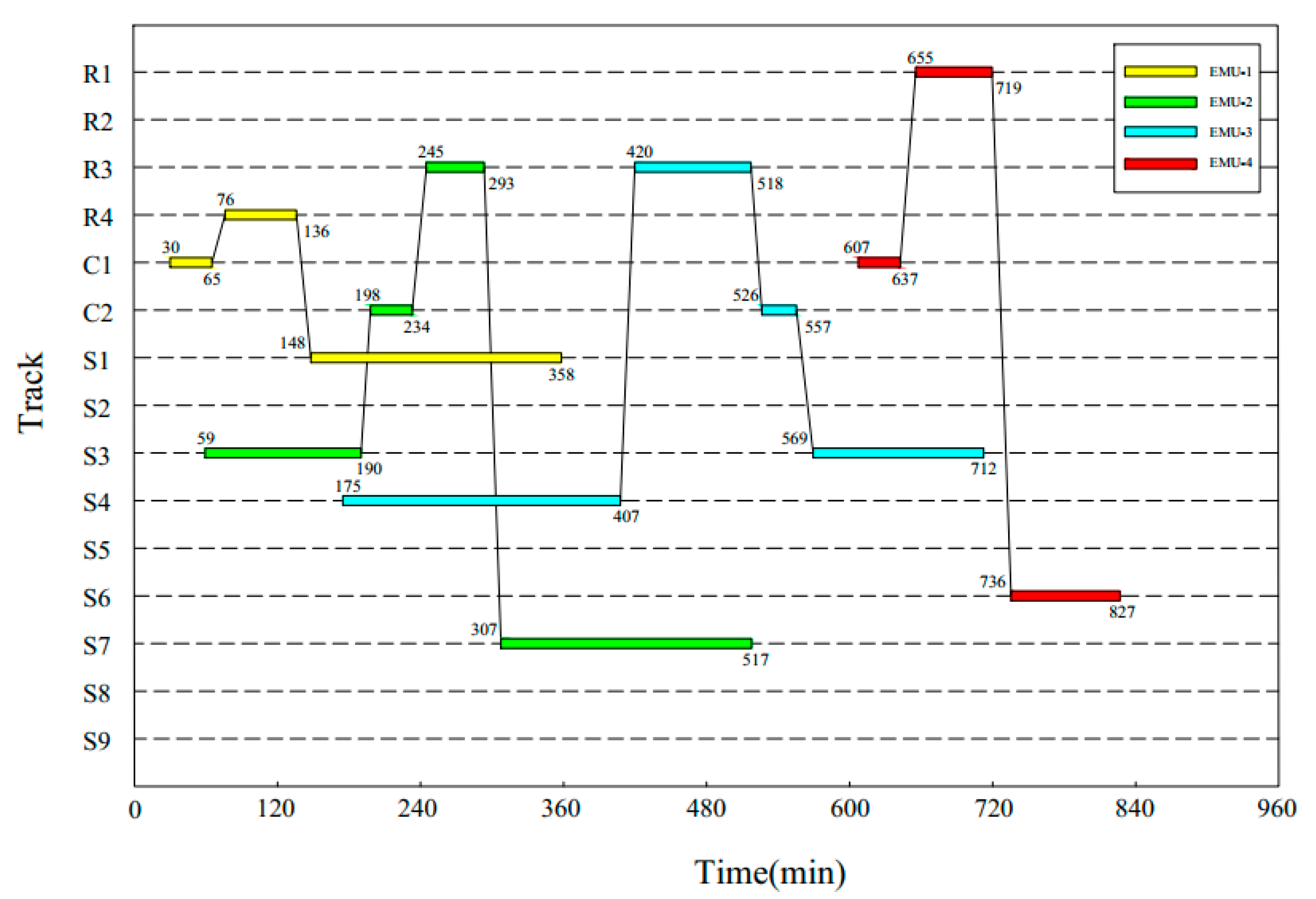
6.2. Computational Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Lin, B.; Wu, J.; Lin, R.; Wang, J.; Wang, H.; Zhang, X. Optimization of high-level preventive maintenance scheduling for high-speed trains. Reliab. Eng. Syst. Saf. 2019, 183, 261–275. [Google Scholar] [CrossRef]
- Heil, J.; Hoffmann, K.; Buscher, U. Railway crew scheduling: Models, methods and applications. Eur. J. Oper. Res. 2020, 283, 405–425. [Google Scholar] [CrossRef]
- Wang, J.; Gronalt, M.; Sun, Y. A two-stage approach to the depot shunting driver assignment problem with workload balance considerations. PLoS ONE 2017, 12, e0181165. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pour, S.M.; Drake, J.H.; Ejlertsen, L.S.; Rasmussen, K.M.; Burke, E.K. A hybrid constraint programming/mixed integer programming framework for the preventive signaling maintenance crew scheduling problem. Eur. J. Oper. Res. 2018, 269, 341–352. [Google Scholar] [CrossRef]
- Souza, R.L.C.; Ghasemi, A.; Saif, A.; Gharaei, A. Robust job-shop scheduling under deterministic and stochastic unavailability constraints due to preventive and corrective maintenance. Comput. Ind. Eng. 2022, 168, 108130. [Google Scholar] [CrossRef]
- Gharaei, A.; Amjadian, A.; Amjadian, A.; Shavandi, A.; Hashemi, A.; Taher, M.; Mohamadi, N. An integrated lot-sizing policy for the inventory management of constrained multi-level supply chains: Null-space method. Int. J. Syst. Sci. Oper. Logist. 2022, 1–14. [Google Scholar] [CrossRef]
- Gharaei, A.; Hoseini Shekarabi, S.A.; Karimi, M. Optimal lot-sizing of an integrated EPQ model with partial backorders and re-workable products: An outer approximation. Int. J. Syst. Sci. Oper. Logist. 2021, 7–11. [Google Scholar] [CrossRef]
- Gharaei, A.; Amjadian, A.; Shavandi, A. An integrated reliable four-level supply chain with multi-stage products under shortage and stochastic constraints. Int. J. Syst. Sci. Oper. Logist. 2021, 1–22. [Google Scholar] [CrossRef]
- Gharaei, A.; Almehdawe, E. Optimal sustainable order quantities for growing items. J. Clean. Prod. 2021, 307, 127216. [Google Scholar] [CrossRef]
- Jütte, S.; Albers, M.; Thonemann, U.W.; Haase, K. Optimizing railway crew scheduling at DB Schenker. Interfaces 2011, 41, 109–122. [Google Scholar] [CrossRef]
- Nishi, T.; Muroi, Y.; Inuiguchi, M. Column generation with dual inequalities for railway crew scheduling problems. Public Transp. 2011, 3, 25–42. [Google Scholar] [CrossRef]
- Liu, M.; Haghani, A.; Toobaie, S. Genetic algorithm-based column generation approach to passenger rail crew scheduling. Transp. Res. Rec. 2010, 2159, 36–43. [Google Scholar] [CrossRef]
- Guillermo, C.G.; José, M.R.L. Hybrid algorithm of tabu search and integer programming for the railway crew scheduling problem. In Proceedings of the 2009 Asia-Pacific Conference on Computational Intelligence and Industrial Applications (PACIIA), Wuhan, China, 28–29 November 2009; Volume 2, pp. 413–416. [Google Scholar] [CrossRef]
- Elizondo, R.; Parada, V.; Pradenas, L.; Artigues, C. An evolutionary and constructive approach to a crew scheduling problem in underground passenger transport. J. Heuretics 2010, 16, 575–591. [Google Scholar] [CrossRef] [Green Version]
- Khmeleva, E.; Hopgood, A.A.; Tipi, L.; Shahidan, M. Fuzzy-logic controlled genetic algorithm for the rail-freight crew-scheduling problem. KI—Künstliche Intelligenz 2018, 32, 61–75. [Google Scholar] [CrossRef] [Green Version]
- Caprara, A.; Kroon, L.; Monaci, M.; Peeters, M.; Toth, P. Passenger railway optimization. In Handbooks in Operations Research and Management Science; Barnhart, C., Laporte, G., Eds.; NorthHolland: Amsterdam, The Netherlands, 2007; Volume 14, pp. 129–187. [Google Scholar]
- Amjadian, A.; Gharaei, A. An integrated reliable five-level closed-loop supply chain with multi-stage products under quality control and green policies: Generalised outer approximation with exact penalty. Int. J. Syst. Sci. Oper. Logist. 2021, 9, 1–21. [Google Scholar] [CrossRef]
- Askari, R.; Sebt, M.V.; Amjadian, A. A Multi-product EPQ Model for Defective Production and Inspection with Single Machine, and Operational Constraints: Stochastic Programming Approach. In Logistics and Supply Chain Management; LSCM 2020. Communications in Computer and Information Science; Molamohamadi, Z., Babaee Tirkolaee, E., Mirzazadeh, A., Weber, G.W., Eds.; Springer: Cham, Switzerland, 2021; pp. 161–193. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Safaei, A.Z.; Bhattacharya, A.; Amjadian, A. Online peer-to-peer lending platform and supply chain finance decisions and strategies. Ann. Oper. Res. 2022, 315, 397–427. [Google Scholar] [CrossRef]
- Chew, K.-L.; Pang, J.; Liu, Q.; Ou, J.; Teo, C.-P. An optimization based approach to the train operator scheduling problem at Singapore MRT. Ann. Oper. Res. 2001, 108, 111–122. [Google Scholar] [CrossRef]
- Amaya, J.; Uribe, P. A model and computational tool for crew scheduling in train transportation of mine materials by using a local search strategy. TOP 2018, 26, 383–402. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, X.; Long, J.; Ding, J. Integrated optimization approach to metro crew scheduling and rostering. Transp. Res. Part C Emerg. Technol. 2021, 123, 102975. [Google Scholar] [CrossRef]
- Borndörfer, R.; Schulz, C.; Seidl, S.; Weider, S. Integration of duty scheduling and rostering to increase driver satisfaction. Public Transp. 2017, 9, 177–191. [Google Scholar] [CrossRef]
- Dauzère-Pérès, S.; De Almeida, D.; Guyon, O.; Benhizia, F. A Lagrangian heuristic framework for a real-life integrated planning problem of railway transportation resources. Transp. Res. Part B Methodol. 2015, 74, 138–150. [Google Scholar] [CrossRef]
- Xu, X.; Li, C.-L.; Xu, Z. Integrated train timetabling and locomotive assignment. Transp. Res. Part B Methodol. 2018, 117, 573–593. [Google Scholar] [CrossRef]
- Ma, J.; Ceder, A.; Yang, Y.; Liu, T.; Guan, W. A case study of Beijing bus crew scheduling: A variable neighborhood-based approach. J. Adv. Transp. 2016, 50, 434–445. [Google Scholar] [CrossRef]
- Hoogeboom, M.; Dullaert, W.; Lai, D.; Vigo, D. Efficient neighborhood evaluations for the vehicle routing problem with multiple time windows. Transp. Sci. 2020, 54, 400–416. [Google Scholar] [CrossRef]



| Type of Data | Notation | Description |
|---|---|---|
| Depot data | N | set of working points in the depot, including the driver lounge , |
| set of working points that could be used as origin points of driving tasks, | ||
| E | set of track segments in the depot, where | |
| walking distance between working point and | ||
| Task data | R | set of driving tasks indicated in the shunting schedule |
| origin working point of driving task | ||
| destination working point of driving task | ||
| start time of driving task | ||
| completion time of driving task | ||
| penalty for canceling driving task | ||
| Driver data | K | set of depot drivers, |
| set of time points for drivers to sign in, | ||
| maximum allowed working time for drivers during the planning horizon | ||
| average walking speed of driver | ||
| fixed cost for driver if he/she is on-duty during the planning horizon | ||
| unit cost for driver when he/she is walking | ||
| unit cost for driver when he/she is waiting | ||
| unit cost for driver to shunt trains in the depot | ||
| unit cost for driver to drive trains at cleaning tracks |
| Instance | Time (s) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 4609.16 | 6168.60 | 0.00 | 21.00 | 33.83% | 493.00 | ||
| 2 | 4811.90 | 7061.22 | 0.00 | 29.00 | 46.74% | 504.00 | ||
| 3 | 8 | 160 | 4644.21 | 6304.68 | 0.00 | 21.00 | 35.75% | 520.00 |
| 4 | 4778.32 | 5957.60 | 0.00 | 19.00 | 24.68% | 517.00 | ||
| 5 | 4791.81 | 6291.20 | 0.00 | 20.00 | 31.29% | 523.00 | ||
| Average: | 4727.08 | 6356.66 | 0.00 | 22.00 | 34.46% | 511.40 | ||
| 6 | 4640.82 | 4932.12 | 0.00 | 4.00 | 6.28% | 642.00 | ||
| 7 | 4856.78 | 5363.40 | 0.00 | 7.00 | 10.43% | 577.00 | ||
| 8 | 10 | 160 | 4682.38 | 5220.34 | 0.00 | 7.00 | 11.49% | 674.00 |
| 9 | 4787.06 | 5008.66 | 0.00 | 4.00 | 4.63% | 657.00 | ||
| 10 | 4824.05 | 5444.64 | 0.00 | 7.00 | 12.86% | 655.00 | ||
| Average: | 4758.22 | 5193.83 | 0.00 | 5.80 | 9.14% | 641.00 | ||
| 11 | 4620.82 | 4795.22 | 1.00 | 1.00 | 3.78% | 791.00 | ||
| 12 | 4850.18 | 5070.78 | 0.00 | 1.00 | 4.55% | 713.00 | ||
| 13 | 12 | 160 | 4687.47 | 4954.82 | 0.00 | 1.00 | 5.70% | 1019.00 |
| 14 | 4763.78 | 4908.48 | 1.00 | 3.00 | 3.04% | 806.00 | ||
| 15 | 4821.67 | 5088.62 | 0.00 | 0.00 | 5.54% | 850.00 | ||
| Average: | 4748.74 | 4963.58 | 0.40 | 1.20 | 4.52% | 835.80 | ||
| 16 | 4623.38 | 4874.24 | 2.00 | 0.00 | 5.43% | 857.00 | ||
| 17 | 4849.61 | 5034.34 | 2.00 | 1.00 | 3.81% | 796.00 | ||
| 18 | 14 | 160 | 4685.95 | 5000.32 | 2.00 | 2.00 | 6.71% | 1086.00 |
| 19 | 4752.28 | 4954.78 | 2.00 | 2.00 | 4.26% | 836.00 | ||
| 20 | 4812.11 | 5081.06 | 2.00 | 0.00 | 5.59% | 990.00 | ||
| Average: | 4744.67 | 4988.95 | 2.00 | 0.80 | 5.16% | 913.00 | ||
| 21 | 4617.25 | 4894.12 | 4.00 | 0.00 | 6.00% | 960.00 | ||
| 22 | 4845.50 | 5054.16 | 4.00 | 1.00 | 4.31% | 910.00 | ||
| 23 | 16 | 160 | 4687.87 | 4950.14 | 5.00 | 2.00 | 5.59% | 1242.00 |
| 24 | 4733.67 | 4935.52 | 4.00 | 2.00 | 4.26% | 989.00 | ||
| 25 | 4809.03 | 5090.32 | 4.00 | 0.00 | 5.85% | 1097.00 | ||
| Average: | 4738.66 | 4984.85 | 4.20 | 1.00 | 5.20% | 1039.60 | ||
| NL | LS | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Instance | Time (s) | Time (s) | Impv. | ||||||||||||
| Network 1 | |||||||||||||||
| 1 | 1210.43 | 1319.28 | 0.00 | 3.00 | 8.99% | 89.00 | 1210.43 | 1319.28 | 0.00 | 3.00 | 8.99% | 81.00 | 0.00% | ||
| 2 | 1547.27 | 1976.70 | 0.00 | 9.00 | 27.75% | 93.00 | 1547.27 | 1976.70 | 0.00 | 9.00 | 27.75% | 115.00 | 0.00% | ||
| 3 | 3 | 40 | 1315.73 | 1619.36 | 0.00 | 6.00 | 23.08% | 99.00 | 1315.73 | 1619.36 | 0.00 | 6.00 | 23.08% | 143.00 | 0.00% |
| 4 | 1240.58 | 1647.62 | 0.00 | 6.00 | 32.81% | 84.00 | 1240.58 | 1647.62 | 0.00 | 6.00 | 32.81% | 109.00 | 0.00% | ||
| 5 | 1229.81 | 1374.58 | 0.00 | 3.00 | 11.77% | 104.00 | 1229.81 | 1374.58 | 0.00 | 3.00 | 11.77% | 149.00 | 0.00% | ||
| Average: | 1308.76 | 1587.51 | 0.00 | 5.40 | 20.88% | 93.80 | 1308.76 | 1587.51 | 0.00 | 5.40 | 20.88% | 119.40 | 0.00% | ||
| 6 | 1985.43 | 2039.56 | 0.00 | 0.00 | 2.73% | 173.00 | 1984.89 | 2034.94 | 0.00 | 0.00 | 2.52% | 257.00 | 0.23% | ||
| 7 | 2122.64 | 2262.82 | 0.00 | 1.00 | 6.60% | 176.00 | 2123.04 | 2259.22 | 0.00 | 1.00 | 6.41% | 270.00 | 0.16% | ||
| 8 | 6 | 80 | 2043.96 | 2186.74 | 0.00 | 0.00 | 6.99% | 170.00 | 2044.46 | 2183.86 | 0.00 | 0.00 | 6.82% | 250.00 | 0.13% |
| 9 | 2066.76 | 2160.18 | 0.00 | 1.00 | 4.52% | 163.00 | 2066.73 | 2158.78 | 0.00 | 1.00 | 4.45% | 214.00 | 0.06% | ||
| 10 | 2165.23 | 2230.88 | 0.00 | 1.00 | 3.03% | 196.00 | 2164.10 | 2228.94 | 0.00 | 1.00 | 3.00% | 211.00 | 0.09% | ||
| Average: | 2076.80 | 2176.04 | 0.00 | 0.60 | 4.77% | 175.60 | 2076.64 | 2173.15 | 0.00 | 0.60 | 4.64% | 240.40 | 0.13% | ||
| 11 | 2856.43 | 3029.94 | 1.00 | 0.00 | 6.07% | 274.00 | 2860.75 | 3025.84 | 1.00 | 0.00 | 5.77% | 377.00 | 0.14% | ||
| 12 | 2834.61 | 3010.22 | 0.00 | 0.00 | 6.20% | 236.00 | 2834.89 | 2991.98 | 0.00 | 0.00 | 5.54% | 360.00 | 0.61% | ||
| 13 | 9 | 120 | 2815.78 | 2989.74 | 1.00 | 0.00 | 6.18% | 225.00 | 2815.61 | 2979.06 | 1.00 | 0.00 | 5.81% | 337.00 | 0.36% |
| 14 | 2754.48 | 2902.80 | 1.00 | 0.00 | 5.38% | 223.00 | 2756.59 | 2897.64 | 1.00 | 0.00 | 5.12% | 344.00 | 0.18% | ||
| 15 | 2788.21 | 2938.80 | 1.00 | 0.00 | 5.40% | 218.00 | 2788.21 | 2938.80 | 1.00 | 0.00 | 5.40% | 347.00 | 0.00% | ||
| Average: | 2809.90 | 2974.30 | 0.80 | 0.00 | 5.85% | 235.20 | 2811.21 | 2966.66 | 0.80 | 0.00 | 5.53% | 353.00 | 0.26% | ||
| Network 2 | |||||||||||||||
| 16 | 4625.77 | 4915.36 | 1.00 | 1.00 | 6.26% | 747.00 | 4620.59 | 4795.22 | 1.00 | 1.00 | 3.78% | 819.00 | 2.51% | ||
| 17 | 4850.56 | 5132.46 | 0.00 | 1.00 | 5.81% | 700.00 | 4850.18 | 5070.78 | 0.00 | 1.00 | 4.55% | 781.00 | 1.22% | ||
| 18 | 12 | 160 | 4686.25 | 5114.44 | 0.00 | 1.00 | 9.14% | 716.00 | 4687.47 | 4954.82 | 0.00 | 1.00 | 5.70% | 1018.00 | 3.22% |
| 19 | 4765.90 | 5005.18 | 1.00 | 3.00 | 5.02% | 682.00 | 4763.78 | 4908.48 | 1.00 | 3.00 | 3.04% | 834.00 | 1.97% | ||
| 20 | 4826.73 | 5199.06 | 0.00 | 0.00 | 7.71% | 793.00 | 4822.72 | 5089.96 | 0.00 | 0.00 | 5.54% | 896.00 | 2.14% | ||
| Average: | 4751.04 | 5073.30 | 0.40 | 1.20 | 6.79% | 727.60 | 4748.95 | 4963.85 | 0.40 | 1.20 | 4.52% | 869.60 | 2.21% | ||
| 21 | 5987.43 | 6390.68 | 1.00 | 1.00 | 6.74% | 944.00 | 5981.75 | 6222.48 | 1.00 | 1.00 | 4.02% | 1255.00 | 2.70% | ||
| 22 | 5644.36 | 6178.52 | 0.00 | 1.00 | 9.46% | 992.00 | 5641.55 | 5988.44 | 0.00 | 1.00 | 6.15% | 1676.00 | 3.17% | ||
| 23 | 15 | 200 | 5641.91 | 6059.82 | 1.00 | 0.00 | 7.41% | 895.00 | 5641.61 | 5867.12 | 1.00 | 0.00 | 4.00% | 1332.00 | 3.28% |
| 24 | 5854.48 | 6404.70 | 0.00 | 1.00 | 9.40% | 999.00 | 5854.78 | 6183.52 | 0.00 | 1.00 | 5.61% | 1453.00 | 3.58% | ||
| 25 | 5997.43 | 6507.26 | 0.00 | 0.00 | 8.50% | 969.00 | 5996.43 | 6348.74 | 0.00 | 0.00 | 5.88% | 1212.00 | 2.50% | ||
| Average: | 5825.12 | 6308.20 | 0.40 | 0.60 | 8.30% | 959.80 | 5823.22 | 6122.06 | 0.40 | 0.60 | 5.13% | 1385.60 | 3.05% | ||
| 26 | 7158.63 | 7701.54 | 2.00 | 3.00 | 7.58% | 1088.00 | 7139.62 | 7401.90 | 2.00 | 3.00 | 3.67% | 2461.00 | 4.05% | ||
| 27 | 6944.08 | 7626.12 | 1.00 | 2.00 | 9.82% | 1175.00 | 6938.38 | 7316.78 | 1.00 | 2.00 | 5.45% | 2053.00 | 4.23% | ||
| 28 | 18 | 240 | 6632.26 | 7229.12 | 2.00 | 0.00 | 9.00% | 1119.00 | 6622.07 | 7042.46 | 2.00 | 0.00 | 6.35% | 1970.00 | 2.65% |
| 29 | 6716.87 | 7169.36 | 2.00 | 0.00 | 6.74% | 1100.00 | 6715.53 | 7008.32 | 2.00 | 0.00 | 4.36% | 2535.00 | 2.30% | ||
| 30 | 6545.21 | 7026.84 | 2.00 | 0.00 | 7.36% | 1102.00 | 6532.70 | 6759.46 | 2.00 | 0.00 | 3.47% | 1605.00 | 3.96% | ||
| Average: | 6799.41 | 7350.60 | 1.80 | 1.00 | 8.10% | 1116.80 | 6789.66 | 7105.78 | 1.80 | 1.00 | 4.66% | 2124.80 | 3.44% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, F.; Fan, X.; Wang, P.; Sheng, M. A Time-Space Network-Based Optimization Method for Scheduling Depot Drivers. Sustainability 2022, 14, 14431. https://doi.org/10.3390/su142114431
Peng F, Fan X, Wang P, Sheng M. A Time-Space Network-Based Optimization Method for Scheduling Depot Drivers. Sustainability. 2022; 14(21):14431. https://doi.org/10.3390/su142114431
Chicago/Turabian StylePeng, Fei, Xian Fan, Puxin Wang, and Mingan Sheng. 2022. "A Time-Space Network-Based Optimization Method for Scheduling Depot Drivers" Sustainability 14, no. 21: 14431. https://doi.org/10.3390/su142114431
APA StylePeng, F., Fan, X., Wang, P., & Sheng, M. (2022). A Time-Space Network-Based Optimization Method for Scheduling Depot Drivers. Sustainability, 14(21), 14431. https://doi.org/10.3390/su142114431





