Impact of Floods on Sediment Trap Efficiency of a Small Shallow Reservoir—A Case Study
Abstract
:1. Introduction
2. Materials and Methods
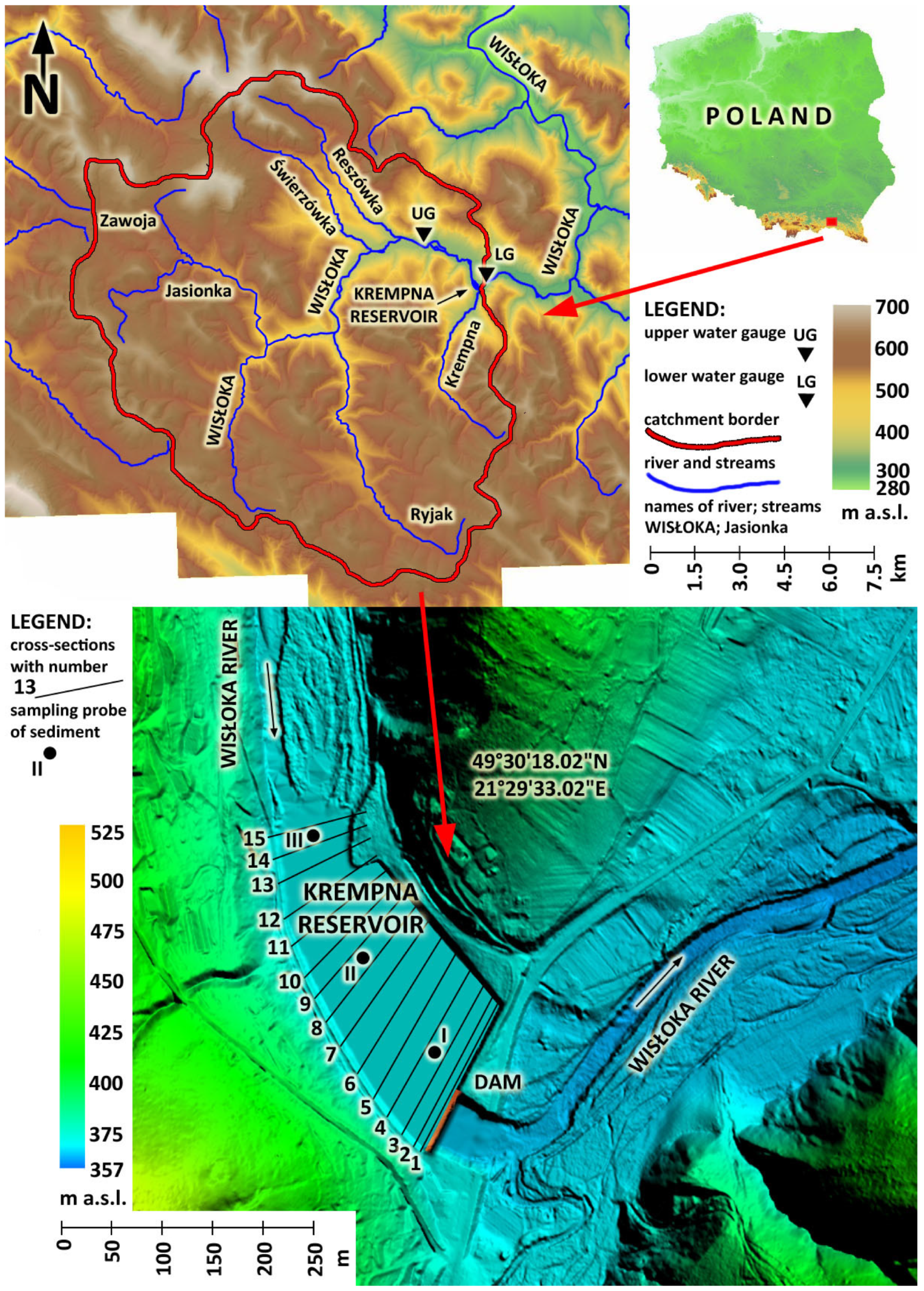
2.1. Characteristics of the Research Object
2.2. Method of Suspended Sediment Transport Calculation
2.3. Method of Silting Measurement and Determination of Sediment Trap Efficiency
3. Results
3.1. Impact of Flood Waves on the Sediment Trap Efficiency
3.2. Sediment Trap Efficiency Changes during Operation
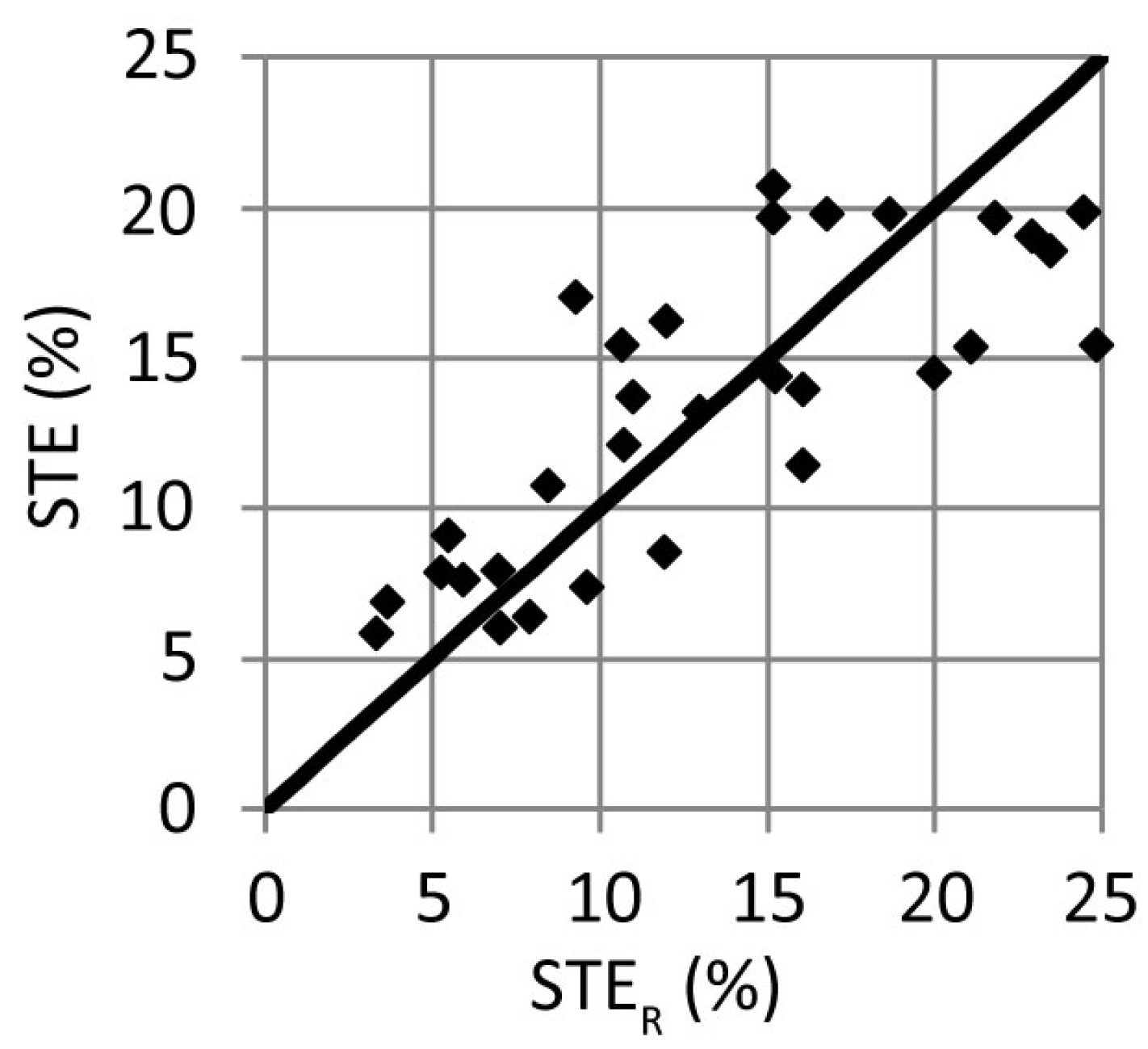
3.3. Verification of Methods for the STE Determination
3.4. Reduction of the STE Value and Its Forecasting
4. Discussion
5. Conclusions
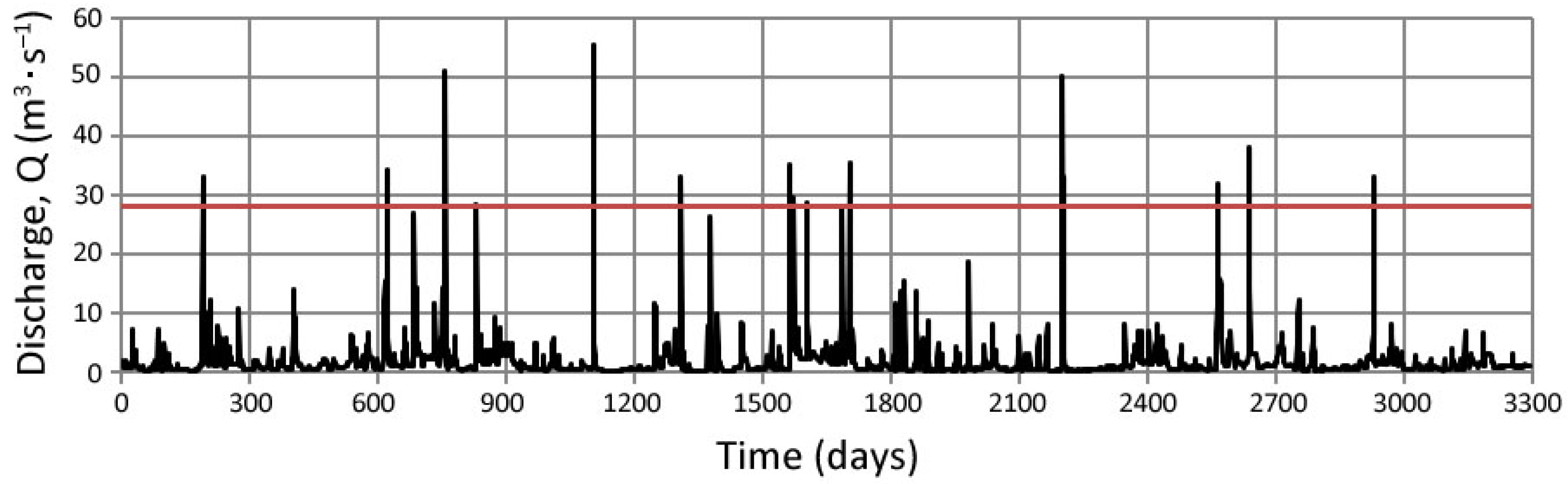
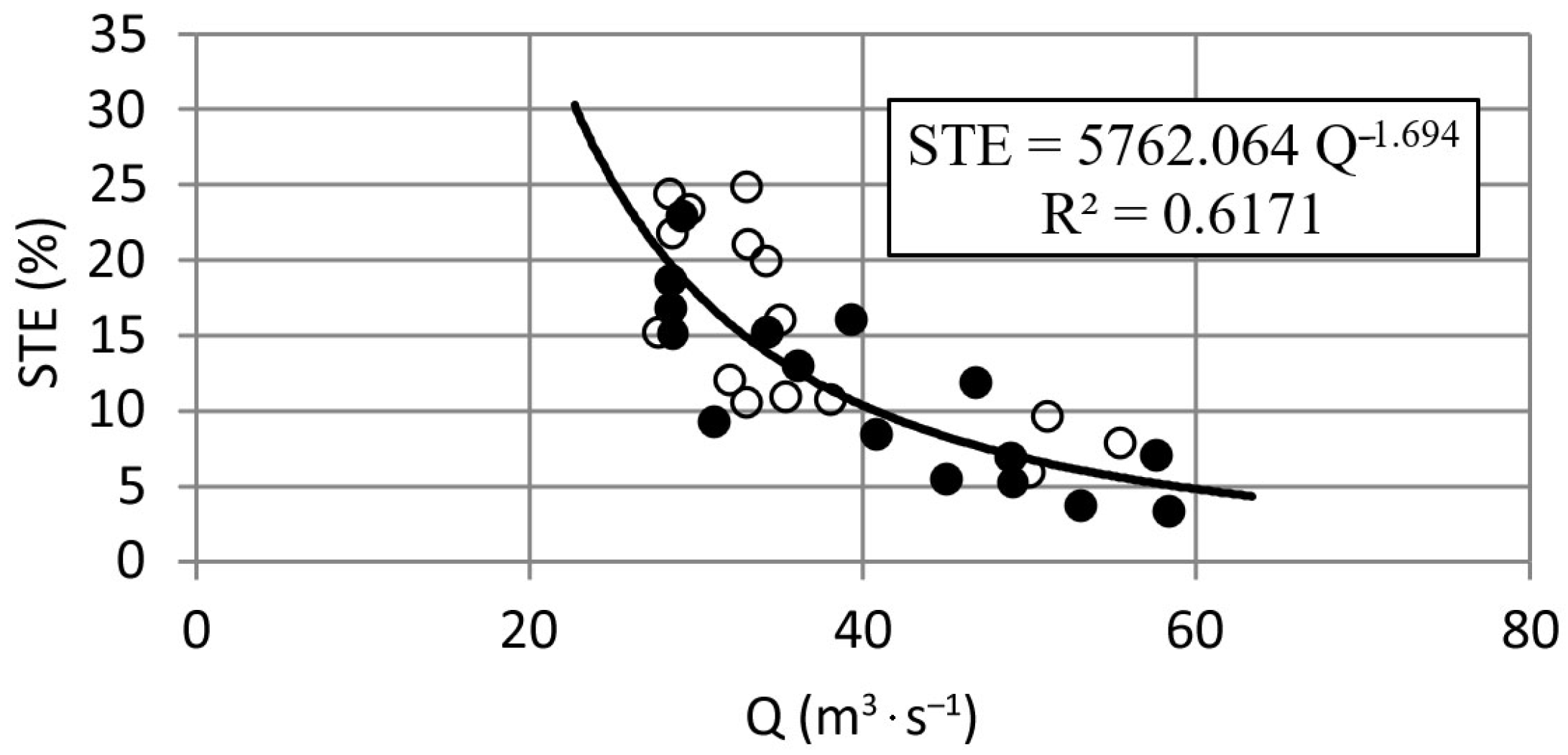
- In the 31 flood waves separated from the two operational periods of the Krempna reservoir, the flow rate of which is greater than the flow with the probability of exceedance of 50% and amounting to 26.14 m3∙s−1, the suspended sediment transport amounts to 47–48% of the total sediment transport in the analyzed operation periods. The sediment trap efficiency, determined from the balance of sediment flowing in and out of the reservoir in the separated flood waves, is from over 3% to less than 25%. The lowest STE values were observed for the waves with the highest flow rate.
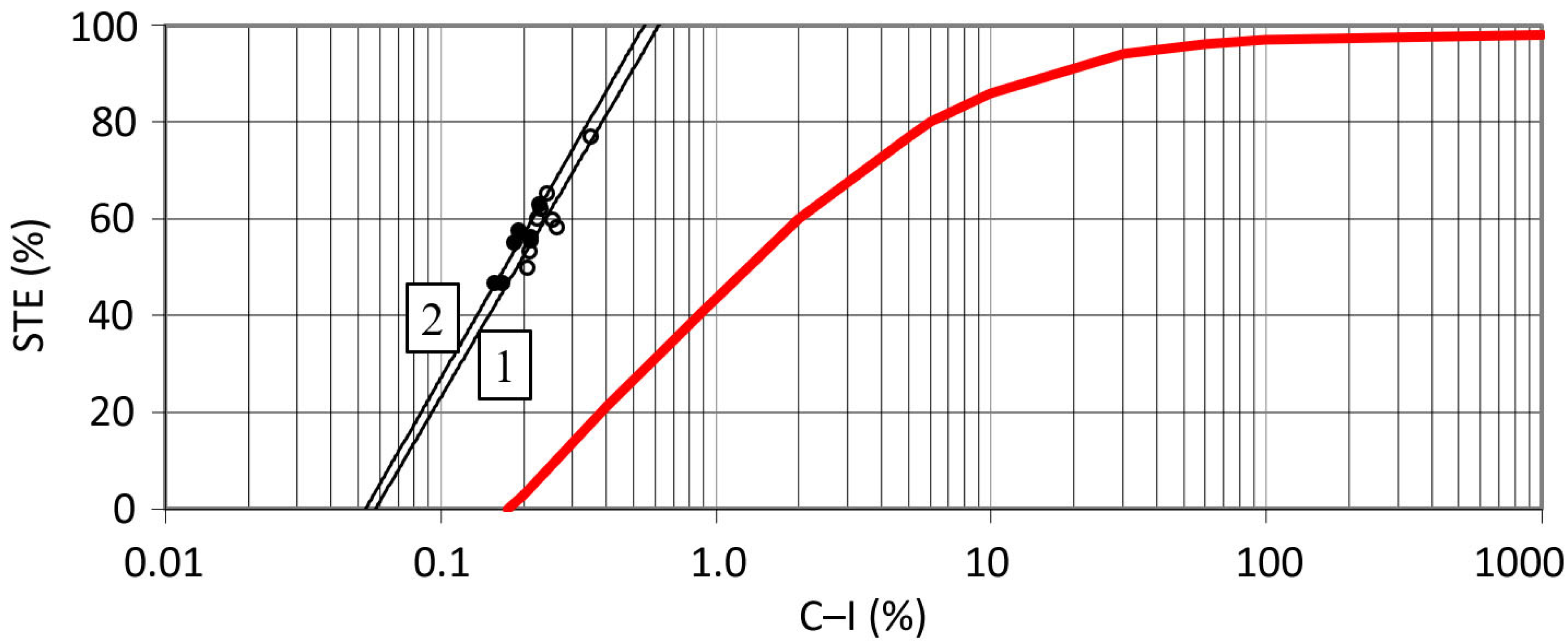
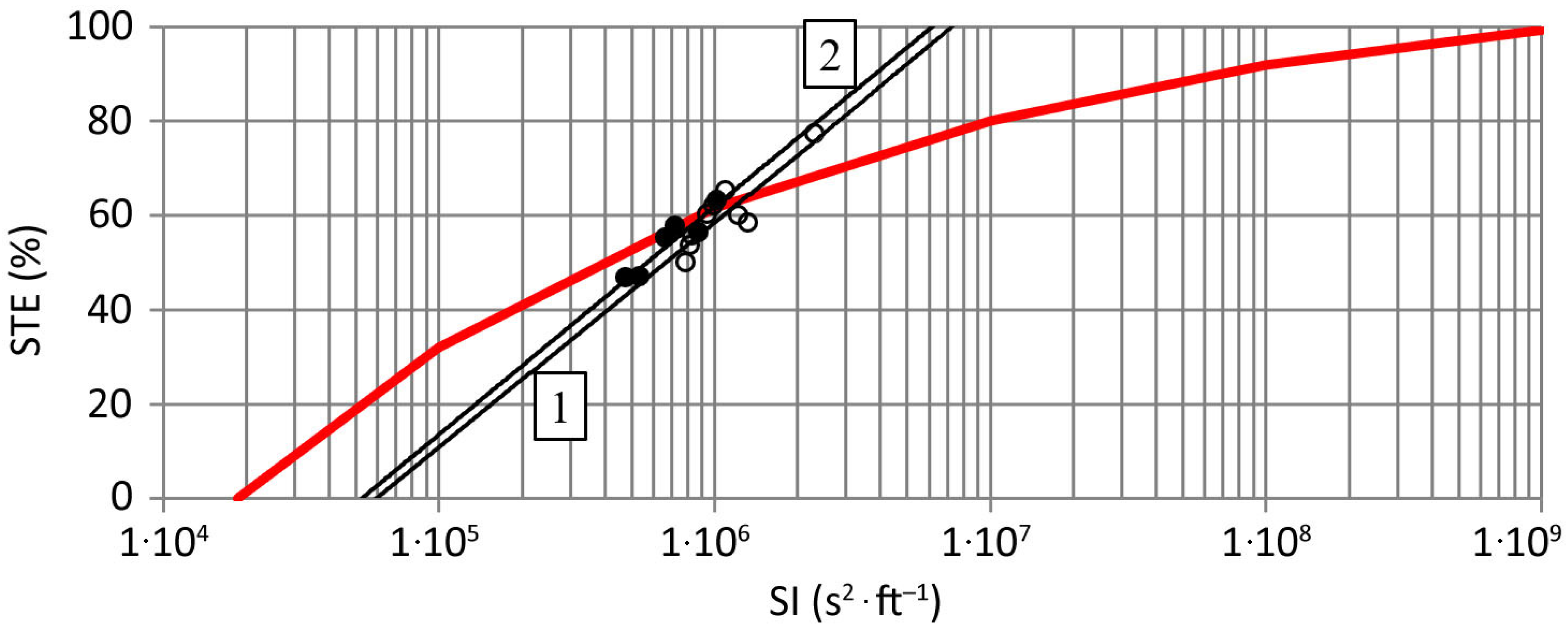
- The initial STE value determined for the initial storage capacity of the reservoir in Krempna using the methods of Łopatin, Brune, Morris and Linsley et al., Ward, and Brown proved to be several times lower than the value determined from the balance of sediment retained in and flowing into the reservoir (STER). This is due to very low values of the capacity–inflow and capacity–watershed ratios of the analyzed reservoir, which belong to the lower range of the STE values of the verified methods, or, as in the case of the Drozd’s method, they are lower than its lower range, making it impossible to determine the STE. In contrast, Brune and Allen’s method provided the STE values of more than 99%. Only Churchill’s method allows for determining the initial STE value close to the STER value. Therefore, it is not possible to determine the STE reduction of the examined reservoir using the above-mentioned methods, except for Churchill’s method.
- The small shallow reservoir in Krempna is characterized by a rapid STE reduction of 27.2% over 18 years of operation (period of 1987–2005) and 16.4% over 12 years of operation (period of 2006–2018). In a small reservoir, the effect of reducing its capacity can be observed in a relatively short period of operation due to rapid silting. With the average flow for this period, it is possible to demonstrate the relationship between the decreasing C–I value and the reduction of STE, C–W, or SI with STE. The developed model of STE reduction in the function of the C–I ratio proved to be burdened with greater error compared with the model of STE reduction in the function of the sedimentation index proposed by Churchill.
- The presented approach on the example of the Krempna reservoir in two operating periods indicates the possibility of developing a method for forecasting the STE value and its reduction during operation. However, it is necessary to have a larger number of small reservoirs examined. Expanding this model based on the obtained results of studies on silting of small reservoirs may contribute to developing a method dedicated to such reservoirs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notations
| C–I | capacity–inflow ratio |
| C–W | capacity–watershed ratio |
| Ccs | average suspended sediment concentration |
| Cp | suspended sediment concentration |
| Δ | difference in the MAE and RMSE values |
| k | correction factors |
| LG | lower water gauge |
| MAE | mean absolute error |
| N | number of data |
| Q | discharge |
| RMSE | root mean square error |
| R2 | determination coefficient |
| SI | sedimentation index |
| SR | silting ratio |
| STE | sediment trap efficiency |
| SSTm | suspended sediment transport |
| SST1 | mass of suspended sediment transport, which flowed into the reservoir in the first year of operation |
| STE | sediment trap efficiency of the reservoir |
| STER | real sediment trap efficiency |
| STE* | mean annual sediment trap efficiency |
| Ui | load of suspension |
| UG | upper water gauge |
| Vp | reservoir’s initial capacity |
| Vt | volume of sediment deposition in a reservoir (Vt) after t years |
| V1 | assumed volume of sediment after the first year of operation |
| xp | predicted STE value |
| xm | STER value calculated based on the measured results |
| ρ0 | the volume density of sediments |
References
- Wiatkowski, M.; Wiatkowska, B.; Gruss, Ł.; Rosik-Dulewska, C.; Tomczyk, P.; Chłopek, D. Assessment of the possibility of implementing small retention reservoirs in terms of the need to increase water resources. Arch. Environ. Prot. 2021, 47, 80–100. [Google Scholar]
- Wiatkowski, M.; Rosik-Dulewska, C.; Kasperek, R. Inflow of Pollutants to the Bukówka Drinking Water Reservoir from the Transboundary Bóbr River Basin. Annu. Set Environ. Prot. 2015, 17, 316–336. [Google Scholar]
- Tallar, R.; Suen, J.-P. Measuring the Aesthetic Value of Multifunctional Lakes Using an Enhanced Visual Quality Method. Water 2017, 9, 233. [Google Scholar] [CrossRef]
- Casadei, S.; Di Francesco, S.; Giannone, F.; Pierleoni, A. Small reservoirs for a sustainable water resources management. Adv. Geosci. 2019, 49, 165–174. [Google Scholar] [CrossRef] [Green Version]
- Habets, F.; Molenat, J.; Carluer, N.; Douez, O.; Leenhardt, D. The cumulative impacts of small reservoirs on hydrology: A review. Sci. Total Environ. 2018, 643, 850–867. [Google Scholar] [CrossRef] [Green Version]
- Nathan, R.; Lowe, L. The hydrologic impacts of farm dams. Aust. J. Water Resour. 2012, 16, 75–83. [Google Scholar]
- Thompson, J.C. Impact and Management of Small Farm Dams in Hawke’s Bay, New Zealand. Ph.D. Thesis, Victoria University of Wellington, Wellington, New Zealand, 2012. [Google Scholar]
- Ayalew, T.B.; Krajewski, W.F.; Mantilla, R.; Wright, D.B.; Small, S.J. Effect of spatially distributed small dams on flood frequency: Insights from the soap creek watershed. J. Hydrol. Eng. 2017, 22, 04017011. [Google Scholar] [CrossRef]
- Hu, H.H.; Deng, A.J.; Chen, J.G.; Shi, H.L.; Ye, M. A Research Overview of the Siltation Loss Controls and Capacity Recovery Processes in China’s Reservoirs. MATEC Web Conf. 2018, 246, 01086. [Google Scholar] [CrossRef]
- Thakkar, H.; Bhattacharyya, S. Reservoir Siltation in India: Latest Studies Revealing Results, a Wake up Call. Dams Rivers People 2006, 4, 1–28. [Google Scholar]
- Alahiane, N.; Elmouden, A.; Aitlhaj, A.; Boutaleb, S. Small dam reservoir siltation in the Atlas Mountains of Central Morocco: Analysis of factors impacting sediment yield. Environ. Earth Sci. 2016, 75, 1035. [Google Scholar] [CrossRef]
- Rǎdoane, M.; Rădoane, N. Dams, sediment sources and reservoir silting in Romania. Geomorphology 2005, 71, 112–125. [Google Scholar] [CrossRef]
- Michalec, B.; Wałęga, A. Assessment of Silting Degree and Usable Life Time the of Small Reservoirs. Irrig. Drain. 2015, 64, 575–583. [Google Scholar] [CrossRef]
- Michalec, B.; Tarnawski, M.; Wałęga, A.; Cupak, A. Verification of the applicability of the Universal Soil Loss Equation and its modifications to determine the amount of suspended sediment. Carpathian J. Earth Environ. Sci. 2017, 12, 235–244. [Google Scholar]
- Bednarczyk, T. Determination of suspended load in cross-section of small reservoir in Zesławice. Sci. Fascicles 1994, 291, 7–18. (In Polish) [Google Scholar]
- Fall, B. Guidelines for Elaborating Annual Reports on Suspended Sediment Load; PIHM: Warszawa, Poland, 1963. [Google Scholar]
- Wiśniewski, B.; Kutrowski, M. Special Constructions in Hydraulical Engineering, Water Reservoirs, Predicting Silting Rate; Biuro Studiów i Projektów Budownictwa Wodnego „Hydroprojekt”: Warszawa, Poland, 1973. (In Polish) [Google Scholar]
- Dąbkowski, L.; Skibiński, J.; Żbikowski, A. Hydrauliczne Podstawy Projektów Wodno-Melioracyjnych; PWRiL: Warszawa, Poland, 1982. (In Polish) [Google Scholar]
- Brune, G.M. Trap efficiency of reservoirs. Trans. Am. Geophys. Union 1953, 34, 407–418. [Google Scholar] [CrossRef]
- Morris, H.M.; Wiggert, J.M. Applied Hydraulics in Engineering; Ronald Press Co.: Brooklyn, NY, USA, 1972. [Google Scholar]
- Linsley, R.K.; Kohler, M.A.; Paulhus, J.L.H. Hydrology for Engineers; McGraw-Hill Inc.: San Francisco, CA, USA, 1986. [Google Scholar]
- Ward, P.R. Sediment transport and a reservoir siltation formula for Zimbabwe-Rhodesia. Civ. Eng. S. Afr. 1980, 22, 9–15. [Google Scholar]
- Batuca, G.D.; Jordaan, M.J., Jr. Silting and Desilting of Reservoirs; A.A. Balkema Publisher: Rotterdam, The Netherlands, 2000; p. 353. [Google Scholar]
- Heinemann, H.G. Reservoir Trap Efficiency. In Erosion and Sediment Yield; Geo Books: Norwich, UK, 1984; pp. 201–218. [Google Scholar]
- Bogárdi, J. Sediment Transport in Alluvial Streams; Akadémiai Kiadó: Budapest, Hungary, 1974; p. 826. [Google Scholar]
- Organ, J.; Gorczyca, Z. Renowacja Zbiornika Rekreacyjnego na Rzece Wisłoka w Miejscowości Krempna; Dokumentacja Techniczna: Jasło, Poland, 1987. [Google Scholar]
- He, Z.; Jia, L.; Jia, Y.; He, J. Effects of flood events on sediment transport and deposition in the waterways of Lingding Bay, Pearl River Delta, China. Ocean Coast Manag. 2020, 185, 105062. [Google Scholar] [CrossRef]
- Łajczak, A. A Study on Silting of Dam Reservoirs in the Vistula River Catchment Basin; Monoghraphs of Water Economy Committee of the Polish Academy of Sciences: Warsaw, Poland, 1995; p. 8. [Google Scholar]
- De Girolamo, A.M.; Pappagallo, G.; Lo Porto, A. Temporal variability of suspended sediment transport and rating curves in a Mediterranean river basin: The Celone (SE Italy). Catena 2015, 128, 135–143. [Google Scholar] [CrossRef]
- Oeurng, C.; Sauvage, S.; Sanchez-Pérez, J.M. Dynamics of suspended sediment transport and yield in a large agricultural catchment, southwest France. Earth Surf. Process. Landf. 2010, 35, 1289–1301. [Google Scholar] [CrossRef] [Green Version]
- Tena, A.; Batalla, R.J.; Vericat, D. Reach-scale suspended sediment balance downstream from dams in a large Mediterranean river. Hydrol. Sci. J. 2012, 57, 831–849. [Google Scholar] [CrossRef] [Green Version]
- Lee, F.-Z.; Lai, J.-S.; Sumi, T. Reservoir Sediment Management and Downstream River Impacts for Sustainable Water Resources—Case Study of Shihmen Reservoir. Water 2022, 14, 479. [Google Scholar] [CrossRef]
- Zhide, Z.; Yang, X. Reservoir Sedimentation in China—Experiences and Lessons. In Energy and Water: Sustainable Development, Proceedings of Theme D: Water for a Changing Global Community: The 27th Congress of International Association for Hydraulic Research, San Francisco, CA, USA, 10–15 August 1997; American Society of Civil Engineers: New York, NY, USA, 1997; pp. 72–77. [Google Scholar]
- Kummu, M.; Varis, O. Sediment-related impacts due to upstream reservoir trapping, the Lower Mekong River. Geomorphology 2005, 85, 275–293. [Google Scholar] [CrossRef]
- Williams, G.P.; Wolman, M.G. Downstream Effects of Dams on Alluvial Rivers; Geological Survey Professional Paper 1286; USGS: Washington, DC, USA, 1984; 61p. [Google Scholar]
- Graf, W.L. Geomorphology and American dams: The scientific, social, and economic context. Geomorphology 2005, 71, 3–26. [Google Scholar] [CrossRef]
- Juško, V.; Sedmák, R.; Kúdela, P. Siltation of Small Water Reservoir under Climate Change: A Case Study from Forested Mountain Landscape of Western Carpathians, Slovakia. Water 2022, 14, 2606. [Google Scholar] [CrossRef]
- Morris, G.L.; Fan, J. Reservoir Sedimentation Handbook: Design and Management of Dams, Reservoirs and Watersheds for Sustainable Use; McGraw Hill: New York, NY, USA, 1998. [Google Scholar]
- Verstraeten, G.; Poesen, J. Estimating trap efficiency of small reservoirs and ponds: Methods and implications for the assessment of sediment yield. Prog. Phys. Geogr. 2000, 24, 219–251. [Google Scholar] [CrossRef]
- Lewis, S.E.; Bainbridge, Z.T.; Kuhnert, P.M.; Sherman, B.S.; Henderson, B.; Dougall, C.; Cooper, M.; Brodie, J.E. Calculating sediment trapping efficiencies for reservoirs in tropical settings: A case study from the Burdekin Falls Dam, NE Australia. Water Resour. Res. 2013, 49, 1017–1029. [Google Scholar] [CrossRef]
- Verstraeten, G.; Poesen, J. Modeling the long-term sediment trap efficiency of small ponds. Hydrol. Process. 2001, 15, 2797–2819. [Google Scholar] [CrossRef]
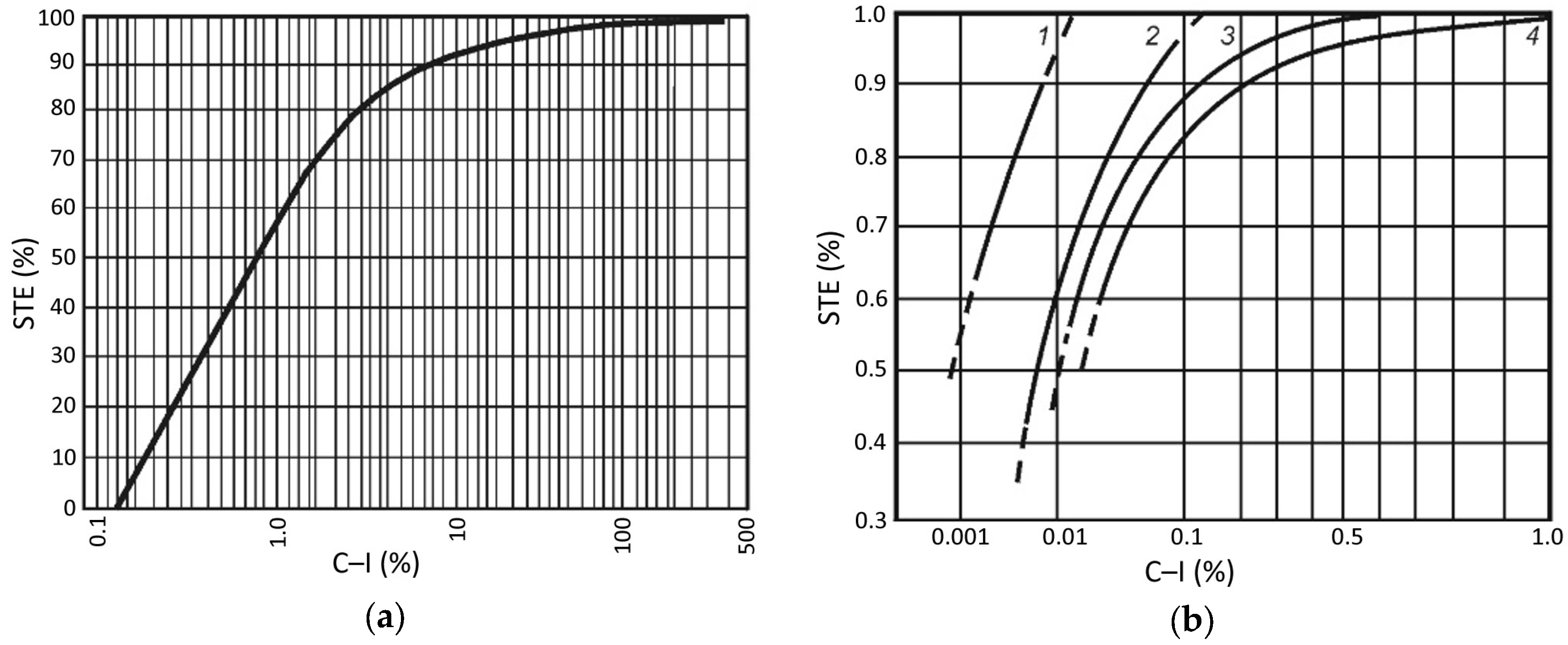



| Author/s of Method | Equation |
|---|---|
| Brune [19] | ; *) |
| Morris and Wiggert [20] | |
| Linsley et al. [21] | , a = 65–130, n = 2–10 |
| Ward [22] | |
| Brown [23] | , K = 0.046–1.0; *) |
| Churchill [24] | ; *) |
| No. | Period 1987–2005 | Period 2006–2018 | ||||||
|---|---|---|---|---|---|---|---|---|
| Qmax (m3∙s−1) | SST in Cross Section [t] | STER (%) | Qmax (m3∙s−1) | SST in Cross Section [t] | STER (%) | |||
| UG | LG | UG | LG | |||||
| 1 | 33.00 | 2258 | 1809 | 24.8 | 34.35 | 839 | 728 | 15.2 |
| 2 | 34.20 | 1589 | 1324 | 20.0 | 29.13 | 1244 | 1012 | 22.9 |
| 3 | 51.00 | 4736 | 4321 | 9.6 | 28.50 | 2869 | 2418 | 18.7 |
| 4 | 28.40 | 520 | 418 | 24.4 | 39.34 | 1522 | 1312 | 16.0 |
| 5 | 55.50 | 6235 | 5778 | 7.9 | 36.10 | 1846 | 1634 | 13.0 |
| 6 | 33.10 | 2368 | 1956 | 21.1 | 46.80 | 547 | 489 | 11.9 |
| 7 | 35.03 | 2137 | 1842 | 16.0 | 58.40 | 2113 | 2045 | 3.3 |
| 8 | 29.60 | 785 | 636 | 23.4 | 57.60 | 5591 | 5223 | 7.0 |
| 9 | 28.60 | 604 | 496 | 21.8 | 48.90 | 1941 | 1815 | 7.0 |
| 10 | 27.70 | 3351 | 2909 | 15.2 | 28.60 | 978 | 849 | 15.2 |
| 11 | 35.40 | 2463 | 2219 | 11.0 | 53.10 | 1346 | 1298 | 3.68 |
| 12 | 50.02 | 4843 | 4572 | 5.9 | 31.10 | 1341 | 1227 | 9.3 |
| 13 | 32.01 | 2425 | 2166 | 12.0 | 40.86 | 2920 | 2693 | 8.4 |
| 14 | 38.06 | 3062 | 2765 | 10.7 | 49.00 | 3409 | 3239 | 5.2 |
| 15 | 33.50 | 6677 | 6035 | 10.6 | 45.00 | 1662 | 1576 | 5.5 |
| 16 | - | - | - | - | 28.50 | 914 | 783 | 16.8 |
| Year | Years of Operation | Volume of Sediment Deposits Vt (m3) | Silting Ratio SR (%) | Total Volume of Suspended Sediment Transport SST (m3) | Capacity–Inflow Ratio C–I (%) | Sediment trap Efficiency STER (%) | Mean Annual Sediment Trap Efficiency STE* (%) |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Period 1987–2005 | |||||||
| 1996 | 9 | 27,041 | 24.1 | 46,462 | 0.265 | 58.2 | 6.47 |
| 1997 | 10 | 30,464 | 27.2 | 50,858 | 0.255 | 59.9 | 5.99 |
| 1998 | 11 | 34,637 | 30.9 | 53,124 | 0.242 | 65.2 | 5.93 |
| 1999 | 12 | 38,002 | 33.9 | 61,294 | 0.231 | 62.0 | 5.17 |
| 2000 | 13 | 40,144 | 35.8 | 66,907 | 0.224 | 60.0 | 4.62 |
| 2002 | 15 | 44,200 | 39.5 | 79,496 | 0.212 | 55.6 | 3.71 |
| 2003 | 16 | 44,901 | 40.1 | 84,084 | 0.210 | 53.4 | 3.34 |
| 2005 | 18 | 45,810 | 40.9 | 91,804 | 0.207 | 49.9 | 2.77 |
| Period 2006–2018 | |||||||
| 2009 | 3 | 6710 | 7.0 | 11,932 | 0.212 | 56.2 | 18.75 |
| 2011 | 5 | 15,133 | 15.7 | 26,321 | 0.192 | 57.5 | 11.50 |
| 2012 | 6 | 18,242 | 18.9 | 33,122 | 0.185 | 55.1 | 9.18 |
| 2017 | 11 | 26,055 | 27.0 | 55,679 | 0.166 | 46.8 | 4.25 |
| 2018 | 12 | 29,943 | 31.1 | 64,108 | 0.157 | 46.7 | 3.89 |
| No. | Method/Parameter | Period | |
|---|---|---|---|
| 1987–2005 | 2006–2018 | ||
| 1 | Łopatin [17] | 22.0 | 10.0 |
| 2 | Drozd [18] | − | − |
| 3 | Brune [19] | 16.5 | 8.9 |
| 4 | Morris and Wiggert [20] | 22.5 | 15.9 |
| 5 | Linsley et al. [21] | 9.8 | 5.2 |
| 6 | Ward [22] | 15.0 | −5.0 |
| 7 | Brown [23] | 12.5 | 10.9 |
| 8 | Brune and Allen [24] | 99.9 | 99.8 |
| 9 | Gotshalk [25] | − | − |
| 10 | Churchill [26] | 69.3 | 61.4 |
| Year | Years of Operation | STER (%) | STE Acc. to Equation (3) Line 1 on Figure 6 (%) | Churchill’s Method | ||
|---|---|---|---|---|---|---|
| SI (s2∙feet−1) | STE Acc. to Churchill (%) | STE Acc. to Equation (5) Line 1 on Figure 7 (%) | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1987 | 0 | 77.1 | 63.5 | 2.3 ∙ 106 | 69.3 | 69.5 |
| 1996 | 9 | 58.2 | 75.9 | 1.3 ∙ 106 | 64.3 | 64.2 |
| 1997 | 10 | 59.9 | 64.2 | 1.2 ∙ 106 | 63.5 | 63.4 |
| 1998 | 11 | 65.2 | 62.6 | 1.1 ∙ 106 | 62.5 | 62.4 |
| 1999 | 12 | 62.0 | 60.3 | 1.0 ∙ 106 | 61.5 | 61.5 |
| 2000 | 13 | 60.0 | 58.4 | 9.4 ∙ 105 | 60.9 | 60.9 |
| 2002 | 15 | 55.6 | 57.1 | 8.4 ∙ 105 | 59.7 | 59.8 |
| 2003 | 16 | 53.4 | 54.8 | 8.2 ∙ 105 | 59.5 | 59.5 |
| 2005 | 18 | 49.9 | 54.4 | 7.9 ∙ 105 | 59.1 | 59.3 |
| RMSE | 7.83 | − | 5.36 | 0.11 | ||
| MAE | 5.43 | − | 4.56 | 0.10 | ||
| Δ (%) | 30.8 | − | 14.9 | 7.2 | ||
| Year | Years of Operation | STER (%) | STE Acc. to Equation (4) Line 1 on Figure 6 (%) | Churchill’s Method | ||
|---|---|---|---|---|---|---|
| SI (s2∙feet−1) | STE Acc. to Churchill (%) | STE Acc. to Equation (6) Line 1 on Figure 7 (%) | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2006 | 0 | 63.0 | 58.2 | 1.0 ∙ 106 | 61.7 | 61.6 |
| 2009 | 3 | 56.2 | 62.4 | 8.8 ∙ 105 | 60.3 | 60.0 |
| 2011 | 5 | 57.5 | 59.3 | 7.2 ∙ 105 | 58.1 | 57.8 |
| 2012 | 6 | 55.1 | 55.1 | 6.7 ∙ 105 | 57.3 | 57.0 |
| 2017 | 11 | 46.8 | 53.4 | 5.4 ∙ 105 | 54.9 | 54.6 |
| 2018 | 12 | 46.7 | 48.9 | 4.8 ∙ 105 | 53.5 | 53.4 |
| RMSE | 3.54 | − | 3.87 | 0.20 | ||
| MAE | 2.40 | − | 2.56 | 0.16 | ||
| Δ (%) | 32.3 | − | 33.9 | 21.0 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michalec, B.; Plesiński, K. Impact of Floods on Sediment Trap Efficiency of a Small Shallow Reservoir—A Case Study. Sustainability 2022, 14, 14537. https://doi.org/10.3390/su142114537
Michalec B, Plesiński K. Impact of Floods on Sediment Trap Efficiency of a Small Shallow Reservoir—A Case Study. Sustainability. 2022; 14(21):14537. https://doi.org/10.3390/su142114537
Chicago/Turabian StyleMichalec, Bogusław, and Karol Plesiński. 2022. "Impact of Floods on Sediment Trap Efficiency of a Small Shallow Reservoir—A Case Study" Sustainability 14, no. 21: 14537. https://doi.org/10.3390/su142114537
APA StyleMichalec, B., & Plesiński, K. (2022). Impact of Floods on Sediment Trap Efficiency of a Small Shallow Reservoir—A Case Study. Sustainability, 14(21), 14537. https://doi.org/10.3390/su142114537






