Testing for Local Spatial Association Based on Geographically Weighted Interpolation of Geostatistical Data with Application to PM2.5 Concentration Analysis
Abstract
:1. Introduction
2. Methods and Data Sources for Evaluation of the Methods and Demonstration of Their Applicability
2.1. Local-Linear Geographically Weighted Interpolation and Interpolated-Value-Based Local Spatial Statistics with the Bootstrap Test for Significance of Local Spatial Association
2.1.1. Local-Linear Geographically Weighted Interpolation (LGWI)
2.1.2. Interpolated-Value-Based Local Spatial Statistics with the Bootstrap Test for Significance of Local Spatial Association
- (i)
- Based on the interpolated data and the spatial proximity matrix , compute the observed value of according to Equation (12), which we denote by .
- (ii)
- Draw a bootstrap sample with replacement from the interpolated data , on which the bootstrap value of , denoted by , is computed bywhere .
- (iii)
- Repeat Step (ii) times and obtain bootstrap values of , which we denote by
- (iv)
- The -value of testing for positive spatial autocorrelation isand the -value of testing for negative spatial autocorrelation iswhere stands for the number of the elements in the set .
2.2. Data Sources for Evaluating the Performance of LGWI and the Bootstrap Test with Interpolated-Value-Based Local Spatial Statistics
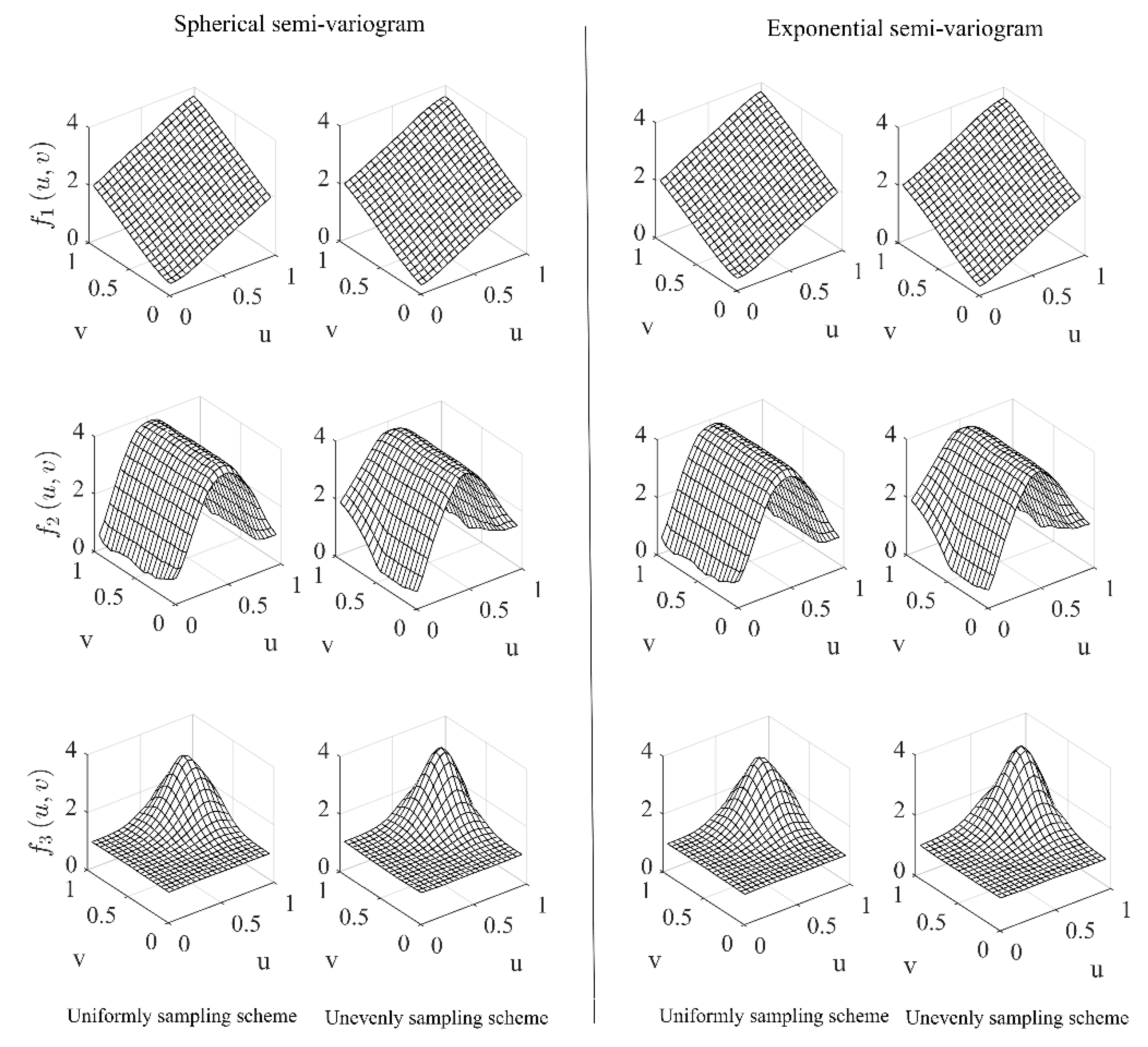
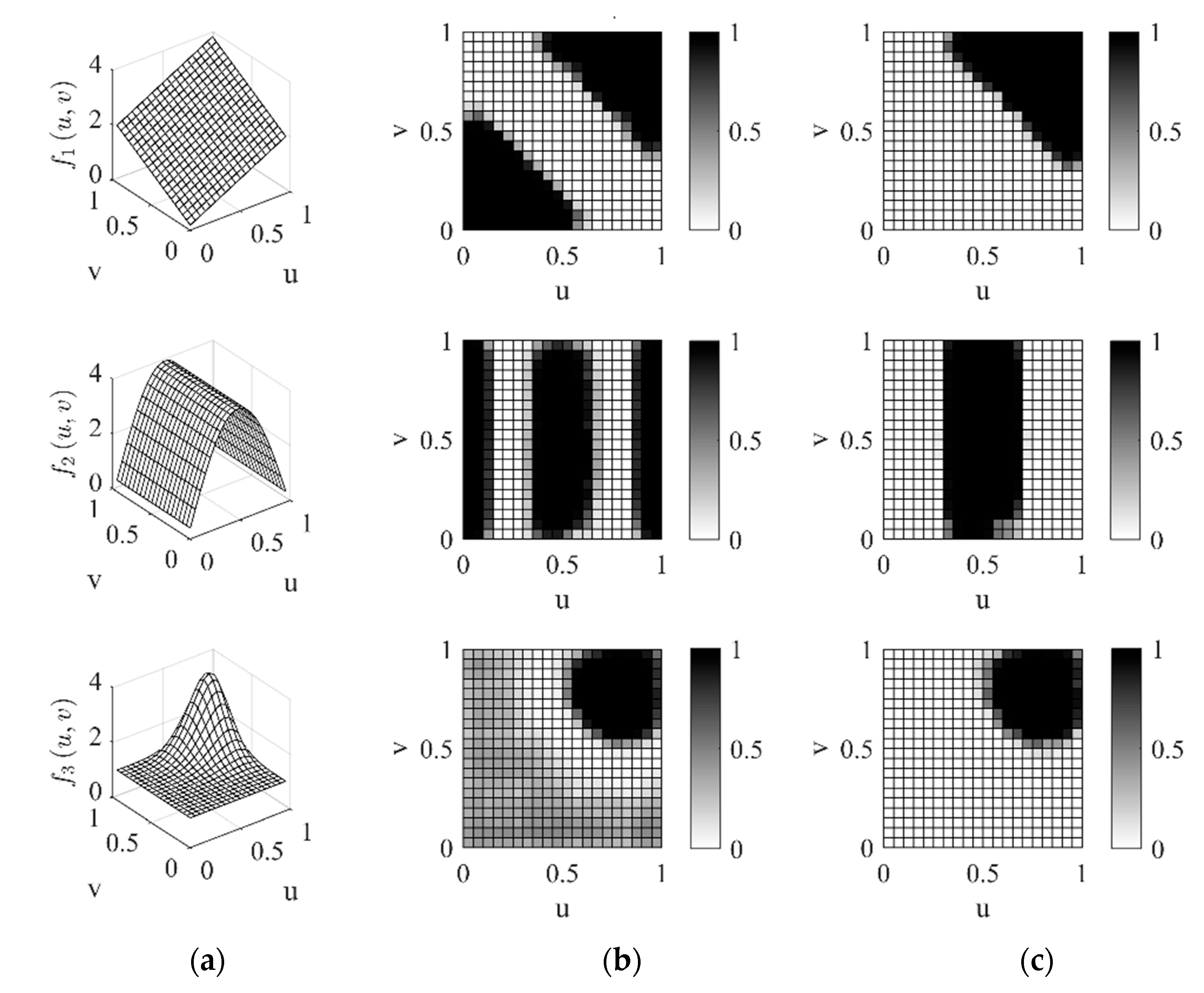
2.2.1. Synthetic Data for Evaluating Accuracy of LGWI and Power of the Test
- (i)
- Designed spatial region, sampling points and interpolation points.
- (a)
- Uniformly distributed sampling points on : 200 pairs of random numbers were independently drawn from the uniform distribution with each pair of the random numbers forming a sampling point on .
- (b)
- Unevenly distributed sampling points on : 100 pairs of random numbers were drawn from the normal distribution , where only the points in were retained and the others were discarded until 100 sampling points were obtained. With the same way, the other 100 pairs of random numbers were drawn from . Because of different means and variances of the two normal distributions, the sampling points form roughly two clusters around the means and respectively and are sparely distributed at the upper-left and lower-right corners.
- (ii)
- Model for generating data.
- (a)
- ;
- (b)
- ;
- (c)
- .
- (iii)
- Indices for measuring accuracy of the interpolation methods and power of the tests.
2.2.2. Real-Life Data for Demonstrating Applicability of LGWI and the Test Methods
- (i)
- Original data with preprocessing.
- (ii)
- Data sets formulated to explore seasonal local spatial association patterns of PM2.5 concentration.
3. Results with Comments
3.1. Simulation Results of Evaluating Accuracy of the LGWI Method and Power of the Test
3.1.1. Accuracy of LGWI
3.1.2. Power of the Bootstrap Test with the Interpolated-Value-Based Local Statistics in Identifying Local Spatial Association
3.2. Seasonal Local Spatial Association Patterns of PM2.5 Concentration in Guangdong Province
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fischer, M.M.; Getis, A. Handbook of Applied Spatial Analysis: Software Tools, Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Fotheringham, A.S. Trends in quantitative methods I: Stressing the local. Prog. Hum. Geogr. 1997, 21, 88–96. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Sachdeva, M. On the importance of thinking locally for statistics and society. Spat. Stat. 2022. [Google Scholar] [CrossRef]
- Unwin, A.; Unwin, D. Exploratory spatial data analysis with local statistics. J. R. Stat. Soc. Ser. D Stat. 1998, 47, 415–421. [Google Scholar] [CrossRef]
- Boots, B. Local measures of spatial association. Ecoscience 2002, 9, 168–176. [Google Scholar] [CrossRef]
- Boots, B.; Okabe, A. Local statistical spatial analysis: Inventory and prospect. Int. J. Geogr. Inf. Sci. 2007, 21, 355–375. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The analysis of spatial association by use of distance statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Ord, J.K.; Getis, A. Local spatial autocorrelation statistics: Distributional issues and application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Jepsen, M.R.; Simonsen, J.; Ethelberg, S. Spatio-temporal cluster analysis of the incidence of Campylobacter cases and patients with general diarrhea in a Danish county, 1995–2004. Int. J. Health Geogr. 2009, 8, 11. [Google Scholar] [CrossRef] [Green Version]
- Hardisty, F.; Klippel, A. Analysing spatio-temporal autocorrelation with LISTA-Viz. Int. J. Geogr. Inf. Sci. 2010, 24, 1515–1526. [Google Scholar] [CrossRef]
- Yan, N.; Mei, C.L.; Wang, N. A unified bootstrap test for local patterns of spatiotemporal association. Environ. Plan. A Econ. Space 2015, 47, 227–242. [Google Scholar] [CrossRef]
- Anselin, L. A local indicator of multivariate spatial association: Extending Geary’s c. Geogr. Anal. 2019, 51, 133–150. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. Local spatial statistics: An overview. In Spatial Analysis: Modeling in a GIS Environment; Longley, P., Batty, M., Eds.; GeoInformation International: Cambridge, IL, USA, 1996; pp. 261–277. [Google Scholar]
- Du, D.; Chen, F. Application of integration of spatial statistical analysis with GIS to regional economic analysis. Geo-Spat. Inf. Sci. 2004, 7, 262–267. [Google Scholar] [CrossRef]
- Xie, Y.; Shekhar, S.; Li, Y. Statistically-robust clustering techniques for mapping spatial hotspots: A survey. ACM. Comput. Surv. 2022, 55, 1–38. [Google Scholar] [CrossRef]
- Sokal, R.R.; Oden, N.L.; Thompson, B.A. Local spatial autocorrelation in a biological model. Geogr. Anal. 1998, 30, 331–354. [Google Scholar] [CrossRef]
- Boots, B.; Tiefelsdorf, M. Global and local spatial autocorrelation in bounded regular tessellations. J. Geogr. Syst. 2000, 2, 319–348. [Google Scholar] [CrossRef]
- Leung, Y.; Mei, C.L.; Zhang, W.X. Statistical test for local patterns of spatial association. Environ. Plan. A Econ. Space 2003, 35, 725–744. [Google Scholar] [CrossRef]
- Tiefelsdorf, M. The saddlepoint approximation of Moran’s I’s and Moran’s Ii’s reference distributions and their numerical evaluation. Geogr. Anal. 2002, 34, 187–206. [Google Scholar] [CrossRef]
- McLaughlin, C.C.; Boscoe, F.P. Effects of randomization methods on statistical inference in disease cluster detection. Health Place 2007, 13, 152–163. [Google Scholar] [CrossRef]
- Lee, S.I. A generalized randomization approach to local measures of spatial association. Geogr. Anal. 2009, 41, 221–248. [Google Scholar] [CrossRef]
- Mei, C.L.; Xu, S.F.; Chen, F. Consistency of bootstrap approximation to the null distributions of local spatial statistics with application to house price analysis. J. Inequal. Appl. 2020, 1, 217. [Google Scholar] [CrossRef]
- Cressie, N.A.C. Statistics for Spatial Data; Wiley: Chichester, UK, 1993. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, B.; Cheng, B.; Hu, X. Interpolation parameters in inverse distance-weighted interpolation algorithm on DEM interpolation error. J. Sens. 2021, 2021, 3535195. [Google Scholar] [CrossRef]
- Fan, J.; Gijbels, I. Local Polynomial Modelling and Its Applications; Chapman and Hall: London, UK, 1996. [Google Scholar]
- Bivand, R.; Müller, W.G.; Reder, M. Power calculations for global and local Moran’s I. Comput. Stat. Data Anal. 2009, 53, 2859–2872. [Google Scholar] [CrossRef]
- Zhang, T.L. Limiting distribution of the G statistics. Stat. Probab. Lett. 2008, 78, 1656–1661. [Google Scholar] [CrossRef] [Green Version]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; Wiley: Chichester, UK, 2002. [Google Scholar]
- Gollini, I.; Lu, B.; Charlton, M.; Brunsdon, C.; Harris, P. GWmodel: An R package for exploring spatial heterogeneity using geographically weighted models. J. Stat. Softw. 2015, 63, 1–50. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.H.; Ma, T.; Yang, L.; Qin, B. Latitude planar projection with its geometrical properties. Sci. China Ser. D Earth Sci. 2006, 36, 164–168. [Google Scholar]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B Stat. Methodol. 1995, 57, 289–300. [Google Scholar] [CrossRef]
- de Castro, M.C.; Singer, B.H. Controlling the false discovery rate: A new application to account for multiple and dependent tests in local statistics of spatial association. Geogr. Anal. 2006, 38, 180–208. [Google Scholar] [CrossRef]
- Huang, B.; Wu, B.; Barry, M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Lam, N.S.N. Extending Getis-Ord statistics to account for local space-time autocorrelation in spatial panel data. Prof. Geogr. 2020, 72, 411–420. [Google Scholar] [CrossRef]





| Interpolated Method | Spatial Process | Uniformly Sampling Scheme | Unevenly Sampling Scheme |
|---|---|---|---|
| LGWI | 0.0762 | 0.0997 | |
| 0.2018 | 0.2797 | ||
| 0.2302 | 0.2450 | ||
| Kriging (spherical semi-variogram) | 0.1659 | 0.1830 | |
| 0.3162 | 0.3879 | ||
| 0.2074 | 0.2144 | ||
| Kriging (exponential semi-variogram) | 0.1607 | 0.1757 | |
| 0.2891 | 0.3840 | ||
| 0.2089 | 0.2146 | ||
| IDW (power parameter = 1) | 0.4824 | 0.4004 | |
| 0.9300 | 1.0080 | ||
| 0.4194 | 0.4067 | ||
| IDW (power parameter = 2) | 0.2591 | 0.2186 | |
| 0.5029 | 0.7242 | ||
| 0.2803 | 0.3017 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.-J.; Mei, C.-L.; Zhang, Z.; Xu, Q.-X. Testing for Local Spatial Association Based on Geographically Weighted Interpolation of Geostatistical Data with Application to PM2.5 Concentration Analysis. Sustainability 2022, 14, 14646. https://doi.org/10.3390/su142114646
Wang F-J, Mei C-L, Zhang Z, Xu Q-X. Testing for Local Spatial Association Based on Geographically Weighted Interpolation of Geostatistical Data with Application to PM2.5 Concentration Analysis. Sustainability. 2022; 14(21):14646. https://doi.org/10.3390/su142114646
Chicago/Turabian StyleWang, Fen-Jiao, Chang-Lin Mei, Zhi Zhang, and Qiu-Xia Xu. 2022. "Testing for Local Spatial Association Based on Geographically Weighted Interpolation of Geostatistical Data with Application to PM2.5 Concentration Analysis" Sustainability 14, no. 21: 14646. https://doi.org/10.3390/su142114646
APA StyleWang, F.-J., Mei, C.-L., Zhang, Z., & Xu, Q.-X. (2022). Testing for Local Spatial Association Based on Geographically Weighted Interpolation of Geostatistical Data with Application to PM2.5 Concentration Analysis. Sustainability, 14(21), 14646. https://doi.org/10.3390/su142114646





