Reverse Logistics Network Design under Disruption Risk for Third-Party Logistics Providers
Abstract
1. Introduction
2. Literature Review
2.1. Reverse Logistics Network Design for 3PL Providers
2.2. Stochastic Reverse Logistics Network Design
2.3. Reverse Logistics Network Design under Disruption Risk
2.4. Incorporating Risk Measures in a Stochastic Reverse Logistics Network Design
2.5. Research Gaps and Contributions
- This study is the first to present a third-party reverse logistics network design problem considering disruptions and risk management simultaneously.
- For the first time, risk-averse two-stage stochastic programming models were developed to solve reverse logistics network designs under uncertain disruptions for 3PL.
- Two risk measures, CVaR and VaR, were investigated.
- A numerical example was used to analyze the performances of the risk-averse two-stage stochastic programming models.
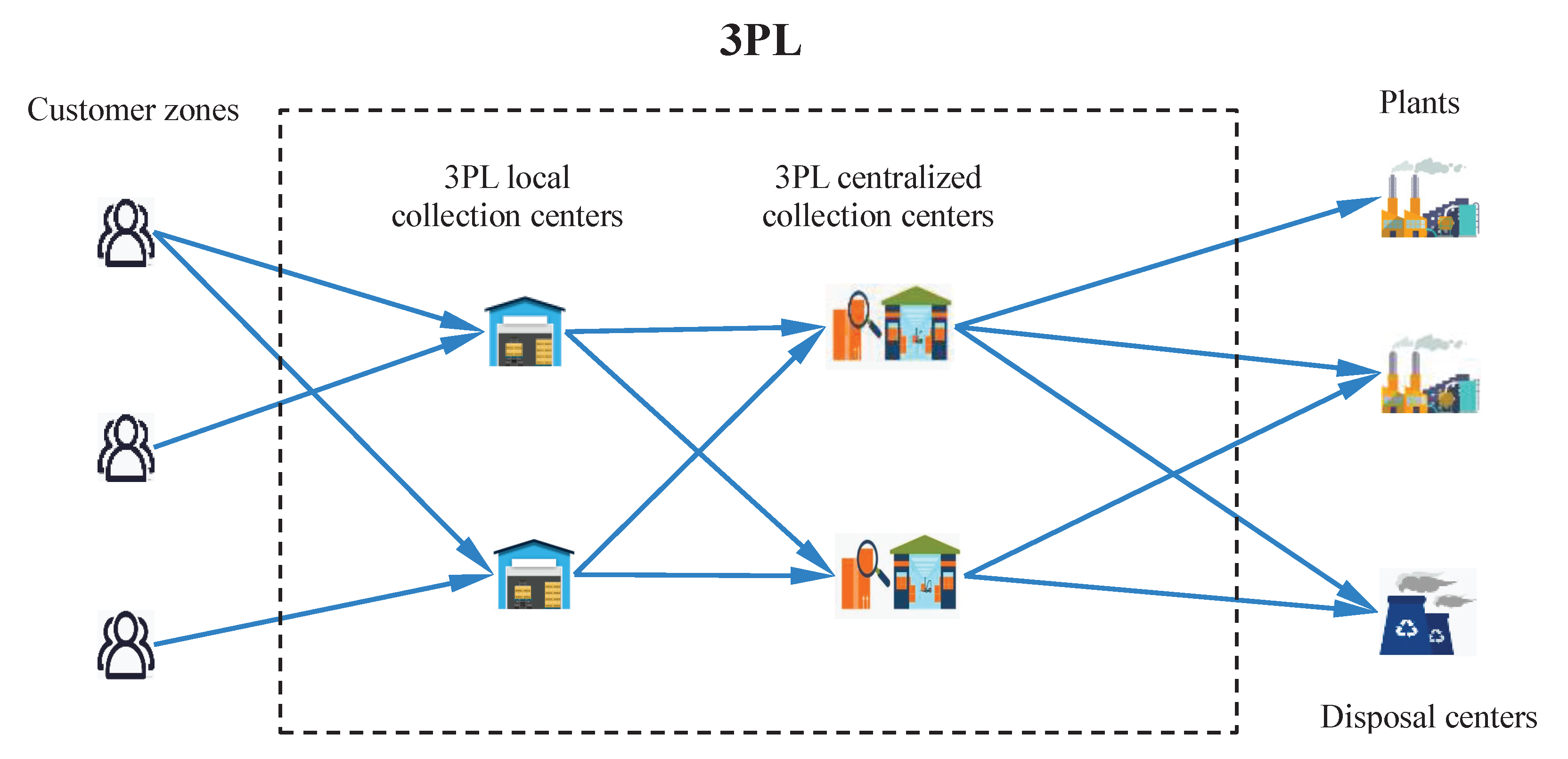
3. Problem Description and Proposed Model
3.1. Assumptions
- 1.
- Multi-echelon, consisting of customer zones, 3PL local collection centers, 3PL centralized collection centers, disposal centers, and plants are considered in the reverse network.
- 2.
- The locations, numbers, and return quantities of the products at the customer zones are known.
- 3.
- The locations, numbers, and capacities of the plants and disposal centers are known.
- 4.
- The potential locations, numbers, and capacities of 3PL local collection centers, 3PL centralized collection centers, and cost parameters (i.e., fixed opening costs, processing costs) are known.
- 5.
- Unit transportation costs for the product between the two adjacent echelons are known.
- 6.
- Penalty costs will be incurred for uncollected returned products.
- 7.
- The disruptions of the 3PL local collection centers and 3PL centralized collection centers are uncertain and can be described by the set of scenarios.
3.2. Notations
3.2.1. Sets
| L | Set of customer zones |
| K | Set of 3PL local collection centers |
| J | Set of 3PL centralized collection centers |
| I | Set of disposal centers |
| M | Set of plants of the manufacturer |
| S | Set of scenarios |
3.2.2. Parameters
| Quantity of returned products in customer zone l | |
| Unit processing cost of returned products at 3PL local collection center k | |
| Capacity of processing for 3PL local collection center k | |
| Fixed opening cost of 3PL local collection center k | |
| Unit processing cost of returned products at 3PL centralized collection center j | |
| Capacity of processing for 3PL centralized collection center j | |
| Fixed opening cost of 3PL centralized collection center j | |
| Capacity of disposal for disposal center i | |
| Capacity of production for plant m | |
| Unit transportation cost for products shipped from customer zone l to 3PL local collection center k | |
| Unit transportation cost for products shipped from 3PL local collection center k to 3PL centralized collection center j | |
| Unit transportation cost for products shipped from the 3PL centralized collection center j to disposal center i | |
| Unit transportation cost for products shipped from the 3PL centralized collection center j to plant m | |
| Unit penalty cost for the uncollected returned products | |
| Disposal ratio of products at 3PL centralized collection center | |
| Probability of disruption scenario s |
3.2.3. Decision Variables
| Binary variable equals 1 if 3PL local collection center k is opened and 0 otherwise | |
| Binary variable equals 1 if 3PL centralized collection center j is opened and 0 otherwise | |
| Quantity of products shipped from customer zone l to 3PL local collection center k in scenario s | |
| Quantity of products shipped from 3PL local collection center k to 3PL centralized collection center j in scenario s | |
| Quantity of products shipped from the 3PL centralized collection center j to disposal center i in scenario s | |
| Quantity of products shipped from the 3PL centralized collection center j to plant m in scenario s |
3.3. Risk-Neutral Two-Stage Stochastic Programming Model
3.4. Risk-Averse Two-Stage Stochastic Programming Model
3.4.1. Mean VaR Objective
3.4.2. Mean CVaR Objective
4. Numerical Experiments
4.1. Sensitivity Analysis
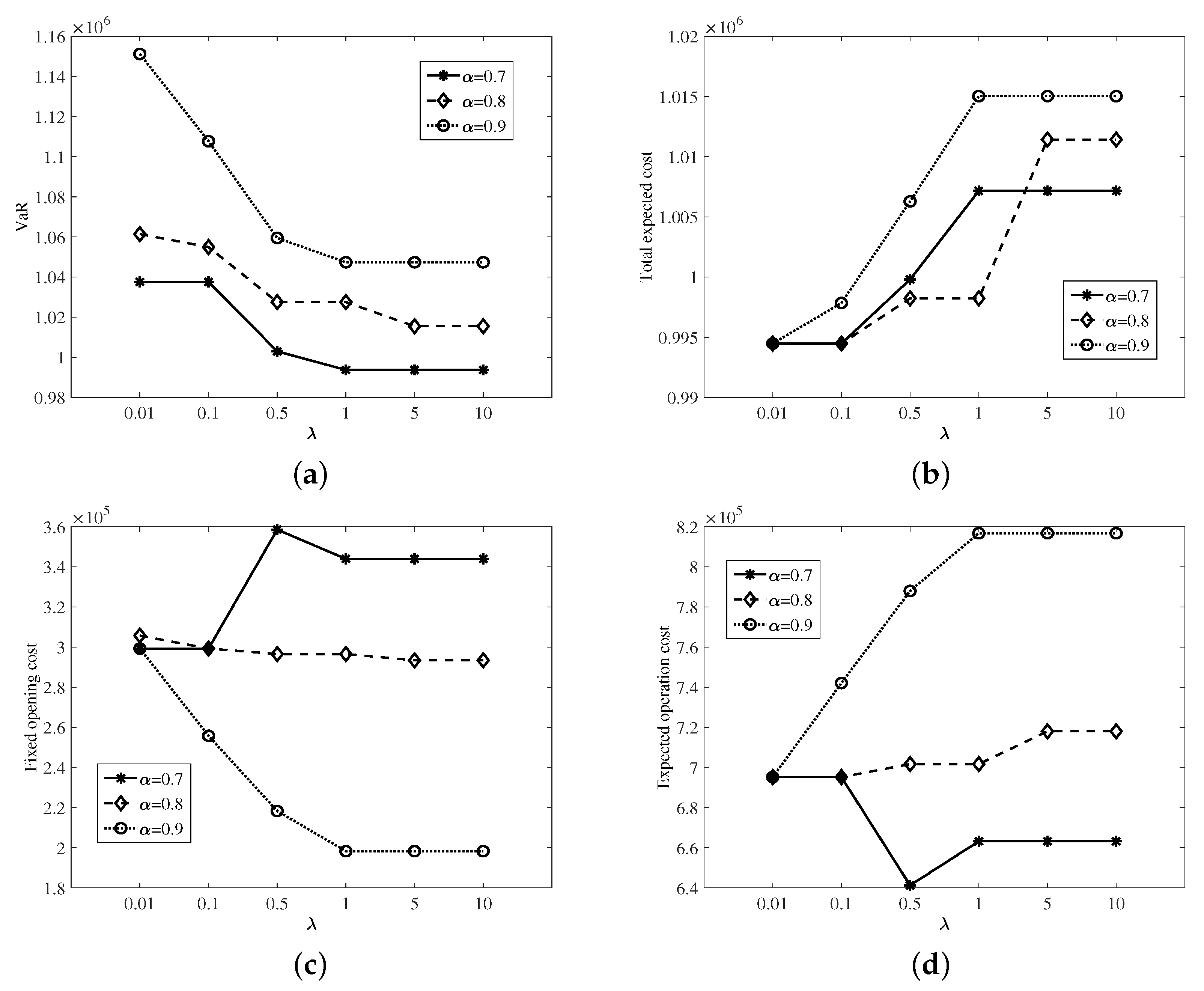
4.1.1. Sensitivity Analysis of Mean VaR Two-Stage Stochastic Programming Model
4.1.2. Sensitivity Analysis of Mean CVaR Two-Stage Stochastic Programming Model
4.2. Comparison with the Risk-Neutral Modeling Approach
4.2.1. Mean VaR Modeling Approach versus Risk-Neutral Modeling Approach
4.2.2. Mean CVaR Modeling Approach versus Risk-Neutral Modeling Approach
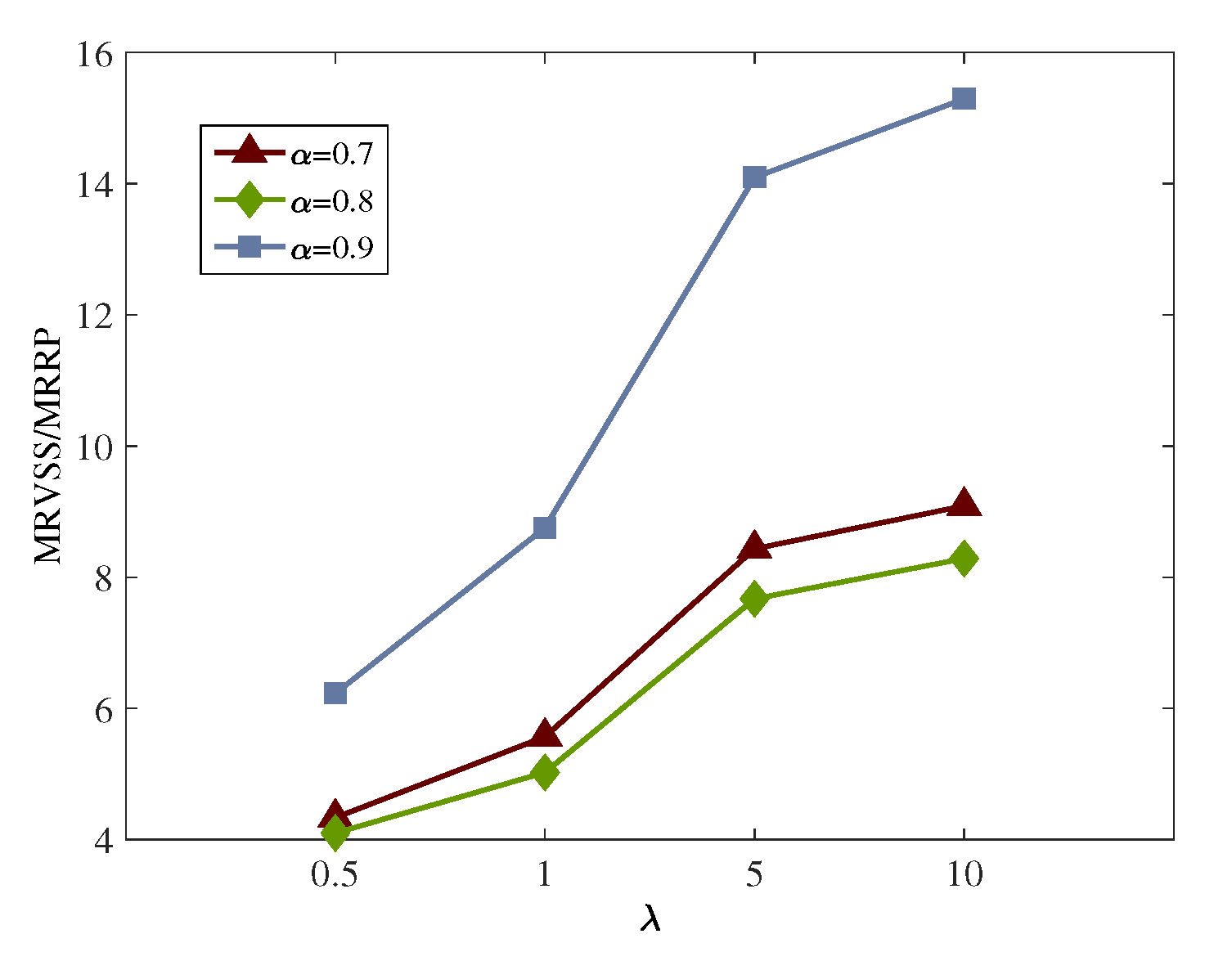
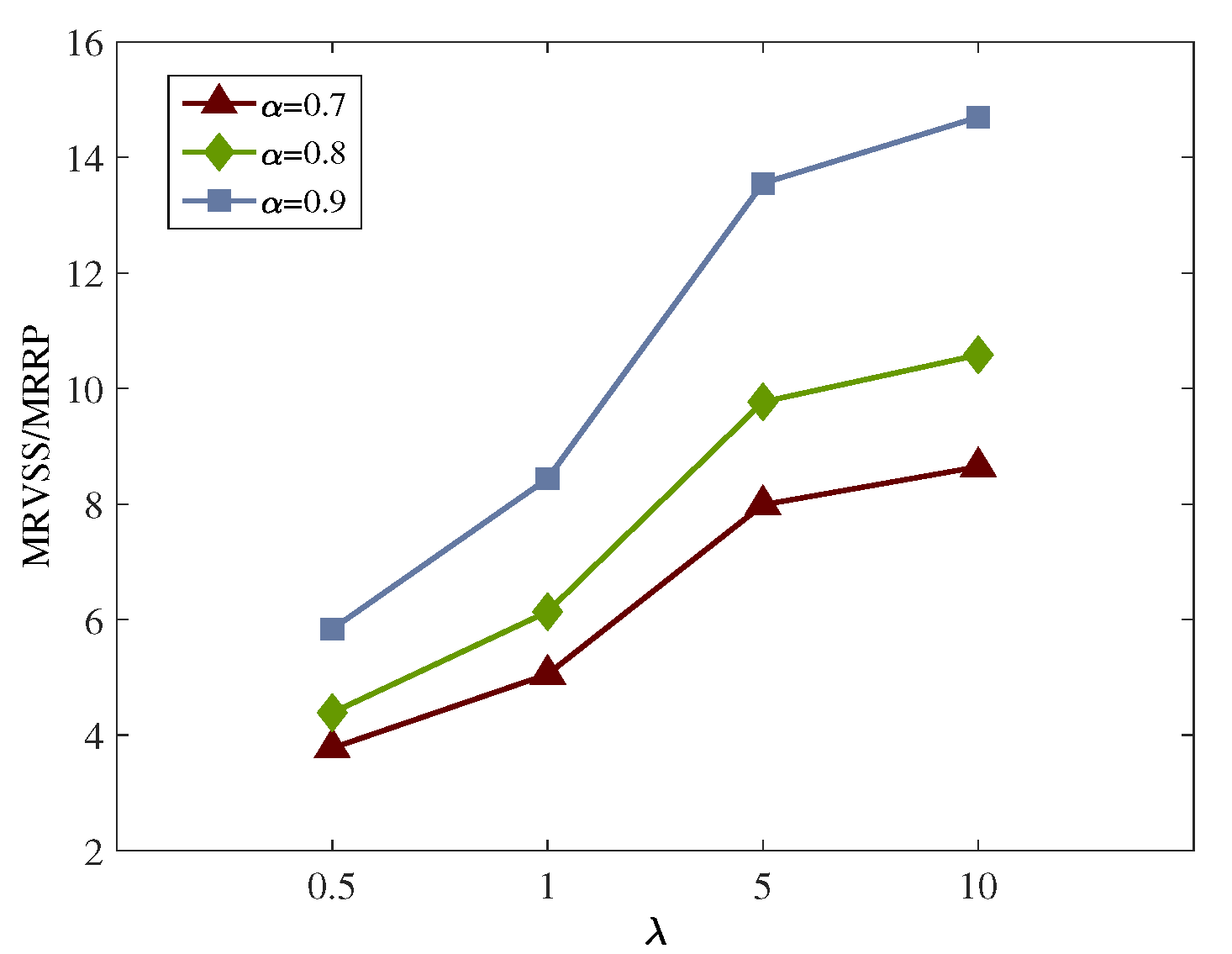
4.3. Stochastic Measures
5. Conclusions
- In this paper, we considered single-type return products in the network. However, in many real cases, we have multiple-type return products, which can be a subject for future research.
- In this paper, the scenario-based stochastic programming method was applied to deal with disruption uncertainty. In future research, mixed uncertainty could be considered for this problem and there is a need to develop other approaches to confront (with uncertainty), such as fuzzy-stochastic programming.
- Because of the limitations of the solvers, we could not consider large problem sizes. Thus, developing a meta-heuristic algorithm for solving large-sized problems can be another interesting area for future research.
- Finally, some methods, such as Benders’ decomposition, can be employed to solve the proposed problem in future research.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Optimal Total Cost of Each Scenario
Appendix B. The EV Problem
| Quantity of products shipped from customer zone l to 3PL local collection center k | |
| Quantity of products shipped from 3PL local collection center k to 3PL centralized collection center j | |
| Quantity of products shipped from 3PL centralized collection center j to disposal center i | |
| Quantity of products shipped from 3PL centralized collection center j to plant m |
References
- Tomislav, K. The concept of sustainable development: From its beginning to the contemporary issues. Zagreb Int. Rev. Econ. Bus. 2018, 21, 67–94. [Google Scholar]
- Manioudis, M.; Meramveliotakis, G. Broad strokes towards a grand theory in the analysis of sustainable development: A return to the classical political economy. New Political Econ. 2022, 27, 866–878. [Google Scholar] [CrossRef]
- Govindan, K.; Soleimani, H.; Kannan, D. Reverse logistics and closed-loop supply chain: A comprehensive review to explore the future. Eur. J. Oper. Res. 2015, 240, 603–626. [Google Scholar] [CrossRef]
- Kara, S.S.; Onut, S. A stochastic optimization approach for paper recycling reverse logistics network design under uncertainty. Int. J. Environ. Sci. Technol. 2010, 7, 717–730. [Google Scholar] [CrossRef]
- Ko, H.J.; Evans, G.W. A genetic algorithm-based heuristic for the dynamic integrated forward/reverse logistics network for 3PLs. Comput. Oper. Res. 2007, 34, 346–366. [Google Scholar] [CrossRef]
- Mahmoudzadeh, M.; Mansour, S.; Karimi, B. To develop a third-party reverse logistics network for end-of-life vehicles in Iran. Resour. Conserv. Recycl. 2013, 78, 1–14. [Google Scholar] [CrossRef]
- Hanafi, J.; Kara, S.; Kaebernick, H. Reverse logistics strategies for end-of-life products. Int. J. Logist. Manag. 2008, 19, 367–388. [Google Scholar] [CrossRef]
- Ivanov, D.; Dolgui, A.; Sokolov, B.; Ivanova, M. Literature review on disruption recovery in the supply chain. Int. J. Prod. Res. 2017, 55, 6158–6174. [Google Scholar] [CrossRef]
- Bugert, N.; Lasch, R. Supply chain disruption models: A critical review. Logist. Res. 2018, 11, 1–35. [Google Scholar]
- Snyder, L.V.; Atan, Z.; Peng, P.; Rong, Y.; Schmitt, A.J.; Sinsoysal, B. OR/MS models for supply chain disruptions: A review. IIE Trans. 2016, 48, 89–109. [Google Scholar] [CrossRef]
- Fleischmann, M.; Bloemhof-Ruwaard, J.M.; Dekker, R.; Van der Laan, E.; Van Nunen, J.A.; Van Wassenhove, L.N. Quantitative models for reverse logistics: A review. Eur. J. Oper. Res. 1997, 103, 1–17. [Google Scholar] [CrossRef]
- Mahaboob Sheriff, K.M.; Gunasekaran, A.; Nachiappan, S. Reverse logistics network design: A review on strategic perspective. Int. J. Logist. Syst. Manag. 2012, 12, 171–194. [Google Scholar]
- Suyabatmaz, A.Ç.; Altekin, F.T.; Şahin, G. Hybrid simulation-analytical modeling approaches for the reverse logistics network design of a third-party logistics provider. Comput. Ind. Eng. 2014, 70, 74–89. [Google Scholar] [CrossRef]
- Kannan, D.; Garg, K.; Jha, P.C.; Diabat, A. Integrating disassembly line balancing in the planning of a reverse logistics network from the perspective of a third party provider. Ann. Oper. Res. 2017, 253, 353–376. [Google Scholar] [CrossRef]
- Eskandarpour, M.; Nikbakhsh, E.; Zegordi, S.H. Variable neighborhood search for the bi-objective post-sales network design problem: A fitness landscape analysis approach. Comput. Oper. Res. 2014, 52, 300–314. [Google Scholar] [CrossRef]
- Min, H.; Ko, H.J. The dynamic design of a reverse logistics network from the perspective of third-party logistics service providers. Int. J. Prod. Econ. 2008, 113, 176–192. [Google Scholar] [CrossRef]
- Du, F.; Evans, G.W. A bi-objective reverse logistics network analysis for post-sale service. Comput. Oper. Res. 2008, 35, 2617–2634. [Google Scholar] [CrossRef]
- Lee, D.H.; Bian, W.; Dong, M. Multiobjective model and solution method for integrated forward and reverse logistics network design for third-party logistics providers. Transp. Res. Rec. 2007, 2032, 43–52. [Google Scholar] [CrossRef]
- Lee, D.H.; Bian, W.; Dong, M. Multiproduct distribution network design of third-party logistics providers with reverse logistics operations. Transp. Res. Rec. 2007, 2008, 26–33. [Google Scholar] [CrossRef]
- Lee, H.; Zhang, T.; Boile, M.; Theofanis, S.; Choo, S. Designing an integrated logistics network in a supply chain system. KSCE J. Civ. Eng. 2013, 17, 806–814. [Google Scholar] [CrossRef]
- Ghafarimoghadam, A.; Ghayebloo, S.; Pishvaee, M.S. A fuzzy-budgeted robust optimization model for joint network design-pricing problem in a forward-reverse supply chain: The viewpoint of third-party logistics. Comput. Appl. Math. 2019, 38, 1–29. [Google Scholar] [CrossRef]
- Ayvaz, B.; Bolat, B.; Aydın, N. Stochastic reverse logistics network design for waste of electrical and electronic equipment. Resour. Conserv. Recycl. 2015, 104, 391–404. [Google Scholar] [CrossRef]
- Trochu, J.; Chaabane, A.; Ouhimmou, M. A two-stage stochastic optimization model for the reverse logistics network design under dynamic suppliers’ locations. Waste Manag. 2019, 95, 569–583. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Solvang, W.D. A carbon-constrained stochastic optimization model with augmented multi-criteria scenario-based risk-averse solution for the reverse logistics network design under uncertainty. J. Clean. Prod. 2017, 164, 1248–1267. [Google Scholar] [CrossRef]
- Fonseca, M.C.; García-Sánchez, Á.; Ortega-Mier, M.; Saldanha-da-Gama, F. A stochastic bi-objective location model for strategic reverse logistics. Top 2010, 18, 158–184. [Google Scholar] [CrossRef]
- Yu, H.; Solvang, W.D. Incorporating flexible capacity in the planning of a multi-product multi-echelon sustainable reverse logistics network under uncertainty. J. Clean. Prod. 2018, 198, 285–303. [Google Scholar] [CrossRef]
- Roudbari, E.S.; Ghomi, S.F.; Sajadieh, M.S. Reverse logistics network design for product reuse, remanufacturing, recycling and refurbishing under uncertainty. J. Manuf. Syst. 2021, 60, 473–486. [Google Scholar] [CrossRef]
- Fattahi, M.; Govindan, K. Integrated forward/reverse logistics network design under uncertainty with pricing for collection of used products. Ann. Oper. Res. 2017, 253, 193–225. [Google Scholar] [CrossRef]
- Pishvaee, M.S.; Jolai, F.; Razmi, J. A stochastic optimization model for integrated forward/reverse logistics network design. J. Manuf. Syst. 2009, 28, 107–114. [Google Scholar] [CrossRef]
- Vahdat, V.; Vahdatzad, M.A. Accelerated Benders’ decomposition for integrated forward/reverse logistics network design under uncertainty. Logistics 2017, 1, 11. [Google Scholar] [CrossRef]
- Sugimura, Y.; Murakami, S. Designing a Resilient International Reverse Logistics Network for Material Cycles: A Japanese Case Study. Resour. Conserv. Recycl. 2021, 170, 105603. [Google Scholar] [CrossRef]
- Govindan, K.; Gholizadeh, H. Robust network design for sustainable-resilient reverse logistics network using big data: A case study of end-of-life vehicles. Transp. Res. Part Logist. Transp. Rev. 2021, 149, 102279. [Google Scholar] [CrossRef]
- Ghomi-Avili, M.; Khosrojerdi, A.; Tavakkoli-Moghaddam, R. A multi-objective model for the closed-loop supply chain network design with a price-dependent demand, shortage and disruption. J. Intell. Fuzzy Syst. 2019, 36, 5261–5272. [Google Scholar] [CrossRef]
- Yavari, M.; Zaker, H. An integrated two-layer network model for designing a resilient green-closed loop supply chain of perishable products under disruption. J. Clean. Prod. 2019, 230, 198–218. [Google Scholar] [CrossRef]
- Yavari, M.; Zaker, H. Designing a resilient-green closed loop supply chain network for perishable products by considering disruption in both supply chain and power networks. Comput. Chem. Eng. 2020, 134, 106680. [Google Scholar] [CrossRef]
- Hatefi, S.M.; Jolai, F. Reliable forward-reverse logistics network design under partial and complete facility disruptions. Int. J. Logist. Syst. Manag. 2015, 20, 370–394. [Google Scholar] [CrossRef]
- Torabi, S.; Namdar, J.; Hatefi, S.; Jolai, F. An enhanced possibilistic programming approach for reliable closed-loop supply chain network design. Int. J. Prod. Res. 2016, 54, 1358–1387. [Google Scholar] [CrossRef]
- Jabbarzadeh, A.; Haughton, M.; Khosrojerdi, A. Closed-loop supply chain network design under disruption risks: A robust approach with real world application. Comput. Ind. Eng. 2018, 116, 178–191. [Google Scholar] [CrossRef]
- Hatefi, S.; Jolai, F. Robust and reliable forward–reverse logistics network design under demand uncertainty and facility disruptions. Appl. Math. Model. 2014, 38, 2630–2647. [Google Scholar] [CrossRef]
- Fazli-Khalaf, M.; Mirzazadeh, A.; Pishvaee, M.S. A robust fuzzy stochastic programming model for the design of a reliable green closed-loop supply chain network. Hum. Ecol. Risk Assessment Int. J. 2017, 23, 2119–2149. [Google Scholar] [CrossRef]
- Rahimi, M.; Ghezavati, V. Sustainable multi-period reverse logistics network design and planning under uncertainty utilizing conditional value at risk (CVaR) for recycling construction and demolition waste. J. Clean. Prod. 2018, 172, 1567–1581. [Google Scholar] [CrossRef]
- Soleimani, H.; Govindan, K. Reverse logistics network design and planning utilizing conditional value at risk. Eur. J. Oper. Res. 2014, 237, 487–497. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Liu, Y. Distributionally robust design for bicycle-sharing closed-loop supply chain network under risk-averse criterion. J. Clean. Prod. 2020, 246, 118967. [Google Scholar] [CrossRef]
- Soleimani, H.; Seyyed-Esfahani, M.; Kannan, G. Incorporating risk measures in closed-loop supply chain network design. Int. J. Prod. Res. 2014, 52, 1843–1867. [Google Scholar] [CrossRef]
- Ramezani, M.; Bashiri, M.; Tavakkoli-Moghaddam, R. A new multi-objective stochastic model for a forward/reverse logistic network design with responsiveness and quality level. Appl. Math. Model. 2013, 37, 328–344. [Google Scholar] [CrossRef]
- Fard, A.F.; Gholian-Jouybari, F.; Paydar, M.M.; Hajiaghaei-Keshteli, M. A bi-objective stochastic closed-loop supply chain network design problem considering downside risk. Ind. Eng. Manag. Syst. 2017, 16, 342–362. [Google Scholar]
- Noyan, N. Risk-averse two-stage stochastic programming with an application to disaster management. Comput. Oper. Res. 2012, 39, 541–559. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Conditional value-at-risk for general loss distributions. J. Bank. Financ. 2002, 26, 1443–1471. [Google Scholar] [CrossRef]


| Authors | Network Type | 3PL | Risk Type | Risk Measures | Mathematical Model | Solution Approach | ||
|---|---|---|---|---|---|---|---|---|
| Forward | Reverse | Operational Risks | Disruption Risks | |||||
| Kannan et al. [14] | ✓ | ✓ | 2MINLP | Lingo | ||||
| Mahmoudzadeh et al. [6] | ✓ | ✓ | 1MILP | CPLEX | ||||
| Suyabatmaz et al. [13] | ✓ | ✓ | Hybrid simulation-analytical | CPLEX | ||||
| Eskandarpour et al. [15] | ✓ | ✓ | 2MINLP | Metaheuristics | ||||
| Du and Evans [17] | ✓ | ✓ | 1MILP | Metaheuristics | ||||
| Min and Ko [16] | ✓ | ✓ | ✓ | 2MINLP | Metaheuristics | |||
| Lee et al. [18] | ✓ | ✓ | ✓ | ✓ | 1MILP | Metaheuristics | ||
| Lee et al. [19] | ✓ | ✓ | ✓ | 1MILP | Metaheuristics | |||
| Lee et al. [20] | ✓ | ✓ | ✓ | 2MINLP | GAMS | |||
| Ko and Evans [5] | ✓ | ✓ | ✓ | 2MINLP | Metaheuristics | |||
| Ghafarimoghadam et al. [21] | ✓ | ✓ | ✓ | 3RO | GAMS | |||
| Ayvaz et al. [22] | ✓ | ✓ | ✓ | 5TSSP | CPLEX | |||
| Trochu et al. [23] | ✓ | ✓ | 5TSSP | - | ||||
| Yu and Solvang [24] | ✓ | ✓ | 5TSSP | Lingo | ||||
| Kara and Onut [4] | ✓ | ✓ | 5TSSP | GAMS | ||||
| Fonseca et al. [25] | ✓ | ✓ | 5TSSP | CPLEX | ||||
| Yu and Solvang [26] | ✓ | ✓ | 5TSSP | Lingo | ||||
| Roudbari et al. [27] | ✓ | ✓ | 5TSSP | Metaheuristics | ||||
| Fattahi and Govindan [28] | ✓ | ✓ | ✓ | 5TSSP | Metaheuristics | |||
| Pishvaee et al. [29] | ✓ | ✓ | ✓ | 5TSSP | Lingo | |||
| Vahdat and Vahdatzad [30] | ✓ | ✓ | ✓ | 5TSSP | Exact Algorithm | |||
| Sugimura and Murakami [31] | ✓ | ✓ | 1MILP | Linear Programming Kit | ||||
| Govindan and Gholizadeh [32] | ✓ | ✓ | 4SBRO | Metaheuristics | ||||
| Ghomi-Avili et al. [33] | ✓ | ✓ | ✓ | 5TSSP | GAMS | |||
| Yavari and Zaker [34] | ✓ | ✓ | ✓ | 5TSSP | - | |||
| Yavari and Zaker [35] | ✓ | ✓ | ✓ | 5TSSP | - | |||
| Hatefi and Jolai [36] | ✓ | ✓ | ✓ | 4SBRO | GAMS | |||
| Torabi et al. [37] | ✓ | ✓ | ✓ | 4SBRO | GAMS | |||
| Jabbarzadeh et al. [38] | ✓ | ✓ | ✓ | 4SBRO | Heuristics | |||
| Hatefi and Jolai [39] | ✓ | ✓ | ✓ | 4SBRO | GAMS | |||
| Fazli-Khalaf et al. [40] | ✓ | ✓ | ✓ | 4SBRO | GAMS | |||
| Rahimi and Ghezavati [41] | ✓ | ✓ | CVaR | 5TSSP | GAMS | |||
| Soleimani and Govindan [42] | ✓ | ✓ | CVaR | 5TSSP | CPLEX | |||
| Ma et al. [43] | ✓ | ✓ | ✓ | CVaR | Multi-scenario optimization model | CPLEX | ||
| Soleimani et al. [44] | ✓ | ✓ | ✓ | MAD, VaR, CVaR | 5TSSP | CPLEX | ||
| Ramezani et al. [45] | ✓ | ✓ | ✓ | Probability of a determined objective | 5TSSP | CPLEX | ||
| Fard et al. [46] | ✓ | ✓ | ✓ | Downside risk | 5TSSP | Metaheuristics, CPLEX | ||
| Our work | ✓ | ✓ | ✓ | VaR, CVaR | 5TSSP | CPLEX | ||
| Parameter | Value Range |
|---|---|
| 100–600 | |
| 5–15 | |
| 1000–1500 | |
| 10,000–20,000 | |
| 5–15 | |
| 1500–2000 | |
| 20,000–30,000 | |
| 2000–3000 | |
| 2000–2500 | |
| 1–20 |
| Scenario | Probability | Disruption Data of 3PL Local Collection Centers | Disruption Data of 3PL Centralized Collection Centers |
|---|---|---|---|
| 1 | 0.0018 | [1,0,1,1,1,0,0,1,1,1,0,1,1,1,0] | [1,0,0,0,0,1,0,1,1,0,1,0,0,1,1] |
| 2 | 0.0165 | [1,0,1,1,1,1,0,1,0,0,1,0,1,1,0] | [1,1,0,1,0,0,0,1,1,1,0,0,1,0,0] |
| 3 | 0.1019 | [1,0,1,1,1,0,1,0,0,0,1,1,0,1,0] | [1,0,1,0,0,0,1,1,1,1,1,0,1,1,1] |
| 4 | 0.0369 | [1,0,1,1,0,1,0,0,1,0,0,0,0,1,1] | [1,1,0,0,0,1,1,1,0,1,1,1,1,1,1] |
| 5 | 0.0043 | [0,0,1,0,1,0,0,1,1,1,0,0,0,0,1] | [1,0,1,0,1,1,1,0,0,1,1,0,0,0,1] |
| 6 | 0.0052 | [0,0,1,1,1,0,1,0,0,0,0,1,0,1,1] | [0,0,0,1,1,1,1,0,0,1,0,1,0,1,0] |
| 7 | 0.0522 | [1,1,0,0,0,0,0,1,1,1,1,1,0,0,0] | [1,0,0,1,1,0,1,0,0,1,0,1,1,1,1] |
| 8 | 0.0226 | [1,1,0,0,1,1,0,1,0,0,1,1,1,0,1] | [1,0,0,1,0,1,0,1,1,1,0,1,1,1,1] |
| 9 | 0.0837 | [1,1,1,0,0,1,1,0,0,1,0,0,1,0,1] | [0,0,0,0,0,0,0,1,0,1,0,0,0,0,1] |
| 10 | 0.1052 | [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] | [0,0,0,0,0,0,0,0,1,0,0,1,1,0,0] |
| 11 | 0.0454 | [1,0,1,1,1,0,1,1,0,1,1,0,0,0,1] | [1,0,0,1,0,0,1,0,1,1,1,1,1,1,1] |
| 12 | 0.0622 | [0,0,1,1,1,0,0,0,0,1,1,1,1,1,0] | [1,0,1,0,1,0,0,0,1,0,1,1,0,1,1] |
| 13 | 0.0175 | [1,1,0,1,1,1,1,0,1,1,0,1,0,0,1] | [1,1,0,1,1,1,1,1,1,1,0,1,1,0,0] |
| 14 | 0.0701 | [1,1,0,0,1,0,0,1,1,0,1,0,1,1,0] | [1,1,1,1,0,0,0,0,1,1,1,1,1,0,0] |
| 15 | 0.0687 | [0,0,1,0,1,0,0,1,1,0,1,0,1,0,1] | [0,0,0,1,1,0,0,1,1,0,1,0,1,1,1] |
| 16 | 0.0300 | [0,0,0,1,0,1,0,1,0,0,1,0,0,0,1] | [0,0,0,1,0,1,1,0,1,0,1,1,0,1,1] |
| 17 | 0.0419 | [0,0,0,0,0,1,0,1,1,0,0,0,0,1,1] | [1,0,1,0,1,0,1,0,0,1,1,1,1,0,0] |
| 18 | 0.0598 | [0,1,1,0,1,0,1,0,1,0,0,0,0,0,1] | [0,0,1,1,1,1,0,0,0,0,0,1,0,0,1] |
| 19 | 0.0856 | [0,0,1,1,0,1,1,0,0,0,1,1,1,1,0] | [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0] |
| 20 | 0.0886 | [0,0,0,0,1,1,1,0,0,1,1,0,0,0,1] | [1,0,0,0,1,1,0,0,1,0,0,1,1,0,1] |
| VaR | CVaR | Worst | Total Expected Cost | Fixed Opening Cost | Expected Operation Cost | Expected Transportation Cost | Expected Processing Cost | Expected Penalty Cost | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.7 | 0.01 | 1,037,594.60 | 1,094,627.08 | 1,151,182.60 | 994,475.09 | 299,268 | 695,207.09 | 66,980.01 | 117,110.48 | 511,116.59 |
| 0.1 | 1,037,594.60 | 1,094,627.08 | 1,151,182.60 | 994,475.09 | 299,268 | 695,207.09 | 66,994.16 | 117,096.34 | 511,116.59 | |
| 0.5 | 1,002,970.40 | 1,121,136.06 | 1,222,722.20 | 999,803.05 | 358,562 | 641,241.05 | 80,300.41 | 143,152.68 | 417,787.96 | |
| 1 | 993,717.40 | 1,127,758.72 | 1,262,939.00 | 1,007,159.40 | 343,970 | 663,189.40 | 72,461.61 | 131,912.60 | 458,815.19 | |
| 5 | 993,717.40 | 1,127,758.72 | 1,262,939.00 | 1,007,159.40 | 343,970 | 663,189.40 | 72,451.31 | 131,922.90 | 458,815.19 | |
| 10 | 993,717.40 | 1,127,758.72 | 1,262,939.00 | 1,007,159.40 | 343,970 | 663,189.40 | 72,420.69 | 131,953.52 | 458,815.19 | |
| 0.8 | 0.01 | 1,061,405.20 | 1,117,673.23 | 1,162,129.40 | 994,473.84 | 305,718 | 695,207.09 | 66,992.08 | 117,098.42 | 511,116.59 |
| 0.1 | 1,054,955.20 | 1,118,634.57 | 1,151,182.60 | 994,475.09 | 299,268 | 695,207.09 | 66,981.78 | 117,108.72 | 511,116.59 | |
| 0.5 | 1,027,541.40 | 1,124,429.54 | 1,148,453.60 | 998,229.30 | 296,539 | 701,690.30 | 66,655.23 | 115,581.35 | 519,453.71 | |
| 1 | 1,027,541.40 | 1,124,429.54 | 1,148,453.60 | 998,229.30 | 296,539 | 701,690.30 | 66,653.55 | 115,583.04 | 519,453.71 | |
| 5 | 1,015,483.30 | 1,148,701.42 | 1,206,844.80 | 1,011,424.01 | 293,411 | 718,013.01 | 63,196.09 | 116,157.54 | 538,659.38 | |
| 10 | 1,015,483.30 | 1,148,701.42 | 1,206,844.80 | 1,011,424.01 | 293,411 | 718,013.01 | 63,196.02 | 116,157.61 | 538,659.38 | |
| 0.9 | 0.01 | 1,151,182.60 | 1,151,182.60 | 1,151,182.60 | 994,475.09 | 299,268 | 695,207.09 | 66,994.16 | 117,096.34 | 511,116.59 |
| 0.1 | 110,7691.60 | 110,7691.60 | 1,107,691.60 | 997,850.55 | 255,777 | 742,073.55 | 60,701.46 | 101,415.48 | 579,956.62 | |
| 0.5 | 1,059,486.40 | 1,071,031.55 | 1,077,241.60 | 1,006,287.47 | 218,290 | 787,997.47 | 51,224.97 | 84,298.83 | 652,473.67 | |
| 1 | 1,047,369.60 | 1,053,348.75 | 1,057,225.60 | 1,015,030.57 | 198,274 | 816,756.57 | 46,402.94 | 74,988.33 | 695,365.30 | |
| 5 | 1,047,369.60 | 1,053,348.75 | 1,057,225.60 | 1,015,030.57 | 198,274 | 816,756.57 | 46,368.60 | 75,022.67 | 695,365.30 | |
| 10 | 1,047,369.60 | 1,053,348.75 | 1,057,225.60 | 1,015,030.57 | 198,274 | 816,756.57 | 46,407.21 | 74,984.06 | 695,365.30 |
| CVaR | VaR | Worst | Total Expected Cost | Fixed Opening Cost | Expected Operation Cost | Expected Transportation Cost | Expected Processing Cost | Expected Penalty Cost | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.7 | 0.01 | 1,094,627.08 | 1,037,594.60 | 1,151,182.60 | 994,475.09 | 299,268 | 695,207.09 | 66,994.16 | 117,096.34 | 511,116.59 |
| 0.1 | 1,094,627.08 | 1,037,594.60 | 1,151,182.60 | 994,475.09 | 299,268 | 695,207.09 | 66,992.71 | 117,097.79 | 511,116.59 | |
| 0.5 | 1,066,580.95 | 1,014,649.80 | 1,095,753.40 | 1,002,941.46 | 254,557 | 748,384.46 | 53,617.49 | 96,667.46 | 598,099.51 | |
| 1 | 1,048,723.75 | 1,042,608.40 | 1,057,225.60 | 1,015,030.57 | 198,274 | 816,756.57 | 46,413.63 | 74,977.64 | 695,365.30 | |
| 5 | 1,048,723.75 | 1,042,608.40 | 1,057,225.60 | 1,015,030.57 | 198,274 | 816,756.57 | 46,368.45 | 75,022.82 | 695,365.30 | |
| 10 | 1,048,723.75 | 1,042,608.40 | 1,057,225.60 | 1,015,030.57 | 198,274 | 816,756.57 | 46,404.46 | 74,986.80 | 695,365.30 | |
| 0.8 | 0.01 | 1,117,673.23 | 1,061,405.20 | 1,162,129.40 | 994,473.84 | 305,718 | 688,755.84 | 71,543.25 | 122,969.82 | 494,242.76 |
| 0.1 | 1,117,673.23 | 1,061,405.20 | 1,162,129.40 | 994,473.84 | 305,718 | 688,755.84 | 71,544.61 | 122,968.47 | 494,242.76 | |
| 0.5 | 1,064,766.19 | 1,054,883.80 | 1,077,241.60 | 1,006,287.47 | 218,290 | 787,997.47 | 51,227.72 | 84,296.08 | 652,473.67 | |
| 1 | 1,050,214.05 | 1,045,932.60 | 1,057,225.60 | 1,015,030.57 | 198,274 | 816,756.57 | 46,367.92 | 75,023.35 | 695,365.30 | |
| 5 | 1,050,214.05 | 1,045,932.60 | 1,057,225.60 | 1,015,030.57 | 198,274 | 816,756.57 | 46,367.92 | 75,023.35 | 695,365.30 | |
| 10 | 1,050,214.05 | 1,045,932.60 | 1,057,225.60 | 1,015,030.57 | 198,274 | 816,756.57 | 46,367.92 | 75,023.35 | 695,365.30 | |
| 0.9 | 0.01 | 1,151,182.60 | 1,151,182.60 | 1,151,182.60 | 994,475.09 | 299,268 | 695,207.09 | 66,994.16 | 117,096.34 | 511,116.59 |
| 0.1 | 1,107,691.60 | 1,107,691.60 | 1,107,691.60 | 997,850.55 | 255,777 | 742,073.55 | 60,701.46 | 101,415.48 | 579,956.62 | |
| 0.5 | 1,053,348.75 | 1,047,369.60 | 1,057,225.60 | 1,015,030.57 | 198,274 | 816,756.57 | 46,368.56 | 75,022.71 | 695,365.30 | |
| 1 | 1,053,348.75 | 1,047,369.60 | 1,057,225.60 | 1,015,030.57 | 198,274 | 816,756.57 | 46,368.60 | 75,022.67 | 695,365.30 | |
| 5 | 1,053,348.75 | 1,047,369.60 | 1,057,225.60 | 1,015,030.57 | 198,274 | 816,756.57 | 46,365.81 | 75,025.45 | 695,365.30 | |
| 10 | 1,053,348.75 | 1,047,369.60 | 1,057,225.60 | 1,015,030.57 | 198,274 | 816,756.57 | 46,365.81 | 75,025.45 | 695,365.30 |
| Total Expected | Cost Worst | VaR | CVaR | ||||
|---|---|---|---|---|---|---|---|
| 994,473.84 | 1,162,129.40 | 1,052,990.90 | 1,061,405.20 | 1,162,129.40 | 1,096,925.72 | 1,117,673.23 | 1,162,129.40 |
| Relative Difference | |||||
|---|---|---|---|---|---|
| Total Expected Cost (%) | VaR (%) | CVaR (%) | Worst (%) | ||
| 0.7 | 0.01 | 0.0001 | |||
| 0.1 | 0.0001 | ||||
| 0.5 | 0.5359 | 2.2071 | 5.2139 | ||
| 1 | 1.2756 | 2.8109 | 8.6746 | ||
| 5 | 1.2756 | 2.8109 | 8.6746 | ||
| 10 | 1.2756 | 2.8109 | 8.6746 | ||
| 0.8 | 0.01 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.1 | 0.0001 | 0.0860 | |||
| 0.5 | 0.3776 | 0.6045 | |||
| 1 | 0.3776 | 0.6045 | |||
| 5 | 1.7044 | 2.7761 | 3.8477 | ||
| 10 | 1.7044 | 2.7761 | 3.8477 | ||
| 0.9 | 0.01 | 0.0001 | |||
| 0.1 | 0.3395 | ||||
| 0.5 | 1.1879 | ||||
| 1 | 2.0671 | ||||
| 5 | 2.0671 | ||||
| 10 | 2.0671 | ||||
| Relative Difference | |||||
|---|---|---|---|---|---|
| Total Expected Cost (%) | VaR (%) | CVaR (%) | Worst (%) | ||
| 0.7 | 0.01 | 0.0001 | |||
| 0.1 | 0.0001 | ||||
| 0.5 | 0.8515 | ||||
| 1 | 2.0671 | ||||
| 5 | 2.0671 | ||||
| 10 | 2.0671 | ||||
| 0.8 | 0.01 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.1 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| 0.5 | 1.1879 | ||||
| 1 | 2.0671 | ||||
| 5 | 2.0671 | ||||
| 10 | 2.0671 | ||||
| 0.9 | 0.01 | 0.0001 | |||
| 0.1 | 0.3395 | ||||
| 0.5 | 2.0671 | ||||
| 1 | 2.0671 | ||||
| 5 | 2.0671 | ||||
| 10 | 2.0671 | ||||
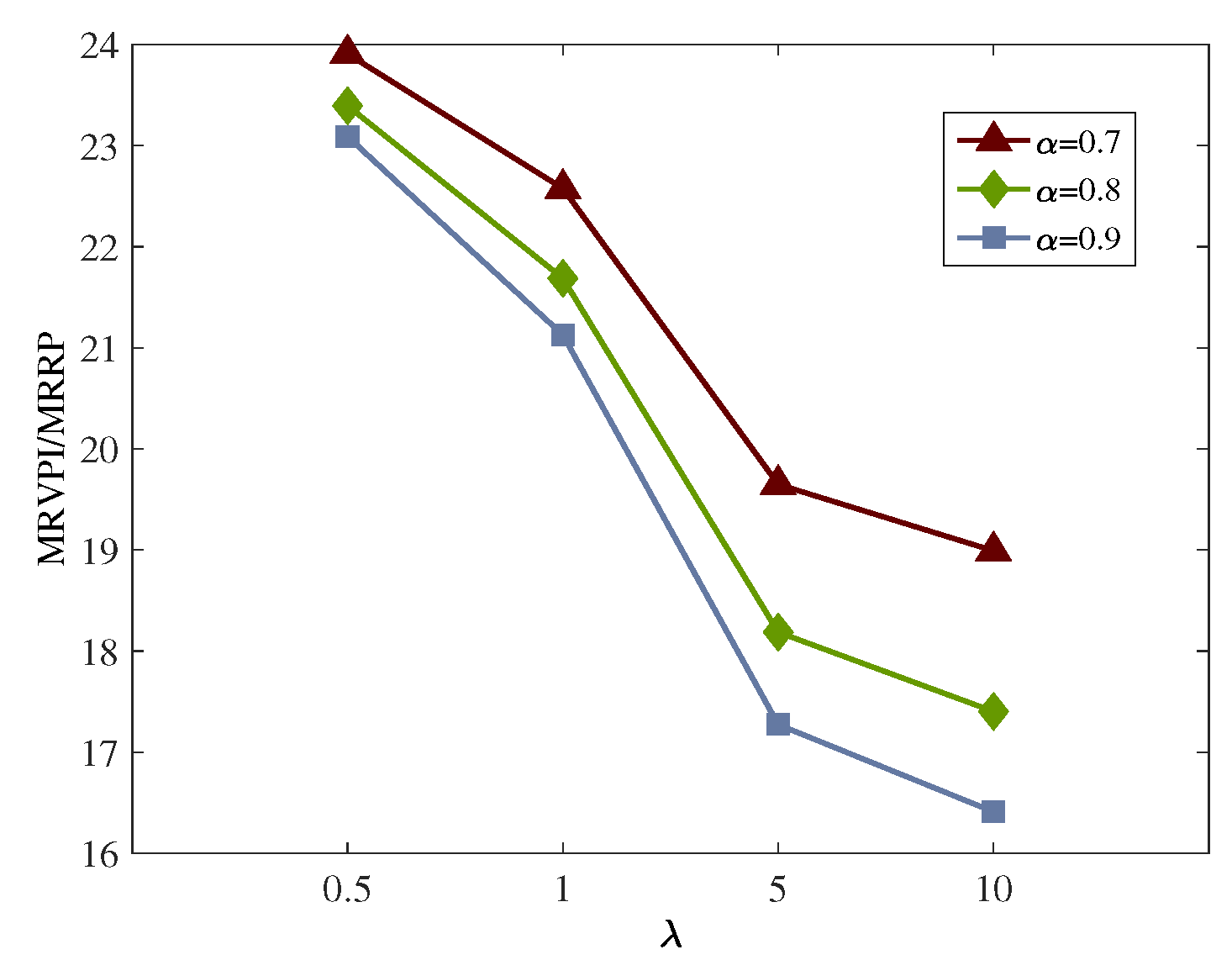
| 0.5 | 0.7 | 1,501,288.25 | 1,566,361.47 | 65,073.22 | 4.3345 | 1,140,708.76 | 360,579.49 | 24.0180 |
| 0.8 | 1,512,000.00 | 1,573,980.52 | 61,980.52 | 4.0992 | 1,160,976.66 | 351,023.34 | 23.2158 | |
| 0.9 | 1,536,030.67 | 1,631,699.27 | 95,668.60 | 6.2283 | 1,185,744.96 | 350,285.71 | 22.8046 | |
| 1 | 0.7 | 2,000,876.80 | 2,112,288.37 | 111,411.57 | 5.5681 | 1,541,339.46 | 459,537.34 | 22.9668 |
| 0.8 | 2,025,770.70 | 2,127,526.47 | 101,755.77 | 5.0231 | 1,581,875.26 | 443,895.44 | 21.9124 | |
| 0.9 | 2,062,400.17 | 2,242,963.97 | 180,563.80 | 8.7550 | 1,631,411.86 | 430,988.31 | 20.8974 | |
| 5 | 0.7 | 5,975,746.40 | 6,479,703.57 | 503,957.17 | 8.4334 | 4,746,385.06 | 1,229,361.34 | 20.5725 |
| 0.8 | 6,088,840.51 | 6,555,894.07 | 467,053.56 | 7.6706 | 4,949,064.06 | 1,139,776.45 | 18.7191 | |
| 0.9 | 6,251,878.57 | 7,133,081.57 | 881,203.00 | 14.0950 | 5,196,747.06 | 1,055,131.51 | 16.8770 | |
| 10 | 0.7 | 10,944,333.40 | 11,938,972.57 | 994,639.17 | 9.0882 | 8,752,692.06 | 2,191,641.34 | 20.0254 |
| 0.8 | 11,166,257.01 | 12,091,353.57 | 925,096.56 | 8.2848 | 9,158,050.06 | 2,008,206.95 | 17.9846 | |
| 0.9 | 11,488,726.57 | 13,245,728.57 | 1,757,002.00 | 15.2933 | 9,653,416.06 | 1,835,310.51 | 15.9749 |
| 0.5 | 0.7 | 1,536,231.94 | 1,594,245.87 | 58,013.93 | 3.7764 | 1,168,964.18 | 367,267.76 | 23.9071 |
| 0.8 | 1,538,670.56 | 1,606,205.26 | 67,534.70 | 4.3892 | 1,178,721.81 | 359,948.75 | 23.3935 | |
| 0.9 | 1,541,704.94 | 1,631,699.27 | 89,994.33 | 5.8373 | 1,185,744.96 | 355,959.98 | 23.0887 | |
| 1 | 0.7 | 2,063,754.32 | 2,168,057.16 | 104,302.84 | 5.0540 | 1,597,850.30 | 465,904.02 | 22.5756 |
| 0.8 | 2,065,244.62 | 2,191,975.95 | 126,731.33 | 6.1364 | 1,617,365.57 | 447,879.05 | 21.6865 | |
| 0.9 | 2,068,379.32 | 2,242,963.97 | 174,584.65 | 8.4406 | 1,631,411.86 | 436,967.46 | 21.1261 | |
| 5 | 0.7 | 6,258,649.31 | 6,758,547.52 | 499,898.21 | 7.9873 | 5,028,939.26 | 1,229,710.05 | 19.6482 |
| 0.8 | 6,266,100.82 | 6,878,141.47 | 612,040.65 | 9.7675 | 5,126,515.61 | 1,139,585.21 | 18.1865 | |
| 0.9 | 6,281,774.31 | 7,133,081.57 | 851,307.26 | 13.5520 | 5,196,747.06 | 1,085,027.25 | 17.2726 | |
| 10 | 0.7 | 11,502,268.05 | 12,496,660.47 | 994,392.42 | 8.6452 | 9,317,800.46 | 2,184,467.59 | 18.9916 |
| 0.8 | 11,517,171.08 | 12,735,848.37 | 1,218,677.29 | 10.5814 | 9,512,953.16 | 2,004,217.92 | 17.4020 | |
| 0.9 | 11,548,518.06 | 13,245,728.57 | 1,697,210.51 | 14.6963 | 9,653,416.06 | 1,895,102.00 | 16.4099 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Chen, X. Reverse Logistics Network Design under Disruption Risk for Third-Party Logistics Providers. Sustainability 2022, 14, 14936. https://doi.org/10.3390/su142214936
Li R, Chen X. Reverse Logistics Network Design under Disruption Risk for Third-Party Logistics Providers. Sustainability. 2022; 14(22):14936. https://doi.org/10.3390/su142214936
Chicago/Turabian StyleLi, Rui, and Xin Chen. 2022. "Reverse Logistics Network Design under Disruption Risk for Third-Party Logistics Providers" Sustainability 14, no. 22: 14936. https://doi.org/10.3390/su142214936
APA StyleLi, R., & Chen, X. (2022). Reverse Logistics Network Design under Disruption Risk for Third-Party Logistics Providers. Sustainability, 14(22), 14936. https://doi.org/10.3390/su142214936






