A New Green Labeling Scheme for Agri-Food Supply Chains: Equilibrium and Information Sharing under Uncertainties

Abstract

Even though organic farming is perceived worldwide as the most eco-friendly agricultural method, its significantly lower yield compared to conventional farming poses a major challenge in ensuring food security for the ever-increasing world population. On the other hand, the adverse environmental impacts of conventional agriculture due to the uncontrolled use of key farm inputs like fertilizer and irrigation water cannot be overlooked. In this context, we develop a new eco-label to promote an efficient agricultural method that provides the right balance between yield and environmental impacts through the optimal use of these farm inputs. The proposed eco-label is applied to a game-theoretic model of a farmer-retailer supply chain under demand and yield uncertainties. We consider the demand as a function of the product’s retail price, greenness, and quality; and model yield using a crop-response function. The analytical results derived help optimize the farm inputs, retail prices, and order quantity so that the stakeholders’ profits are maximized. We also investigate the effects of yield information sharing in this supply chain and find that the stakeholders must share yield information when environmentally conscious consumers dominate the market.

1. Introduction

The increasing world population and the associated need for ensuring food security using limited resources have forced agricultural communities around the world to rely on high-yield farming techniques which depend on excessive fertilization, which adversely affects the environment in numerous ways. The life cycle assessment of a wheat-to-bread supply chain reveals that the use of ammonium nitrate fertilizers accounts for 41.9% of the total Human Toxicity Potential of the supply chain [1]. Today’s consumer is conscious and vocal about health and environmental concerns. Therefore, there is an increasing importance for sustainable practices in agriculture to ensure safe and healthy food for human consumption. The emergence of various farming practices like Good Agricultural Practices (GAP) [2], Three Controls Technology [3], System of Rice Intensification [4], and organic farming [5] are some examples of this development. Among all the farming methods developed, organic farming has been identified by most consumers as the most eco-friendly mode of agriculture [6,7] as it completely avoids the use of synthetic fertilizers. The premium prices that the consumers are willing to pay for organic farm products support this observation. However, many scientific studies across the world point out a significant reduction in yield in organic farms due to the non-usage of fertilizers [7,8]. These studies highlight that the environmental impact measured per hectare of cultivated land was less for organic farming when compared to conventional farming. However, this impact was higher when the impacts were measured per tonne of farm output, primarily because of the low yield from the organic farming practices. This means that organic farming would require more land area than conventional farming to produce the same output (yield) as that of conventional farming. This can significantly affect land use patterns, which in turn causes severe environmental impacts. Moreover, attempts to increase the yield in organic farming would require high compost quality and improved quality of organic fertilizers, which in turn would increase the investment in time, money, and effort. All of this may make organic farming economically less viable [5]. In fact, it is with this issue in mind Stubenrauch et al. [9] developed a legal framework to merge the conventional and organic agricultural systems. Such a transformation is necessary for the present-day agricultural settings to ensure safe and high-quality food for the masses.

Another important aspect that has a major impact on the yield and sustainability of agricultural practices is the type of irrigation facilities used. It is observed that the yield of mostly all agricultural products are dependent on the type of irrigation facilities used [10], and many of these products have a very high water footprint [11]. Hence, the excessive water consumption is a matter of grave concern.

Given the above discussion, we identify the need for promoting an agricultural practice that is more efficient in terms of output and resource usage. Specifically, the focus should be on improving the farm yield while minimizing the product’s environmental impacts per unit quantity. This requires optimizing the primary farm inputs like fertilizer and irrigation water, as these are the key factors that influence the yield when adequately applied but create severe environmental impacts when overused. Since eco-labels play a crucial role in promoting green approaches, we argue that these labeling schemes should consider quantities of fertilizer and irrigation water used while determining the greenness of an agri-food product. While numerous eco-labels are prevalent worldwide for agri-food products, they fall short of meeting this requirement (www.ecolabelindex.com; Accessed on 20 April 2021). To bridge this gap, in this work, we develop a new eco-labeling scheme for agri-food supply chains. Our labeling scheme opens up the possibility of incorporating yield considerations while certifying agri-food products, which is crucial considering the rising challenge of feeding the growing world population. On the practical side, the proposed scheme can be applied in various agricultural settings with little modifications due to its coherent nature.

To demonstrate the effectiveness of the proposed eco-label, we model a two-echelon green agri-food supply chain consisting of a farmer and a retailer. Such supply chains are typical in supermarket contracts where the supermarket procures fresh agricultural products directly from the farmer [12,13]. The farmer and the retailer enter into a contract where the farmer agrees to supply a fixed quantity of green products to the retailer at a fixed price for a period of time as mentioned in the contract. The farmer is expected to replenish the retailer’s inventory at fixed intervals. While it is common in the literature to consider the demand at the retailer for any green product to be dependent on its retail price and greenness level [14,15], a third factor in the form of product quality needs to be considered in the case of agricultural products [16]. As the quality of these products decreases over time due to physical deterioration, the consumers refrain from buying them when their expiry dates grow nearer [17]. In addition, it is necessary to consider uncertainties in some form (due to the availability of alternative products, other consumer preferences, etc.) as the fourth factor affecting the demand for these products. There is a dearth of supply chain models in the literature that account for all these factors while modeling product demand. To address this gap, we model the retailer’s demand as a function of these four factors.

The proposed eco-labeling scheme, which considers a reduction in fertilizer and irrigation water usage, is used to certify the farmer’s products. The retailer decides the order quantity and the retail price of the product, while the farmer chooses the amount of fertilizer and irrigation water to be used so that his yield will be sufficient to meet the retailer’s demand. In this sense, this is a typical futures contract where the retailer is deciding on an order quantity for the future, and the farmer is planning for the present. As his yield is uncertain, the farmer forecasts the yield before sowing seeds. This forecast information, along with the retailer’s order quantity information, is then used to decide the farm inputs. By considering uncertainties in yield and demand together in our supply chain model, we explore some critical areas that are rarely studied in the sustainable agri-food supply chain literature. We derive closed-form solutions for the farmer’s and retailer’s problems under different market settings to aid them in decision-making.

Finally, through rigorous numerical analysis, we study the effects of yield information sharing on the stakeholder’s profits. While researchers have conducted extensive studies on the effects of demand information sharing, the topic of yield information sharing has remained less explored in the context of sustainable agri-food supply chains. Our study provides some valuable insights to the stakeholders by helping them identify the scenarios where it is beneficial to share the yield information.

The remainder of this paper is organized as follows: In Section 2, a literature review is conducted to discuss the existing works in this area and identify the research gaps. Section 3 details our model and the associated assumptions, and in Section 4, the model is analyzed to obtain closed-form solutions for the farmer’s and retailer’s problems. In Section 5, a numerical study is conducted to study the effects of information sharing. The significance of the results obtained is discussed in Section 6, and finally, the conclusions are drawn.

2. Literature Review

Recognizing the pivotal role of sustainable agricultural supply chains in shaping the future of humanity, the scientific community has conducted extensive research in this field. Some of the most recent studies in this direction include the impact of COVID-19 on these supply chains [18,19], drivers and barriers to sustainability [20,21,22], sustainable supply chain logistics [23,24], stakeholders’ contributions to improving sustainability [25], etc. Another exciting but not intensely explored area in the literature is the effect of knowledge management on the internationalization of green agri-food industries [26]. A wide array of review articles [27,28,29,30,31,32,33,34] dealing with various aspects of these supply chains have been published recently. In particular, Nematollahi and Tajbakhsh [28] stress the importance of developing new solution approaches to deal with the agri-food supply chain problems, which are complicated due to the presence of demand and yield uncertainties and sustainability issues. Nematollahi and Tajbakhsh [28] also highlights the limited number of studies investigating the effect of product perishability in these supply chains. Although there has been considerable attention to modeling the perishability of goods in supply chains [35,36,37], most of these models do not consider the sustainability aspects in defining the demand function. While Song et al. [38] address the perishability aspect by using a demand function that depends on the greenness and freshness of the product, they fail to incorporate the uncertainties in their model.

It is also important to consider the factors like the amount of fertilizer and water used during cultivation while determining the greenness level of an agri-food product, as these factors have a significant impact on the environment [1,11]. Excessive use of synthetic nitrogen fertilizers results in high greenhouse gas emissions, which must be avoided. However, avoiding their use entirely, as in the case of organic farming, is not advisable as it results in significant yield losses. To counter this, Stubenrauch et al. [9] demand amending the organic farming provisions by permitting the controlled use of synthetic fertilizers and pesticides. Similarly, Karamian et al. [39] stress the importance of reducing water consumption to improve the sustainability of agricultural systems. The research aimed at optimizing fertilizer and water usage is mostly case-study based (e.g., [40,41,42,43]), and there exists a need for a standard way to handle such problems. It is in this context that we develop a new green labeling scheme based on the ideas of Stubenrauch et al. [9] and Karamian et al. [39].

The yield in agricultural systems has been modeled using various crop response functions like the von Liebig [44], Mitscherlich–Baule [45], etc. However, these functions are not invoked often in the context of agricultural supply chains. In addition, Peng et al. [46] discuss yield uncertainties in a contract farming supply chain by studying the effects of government subsidies and the level of uncertainties on the supply chain performance. Zare et al. [47] point out the importance of risk-sharing in a cocoa-beans supply chain in the Ivory Coast. Behzadi et al. [48] developed a stochastic model for an agribusiness supply chain to investigate the effect of various strategies on managing yield disruptions. The major highlight of their work was the consideration of the perishability aspect of the product alongside yield uncertainties. Combined analysis of perishability, demand, and yield uncertainties together are sparse in the literature. Golmohammadi et al. [49] discuss the importance of considering supply and demand uncertainties jointly to make efficient decisions. An equally important aspect to consider is the sharing of yield information. While the supply chain literature is rich with studies on cost and demand information sharing, only a few studies consider the sharing of yield information [50].

Table 1. Comparison with Previous Studies.

Reference	Crop Response Functions to Model Yield	Yield Uncertainties	Yield Information Sharing	Product Perishability	Demand Uncertainties	Greenness Concerns
[38]				✓		✓
[47]		✓			✓
[48]		✓		✓
[51]		✓			✓
[52]		✓			✓
[53]		✓			✓
[54]					✓	✓
[55]		✓			✓	✓
[43]	✓					✓
Our Model	✓	✓	✓	✓	✓	✓

compares our model with the most relevant previous studies in the field of agri-food supply chains.

Our work contributes to the literature in many ways. Firstly, the proposed eco-labeling scheme is a unique approach that promises an improvement in agricultural sustainability by assuring good crop yields while limiting the adverse environmental impacts of uncontrolled fertilizer and irrigation water usage. Secondly, the use of the crop-response function (von Liebig Production Function) in our supply chain design helps to model crop yield more realistically. This approach, which is unprecedented in the supply chain literature, has a remarkable advantage. Since such functions quantify crop yield based on the main farm inputs such as fertilizer and irrigation water, their usage in a supply chain model helps us optimize these farm inputs for good yields. Thirdly, our work adds to the sparse literature dealing with combined aspects of perishability, demand, and yield uncertainties in sustainable agri-food supply chains. Finally, the literature on yield information sharing is extended by conducting numerical studies to identify instances where sharing yield information benefits the stakeholders in the context of the farmer-retailer supply chain.

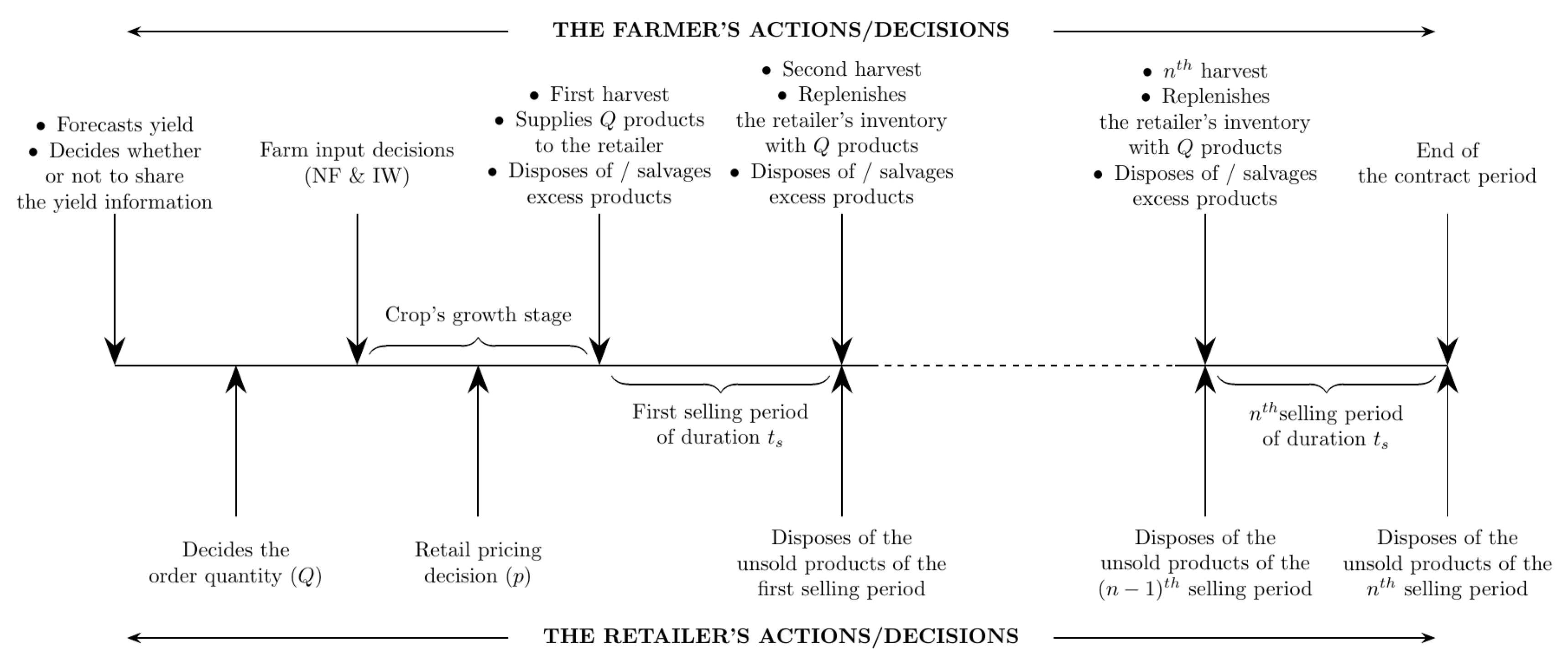
3. Model Formulation and Assumptions

We consider a two-echelon agri-food supply chain problem in which a farmer signs a supermarket contract with the retailer. The model is described in Figure 1 and a comprehensive list of decision variables and parameters used in the model is given in

Table 2. Notations Used.

Symbol	Description	Symbol	Description
$NF$	Nitrogen fertilizer requirement	$\alpha$	Price Sensitivity factor ($\alpha \ge 0$)
$IW$	Irrigation water requirement	$\beta$	Greenness level Sensitivity Factor ($\beta \ge 0$)
p	Retail price per unit of the agricultural product	$q_0$	The initial quality of the agri-food product
Q	Retailer’s order quantity per selling period	$\lambda$	Deterioration rate of the agri-food product
${\alpha }_0,{\alpha }_1,{\beta }_0,{\beta }_1$	Coefficients in the von Liebig production function	$D_0$	Potential Market size
m	Yield Plateau (Maximum possible crop yield)	$t_s$	Duration of a selling period
$N{F}_{max}$	Optimum fertilizer requirement for a yield of m	$\eta$	Efficiency of the irrigation method used, $(0\le \eta \le 1)$
$I{W}_{max}$	Optimum irrigation water required for a yield of m	$C_{s\left(R\right)}$	Shortage cost per unit for the retailer
$N{F}_c$	Fertilization level that minimizes/limits GHGI	$\delta$	Quality Sensitivity Factor ($\delta \ge 0$)
${\mathrm{\Gamma }}_y$	Forecast signal obtained by the farmer	$C_f$	Unit cost of Fertilizer
$C_{s\left(F\right)}$	Shortage cost per unit for the farmer	$C_w$	Unit cost of irrigation water consumed
$C_{d\left(F\right)}$	Farmer’s cost of disposal per unit of excess product	$C_{d\left(R\right)}$	Retailer’s cost of disposal per unit of excess product
w	Wholesale price per unit of the agri-food product	${ϵ}_1$	Yield uncertainty, ${ϵ}_1\sim \mathcal{N}(0,{\sigma }_1^2)$
$C_{sal\left(F\right)}$	Salvage Revenue for the farmer	$I{W}_{av}$	Maximum amount of water available for irrigation
$w_f,w_i$	Weights associated with ${\theta }_f$ and ${\theta }_i$ respectively	$\varphi$	Noise in the forecast signal, $\varphi \sim \mathcal{N}(0,{\sigma }_{\varphi }^2)$
n	Total number of harvests in a crop season	${ϵ}_2$	Demand uncertainty, ${ϵ}_2\in [A,B]$; mean $=\mu$ & variance $={\sigma }_2^2$

. In the beginning, the farmer forecasts the uncertainty in his (Without loss of generality, we refer to the farmer as ‘he’, and the retailer as ‘she’) yield (${ϵ}_1$) and decides whether to share the forecast information with the retailer. Since it is almost impossible to predict the exact yield accurately, we associate an error ($\varphi$) with his forecast. The retailer chooses her order quantity (Q) based on the available information on yield uncertainty and shares her requirements with the farmer. In case of a discouraging forecast, information sharing helps the farmer avoid shortages by forcing the retailer to reduce the quantity of her order. On the other hand, when the forecasts are good, sharing yield information encourages the retailer to order more (provided there is demand), resulting in better revenue for both players. In response to the retailer’s requirement, the farmer determines the fertilizer requirement ($NF$) and irrigation water requirement ($IW$). The crops are then allowed to grow with the controlled application of these inputs. We assume that the crops, especially fruits and vegetables, can be harvested multiple times at regular intervals once they are fully grown, [56,57] and hence there is a steady supply of products from the farm throughout the demand season.

Once the crops are fully grown, they start bearing fruits/vegetables, which the farmer harvests at regular intervals of $t_s$. The number of harvests in a crop season is n. After each harvest, he supplies Q quantity of these products to the retailer, and the remaining are either salvaged or disposed of. He cannot replenish the retailer’s inventory daily, as the choice of maturity stages and harvesting intervals varies across different fruits and vegetables [56,57]. To assure a daily supply of his products, he can preserve the products of a single harvest and sell only a part of it daily until the next harvest. In our study, this possibility is ruled out; instead, we assume that the farmer sells his entire produce soon after each harvest, as it helps eliminate the holding and preservation costs. Due to the consumer’s dependence on the sensory attributes of the agri-products to evaluate freshness [58,59], their perceived value of freshness will be high at the beginning of a selling period. This results in more sales at the onset of each selling period, encouraging the retailer to let the farmer sell his entire production to her at the beginning of each selling period.

The period $t_s$ between each harvest constitutes the retailer’s selling period, and her inventory is replenished at the beginning of each period. There are n such selling periods during the contract duration (Figure 1). Each time the stock replenishment occurs at the retailer, she may have some unsold products from the previous selling period in her inventory. If she does not dispose of these old products during each replenishment, her inventory will have perishable products of the same type but with different ages and quality levels. This makes it difficult for the customers to separate out the fresh products from the old ones and hence impacts the retailer’s profits [60]. To avoid this issue, a rational retailer disposes of the unsold products (at a disposal cost of $C_{d\left(R\right)}$) every time the farmer replenishes the stock. In addition, her limited inventory space is another reason for forcing her to dispose of the old products. In cases when she is unable to meet the demand of the consumers, there are chances that her goodwill is affected, and the consumers might approach a different retailer during their next purchase. Therefore, she must minimize the shortage of products. This possibility is modeled by incorporating a shortage cost of $C_{s\left(R\right)}$ for her.

It is assumed that an average-price contract, similar to that employed by retail giants like Walmart, La Colonia, etc. [61] exists between the retailer and the farmer. According to this contract, the retailer pays the average traditional market price (w) to the farmer regardless of whether the market price rises or falls during the demand season. This helps the farmer, for it considerably reduces his risk in terms of price fluctuations. On the other hand, the retailer enjoys an assured supply of quality products throughout the demand season [62].

Generally, in supermarket contracts, the retailer’s order quantity remains fixed throughout the crop season. She terminates the contract of the farmer who is unable to supply products as per requirement. This forces the farmer to compensate for the deficit by getting products from open markets in the event of shortages, which incurs a “shortage cost” ($C_{s\left(F\right)}$) for him [12,13]. When the yield per harvest ($Y/n$) is greater than the order quantity per period (Q), the farmer sells the excess products at salvage value ($C_{sal\left(F\right)}$) in open markets, which promotes direct interaction between him and the consumers [12,63]. In cases where there are difficulties in accessibility to these open markets due to reasons like remote farm location, high transportation costs, etc., he disposes of the surplus products, at a cost of $C_{d\left(F\right)}$. Our model considers both of these cases, as explained later in Section 4.2.

The individual rationality constraint ensures the farmer’s participation in the contract, and requires that the wholesale price should be set higher than the salvage value ($w>C_{sal\left(F\right)}$). Similarly, incentive compatibility constraint forces the farmer to optimize resource utilization, and would demand that the shortage cost is at least equal to the wholesale price ($C_{s\left(F\right)}\ge w$). This constraint makes fetching products from open markets an expensive alternative.

The total yield (Y) of the farmer is determined by the linear von Liebig production function and other external uncertainties. The uncertainties include the factors that are not under the farmer’s direct control, for example, climatic variations. The capability of the linear von Liebig specification in modeling crop response is discussed in detail by Grimm et al. [44] and Holloway [64]. Though non-linear specifications of this function exist, the selection of the most appropriate functional form for a crop response problem must be made after considering the available empirical data [65]. In this work, we limit our interest to the linear model, as many empirical studies [44,66,67] identify the linear formulation as a good fit for the available data. According to the linear von Liebig function, the yield of a crop is given by:

$$y=min\{{\alpha }_0+{\alpha }_{1}NF,{\beta }_0+{\beta }_{1}IW,m\}$$

(1)

As per this function, the yield potential of a crop is limited by that factor that is not applied to the greatest extent. Here, the limiting factors are either $NF$ or $IW$, which represent the fertilizer and irrigation water requirement, respectively. The variable m, termed as the “yield plateau”, is the maximum possible crop yield that can be achieved by varying $NF$ and $IW$. The expression for m is given as $m={\alpha }_0+{\alpha }_{1}N{F}_{max}={\beta }_0+{\beta }_{1}I{W}_{max}$. Furthermore, ${\alpha }_0,{\beta }_0,{\alpha }_1,{\beta }_1(>0)$ are constants that are to be determined by field experiments and $N{F}_{max}$ and $I{W}_{max}$ are the optimum values of fertilizer and irrigation water that results in maximum yield. The intercept ${\alpha }_0$ (${\beta }_0$) gives the expected yield when $NF$ ($IW$) is the limiting factor, in absence of the fertilizer (irrigation & rainfall). The uncertainty in yield can be modeled using a Gaussian disturbance ${ϵ}_1$ [44] with the mean of zero and the variance ${\sigma }_1^2$. Let $f(.)$ and $F(.)$ be the corresponding pdf and CDF of the distribution. Thus, total yield in the presence of uncertainties is given by:

$$Y=y+{ϵ}_1$$

(2)

Even though the exact value of ${ϵ}_1$ is not known to the farmer in advance, he can estimate it before sowing the seeds. This is important for him, as his input decisions are heavily dependent on these forecasts. Denoting the forecast signal obtained by him as ${\mathrm{\Gamma }}_y$, we can write, ${\mathrm{\Gamma }}_y={ϵ}_1+\varphi$. Here, $\varphi$ captures the noise in the forecast signal, which can be considered to be normally distributed with mean zero and variance ${\sigma }_{\varphi }^2$. Such an approach is common in literature [68,69] and when both ${ϵ}_1$ and $\varphi$ are normally distributed we have:

$$E[{ϵ}_1\mid {\mathrm{\Gamma }}_y]=\frac{{\sigma }_1^2{\mathrm{\Gamma }}_y}{{\sigma }_1^2+{\sigma }_{\varphi }^2}$$

(3)

$$Var[{ϵ}_1\mid {\mathrm{\Gamma }}_y]=\frac{{{\sigma }_1}^2{\sigma }_{\varphi }^2}{{\sigma }_1^2+{\sigma }_{\varphi }^2}$$

(4)

Let us use $h(.)$ and $H(.)$ to define the pdf and CDF of the corresponding posterior distribution of yield uncertainty (${ϵ}_1\mid {\mathrm{\Gamma }}_y$). The farmer can decide whether to share the forecast information, which includes the updated distribution parameters ($E[{ϵ}_1\mid {\mathrm{\Gamma }}_y],Var[{ϵ}_1\mid {\mathrm{\Gamma }}_y],$ and $h(.)$) with the retailer. In such cases, the retailer makes their decisions based on the shared information. However, in the absence of shared information, they depend on their prior beliefs ($E\left[{ϵ}_1\right],Var\left[{ϵ}_1\right],f(.)$). Nevertheless, it is assumed that all other information associated with the farmer is known to the retailer. This is a reasonable assumption as the retailer can access the details of the farm parameters (${\alpha }_0,{\alpha }_1,{\beta }_0,{\beta }_1,\eta ,{\sigma }_1$) from the farm records used for green certification [70]. Additionally, the production costs ($C_f,C_w$) are generally known to everyone through the maximum retail prices set by the suppliers and irrigation costs set by the authorities. The other farmer related costs ($C_{d\left(F\right)},C_{s\left(F\right)},C_{sal\left(F\right)}$) are also known to them as they have access to the agri-food markets.

3.1. Green Labeling

Since the consumers are environmentally aware, it is essential to have a labeling scheme that classifies the products into two categories: green and not-green. The primary requirement of such a labeling scheme is to have a greenness function that can measure the product’s environmental sustainability levels. Global Warming Potential (GWP) during a product’s life cycle is considered one of the major indicators of its environmental sustainability [42]. Products with lower values of GWP are generally considered to be green. Since the nitrogen fertilizer application contributes to a high GWP, reducing its usage improves product greenness [71]. The greenness level achieved by adequate fertilizer management is given by:

$${\theta }_f=\frac{N{F}_{max}-NF}{N{F}_{max}}$$

(5)

Another important indicator that determines the greenness level of an agri-food product is the ability to save water during irrigation. Methods such as drip irrigation help in saving water by minimizing water losses due to runoffs or evaporation [11]. The agri-food products can be considered green only if significant water savings are obtained during their cultivation. The greenness level achieved by adequate irrigation water management is given by:

$${\theta }_i=\frac{I{W}_{av}-\frac{IW}{\eta }}{I{W}_{av}}$$

(6)

where $\eta$ denotes the efficiency of the irrigation technique employed, and $I{W}_{av}$ corresponds to the maximum amount of water available for irrigation. When $\eta =1$, the irrigation technique employed is highly efficient, and there is no wastage of water. For $\eta <1$, the amount of water wasted is $(IW/\eta )-IW$, and with the decrease in value of $\eta$, the wastage increases. In our model, we assume that $I{W}_{av}\ge (I{W}_{max}/\eta$). This ensures that the farmer is not constrained due to the unavailability of water even when he aims for the maximum yield of m.

A composite indicator defined as an additive function of fertilizer (${\theta }_f$) and irrigation water management (${\theta }_i$) is used for describing the product’s greenness level ($\theta$):

$$\theta =w_f{\theta }_f+w_i{\theta }_i$$

(7)

where, $w_f+w_i=1$ and $w_f,w_i\ge 0$. Since, by definition $0\le {\theta }_f,{\theta }_w\le 1$, we have that $0\le \theta \le 1$. Note that $w_{(·)}$ can be adjusted depending on the factor to be prioritized. For example, $w_i$ can be assigned a higher value when the farmland considered is in a water-scarce region. This definition of $\theta$ follows a weak sustainability approach where a sufficiently high value of one indicator compensates for the poor performance of the other [72]. This sustainability approach is necessary in agricultural settings where a farmer faces issues such as water scarcity or soil depletion. For example, in areas where $I{W}_{av}$ is low (water scarce areas), ${\theta }_i$ will be low even when efficient irrigation techniques are used ($\eta \approx 1$). In this case, a weak sustainability approach rewards the farmer with a high greenness value if his ${\theta }_f$ value is high.

To communicate the greenness of the product with consumers, we make use of eco-labels. Since most of the eco-labeling agencies like the EU Organic Product label, India Organic, USDA Organic (See www.ecolabelindex.com for more details; Accessed on 20 April 2021), etc., do not explicitly consider the reduction in fertilizers and water consumption when evaluating product greenness, a new scheme is proposed here. This scheme uses the greenness function defined by Equation (7) and considers the reduction in fertilizer and water usage at its core when evaluating greenness. Additionally, to address the concerns of health-conscious consumers, Integrated Pest Management (IPM) [73] or Agroecological Crop Protection (ACP) [74] are made mandatory requirements to ensure that the products are free of pesticide residues. Thus, according to our scheme, the product is certified green if the IPM or ACP practices are followed and the product greenness ($\theta$) is at least equal to the minimum greenness level required to obtain the green certification (${\theta }_c$).

Decreasing fertilizer application ($NF$) improves the product greenness (see Equations (5) and (7)) but at the expense of crop yield (Equation (1)). To balance this tradeoff between yield and greenness, we use the concept of Greenhouse Gas Emission Intensity (GHGI) which measures the Global Warming Potential (GWP) per unit yield of the farmland [75]. A low value of GHGI is always preferred as it ensures minimal emissions per unit yield. As GWP and yield are increasing functions of the fertilization level, GHGI varies at different levels of applied fertilizers. We determine a maximum allowable fertilization level $N{F}_c$ such that GHGI is within the limits of the prevalent emission regulations. As a special case, when the GHGI function is convex, as in Chi et al. [71] and Kim et al. [41], $N{F}_c$ can be determined as the fertilization level that minimizes GHGI. According to the linear von Liebig function, corresponding to this value of $N{F}_c$, there is a value of irrigation water requirement ($I{W}_c$) such that both $N{F}_c$ and $I{W}_c$ become the limiting factors. Mathematically, this can be expressed as ${\alpha }_0+{\alpha }_{1}N{F}_c={\beta }_0+{\beta }_{1}I{W}_c$. Now, the minimum greenness level required for certification (${\theta }_c$) can be calculated as:

$${\theta }_c=w_f{\theta }_f^c+w_i{\theta }_i^c$$

(8)

where ${\theta }_f^c=\frac{N{F}_{max}-N{F}_c}{N{F}_{max}}$ and ${\theta }_w^c=\frac{I{W}_{av}-\frac{I{W}_c}{{\eta }_c}}{I{W}_{av}}$. Note that, ${\theta }_w^c$ represents the maximum greenness level achieved by irrigation water management when $IW=I{W}_c$ and the irrigation efficiency (${\eta }_c$) corresponds to the efficiency of the existing most efficient irrigation technique. The new labeling scheme can be explained using the cases below:

• When $\theta ={\theta }_c$
  This happens only when the farmer’s fertilizer ($NF$) and irrigation water ($IW$) usage are precisely equal to their corresponding maximum permissible limits defined by the labeling scheme ($NF=N{F}_c;IW=I{W}_c$). Moreover, the farmer should be using the most efficient irrigation technique ($\eta ={\eta }_c$). This results in the GHGI value being at its minimum or the maximum permissible limit depending upon whether it is convex or not. In both cases, the emissions are within limits, and hence the farmer gets a green certification.
• When $\theta >{\theta }_c$
  For this to happen, the farmer should use less quantity of fertilizers and irrigation water than the maximum permissible limits mentioned in the labeling scheme ($NF<N{F}_c \mathrm{and} IW<I{W}_c$). When the GHGI function is convex, this results in a higher GHGI value than in the previous case where $\theta ={\theta }_c$. Although the GHGI is high, the Global Warming Potential (GWP) in this case will be lesser than that in the $\theta ={\theta }_c$ scenario due to the reduced fertilizer and irrigation water usage. The reduced GWP helps the farmer obtain green certification, which is justifiable. A non-convex GHGI function will also result in a green certification because GWP is lesser.
• When $\theta <{\theta }_c$
  This scenario is marked by the intense use of fertilizers ($NF$) and irrigation water ($IW$), resulting in $NF>N{F}_c$ and $IW>I{W}_c$. Here, regardless of the convexity of the GHGI function, the emissions and the emission intensity are on the higher side. According to Carlson et al. [76], it is important to concentrate mitigation efforts on crops and locations that exhibit high emissions and high emission intensities. Moreover, from Equations (6) and (7), it can be understood that a poorly designed irrigation technique with a small value of irrigation efficiency ($\eta <<{\eta }_c$) can also result in $\theta <{\theta }_c$ even when fertilizer and irrigation water requirement are well within limits ($NF<N{F}_c \mathrm{and} IW<I{W}_c$). Here, the farmer is to be penalized for wastage of water stemming from the improper design of the irrigation facility. Therefore, to force farmers to go green, the products with $\theta <{\theta }_c$ will not receive green certification.

Chen et al. [77] discuss the significance of eco-labels that encourage efficient farm management practices in promoting sustainable agricultural methods among farmers. Due to the flexibility offered by this scheme in terms of fertilizer usage, existing organic consumers may find it unattractive. However, such schemes can target the share of the eco-sensitive population who cannot buy organic products at premium prices, provided that the retail prices are lower [78]. Furthermore, educating the consumers about the importance of promoting sustainable farming techniques that ensure better yield compared to organic farming is critical. This could make more consumers embrace the new labeling scheme.

It should be noted that in our labeling scheme, the greenness is quantified based on only two factors, which are fertilizer and irrigation water consumption. Although adherence to IPM or ACP practices is made mandatory for certification, they are not used in calculating greenness $\theta$. This approach is justifiable as we attempt to quantify greenness based on the factors that directly influence yield. Although judiciously administered pest control techniques help the farmer prevent yield losses due to pest attacks, there is no significant evidence in the literature that claims an improvement in total yield by using these control techniques. This means that practicing IPM or ACP does not help improve the yield, but it only safeguards the farmer against yield losses.

3.2. Modeling Demand

Since the products are perishable, their quality is expected to deplete with time. According to Chen et al. [37], the quality level of the product as a function of time t can be written as $q\left(t\right)=q_0-\lambda t$, where $q_0$ is the initial quality, and $\lambda$ represents the deterioration rate. Not all vegetables have the same shelf-life, and hence the deterioration rate depends on the type of vegetable under consideration. The demand for the product is a function of the retail price, greenness, and product quality. Since product quality is time-dependent, the demand for the product varies over time. We can write the demand of an agri-food product with deterioration rate $\lambda$ and quality function $q\left(t\right)$ at any time t as [37,79]:

$$d\left(t\right)=D_0-\alpha p+\beta {\theta }_p+\delta q\left(t\right)$$

where $D_0$ = Potential Market Size; $\alpha$ = Price Sensitivity Factor, $\alpha >0$; $\beta$ = Greenness Sensitivity Factor, $\beta >0$; $\delta$ = Quality Sensitivity Factor, $\delta >0$. Note that, in this study, we attempt to develop a model in which the farmer is supplying a single type of agri-food product to the retailer.

An environmentally-conscious consumer prefers an eco-labeled product over one without a label. To capture this sensitivity of demand to product greenness, the term $\beta {\theta }_p$ is included in the demand function such that:

$${\theta }_p=\left\{\begin{array}{cc}1\hfill & \mathrm{If}\mathrm{the}\mathrm{product}\mathrm{bears}\mathrm{an}\mathrm{eco}\text{-}\mathrm{label}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

Thus, a product with an eco-label increases the demand by $\beta$, in comparison with a product without one. Considering the above factors, demand for the product in the retailer during a selling period of duration $t_s$ is given by:

$$D={\int }_0^{t_s}d\left(t\right)dt=(D_0-\alpha p+\beta {\theta }_p+\delta q_0)t_s-\frac{1}{2}\delta \lambda t_s^2$$

(9)

As consumer demand for agri-food products can continue to vary, it is important to consider the stochastic nature of the demand function. A random variable ${ϵ}_2$ can represent the stochasticity in demand. This random variable has PDF and CDF as $g[.]$ and $G[.]$, respectively, defined over the support $[A,B]$ with mean $\mu$ and standard deviation ${\sigma }_2$ [68]. Thus, the demand in each selling period is given by:

$$D_T=D+{ϵ}_2$$

(10)

where D is the deterministic part of the demand. To ensure a positive value of demand, we impose a condition that $D_T\ge 0$ on all admissible parameter values. As discussed earlier, there are n selling periods in the entire length of the selling season. To reduce the problem complexity and ensure analytical tractability, we assume that the selling periods are identical in terms of the realized ${ϵ}_2$ values.

The farmer’s major expenses while growing his crops include the cost of fertilizers, (denoted by $C_f$ per unit quantity of fertilizer used) and that for irrigation (denoted by $C_w$ per unit quantity of water consumed). We assume that all other associated costs are included in this cost component. Any additional expense of the farmer, such as the transportation cost, is assumed to be less significant and therefore not considered.

4. Model Analysis

We aim to determine the equilibrium decisions of the farmer and the retailer so that their profits are maximized. A backward induction approach is used to obtain a solution for our problem [69]. Thus, we begin by solving the retailer’s problem of deciding the retail price and then solve the farmer’s problem of determining the input levels. Finally, we find the solution for the retailer’s order quantity requirement problem. Note that, in our approach, the quantity decision precedes the price decision, but it is immaterial whether the price is decided before or after the realization of the yield. This sequential approach, which is similar to [80], is used to overcome the complexities associated with the determination of closed-form solutions in a joint decision-making case in the presence of uncertainties.

4.1. Determination of Retail Price

The profit function of the retailer in a sales period can be written as:

$${\pi }_R(p,Q)=\left\{\begin{array}{cc}p{D}_T-C_{d\left(R\right)}\left[Q-D_T\right]-wQ\hfill & D_T\le Q\hfill \\ pQ-C_{s\left(R\right)}\left[D_T-Q\right]-wQ\hfill & D_T>Q\hfill \end{array}\right.$$

Depending on whether $D_T\le Q$ or not, the retailer will have excess inventory or shortages, respectively. In both cases, we assume that the retailer bears the cost: either the cost to dispose of excess products (at a rate of $C_{d\left(R\right)}$) or the shortage cost (at a rate of $C_{s\left(R\right)}$). The last term for both cases represents the retailer’s total purchase cost. The terms $p{D}_T$ and $pQ$ are the revenues that the retailer gains in cases 1 and 2, respectively.

For ease of calculation, we represent $Q\equiv D+z$. Using this expression and Equation (10), the retailer’s profit function can be rewritten as:

$${\pi }_R(p,z)=\left\{\begin{array}{cc}p[D+{ϵ}_2]-C_{d\left(R\right)}\left[z-{ϵ}_2\right]-w[D+z]\hfill & \mathrm{for}{ϵ}_2\le z\hfill \\ p[D+z]-C_{s\left(R\right)}\left[{ϵ}_2-z\right]-w[D+z]\hfill & \mathrm{for}{ϵ}_2>z\hfill \end{array}\right.$$

Here, D represents the deterministic part of the demand (Equation (9)), and z is the stocking factor. The stocking factor can be a positive or a negative value. It takes a positive value when the demand uncertainty (${ϵ}_2$) turns to be positive, thereby compelling the retailer to order more products than D. Alternatively, a negative ${ϵ}_2$ results in the retailer setting an order quantity less than D, resulting in z being negative. Moreover, if $z>{ϵ}_2$, the retailer will have leftovers; and if $z<{ϵ}_2$, shortages occur. Thus, the selection of z is an optimization problem for the retailer [81,82]. Now, the expected profit function of the retailer is:

$$\begin{array}{c}E\left[{\pi }_R(p,z)\right]=p\left[D+{\int }_A^z{ϵ}_{2}g\left({ϵ}_2\right)d{ϵ}_2+{\int }_z^{B}zg\left({ϵ}_2\right)d{ϵ}_2\right]-C_{d\left(R\right)}{\int }_A^z\left[z-{ϵ}_2\right]g\left({ϵ}_2\right)d{ϵ}_2\hfill \\ \hfill -C_{s\left(R\right)}{\int }_z^B\left[{ϵ}_2-z\right]g\left({ϵ}_2\right)d{ϵ}_2-w[D+z]\end{array}$$

(11)

Theorem 1.

For ${ϵ}_2$ following any distribution, the profit function of the retailer is concave in p, and the optimal value of p can be written as a function of z as $p^{*}=p^0-\frac{\mathrm{\Theta }\left(z\right)}{2\alpha t_s}$ where, $p^0=\frac{(D_0+\alpha w+\beta {\theta }_p+\delta q_0)t_s-\frac{1}{2}\delta \lambda t_s^2+\mu }{2\alpha t_s}$, and $\mathrm{\Theta }\left(z\right)={\int }_z^B[{ϵ}_2-z]g\left({ϵ}_2\right)d{ϵ}_2.$

(Proofs for all theories, lemmas, and corollaries are given in Appendix A).

Corollary 1.

The retail price ($p^{*}$) in the proposed greenness scheme is less than that of an organic labeling scheme ($p_{org}^{*}$) and greater than that in the case of conventional farming ($p_{con}^{*}$). Mathematically, $p_{org}^{*}>p^{*}>p_{con}^{*}$.

From Corollary 1 it is evident that the new greenness scheme benefits the consumer by providing eco-friendly products at reduced costs in comparison with the organic labeling scheme. Furthermore, it helps the retailer earn better profits by selling products at a higher price compared to the case of conventional farming.

4.2. Determination of Farmer’s Inputs

The retailer transmits the order quantity requirement $\left(Q\right)$ to the farmer, based on which he has to make his input decisions ($NF$ and $IW$). In addition to this, considering the environmental consciousness of the consumers, the retailer can demand the farmer to produce “eco-labeled” products. The profit function of the farmer per harvest can be written as:

$${\pi }_F=\left\{\begin{array}{cc}wQ-C_{s\left(F\right)}\left[Q-\frac{Y}{n}\right]-\frac{C_f\times NF}{n}-\frac{C_w\times IW}{\eta \times n}\hfill & \mathrm{for}\frac{Y}{n}\le Q\hfill \\ wQ-C_{d\left(F\right)}\left[\frac{Y}{n}-Q\right]-\frac{C_f\times NF}{n}-\frac{C_w\times IW}{\eta \times n}\hfill & \mathrm{for}\frac{Y}{n}>Q\hfill \end{array}\right.$$

where the total yield Y is given by Equation (2). Assuming a steady supply from the farm throughout the selling season, the yield per harvest can be determined as $Y/n$, where n is the number of harvests. Depending on whether $(Y/n)\le Q$ or not, the farmer faces a condition of shortage or over-production, respectively. To compensate for the shortage, he purchases products from open markets (at the rate of $C_{s\left(F\right)}$), whereas in case of over-production, he sells the excess products in open markets at a salvage value of $C_{sal\left(F\right)}$ per unit. If selling in open markets is not profitable, he disposes of excess products at a cost of $C_{d\left(F\right)}$ per unit. To model cases when he earns the salvage revenue, we have to substitute $C_{d\left(F\right)}=-C_{sal\left(F\right)}$ in the profit function. The other terms are the same in both cases. The first, third, and fourth terms represent farmers’ revenue, fertilization costs, and irrigation costs, respectively, during each harvest. Since the fertilizer and irrigation water inputs ($NF$ and $IW$) are estimated for the entire crop season, the third and fourth terms are divided by n to obtain the related costs for a single harvest.

Lemma 1.

In the linear von Liebig crop response function, for each value of the ideal yield y, we have a unique set of values of $NF$ and $IW$, which maximizes the farmer’s profit, and these values can be estimated using the relation: $y={\alpha }_0+{\alpha }_{1}NF={\beta }_0+{\beta }_{1}IW$.

From Lemma 1, it is clear that $NF$ and $IW$ are linear functions of the yield y alone, and thus we can convert the actual farmer’s problem of optimizing $NF$ and $IW$ into a new problem of optimizing y. Using Equation (2), the forecast information and Lemma 1, we can rewrite the profit function of the farmer as:

$${\pi }_F\left(y\right)=\left\{\begin{array}{cc}wQ-\frac{C_f\times \frac{y-{\alpha }_0}{{\alpha }_1}}{n}-\frac{C_w\times \frac{y-{\beta }_0}{{\beta }_1}}{\eta \times n}-C_{s\left(F\right)}\left[Q-\frac{y+({ϵ}_1\mid {\mathrm{\Gamma }}_y)}{n}\right]\hfill & \mathrm{for} ({ϵ}_1\mid {\mathrm{\Gamma }}_y)\le nQ-y\hfill \\ wQ-\frac{C_f\times \frac{y-{\alpha }_0}{{\alpha }_1}}{n}-\frac{C_w\times \frac{y-{\beta }_0}{{\beta }_1}}{\eta \times n}-C_{d\left(F\right)}\left[\frac{y+({ϵ}_1\mid {\mathrm{\Gamma }}_y)}{n}-Q\right]\hfill & \mathrm{for} ({ϵ}_1\mid {\mathrm{\Gamma }}_y)>nQ-y\hfill \end{array}\right.$$

The expected profit function is given by:

$$\begin{array}{c}E\left[{\pi }_F\left(y\right)\right]=wQ-\frac{C_f\times \frac{y-{\alpha }_0}{{\alpha }_1}}{n}-\frac{C_w\times \frac{y-{\beta }_0}{{\beta }_1}}{\eta \times n}-\left[C_{s\left(F\right)}{\int }_{-\infty }^{nQ-y}\left[Q-\frac{y+{ϵ}_1}{n}\right]f\left({ϵ}_1\right)d{ϵ}_1|{\mathrm{\Gamma }}_y\right]\hfill \\ \hfill -\left[C_{d\left(F\right)}{\int }_{nQ-y}^{\infty }\left[\frac{y+{ϵ}_1}{n}-Q\right]f\left({ϵ}_1\right)d{ϵ}_1|{\mathrm{\Gamma }}_y\right]\end{array}$$

(12)

Lemma 2.

To obtain a green certification, the farmer should limit his target yield such that $y\le y_c$, where $y_c=\frac{1+\frac{w_f{\alpha }_0}{N{F}_{max}{\alpha }_1}+\frac{(1-w_f){\beta }_0}{I{W}_{av}{\beta }_1\eta }-{\theta }_c}{\frac{w_f}{N{F}_{max}{\alpha }_1}+\frac{(1-w_f)}{I{W}_{av}{\beta }_1\eta }}$ and ${\theta }_c$ is given by Equation (8).

Now, using Equation (12) and Lemma (2), we can write the farmer’s profit maximization problem as:

$$MaximizeE\left[{\pi }_F\left(y\right)\right]$$

subject to

$$0\le y\le y_c$$

In case the farmer does not wish to aim for the eco-label certification, we can replace the above constraint with $y\le m$. Here, the upper limit on the yield is defined by the maximum defined under the von Liebig function. Because of the way ${\theta }_c$ is defined, this constraint is always satisfied in the case of green products. We now define a term K, called the cost index, which plays a significant role in the analysis of the farmer’s profit function. Let

$$K:=\left[\frac{\frac{C_f}{{\alpha }_1}+\frac{C_w}{{\beta }_1\eta }+C_{d\left(F\right)}}{C_{s\left(F\right)}+C_{d\left(F\right)}}\right]$$

(13)

Theorem 2.

Based on the presence or absence of open markets and the value of the cost index (K), the farmer’s optimal decisions when he is producing green products are characterized as follows:

• For K $\in [0,1]$, irrespective of the presence or absence of open markets, the profit function of the farmer is concave in y, and the optimal value of y, which maximizes the farmer’s profit, is given by:

  $$y^{*}=min\{nQ-H^{-1}\left(K\right),y_c\}$$
• For $K\notin [0,1]$, and in the absence of open markets, the farmer’s profit function is always monotonically decreasing in y and the optimum value of y for the farmer is $y^{*}=min\{{\alpha }_0,{\beta }_0\}$.
• For $K\notin [0,1]$, and in the presence of open markets, the profit function of the farmer is monotonically increasing in y, if for all $y\in [min\{{\alpha }_0,{\beta }_0\},y_c]$

  $$C_{sal\left(F\right)}+\left(C_{s\left(F\right)}-C_{sal\left(F\right)}\right)H(nQ-y)>\frac{C_f}{{\alpha }_1}+\frac{C_w}{{\beta }_1\eta }$$

  and the corresponding value of y, which maximizes the farmer’s profit is $y^{*}=y_c$.
• For $K\notin [0,1]$, and in the presence of open markets, the profit function of the farmer is monotonically decreasing in y, if for all $y\in [min\{{\alpha }_0,{\beta }_0\},y_c]$

  $$C_{sal\left(F\right)}+\left(C_{s\left(F\right)}-C_{sal\left(F\right)}\right)H(nQ-y)<\frac{C_f}{{\alpha }_1}+\frac{C_w}{{\beta }_1\eta }$$

  and the optimum value of y is $y^{*}=min\{{\alpha }_0,{\beta }_0\}$.

Based on the value of the cost index K, the farmer’s market can be classified as given in

Table 3. Classification of farmer’s markets based on the cost index (K).

K	Type of Market	Farmer’s Optimal Yield Decision (${\mathit{y}}^{*})$
$K<0$	Highly Favourable	$y_c$
$0\le K\le 1$	Favourable	$min\{nQ-H^{-1}\left[K\right],y_c\}$
$K>1$	Unfavourable	$min\{{\alpha }_0,{\beta }_0\}$

. A high salvage value ($C_{sal\left(F\right)}$) such that $C_{sal\left(F\right)}>(C_f/{\alpha }_1)+(C_w/{\beta }_1\eta )$ results in $K<0$. In this case, statement 3 of Theorem 2 is always satisfied, and the optimal yield for the farmer is $y^{*}=y_c$. In other words, a higher salvage value encourages the farmer to produce to his maximum allowable capacity as he can sell his excess products in open markets at good prices, helping him earn better profits. This market condition can be considered as a “highly favorable market condition.” A necessary, but not sufficient, condition for $0\le K\le 1$ is $C_{s\left(F\right)}>(C_f/{\alpha }_1)+(C_w/{\beta }_1\eta )$. While in the absence of open markets, this condition is also sufficient, an additional condition $C_{sal\left(F\right)}<(C_f/{\alpha }_1)+(C_w/{\beta }_1\eta )$ is required for sufficiency when open markets are present. Under this setting, according to statement 1 of Theorem 2, the farmer’s profit function is concave in y, and he may not always benefit by carrying out production at his maximum capacity due to the following reasons: (i) In the absence of open markets, he is forced to dispose of his excess products at the cost of $C_{d\left(F\right)}$ which attract revenue losses (ii) When open markets are present, the salvage revenue ($C_{sal\left(F\right)}$) is too low that he cannot recover his production costs by selling in these markets. This can be considered as a “favorable market situation” where the farmer benefits only by selling his products to the retailer, but not in open markets. The condition $K>1$ occurs when the production costs are much higher than the shortage costs so that $(C_f/{\alpha }_1)+(C_w/{\beta }_1\eta )>C_{s\left(F\right)}$. In such cases, the market condition is “unfavorable” as the production costs exceed the farmer’s wholesale price (as $C_{s\left(F\right)}>w$), and he decides not to use any farm inputs, resulting in a very low yield and subsequently minimal profits. Statements 2 and 4 of Theorem 2 denote these conditions.

The yield under organic farming is generally lower (by about $25\%$) than that in conventional agriculture, and this gap is more pronounced in the case of cereals and vegetables (26–33%) [83]. Thus, the maximum possible yield in organic farming ($m_{org}$) can be represented as a fraction of m, the maximum possible yield in conventional agriculture. In other words, $m_{org}=k_{org}\times m$ where $k_{org}\in [0,1]$. Additionally, in the context of production costs, there are no significant differences between organic and conventional agriculture [84]. Considering these factors, the following corollary can be derived from Theorem 2.

Corollary 2.

For a given order quantity Q, when $y_c>m_{org}$, we have the relation $y_{con}^{*}\ge y^{*}\ge y_{org}^{*}$, where $y_c$ is given by Lemma 2 and $y_{con}^{*},y^{*},y_{org}^{*}$ represents the optimal yield under conventional, proposed, and organic agricultural practices, respectively.

Corollary 2 is significant, especially in cases of vegetable production, where there is a large yield gap (low $k_{org}$ values) between conventional and organic agricultural methods. In such cases, the yield is highest for conventional agriculture, but it is criticized for its high environmental impacts. On the contrary, the organic scheme, which boasts low ecological impacts, suffers significantly lower yields. Interestingly, the greenness scheme proposed by us provides the right balance between yield and environmental impacts by ensuring a better yield when compared to the organic scheme and lower ecological impacts compared to conventional methods.

Theorem 3.

When the linear von Liebig production function determines the yield of a crop and the farmer aims at maximizing his profit, the optimum quantities of nitrogen fertilizer ($N{F}^{*}$) and irrigation water ($I{W}^{*}$) required are $N{F}^{*}=max\{0,(y^{*}-{\alpha }_0)/{\alpha }_1\}$ and $I{W}^{*}=max\{0,(y^{*}-{\beta }_0)/{\beta }_1\}$, where $y^{*}$ is given in Theorem 2.

4.3. Determination of the Order Quantity

Lemma 3.

To ensure that the farmer signs a contract with the retailer to supply green products, the retailer should limit her order quantity (Q) such that $Q\le Q_c$, where the expressions for $Q_c$ based on the cost index values are given in

Table 4. Expressions for $Q_c$ based on the cost index K.

K	When Information Is Shared	When No Information Is Shared
$K<0$	$\frac{y_c+E\left[{ϵ}_1\right|{\mathrm{\Gamma }}_y]}{n}$	$\frac{y_c+E\left[{ϵ}_1\right]}{n}$
$0\le K\le 1$	$min\left\{\frac{1+\frac{w_f}{N{F}_{max}{\alpha }_1}({\alpha }_0+H^{-1}\left[K\right])+\frac{(1-w_f)}{I{W}_{av}{\beta }_1\eta }({\beta }_0+H^{-1}\left[K\right])-{\theta }_c}{\frac{n{w}_f}{N{F}_{max}{\alpha }_1}+\frac{n(1-w_f)}{I{W}_{av}{\beta }_1\eta }},\frac{y_c+E\left[{ϵ}_1\right|{\mathrm{\Gamma }}_y]}{n}\right\}$	$min\left\{\frac{1+\frac{w_f}{N{F}_{max}{\alpha }_1}({\alpha }_0+F^{-1}\left[K\right])+\frac{(1-w_f)}{I{W}_{av}{\beta }_1\eta }({\beta }_0+F^{-1}\left[K\right])-{\theta }_c}{\frac{n{w}_f}{N{F}_{max}{\alpha }_1}+\frac{n(1-w_f)}{I{W}_{av}{\beta }_1\eta }},\frac{y_c+E\left[{ϵ}_1\right]}{n}\right\}$
$K>1$	$\frac{min\{{\alpha }_0,{\beta }_0\}+E\left[{ϵ}_1\right|{\mathrm{\Gamma }}_y]}{n}$	$\frac{min\{{\alpha }_0,{\beta }_0\}+E\left[{ϵ}_1\right]}{n}$

.

Using the relation $Q=D+z$, the condition mentioned in Lemma 3 becomes $D+z\le Q_c$. Using Equation (9) we can rewrite this as $(D_0-\alpha p+\beta {\theta }_p+\delta q_0)t_s-\frac{1}{2}\delta \lambda t_s^2+z\le Q_c$. Now, from Theorem 1, we finally have the inequality as $z+\frac{\mathrm{\Theta }\left(z\right)}{2}\le Q_c-(D_0-\alpha p^0+\beta {\theta }_p+\delta q_0)t_s+\frac{1}{2}\delta \lambda t_s^2$. This condition should be satisfied by the retailer when deciding the stocking factor z. Using Theorem 1, we can write the retailer’s expected profit function in terms of the stocking factor z alone, and it will take the form $E\left[{\pi }_R(p\left(z\right),z)\right]$. Now, the retailer’s problem of determining the optimal order quantity becomes a constrained optimization problem as follows:

$$MaximizeE\left[{\pi }_R(p\left(z\right),z)\right]$$

subject to

$$z+\frac{\mathrm{\Theta }\left(z\right)}{2}\le Q_c-(D_0-\alpha p^0+\beta {\theta }_p+\delta q_0)t_s+\frac{1}{2}\delta \lambda t_s^2$$

(14)

As discussed above, the constraint (14), ensures that the farmer signs the contract to sell green products to the retailer. Let $z_c$ correspond to z, which makes the constraint (14) binding.

Theorem 4.

The optimal order quantity of the retailer, which maximizes her profit when selling green products, is given by $Q=D+z^{*}$, where D is given by Equation (9), and $z^{*}$ is determined as follows:

• If the distribution function G(.) satisfies the condition $2r{\left(z\right)}^2+\frac{dr\left(z\right)}{dz}>0$, for all $z\in [A,B]$ and $z_c\ge A$, then $z^{*}$ is given as follows:

  $$z^{*}=\left\{\begin{array}{cc}{z}_{max}\hfill & \mathrm{if}{z}_{max}\le z_c \& E\left[{\pi }_R(p\left(z_{max}\right),z_{max})\right]\ge E\left[{\pi }_R(p\left(A\right),A)\right]\hfill \\ z_c\hfill & \mathrm{if}{z}_{min}\le z_c\le z_{max} \& E\left[{\pi }_R(p\left(z_c\right),z_c)\right]\ge E\left[{\pi }_R(p\left(A\right),A)\right]\hfill \\ A\hfill & otherwise\hfill \end{array}\right.$$

  Here, $r\left(z\right)=\frac{g\left[z\right]}{1-G\left[z\right]}$, and $z_{max}$ is the largest among the two roots of the equation $\frac{dE\left[{\pi }_R(p\left(z\right),z)\right]}{dz}=0$ and $z_{min}$ is the other root.
• If, along with the conditions given in statement 1, the inequality $(D_0+\beta {\theta }_p+\delta q_0)t_s-\frac{1}{2}\delta \lambda t_s^2-\alpha t_s\left(w-2C_{s\left(R\right)}\right)+A>0$ is also satisfied, then the retailer’s profit function is concave in z, and the value of $z^{*}$ is given by:

  $$z^{*}=\left\{\begin{array}{cc}{z}^1\hfill & \mathit{if}{z}^1\le z_c\hfill \\ z_c\hfill & \mathit{otherwise}\hfill \end{array}\right.$$

  where $z^1$ is the solution of equation $\frac{dE\left[{\pi }_R(p\left(z\right),z)\right]}{dz}=0$
• If $z_c\ge A$ and G(.) is an arbitrary distribution function, $z^{*}$ which maximizes the retailer’s profit can be found by an exhaustive search over all z values in the region $[A,B]$
• When $z_c<A$, irrespective of the distribution of G(.), $z^{*}=z_c$

It is interesting to note that the term $r\left(z\right)=\frac{g\left[z\right]}{1-G\left[z\right]}$ represents the hazard rate of a distribution. All distributions with a non-decreasing hazard rate, which includes the PF₂ family of distributions and also the log-normal distribution, satisfy the condition $2r{\left(z\right)}^2+\frac{dr\left(z\right)}{dz}>0$ [81].

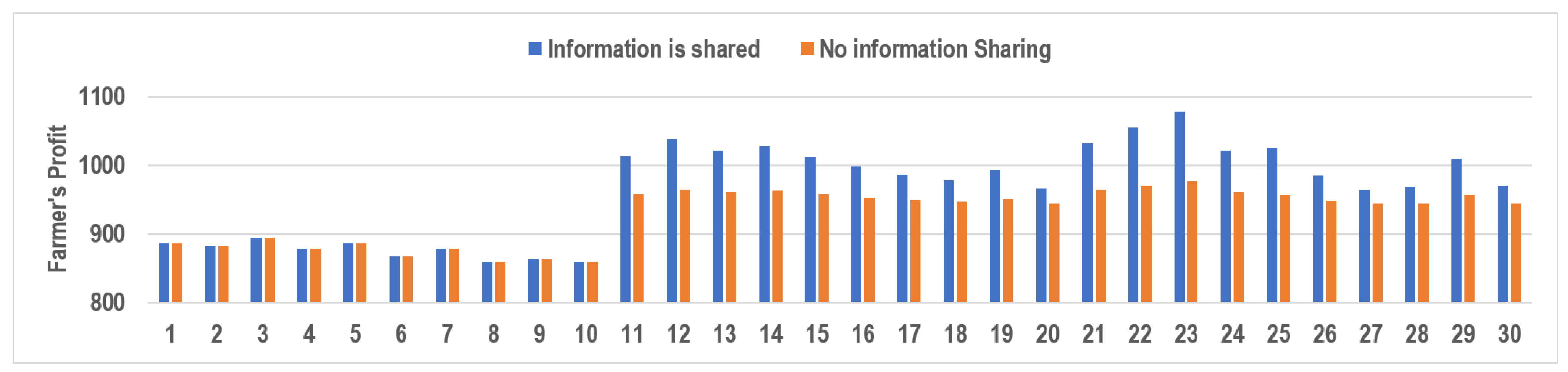
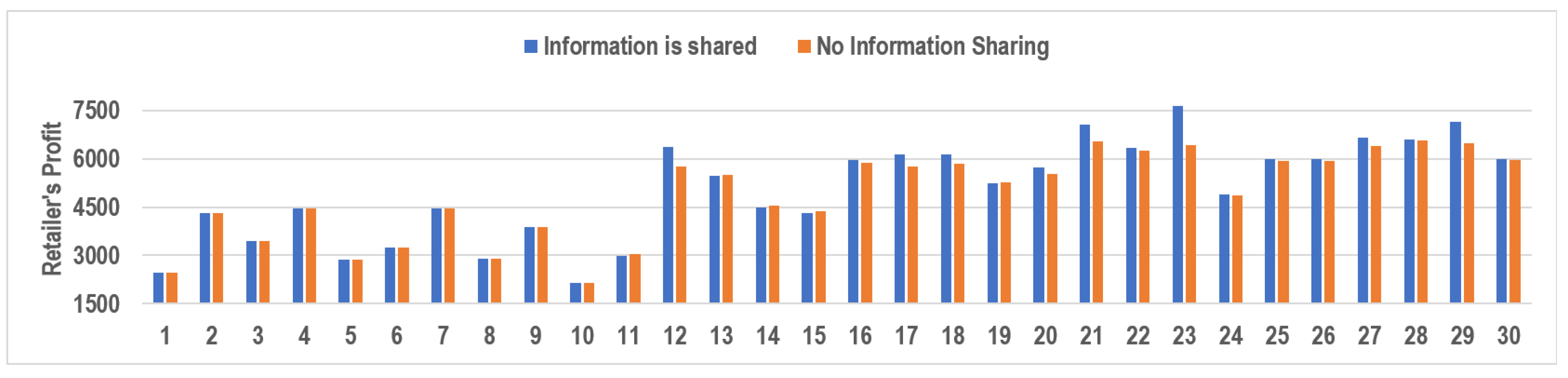
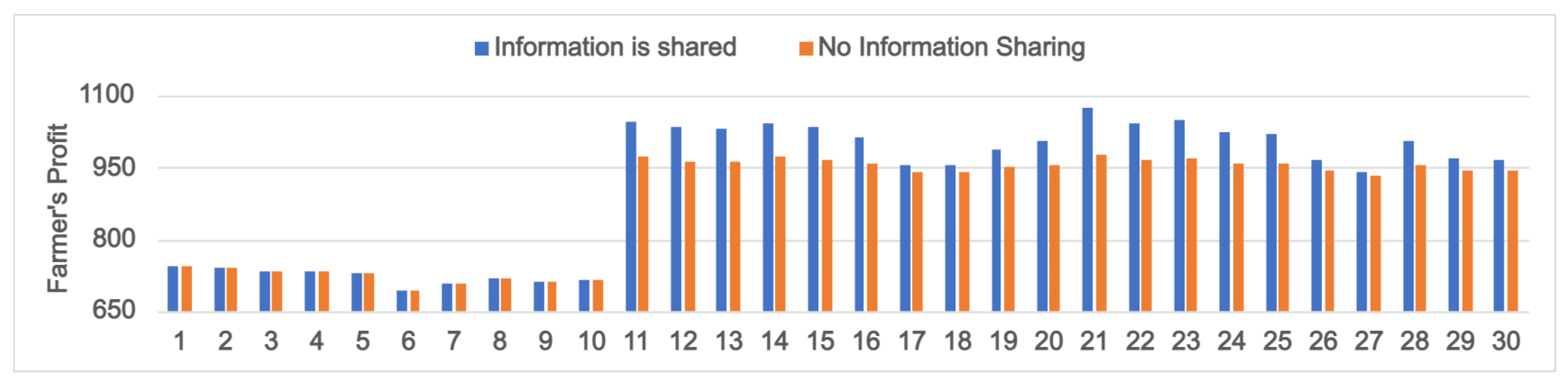
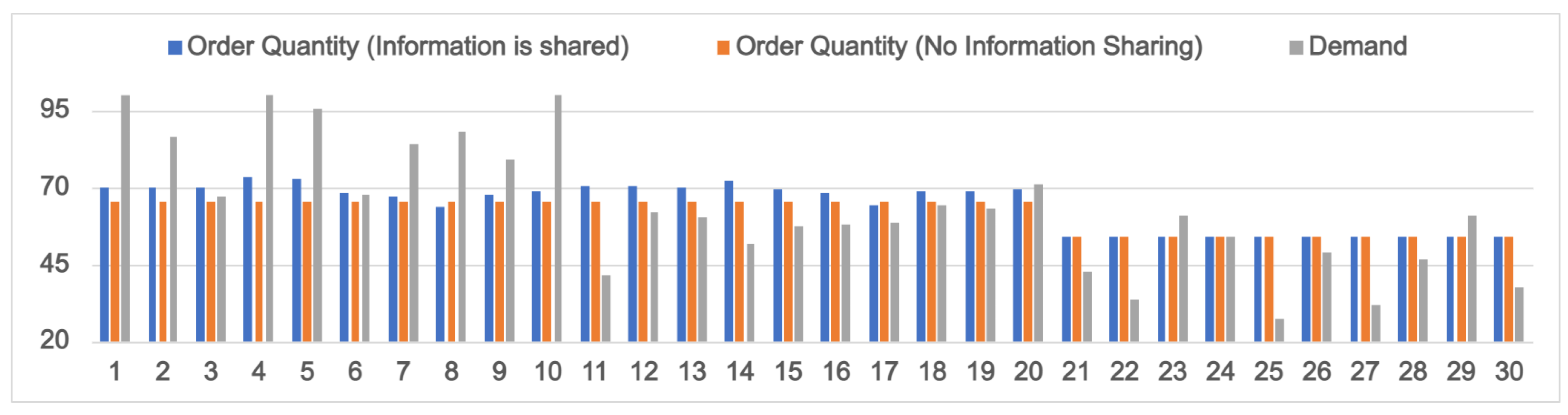
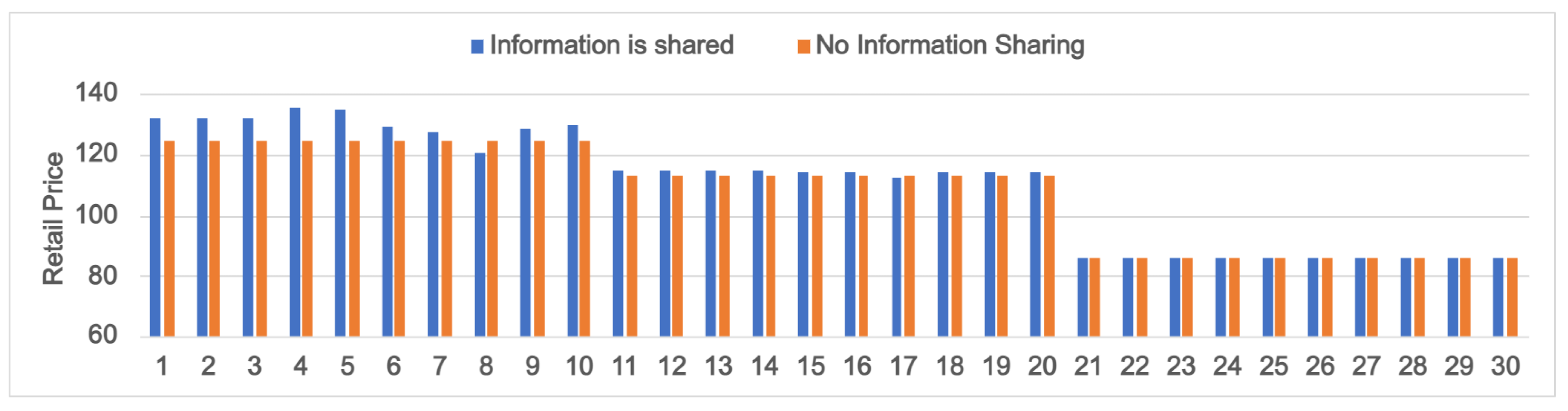
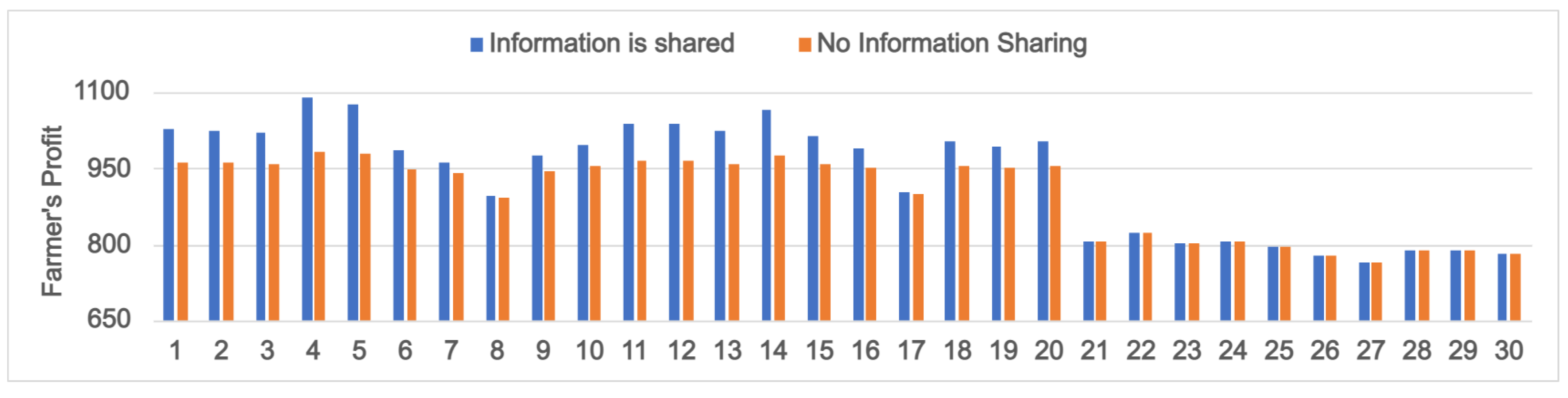
5. Effects of Information Sharing

Due to the complexities associated with an analytical approach, we numerically study the effects of information sharing on the performance of the supply chain that incorporates the proposed labeling scheme. Specifically, we investigate the sensitivity of the information-sharing decision with respect to (a) varying potential market sizes ($D_0$); (b) varying greenness level sensitivity factor ($\beta$); and (c) varying product deterioration rates ($\lambda$). The parameter values used in each case are as follows, unless stated otherwise:

Demand function parameters: Potential market size, $D_0=20$; Price sensitivity factor, $\alpha =0.3125$; Greenness level sensitivity factor, $\beta =10$; Quality sensitivity factor, $\delta =5$; Duration of each sale period, $t_s=2$; Initial product quality $q_0=1$; Product deterioration rate, $\lambda =0.3$;

Farm parameters: Production function coefficients, ${\alpha }_0=100,{\alpha }_1=10,{\beta }_0=20,{\beta }_1=6.8$; Irrigation efficiency, $\eta =0.75$; Fertilizer requirement for maximum yield, $N{F}_{max}=80$; Maximum amount of irrigation water available, $I{W}_{av}=400$; number of harvests, $n=10$

Farmer’s cost parameters: Salvage value, $C_{sal\left(F\right)}=5$; Shortage cost, $C_{s\left(F\right)}=30$; Wholesale price, $w=20$; Cost of fertilizers, $C_f=30$; Cost of irrigation water, $C_w=15$

Retailer’s cost parameters: Disposal cost, $C_{d\left(R\right)}=5$; Shortage cost, $C_{s\left(R\right)}=30$

Greenness function parameters:$w_f=0.5,N{F}_c=60,{\eta }_c=0.75$

The common belief about yield uncertainty before the forecast is that it is normally distributed with a mean of zero and a standard deviation, ${\sigma }_1=25$. The forecast signal noise is normally distributed with a mean of zero and standard deviation, ${\sigma }_{\varphi }=3$. We have assumed a uniform distribution for the demand uncertainty, ${ϵ}_2$ such that ${ϵ}_2\in [-20,20]$. This assumption satisfies statement 2 of Theorem 4. The numerical analysis procedure is detailed in Appendix B, and a detailed discussion of the results is given in Section 5.1, Section 5.2 and Section 5.3.

5.1. Varying Potential Market Sizes ($D_0$)

We consider 30 different problem instances (PI) (numbered 1–30) to study the effects of information sharing under varying potential market sizes ($D_0$). For problem instances numbered 1–10, $D_0$ is set as 40, while it is equal to 50 for instances from 11–20 and 60 for the remaining ten cases. Additionally, we consider a positive yield forecast (${\mathrm{\Gamma }}_y>0$) for the first five problem instances in each market size category and a negative forecast (${\mathrm{\Gamma }}_y<0$) for the remaining five cases. A positive yield forecast denotes favorable conditions where the yield is better than the expected value of y, and a negative forecast indicates unfavorable farming conditions where the yield is less than y. For each problem instance, the order quantities (Q) under different information-sharing scenarios and the corresponding demands are plotted in Figure 2 and the corresponding retail prices are plotted in Figure 3. Similarly, the farmer’s and retailer’s profits associated with each problem instance are also plotted (Figure 4 and Figure 5).

As seen in Section 4.3, the retailer’s problem of determining the order quantity is a single-constraint optimization problem in z (and therefore in Q). When the retailer’s profit function is concave in Q (or z) (as in our case), it can be solved by first considering it as an unconstrained optimization problem in Q (or z) and then limiting the value of Q thus obtained so that $Q\le Q_c$, where $Q_c$ is determined by Lemma 3. Note that the value of $Q_c$ depends on the information setting (see Lemma 3), but the value of Q is independent of the same. Following the same procedure as in our problem, the retailer’s optimal order quantity turns out to be the maximum allowable value, $Q_c$, when the potential market size is high ($D_0=50\mathrm{or}60$). Since the value of $Q_c$ varies in different information settings, the retailer’s order quantities vary across these settings, as seen in Figure 2 (PI: 11–30). On the other hand, when the market size is small ($D_0=40$), the value of Q obtained by solving the unconstrained optimization problem will be much lesser than $Q_c$ irrespective of the information set considered to determine $Q_c$. Thus, Q remains the same regardless of whether the information is shared or not (Figure 2, PI: 1–10). As a result, when the market size is small ($D_0=40$), the profit of the farmer and the retailer does not vary across different information settings as seen in Figure 4 and Figure 5 (PI: 1–10).

When the potential market size is large ($D_0=50\mathrm{or}60$), sharing the yield forecast with the retailer benefits the farmer (Figure 4, PI: 11–30). By giving a clear yield estimate, he encourages the retailer to order more products that help him earn better profits. This is evident in Figure 2 (PI: 11–30), where the retailer’s order quantity (Q) is always higher under the information-sharing scenario. When information is shared, and the farmer sees a negative forecast signal (${\mathrm{\Gamma }}_y<0$), he limits the retailer’s order quantity to avoid shortages (Figure 2, PI: 16–20 & 26–30 ). In contrast, he lets the retailer order more products when ${\mathrm{\Gamma }}_y>0$ (Figure 2, PI: 11–15 & 21–25). Thus in Figure 4, we can see that his profit is higher when the forecast signal is positive (${\mathrm{\Gamma }}_y>0$) (PI: 11–15 & 21–25) when compared with the cases where it is negative (${\mathrm{\Gamma }}_y<0$) (PI: 16–20 & 26–30).

The retailer benefits from shared information only when the realized demand ($D_T$) exceeds the maximum order quantity limit ($Q_c$) of the no-information sharing case ( Figure 2 and Figure 5, PI: $12,17,18,20,21,23,27,29$). The higher inventory levels, resulting from a larger order quantity in the information-sharing case, become useful only when $D_T$ is large. If $D_T$ is low, the large inventory levels result in more unsold products to be disposed of, causing revenue losses to the retailer. In such cases, even though she has to spend more in disposing of excess products, her profits are on par with that of the no-sharing scenario (Figure 5, PI: $11,13,14,15,19,22,24,25,26,28,30$). Higher retail prices in the information sharing scenario (Figure 3), as well as the small disposal costs ($C_{d\left(R\right)}=5$, in both cases), can be considered as the reasons for this observation. Higher values of $C_{d\left(R\right)}$ may offset the benefits of higher retail prices, and it may result in more revenue losses to the retailer under information sharing when $D_T$ is low. Accurate demand forecasts may help the retailer improve their profits, as it helps them determine the order quantity more precisely, thus reducing the quantity of unsold products at the end of a selling period.

Furthermore, we obtain interesting insights by comparing the cases where the product is eco-labeled and when it is not (conventional products) (Figure 6, Figure 7 and Figure 8). Here, we consider the potential market sizes ($D_0$) to be 50 (PI: 1–8), 60 (PI: 9–16), 70 (PI: 17–24) and 80 (PI: 25–32). The first four problem instances in each category are good yield scenarios (indicated by ${\mathrm{\Gamma }}_y>0$), and the remaining four are poor yield scenarios (${\mathrm{\Gamma }}_y<0$). Since it has already been shown that when $D_0>50$, sharing yield information benefits the farmer, we assume that he always shares the yield information with the retailer.

Figure 6 shows that the retailer makes better profits by selling eco-labeled products when $D_0=50$ (PI: 1–8) or 60 (PI: 9–16) and also under positive forecasts when $D_0=70$ (PI: 17–20). For all other instances considered (PI: 21–32), the retailer enjoys better profits on the sale of conventional products. This happens mainly because the term $D_0$ represents the demand quantity ignoring the green label and the quality considerations (see Equation (9)). A high value of $D_0(=80)$ compared to $\beta$ and $\delta$ signifies that a considerable number of consumers are insensitive to the labeling or quality attributes of the product. In such cases, it is beneficial for the retailer to overlook the labeling provision, as it helps her lift the constraints on order quantity set by the demands of the labeling scheme (see Lemma 3). This, in turn, helps her gain better profits by reducing product shortages and selling more quantities to consumers. Simultaneously, the farmer, relieved from meeting the labeling requirements, enjoys better profits by supplying more product quantities grown under conventional agricultural methods (Figure 7; PI: 25–32).

On the contrary, when $D_0=50$ or 60, the retailer’s stocking quantity (Q) requirement, calculated considering the product is eco-labeled, falls within the limiting order quantity requirement ($Q_c$) set by Lemma 3. This means that if she opts for an eco-label, she can increase the product demand (by $\beta$) without fearing the occurrence of stockouts. Due to the higher demand for eco-labeled products and the corresponding higher retail prices compared to conventional products (see Corollary 1), the retailer enjoys better profits by opting to sell eco-labeled products (Figure 6; PI: 1–16). In such cases, the farmer enjoys better profits by growing his crops following the labeling regulations (see Figure 7; PI: 1–12) as it helps him reduce cultivation costs (due to less fertilization and irrigation costs).

Problem instances 13–16 in Figure 7 show the cases of the farmer benefitting from conventional farming even when $D_0=60$. From the model definition (${\mathrm{\Gamma }}_y<0$, for PI: 13–16), it is evident that the farmer suffers poor yields in these situations. In such circumstances, a farmer can obtain a reasonable yield only if he aims for a much higher yield during his initial planning. This requires an excessive use of farm inputs, such as fertilizers and irrigation water, which is not allowed in the standards of the proposed labeling scheme. Since the yield forecast information has already been communicated with the retailer, she reduces her order quantity, reducing the farmer’s profit. Conversely, the absence of constraints on the farm inputs in conventional agriculture helps counteract possible yield losses. This allows the farmer to make higher profits by supplying more product quantities (Q) to the retailer, provided that she sells conventional products (Figure 8; PI: 13–16). However, when $D_0=60$, the extra quantity that the retailer can sell by opting for conventional products over eco-labeled ones is negligibly small. Considering the higher retail prices of eco-labeled products (see Corollary 1), this small difference will be insufficient to ensure higher retailer profits by selling conventional products over eco-labeled ones. This is evident in Figure 6; (PI: 13–16), where the retailer’s profits are higher when selling eco-labeled products. Hence, in such a scenario, the farmer’s and retailer’s decisions about the type of product will be conflicting. From Figure 6 and Figure 7 (PI: 13–16), it is clear that the effect of the product type decision is more pronounced on the retailer’s profit. Hence, the retailer should incentivize the farmer to cultivate eco-labeled products on his farm. A similar observation can be made for positive yield forecasts with $D_0=70$ (PI: 17–20).

Finally, for poor yield scenarios (${\mathrm{\Gamma }}_y<0$) with $D_0=70$ (PI: 21–24), significantly more quantities of conventional products will be available for sale compared to the eco-labeled ones (Figure 8; PI: 21–24). Since the potential market size ($D_0$) is also large, the difference between the quantities of conventional and eco-labeled products sold will be significant enough to make the sale of conventional products more profitable for the retailer (Figure 6; PI: 21–24). In this scenario, the farmer will also prefer conventional agriculture as it allows him to supply more products, thus, increasing his income (Figure 7; PI: 21–24).

5.2. Varying Greenness Level Sensitivity Factor ($\beta$)

A market setting in which environmentally conscious consumers are predominant is marked with higher values of $\beta$ and lower values of $D_0$. Products bearing eco-labels (${\theta }_p=1$) significantly increase the demand in this environment. This section investigates the effects of information sharing at varying greenness sensitivity levels ($\beta$). The profits of the farmer and retailer at different $\beta$ values in different information settings are evaluated, and the corresponding plots are developed (Figure 9 and Figure 10). The $\beta$ values considered are 20 (PI: 1–10), 40 (PI: 11–20) and 60 (PI: 21–30). Similarly to Section 5.1, we consider a positive (negative) forecast signal for the first (last) five problem instances in each $\beta$ category.

The results obtained are similar to the case of varying potential demand sizes (Section 5.1), with both the farmer (Figure 9) and the retailer (Figure 10) benefitting from the sharing of information at high values of $\beta$ ($=60$). At low $\beta$ values sharing yield information offers no advantage as the profits of both stakeholders remain the same in both information settings (Figure 9 and Figure 10; PI: 1–10). The explanation for this behavior is similar to that of the low $D_0$ case discussed in Section 5.1.

Importantly, there is a noticeable difference in the farmer’s and retailer’s preference for product types (eco-labeled/conventional) under high $\beta$ values compared with those under high $D_0$ values. For very high values of $D_0(=80)$, both the farmer and retailer were found to benefit from preferring conventional products (Section 5.1). However, when $\beta$ is high compared to $D_0$ and $\delta$, the farmer and retailer gain good profits only if they prefer eco-labeled products. This is due to the fact that the demand in a high $\beta$ setting can be boosted only if the product is eco-labeled (${\theta }_p=1$) (see Equation (9)).

5.3. Varying Product Deterioration Rates ($\lambda$)

When quality-conscious consumers dominate the market, we have higher values for the quality sensitivity factor ($\delta$) compared to $D_0$ and $\beta$. The demand for products in such an environment is highly influenced by the product deterioration rate ($\lambda$) (see Equation (9)). In this section, we analyze the effects of information sharing on stakeholders’ profits, considering the perishability attributes of the eco-labeled products. Here, we assume a high value of $\delta (=60)$ compared to $D_0(=20)$ and $\beta (=10)$. Figure 11 displays the order quantities under different information-sharing scenarios and the corresponding product demand when $\lambda =0.1$ (PI: 1–10), $0.4$ (PI: 11–20), and $0.7$ (PI: 21–30). Figure 12 shows the related retail prices. The profits of the farmer and the retailer are displayed in Figure 13 and Figure 14, respectively. Similarly to Section 5.1 and Section 5.2, we consider a positive (negative) forecast signal for the first (last) five instances in each $\lambda$ category.

When the deterioration rate is low ($\lambda =0.1$), the total demand for the product will be high (see Equation (9)), as seen in Figure 11 (PI: 1–10). In this case, the retailer prefers that the farmer shares his yield information so that she can order the maximum possible quantities that the farmer can supply. This is evident in Figure 11 (PI: 1–10), as in almost all instances (except PI: 8), the retailer’s order quantity (Q) under information sharing is higher than that under the no information sharing (In PI: 8, when information is shared, the retailer is forced to restrict her order quantity to a lower value due to a high negative yield forecast by the farmer). Here, the farmer is also at an advantage by sharing the yield information as it enables him to gain better profits (Figure 13; PI: 1–10) by supplying more products to the retailer. Interestingly, in Figure 12, we can find that the retail prices under information-sharing remain fairly high compared to the no information-sharing case for PI: 1–10 (except PI: 8). The sale of more quantities at higher retail prices under the information-sharing scenario results in greater profits for the retailer (Figure 14; PI: 1–10).

Information sharing is not always rewarding for the retailer with higher product deterioration rates ($\lambda =0.4$). The high value of $\lambda$ results in a decrease in product demand and retail prices, as seen in Figure 11 and Figure 12 (PI: 11–20). However, uncertainties associated with demand and high shortage costs ($C_{s\left(R\right)}$) force the retailer to follow a conservative approach where she stocks more products based on availability. For PI: 11–20, except for PI: 17, the yield information shared by the farmer is such that the product quantity that he can supply is greater than the corresponding value calculated under the no information sharing scenario. This results in the retailer ordering larger quantities when information is shared (Figure 11; PI: 11–20). On the other hand, when the retailer remains uninformed about the yield forecast, she makes her order quantity decision based on her knowledge of yield. The excess quantities ordered, when information is shared, prove useful to her only when the demand exceeds the order quantity of the no information-sharing case, which happens only for PI:20. For all the other instances (PI: 11–19), the total disposal costs for the retailer are higher in the information-shared situation. Low disposal costs per unit quantity and marginally better retail prices under information-sharing (Figure 12; PI: 11–20) are the reasons why the profit in this scenario remains almost the same as in the other case.

Although information sharing may not help the retailer when $\lambda =0.4$, the farmer reaps its benefits. It allows him to sell more products to the retailer through which he receives higher profits (Figure 13; PI: 11–20). Finally, for highly perishable products ($\lambda =0.7$), the high $\lambda$ results in low demand; hence, information-sharing offers no benefits to the stakeholders (PI: 21–30). This can be explained using the same logic discussed in Section 5.1, where information-sharing was found not beneficial for low potential market sizes ($D_0$).

6. Discussion

This section discusses the significance of the major results obtained for our supply chain model.

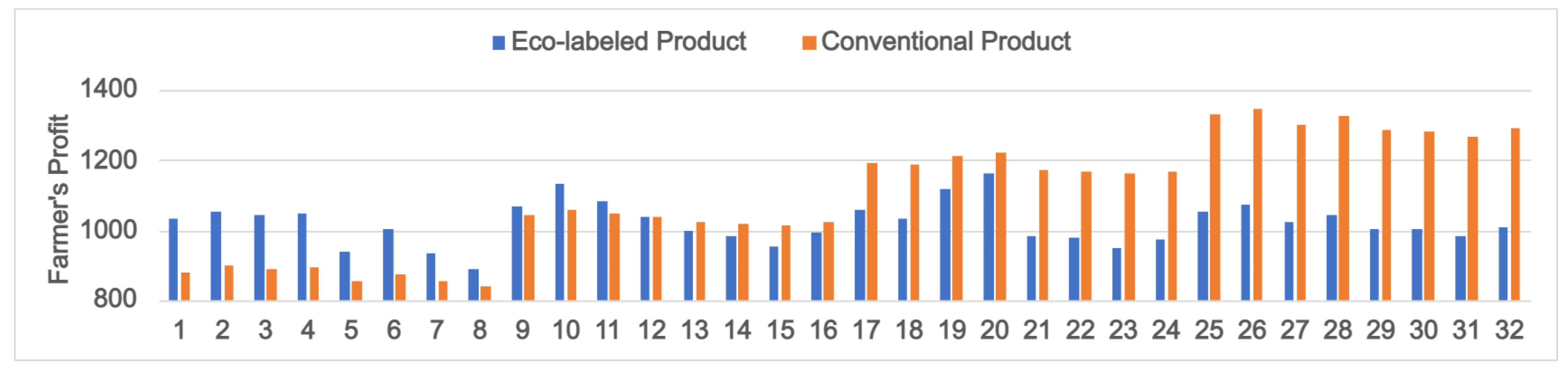
6.1. Effectiveness of the Proposed Eco-Labeling Scheme

Among the per unit area and the per unit mass of output measures available for measuring environmental impacts (see Section 1), the latter gains prominence in the interest of ensuring food security with minimal ecological damage. It is already seen in Section 1 that the organic scheme, due to its low yield, performed poorly under this measure. On the contrary, the proposed eco-label is defined to control the fertilizer application such that the greenhouse gas emissions per unit yield are minimal (Section 3.1). Moreover, Corollary 2 proves that the proposed scheme guarantees a better yield than organic farming. Effectively, this proves the superiority of the proposed scheme over the organic one in terms of ensuring agricultural sustainability, as it has minimal environmental impacts per unit yield. Although Corollary 2 points towards a higher yield in the case of conventional farming, its severe environmental impacts due to the uncontrolled use of synthetic fertilizers make it an unsustainable alternative.

Many previous studies [40,41,42,43] stress the importance of optimizing fertilizer usage to balance the yield-emission trade-off. Although all of these studies identify the optimal fertilizer requirement through field experiments, none discusses how observations can be put into practice. However, the proposed eco-label helps the consumer identify agri-products grown using such sustainable practices, creating a demand for such products in the market. This incentivizes the farmer and retailer to implement such practices.

Secondly, Corollary 1 suggests that the retail price under the proposed scheme is lower than that under the organic scheme. This makes the products cultivated under the new scheme affordable to the group of eco-sensitive consumers who find the price of organic products too high. The need for such products and their importance in promoting green agricultural practices are discussed in [78].

6.2. Farmer’s Cost Index (K) and Optimal Input Decisions

As seen in Equation (13), the farmer’s cost index (K) is calculated based on his cost and field parameters. It helps the farmer identify his market setting and the corresponding optimal yield levels (Table 3). Precise knowledge of the market environment helps the farmer identify scenarios where production to his maximum capacity proves beneficial. Moreover, it lets him recognize the cases where he has to avoid overproduction (beyond the retailer’s requirement) to prevent profit losses. Further, using Theorem 3, he can determine the exact amount of fertilizer and irrigation water needed to achieve the required yield. The precise control over the fertilizer and irrigation water application makes the agricultural setting more sustainable as it aids in checking greenhouse gas emissions and conserving water resources.

In existing green agri-food supply chain models like [54,79], attempts are made to determine the optimal greenness levels of the farmers to ensure agricultural sustainability while maximizing farmers’ profits. However, these models fail to explain how to achieve the recommended greenness levels. Our model addresses this issue by creating a clear connection between the greenness levels and the critical farm inputs (Section 3.1).

6.3. Retailer’s Optimal Decisions

Theorems 1 and 4 deal with the optimal retailer decisions on the retail price and order quantities that maximize her profit. These results are applicable in various retailer settings, as no specific distribution of demand uncertainties is considered during their development. They are derived following the seminal work of Petruzzi et al. [81] on pricing and order quantity decisions for a newsvendor problem. An important factor differentiating our work from [81] is the presence of constraints on order quantity (see lemma 3) due to the necessity of meeting the greenness requirement. As a result, the order quantity decisions in our model vary considerably from that of [81] (see Theorem 4).

6.4. Importance of Yield Information Sharing

The effects of yield information sharing in various market settings are detailed in Section 5. It identifies the contexts where information sharing becomes beneficial for both stakeholders and points out the importance of accurate demand forecasting at the retailer’s end. The study offers many practical implications to stakeholders by helping them make crucial decisions in various contexts, some of which are discussed here. In a market dominated by consumers who are less sensitive to eco-labels, the choice of the product type (eco-labeled/conventional) to be sold should depend on the potential market size ($D_0$). Although a very large potential market size may favor conventional products, opting for eco-labeled products in comparatively smaller markets may prove beneficial to the farmer and the retailer, provided they share the yield information (see Section 5.1). It is advisable that the farmer shares his yield information with the retailer when the market size is large and eco-sensitive consumers dominate the market (Section 5.2). It is always important to share the yield information when the products are less perishable (Section 5.3). For products with high perishability, information sharing does not help improve the stakeholder profits unless the market size is huge. Such an in-depth study on yield information sharing in sustainable agri-food supply chains has not been attempted previously in the literature.

7. Conclusions

The proposed eco-labeling scheme is a novel approach to sustainable agriculture, focusing on balancing the tradeoff between yield and environmental impacts of agriculture. The unique way in which greenness is defined under the scheme ensures that the farmer always uses his key farm inputs (fertilizer and irrigation water) judiciously, thereby ensuring a good yield with minimal ecological consequences. By bringing the considerations of crop yield into the labeling framework, we show a new way to improve agricultural sustainability. This is the first theoretical contribution of our work.

Due to its advantages over the organic and conventional schemes (see Section 6.1), the proposed eco-labeling scheme can potentially bring a positive change in the agricultural sector. Practically, to make this possible, it is vital to make environmentally-conscious consumers aware of the disadvantages of extensive implementation of organic farming practices (discussed in Section 1). Although it may take some time and effort to convince people to think beyond organic farming, an immediate opportunity for a niche market segment that constitutes these uniquely labeled products is identified in Section 6.1.

The farmer-retailer supply chain model, to which the proposed eco-labeling scheme is applied, considers the aspects of demand and yield uncertainties, and product perishability, thereby moving a step closer to a realistic setting. In addition, we prove the existence of closed-form solutions for the farmer’s and retailer’s problems, which is another important theoretical contribution considering the complexity of the problem. On the practical side, by classifying the farmer’s market based on the cost index (K), the model simplifies the farmer’s task of making important production decisions (Section 6.2). As discussed in Section 6.3, the generic nature of the retailer’s closed-form solution extends the applicability of our model across various retailer settings.

Finally, the numerical analysis (Section 5) throws more light on the importance of yield information sharing. Notably, the analysis focuses on identifying the scenarios in which sharing yield information benefits the stakeholders. The consideration of different market types, including the eco-sensitive consumer market, perishable products market, add more value to the analysis. Additionally, the study aids the stakeholders in recognizing scenarios where the production and sale of conventional products gain them better profits. Section 6.4 lists out some practical implications of our numerical study.

Furthermore, studies can be undertaken to extend the present model in various directions. Identification of other production variables with considerable environmental impacts and their incorporation into the eco-labeling scheme is an idea that future researchers can contemplate. It will help to further strengthen the proposed scheme, thus, improving its effectiveness in ensuring agricultural sustainability. Another important step would be to consider other crop-production functions like the Mitscherlich–Baule function, quadratic function, etc., [85] so that the model can be extended to a wide variety of crops. Extending the model by considering a retailer sourcing her products from competing farmers, which is a common scenario for large retail chains, will also be interesting. In such cases, each farmer may have different farm parameters and levels of uncertainties, according to which the production decisions of individual farmers may vary. The retailer has to decide on the quantities to be sourced from each farmer under uncertainties. It will also be interesting to study the effects of product preservation on supply chain decisions. Different preservation levels may result in completely new retailer behavior, and it has to be closely investigated.