Experimental Study on Deformation Characteristics of Gangue Backfill Zone under the Condition of Natural Water in Deep Mines
Abstract
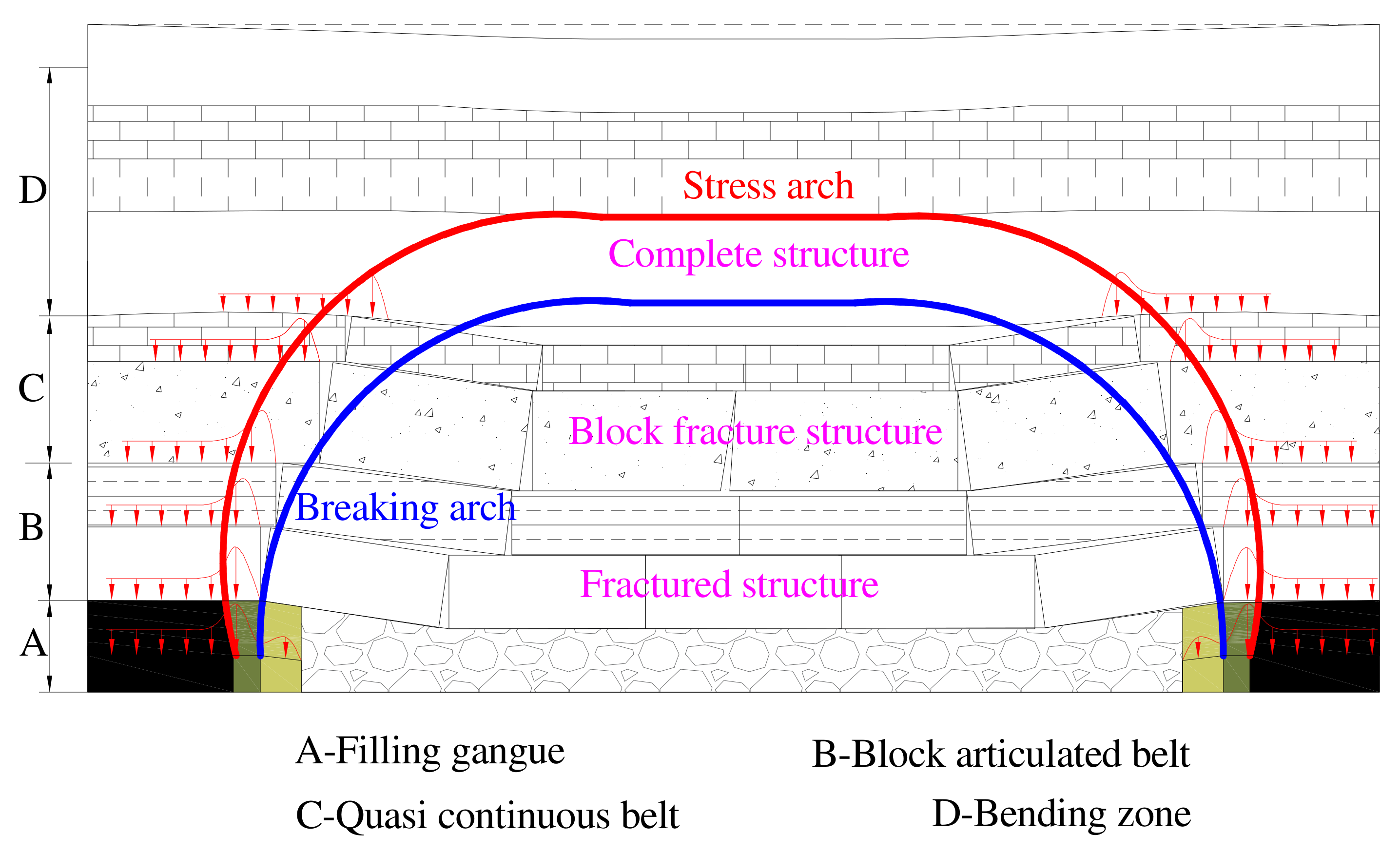
:1. Introduction
2. Test Method
2.1. Test Instrument
2.2. Test Design
3. Compaction Test under Natural Conditions
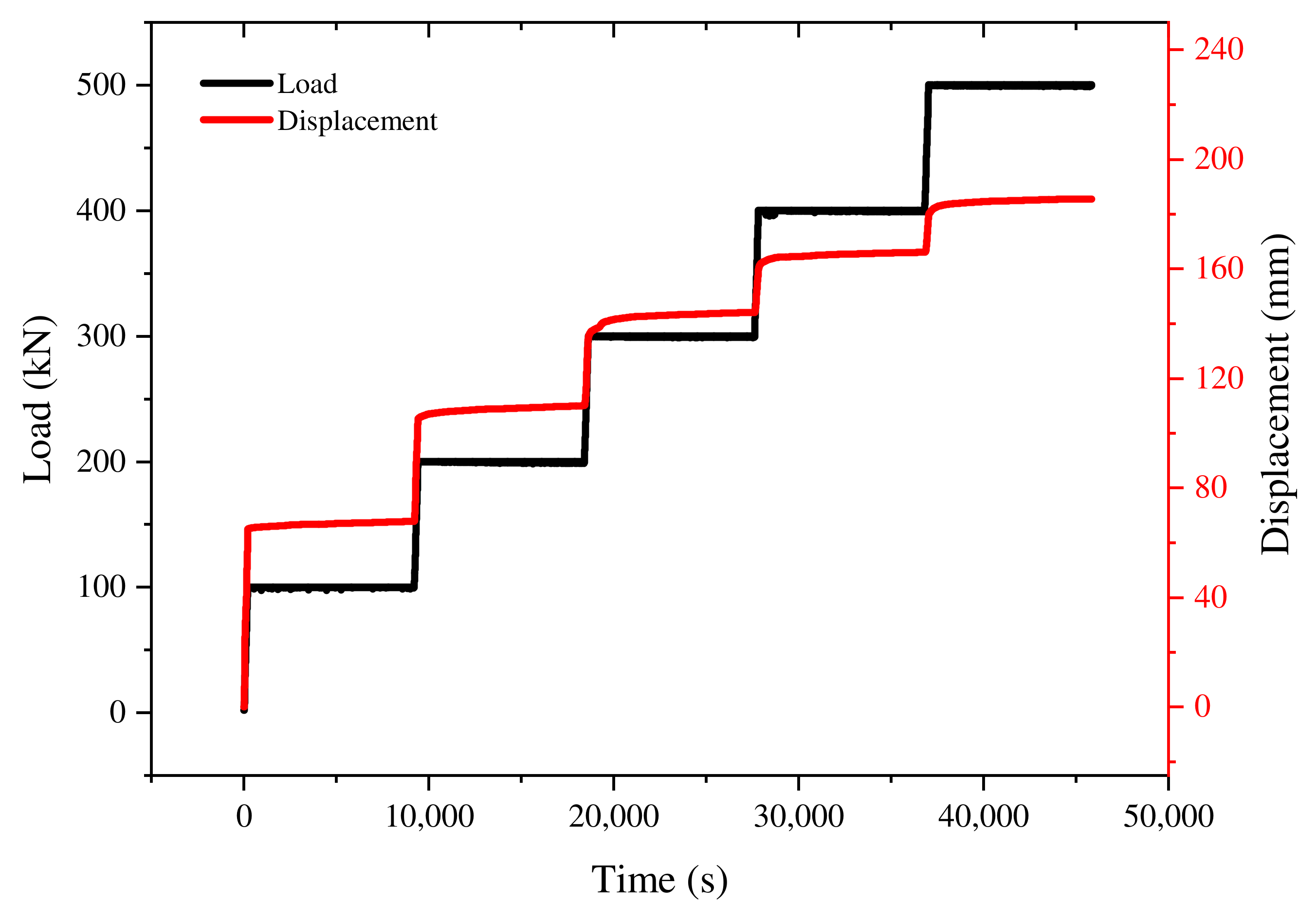
3.1. Test Results
3.2. Characteristics of Displacement Variation in the Loading Stage
3.3. Characteristics of Displacement Variation in the Dead Load Stage
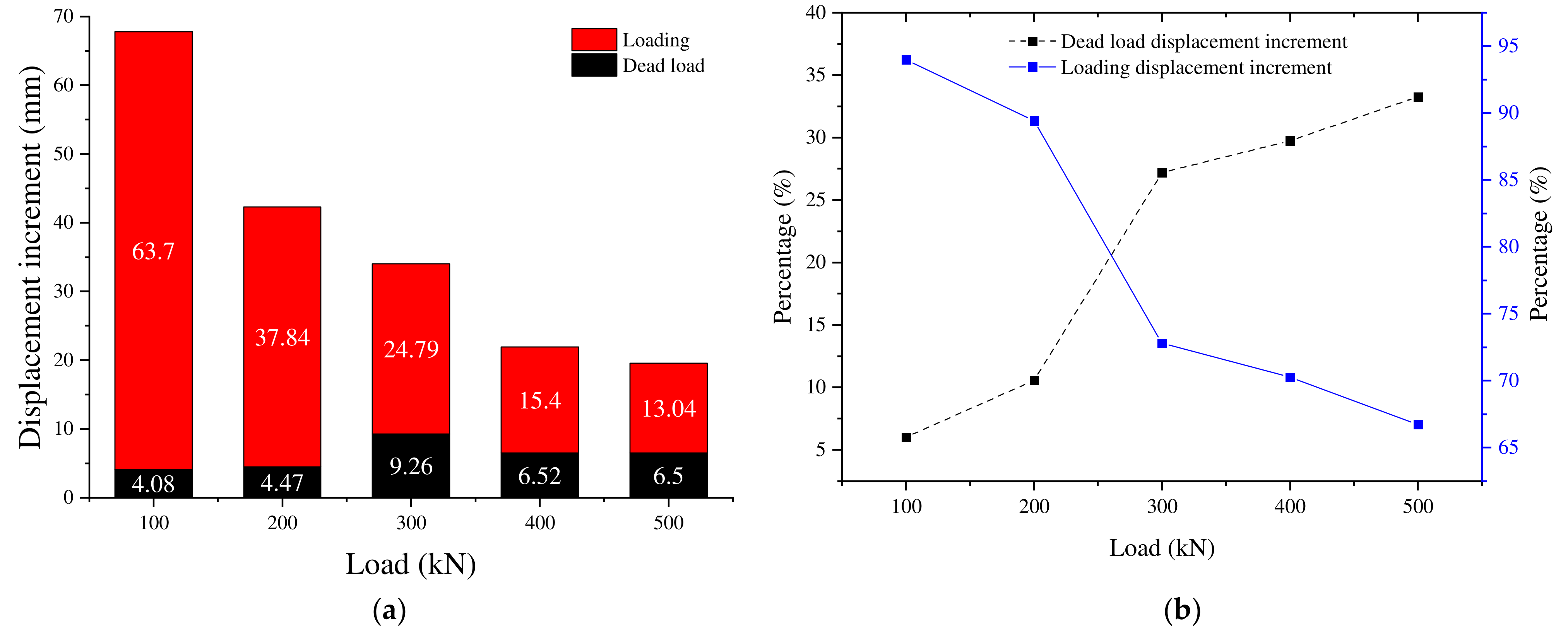
3.4. Comparison of Deformation in the Loading and Dead Load Stages
4. Compaction Test in a Saturated State
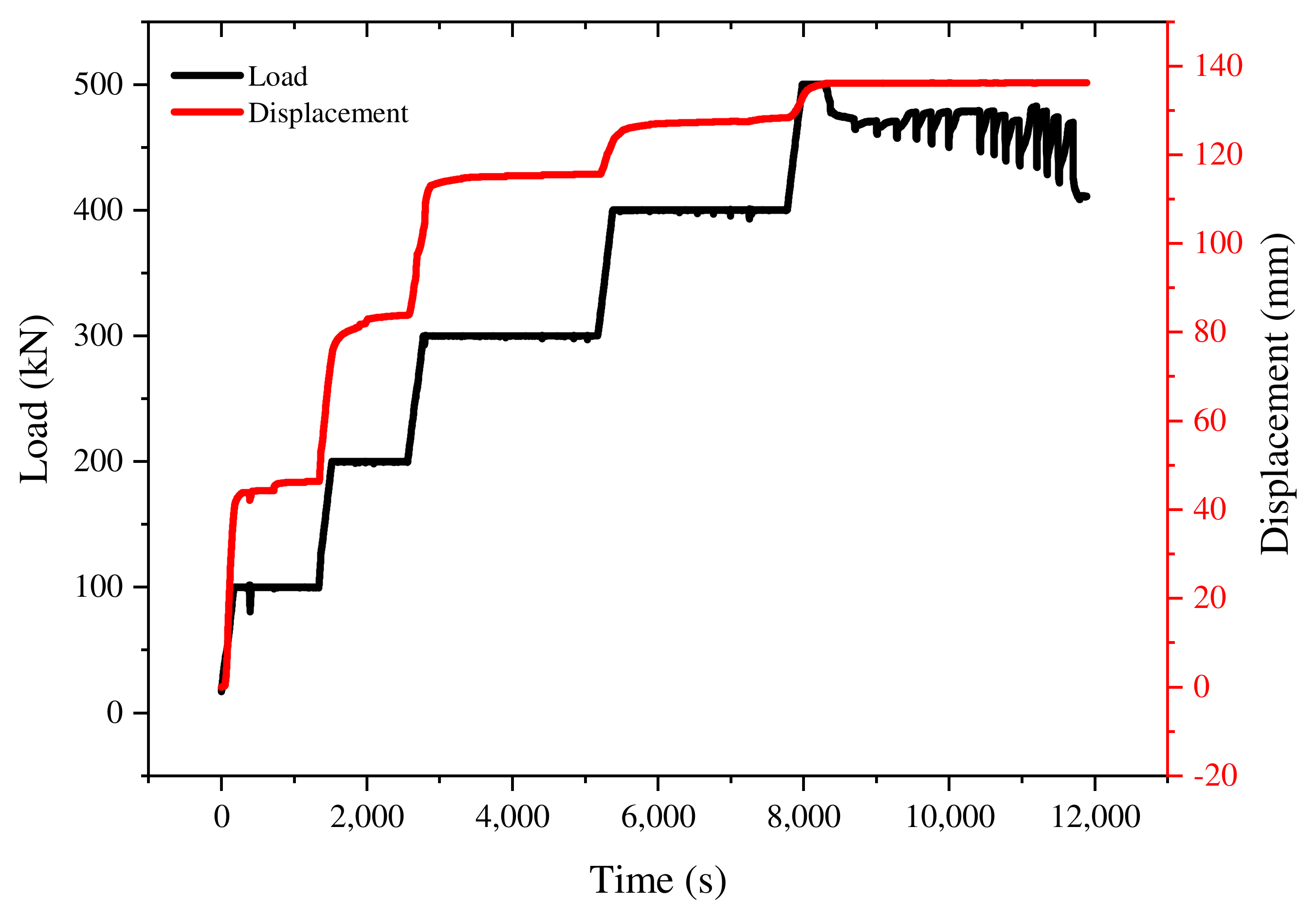
4.1. Test Results
4.2. Characteristics of the Displacement Variation in the Loading Stage
4.3. Characteristics of the Displacement Variation in the Dead Load Stage
4.4. Comparison of the Deformation in the Loading and Dead Load Stages
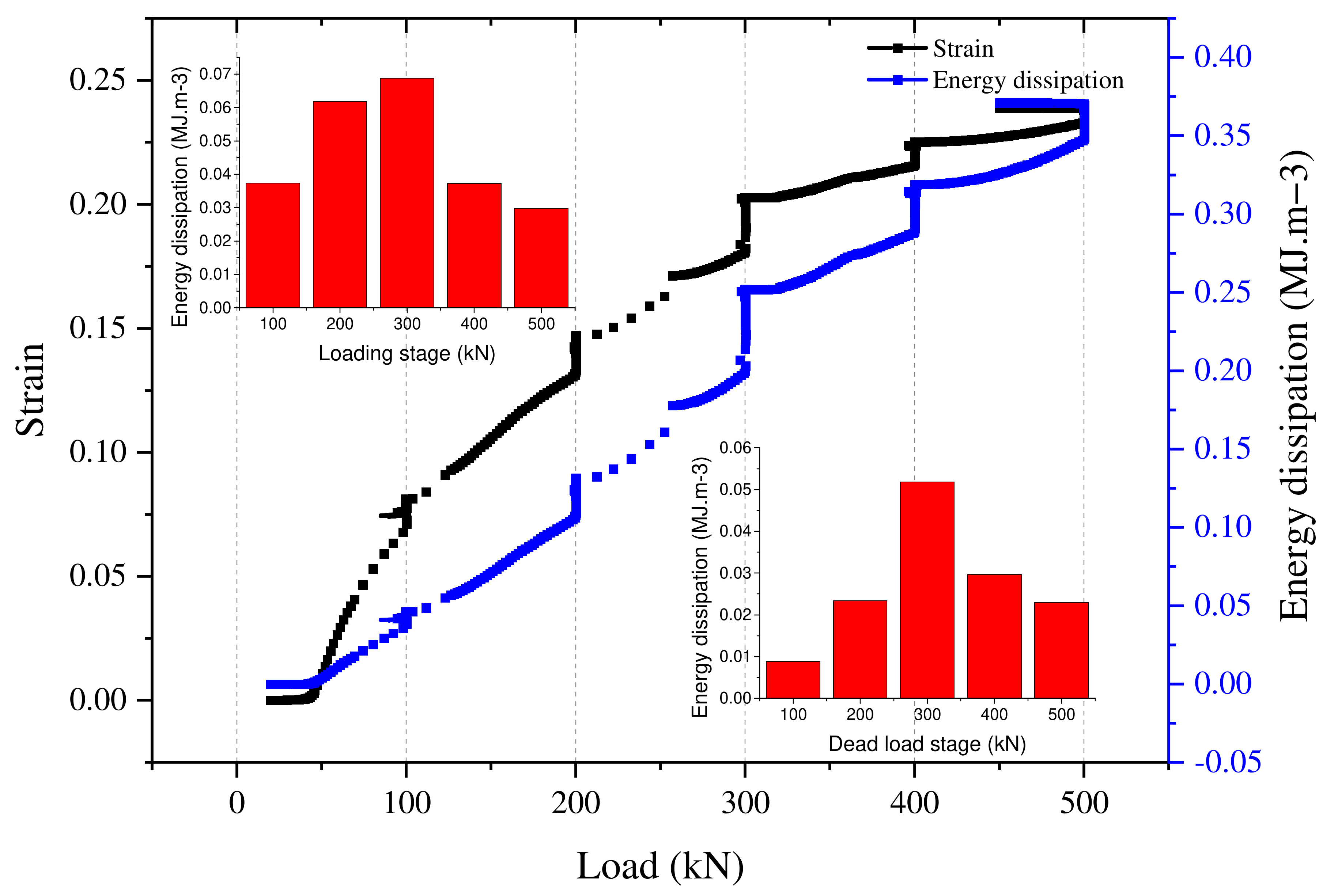
5. Energy Dissipation of the Filling Gangue
6. Discussion and Conclusions
- (1)
- Gradient loading stage: the results of the natural state test are consistent with those in the saturated state. During the loading process, the displacement–load curve for 0~100 kN is an inverted S-type, and 100~200, 200~300, 300~400, and 400~500 kN are of a positive S-type. Similar to the natural state, the displacement in the loading stage is the main component of the total displacement. However, the proportion of the loading displacement decreases gradually with an increase in load gradient in the water-saturated state.
- (2)
- Dead load stage: the displacement–time curve for each dead load test stage in the natural state is consistent, and the displacement increment of the dead load stage is small. However, the percentage of the dead load displacement gradually increases. Compared with the natural state, the axial displacement of the water-saturated state has evident “step” characteristics. The deformation in the dead load stage of the water-saturated state is higher than that of the natural state. When the natural and water-saturated states are 300 kN, the dead load deformation is the largest.
- (3)
- For both natural and water-bearing states, in the loading stage, with an increase in load, the strain and energy dissipation consistently increase. The difference is that the strain shows a logarithmic increase, while the energy dissipation shows an exponential increase. In the natural state, whether in the loading stage or in the dead load stage, the larger the load gradient, the greater the increase in range. In the water-bearing state, whether in the loading stage or the dead load stage, the energy dissipation shows a trend of normal distribution.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chi, M.; Li, Q.; Cao, Z.; Fang, J.; Wu, B.-Y.; Zhang, Y.; Wei, S.-R.; Liu, X.-Q.; Yang, Y.-M. Evaluation of water resources carrying capacity in ecologically fragile mining areas under the influence of underground reservoirs in coal mines. J. Clean. Prod. 2022, 379, 134449. [Google Scholar] [CrossRef]
- Karagianni, A.; Lazos, I.; Chatzipetros, A. Remote Sensing Techniques in Disaster Management: Amynteon Mine Landslides, Greece; Springer Science and Business Media Deutschland GmbH: Istanbul, Turkey, 2019. [Google Scholar]
- Shen, B.; Barton, N. fracturing mechanisms around underground openings. Geomech. Eng. 2018, 16, 35–47. [Google Scholar]
- Jaouhar, E.M.; Li, L.; Aubertin, M. An analytical solution for estimating the stresses in vertical backfilled stopes based on a circular arc distribution. Geomech. Eng. 2018, 15, 889–898. [Google Scholar]
- Moon, H.; Yang, I.J. A study on the characteristics of subsidence according to discontinuous rock masses collapse in abandoned mine. J. Korean Soc. Miner. Energy Resour. Eng. 2014, 51, 385–394. [Google Scholar]
- Yavuz, H. An estimation method for cover pressure re-establishment distance and pressure distribution in the goaf of longwall coal mines. Int. J. Rock Mech. Min. Sci. 2004, 41, 193–205. [Google Scholar] [CrossRef]
- Zhou, N.; Zhang, J.; Yan, H.; Li, M. Deformation behavior of hard roofs in solid backfill coal mining using physical models. Energies 2017, 10, 557. [Google Scholar] [CrossRef] [Green Version]
- Rozenblat, Y.; Portnikov, D.; Levy, A.; Kalman, H.; Aman, S.; Tomas, J. Strength distribution of particles under compression. Powder Technol. 2011, 208, 215–224. [Google Scholar] [CrossRef]
- Donohue, S.; O’sullivan, C.; Long, M. Particle breakage during cyclic triaxial loading of a carbonate sand. Géotechnique 2009, 59, 477–482. [Google Scholar] [CrossRef]
- Gupta, V.K. Effect of size distribution of the particulate material on the specific breakage rate of particles in dry ball milling. Powder Technol. 2017, 305, 714–722. [Google Scholar] [CrossRef]
- Hu, C.M.; Wang, X.Y.; Mei, Y.; Yuan, Y.L.; Zhang, S.S. Compaction techniques and construction parameters of loess as filling material. Geomech. Eng. 2018, 15, 1143–1151. [Google Scholar]
- Li, M.; Zhang, J.; Huang, Y.; Zhou, N. Effects of particle size of crushed gangue backfill materials on surface subsidence and its application under buildings. Environ. Earth Sci. 2017, 76, 603. [Google Scholar] [CrossRef]
- De Bono, J.P.; Mcdowell, G.R. The fractal micro mechanics of normal compression. Comput. Geotech. 2016, 78, 11–24. [Google Scholar] [CrossRef]
- Nieuwmeyer, F.J.; Van der Voort Maarschalk, K.; Vromans, H. Granule breakage during drying processes. Int. J. Pharm. 2007, 329, 81–87. [Google Scholar] [CrossRef]
- Ovalle, C.; Dano, C.; Hicher, P.Y.; Cisternas, M. Experimental framework for evaluating the mechanical behavior of dry and wet crushable granular materials based on the particle breakage ratio. Can. Geotech. J. 2014, 52, 587–598. [Google Scholar] [CrossRef]
- Si, L.; Zhang, H.; Wei, J.; Li, B.; Han, H. Modeling and experiment for effective diffusion coefficient of gas in water-saturated coal. Fuel 2021, 284, 118887. [Google Scholar] [CrossRef]
- Si, L.; Wei, J.; Xi, Y.; Wang, H.; Wen, Z.; Li, B.; Zhang, H. The influence of long-time water intrusion on the mineral and pore structure of coal. Fuel 2021, 290, 119848. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, S.; Zhang, X. Classification and fractal characteristics of coal rock fragments under uniaxial cyclic loading conditions. Arab. J. Geosci. 2018, 11, 201. [Google Scholar] [CrossRef]
- Talbot, A.N.; Brown, H.A.; Richart, F.E. The Strength of Concrete: Its Relation to the Cement Aggregates and Water (No. 137–138); University of Illinois: Chicago, IL, USA, 1923. [Google Scholar]
- Ma, D.; Rezania, M.; Yu, H.S.; Bai, H.B. Variations of hydraulic properties of granular sandstones during water inrush: Effect of small particle migration. Eng. Geol. 2017, 217, 61–70. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Yin, L.; Guo, W. Stress–seepage coupling of cataclastic rock masses based on digital image technologies. Rock Mech. Rock Eng. 2018, 51, 2355–2372. [Google Scholar] [CrossRef]
- Golsanami, N.; Jayasuriya, M.N.; Yan, W.; Fernando, S.G.; Liu, X.; Cui, L.; Zhang, X.; Yasin, Q.; Dong, H.; Dong, X. Characterizing clay textures and their impact on the reservoir using deep learning and Lattice-Boltzmann simulation applied to SEM images. Energy 2022, 240, 122599. [Google Scholar] [CrossRef]
- Liu, Q.; Li, J.; Li, Y.; Gao, M. Recognition Methods for Coal and Coal Gangue Based on Deep Learning. IEEE Access 2021, 9, 77599–77610. [Google Scholar] [CrossRef]
- Murali, S.; Asokan, P.; Morchhale, R.K. Chapter 12—High volume fly ash utilization for reclamation of wastelands with special reference to mine spoil and ash back-haul areas for agriculture and forestry. In Modern Cartography Series; Bhunia, G.S., Chatterjee, U., Kashyap, A., Shit, P.K., Eds.; Academic Press: Cambridge, MA, USA, 2021; pp. 243–263. [Google Scholar]
- Saha, L.; Bauddh, K. Chapter 4—Characteristics of mining spoiled and oil drilling sites and adverse impacts of these activities on the environment and human health. In Phytorestoration of Abandoned Mining and Oil Drilling Sites; Bauddh, K., Korstad, J., Sharma, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 87–101. [Google Scholar]
- Zhang, Z. Analysis of plastic deformation and energy property of marble under pseudo-triaxial compression. Chin. J. Rock Mech. Eng. 2008, 27, 273–280. [Google Scholar]
- Huang, J.; Tian, C.; Xing, L.; Bian, Z.; Miao, X. Green and sustainable mining: Underground coal mine fully mechanized solid dense stowing-mining method. Sustainability 2017, 9, 1418. [Google Scholar] [CrossRef]
- Miao, X.X.; Mao, X.B.; Hu, G.W.; Ma, Z.G. Research on broken expand and press solid characteristics of rocks and coals. J. Exp. Mech. 1997, 12, 394–399. [Google Scholar]
- Su, C.; Gu, M.; Tang, X.; Guo, W. Experiment study of compaction characteristics of crushed stones from coal seam roof. Chin. J. Rock Mech. Eng. 2012, 31, 18–26. [Google Scholar]









| Experimental Stage | Displacement | |||
|---|---|---|---|---|
| Origin/mm | End/mm | D-Value/mm | Strain | |
| 0~100 kN loading | 0.000 | 63.700 | 63.700 | 0.103 |
| 100 kN dead load | 63.700 | 67.890 | 4.190 | 0.007 |
| 100~200 kN loading | 67.890 | 104.460 | 36.570 | 0.059 |
| 200 kN dead load | 104.460 | 110.100 | 5.640 | 0.009 |
| 200~300 kN loading | 110.100 | 134.880 | 24.780 | 0.040 |
| 300 kN dead load | 134.880 | 144.140 | 9.260 | 0.015 |
| 300~400 kN loading | 144.140 | 159.540 | 15.400 | 0.025 |
| 400 kN dead load | 159.540 | 166.060 | 6.520 | 0.011 |
| 400~500 kN loading | 166.060 | 179.100 | 13.040 | 0.021 |
| 500 kN dead load | 179.100 | 185.600 | 6.500 | 0.010 |
| Experimental Stage | Deformation | |||
|---|---|---|---|---|
| Origin/mm | End/mm | D-Value/mm | Strain | |
| 0~100 kN loading | 0 | 39.86 | 39.86 | 0.0699 |
| 100 kN dead load | 39.86 | 46.33 | 6.47 | 0.0114 |
| 100~200 kN loading | 46.33 | 75.46 | 29.13 | 0.0511 |
| 200 kN dead load | 75.46 | 83.82 | 8.36 | 0.0147 |
| 200~300 kN loading | 83.82 | 103.18 | 19.36 | 0.0340 |
| 300 kN dead load | 103.18 | 115.61 | 12.43 | 0.0218 |
| 300~400 kN loading | 115.61 | 123.02 | 7.41 | 0.0130 |
| 400 kN dead load | 123.02 | 127.85 | 4.83 | 0.0085 |
| 400~500 kN loading | 127.85 | 132.82 | 4.97 | 0.0087 |
| 500 kN dead load | 132.82 | 136.21 | 3.39 | 0.0059 |
| Experimental Stage | Strain | Stage Ratio (%) | E-d (MJ·m−3) | Stage Ratio (%) | Strain | Stage Ratio (%) | E-d (MJ·m−3) | Stage Ratio (%) |
|---|---|---|---|---|---|---|---|---|
| 0~100 kN loading | 0.103 | 93.64 | 0.03807 | 87.72 | 0.0699 | 85.98 | 0.03739 | 80.90 |
| 100 kN dead load | 0.007 | 6.36 | 0.00533 | 12.28 | 0.0114 | 14.02 | 0.00883 | 19.10 |
| 100~200 kN loading | 0.059 | 86.76 | 0.07057 | 82.99 | 0.0511 | 77.66 | 0.06182 | 72.58 |
| 200 kN dead load | 0.009 | 13.24 | 0.01446 | 17.01 | 0.0147 | 22.34 | 0.02336 | 27.42 |
| 200~300 kN loading | 0.040 | 72.73 | 0.08168 | 69.46 | 0.0340 | 60.93 | 0.06875 | 57.02 |
| 300 kN dead load | 0.015 | 27.27 | 0.03591 | 30.54 | 0.0218 | 39.07 | 0.05183 | 42.98 |
| 300~400 kN loading | 0.025 | 69.44 | 0.07052 | 67.80 | 0.0130 | 60.47 | 0.03722 | 55.64 |
| 400 kN dead load | 0.011 | 30.56 | 0.03349 | 32.20 | 0.0085 | 39.53 | 0.02967 | 44.36 |
| 400~500 kN loading | 0.021 | 67.74 | 0.07733 | 64.94 | 0.0087 | 59.59 | 0.02984 | 56.85 |
| 500 kN dead load | 0.010 | 32.26 | 0.04175 | 35.06 | 0.0059 | 40.41 | 0.02295 | 43.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Jiang, N.; Lu, W.; Zhang, M.; Kong, D.; Xu, M.; Wang, C. Experimental Study on Deformation Characteristics of Gangue Backfill Zone under the Condition of Natural Water in Deep Mines. Sustainability 2022, 14, 15517. https://doi.org/10.3390/su142315517
Lu Y, Jiang N, Lu W, Zhang M, Kong D, Xu M, Wang C. Experimental Study on Deformation Characteristics of Gangue Backfill Zone under the Condition of Natural Water in Deep Mines. Sustainability. 2022; 14(23):15517. https://doi.org/10.3390/su142315517
Chicago/Turabian StyleLu, Yao, Ning Jiang, Wei Lu, Meng Zhang, Dezhi Kong, Mengtang Xu, and Changxiang Wang. 2022. "Experimental Study on Deformation Characteristics of Gangue Backfill Zone under the Condition of Natural Water in Deep Mines" Sustainability 14, no. 23: 15517. https://doi.org/10.3390/su142315517







