Overview of Model- and Non-Model-Based Online Battery Management Systems for Electric Vehicle Applications: A Comprehensive Review of Experimental and Simulation Studies
Abstract
:1. Introduction
- (1)
- The challenge for the state-of-charge (SOC) estimation is the great amount of current in EVs, leading to complex dynamics that are difficult to capture using a battery model.
- (2)
- It is very difficult to predict battery aging or state of health (SOH) online by measuring current, voltage, and temperature. No sensor has been developed yet to predict online capacity and internal resistance.
- (3)
- The battery state of power (SOP) and state of energy (SOE) also depend on aging (SOH) and SOC. Therefore open-loop experimental methods such as ampere-hour counting (AHC), and open-circuit voltage (OCV) are not suitable for online state monitoring of BMS. The development of an algorithm to work on the relationship of battery state with the combined estimation of all these measurements is challenging for online BMS.
- (4)
- The state of safety (SOS) depends on multi-fault diagnosis, which is still challenging to achieve online.
- (5)
- Fast and optimized charging is crucial for EVs. It is challenging to optimize charging methods to prolong cycle life and enhance safety, speed up charging time, and increase charging performance.
- (1)
- Model-based and non-model-based (data-driven methods) algorithm development for online state monitoring for complex, nonlinear, and time-varying battery systems. SOC, SOE, SOH, and SOP estimation is the prime objective of the BMS.
- (2)
- Algorithm development for battery state of safety (SOS), control, and fault diagnosis, which is essential for BMS condition monitoring.
- (3)
- Algorithm development for charging control, which is crucial as the charging process of the LiBs directly impacts the SOH and SOS of LIBs. Model- and non-model-based charging optimization strategies are key to the safety and longevity of LiBs.
2. Lithium-Ion Charging Strategy for Electric Vehicles
2.1. Simulation Comparison between CC–CV and CP–CV Charging Profile for EVs
2.2. Issues, Challenges, and Future Directions
3. Li-Ion Battery Modeling
3.1. Electrical Equivalent Circuit Model (EECM) or Equivalent Circuit Model (ECM) of Li-Ion Batteries
3.2. Fractional-Order Battery Model
3.3. Issues, Challenges, and Future Directions
- An excellent battery model should predict battery dynamics in both time and frequency areas in complete operating conditions. The ideal model for BMS should be performed with modest parameter identification, less computation burden, and good accuracy in different operating conditions. The existing model needs to be modified with a better algorithm to make parameter and state identification secure and robust.
- The main disadvantage of FOM is a computationally expansive procedure for employment in BMS, and an intelligent management algorithm is technically very challenging. Future research in this direction needs to be carried out.
4. Model-Based Online Parameter and State Estimation
4.1. Model-Based Online Parameter and State Estimation of Li-Ion Battery
4.2. Issues, Challenges, and Future Directions
5. Kalman Filter Algorithms for Model-Based Online Parameter and State Estimations
5.1. Algorithm Comparison of Simulation Results of EKF and SPKF
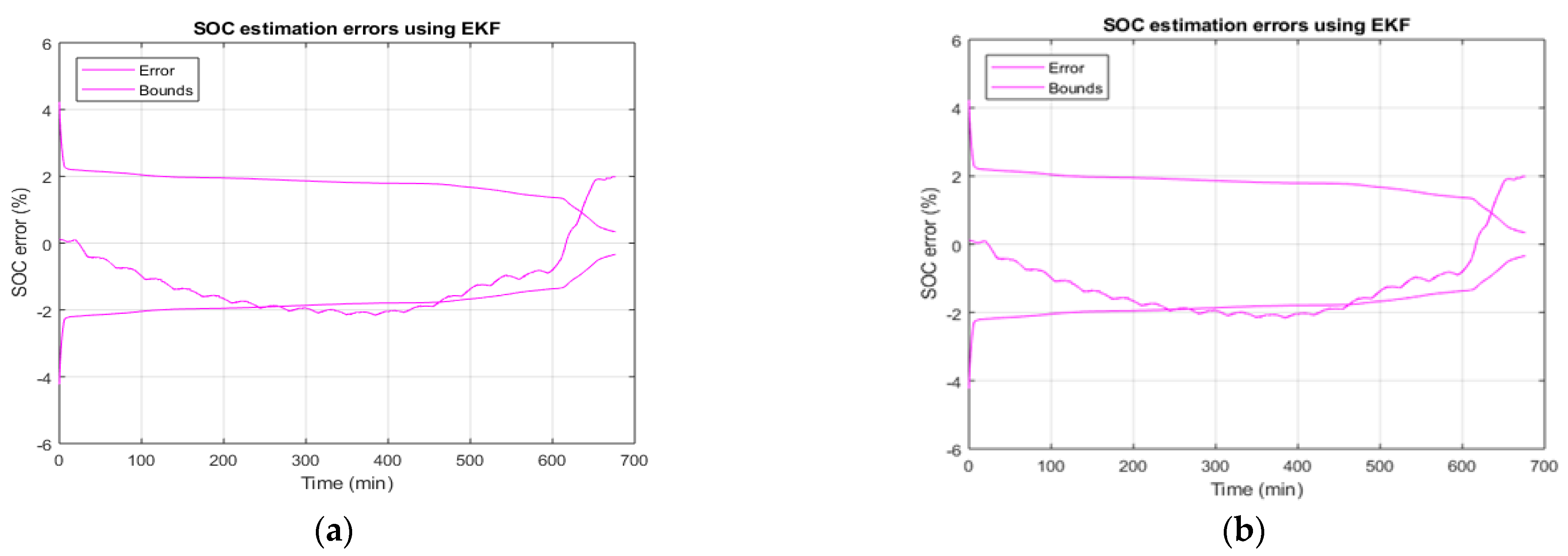
5.2. Performance Analysis of Kalman Filters
5.3. Issues, Challenges, and Future Directions
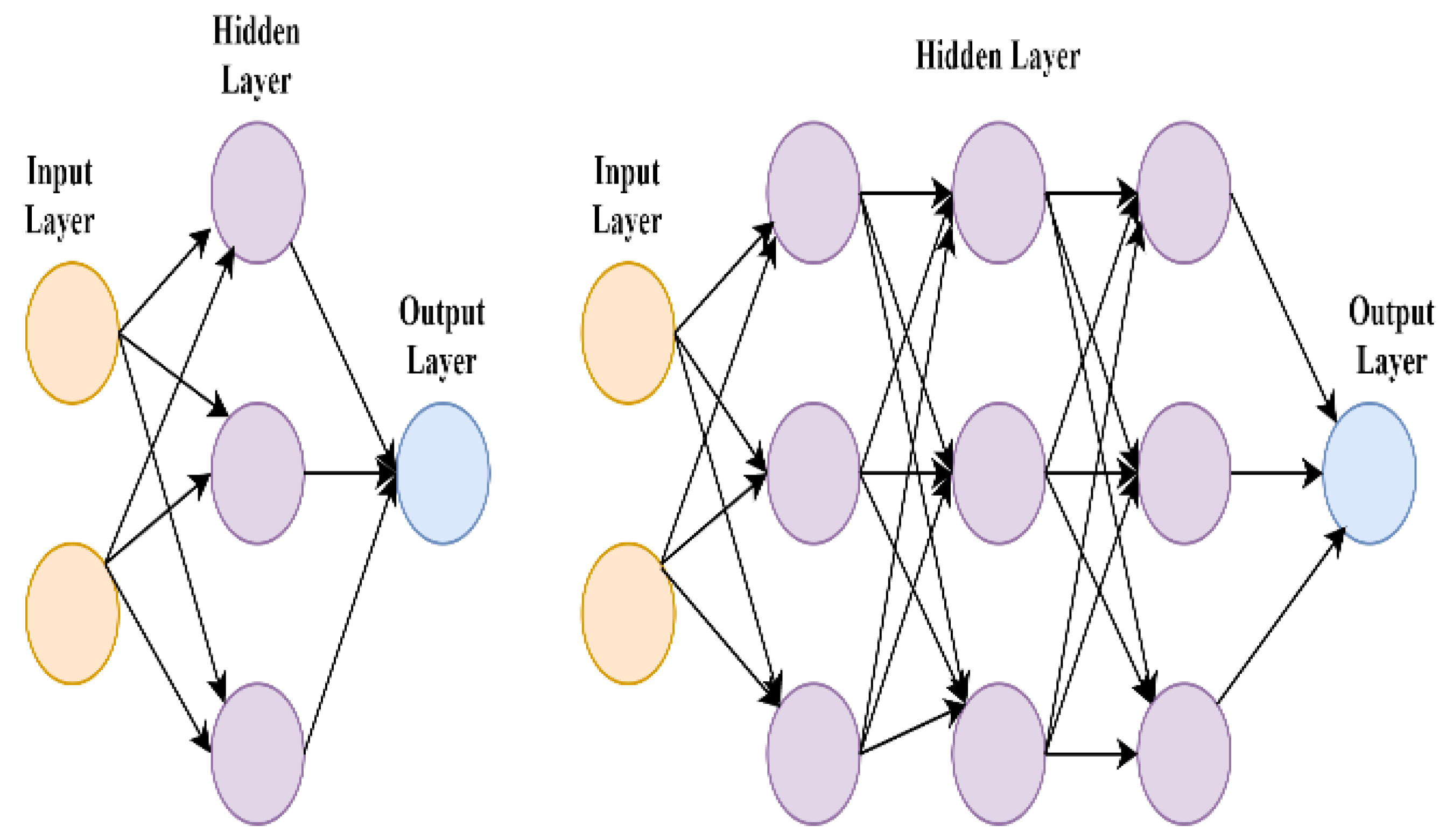
6. BMS Algorithms for Non-Model-Based (Data-Driven Approach) State Estimation
6.1. Lithium-Ion Battery Modeling Based on Big Data
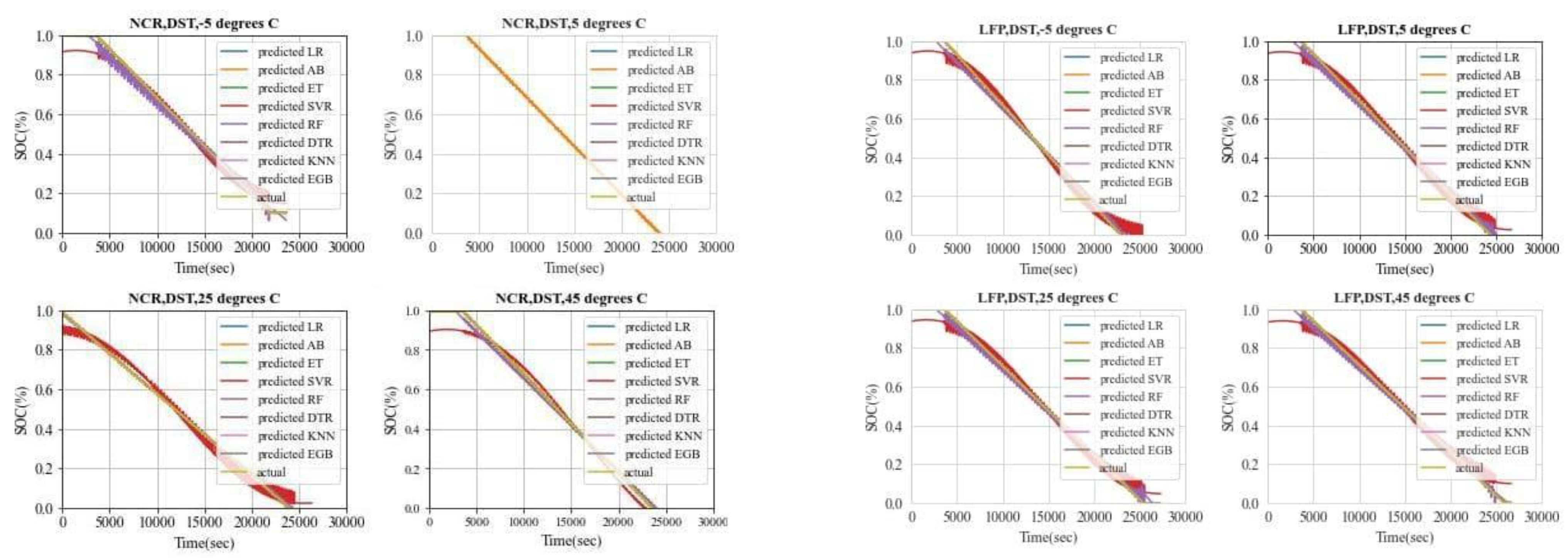
6.2. A simulation Comparison of Machine Learning Algorithms
6.3. Issues, Challenges, and Future Directions
- Issues and Challenges
- Future trends
7. Fault Diagnosis and the State of Balance
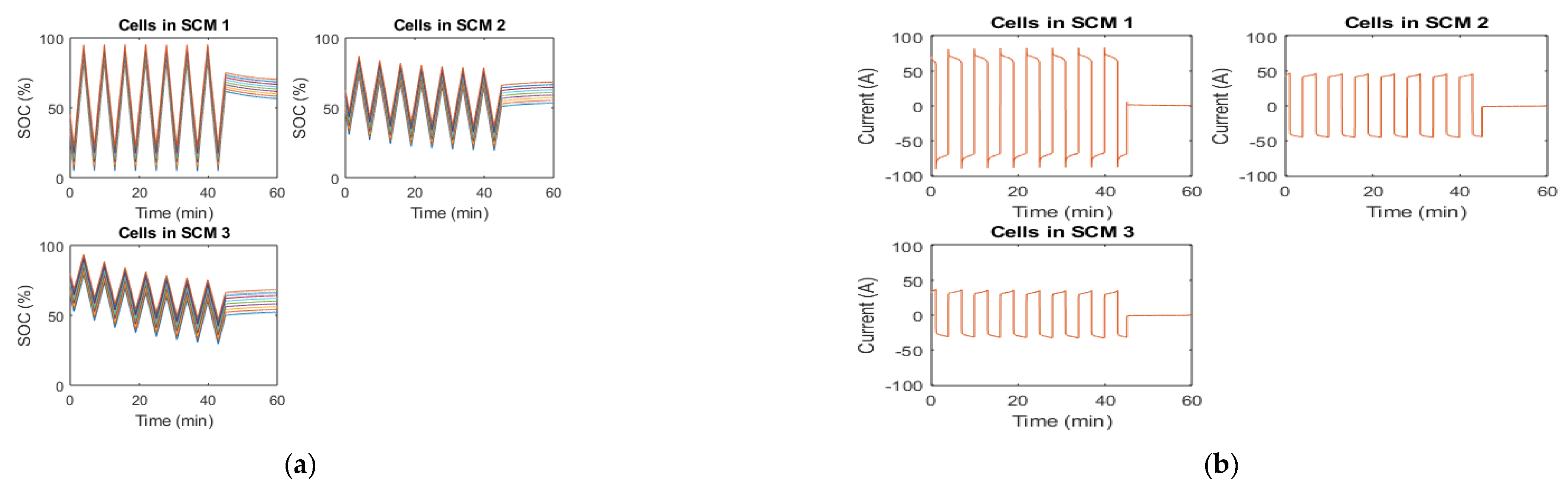
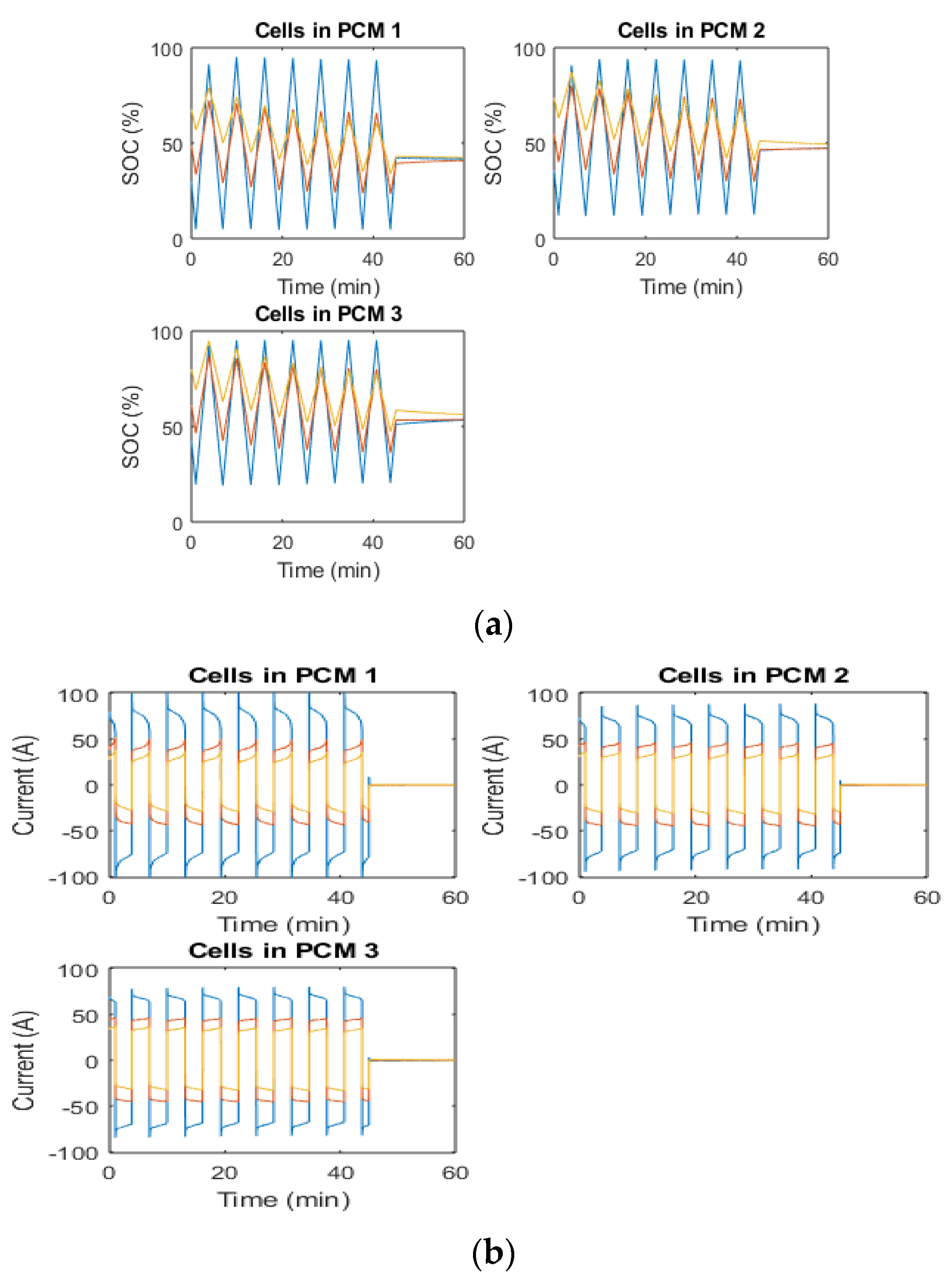
7.1. Research Challenges and Advances in Series and Parallel Connection (Battery Pack)
7.2. Mode-l and Non-Model-Based Fault Diagnosis and State of Safety of Li-Ion Battery
7.3. Issues, Challenges, and the Future Trend of Online Fault Diagnosis
- Issues and Challenges
- Future trends
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| AB | Adaboost |
| AEKF | Adaptive extended Kalman filter |
| AHC | Ampere-hour counting |
| AM | Analytical models |
| ANN | Artificial neural network |
| AR | Auto-regression |
| ARIMA | Autoregressive integrated moving average |
| BLSTM | Deep long short-term memory |
| BMS | Battery management system |
| CC-CV | Constant current–constant voltage |
| CDKF | Central difference Kalman filter |
| CNN | Convolution neural network |
| CP-CV | Constant power–constant voltage |
| CPE | Constant phase element |
| CVA | Canonical variate analysis |
| DBN | Deep belief network |
| DBNN | Deep belief neural network |
| DCNN | Deep convolution neural network |
| DD | Data-driven |
| DEKF | Dual extended Kalman filter |
| DL | Deep learning |
| DNN | Deep neural netowrk |
| DST | Dynamic stress test |
| DT | Decision tree |
| ECM | Equivalent circuit model |
| EECM | Electrical equivalent circuit models |
| EGB | Extreme gradient boosting |
| EIS | Electrochemical impedance spectroscopy |
| EKF | Extended Kalman filter |
| EMD | Empirical mode decomposition |
| ESC | Enhanced self-correcting |
| ETM | Electro-thermal modeling |
| ETR | Extra trees regressor |
| EV | Electric vehicle |
| FA | Firefly algorithm |
| FCN | Fully convolutional network |
| FOM | Fractional-order model |
| FUDS | Federal urban driving schedule |
| GA | Genetic algorithm |
| GPR | Gaussian process regression |
| HPPC | Hybrid pulse power characterization |
| HEVs | Hybrid electric vehicles |
| IIR | Infinite impulse response |
| KNN | K neighbor regressor |
| LCO | Lithium cobalt oxide |
| LFP | Lithium iron phosphate |
| LiBs | Lithium-ion batteries |
| LMO | Lithium manganese oxide |
| LR | Linear regression |
| LSTM | Long short-term memory |
| LTO | Lithium titanate oxide |
| MAE | Mean absolute error |
| ML | Machine learning |
| MSE | Mean square error |
| NCA | Lithium nickel cobalt aluminum oxide |
| NMC | Lithium nickel manganese cobalt oxide |
| OCV | Open-circuit voltage |
| ODEs | Ordinary differential equations |
| PDEs | Partial differential equations |
| PHEVs | Plug-in hybrid electric vehicle |
| PNGV | Partnership new generation of vehicle |
| PSO | Partical swam optimization |
| RF | Random forest |
| RMSE | Root-mean-square error |
| RNN | Recurrent neural network |
| RUL | Remaining userful life |
| SAA | Simulated annealing algorithm |
| SAE | Stacked auto encoder |
| LS | Lebesgue sampling |
| RS | Riemann sampling |
| SMO | Sliding mode observer |
| SOC | State of charge |
| SOE | State of energy |
| SOF | State of function |
| SOH | State of health |
| SOP | State of power |
| SOS | State of safety |
| SOT | State of temperature |
| SPKF | Sigma point Kalman filter |
| SVR | Support vector regression |
| TM | Thermal model |
| UDDS | Urban dynamometer driving schedule |
| UKF | Unscented Kalman filter |
| WD | Wavelet decomposition |
References
- Nykvist, B.; Nilsson, M. Rapidly falling costs of battery packs for electric vehicles. Nat. Clim. Chang. 2015, 5, 329–332. [Google Scholar] [CrossRef]
- Sulaiman, N.; Hannan, M.; Mohamed, A.; Majlan, E.; Daud, W.W. A review on energy management system for fuel cell hybrid electric vehicle: Issues and challenges. Renew. Sustain. Energy Rev. 2015, 52, 802–814. [Google Scholar] [CrossRef]
- Hannan, M.A.; Hoque, M.D.M.; Hussain, A.; Yusof, Y.; Ker, A.P.J. State-of-the-Art and Energy Management System of Lithium-Ion Batteries in Electric Vehicle Applications: Issues and Recommendations. IEEE Access Spec. Sect. Adv. Energy Storage Technol. Appl. 2018, 6, 19362–19378. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, W.; Yu, Q.; Sun, F. Research progress, challenges and prospects of fault diagnosis on battery system of electric vehicles. Appl. Energy 2020, 279, 115855. [Google Scholar] [CrossRef]
- Yong, J.Y.; Ramachandaramurthy, V.K.; Tan, K.M.; Mithulananthan, N. A review on the state-of-the-art technologies of electric vehicle, its impacts and prospects. Renew. Sustain. Energy Rev. 2015, 49, 365–385. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, J.; Xiong, R.; Shen, W.; He, H. Towards a smarter battery management system: A critical review on optimal charging methods of lithium ion batteries. Energy 2019, 183, 220–234. [Google Scholar] [CrossRef]
- Nejad, S.; Gladwin, D.; Stone, D. A systematic review of lumped-parameter equivalent circuit models for real-time estimation of lithium-ion battery states. J. Power Sources 2016, 316, 183–196. [Google Scholar] [CrossRef] [Green Version]
- Shrivastava, P.; Soon, T.K.; Bin Idris, M.Y.I.; Mekhilef, S. Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries. Renew. Sustain. Energy Rev. 2019, 113, 109233. [Google Scholar] [CrossRef]
- Hu, X.; Feng, F.; Liu, K.; Zhang, L.; Xie, J.; Liu, B. State estimation for advanced battery management: Key challenges and future trends. Renew. Sustain. Energy Rev. 2019, 114, 109334. [Google Scholar] [CrossRef]
- Das, U.K.; Shrivastava, P.; Tey, K.S.; Bin Idris, M.Y.I.; Mekhilef, S.; Jamei, E.; Seyedmahmoudian, M.; Stojcevski, A. Advancement of lithium-ion battery cells voltage equalization techniques: A review. Renew. Sustain. Energy Rev. 2020, 134, 110227. [Google Scholar] [CrossRef]
- Liu, K.; Ashwin, T.R.; Hu, X.; Lucu, M.; Widanage, W.D. An evaluation study of different modelling techniques for calendar ageing prediction of lithium-ion batteries. Renew. Sustain. Energy Rev. 2020, 131, 110017. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Tran, M.-K.; Fowler, M. A Review of Lithium-Ion Battery Fault Diagnostic Algorithms: Current Progress and Future Challenges. Algorithms 2020, 13, 62. [Google Scholar] [CrossRef] [Green Version]
- Jin, G.; Li, L.; Xu, Y.; Hu, M.; Fu, C.; Qin, D. Comparison of SOC Estimation between the Integer-Order Model and Fractional-Order Model Under Different Operating Conditions. Energies 2020, 13, 1785. [Google Scholar] [CrossRef] [Green Version]
- Naseri, F.; Schaltz, E.; Stroe, D.-I.; Gismero, A.; Farjah, E. An Enhanced Equivalent Circuit Model With Real-Time Parameter Identification for Battery State-of-Charge Estimation. IEEE Trans. Ind. Electron. 2021, 69, 3743–3751. [Google Scholar] [CrossRef]
- Bian, X.; Wei, Z.; He, J.; Yan, F.; Liu, L. A Two-Step Parameter Optimization Method for Low-Order Model-Based State-of-Charge Estimation. IEEE Trans. Transp. Electrif. 2020, 7, 399–409. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Kuang, K.; Han, X.; Chu, Z.; Lu, L.; Ouyang, M. A model-based continuous differentiable current charging approach for electric vehicles in direct current microgrids. J. Power Sources 2021, 482, 229019. [Google Scholar] [CrossRef]
- Behi, H.; Karimi, D.; Kalogiannis, T.; He, J.; Patil, M.S.; Muller, J.-D.; Haider, A.; Van Mierlo, J.; Berecibar, M. Advanced hybrid thermal management system for LTO battery module under fast charging. Case Stud. Therm. Eng. 2022, 33, 101938. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, G.; Zhou, C.; Li, M.; Chen, Z. Lithium-Ion Battery Optimal Charging using Moth-flame Optimization Algorithm and Fractional-Order Model. IEEE Trans. Transp. Electrif. 2022, 1. [Google Scholar] [CrossRef]
- Faria, J.P.D.; Velho, R.L.; Calado, M.R.A.; Pombo, J.A.N.; Fermeiro, J.B.L.; Mariano, S.J.P.S. A New Charging Algorithm for Li-Ion Battery Packs Based on Artificial Neural Networks. Batteries 2022, 8, 18. [Google Scholar] [CrossRef]
- Shen, W.; Vo, T.T.; Kapoor, A. Charging algorithms of lithium-ion batteries: An overview. In Proceedings of the 2012 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 18–20 July 2012; pp. 1567–1572. [Google Scholar] [CrossRef]
- Zhang, S.S. The effect of the charging protocol on the cycle life of a Li-ion battery. J. Power Sources 2006, 161, 1385–1391. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Hsieh, C.-H.; Luo, Y.-F. Search for an Optimal Five-Step Charging Pattern for Li-Ion Batteries Using Consecutive Orthogonal Arrays. IEEE Trans. Energy Convers. 2011, 26, 654–661. [Google Scholar] [CrossRef]
- Wang, S.-C.; Liu, Y.-H. A PSO-Based Fuzzy-Controlled Searching for the Optimal Charge Pattern of Li-Ion Batteries. IEEE Trans. Ind. Electron. 2014, 62, 2983–2993. [Google Scholar] [CrossRef]
- Chen, L.-R. Design of Duty-Varied Voltage Pulse Charger for Improving Li-Ion Battery-Charging Response. IEEE Trans. Ind. Electron. 2008, 56, 480–487. [Google Scholar] [CrossRef]
- Khan, A.B.; Choi, W. Optimal Charge Pattern for the High-Performance Multistage Constant Current Charge Method for the Li-Ion Batteries. IEEE Trans. Energy Convers. 2018, 33, 1132–1140. [Google Scholar] [CrossRef]
- Li, Y.; Li, K.; Xie, Y.; Liu, J.; Fu, C.; Liu, B. Optimized charging of lithium-ion battery for electric vehicles: Adaptive multistage constant current–constant voltage charging strategy. Renew. Energy 2019, 146, 2688–2699. [Google Scholar] [CrossRef]
- Vo, T.T.; Chen, X.; Shen, W.; Kapoor, A. New charging strategy for lithium-ion batteries based on the integration of Taguchi method and state of charge estimation. J. Power Sources 2015, 273, 413–422. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Teng, J.-H.; Lin, Y.-C. Search for an Optimal Rapid Charging Pattern for Lithium–Ion Batteries Using Ant Colony System Algorithm. IEEE Trans. Ind. Electron. 2005, 52, 1328–1336. [Google Scholar] [CrossRef]
- Notten, P.; Veld, J.O.H.; van Beek, J. Boostcharging Li-ion batteries: A challenging new charging concept. J. Power Sources 2005, 145, 89–94. [Google Scholar] [CrossRef]
- Keil, P.; Jossen, A. Charging protocols for lithium-ion batteries and their impact on cycle life—An experimental study with different 18650 high-power cells. J. Energy Storage 2016, 6, 125–141. [Google Scholar] [CrossRef]
- Tar, B.; Fayed, A. An overview of the fundamentals of battery chargers. In Proceedings of the 2016 IEEE 59th International Midwest Symposium on Circuits and Systems (MWSCAS), Abu Dhabi, United Arab Emirates, 16–19 October 2016; pp. 1–4. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.-R. A Design of an Optimal Battery Pulse Charge System by Frequency-Varied Technique. IEEE Trans. Ind. Electron. 2007, 54, 398–405. [Google Scholar] [CrossRef]
- Cho, I.-H.; Lee, P.-Y.; Kim, J.-H. Analysis of the Effect of the Variable Charging Current Control Method on Cycle Life of Li-ion Batteries. Energies 2019, 12, 3023. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.-R.; Wu, S.-L.; Shieh, D.-T.; Chen, T.-R. Sinusoidal-Ripple-Current Charging Strategy and Optimal Charging Frequency Study for Li-Ion Batteries. IEEE Trans. Ind. Electron. 2012, 60, 88–97. [Google Scholar] [CrossRef]
- Abdel-Monem, M.; Trad, K.; Omar, N.; Hegazy, O.; Mantels, B.; Mulder, G.; Van den Bossche, P.; Van Mierlo, J. Lithium-ion batteries: Evaluation study of different charging methodologies based on aging process. Appl. Energy 2015, 152, 143–155. [Google Scholar] [CrossRef]
- Abdel-Monem, M.; Trad, K.; Omar, N.; Hegazy, O.; Bossche, P.V.D.; Van Mierlo, J. Influence analysis of static and dynamic fast-charging current profiles on ageing performance of commercial lithium-ion batteries. Energy 2017, 120, 179–191. [Google Scholar] [CrossRef]
- Tomaszewska, A.; Chu, Z.; Feng, X.; O’Kane, S.; Liu, X.; Chen, J.; Ji, C.; Endler, E.; Li, R.; Liu, L.; et al. Lithium-ion battery fast charging: A review. eTransportation 2019, 1, 100011. [Google Scholar] [CrossRef]
- Patnaik, L.; Praneeth, A.V.J.S.; Williamson, S.S. A Closed-Loop Constant-Temperature Constant-Voltage Charging Technique to Reduce Charge Time of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2018, 66, 1059–1067. [Google Scholar] [CrossRef]
- Marcis, V.A.; Praneeth, A.; Patnaik, L.; Williamson, S.S. Analysis of CT-CV Charging Technique for Lithium-ion and NCM 18650 Cells. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), Cochin, India, 2–4 January 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Plett, G.L. Dr. Gregory L. Plett’s Homepage. Available online: http://mocha-java.uccs.edu/ (accessed on 8 July 2020).
- Wang, Y.; Li, J.; Zhang, J.; Pecht, M. Lithium-iron-phosphate battery electrochemical modelling under a wide range of ambient temperatures. J. Electroanal. Chem. 2021, 882, 115041. [Google Scholar] [CrossRef]
- Ngandjong, A.C.; Lombardo, T.; Primo, E.N.; Chouchane, M.; Shodiev, A.; Arcelus, O.; Franco, A.A. Investigating electrode calendering and its impact on electrochemical performance by means of a new discrete element method model: Towards a digital twin of Li-Ion battery manufacturing. J. Power Sources 2020, 485, 229320. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, C.; Chen, S.; Zhang, X.; Fan, G.; Zhu, C. Development and parameterization of a control-oriented electrochemical model of lithium-ion batteries for battery-management-systems applications. Appl. Energy 2022, 309, 118521. [Google Scholar] [CrossRef]
- Lai, X.; Zheng, Y.; Sun, T. A comparative study of different equivalent circuit models for estimating state-of-charge of lithium-ion batteries. Electrochim. Acta 2018, 259, 566–577. [Google Scholar] [CrossRef]
- Seaman, A.; Dao, T.-S.; McPhee, J. A survey of mathematics-based equivalent-circuit and electrochemical battery models for hybrid and electric vehicle simulation. J. Power Sources 2014, 256, 410–423. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Patil, D.; Fahimi, B. Electrothermal Modeling of Lithium-Ion Batteries for Electric Vehicles. IEEE Trans. Veh. Technol. 2018, 68, 170–179. [Google Scholar] [CrossRef]
- Mesbahi, T.; Rizoug, N.; Bartholomeus, P.; Sadoun, R.; Khenfri, F.; Le Moigne, P. Dynamic Model of Li-Ion Batteries Incorporating Electrothermal and Ageing Aspects for Electric Vehicle Applications. IEEE Trans. Ind. Electron. 2017, 65, 1298–1305. [Google Scholar] [CrossRef]
- Huria, T.; Ceraolo, M.; Gazzarri, J.; Jackey, R. High fidelity electrical model with thermal dependence for characterization and simulation of high-power lithium battery cells. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012. [Google Scholar]
- Lai, X.; Wang, S.; Ma, S.; Xie, J.; Zheng, Y. Parameter sensitivity analysis and simplification of equivalent circuit model for the state of charge of Lithium-Ion batteries. Electrochim. Acta 2019, 330, 135239. [Google Scholar] [CrossRef]
- Shen, P.; Ouyang, M.; Lu, L.; Li, J.; Feng, X. The Co-estimation of State of Charge, State of Health, and State of Function for Lithium-Ion Batteries in Electric Vehicles. IEEE Trans. Veh. Technol. 2017, 67, 92–103. [Google Scholar] [CrossRef]
- Tran, M.-K.; Mevawala, A.; Panchal, S.; Raahemifar, K.; Fowler, M.; Fraser, R. Effect of integrating the hysteresis component to the equivalent circuit model of Lithium-ion battery for dynamic and non-dynamic applications. J. Energy Storage 2020, 32, 101785. [Google Scholar] [CrossRef]
- Miniguano, H.; Barrado, A.; Lazaro, A.; Zumel, P.; Fernandez, C. General Parameter Identification Procedure and Comparative Study of Li-Ion Battery Models. IEEE Trans. Veh. Technol. 2019, 69, 235–245. [Google Scholar] [CrossRef]
- Lai, X.; Gao, W.; Zheng, Y.; Ouyang, M.; Li, J.; Han, X.; Zhou, L. A comparative study of global optimization methods for parameter identification of different equivalent circuit models for Li-ion batteries. Electrochim. Acta 2018, 295, 1057–1066. [Google Scholar] [CrossRef]
- Zou, C.; Hu, X.; Dey, S.; Zhang, L.; Tang, X. Nonlinear Fractional-Order Estimator with Guaranteed Robustness and Stability for Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2017, 65, 5951–5961. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Yu, Q. Fractional-Order Model-Based Incremental Capacity Analysis for Degradation State Recognition of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2018, 66, 1576–1584. [Google Scholar] [CrossRef]
- Xiong, R.; Tian, J.; Shen, W.; Sun, F. A Novel Fractional Order Model for State of Charge Estimation in Lithium Ion Batteries. IEEE Trans. Veh. Technol. 2018, 68, 4130–4139. [Google Scholar] [CrossRef]
- Wei, Y.; Ling, L. State-of-Charge Estimation for Lithium-Ion Batteries Based on Temperature-Based Fractional-Order Model and Dual Fractional-Order Kalman Filter. IEEE Access 2022, 10, 37131–37148. [Google Scholar] [CrossRef]
- Wu, J.; Fang, C.; Jin, Z.; Zhang, L.; Xing, J. A multi-scale fractional-order dual unscented Kalman filter based parameter and state of charge joint estimation method of lithium-ion battery. J. Energy Storage 2022, 50, 104666. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, K.; Liu, K.; Lin, X.; Dey, S.; Onori, S. Advanced Fault Diagnosis for Lithium-Ion Battery Systems: A Review of Fault Mechanisms, Fault Features, and Diagnosis Procedures. IEEE Ind. Electron. Mag. 2020, 14, 65–91. [Google Scholar] [CrossRef]
- Hossain, M.; Haque, E.; Arif, M.T. Online Model Parameter and State of Charge Estimation of Li-ion Battery using Unscented Kalman Filter Considering Effects of Temperatures and C-rates. IEEE Trans. Energy Convers. 2022, 1. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.; Yu, Q.; He, H.; Sun, F. Critical Review on the Battery State of Charge Estimation Methods for Electric Vehicles. IEEE Access 2017, 6, 1832–1843. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Zhang, C. Online remaining energy prediction: A case study in embedded battery management system. Appl. Energy 2017, 194, 688–695. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Chen, Z. An adaptive remaining energy prediction approach for lithium-ion batteries in electric vehicles. J. Power Sources 2016, 305, 80–88. [Google Scholar] [CrossRef]
- Feng, F.; Teng, S.; Liu, K.; Xie, J.; Xie, Y.; Liu, B.; Li, K. Co-estimation of lithium-ion battery state of charge and state of temperature based on a hybrid electrochemical-thermal-neural-network model. J. Power Sources 2020, 455, 227935. [Google Scholar] [CrossRef]
- Cabrera-Castillo, E.; Niedermeier, F.; Jossen, A. Calculation of the state of safety (SOS) for lithium ion batteries. J. Power Sources 2016, 324, 509–520. [Google Scholar] [CrossRef] [Green Version]
- Rijanto, E.; Rozaqi, L.; Nugroho, A.; Kanarachos, S. RLS with optimum multiple adaptive forgetting factors for SoC and SoH estimation of Li-Ion battery. In Proceedings of the 2017 5th International Conference on Instrumentation, Control, and Automation (ICA), Yogyakarta, Indonesia, 9–11 August 2017; pp. 73–77. [Google Scholar] [CrossRef]
- Zhang, C.; Allafi, W.; Dinh, Q.; Ascencio, P.; Marco, J. Online estimation of battery equivalent circuit model parameters and state of charge using decoupled least squares technique. Energy 2018, 142, 678–688. [Google Scholar] [CrossRef]
- Natella, D.; Onori, S.; Vasca, F. A co-estimation framework for state of charge and parameters of Lithium-ion battery with robustness to aging and usage conditions. IEEE Trans. Ind. Electron. 2022, 1–10. [Google Scholar] [CrossRef]
- Ahwiadi, M.; Wang, W. An enhanced particle filter technology for battery system state estimation and RUL prediction. Measurement 2022, 191, 110817. [Google Scholar] [CrossRef]
- Chen, M.; Han, F.; Shi, L.; Feng, Y.; Xue, C.; Gao, W.; Xu, J. Sliding Mode Observer for State-of-Charge Estimation Using Hysteresis-Based Li-Ion Battery Model. Energies 2022, 15, 2658. [Google Scholar] [CrossRef]
- Xue, Z.; Zhang, Y.; Cheng, C.; Ma, G. Remaining useful life prediction of lithium-ion batteries with adaptive unscented kalman filter and optimized support vector regression. Neurocomputing 2019, 376, 95–102. [Google Scholar] [CrossRef]
- Meng, J.; Ricco, M.; Luo, G.; Swierczynski, M.; Stroe, D.-I.; Stroe, A.-I.; Teodorescu, R. An Overview and Comparison of Online Implementable SOC Estimation Methods for Lithium-Ion Battery. IEEE Trans. Ind. Appl. 2017, 54, 1583–1591. [Google Scholar] [CrossRef]
- Xuan, D.-J.; Shi, Z.; Chen, J.; Zhang, C.; Wang, Y.-X. Real-time estimation of state-of-charge in lithium-ion batteries using improved central difference transform method. J. Clean. Prod. 2019, 252, 119787. [Google Scholar] [CrossRef]
- Tian, Y.; Lai, R.; Li, X.; Xiang, L.; Tian, J. A combined method for state-of-charge estimation for lithium-ion batteries using a long short-term memory network and an adaptive cubature Kalman filter. Appl. Energy 2020, 265, 114789. [Google Scholar] [CrossRef]
- Sun, D.; Chen, X.; Ruan, Y. Research on modeling and state of charge estimation for lithium-ion battery. In Proceedings of the 2014 International Power Electronics and Application Conference and Exposition, Shanghai, China, 5–8 November 2014; pp. 1401–1406. [Google Scholar] [CrossRef]
- Cui, X.; Jing, Z.; Luo, M.; Guo, Y.; Qiao, H. A New Method for State of Charge Estimation of Lithium-Ion Batteries Using Square Root Cubature Kalman Filter. Energies 2018, 11, 209. [Google Scholar] [CrossRef] [Green Version]
- Qiu, X.; Wu, W.; Wang, S. Remaining useful life prediction of lithium-ion battery based on improved cuckoo search particle filter and a novel state of charge estimation method. J. Power Sources 2020, 450, 227700. [Google Scholar] [CrossRef]
- Linghu, J.; Kang, L.; Liu, M.; Luo, X.; Feng, Y.; Lu, C. Estimation for state-of-charge of lithium-ion battery based on an adaptive high-degree cubature Kalman filter. Energy 2019, 189, 116204. [Google Scholar] [CrossRef]
- Zarei, J.; Kowsari, E.; Razavi-Far, R. Induction Motors Fault Detection Using Square-Root Transformed Cubature Quadrature Kalman Filter. IEEE Trans. Energy Convers. 2018, 34, 870–877. [Google Scholar] [CrossRef]
- Savargaonkar, M.; Chehade, A. An Adaptive Deep Neural Network with Transfer Learning for State-of-Charge Estimations of Battery Cells. In Proceedings of the 2020 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 23–26 June 2020; pp. 598–602. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Chen, W.; Wang, L.-Y.; Qu, C. Online joint-prediction of multi-forward-step battery SOC using LSTM neural networks and multiple linear regression for real-world electric vehicles. J. Energy Storage 2020, 30, 101459. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Saad, M.H.; Ayob, A.; Uddin, M.N. Extreme Learning Machine Model for State-of-Charge Estimation of Lithium-Ion Battery Using Gravitational Search Algorithm. IEEE Trans. Ind. Appl. 2019, 55, 4225–4234. [Google Scholar] [CrossRef]
- Li, I.-H.; Wang, W.-Y.; Su, S.-F.; Lee, Y.-S. A Merged Fuzzy Neural Network and Its Applications in Battery State-of-Charge Estimation. IEEE Trans. Energy Convers. 2007, 22, 697–708. [Google Scholar] [CrossRef]
- Hannan, M.A.; How, D.N.T.; Lipu, M.S.H.; Ker, P.J.; Dong, Z.Y.; Mansur, M.; Blaabjerg, F. SOC Estimation of Li-ion Batteries With Learning Rate-Optimized Deep Fully Convolutional Network. IEEE Trans. Power Electron. 2020, 36, 7349–7353. [Google Scholar] [CrossRef]
- Ni, Z.; Yang, Y. A Combined Data-Model Method for State-of-Charge Estimation of Lithium-Ion Batteries. IEEE Trans. Instrum. Meas. 2021, 71, 1–11. [Google Scholar] [CrossRef]
- Chehade, A.A.; Hussein, A.A. A Multioutput Convolved Gaussian Process for Capacity Forecasting of Li-Ion Battery Cells. IEEE Trans. Power Electron. 2021, 37, 896–909. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussaion, A.; Ansari, S.S.; Rahman, S.A.; Saad, M.H.; Muttaqi, K. Real-time State of Charge Estimation of Lithium-ion Batteries Using Optimized Random Forest Regression Algorithm. IEEE Trans. Intell. Veh. 2022, 1. [Google Scholar] [CrossRef]
- Li, R.; Xu, S.; Li, S.; Zhou, Y.; Zhou, K.; Liu, X.; Yao, J. State of Charge Prediction Algorithm of Lithium-Ion Battery Based on PSO-SVR Cross Validation. IEEE Access 2020, 8, 10234–10242. [Google Scholar] [CrossRef]
- Bian, C.; Yang, S.; Miao, Q. Cross-Domain State-of-Charge Estimation of Li-Ion Batteries Based on Deep Transfer Neural Network with Multiscale Distribution Adaptation. IEEE Trans. Transp. Electrif. 2020, 7, 1260–1270. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Gong, J. A multi-model probability SOC fusion estimation approach using an improved adaptive unscented Kalman filter technique. Energy 2017, 141, 1402–1415. [Google Scholar] [CrossRef]
- Bi, Y.; Choe, S.-Y. An adaptive sigma-point Kalman filter with state equality constraints for online state-of-charge estimation of a Li(NiMnCo)O2/Carbon battery using a reduced-order electrochemical model. Appl. Energy 2019, 258, 113925. [Google Scholar] [CrossRef]
- Sangwan, V.; Kumar, R.; Rathore, A.K. State-of-charge estimation for li-ion battery using extended Kalman filter (EKF) and central difference Kalman filter (CDKF). In Proceedings of the 2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 1–5 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, S.; Li, W.; Miao, Q. State-of-charge estimation of lithium-ion batteries using LSTM and UKF. Energy 2020, 201, 117664. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Z.; Zhao, Z.; Wang, L.; Lai, C.S.; Wang, D. Robustness Evaluation of Extended and Unscented Kalman Filter for Battery State of Charge Estimation. IEEE Access 2018, 6, 27617–27628. [Google Scholar] [CrossRef]
- Peng, J.; Luo, J.; He, H.; Lu, B. An improved state of charge estimation method based on cubature Kalman filter for lithium-ion batteries. Appl. Energy 2019, 253, 113520. [Google Scholar] [CrossRef]
- Plett, G.L. Battery Management Systems, Volume II: Equivalent-Circuit Methods; Artech House: Norwood, MA, USA, 2015; Available online: https://books.google.com/books?id=1kSPCwAAQBAJ&pgis=1 (accessed on 26 September 2022).
- Shete, S.; Jog, P.; Kumawat, R.K.; Palwalia, D. Battery Management System for SOC Estimation of Lithium-Ion Battery in Electric Vehicle: A Review. In Proceedings of the 2021 6th IEEE International Conference on Recent Advances and Innovations in Engineering (ICRAIE), Kedah, Malaysia, 1–3 December 2021; Volume 6, pp. 1–4. [Google Scholar] [CrossRef]
- Fang, L.; Li, J.; Peng, B. Online Estimation and Error Analysis of both SOC and SOH of Lithium-ion Battery based on DEKF Method. Energy Procedia 2019, 158, 3008–3013. [Google Scholar] [CrossRef]
- How, D.N.T.; Hannan, M.A.; Lipu, M.S.H.; Sahari, K.S.M.; Ker, P.J.; Muttaqi, K.M. State-of-Charge Estimation of Li-Ion Battery in Electric Vehicles: A Deep Neural Network Approach. IEEE Trans. Ind. Appl. 2020, 56, 5565–5574. [Google Scholar] [CrossRef]
- Sahinoglu, G.O.; Pajovic, M.; Sahinoglu, Z.; Wang, Y.; Orlik, P.V.; Wada, T. Battery State-of-Charge Estimation Based on Regular/Recurrent Gaussian Process Regression. IEEE Trans. Ind. Electron. 2017, 65, 4311–4321. [Google Scholar] [CrossRef]
- Zhao, R.; Kollmeyer, P.J.; Lorenz, R.D.; Jahns, T.M. A Compact Methodology Via a Recurrent Neural Network for Accurate Equivalent Circuit Type Modeling of Lithium-Ion Batteries. IEEE Trans. Ind. Appl. 2018, 55, 1922–1931. [Google Scholar] [CrossRef]
- Liu, K.; Shang, Y.; Ouyang, Q.; Widanage, W.D. A Data-Driven Approach with Uncertainty Quantification for Predicting Future Capacities and Remaining Useful Life of Lithium-ion Battery. IEEE Trans. Ind. Electron. 2020, 68, 3170–3180. [Google Scholar] [CrossRef]
- Fasahat, M.; Manthouri, M. State of charge estimation of lithium-ion batteries using hybrid autoencoder and Long Short Term Memory neural networks. J. Power Sources 2020, 469, 228375. [Google Scholar] [CrossRef]
- Hu, X.; Che, Y.; Lin, X.; Onori, S. Battery Health Prediction Using Fusion-Based Feature Selection and Machine Learning. IEEE Trans. Transp. Electrif. 2020, 7, 382–398. [Google Scholar] [CrossRef]
- Lyu, Z.; Gao, R.; Chen, L. Li-Ion Battery State of Health Estimation and Remaining Useful Life Prediction Through a Model-Data-Fusion Method. IEEE Trans. Power Electron. 2020, 36, 6228–6240. [Google Scholar] [CrossRef]
- Charkhgard, M.; Farrokhi, M. State-of-Charge Estimation for Lithium-Ion Batteries Using Neural Networks and EKF. IEEE Trans. Ind. Electron. 2010, 57, 4178–4187. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.E.; Yang, Y. Advanced Machine Learning Approach for Lithium-Ion Battery State Estimation in Electric Vehicles. IEEE Trans. Transp. Electrif. 2015, 2, 140–149. [Google Scholar] [CrossRef]
- Chen, J.; Ouyang, Q.; Xu, C.; Su, H. Neural Network-Based State of Charge Observer Design for Lithium-Ion Batteries. IEEE Trans. Control Syst. Technol. 2017, 26, 313–320. [Google Scholar] [CrossRef]
- Li, W.; Sengupta, N.; Dechent, P.; Howey, D.; Annaswamy, A.; Sauer, D.U. Online capacity estimation of lithium-ion batteries with deep long short-term memory networks. J. Power Sources 2020, 482, 228863. [Google Scholar] [CrossRef]
- Bian, C.; He, H.; Yang, S. Stacked bidirectional long short-term memory networks for state-of-charge estimation of lithium-ion batteries. Energy 2019, 191, 116538. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A.; Kollmeyer, P. Long Short-Term Memory Networks for Accurate State-of-Charge Estimation of Li-ion Batteries. IEEE Trans. Ind. Electron. 2018, 65, 6730–6739. [Google Scholar] [CrossRef]
- Bian, C.; He, H.; Yang, S.; Huang, T. State-of-charge sequence estimation of lithium-ion battery based on bidirectional long short-term memory encoder-decoder architecture. J. Power Sources 2019, 449, 227558. [Google Scholar] [CrossRef]
- Shu, X.; Li, G.; Zhang, Y.; Shen, S.; Chen, Z.; Liu, Y. Stage of Charge Estimation of Lithium-Ion Battery Packs Based on Improved Cubature Kalman Filter With Long Short-Term Memory Model. IEEE Trans. Transp. Electrif. 2020, 7, 1271–1284. [Google Scholar] [CrossRef]
- She, C.; Wang, Z.; Sun, F.; Liu, P.; Zhang, L. Battery Aging Assessment for Real-World Electric Buses Based on Incremental Capacity Analysis and Radial Basis Function Neural Network. IEEE Trans. Ind. Informatics 2019, 16, 3345–3354. [Google Scholar] [CrossRef]
- Anton, J.C.A.; Nieto, P.J.G.; Viejo, C.B.; Vilan, J.A.V. Support Vector Machines Used to Estimate the Battery State of Charge. IEEE Trans. Power Electron. 2013, 28, 5919–5926. [Google Scholar] [CrossRef]
- Feng, F.; Hu, X.; Liu, J.; Lin, X.; Liu, B. A review of equalization strategies for series battery packs: Variables, objectives, and algorithms. Renew. Sustain. Energy Rev. 2019, 116, 109464. [Google Scholar] [CrossRef]
- Ouyang, Q.; Han, W.; Zou, C.; Xu, G.; Wang, Z. Cell Balancing Control For Lithium-Ion Battery Packs: A Hierarchical Optimal Approach. IEEE Trans. Ind. Inform. 2019, 16, 5065–5075. [Google Scholar] [CrossRef]
- Lee, Y.-S.; Cheng, M.-W. Intelligent Control Battery Equalization for Series Connected Lithium-Ion Battery Strings. IEEE Trans. Ind. Electron. 2005, 52, 1297–1307. [Google Scholar] [CrossRef]
- Song, C.; Shao, Y.; Song, S.; Chang, C.; Zhou, F.; Peng, S.; Xiao, F. Energy Management of Parallel-Connected Cells in Electric Vehicles Based on Fuzzy Logic Control. Energies 2017, 10, 404. [Google Scholar] [CrossRef]
- McCurlie, L.; Preindl, M.; Emadi, A. Fast Model Predictive Control for Redistributive Lithium-Ion Battery Balancing. IEEE Trans. Ind. Electron. 2016, 64, 1350–1357. [Google Scholar] [CrossRef]
- Xue, Q.; Li, G.; Zhang, Y.; Shen, S.; Chen, Z.; Liu, Y. Fault diagnosis and abnormality detection of lithium-ion battery packs based on statistical distribution. J. Power Sources 2020, 482, 228964. [Google Scholar] [CrossRef]
- Schmid, M.; Gebauer, E.; Hanzl, C.; Endisch, C. Active Model-Based Fault Diagnosis in Reconfigurable Battery Systems. IEEE Trans. Power Electron. 2020, 36, 2584–2597. [Google Scholar] [CrossRef]
- Xu, Y.; Ge, X.; Shen, W.; Yang, R. A Soft Short-Circuit Diagnosis Method for Lithium-Ion Battery Packs in Electric Vehicles. IEEE Trans. Power Electron. 2022, 37, 8572–8581. [Google Scholar] [CrossRef]
- Yao, L.; Xiao, Y.; Gong, X.; Hou, J.; Chen, X. A novel intelligent method for fault diagnosis of electric vehicle battery system based on wavelet neural network. J. Power Sources 2020, 453, 227870. [Google Scholar] [CrossRef]
- Shang, Y.; Lu, G.; Kang, Y.; Zhou, Z.; Duan, B.; Zhang, C. A multi-fault diagnosis method based on modified Sample Entropy for lithium-ion battery strings. J. Power Sources 2020, 446, 227275. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, Y.; Deng, J.; Xu, H.; Wen, H. Feature Engineering and Artificial Intelligence-Supported Approaches Used for Electric Powertrain Fault Diagnosis: A Review. IEEE Access 2022, 10, 29069–29088. [Google Scholar] [CrossRef]
- Gao, W.; Zheng, Y.; Ouyang, M.; Li, J.; Lai, X.; Hu, X. Micro-short-circuit diagnosis for series-connected lithium-ion battery packs using mean-difference model. IEEE Trans. Ind. Electron. 2019, 66, 2132–2142. [Google Scholar] [CrossRef]
- Yao, L.; Fang, Z.; Xiao, Y.; Hou, J.; Fu, Z. An Intelligent Fault Diagnosis Method for Lithium Battery Systems Based on Grid Search Support Vector Machine. Energy 2021, 214, 118866. [Google Scholar] [CrossRef]
- Xiong, R.; Yu, Q.; Shen, W.; Lin, C.; Sun, F. A Sensor Fault Diagnosis Method for a Lithium-Ion Battery Pack in Electric Vehicles. IEEE Trans. Power. Electron. 2019, 34, 9709–9718. [Google Scholar] [CrossRef]
- Sidhu, A.; Izadian, A.; Anwar, S. Adaptive nonlinear model-based fault diagnosis of li-ion batteries. IEEE Trans. Ind. Electron. 2015, 62, 1002–1011. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Liu, P.; Wang, Z.; Zhang, L.; Hong, J. Fault and defect diagnosis of battery for electric vehicles based on big data analysis methods. Appl. Energy 2017, 207, 354–362. [Google Scholar] [CrossRef]
- Lin, T.; Chen, Z.; Zheng, C.; Huang, D.; Zhou, S. Fault diagnosis of lithium-ion battery pack based on hybrid system and dual extended Kalman filter algorithm. IEEE Trans. Transp. Electrif. 2020, 7782. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Z.; Liu, P.; Wang, Z.; Zhang, L. Battery Fault Diagnosis for Electric Vehicles Based on Voltage Abnormality by Combining the Long Short-Term Memory Neural Network and the Equivalent Circuit Model. IEEE Trans. Power Electron. 2021, 36, 1303–1315. [Google Scholar] [CrossRef]
- Xia, B.; Shang, Y.; Nguyen, T.; Mi, C. A correlation based fault detection method for short circuits in battery packs. J. Power Sources 2017, 337, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Ojo, O.; Lang, H.; Kim, Y.; Hu, X.; Mu, B.; Lin, X. A Neural Network-Based Method for Thermal Fault Detection in Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2020, 46, 1. [Google Scholar] [CrossRef]

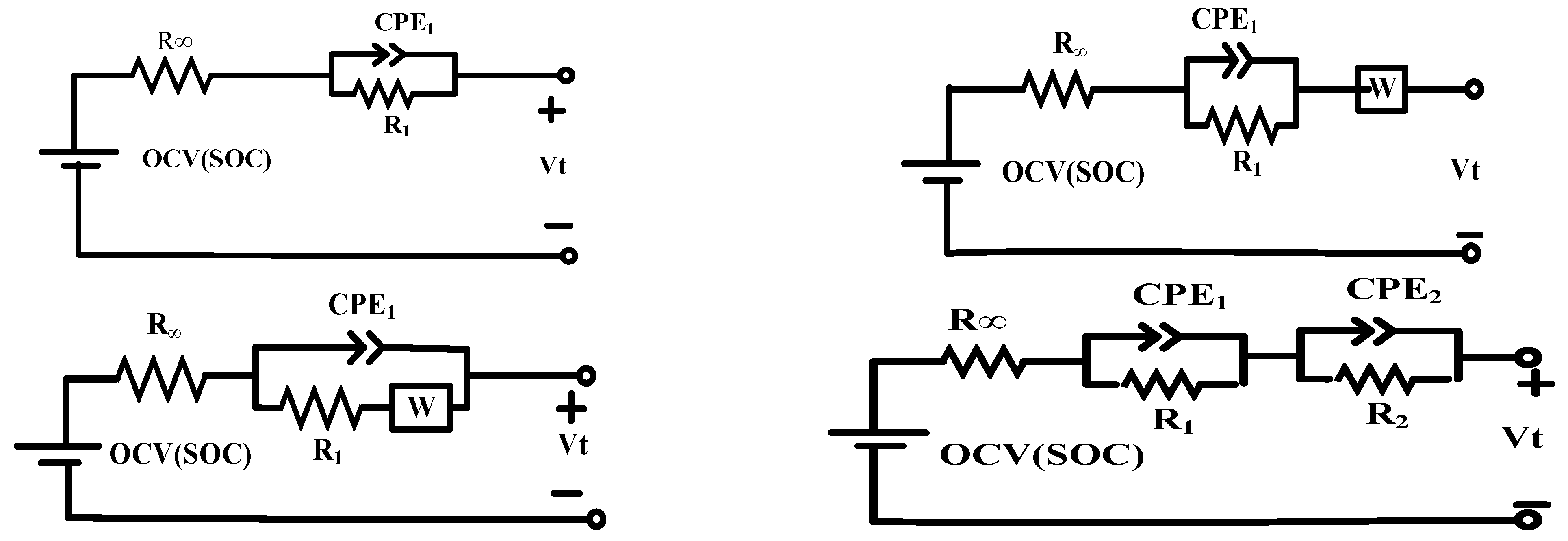

| Charging Algorithm | Characteristics of Algorithm | Variants of the Charging Algorithm | Comparison |
|---|---|---|---|
| Simple charging method | This charging protocol includes controlled constant current and voltage to avoid a sharp increase in the battery’s temperature and voltage. Trickle charging is a low-current charging method when the battery is in a deep discharge state. It shifts to CC mode until voltage reaches a threshold value. | Constant current charging (CC) Trickle charging Standard CC charging Constant voltage charging (CV) | Simple, cost-effective, but not currently popular compared to other charging protocols. |
| Constant current–constant voltage (CC–CV) [23] | CC is applied to charge the battery until the predefined voltage level after switching to the CV mode until the charge current reaches a minimum threshold. | Double-loop control charger (DL-CC/CV) [24] Boost charger (BC-CC/CV) [25] Fuzzy logic (FL-CC/CV) [26] Gray-predicted (GP-CC/CV) Phased locked loop (PLL-CC/CV) | Most popular, simple, and inexpensive regarding other charging protocols. |
| Duty-varied voltage pulse charger (DVVPC) [27] | The duty-varied voltage pulse charger can notice the appropriate pulse-charge duty and supply the battery’s required pulse charge. | DFVPCS (duty-fixed voltage pulse charger) | The charging speed is improved compared to CC–CV. |
| Multistage constant current (MSCC) [24,28,29] | This protocol comprises variable current magnitude with two or more constant current stages where shifting conditions are based on upper cutoff voltage or SOC interval. | Optimal five-stage charging protocol using consecutive orthogonal arrays [25]. Optimal multistage charging pattern using PSO-based fuzzy controlled [26]. Optimal charging pattern for MSCC [28]. MSCC charging pattern is based on the integration of the Taguchi method and SOC estimation [30]. The ant colony algorithm is been used for implementing the MSCC-based optimal charging method [31]. | MSSC protocol can decrease the charging time and enhance the charging efficiency. Lower charging time and capacity fade compared to CC–CV. |
| Boost charging [32] | This protocol is used for fast charging in which a fully discharged cell is charged with a very high current for a short period without degradation. | CVCCCV | It is a rapid charging protocol that can charge one-third of battery-rated capacity in 5 min compared to other protocols [32]. |
| Pulse charging [33,34] | Noncontinuous CC and CV can be defined as pulse charging. | Constant current + pulse charging (CCPC) [33] Constant-current and constant-frequency pulse charging (CCCF-PC) Constant-current and variable-frequency pulse charging (CCVF-PC) Variable-current and constant-frequency pulse charging (VCCF-PC) Variable-frequency variable-current pulse charging Pulse charge with constant voltage (CVPC) [27] | Cost-effective and straightforward with respect to other charging schemes. |
| Variable current profile [35] | Noncontinuous CC and CV can be defined as pulse charging. | Constant current + pulse charging (CCPC) [33] Constant-current and constant-frequency pulse charging (CCCF-PC) Constant-current and variable-frequency pulse charging (CCVF-PC) Variable-current and constant-frequency pulse charging (VCCF-PC) Variable-frequency variable-current pulse charging Pulse charge with constant voltage (CVPC) [27] | Slower aging effect compared to CC–CV [36]. |
| Sinusoidal ripple current [37] | This charging protocol superimposes the low-frequency sinusoidal current on a DC current. | SRC + CP SRC + CT | The cycle life, temperature rising, charging time, and charging efficiency are better than CC–CV [37]. |
| Constant current–constant voltage with negative pulse (CC–CV-NP) [38,39] | This charging protocol improves the low-frequency sinusoidal current at the time of CC to delay the polarization that enhances the battery charging capacity and slows down the aging. | MCC–CVNP | CC–CVNP charging protocol with small amplitude and a minimum number of negative pulses is more efficient than other protocols in lowering the diffusion time constant and concentration polarization resistance. This property increases the charging efficiency and longevity [38]. |
| Constant-power–constant-voltage (CP–CV) [24,40] | In the CP–CV charging protocol, the current starts at a high rate and steadily decreases with the charging time. In the meantime, a CP co-relation exists between the current and voltage. CV charging is followed by voltage reached to its maximum cutoff until the current decreases to a predefined value. | CP | At a low charging rate, capacity fade is in the order of CP > MCC > CC. At a high charging rate, capacity fade is in order of MCC > CC > CP [24]. |
| Constant temperature–constant voltage (CT–CV) [41,42] | The optimal CT–CV charging protocol controls the charging current magnitude corresponding to the temperature of the cell. It is a closed-loop technique that modulates the charging current concerning the battery’s temperature. | CT + SRC CT + PC | CT–CV is a fast-charging and low-temperature rise method compared to CC–CV. |
| Models | Equation and Description | Parameters/Optimization | Applications |
|---|---|---|---|
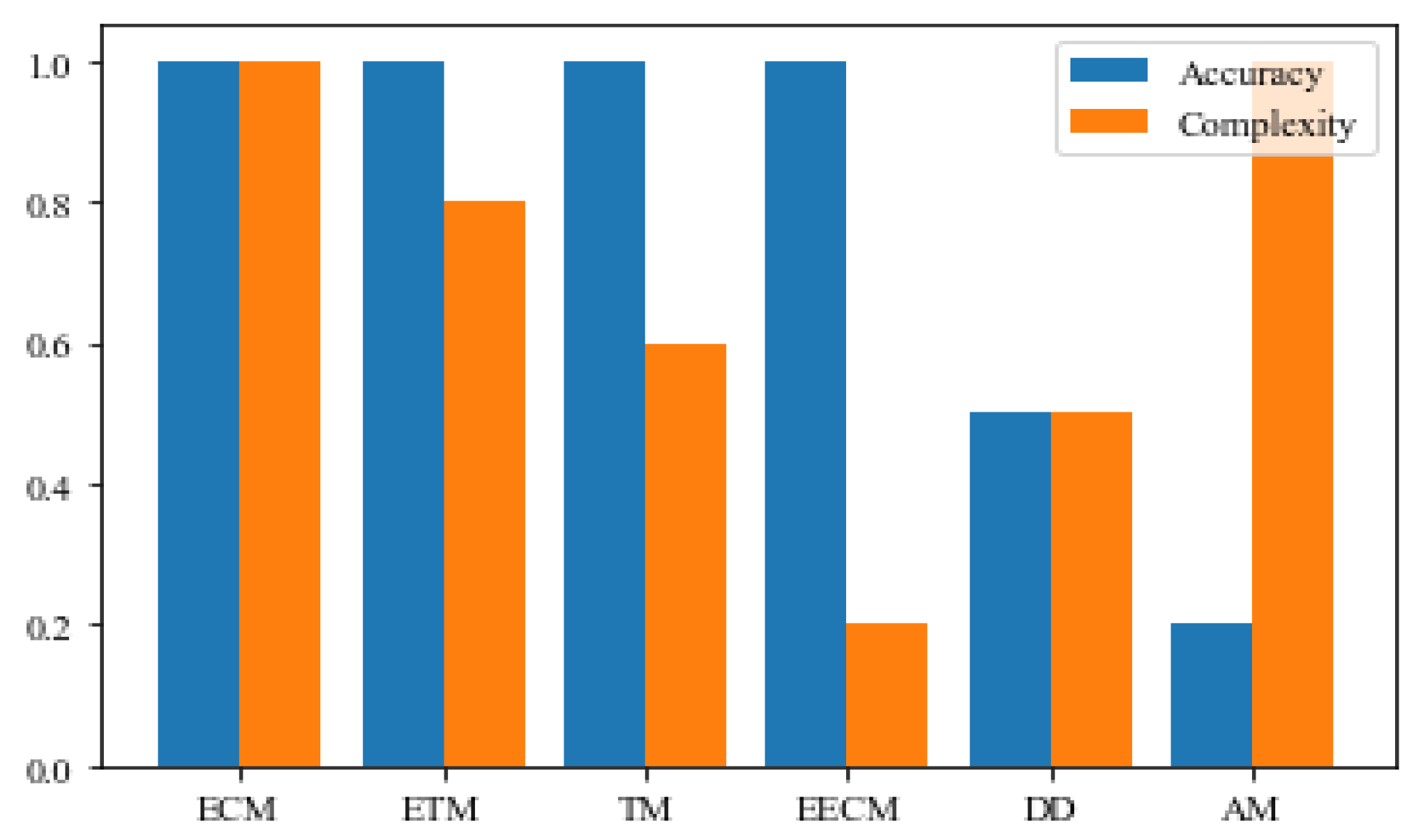
| 1RC | , , , = voltage of RC network, = = time constant of RC network | 4/FMIN | This model is the perfect selection for NMC chemistry. |
| 1RCH | = voltage of hysteresis network | FMIN | 1RCH-based online SOC, SOH estimation, which is applicable in EVs and PHEVs. Further enhancement can be achieved with SOP and SOF analysis. Thermal and aging effects can also be integrated with this model. This model is the best fit for LFP cells. |
| 2RC | = voltage of 2RC network, = = time constant of 2RC | 6/PSO | The 2RC model demonstrates a balance between accuracy and complexity, making it the preferred choice for EV applications. |
| 2RCH | 8/PSO | The 2RCH model does not advance its accuracy but reduces its reliability in the case of parameter estimation; thus, it is not a correct choice for EV application. | |
| 3RC | = voltage of 3RC network, = time constant of 3RC | 8/FA | Not appropriate for online identification of parameters and states |
| 3RCH | 10/FA | Not appropriate for online identification of parameters and states. | |
| 4RC | = voltage of 4RC network, = = time constant of 4RC | 10/FA | Not suitable for online BMS applications for EVs. |
| 4RCH | 12/FA | Not suitable for online BMS applications for EVs. |
| States | Equations | Challenges in Automotive Applications | Methods |
|---|---|---|---|
| State of charge (SOC) [65] | The main challenge of SOC estimation in automotive applications is the great amount of current produced in these types of applications, leading to stimulating complex dynamics that are difficult to capture using EECM. | 1. Direct calculation method 2. Coulomb-counting methods 3. OCV–SOC relationship 4. Model-based method 5. Data-driven method | |
| State of health (SOH) [66] | The major challenge related to the online estimation of SOH by measuring current, voltage, and temperature measurement is the complexity, which means it is very hard to predict the battery aging growth. Currently, no sensor is available to directly measure capacity and internal resistance. | 1. Experimental method 2. Model-based estimation 3. Incremental capacity analysis (ICA) and differential voltage analysis (DVA) method 4. Empirical models 5. Data-driven method 6. Waveform-based method. | |
| State of power (SOP) [7] | , | The SOP prediction depends on current, voltage, temperature, and SOC, and these parameters are still not optimized. The SOP also depends on battery aging, which is difficult to predict online. | 1. Characteristic map (CM)-based method 2. Model-based method 3. Multiple constant estimation approach 4. Data-driven approach |
| State of function (SOF) [53] | The main challenge in SOF estimation is the deficiency of an accurate model to relate SOC, SOH, SOF, and temperature. | 1. Model-based method 2. Data-driven approach | |
| State of energy (SOE) [67,68] | The power integration is used for estimating SOE, which enhances the computational complexity. In another way, its open-loop nature results in accumulated errors leading to measurement flaws, uncertain noise, and restricted sensor resolution. | 1. Direct estimate 2. Power integration approach 3. Characteristic mapping approach 4. Adaptive algorithm estimation 5. Machine learning method | |
| State of temperature (SOT) [69] | Online estimation is quite difficult due to computational efficiency. | 1. Impedance–temperature detection (ITD)-based method 2. Model-based method 3. Integrated method | |
| State of safety (SOS) [70] | Practical online estimation is not possible for SOS. The fidelity of SOS is not guaranteed. | 1. Qualitative estimation 2. Quantitative estimation |
| Methods | Strongpoint | Drawback or Error-Source | Applications | Predicted Error | |
|---|---|---|---|---|---|
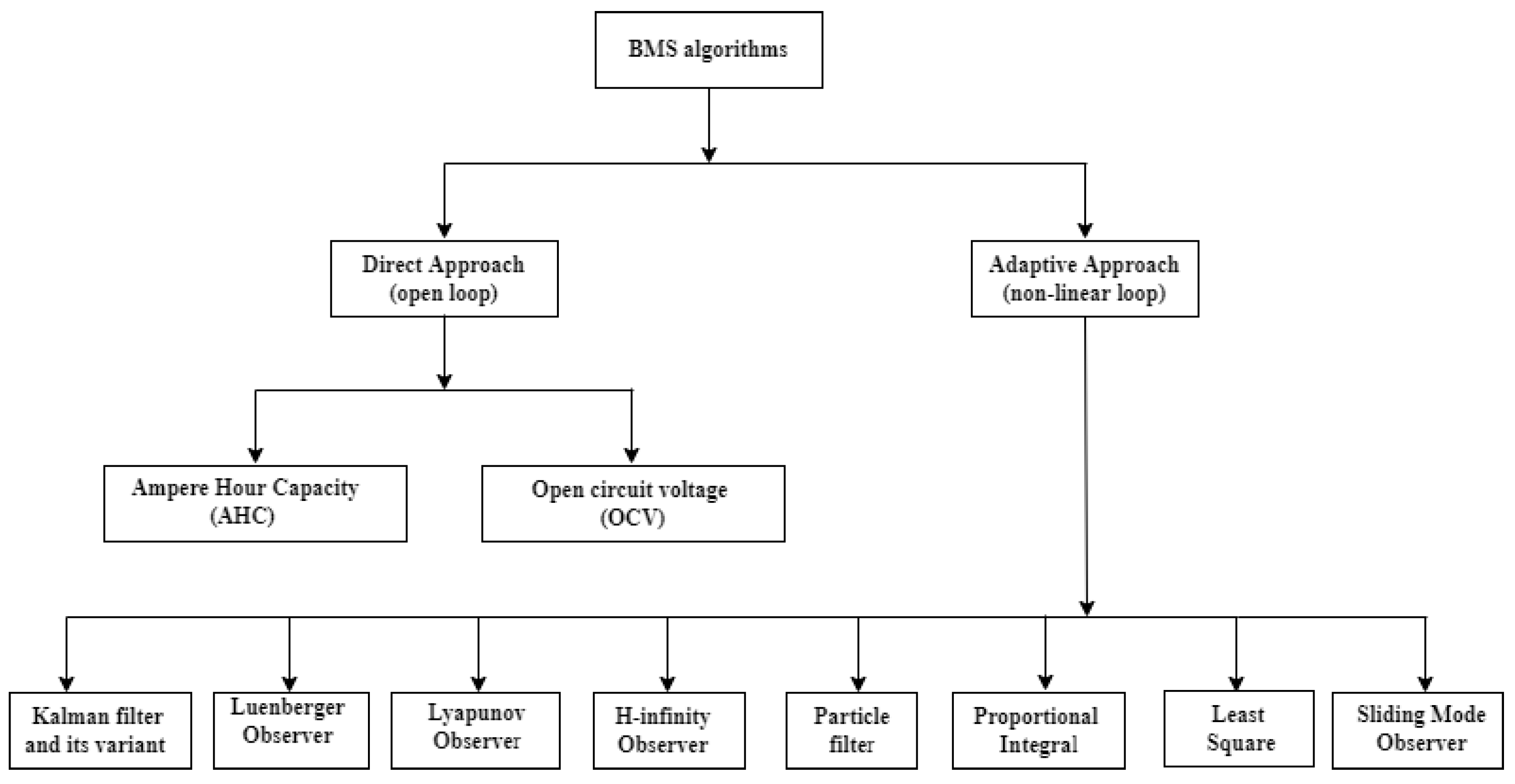
| Direct approach (open loop) | AHC [76,77] | AHC requires the information of current battery capacity It is a simple current-based estimation method (charging/discharging) and integrated over time Low-power computation Cheap sensor for current measurement Can be combined with other techniques | Open-loop and uncertain initial SOC (cumulative effect) Sensitive to the current sensor | AHC collaboration with adaptive algorithms is a satisfactory choice for HEVs | Enhanced AHC method for SOC and SOH estimation and estimation error reduced to 1.08% SOC estimation error under 6.5% using online EKF-AH |
| OCV [73,78] | Secure and capable method for BEVs and HEVs Relationship between OCV-SOH determined by observing charging curves at the altered lifespan of Li-ion battery to predict model parameters and capacity fade to evaluate SOH [57] Simple and easy to implement, look-up table-based method | Not suitable for battery chemistry having flat OCV–SOC curves Open loop Quickly responds to the voltage-sensor precision | AHC corrected by OCV and state estimation is a satisfactory choice for BEVs and PHEVs | Integration of (AHC + OCV + KF) precisely estimates SOC compared with the OCV estimation method with an error of ±1.76% | |
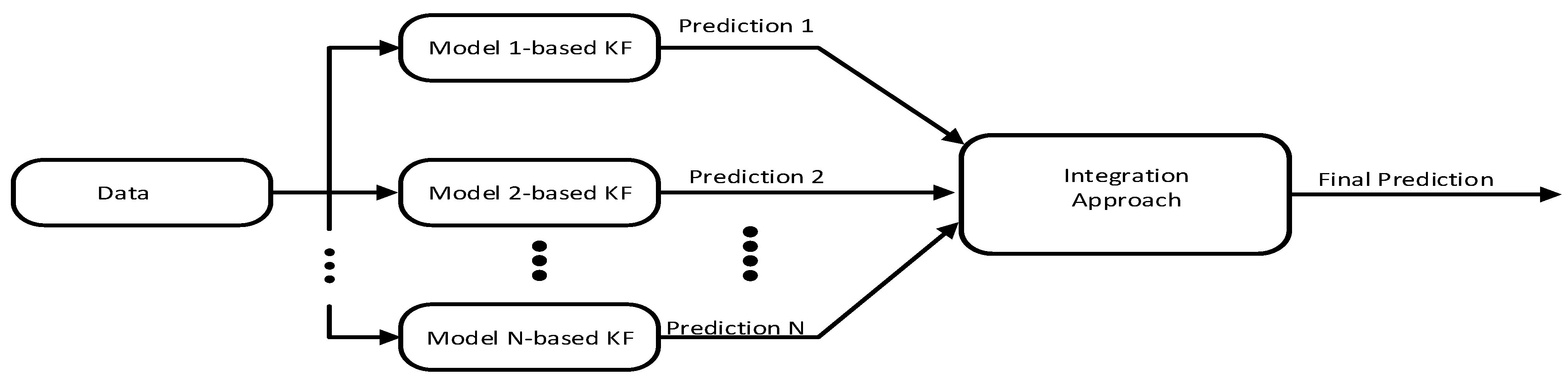
| Adaptive approach (nonlinear, -loop) | KF and its variants [79,80,81] | The KF requires models and measurement noise These algorithms help reduce measurement noise effects and predict the states (SOC and SOH) that cannot be estimated straightforwardly It is closed-loop, accurate, and error-bounds | The KF is dependent upon model accuracy It is a highly complex and expansive computation Several variables need to be controlled | All types of EVs | DEKF (±5%) AEKF (MAE (0.02)) DEKF ((±0.01) |
| Luenberger observer [82,83] | Faster than KF and suitable for all chemistry Does not depend on model and measurement noise Neither noise is Gaussian | These observers have high computational complexity They require a robust controller. PF acquires high computational complexity (approximately thousandfold) in comparison with EKF/SPKF | All types of EVs | 1.25% | |
| Lyapunov observer [84] | Better accuracy, convergence time, robustness, chattering, and computational complexity | 0.59% | |||
| H-infinity [85,86] Observer | These observers can enhance the feature of the feedback gain, leading to accurate SOC estimation. | 1% | |||
| Sliding-mode observer [87,88] | Upgrade tracking control for stability and robustness | ≤±3% | |||
| Particle filter (PF) [89,90] | Robust and low computation time | ≤1% | |||
| Proportional integral (PI) [91] | More robust with model uncertainty | ≤2% | |||
| Least square [92,93,94] | Takes less execution time and lower algorithm complexity | 0.05 |
| A Variant of the Kalman Filter | Estimation Accuracy | Estimation Error MAE (%) | Convergence Speed | Complexity | State Estimation | Computational Cost |
|---|---|---|---|---|---|---|
| EKF [99] | Strong robustness against current noise | 0.01 | UKF convergence rate is better in the case of unknown initial SOC | Medium | SOC | Medium |
| UKF [98] | Superior to EKF in terms of robustness | 0.63 | Less than EKF due to state vector sigma point (2n + 1). | The implementation is not simpler due to more tuning parameters, but filter robustness is high. | SOC | 4 times higher than EKF |
| AEKF [95] | Better accuracy and higher robustness than EKF | 0.54 | Improved due to outstanding OCV–SOC relationship | High | OCV and SOC | High |
| AUKF [76] | Better than UKF and AEKF | 0.038 | Better than UKF and AEKF | High | RUL | High |
| CDKF [77] | Better in estimation accuracy, filter robustness, and implementation | 0.0096 | More than EKF | It is simpler in implementation than UKF due to only one tuning parameter | SOC | High |
| SR-CDKF [78] | Better accuracy than EKF, UKF, and CDKF Robust to current noise | 2% | Less than EKF and UKF | Non-negative covariance and reduced computational complexity | SOC | High |
| SR-UKF [77] | Strongly nonlinear and more accurate than EKF, UKF, and CDKF | 0.0022 | More than EKF, UKF, and CDKF | High | SOC | High |
| Asymmetric ASR-SPKF [96] | More accurate than AEKF | 2 | Faster convergence speed | Less complex than AEKF and ASPKF | SOC | Less than ASPKF |
| SP-UKF | Like true value | 1 | Moderate convergence speed | More complex than SP-UKF | SOC, SOH, SOP, and SOE | Computationally intensive |
| SP-CDKF | Superior performance to EKF and SP-UKF | 1 | Faster convergence speed | Only one control parameter rather than three control parameters of SP-UKF | SOC and SOE | Computationally intensive |
| ACKF [79] | Good robustness | 4 | Good convergence capacity | Better than CKF | SOC | Better than CKF |
| CKF [100] | More robust than EKF and UKF | 1 | Faster than UKF but slower than EKF | CKF with the Thevenin model is a better option for embedding in microcontrollers | SOC | 4 times higher than EKF |
| ST-CKF [80] | Robust | 1.8 | Moderate convergence speed | High | SOC | High |
| SR-CKF [81] | Higher accuracy and robustness than EKF, UKF, and CKF | 0.00015 | Higher convergence rate than EKF, UKF, and CKF | Less | SOC | More than EKF, UKF, and CKF |
| BS (backward smoothing)-SRCKF [82] | Improved accuracy | 0.55 | Improved convergence speed, faster than UKF and SRCKF | High than SRCKF but less than UKF | SOC, SOH, and RUL | High |
| QKF, Szego quadrature (SQKF) [83] | High accuracy, overcome the impact of large measurement and initial error | 0.892 | Convergence to 4% in 672 steps | High | SOC | High |
| Square-root transformed cubature quadrature Kalman filter (SR-TCQKF) [84] | More stable and accurate than CQKF | 1 | Improved convergence speed due to square root KF | Less, better numerical stability | SOC | Less |
| Sl No. | Model | MAE | MSE | RMSE | R2 | RMSLE | MAPE | TT (s) |
|---|---|---|---|---|---|---|---|---|
| 1 | Extra trees regressor | 0.0026 | 0.0000 | 0.0052 | 0.9997 | 0.0037 | −0.0260 | 0.1545 |
| 2 | Extreme gradient boosting | 0.0040 | 0.0000 | 0.0063 | 0.9996 | 0.0045 | −0.0330 | 0.2134 |
| 3 | Random forest | 0.0034 | 0.0000 | 0.0066 | 0.9995 | 0.0047 | −0.0312 | 0.2003 |
| 4 | Light gradient boosting machine | 0.0050 | 0.0001 | 0.0076 | 0.9994 | 0.0055 | −0.0419 | 0.1213 |
| 5 | Decision tree | 0.0034 | 0.0001 | 0.0080 | 0.9993 | 0.0057 | −0.0196 | 0.0104 |
| 6 | Gradient boosting regressor | 0.0034 | 0.0001 | 0.0080 | 0.9993 | 0.0057 | −0.0196 | 0.0104 |
| 7 | Adaboost regressor | 0.0327 | 0.0016 | 0.0398 | 0.9835 | 0.0261 | −0.4166 | 0.1861 |
| 8 | Ridge regression | 0.0272 | 0.0016 | 0.0400 | 0.9831 | 0.0325 | −0.8945 | 0.0073 |
| 9 | Least angle regression | 0.0267 | 0.0016 | 0.0400 | 0.9831 | 0.0326 | −0.9191 | 0.0059 |
| 10 | Bayesian ridge | 0.0267 | 0.0016 | 0.0400 | 0.9831 | 0.0326 | −0.9190 | 0.0087 |
| 11 | Linear regression | 0.0267 | 0.0016 | 0.0400 | 0.9831 | 0.0326 | −0.9191 | 0.0043 |
| 12 | Random sample consensus | 0.0257 | 0.0016 | 0.0401 | 0.9830 | 0.0329 | −0.9936 | 0.1339 |
| 13 | K neighbors regressor | 0.0133 | 0.0017 | 0.0402 | 0.9819 | 0.0285 | −0.0779 | 0.0072 |
| 14 | Huber regressor | 0.0251 | 0.0017 | 0.0414 | 0.9819 | 0.0341 | −1.1640 | 0.0387 |
| 15 | Theilsen regressor | 0.0255 | 0.0018 | 0.0417 | 0.9816 | 0.0341 | −1.1423 | 1.1475 |
| 16 | Orthogonal matching pursuit | 0.0472 | 0.0051 | 0.0708 | 0.9476 | 0.0512 | −0.7833 | 0.0077 |
| 17 | Passive aggressive regressor | 0.0645 | 0.0053 | 0.0729 | 0.9448 | 0.0512 | −0.4119 | 0.0076 |
| 18 | Support vector machine | 0.2675 | 0.0945 | 0.3074 | 0.0177 | 0.2126 | −3.4891 | 0.2531 |
| 19 | Lasso regression | 0.2699 | 0.0959 | 0.3097 | 0.0032 | 0.2151 | −3.7653 | 0.0094 |
| 20 | Elastic net | 0.2699 | 0.0959 | 0.3097 | 0.0032 | 0.2151 | −3.7638 | 0.0068 |
| 21 | Lasso least angle regression | 0.2704 | 0.0964 | 0.3103 | −0.001 | 0.2156 | −3.7954 | 0.0062 |
| Ref. | Data-Driven Method | Battery Testing | RMSE/Error Rate (%) | Comparison | Online Parameters | Technical Comment |
|---|---|---|---|---|---|---|
| [94] | Deep transfer neural network + MDA (multiscale distribution adaptation) | BJDST, USO6, and FUDS | 1.04 | RNN, GRU, and LSTM | SOC | More robust than other methods |
| [104] | Deep neural network | DST, FUDS, BJDST, and US06 | 0.08 | LSTM and CNN-GRU | SOC | Reduced error rate, Enhanced performance of SOC estimation |
| [105] | Recurrent Gaussian process regression (RGPR) | FUDS and US06 | 0.14 | SVM, RVM, and NN | SOC | High accuracy, identification important input features |
| [106] | RNN (recurrent neural network) with gated recurrent unit | HWFET, LA92, UDDS, and US06 | 0.029 | RNN | SOE | Energy prediction, range estimation |
| [107] | LSTM + GPR | Cycle test dataset | 0.0032 | GPR, LSTM, GPR + EMD, and LSTM + EMD (empirical mode decomposition) | RUL | Good adaptability, reliable, high certainty |
| [108] | Autoencoder + LSTM | DST and FUDS | 0.72%, 0.90%, 1.30% | LSTM and RBFNN | SOC | Autoencoder is useful for optimum feature selection |
| [88] | Fuzzy neural network + form genetic algorithm | Charging/discharging | BPNN | SOC | High convergence rate | |
| [87] | Extreme learning machine (ELM)–GSA (gravitational search algorithm) | DST, FUDS, and USO6 | 1.1%, 1.4%, 1.8% | Back propagation neural network (BPNN) and radial basis function neural network | SOC | Greater accuracy, low error |
| [109] | Feature selection + ML | Calce + NASA dataset | ELM and SVR | SOH | Accuracy, computational efficiency | |
| [110] | Model + DNN metabolic gray model, multioutput Gaussian process regression | NEDS + UDDS + JP1015 | ±2 | GPR and SVR | SOH + RUL | Great accuracy and robustness, closed-loop control, dynamic model |
| [111] | NN + EKF | Battery charging | 3% | NN | SOC | Good prediction of SOC and fast convergence due to EKF RBF type NN taken to decide a suitable model for EKF |
| [112] | Fuzzy C-means | FUDS | 1.68 | SOC | The better initial value for optimization | |
| [98] | LSTM + UKF | DST, US06, and FUDS | 0.93 | LSTM | SOC | Model-free, no need for OCV-SOC look-up table |
| [113] | NN | Charge/discharge | 2.36% | EKF | SOC | Fast convergence speed, higher precision |
| [114] | Deep LSTM | Charge/discharge test | 0.76% | LSTM-RNN | Capacity | DLSTM worked well with timeseries data Computationally fast |
| [115] | Bidirectional LSTM encoder–decoder | UDDS, LA92, US06, and HWFET | 1.07% | LSTM-RNN and BSLTSM | SOC | Encoder and decoder architecture BSLSDM-ED can exhibit long-term dependencies from both past and future directions that estimate the accuracy of SOC |
| [116] | LSTM | HWFET, UDDS, LA92, and US06 | 1.606% | ECM | SOC | No need for modeling and an expansive filter |
| [89] | Deep convolution neural network | US06 | 0.85 | LSTM, GRU, and CNN | SOC | Lowest RMSE compared to LSTM, GRU, and CNN, computationally competent, high speed, less cost |
| [117] | Stacked bidirectional LSTM | FUDS, US06, and BJDST | 0.46 | LSTM | SOC | Bidirectional LSTM works on both forward and backward sequential data to estimate SOC accurately |
| [79] | LSTM + ACKF | DST, US06, and FUDS | 2.2, 4% | LSTM | SOC | Improved accuracy due to a combination of LSTM and ACKF |
| [118] | LSTM + SRCKF | DST and FUDS | 0.4, 2% | LSTM | SOC | Better accuracy in the lower range of SOC |
| [119] | Radial basis function NN (RBFNN) | EV data | 4% | ANN | Battery aging | Good choice for online BMS |
| [120] | SVR | DST | 0.71, 6%, 0.4, 4% | SOC, Cell voltage | Quick SOC, worked well with low-cost BMS |
| Diagnostic Techniques | Battery Faults | Benefit | Drawback | Limitations | References |
|---|---|---|---|---|---|
| RLS Filter | ISC (Internal short circuit) MSC (micro-short circuit) | Simple, low cost, and complexity | Model-based ambiguity and minimal estimation accuracy of states | Need information about other series and parallel connected cell leads to inconsistency and balancing | [132] |
| SVM | Connection fault | Identify the severity of voltage fault with the time | Cannot identify current working state for big and high dimension data | Suitable only for small, simple data | [133] |
| RLS-UKF | Sensor fault detection | More accurate and less prediction time for a current sensor | Longer time for prediction of fault due to voltage sensor | Limitation of Gaussian white noise | [134] |
| AEKF | overcharge and over-discharge faults | Adaptive model-based technique | Model-based limitation for parameters and states estimation | Required to generate a residual signal | [135] |
| Neural Network | Fault due to the voltage sensor | Identify abnormal voltage data | required big historical data | Overfitting | [136] |
| Statistical method | Diagnosis of the real-time fault with the time | Identify the future fault | Need large history data | Overfitting | [126] |
| Entropy Theory | Short circuit | Fast diagnosis of the short circuit | Vulnerable to measurement noise | Failed in considerable inconsistency and with varied temperature and the current rate | [130] |
| DEKF | Sensor fault | Estimate accurately continuous state and parameter | complexity | computational cost | [137] |
| LSTM | Thermal runaway | Increase accuracy, decrease computational time | Increase complexity by coupling model and data-driven method | Failed when voltage within is within the set threshold | [138] |
| WAVELET | Diagnosis real voltage value | Noise removal from the real voltage | Affected by the set value of interval parameters | Cross-voltage test | [129] |
| Correlation method | Short circuit | Robust for real-time application | Irregular voltage drops | Vulnerable to measurement noise | [139] |
| Neural network | Thermal Fault | Stretch forward technique and residual monitor used for identifying fault | Slow fault and long-term degradation require to be enhanced | Only work on big historical data | [140] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhushan, N.; Mekhilef, S.; Tey, K.S.; Shaaban, M.; Seyedmahmoudian, M.; Stojcevski, A. Overview of Model- and Non-Model-Based Online Battery Management Systems for Electric Vehicle Applications: A Comprehensive Review of Experimental and Simulation Studies. Sustainability 2022, 14, 15912. https://doi.org/10.3390/su142315912
Bhushan N, Mekhilef S, Tey KS, Shaaban M, Seyedmahmoudian M, Stojcevski A. Overview of Model- and Non-Model-Based Online Battery Management Systems for Electric Vehicle Applications: A Comprehensive Review of Experimental and Simulation Studies. Sustainability. 2022; 14(23):15912. https://doi.org/10.3390/su142315912
Chicago/Turabian StyleBhushan, Neha, Saad Mekhilef, Kok Soon Tey, Mohamed Shaaban, Mehdi Seyedmahmoudian, and Alex Stojcevski. 2022. "Overview of Model- and Non-Model-Based Online Battery Management Systems for Electric Vehicle Applications: A Comprehensive Review of Experimental and Simulation Studies" Sustainability 14, no. 23: 15912. https://doi.org/10.3390/su142315912
APA StyleBhushan, N., Mekhilef, S., Tey, K. S., Shaaban, M., Seyedmahmoudian, M., & Stojcevski, A. (2022). Overview of Model- and Non-Model-Based Online Battery Management Systems for Electric Vehicle Applications: A Comprehensive Review of Experimental and Simulation Studies. Sustainability, 14(23), 15912. https://doi.org/10.3390/su142315912










