Mechanics Modeling and Simulation Analysis of a Novel Articulated Chassis for Forestry
Abstract
:1. Introduction
2. Materials and Methods
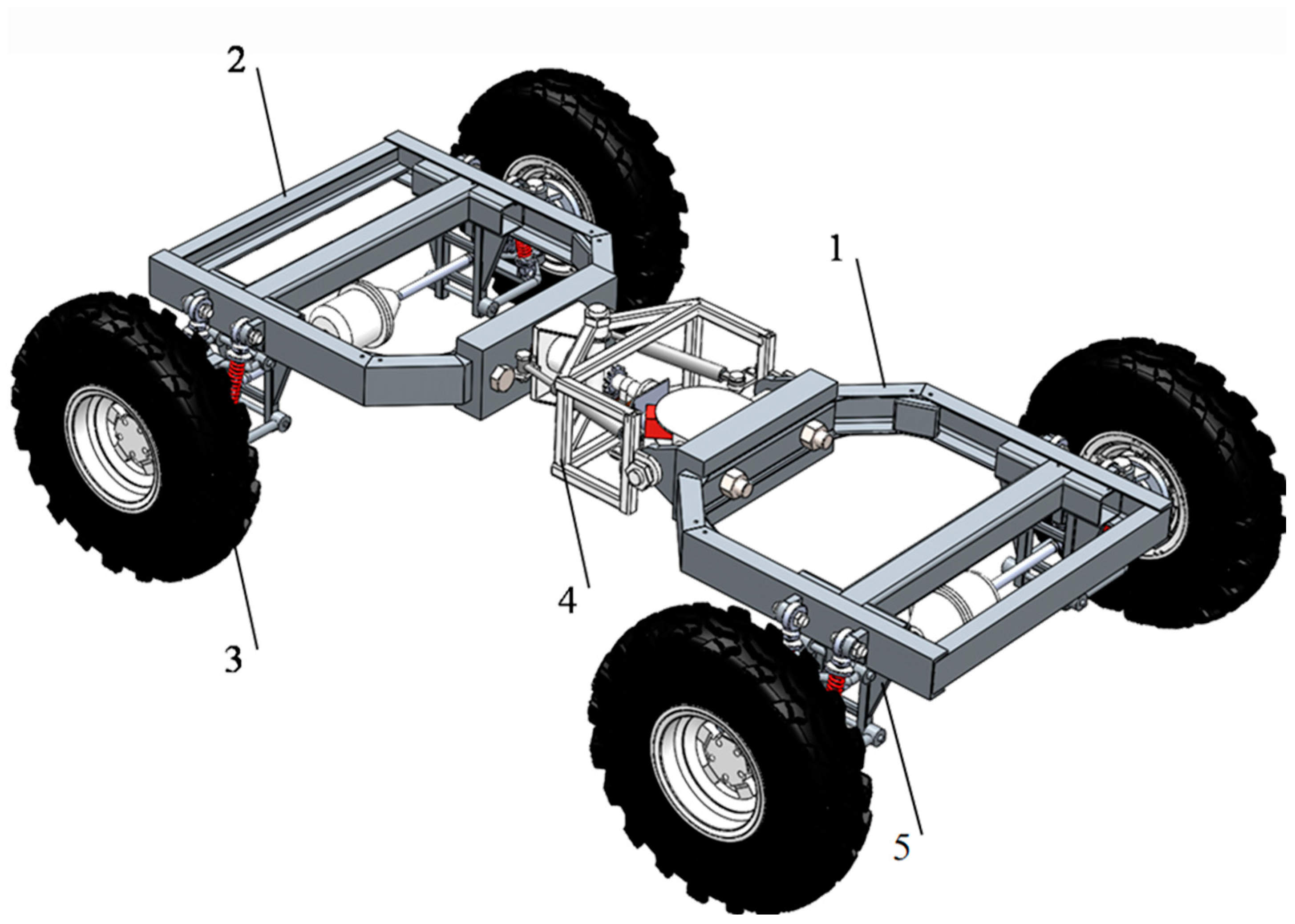
2.1. Chassis Structure
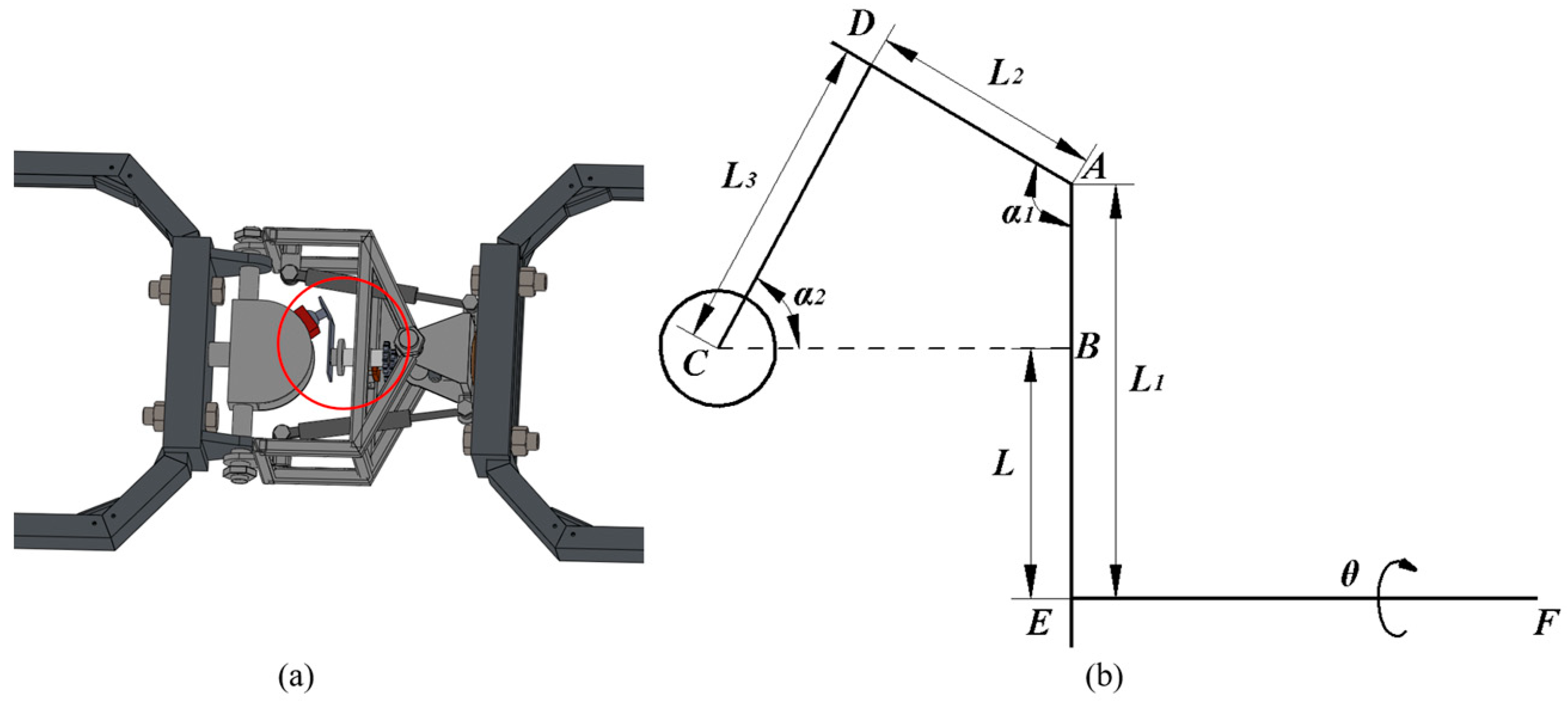
2.2. Three-Degree-of-Freedom Articulated Structure with Active Pitching Function
2.3. Kinematics and Dynamics Analysis of Key Mechanism of Chassis
2.3.1. Kinematics Analysis of Articulated Structure
2.3.2. Dynamics Analysis of Articulated Structure
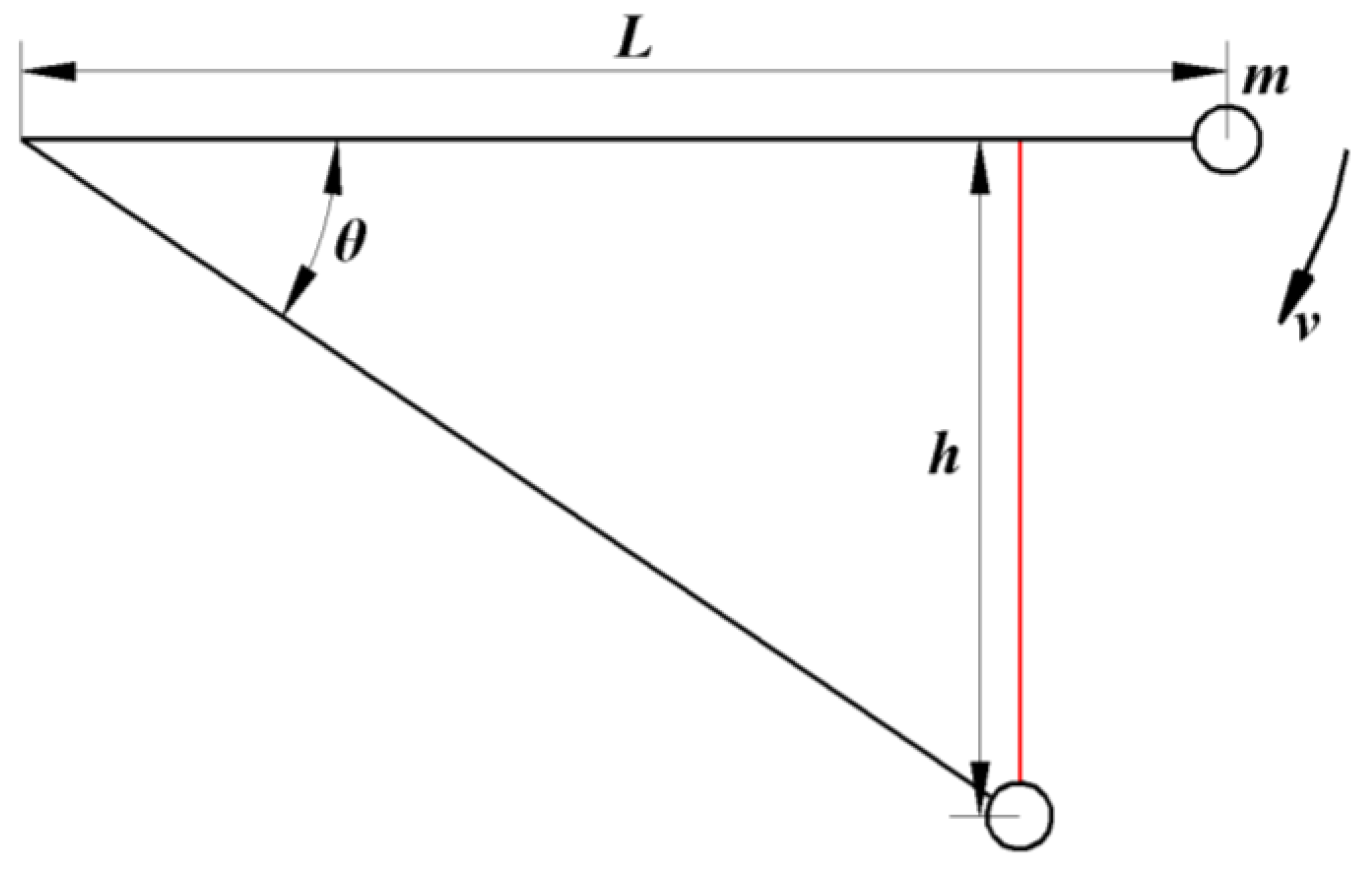
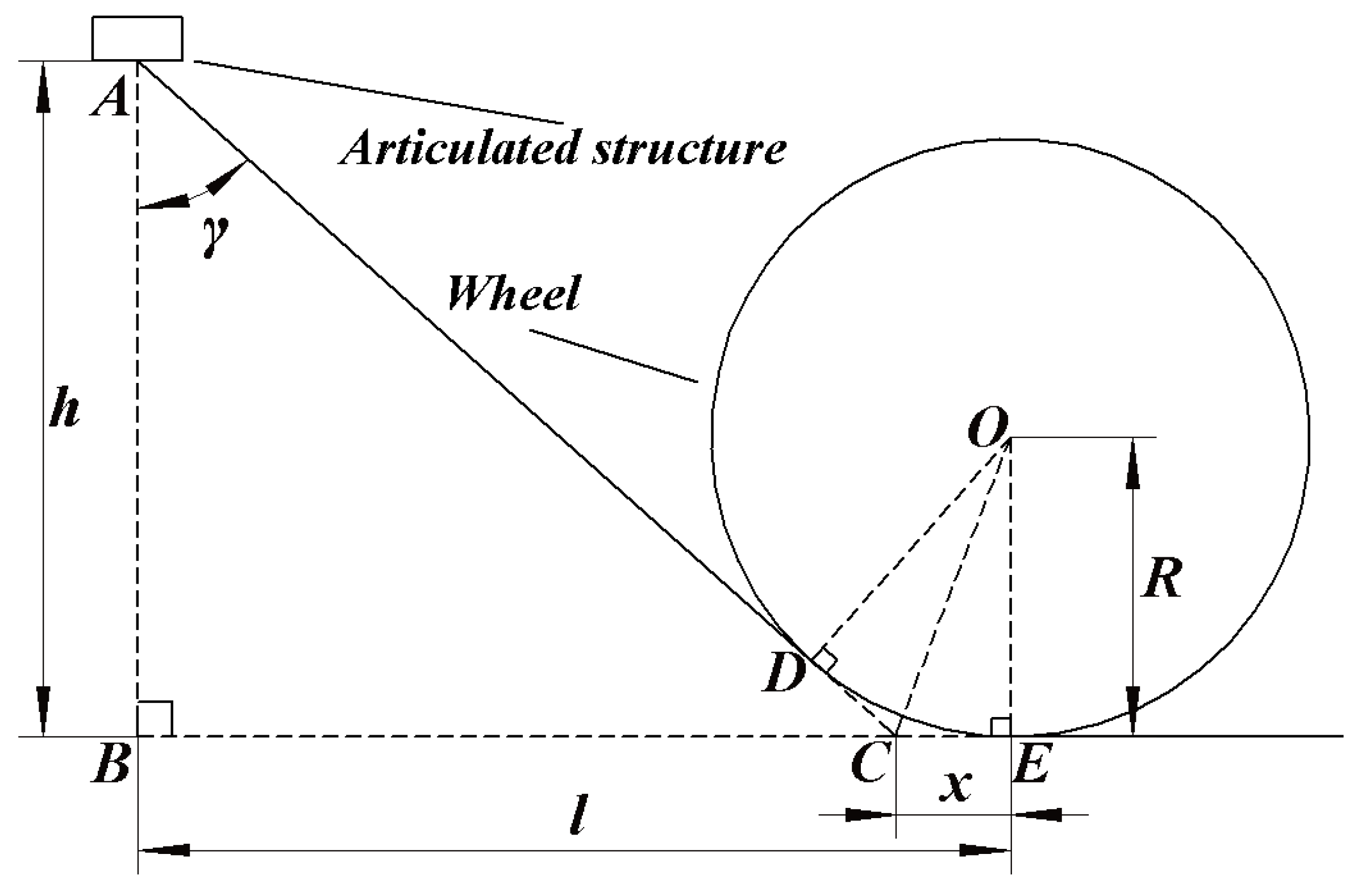
2.3.3. Theoretical Model of Ultimate Pitch Angle of Chassis
2.4. Kinematic Simulation Experiment of Articulated Structure
2.5. Chassis Working Condition Simulation Experiment
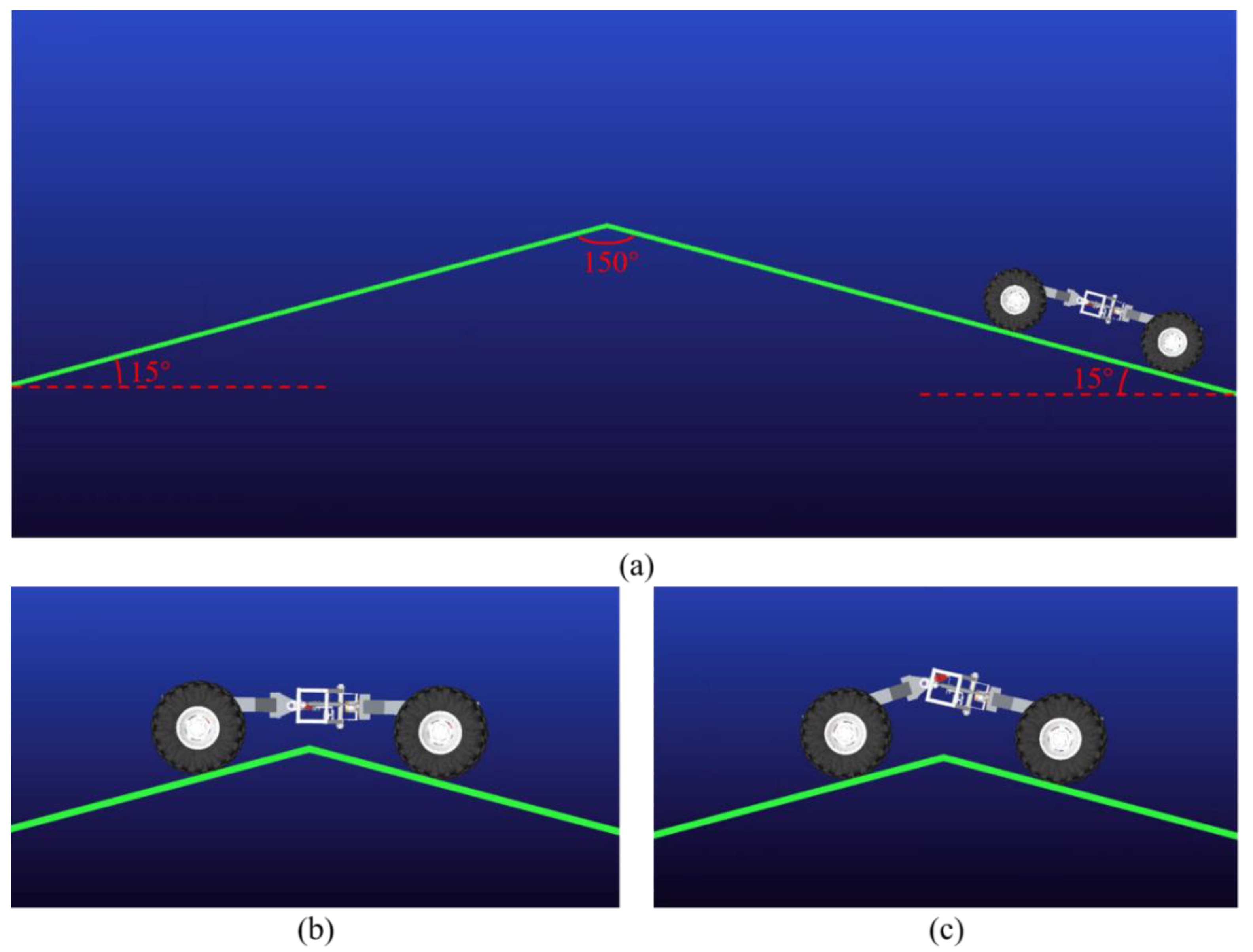
2.5.1. Climbing a Slope
2.5.2. Steep-Convex-Obstacle Crossing
2.5.3. Unilateral-Obstacle Crossing
3. Results and Discussion
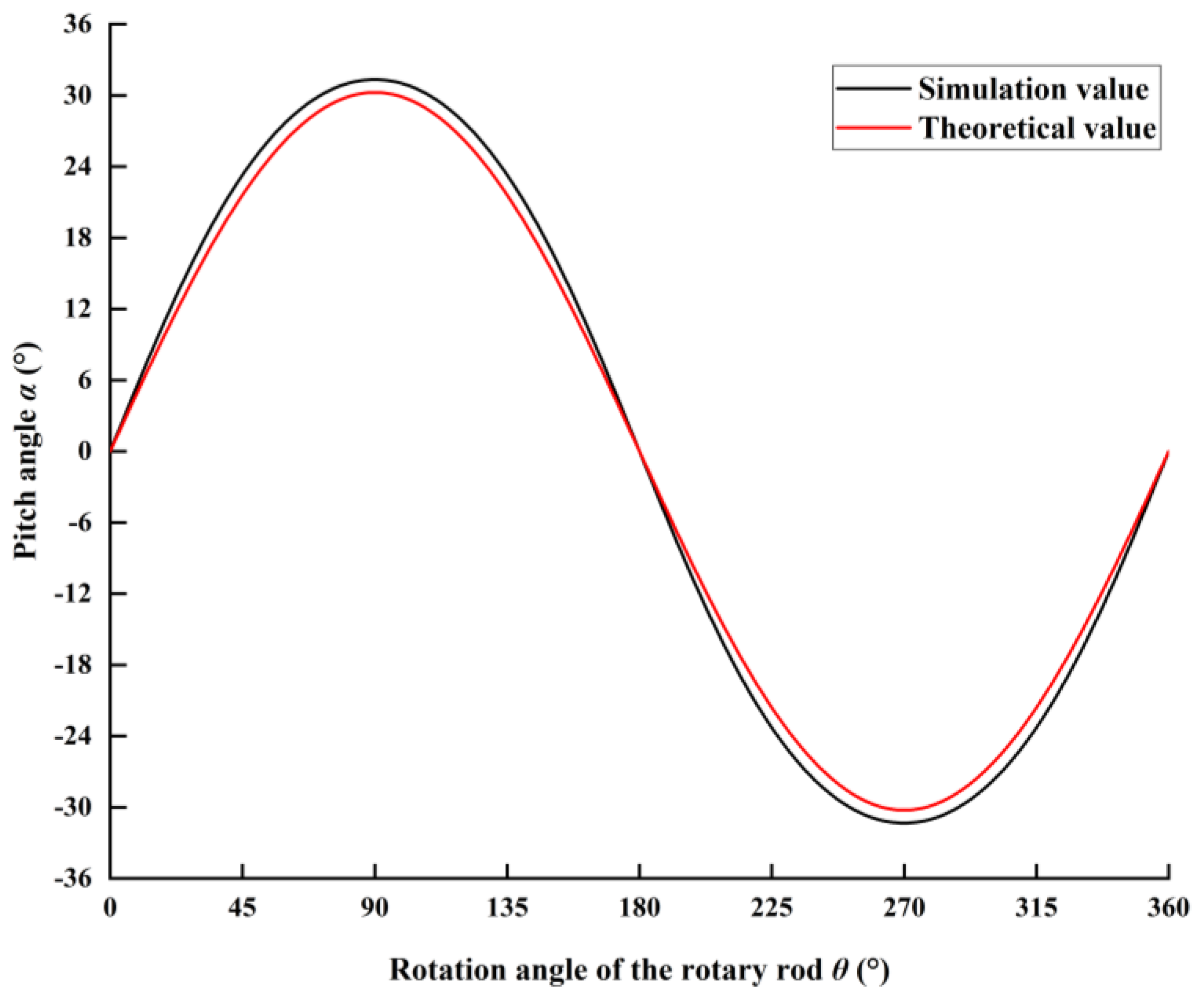
3.1. Analysis of Kinematics Simulation Experiment Results of Articulated Structure
3.2. Analysis of Simulation Results of Chassis Working Conditions
3.2.1. Climbing the Slope
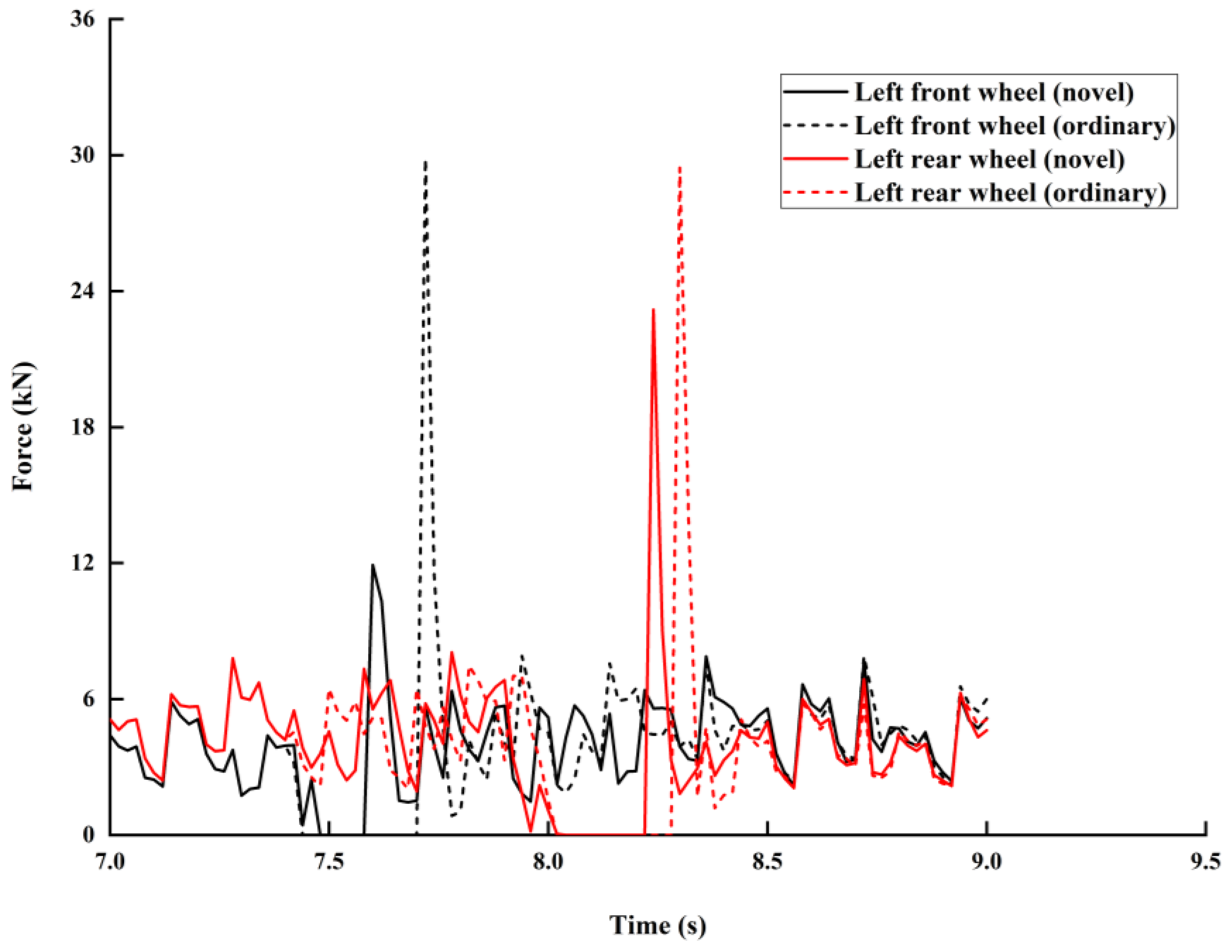
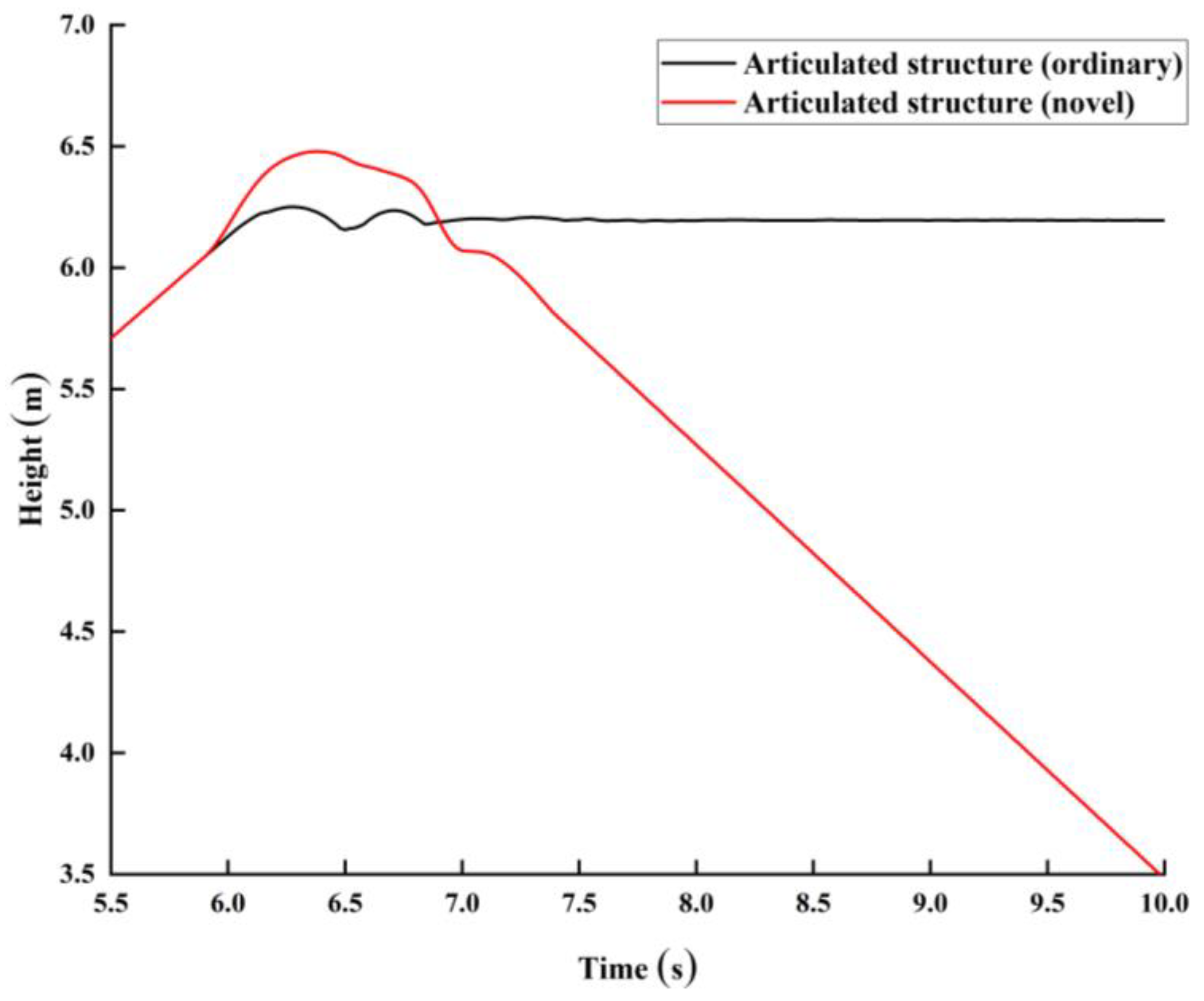
3.2.2. Steep-Convex-Obstacle Crossing
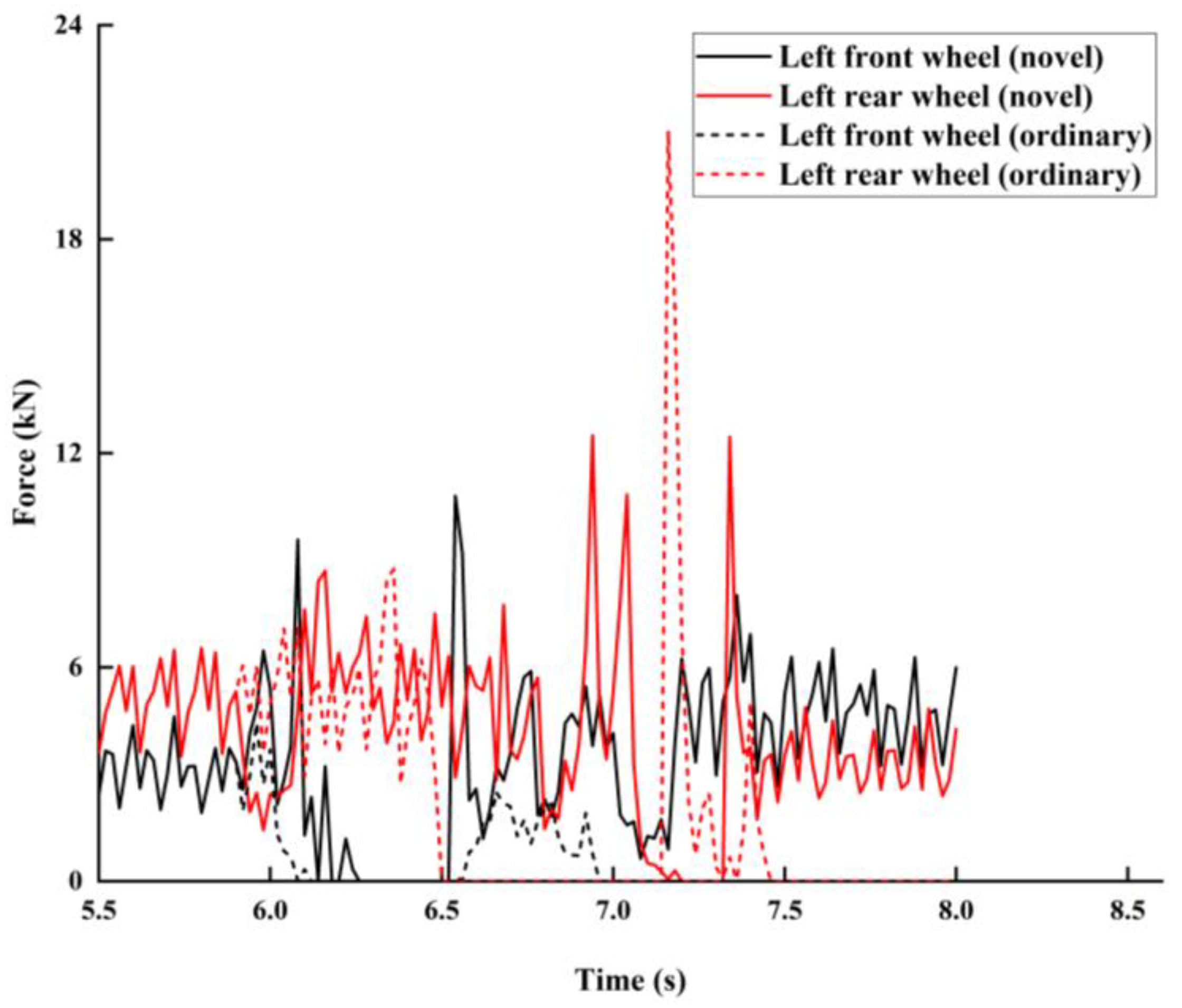
3.2.3. Unilateral-Obstacle Crossing
4. Conclusions
- (1)
- According to the principle of multiple-degree-of-freedom profiling, a novel articulated chassis was designed for forestry. The innovative articulated structure realizes active pitching, active deflection, and passive torsion of the front and rear frames and meets the requirements of profiling driving on uneven roads.
- (2)
- Through a kinematics and dynamics analysis of the articulated structure, a theoretical model of the relationship between the rotation angle of the rotary shaft and the pitch angle of the front and rear frames was established. The quantitative relationship between the output torque of the servo motor and the angular acceleration and angle of the terminal pitch plate was determined, making it possible to control the leaning and pitching motion of the front and rear frames by adjusting the output torque of the servo motor. The theoretical limit pitch angle of the chassis was determined, providing a judgment basis for chassis profiling obstacle crossing.
- (3)
- ADAMS was used to establish a forest chassis simulation model, and a kinematics simulation experiment for the articulated structure was conducted. A comparison between simulation and theoretical results shows that the maximum error occurs at the position where the rotation angle of the rotary shaft is 90° and less than 1%, demonstrating the accuracy of the theoretical model.
- (4)
- The complex terrain environment of a forest area was simplified into three working conditions: Climbing over slopes, steep convex obstacles, and unilateral obstacles. The three working conditions were established in ADAMS, and a simulation experiment was performed. For climbing over a slope at a wheel speed of 1.39 rev/s, the duration of the effective driving force of the front wheel of the novel chassis was 61.5% longer than an ordinary chassis. For steep-convex-obstacle crossing, compared with an ordinary chassis, the active pitch function of the novel chassis ensured that the wheels had a good contact with the road and carried the load past the obstacles smoothly. For unilateral-obstacle crossing, the novel chassis provided a continuous and stable effective driving force for obstacle crossing due to its good road profile. The research results provide guidance for the mechanization of forestry equipment and a theoretical and technical foundation for research on special forestry equipment chassis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pan, J. Prospect of agricultural Mechanization development in hilly areas. Agric. Dev. Equip. 2020, 6, 68, 70. (In Chinese) [Google Scholar]
- Song, J.W.; Liu, H.X. Accelerate the breakthrough of agricultural mechanization development bottleneck in hilly and mountainous areas. China Agric. Mech. 2010, 16–19. (In Chinese) [Google Scholar]
- Bergerman, M.; Billingsley, J.; Reid, J.; van Henten, E. Robotics in agriculture and forestry. In Springer Handbook of Robotics; Springer: Cham, Switzerland, 2016; pp. 1463–1492. [Google Scholar]
- Khot, L.R.; Tang, L.; Steward, B.L.; Han, S. Sensor fusion for improving the estimation of roll and pitch for an agricultural sprayer. Biosyst. Eng. 2008, 101, 13–20. [Google Scholar] [CrossRef]
- Vidoni, R.; Bietresato, M.; Gasparetto, A.; Mazzetto, F. Evaluation and stability comparison of different vehicle configurations for robotic agricultural operations on side-slopes. Biosyst. Eng. 2015, 129, 197–211. [Google Scholar] [CrossRef]
- Liu, P.Y.; Wang, C.Y.; Li, H.T.; Zhang, M.; Wei, W.; Zhang, S. Design and experiment of dynamic leveling chassis for agricultural profile walking in hilly areas. Trans. Chin. Soc. Agric. Mach. 2018, 49, 74–81. (In Chinese) [Google Scholar]
- Gao, Q.M.; Pan, D.; Zhang, X.; Deng, F.Y.; Huang, D.H.; Wang, L.Q. Design and Simulation of full track modular unmanned agricultural power chassis. Trans. Chin. Soc. Agric. Mach. 2020, 51, 561–570. (In Chinese) [Google Scholar]
- Wang, Y.; Qin, H.; Xu, S.B.; Gou, Y.F.; Li, H.T. Research and trial production of all terrain profiling walking vehicle. J. Dalian Univ. Technol. 2011, 51, 84–87. (In Chinese) [Google Scholar]
- Agheli, M.; Nestinger, S.S. Study of the foot force stability margin for multi-legged/wheeled robots under dynamic situations. In Proceedings of the 2012 IEEE/ASME 8th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications, Suzhou, China, 8–10 July 2012; IEEE: New York, NY, USA, 2012; pp. 99–104. [Google Scholar]
- Wang, Z.; Ding, X.; Rovetta, A.; Giusti, A. Mobility analysis of the typical gait of a radial symmetrical six-legged robot. Mechatronics 2011, 21, 1133–1146. [Google Scholar] [CrossRef]
- Cheng, C.; Cebon, D. Improving roll stability of articulated heavy vehicles using active semi-trailer steering. Veh. Syst. Dyn. 2008, 46, 373–388. [Google Scholar] [CrossRef]
- Ismoilov, A.; Sellgren, U.; Andersson, K.; Löfgren, B. A comparison of novel chassis suspended machines for sustainable forestry. J. Terramechanics 2015, 58, 59–68. [Google Scholar] [CrossRef]
- Reiter, J.; Boehringer, K.F.; Campbell, M. MEMS control moment gyroscope design and wafer-based spacecraft chassis study. In Micromachined Devices and Components V; SPIE—The International Society for Optical Engineering: Washington, DC, USA, 1999; p. 3876. [Google Scholar]
- Alamdari, A.; Krovi, V. Active reconfiguration for performance enhancement in articulated wheeled vehicles. In Dynamic Systems and Control Conference; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- Zhao, K.; Liu, J.H.; Huang, Q.Q.; Hao, S.; Dian, W. Optimization design and obstacle overcoming performance simulation analysis of forestry parallel articulated chassis. J. Beijing For. Univ. 2018, 40, 131–140. (In Chinese) [Google Scholar]
- Carabin, G.; Gasparetto, A.; Mazzetto, F.; Vidoni, R. Design, implementation and validation of a stability model for articulated autonomous robotic systems. Robot. Auton. Syst. 2016, 83, 158–168. [Google Scholar] [CrossRef]
- Smith, T.; Chavez, D. A Practical Comparison of motion planning techniques for robotic legs in environments with obstacles. In Proceedings of the 2009 Third IEEE International Conference on Space Mission Challenges for Information Technology, Pasadena, CA, USA, 19–23 July 2009; pp. 155–162. [Google Scholar]
- Li, L.; Zhao, H.; Li, B.H. Simulation study on obstacle crossing performance of articulated crawler submarine mining vehicle. Comput. Simul. 2008, 25, 195–199. (In Chinese) [Google Scholar]
- Edlund, J.; Keramati, E.; Servin, M. A long-tracked bogie design for forestry machines on soft and rough terrain. J. Terramech. 2013, 50, 73–83. [Google Scholar] [CrossRef]
- Liu, P.Y.; Peng, F.J.; Li, H.T.; Wang, Z.Z.; Wei, W.J.; Zhao, J.P. Design and experiment of adaptive leveling chassis for agriculture in hilly areas. Trans. of the Chin. Soc. Agric. Mach. 2017, 48, 42–47. (In Chinese) [Google Scholar]
- Liu, P.Y.; Ke, C.P.; Ke, T.; Li, H.T.; Wei, W.J.; Zhao, C. Design and experiment of pretesting active leveling chassis for agriculture in hilly areas. Transactions of the Chin. Soc. Agric. Mach. 2020, 51, 371–378. (In Chinese) [Google Scholar]
- Liu, P.Y.; Li, H.T.; Zhang, S.Y.; Wei, W. Theoretical Analysis and Experiment of All Terrain Adaptive Locomotion Vehicle; Editorial Office of Transactions of the Chinese Society of Agricultural Engineering: Beijing, China, 2012; p. 28. [Google Scholar]
- Zhang, N. Analysis of swing frame structure of mining special vehicle based on SimSolid. Coal Mine Mech. Electr. 2020, 41, 59–62. (In Chinese) [Google Scholar]
- Hao, Z.J. Analysis and Discussion on Swing Structure of Mining Articulated Vehicle. Coal Mine Mach. 2020, 41, 89–92. (In Chinese) [Google Scholar]
- Moreno, G.; Manenti, V.; Guerero, G.; Nicolazzi, L.; Vieira, R.; Martins, D. Stability of heavy articulated vehicles: Effect of load distribution. Transp. Res. Procedia 2018, 33, 211–218. [Google Scholar] [CrossRef]
- Cojocaru-Greblea, T.; Bontos, M.D.; Vasiliu, N.; Dobre, A. Redundant Steering Systems for Articulated Vehicles. Int. Multidiscip. Sci. GeoConference SGEM 2017, 17, 497–504. [Google Scholar]
- Pijuan, J.; Comellas, M.; Nogués, M.; Roca, J.; Potau, X. Active bogies and chassis levelling for a vehicle operating in rough terrain. J. Terramech. 2012, 49, 161–171. [Google Scholar] [CrossRef]
- Zhu, Y. Design and Analysis of Wheel-Leg Variable Amplitude and 3-DOF Articulated Forest Chassis; Beijing Forestry University: Beijing, China, 2018. (In Chinese) [Google Scholar]
- Zhu, Y.; Kan, J.M. Design and obstacle overcoming performance analysis of 3-DOF articulated forest chassis. J. Beijing For. Univ. 2016, 38, 126–132. (In Chinese) [Google Scholar]
- Zhu, Y.; Kan, J.; Li, W.; Kang, F. A novel forestry chassis with an articulated body with three degrees of freedom and installed luffing wheel-legs (FC-3DOF&LW). Adv. Mech. Eng. 2018, 10, 1–10. (In Chinese) [Google Scholar]
- Zhu, Y.; Kan, J. Prediction of the lateral stability of a forestry chassis with an articulated body and fitted with luffing wheel-legs. Biosyst. Eng. 2022, 224, 143–160. [Google Scholar] [CrossRef]
- Zhu, Y.; Kan, J.; Li, W.; Kang, F. Strategies of traversing obstacles and the simulation for a forestry chassis. Int. J. Adv. Robot. Syst. 2018, 15, 68–73. [Google Scholar] [CrossRef] [Green Version]
- San, T.; Ishii, Y. A study on current state of forest resources and forest policy in myanmar. Trans. Meet. Hokkaido Branch Jpn. For. Soc. 2018, 46, 107–110. [Google Scholar]
- Guan, Y.X. Analysis of influencing factors and countermeasures of forest coverage in Fujian Province. For. Surv. Des. 2015, 10–13. (In Chinese) [Google Scholar]
- Zhang, L.J.; You, T.G.; Lin, L.X.; Chen, S.Z.; Huang, Y. Study on the relationship between air quality and forest coverage in Fujian Province. Wuyi Sci. 2018, 34, 144–150. (In Chinese) [Google Scholar]
- Fan, J.F.; Huang, S.C.; Mei, E.Z.; Tang, X.N. Motion and simulation analysis of universal joint coupling based on cross shaft. Mach. Des. 2021, 38, 91–96. (In Chinese) [Google Scholar]
- Sun, T.; Xiang, X.; Su, W.; Wu, H.; Song, Y. A transformable wheel-legged mobile robot: Design, analysis and experiment. Robot. Auton. Syst. 2017, 98, 30–41. (In Chinese) [Google Scholar] [CrossRef]
- Dobretsov, R.Y.; Voinash, S.A.; Sokolova, V.A.; Krivonogova, A.S.; Pushkov, Y.L.; Andronov, A.V. Power distribution mechanism for the transmission of forest tracked and wheeled vehicles. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; Volume 1679, p. 042046. [Google Scholar]
- Franceschetti, B.; Lenain, R.; Rondelli, V. Comparison between a rollover tractor dynamic model and actual lateral tests. Biosyst. Eng. 2014, 127, 79–91. [Google Scholar] [CrossRef]
- Zhao, T.W.; Xue, Y.H.; Xue, Y.H.; Bao, Q.Q. Kinematics and Dynamics Simulation Analysis of Wheel Assembly Manipulator for Large Heavy-Duty Vehicle Based on ADAMS. J. Mach. Des. 2021, 38, 27–31. (In Chinese) [Google Scholar]
- Huang, H.S.; Li, T.; Liu, J.H. Dynamic Modeling and Simulation Analysis of 6-HUS Parallel Moving Platform. J. Beijing For. Univ. 2015, 37, 143–150. (In Chinese) [Google Scholar]
- ElMadany, M.M.; Dokainish, M.A.; Allan, A.B. Ride dynamics of articulated vehicles—A literature survey. Veh. Syst. Dyn. 1979, 8, 287–316. [Google Scholar] [CrossRef]
- Alamdari, A.; Krovi, V.N. Design of articulated leg–wheel subsystem by kinetostatic optimization. Mech. Mach. Theory 2016, 100, 222–234. [Google Scholar] [CrossRef]
- Han, D.T.; Liu, J.H.; Wang, D.; Li, D.W. Research on Obstacle Crossing and Position Optimization of a Double-cylinder wheel Leg of Forest Active Gait Chassis. J. Beijing For. Univ. 2018, 40, 117–124. (In Chinese) [Google Scholar]
- Alamdari, A.; Zhou, X.; Krovi, V.N. Kinematic modeling, analysis and control of highly reconfigurable articulated wheeled vehicles. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Portland, OR, USA, 4–7 August 2013; American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar]













| Parameter | Value |
|---|---|
| L1 (mm) | 75.09 |
| L2 (mm) | 25 |
| L3 (mm) | 42.5 |
| (°) | 150 |
| (°) | 30 |
| Parameter | Value |
|---|---|
| Stiffness coefficient (N/mm) | 100,000 |
| Force index | 1.5 |
| Damping coefficient (N-s/mm) | 10,000 |
| Penetration depth (mm) | 0.001 |
| Coefficient of static friction | 0.3 |
| Coefficient of dynamic friction | 3 |
| Static friction velocity (mm/s) | 0.1 |
| Dynamic friction velocity (mm/s) | 10 |
| Chassis length (mm) | 2260 |
| Chassis width (mm) | 1580 |
| Wheel diameter (mm) | 660 |
| Wheel width (mm) | 160 |
| Chassis mass (kg) | 510 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Zhu, Y.; Xie, Z. Mechanics Modeling and Simulation Analysis of a Novel Articulated Chassis for Forestry. Sustainability 2022, 14, 16118. https://doi.org/10.3390/su142316118
Lin X, Zhu Y, Xie Z. Mechanics Modeling and Simulation Analysis of a Novel Articulated Chassis for Forestry. Sustainability. 2022; 14(23):16118. https://doi.org/10.3390/su142316118
Chicago/Turabian StyleLin, Xintao, Yue Zhu, and Zheng Xie. 2022. "Mechanics Modeling and Simulation Analysis of a Novel Articulated Chassis for Forestry" Sustainability 14, no. 23: 16118. https://doi.org/10.3390/su142316118





