Cyclic True Triaxial Tests on Aeolian Sand Considering Initial Shear Effect
Abstract
:1. Introduction
2. Test Procedures
2.1. Test Apparatus and Specimen Preparation
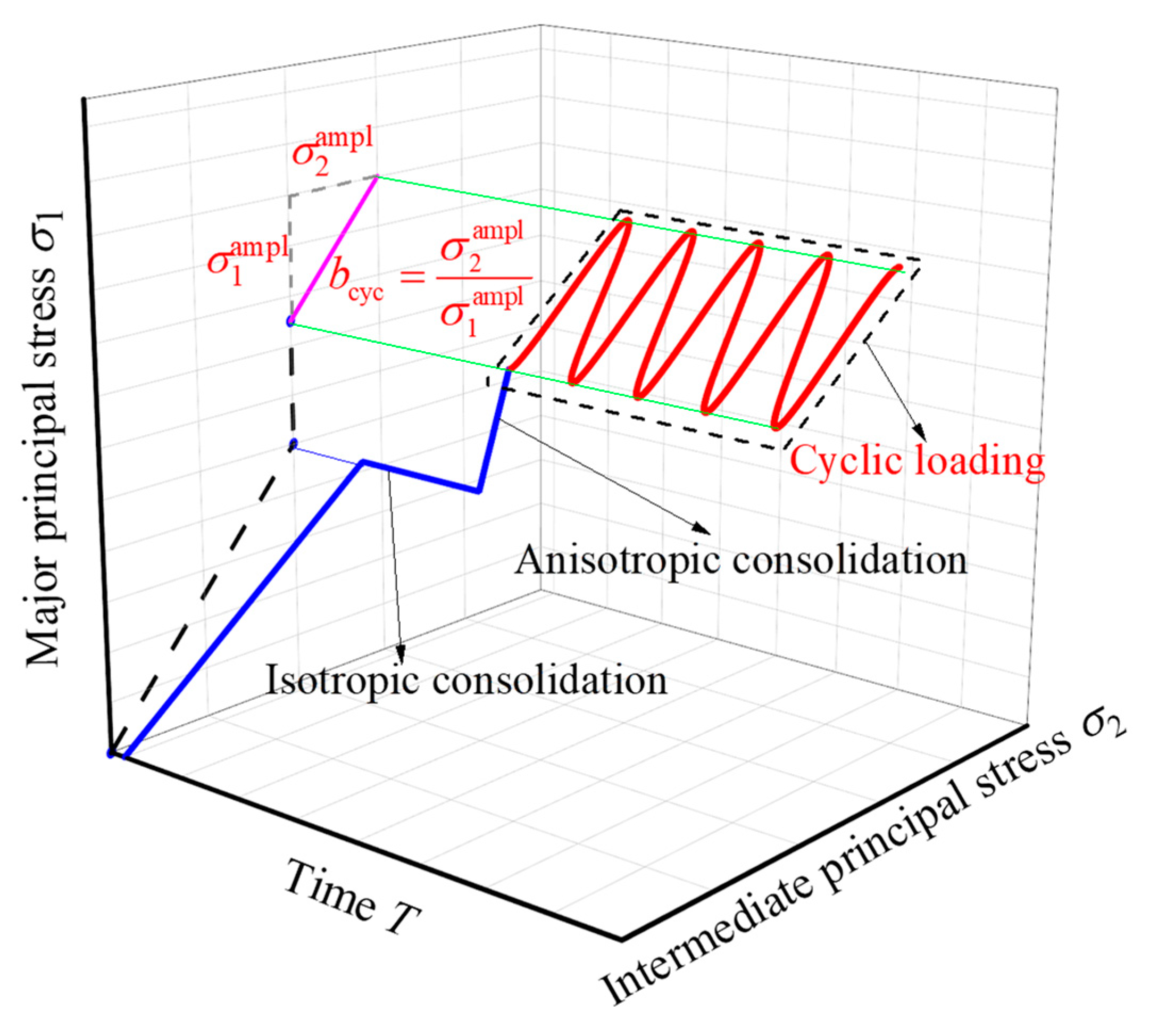
2.2. Test Program
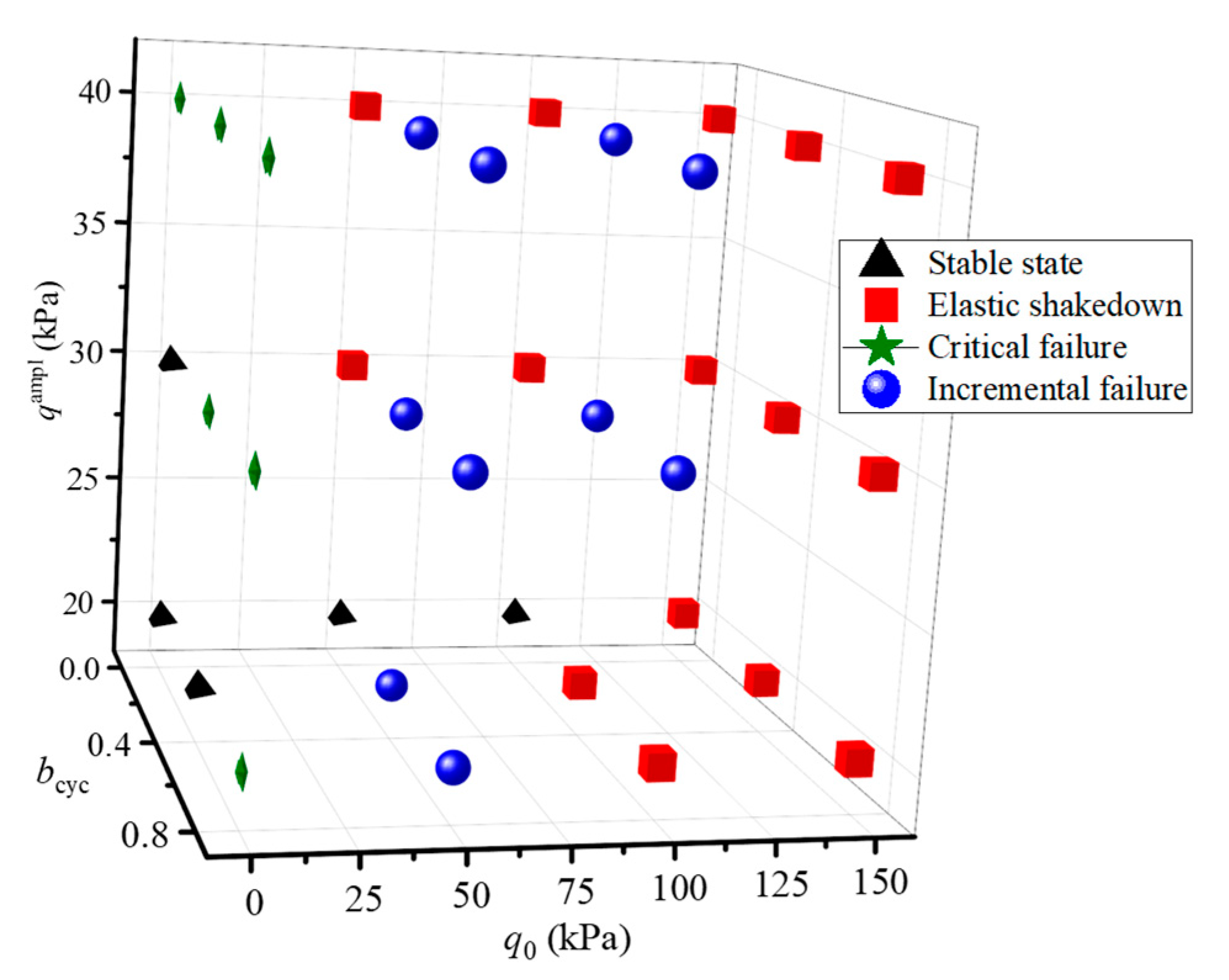
3. Test Results and Discussion
3.1. Strains Development under One-Dimensional Cyclic Loading
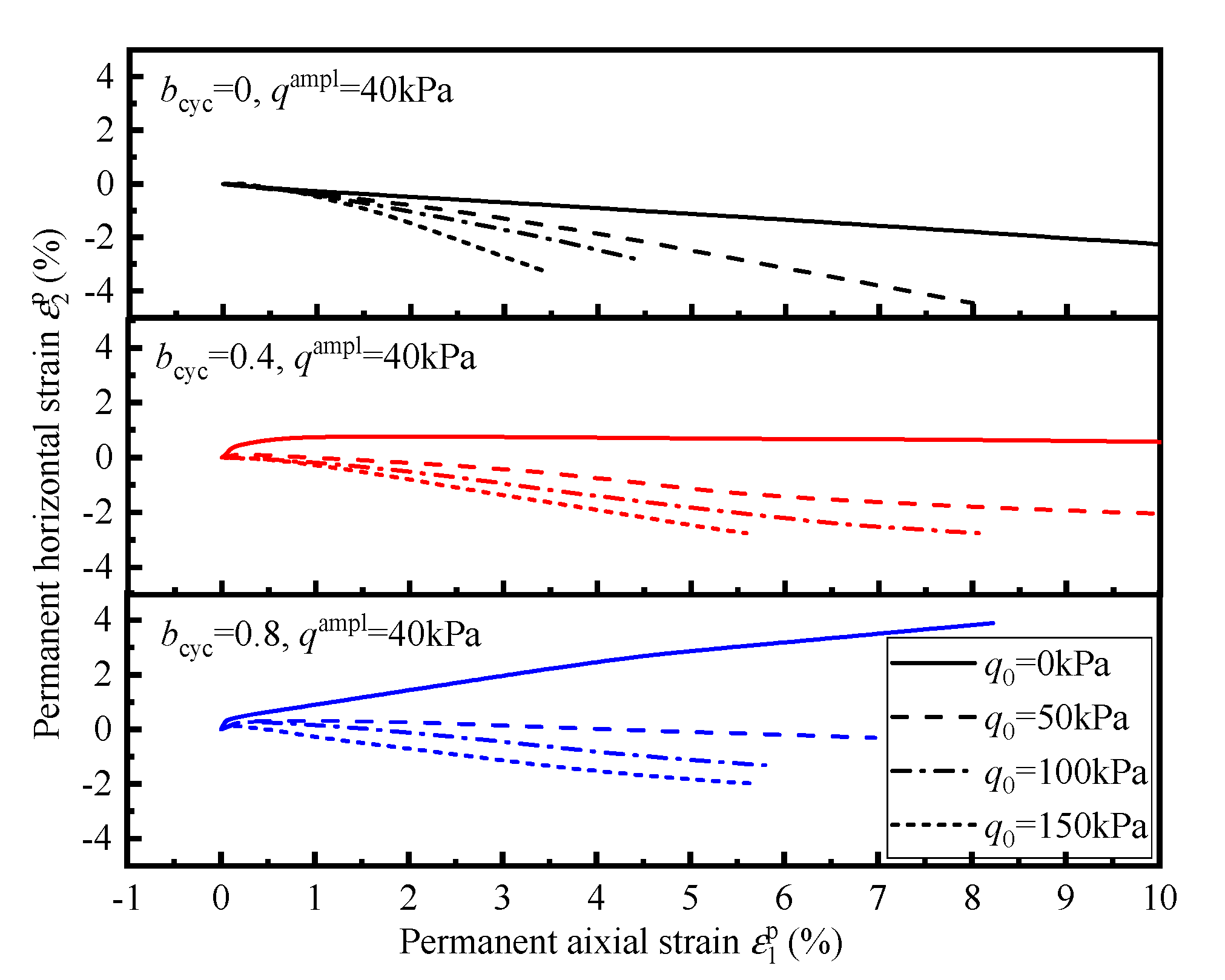
3.2. Strains Development under Two-Dimensional Cyclic Loading
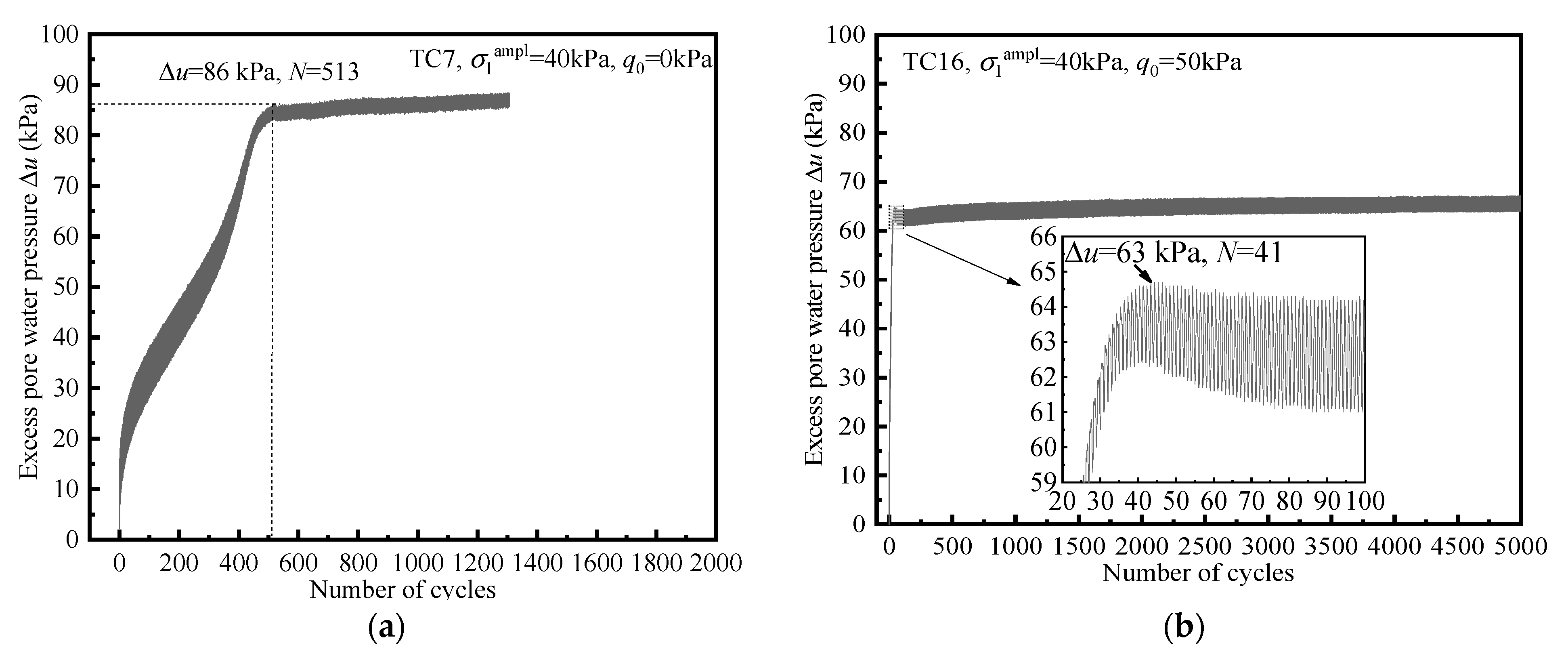
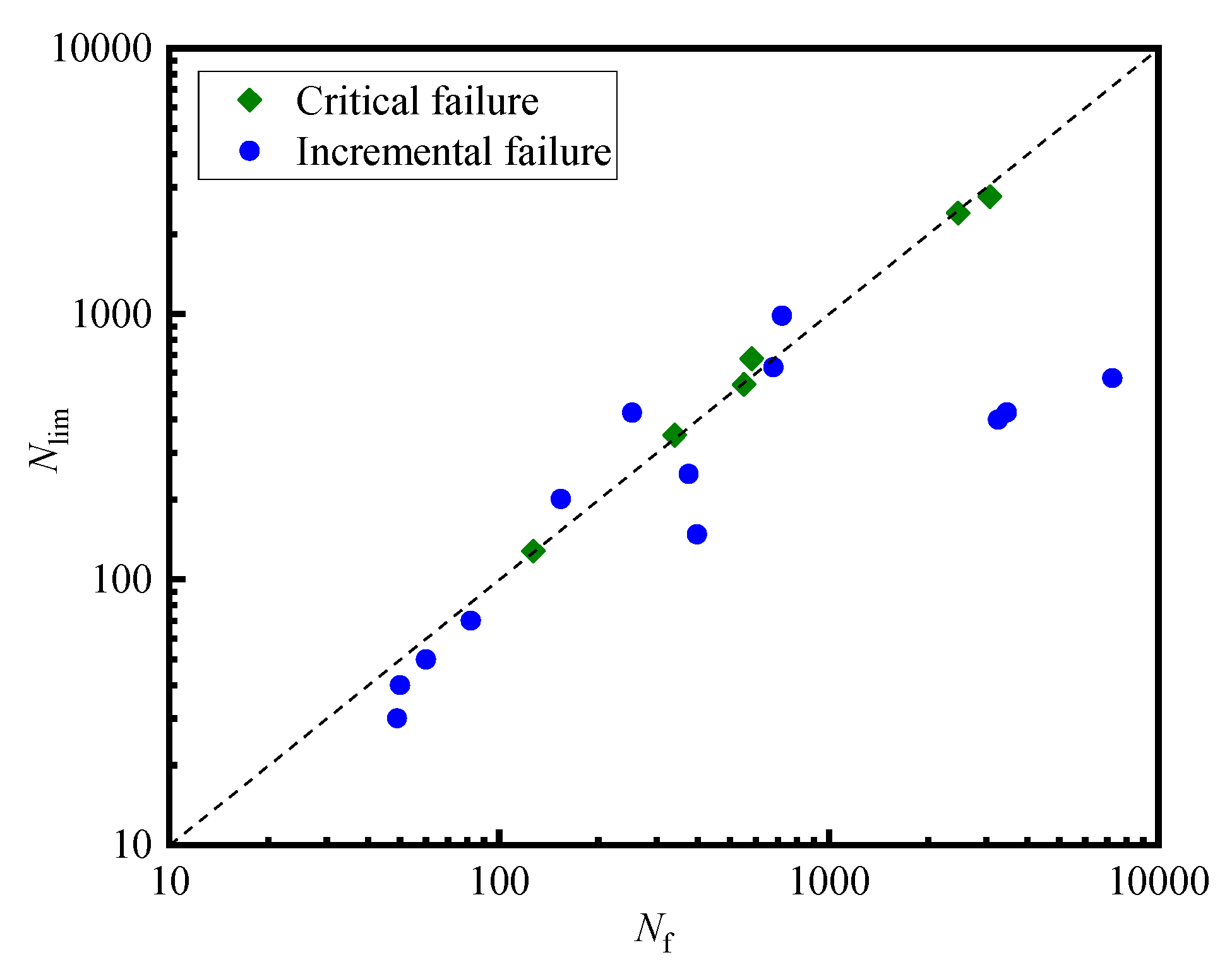
3.3. The Development of Pore Pressure
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Idriss, I.M.; Boulanger, R.W. Soil Liquefaction during Earthquakes; Earthquake Engineering Research Institute (EERI): Oakland, CA, USA, 2008. [Google Scholar]
- Dong, T.; Zheng, Y.; Liang, K.; Liu, C. Shear strength and shear bands of anisotropic sand. Acta Geotech. 2022, 17, 2841–2853. [Google Scholar] [CrossRef]
- Xiu, Z.; Wang, S.; Ji, Y.; Wang, F.; Ren, F. Experimental investigation on liquefaction and post-liquefaction deformation of stratified saturated sand under cyclic loading. Bull. Eng. Geol. Environ. 2020, 79, 2313–2324. [Google Scholar] [CrossRef]
- Pan, K.; Xu, T.; Liao, D.; Yang, Z. Failure mechanisms of sand under asymmetrical cyclic loading conditions: Experimental observation and constitutive modelling. Géotechnique 2022, 72, 162–175. [Google Scholar] [CrossRef]
- Xu, Z.; Pan, L.; Gu, C.; Cai, Y. Deformation behavior of anisotropically overconsolidated clay under one-way cyclic loading. Soil Dyn. Earthq. Eng. 2020, 129, 105943. [Google Scholar] [CrossRef]
- Yang, J.; Yang, A.; Shan, Y.; Yang, M.; Zhao, J.; Yu, H. Experimental Study on Mechanical Behavior of Lean Cemented Sand and Gravel Material in Unloading and Reloading Paths. Adv. Mater. Sci. Eng. 2021, 2021, 8893840. [Google Scholar] [CrossRef]
- Ye, B.; Ni, X.; Ye, G.; Huang, Y.; Lu, P. Prediction of the initial point of the last cycle in undrained cyclic triaxial tests on flow liquefaction. Soil Dyn. Earthq. Eng. 2019, 120, 12–22. [Google Scholar] [CrossRef]
- Ding, Z.; He, S.; Sun, Y.; Xia, T.; Zhang, Q. Comparative study on cyclic behavior of marine calcareous sand and terrigenous siliceous sand for transportation infrastructure applications. Constr. Build. Mater. 2021, 283, 122740. [Google Scholar] [CrossRef]
- Zhang, Y.; Gu, C.; Wang, J.; Cai, Y. Three-dimensional cyclic behavior of saturated clays: Comparison between undrained and partly drained conditions. Can. Geotech. J. 2021, 58, 1716–1729. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Y.; Wu, Y.; Zhang, B.; Lv, H.; Sun, X. Development and application of a large-scale static and dynamic true triaxial apparatus for gravel. Int. J. Geomech. 2018, 18, 04018004. [Google Scholar] [CrossRef]
- Yoshimine, M.; Ishihara, K.; Vargas, W. Effects of principal stress direction and intermediate principal stress on undrained shear behavior of sand. Soils Found. 1998, 38, 179–188. [Google Scholar] [CrossRef]
- Sivathayalan, S.; Vaid, Y.P. Influence of generalized initial state and principal stress rotation on the undrained response of sands. Can. Geotech. J. 2002, 39, 63–76. [Google Scholar] [CrossRef]
- Shibuya, S.; Hight, D.W.; Jardine, R.J. Local boundary surfaces of a loose sand dependent on consolidation path. Soils Found. 2003, 43, 85–93. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, K.L.; Seed, H.B. Dynamic strength of anisotropically consolidated sand. J. Soil. Mech. Found. Div. 1967, 93, 169–190. [Google Scholar] [CrossRef]
- Ma, Y. Effect of initial consolidation shear stress on dynamic strength of saturated sand. Water Conser. Water Transp. Res. 1988, 1988, 63–68. [Google Scholar]
- Vaid, Y.P.; Chern, J.C. Cyclic and monotonic undrained response of saturated sands. In Advances in the Art of Testing Soils under Cyclic Conditions; ASCE: Reston, VA, USA, 1985; pp. 120–147. [Google Scholar]
- Vaid, Y.P.; Stedman, J.D.; Sivathayalan, S. Confining stress and static shear effects in cyclic liquefaction. Can. Geotech. J. 2001, 38, 580–591. [Google Scholar] [CrossRef]
- Harder, L.F.; Boulanger, R.W. Application of Kσ and Kα correction factors. In Proceedings of the NCEER Workshop on Evaluation of Liquefaction Resistance of Soils; National Center for Earthquake Engineering Research, State University of New York: Buffalo, NY, USA, 1997; pp. 167–190. [Google Scholar]
- Been, K.; Jefferies, M.G. A state parameter for sands. Géotechnique 1985, 35, 99–112. [Google Scholar] [CrossRef]
- Yang, J.; Sze, H.Y. Cyclic behaviour and resistance of saturated sand under nonsymmetrical loading conditions. Géotechnique 2011, 61, 59–73. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Sze, H.Y. Cyclic strength of sand under sustained shear stress. J. Geotech. Geoenviron. Eng. 2011, 137, 1275–1285. [Google Scholar] [CrossRef] [Green Version]
- Shi, W.; Zhu, J.; Chiu, C.; Liu, H. Strength and deformation behaviour of coarse-grained soil by true triaxial tests. J. Cent. South Univ. 2010, 17, 1095–1102. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, H.; Chen, Y.; Zhang, W. Particle size effects in granular soils under true triaxial conditions. Géotechnique 2014, 64, 667–672. [Google Scholar] [CrossRef]
- Huang, W.; Sun, D.; Sloan, S.W. Analysis of the failure mode and softening behaviour of sands in true triaxial tests. Int. J. Solids. Struct. 2007, 44, 1423–1437. [Google Scholar] [CrossRef]
- Li, X.; Ma, Z.; Lu, W.; Wang, Y. True-triaxial drained test of tengger desert sand. Adv. Civil. Eng. 2020, 2020, 8851165. [Google Scholar] [CrossRef]
- Li, X.; Lu, W.; Ma, Z.; Tuo, N. The undrained characteristics of tengger desert sand from true triaxial testing. Adv. Civil. Eng. 2021, 2021, 6320397. [Google Scholar] [CrossRef]
- Chazallon, C.; Hornych, P.; Mouhoubi, S. Elastoplastic model for the long-term behavior modeling of unbound granular materials in flexible pavements. Int. J. Geomech. 2006, 6, 279–289. [Google Scholar] [CrossRef]
- Melan, E. Theorie statisch unbestimmter Systemeaus aus idealplastischen Baustoffen. Sitzungsber. Akad. Wiss. Wien Math.-Naturwiss. Kl. Abt. IIA 1936, 145, 195–218. [Google Scholar]
- Rahman, M.S.; Erlingsson, S. Moisture influence on the resilient deformation behaviour of unbound granular materials. Int. J. Pave. Eng. 2016, 17, 763–775. [Google Scholar] [CrossRef]
- Guo, L.; Cai, Y.Q.; Jardine, R.J.; Yang, Z.; Wang, J. Undrained behavior of intact soft clay under cyclic paths that match vehicle loading conditions. Can. Geotech. J. 2018, 55, 90–106. [Google Scholar] [CrossRef] [Green Version]
- Xia, P.; Deng, W.; Shao, L.; Zhang, X. Role of Elastic Upper Limit in Shakedown Study for Granular soils. Transp. Geotech. 2022, 34, 100746. [Google Scholar] [CrossRef]
- Mamou, A.; Powrie, W.; Priest, J.A.; Clayton, C. The effects of drainage on the behaviour of railway track foundation materials during cyclic loading. Géotechnique 2017, 67, 845–854. [Google Scholar] [CrossRef] [Green Version]
- Mamou, A.; Priest, J.A.; Clayton, C.R.I.; Powrie, W. Behaviour of saturated railway track foundation materials during undrained cyclic loading. Can. Geotech. J. 2018, 55, 689–697. [Google Scholar] [CrossRef] [Green Version]
- Mamou, A.; Clayton, C.; Powrie, W.; Priest, J. The role of clay content on the response of railway track foundations during free-to-drain cyclic changes in principal stress rotation. Transp. Geotech. 2019, 20, 100246. [Google Scholar] [CrossRef]
- Werkmeister, S.; Dawson, A.R.; Wellner, F. Permanent deformation behavior of granular materials and the shakedown concept. Transp. Res. Rec. 2001, 1757, 75–81. [Google Scholar] [CrossRef]
- Werkmeister, S.; Dawson, A.R.; Wellner, F. Pavement design model for unbound granular materials. J. Transp. Eng. 2004, 130, 665–674. [Google Scholar] [CrossRef]
- Werkmeister, S. Permanent Deformation Behaviour of Unbound Granular Materials in Pavement Constructions. Ph.D. Thesis, Department of Civil Engineering, Dresden University of Technology, Dresden, Germany, 2004. [Google Scholar]
- Flora, A.; Lirer, S.; Silvestri, F. Undrained cyclic resistance of undisturbed gravelly soils. Soil Dyn. Earthq. Eng. 2012, 43, 366–379. [Google Scholar] [CrossRef]
- Sivathayalan, S.; Ha, D. Effect of static shear stress on the cyclic resistance of sands in simple shear loading. Can. Geotech. J. 2011, 48, 1471–1484. [Google Scholar] [CrossRef]
- Hyodo, M.; Tanimizu, H.; Yasufuku, N.; Murata, H. Undrained cyclic and monotonic triaxial behavior of saturated loose sand. Soils Found. 1994, 34, 19–32. [Google Scholar] [CrossRef] [Green Version]
- Seed, H.B.; Martin, P.P.; Lysmer, J. The Generation and Dissipation of Pore Water Pressures during Soil Liquefaction; College of Engineering, University of California: Berkeley, CA, USA, 1975. [Google Scholar]
- Polito, C.P.; Green, R.A.; Lee, J. Pore pressure generation models for sands and silty soils subjected to cyclic loading. J. Geotech. Geoenviron. Eng. 2008, 134, 1490–1500. [Google Scholar] [CrossRef]
- Chiaradonna, A.; Flora, A.; d’Onofrio, A.; Bilotta, E. A pore water pressure model calibration based on in-situ test results. Soils Found. 2020, 60, 327–341. [Google Scholar] [CrossRef]
- Pan, K.; Yang, Z.X. Effects of initial static shear on cyclic resistance and pore pressure generation of saturated sand. Acta Geotech. 2018, 13, 473–487. [Google Scholar]
- Pan, K.; Cai, Y.; Yang, Z.; Pan, X. Liquefaction of sand under monotonic and cyclic shear conditions: Impact of drained preloading history. Soil Dyn. Earthq. Eng. 2019, 126, 105775. [Google Scholar] [CrossRef]
- Pan, K.; Zhou, G.; Yang, Z.; Cai, Y. Comparison of cyclic liquefaction behavior of clean and silty sands considering static shear effect. Soil Dyn. Earthq. Eng. 2020, 139, 106338. [Google Scholar] [CrossRef]
- Li, X.; Xu, W.; Chen, Q.; Yang, W. Cyclic behavior of saturated aeolian sand under true triaxial conditions. Geofluids 2022, 2022, 1–17. [Google Scholar]
- Li, X.; Xu, W.; Chang, L.; Yang, W. Shear behaviour of aeolian sand with different density and confining pressure. Appl. Sci. 2022, 12, 3020. [Google Scholar] [CrossRef]
- Powrie, W.; Yang, L.A.; Clayton, C.R.I. Stress changes in the ground below ballasted railway track during train passage. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2007, 221, 247–262. [Google Scholar] [CrossRef]
- Hyodo, M.; Murata, H.; Yasufuku, N.; Fujii, T. Undrained cyclic shear strength and residual strain of saturated sand by cyclic triaxial tests. Soils Found. 1991, 31, 60–76. [Google Scholar] [CrossRef]
- Ishihara, K. Soil Behavior in Earthquake Geotechnics; Clarendon Press: Oxford, UK, 1996. [Google Scholar]




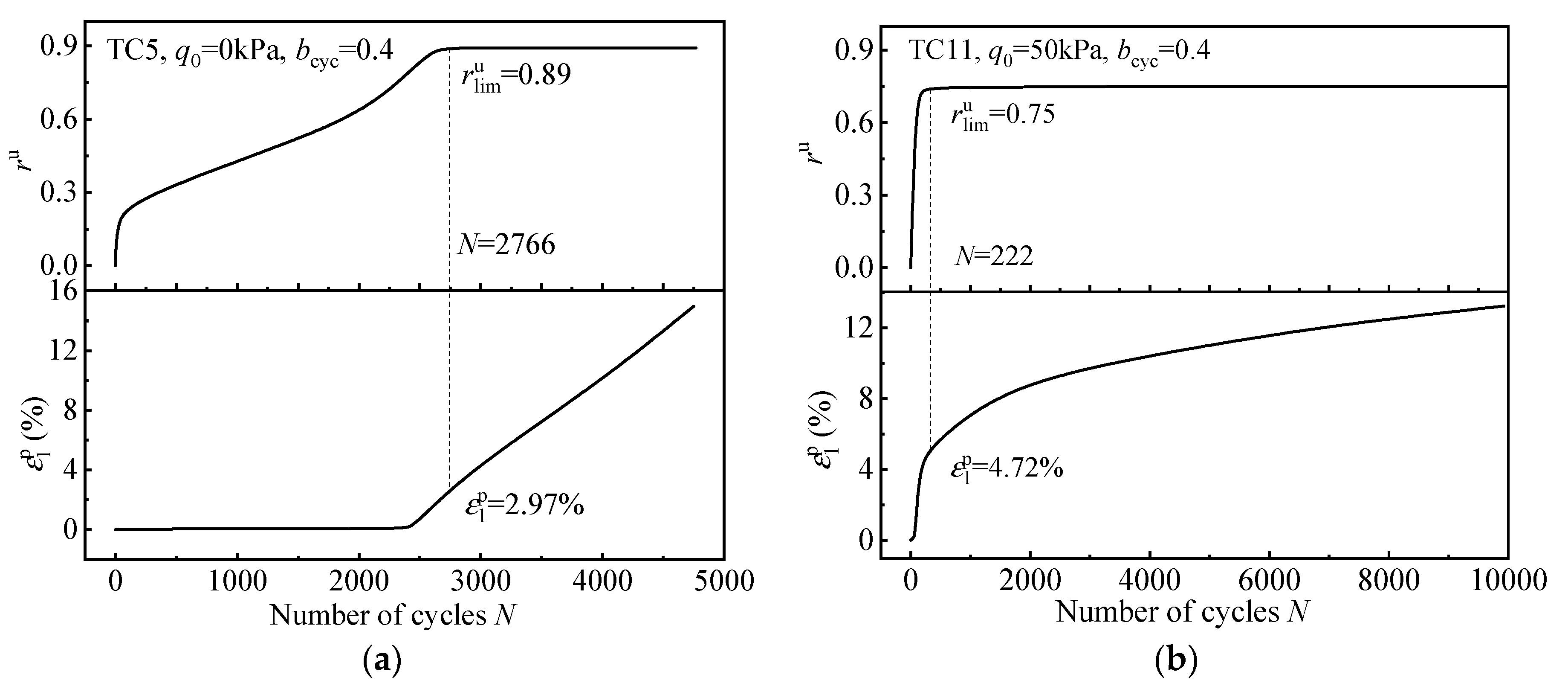

| Coefficient of Uniformity Cu | Coefficient of Curvature Cc | Specific Gravity Gs | Mean Particle Diameter d50 | Void Ratio | |
|---|---|---|---|---|---|
| max | min | ||||
| 2.1 | 1.0 | 2.67 | 0.17 mm | 0.907 | 0.589 |
| Number of Tests | (kPa) | (kPa) | qampl (kPa) | bcyc | q0 (kPa) |
|---|---|---|---|---|---|
| TC1 | 20 | 0 | 20 | 0 | 0 |
| TC2 | 22.9 | 9.2 | 20 | 0.4 | 0 |
| TC3 | 21.8 | 17.44 | 20 | 0.8 | 0 |
| TC4 | 30 | 0 | 30 | 0 | 0 |
| TC5 | 34.4 | 13.8 | 30 | 0.4 | 0 |
| TC6 | 32.7 | 26.2 | 30 | 0.8 | 0 |
| TC7 | 40 | 0 | 40 | 0 | 0 |
| TC8 | 45.6 | 18.4 | 40 | 0.4 | 0 |
| TC9 | 43.7 | 34.9 | 40 | 0.8 | 0 |
| TC10 | 20 | 0 | 20 | 0 | 50 |
| TC11 | 22.9 | 9.2 | 20 | 0.4 | 50 |
| TC12 | 21.8 | 17.44 | 20 | 0.8 | 50 |
| TC13 | 30 | 0 | 30 | 0 | 50 |
| TC14 | 34.4 | 13.8 | 30 | 0.4 | 50 |
| TC15 | 32.7 | 26.2 | 30 | 0.8 | 50 |
| TC16 | 40 | 0 | 40 | 0 | 50 |
| TC17 | 45.6 | 18.4 | 40 | 0.4 | 50 |
| TC18 | 43.7 | 34.9 | 40 | 0.8 | 50 |
| TC19 | 20 | 0 | 20 | 0 | 100 |
| TC20 | 22.9 | 9.2 | 20 | 0.4 | 100 |
| TC21 | 21.8 | 17.44 | 20 | 0.8 | 100 |
| TC22 | 30 | 0 | 30 | 0 | 100 |
| TC23 | 34.4 | 13.8 | 30 | 0.4 | 100 |
| TC24 | 32.7 | 26.2 | 30 | 0.8 | 100 |
| TC25 | 40 | 0 | 40 | 0 | 100 |
| TC26 | 45.6 | 18.4 | 40 | 0.4 | 100 |
| TC27 | 43.7 | 34.9 | 40 | 0.8 | 100 |
| TC28 | 20 | 0 | 20 | 0 | 150 |
| TC29 | 22.9 | 9.2 | 20 | 0.4 | 150 |
| TC30 | 21.8 | 17.44 | 20 | 0.8 | 150 |
| TC31 | 30 | 0 | 30 | 0 | 150 |
| TC32 | 34.4 | 13.8 | 30 | 0.4 | 150 |
| TC33 | 32.7 | 26.2 | 30 | 0.8 | 150 |
| TC34 | 40 | 0 | 40 | 0 | 150 |
| TC35 | 45.6 | 18.4 | 40 | 0.4 | 150 |
| TC36 | 43.7 | 34.9 | 40 | 0.8 | 150 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Li, X.; Lü, X.; Yang, W. Cyclic True Triaxial Tests on Aeolian Sand Considering Initial Shear Effect. Sustainability 2022, 14, 16730. https://doi.org/10.3390/su142416730
Xu W, Li X, Lü X, Yang W. Cyclic True Triaxial Tests on Aeolian Sand Considering Initial Shear Effect. Sustainability. 2022; 14(24):16730. https://doi.org/10.3390/su142416730
Chicago/Turabian StyleXu, Wendong, Xuefeng Li, Xilin Lü, and Wenwei Yang. 2022. "Cyclic True Triaxial Tests on Aeolian Sand Considering Initial Shear Effect" Sustainability 14, no. 24: 16730. https://doi.org/10.3390/su142416730






