Hydrodynamic Response of Ocean-Towed Cable-Array System under Different Munk Moment Coefficients
Abstract
:1. Introduction
2. Computational Theory
2.1. Mathematical Model
2.2. Expression of Munk Moments
2.2.1. Basic Assumptions
- (1)
- The towed body is considered as a rigid body;
- (2)
- The shape of the towed body is symmetric with respect to the xOy plane and the xOz plane. In the calculation of the additional mass, the asymmetry of the xOz plane that may be caused by the geometric shape of the towed body is ignored;
- (3)
- The inertial product of the towed body is not taken into account, which means Jxy = Jyx = Jxz = Jzx = Jyz = Jzy = 0;
- (4)
- The towed body is completely submerged in the fluid medium and in a fully wet state;
- (5)
- The change of the mass and mass distribution of the towed body in the course of navigation is negligible;
- (6)
- Without considering the Earth’s autobiography and the curvature of the Earth, the ground coordinate system is regarded as the inertial coordinate system.
2.2.2. Selection of Coordinate System
2.2.3. Definition of Kinematic Parameters
- (1)
- Position coordinates and velocity:, ,
- (2)
- Attitude angle and angular velocity:,
- (3)
- Rudder angle and trajectory angle,
- (4)
- Angle of attack α and sideslip angle β
2.2.4. Kinetic Equation and Kinematic Equation
2.2.5. Munk Moment
3. Numerical Model Setup
4. Results and Discussion
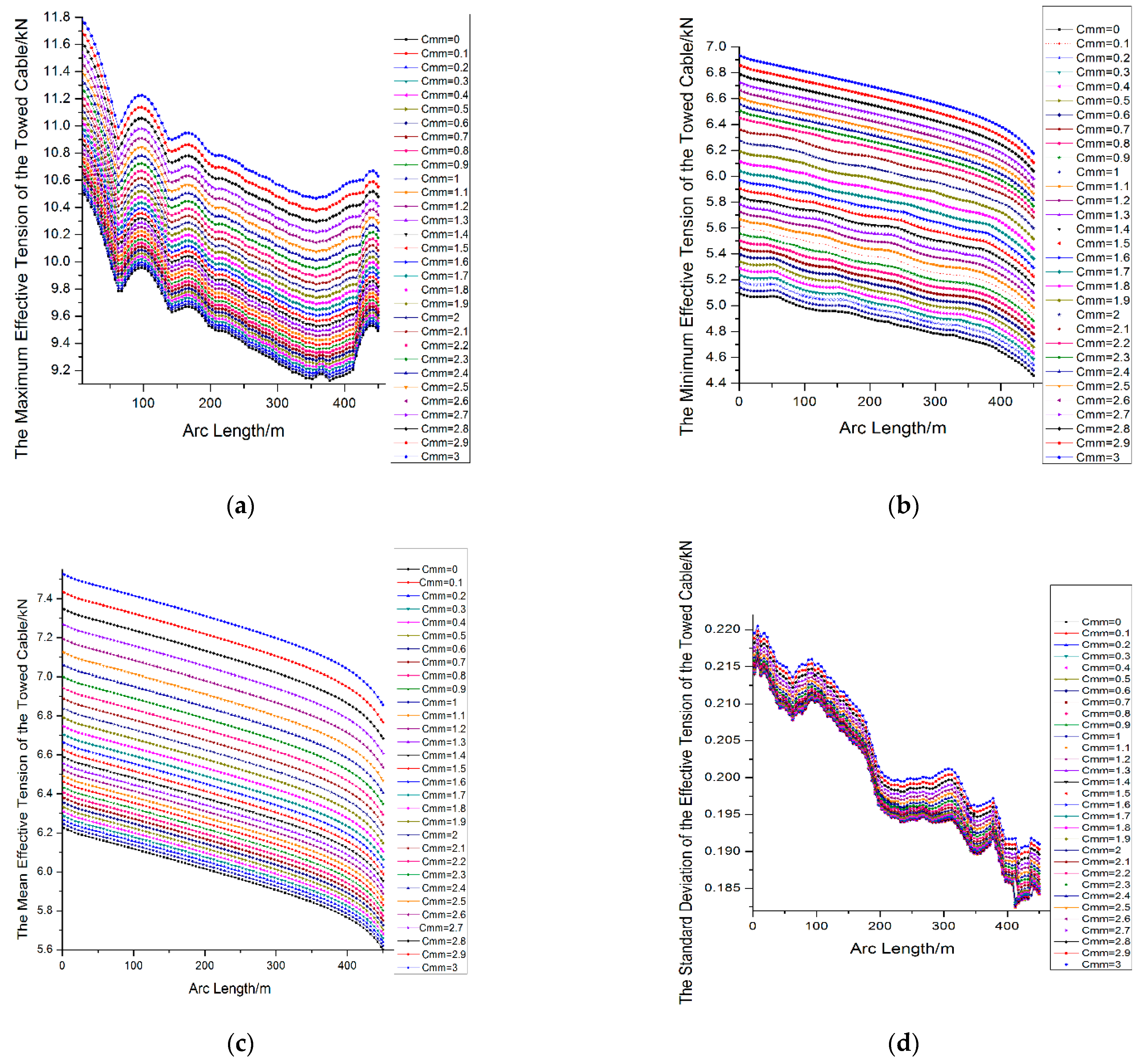
4.1. The Variation of the Effective Tension of the Towing Cable
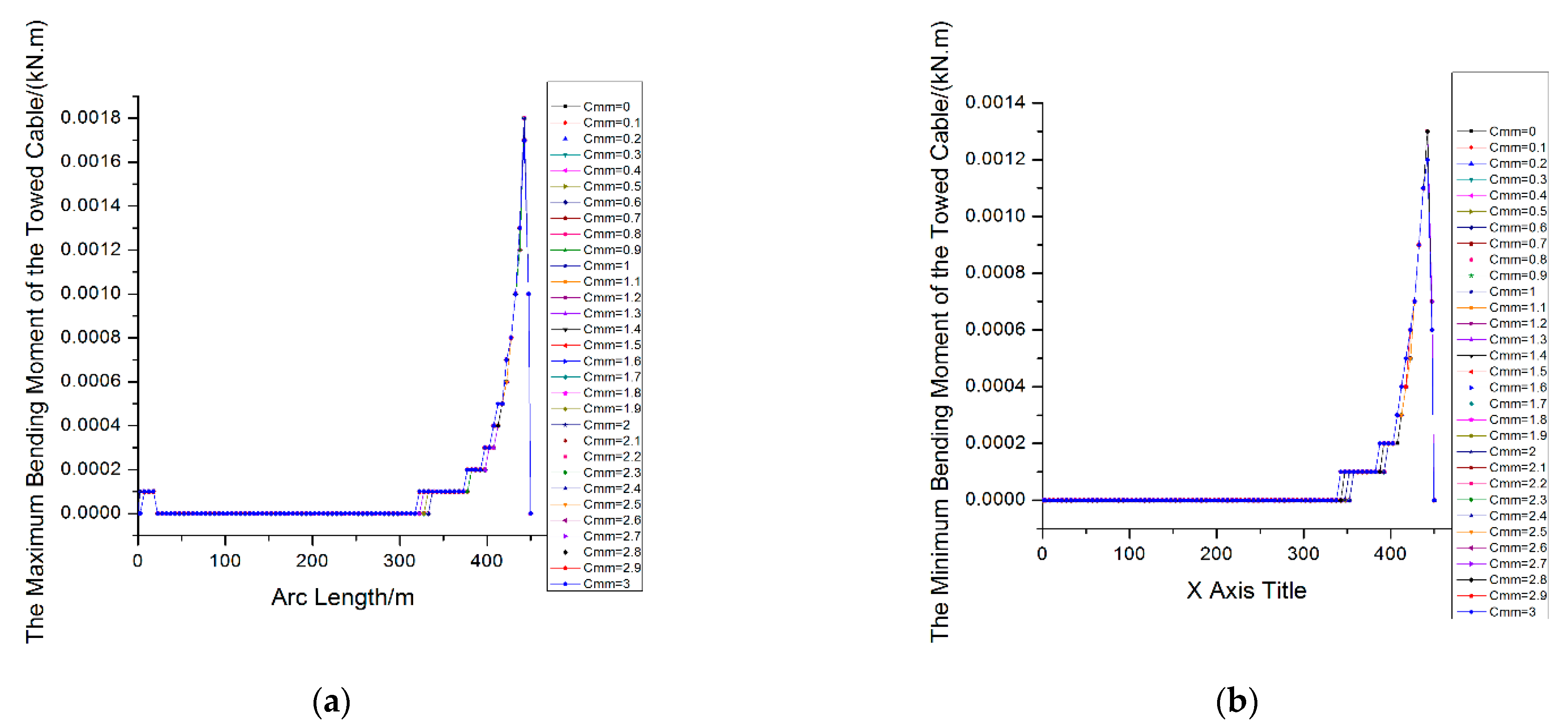
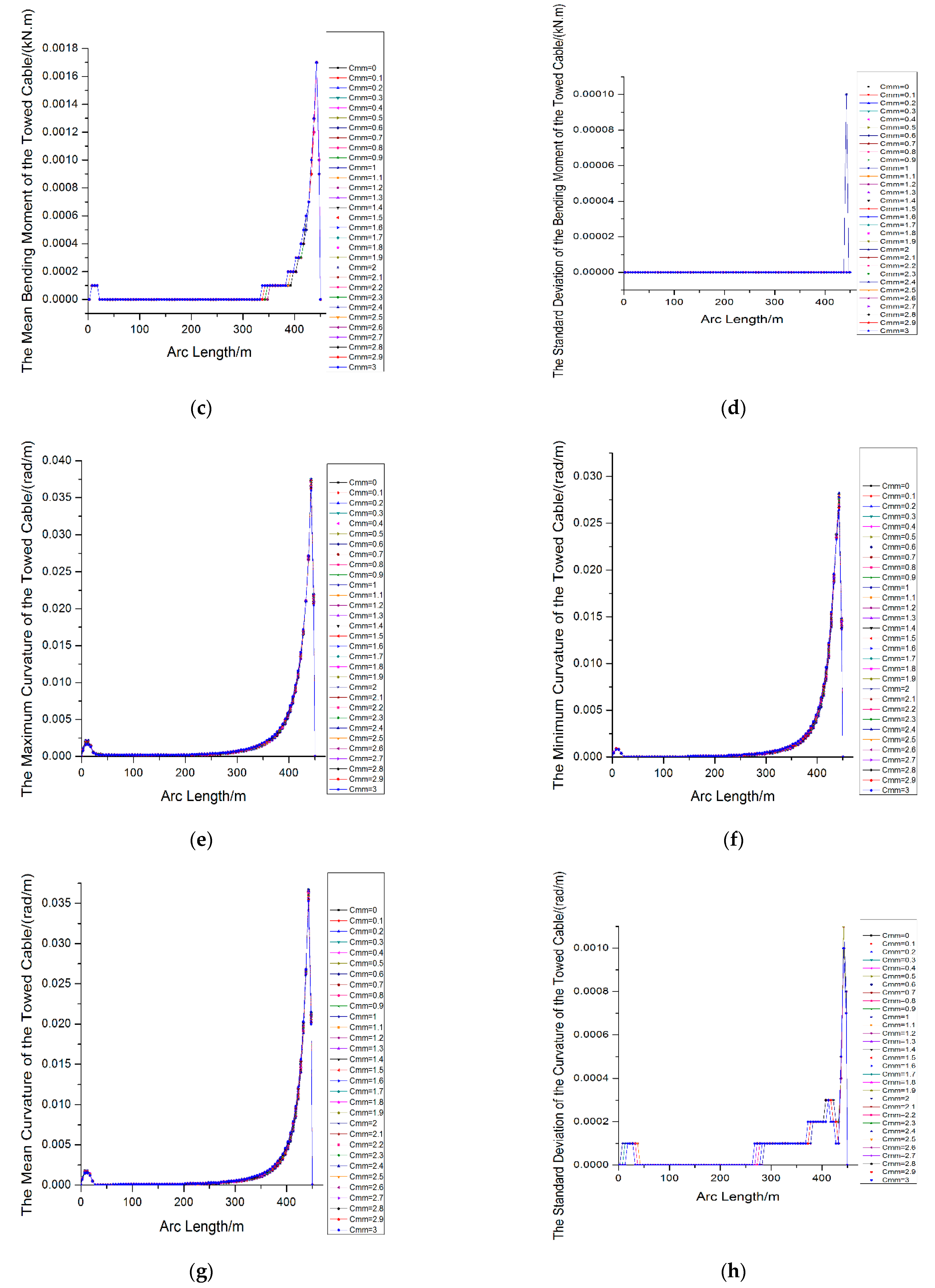
4.2. The Variation of Bending of the Towing Cable
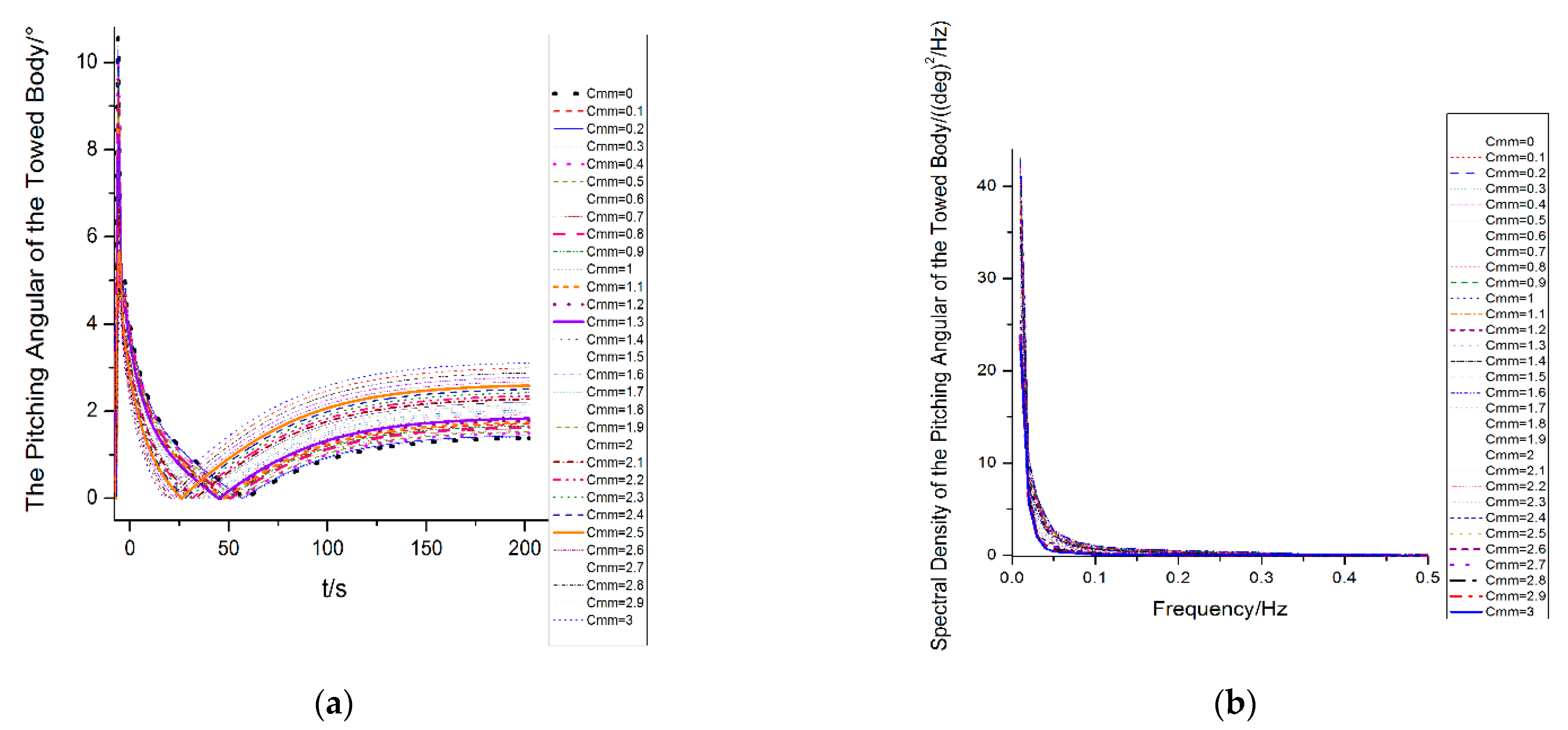
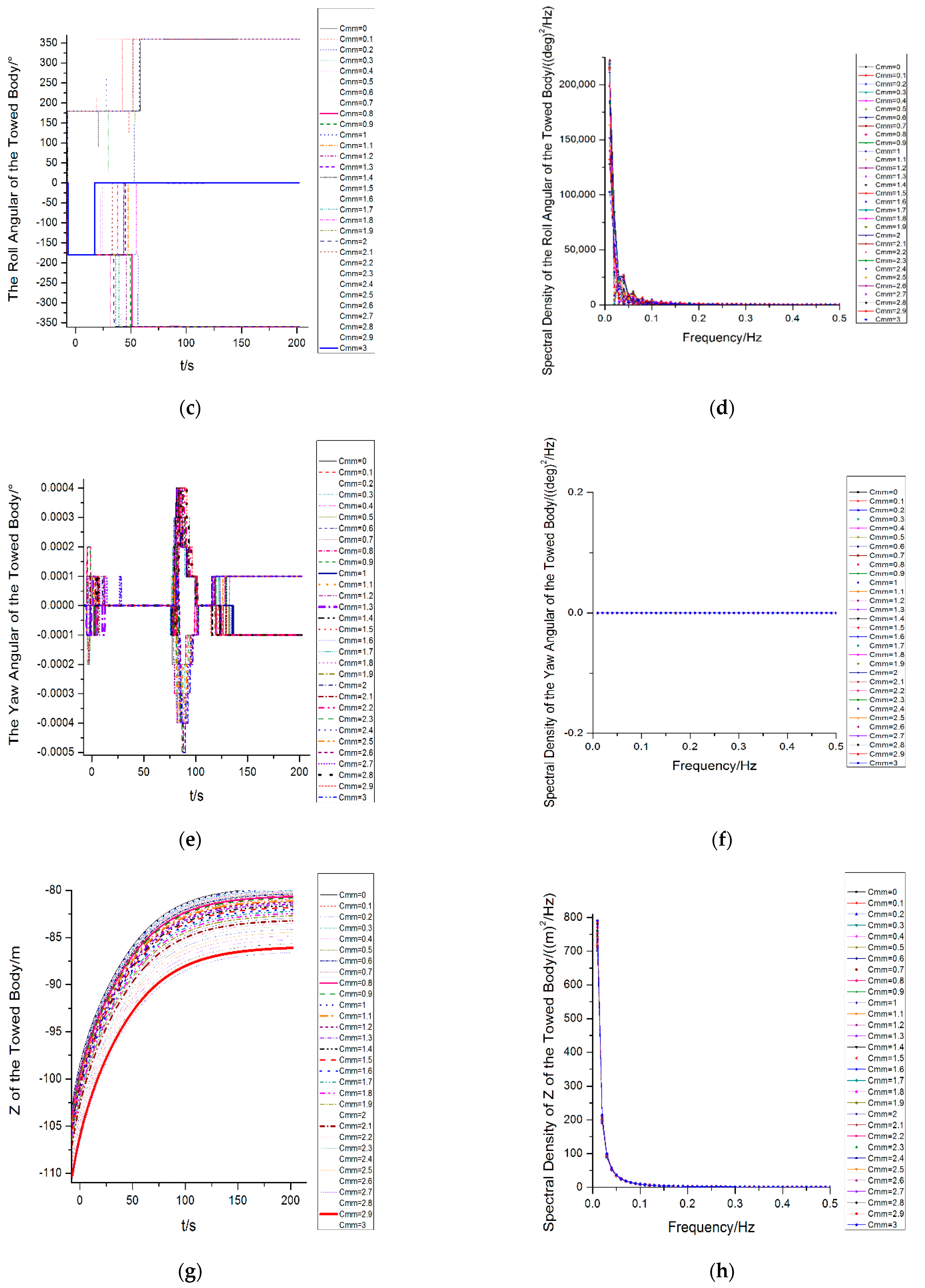
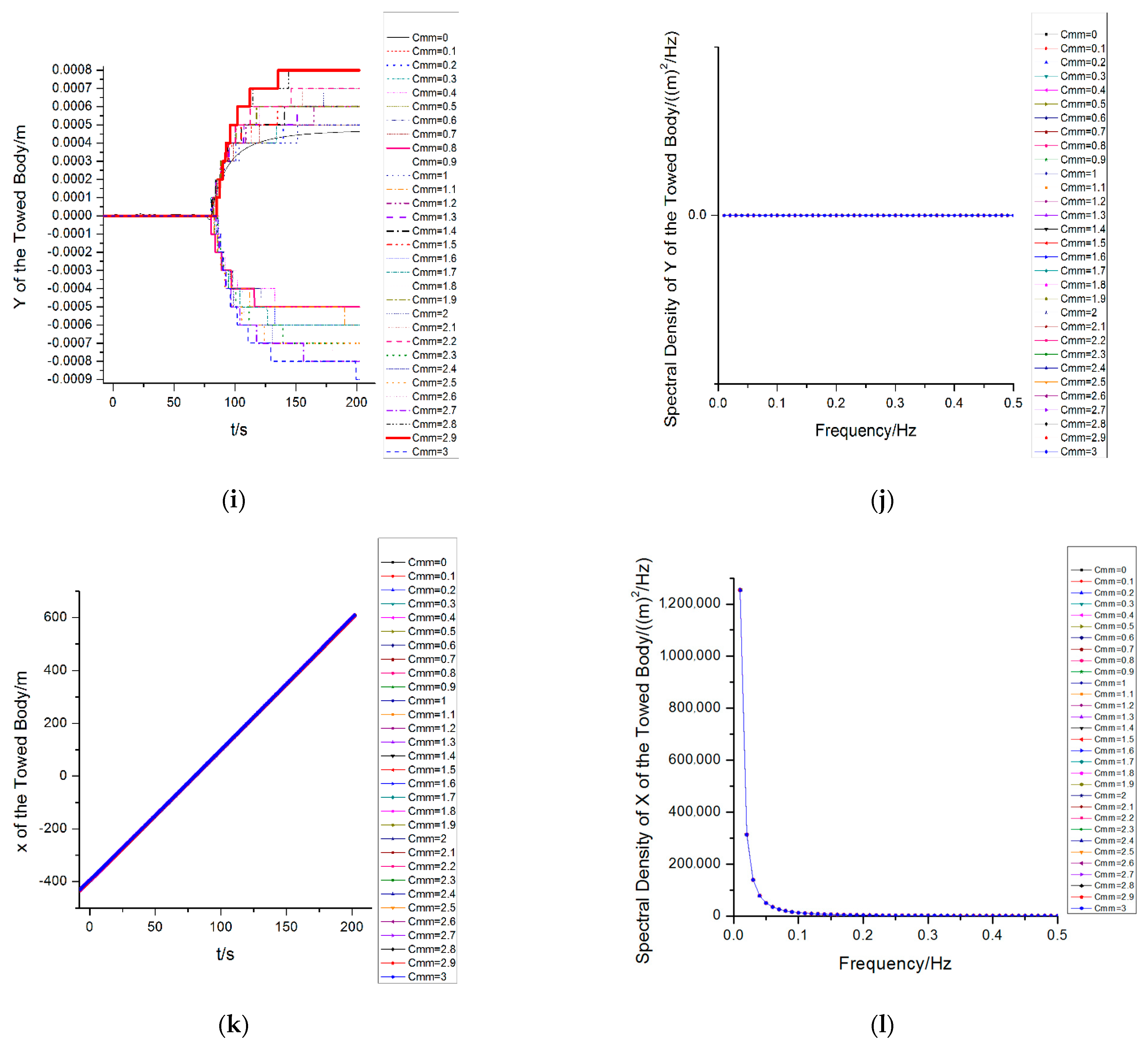
4.3. The Variation of the Towed Body
5. Conclusions
- (1)
- The amplitude of the maximum effective tension under the action of a certain single Munk moment coefficient has a tendency of recurrent fluctuations along the length direction. The coordination and synchronization of the effective tension of the towing cable may be better than that when there is no Munk moment; when the Munk moment coefficient is 0.5–0.9, the effective tension of the towing cable has almost the same synchronism along the length direction; with the increase in the Munk moment coefficients, the synchronism of the tension of the towing cable firstly decrease and then increase.
- (2)
- When the Munk moment coefficient is small, the drag by the Munk moment makes the underwater towed body rotate, and the flow facing surface area changes constantly. Sometimes, this is a large change, and sometimes it is small; when it is large, the drag force and the damping force on the towed body of the current become larger, which makes the towing cable tension larger.
- (3)
- Under different Munk moment coefficients, the bending moment exhibits a poor continuity along the cable length direction, but the change of the bending moment along the cable length shows better coordination and synchronization; the curvature exhibits better continuity along the cable length, but its coordination and synchronization of the curvature along the cable length is poor.
- (4)
- With the increase in the Munk moment coefficient, the pitching angle of the towed body in the stable state increases successively and eventually approaches a certain stable value with the increase in the Munk coefficient. The pitching and roll of the towed body interact with each other; the time turning point of the roll angle into the steady state is in advance of the increase in the Munk moment coefficient in proper sequence; under different Munk moment coefficients, the roll angle of the towed body is basically maintained at three values when the towing attitude of the towed body is basically stable. The Munk moment has little effect on the yaw angle, the yaw angle of the towed body will not fluctuate with the change of the external frequency in the frequency domain, and no low-frequency response will occur.
- (5)
- With the increase in the Munk moment coefficients, the water depth after the stability of the towed body increases continuously, and the maximum water depth is about 5 m different from the minimum water depth; the change of the heave of the towed body is not sensitive to the change of frequency. The time taken to reach the lateral (sway) steady state is advanced in turn and before its stabilization. The change of the Munk moment has a very weak influence on the dynamic response of the X-direction of the towed body
- (6)
- From the order of magnitude, the influence of the Munk moment on the heave direction of the towed body is much larger than that of the sway and surge directions, which indicates that the change of the Munk moment mainly affects the heave response of the towed body. The influence of the Munk moment on the sway and yaw response of the towed body is very weak, but the influence on the sway direction is greater than that of the surge direction.
- (7)
- The study enriched the research on the dynamic characteristics of ocean towing systems and helps to design a more stable towing system, which will play a more efficient role in the exploration of marine resources and sustainability in ocean engineering.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bettles, R.W.; Chapman, D.A. The experimental verification of a towed body and cable dynamic response theory. Ocean Eng. 1985, 12, 453–469. [Google Scholar] [CrossRef]
- Wu, J.; Chwang, A.T. A hydrodynamic model of a two-part underwater towed system. Ocean Eng. 2000, 27, 455–472. [Google Scholar] [CrossRef]
- Wu, J.; Chwang, A.T. Experimental investigation on a two-part underwater towed system. Ocean Eng. 2001, 28, 735–750. [Google Scholar] [CrossRef]
- Wu, J.; Ye, J.; Yang, C.; Chen, Y.; Tian, H.; Xiong, X. Experimental study on a controllable underwater towed system. Ocean Eng. 2005, 32, 1803–1817. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Dai, J.; Pang, Y.; Xu, Y. Calculation of coupling between the cable and the towed body in the towed system. Ocean Eng. 2002, 20, 38–40. [Google Scholar]
- Abiow, C.M.; Schechter, S. Numerical simulation of undersea cable dynamics. Ocean Eng. 1983, 10, 443–457. [Google Scholar] [CrossRef]
- Choc, Y.I.; Casarella, M.J. Configuration of a Towline Attached to a Vehicle Moving in a Circular Path. J. Hydronautics 1972, 6, 51–57. [Google Scholar]
- Chapman, D.A. Towed cable behavior during ship turning maneuvers. Ocean Eng. 1984, 11, 327–361. [Google Scholar] [CrossRef]
- Kishore, S.S.; Ganapathy, C. Analytical investigations on loop-manoeuvre of underwater towed cable-array system. Appl. Ocean Res. 1996, 18, 353–360. [Google Scholar] [CrossRef]
- Koh, C.G.; Rong, Y. Dynamic analysis of large displacement cable motion with experimental verification. J. Sound Vib. 2004, 272, 187–206. [Google Scholar] [CrossRef]
- Sun, F.J.; Zhu, Z.H.; LaRosa, M. Dynamic modeling of cable towed body using nodal position finite element method. Ocean Eng. 2011, 38, 529–540. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, G. Parameters influence on maneuvered towed cable system dynamics. Appl. Ocean Res. 2015, 49, 27–41. [Google Scholar] [CrossRef]
- Yuan, Z.; Jin, L.; Chi, W.; Tian, H. Finite difference method for solving the nonlinear dynamic equation of underwater towed system. Int. J. Comp. Meth-Sing 2014, 11, 1350060. [Google Scholar] [CrossRef]
- Yuan, Z.J.; Jin, L.A.; Chi, W.; Jiang, X.G.; Zheng, Z.L. The underwater towed system behavior during SHIP turning maneuvers. J. Mar. Sci. Tech.-Jpn. 2017, 25, 464–474. [Google Scholar]
- Rodríguez Luis, Á.; Armesto, J.A.; Guanche, R.; Barrera, C.; Vidal, C. Simulation of marine towing cable dynamics using a finite elements method. J. Mar. Sci. Eng. 2020, 8, 140. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Li, G.; Lian, L. Numerical model of towed cable body system validation from sea trial experimental data. Ocean Eng. 2021, 226, 108859. [Google Scholar] [CrossRef]
- Huang, S. Dynamic analysis of three-dimensional marine cables. Ocean Eng. 1994, 21, 587–605. [Google Scholar] [CrossRef]
- Chai, Y.T.; Varyani, K.S.; Barltrop, N. Three-dimensional Lump-Mass formulation of a catenary riser with bending, torsion and irregular seabed interaction effect. Ocean Eng. 2002, 29, 1503–1525. [Google Scholar] [CrossRef]
- Wang, F.; Huang, G.; Deng, D. Dynamic response analysis of towed cable during deployment/retrieval. J. Shanghai Jiaotong Univ. (Sci.) 2008, 13, 245. [Google Scholar] [CrossRef]
- Zhu, K.; Zheng, D.; Cai, Y.; Yu, C.; Wang, R.; Liu, Y.L.; Zhang, F. Nonlinear Hydrodynamic Response of Marine Cable -Body System Undergoing Random Dynamic Excitation. J. Hydrodyn. 2009, 21, 851–855. [Google Scholar] [CrossRef]
- Yang, B.; Zhu, K.; Zhu, Y.; Qin, D. Dynamic response of towed line array. J. Hydrodyn. 2013, 25, 616–619. [Google Scholar] [CrossRef]
- Hill, J.; Laycock, S.; Chai, S.; Balash, C.; Morand, H. Hydrodynamic loads and response of a Mid Water Arch structure. Ocean Eng. 2014, 83, 76–86. [Google Scholar] [CrossRef]
- Du, X.; Cui, H.; Zhang, Z. A numerical method for analyzing the influence of underwater vehicle flow field on dynamic behavior of towed sonar cable array. Ocean Eng. 2019, 175, 163–175. [Google Scholar] [CrossRef]
- Rinaldi, G.; Gordelier, T.; Sansom, M.; Johanning, L. Development of a modular mooring system with clump weights. Ocean Eng. 2021, 223, 108536. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, H.; Li, N.; An, W.; Lim, F.; Wang, C.; Estefen, S.F. The motion response and hydrodynamic performance comparisons of the new subsea suspended manifold with two mooring scenarios. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 1–16. [Google Scholar] [CrossRef]
- Park, S.H.; Lee, S.J.; Lee, S. Experimental investigation of towing- and course-stability of a FPSO towed by a tug-boat with lateral motion. Int. J. Nav. Arch. Ocean 2021, 13, 12–23. [Google Scholar] [CrossRef]
- Rentschler, M.U.T.; Adam, F.; Chainho, P. Design optimization of dynamic inter-array cable systems for floating offshore wind turbines. Renew. Sustain. Energy Rev. 2019, 111, 622–635. [Google Scholar] [CrossRef]

| Mass (t) | Mass Moments of Inertia (t.m2) | Total Length (m) | Centre of Mass (m) | ||||
|---|---|---|---|---|---|---|---|
| Ix | Iy | Iz | x | y | z | ||
| 1.5 | 0.1 | 5 | 5 | 3.9 | 0 | 0 | 0 |
| Cylinder Segment | ID (m) | OD (m) | Length (m) | Cumulative Length (m) |
|---|---|---|---|---|
| 1 | 0 | 0.2 | 0.1 | 0.1 |
| 2 | 0 | 0.35 | 0.3 | 0.4 |
| 3 | 0 | 0.5 | 1.0 | 1.4 |
| 4 | 0 | 0.5 | 1.0 | 2.4 |
| 5 | 0 | 0.4 | 1.0 | 3.4 |
| 6 | 0 | 0.2 | 0.5 | 3.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Zhao, B.; Zhu, K. Hydrodynamic Response of Ocean-Towed Cable-Array System under Different Munk Moment Coefficients. Sustainability 2022, 14, 1932. https://doi.org/10.3390/su14031932
Zhang D, Zhao B, Zhu K. Hydrodynamic Response of Ocean-Towed Cable-Array System under Different Munk Moment Coefficients. Sustainability. 2022; 14(3):1932. https://doi.org/10.3390/su14031932
Chicago/Turabian StyleZhang, Dapeng, Bowen Zhao, and Keqiang Zhu. 2022. "Hydrodynamic Response of Ocean-Towed Cable-Array System under Different Munk Moment Coefficients" Sustainability 14, no. 3: 1932. https://doi.org/10.3390/su14031932






