Tripartite Evolutionary Game Analysis for Plastic Pollution Prevention and Control under the Background of China’s Plastic Ban
Abstract
:1. Introduction
2. Related Research
2.1. Actions Taken Aganist Plastic Pollution
2.2. Research Concerning Policies on Plastic Pollution
2.3. The Use of Game Theory to Study Environmental Protection Issues
3. Model Building
3.1. Basic Assumptions
3.2. Construction of Evolutionary Game Model
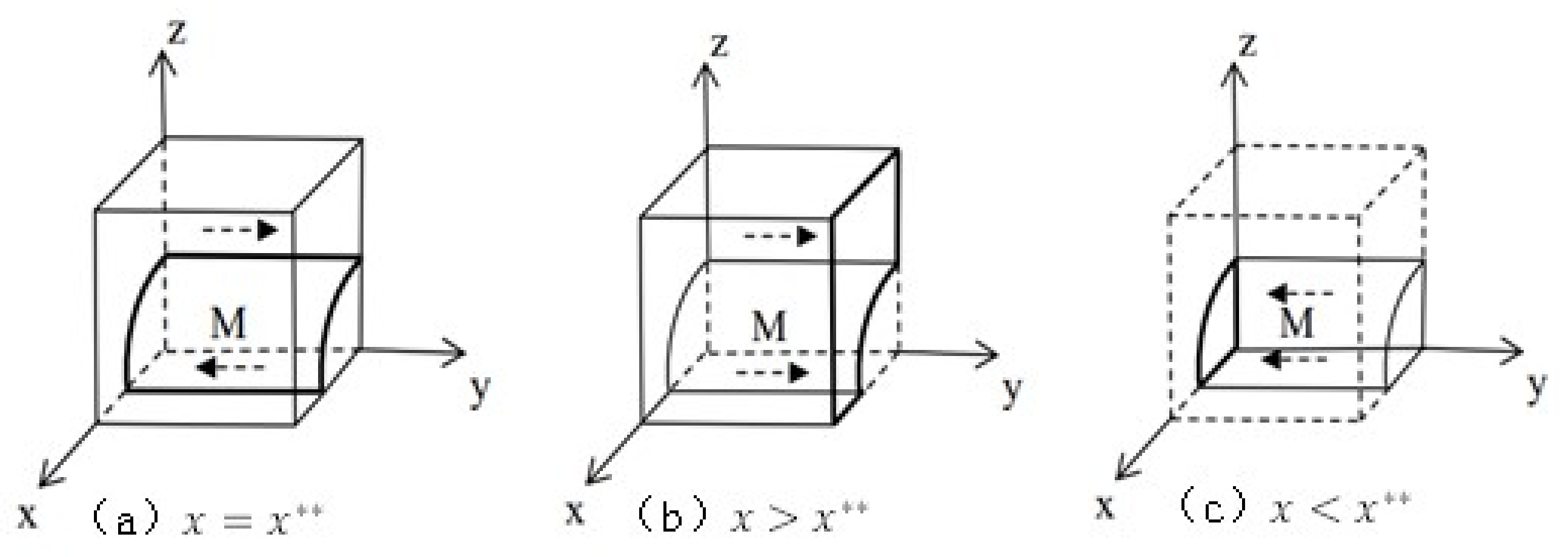
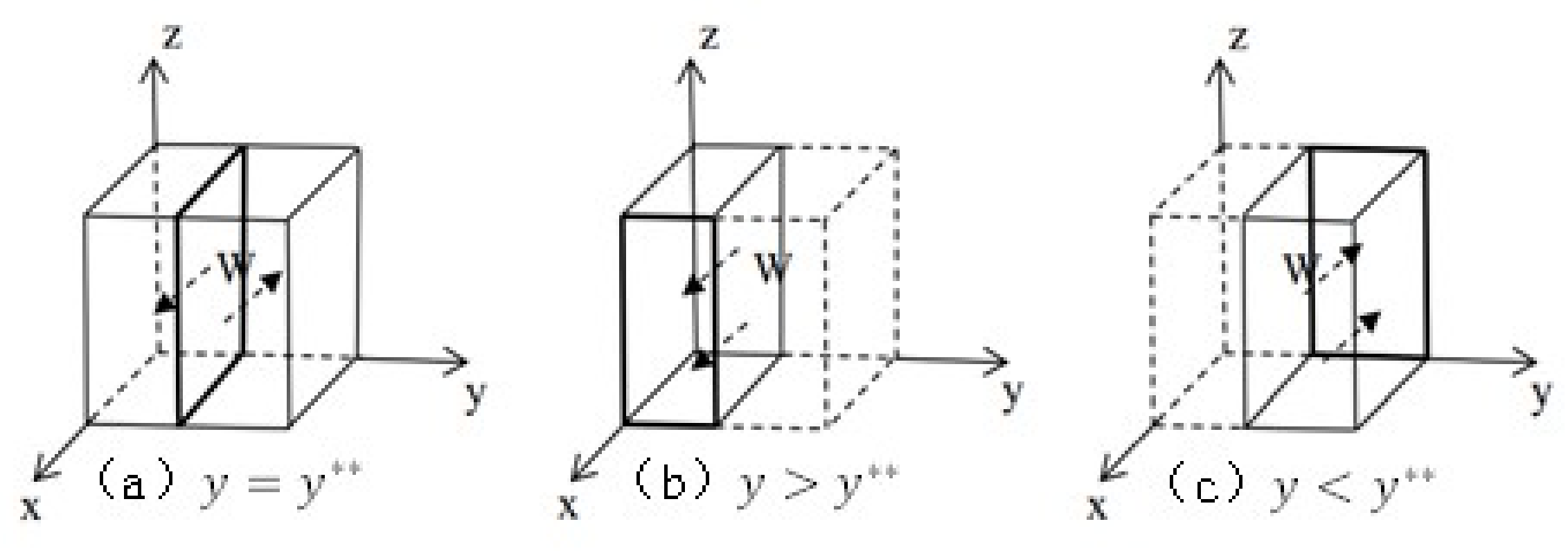
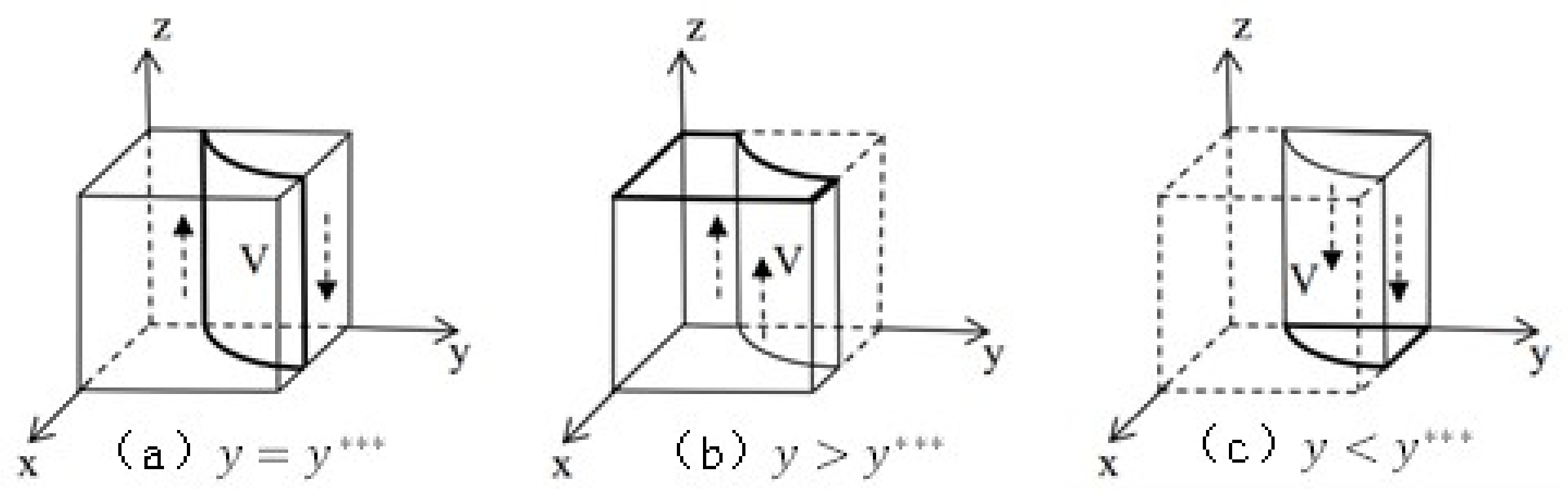
3.3. Model Analysis
4. Numeric Simulation
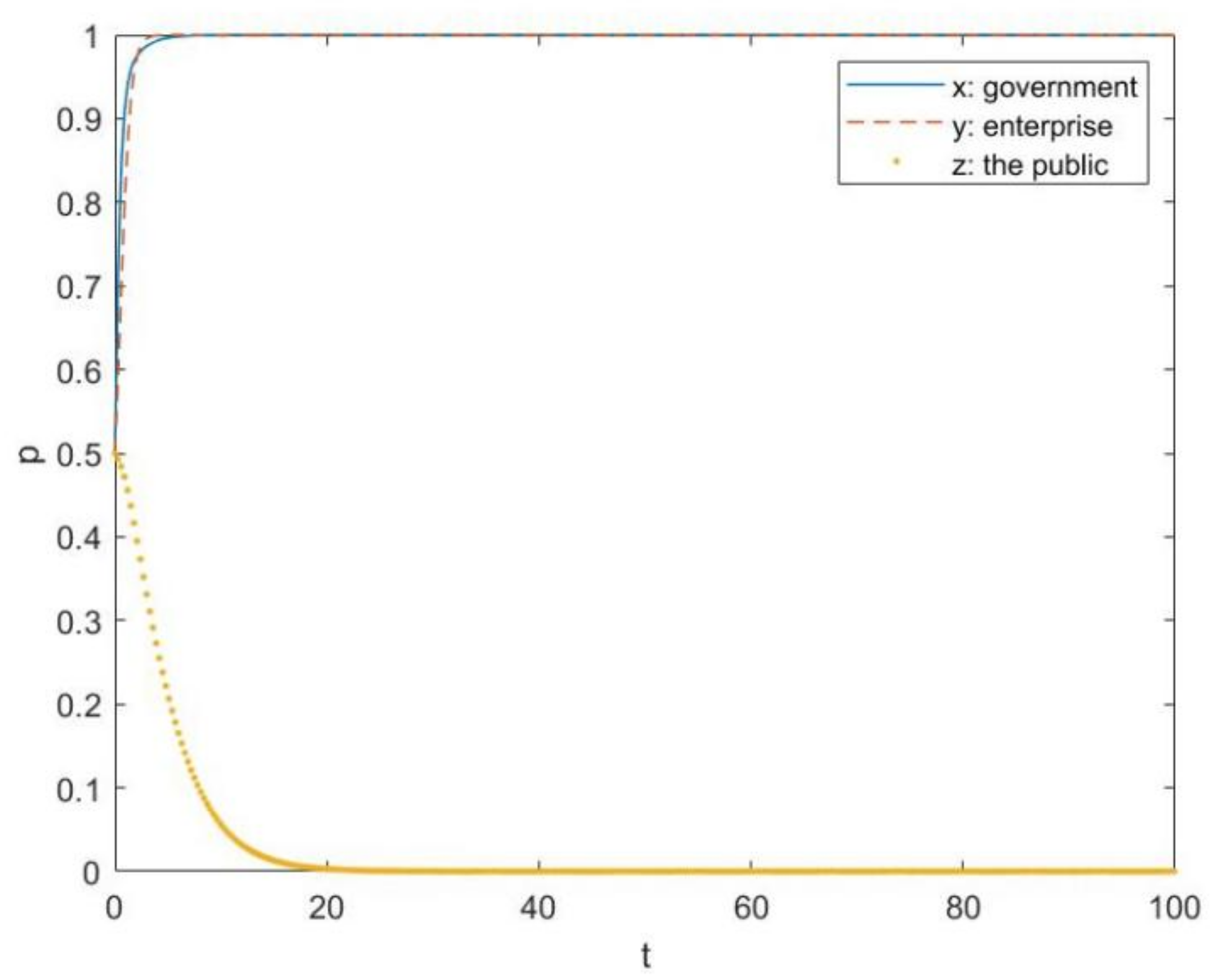
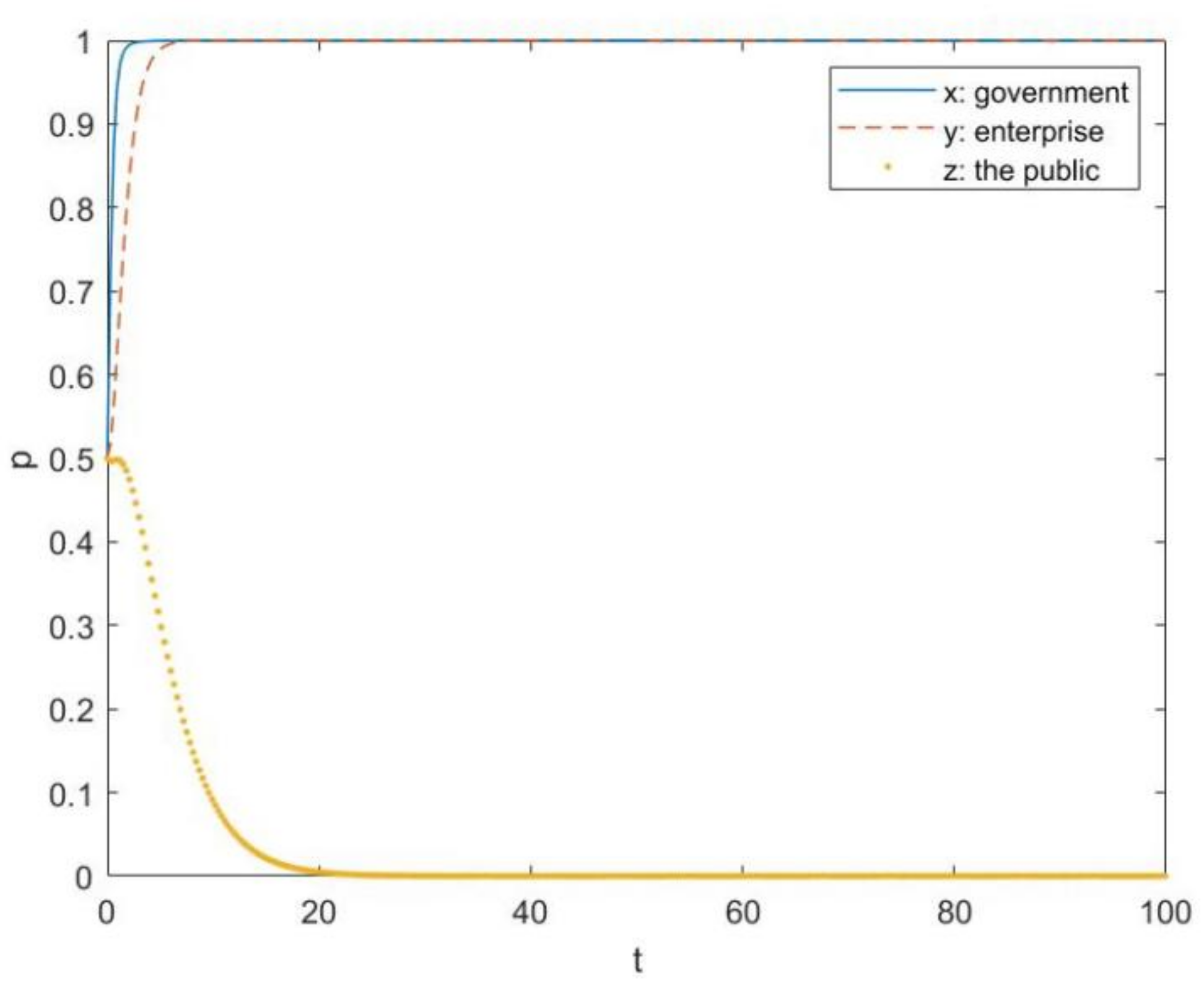
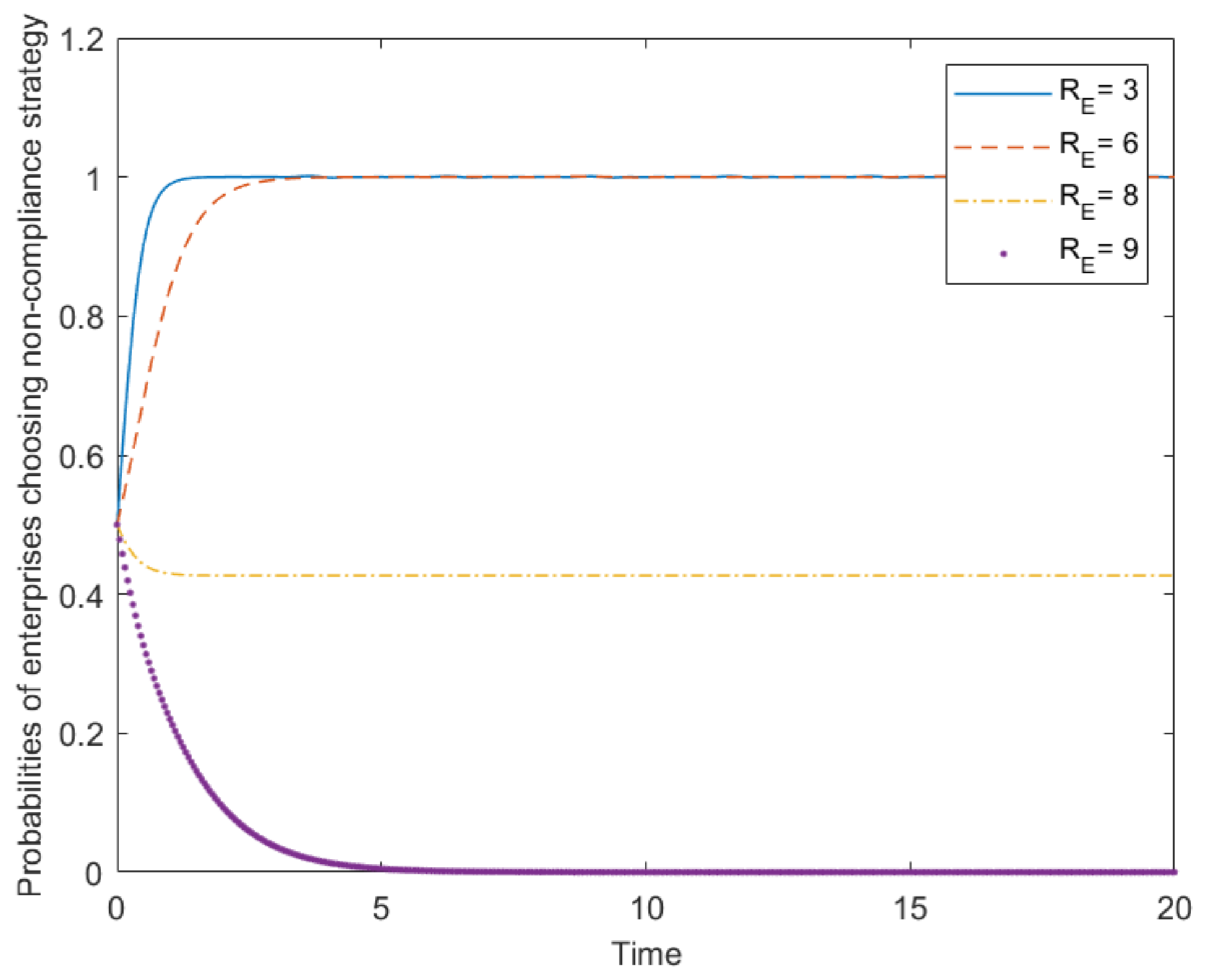
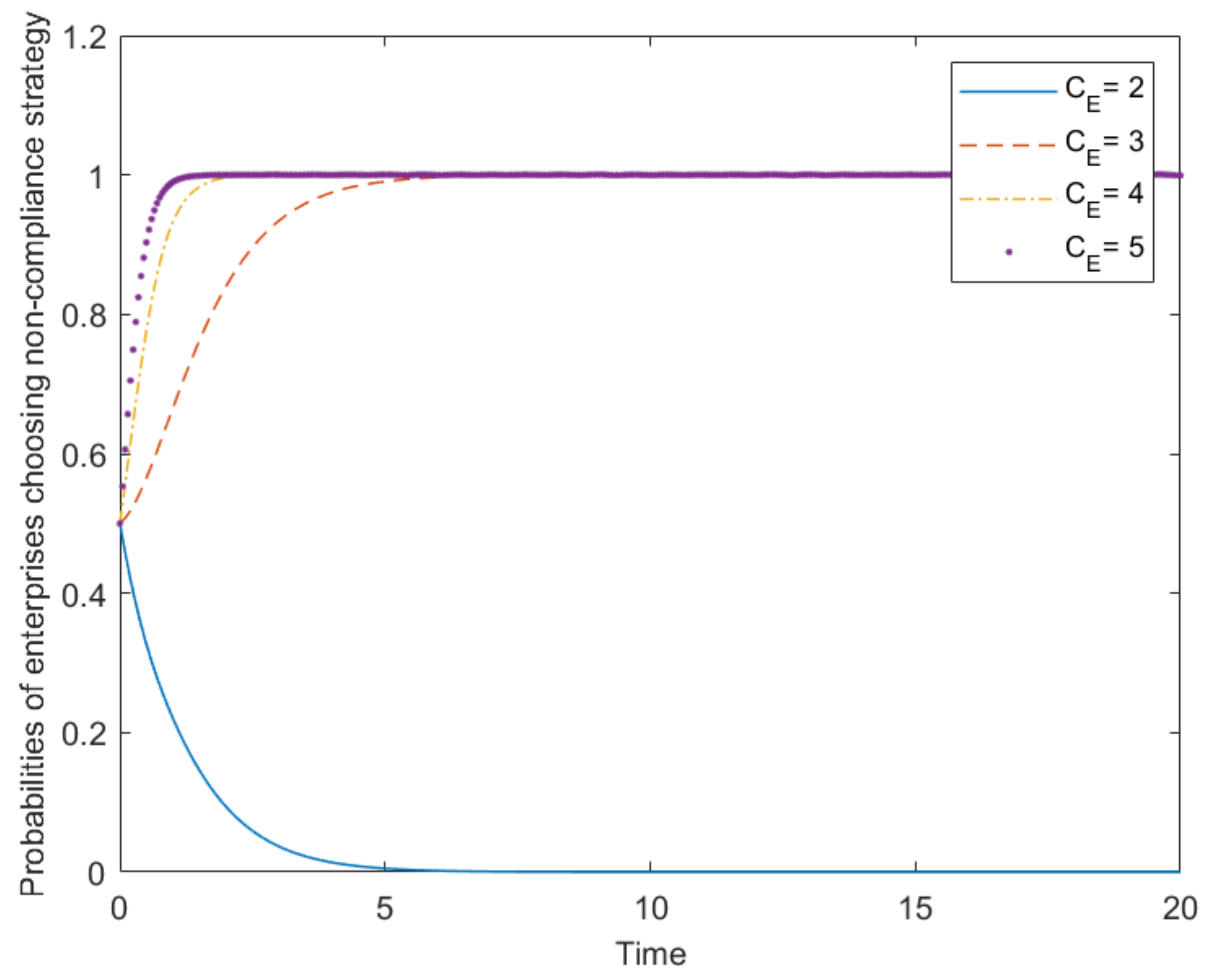
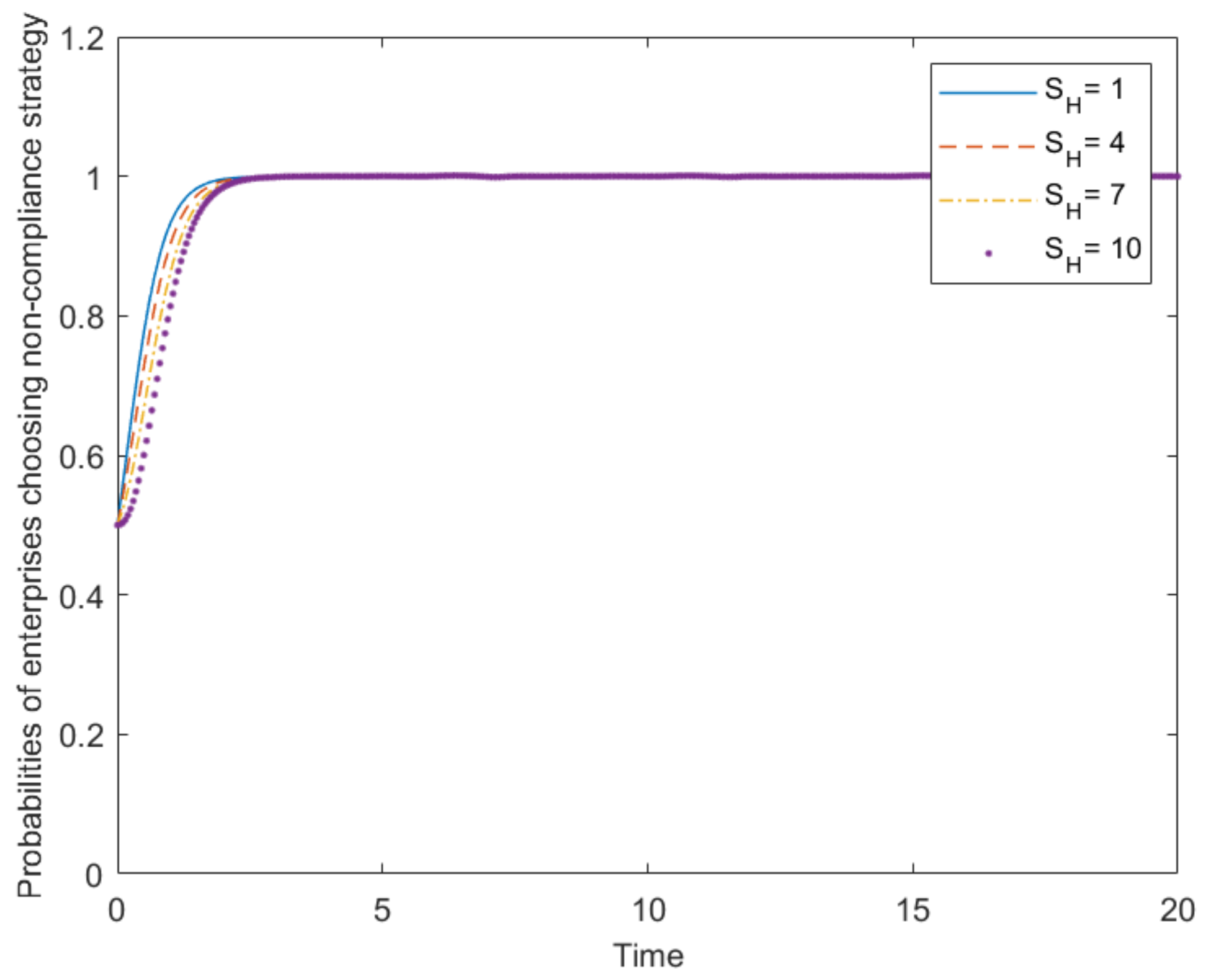
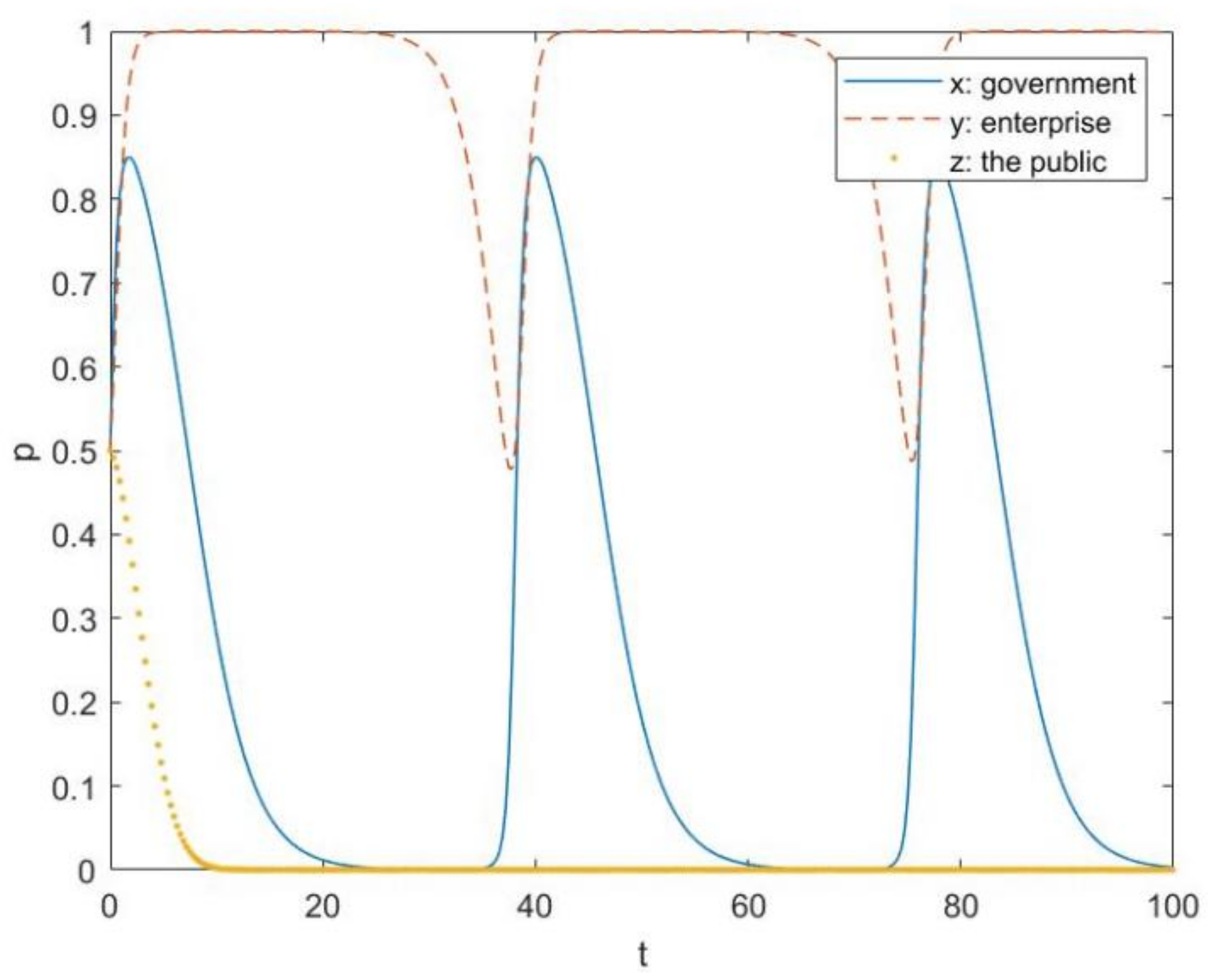
4.1. Evolution Path Graphs of Three Participants on the Noneffective Stage of Plastic Pollution Control and the Influence with Respect to Parameter Changes
4.2. Evolution Path Graphs of Three Participants on the Effective Stage of Plastic Pollution Control
4.3. Evolution Path Graphs of the Three Participants on the Autonomic Stage of Plastic Pollution Control
5. Discussion
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Equilibrium Points | Case 1-1 | Case 1-2 | Case 2-1 | Case 2-2 | Case 3-1 | Case 3-2 | Case 4-1 | Case 4-2 |
|---|---|---|---|---|---|---|---|---|
| There are eigenvalues with different signs. | ||||||||
References
- Hahladakis, J.N.; Velis, C.A.; Weber, R.; Iacovidou, E.; Purnell, P. An overview of chemical additives present in plastics: Migration, release, fate and environmental impact during their use, disposal and recycling. J. Hazard. Mater. 2018, 344, 179–199. [Google Scholar] [CrossRef] [PubMed]
- Organization for Economic Co-Operation and Development (OCDE). OCDE Statistics. Available online: https://stats.oecd.org/Index.aspx? (accessed on 6 December 2021).
- Plastics Europe. Plastics—The Facts 2019: An Analysis of European Plastics Production, Demand and Waste Data; Plastics Europe: Brussels, Belgium, 2019. [Google Scholar]
- Chen, Y.; Awasthi, A.K.; Wei, F.; Tan, Q.; Li, J. Single-use plastics: Production, usage, disposal, and adverse impacts. Sci. Total Environ. 2020, 752, 141772. [Google Scholar] [CrossRef] [PubMed]
- Jambeck, J.R.; Geyer, R.; Wilcox, C.; Siegler, T.R.; Perryman, M.; Andrady, A.; Narayan, R.; Law, K.L. Plastic waste inputs from land into the ocean. Science 2015, 347, 768–771. [Google Scholar] [CrossRef] [PubMed]
- Shen, M.; Huang, W.; Chen, M.; Song, B.; Zhang, Y. (Micro)plastic crisis: Un-ignorable contribution to global greenhouse gas emissions and climate change. J. Clean. Prod. 2020, 254, 120138. [Google Scholar] [CrossRef]
- Jjk, A.; Yvf, A.; Rrt, B.; Tan, R. Minimising the present and future plastic waste, energy and environmental footprints related to COVID-19. Renew. Sustain. Energy Rev. 2020, 127, 109883. [Google Scholar]
- Wagner, T.P. Reducing single-use plastic shopping bags in the USA. Waste Manag. 2017, 70, 3–12. [Google Scholar] [CrossRef]
- CIEL. Plastic & Health: The Hidden Costs of a Plastic Planet; Center for International Environmental Law Technical Report. 2019. Available online: https://www.ciel.org/wp-content/uploads/2019/05/Plastic-and-Climate-FINAL-2019.pdf (accessed on 6 December 2021).
- Schnurr, R.E.J.; Alboiu, V.; Chaudhary, M.; Corbett, R.A.; Quanz, M.E.; Sankar, K.; Srain, H.S.; Thavarajah, V.; Xanthos, D.; Walker, T.R. Reducing marine pollution from single-use plastics (SUPs): A review. Mar. Pollut. Bull. 2018, 137, 157–171. [Google Scholar] [CrossRef]
- Xanthos, D.; Walker, T.R. International policies to reduce plastic marine pollution from single-use plastics (plastic bags and microbeads): A review. Mar. Pollut. Bull. 2017, 118, 17–26. [Google Scholar] [CrossRef]
- Prata, C.J.; Silva, A.L.P.; da Costa, J.P.; Mouneyrac, C.; Walker, T.R.; Duarte, A.C.; Rocha-Santos, T. Solutions and Integrated Strategies for the Control and Mitigation of Plastic and Microplastic Pollution. Int. J. Environ. Res. Public Health 2019, 16, 2411. [Google Scholar] [CrossRef] [Green Version]
- Pani, S.K.; Pathak, A.A. Managing plastic packaging waste in emerging economies: The case of EPR in India. J. Environ. Manag. 2021, 288, 112405. [Google Scholar] [CrossRef]
- Li, C.; Sun, M.; Xu, X.; Zhang, L. Characteristics and influencing factors of mulch film use for pollution control in China: Microcosmic evidence from smallholder farmers. Res. Conserv. Recycl. 2021, 164, 105222. [Google Scholar] [CrossRef]
- Mederake, L.; Knoblauch, D. Shaping EU Plastic Policies: The Role of Public Health vs. Environmental Arguments. Int. J. Environ. Res. Public Health 2019, 16, 3928. [Google Scholar] [CrossRef] [Green Version]
- De Lucia, C.; Pazienza, P. Market-based tools for a plastic waste reduction policy in agriculture: A case study in the south of Italy. J. Environ. Manag. 2019, 250, 109468. [Google Scholar] [CrossRef]
- Gilli, M.; Nicolli, F.; Farinelli, P. Behavioural attitudes towards waste prevention and recycling. Ecol. Econ. 2018, 154, 294–305. [Google Scholar] [CrossRef]
- Lazarevic, D.; Aoustin, E.; Buclet, N.; Brandt, N. Plastic waste management in the context of a European recycling society: Comparing results and uncertainties in a life cycle perspective. Resour. Conserv. Recycl. 2010, 55, 246–259. [Google Scholar] [CrossRef]
- Viera, J.; Marques, M.; Nazareth, C.; Jimenez, P.C.; Castro, I.B. On replacing single-use plastic with so-called biodegradable ones: The case with straws. Environ. Sci. Policy 2020, 106, 177. [Google Scholar] [CrossRef]
- Taylor, R. Bag leakage: The effect of disposable carryout bag regulations on unregulated bags. J. Environ. Econ. Manag. 2019, 93, 254–271. [Google Scholar] [CrossRef]
- Macintosh, A.; Simpson, A.; Neeman, T.; Dickson, K. Plastic bag bans: Lessons from the Australian Capital Territory. Resour. Conserv. Recycl. 2020, 154, 104638. [Google Scholar] [CrossRef]
- Taylor, R.; Villas-Boas, S.B. Bans vs. Fees: Disposable Carryout Bag Policies and Bag Usage. In Proceedings of the AAEA & WAEA Joint Meeting, San Francisco, CA, USA, 26–28 July 2015. [Google Scholar]
- Aumann, R.J. Presidential address. Games Econ. Behav. 2003, 45, 2–14. [Google Scholar] [CrossRef]
- Zhao, R.; Neighbour, G.; Han, J.; McGuire, M.; Deutz, P. Using game theory to describe strategy selection for environmental risk and carbon emissions reduction in the green supply chain. J. Loss Prev. Process Ind. 2012, 25, 927–936. [Google Scholar] [CrossRef]
- Hafezalkotob, A. Competition of two green and regular supply chains under environmental protection and revenue seeking policies of government. Comput. Ind. Eng. 2015, 82, 103–114. [Google Scholar] [CrossRef]
- Ciardiello, F.; Genovese, A.; Simpson, A. Pollution responsibility allocation in supply networks: A game-theoretic approach and a case study. Int. J. Prod. Econ. 2018, 217, 211–217. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Wang, W.; Huang, R. Supply chain enterprise operations and government carbon tax decisions considering carbon emissions. J. Clean. Prod. 2017, 152, 271–280. [Google Scholar] [CrossRef]
- Madani, S.R.; Rasti-Barzoki, M. Sustainable supply chain management with pricing, greening and governmental tariffs determining strategies: A game-theoretic approach. Comput. Ind. Eng. 2017, 105, 287–298. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Q.; Ji, J. Pricing and carbon emission reduction decisions in supply chains with vertical and horizontal cooperation. Int. J. Prod. Econ. 2017, 191, 286–297. [Google Scholar] [CrossRef]
- Du, S.; Zhu, J.; Jiao, H.; Ye, W. Game-theoretical analysis for supply chain with consumer preference to low carbon. Int. J. Prod. Res. 2014, 53, 3753–3768. [Google Scholar] [CrossRef]
- Bertinelli, L.; Camacho, C.; Zou, B. Carbon capture and storage and transboundary pollution: A differential game approach. Eur. J. Oper. Res. 2014, 237, 721–728. [Google Scholar] [CrossRef]
- Huang, X.; He, P.; Zhang, W. A cooperative differential game of transboundary industrial pollution between two regions. J. Clean. Prod. 2016, 120, 43–52. [Google Scholar] [CrossRef]
- Yeung DW, K.; Petrosyan, L.A. A cooperative stochastic differential game of transboundary industrial pollution. Automatica 2008, 44, 1532–1544. [Google Scholar] [CrossRef]
- Jamali, M.-B.; Rasti-Barzoki, M. A game theoretic approach for green and non-green product pricing in chain-to-chain competitive sustainable and regular dual-channel supply chains. J. Clean. Prod. 2018, 170, 1029–1043. [Google Scholar] [CrossRef]
- Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Babu, S.; Mohan, U. An integrated approach to evaluating sustainability in supply chains using evolutionary game theory. Comput. Oper. Res. 2018, 89, 269–283. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Q.; Chen, B.; Wang, Y. Evolutionary game analysis on behavioral strategies of multiple stakeholders in E-waste recycling industry. Resour. Conserv. Recycl. 2020, 155, 104618. [Google Scholar] [CrossRef]
- Friedman, R.S.; Guerrero, A.M.; McAllister, R.R.J.; Rhodes, J.R.; Santika, T.; Budiharta, S.; Wilson, K.A. Beyond the community in participatory forest management: A governance network perspective. Land Use Policy 2020, 97, 104738. [Google Scholar] [CrossRef]
- Xu, R.; Wang, Y.; Wang, W.; Ding, Y. Evolutionary game analysis for third-party governance of environmental pollution. J. Ambient Intell. Humaniz. Comput. 2018, 12, 474. [Google Scholar] [CrossRef]
- Wang, C.; Shi, F. An Evolutionary Game Model for Industrial Pollution Management under Two Punishment Mechanisms. Int. J. Environ. Res. Public Health 2019, 16, 2775. [Google Scholar] [CrossRef] [Green Version]
- Js, A.; Wz, B.; Bz, B. The coordination of stakeholder interests in environmental regulation: Lessons from China’s environmental regulation policies from the perspective of the evolutionary game theory. J. Clean. Prod. 2020, 249, 119385. [Google Scholar]
- Chen, W.; Hu, Z.-H. Using evolutionary game theory to study governments and manufacturers’ behavioral strategies under various carbon taxes and subsidies. J. Clean. Prod. 2018, 201, 123–141. [Google Scholar] [CrossRef]
- Tu, Y.; Peng, B.; Wei, G.; Wu, W. EPR System Participants’ Behavior: Evolutionary Game and Strategy Simulation. J. Clean. Prod. 2020, 271, 122659. [Google Scholar] [CrossRef]
- Wang, Z.; Huo, J.; Duan, Y. The impact of government incentives and penalties on willingness to recycle plastic waste: An evolutionary game theory perspective. Front. Environ. Sci. Eng. 2020, 14, 173–184. [Google Scholar] [CrossRef]
- Gao, S.; Ling, S.; Liu, X.; Dou, X.; Wu, R. Understanding local government’s information disclosure in China’s environmental project construction from the dual-pressure perspective. J. Clean. Prod. 2020, 263, 121311. [Google Scholar] [CrossRef]
- Jiang, K.; You, D.; Merrill, R.; Li, Z. Implementation of a multi-agent environmental regulation strategy under Chinese fiscal decentralization: An evolutionary game theoretical approach. J. Clean. Prod. 2019, 214, 902–915. [Google Scholar] [CrossRef]
- Tian, Y.; Govindan, K.; Zhu, Q. A system dynamics model based on evolutionary game theory for green supply chain management diffusion among Chinese manufacturers. J. Clean. Prod. 2014, 80, 96–105. [Google Scholar] [CrossRef]
- Yin, S.; Zhang, N.; Li, B.; Dong, H. Enhancing the effectiveness of multi-agent cooperation for green manufacturing: Dynamic co-evolution mechanism of a green technology innovation system based on the innovation value chain. Environ. Impact Assess. Rev. 2021, 86, 106475. [Google Scholar] [CrossRef]
- Cui, M. A Tripartite Evolutionary Game Analysis of Environmental Credit Supervision under the Background of Cooperative Governance. Syst. Eng. Theory Pract. 2021, 3, 1–21. [Google Scholar]
- Liang, Y.R.; Liu, Y.Q. The evolutionary game and stability analysis of medical protective equipment market supervision under the COVID-19 epidemic. China Manag. Sci. 2021, 5, 1–11. [Google Scholar]
- Feng, L.P.; Qian, C.L.; Pang, Q.H.; Cheng, T.J. Analysis on the timing of government intervention in network public opinion in emergencies based on the tripartite game model. Inform. Theory Pract. 2021, 5, 1–14. [Google Scholar]
- Xu, X.Y.; Yang, Y. Research on the Tripartite Evolutionary Game of the Road-rail Combined Transport System under the Domination of the Government. Transp. Syst. Eng. Inf. 2021, 21, 7–15. [Google Scholar]
- Wu, J.M.; Tang, X.; Sheng, Y.X.; Wei, X.Z.; Mao, X.Y. Research on the Government-Industry-University Collaborative Innovation Mechanism of New Energy Vehicles in the Post-Subsidy Era Based on the Tripartite Evolutionary Game. Oper. Res. Manag. 2021, 30, 96–102. [Google Scholar]
- Hu, R.; Tong, H.J. Jurisprudence Thinking of “Plastic Restriction”. Ecol. Econ. 2011, 3, 180–183. [Google Scholar]
- Fonoberova, M.; Fonoberov, V.A.; Mezić, I. Global sensitivity/uncertainty analysis for agent-based models. Reliab. Eng. Syst. Saf. 2013, 118, 8–17. [Google Scholar] [CrossRef]





| Entity | Parameters | Explanation |
|---|---|---|
| Government | The cost of the government supervision of plastic pollution control, including the cost of providing policy and financial support, the cost of regulation of enterprises, etc. | |
| The benefits of the government supervision of plastic pollution control, including economic, reputational, and social benefits, etc. | ||
| The benefits gained when governments do not conduct plastic pollution supervising, including more leisure time, less difficult work, gains from collusion between local officials and enterprises, etc. | ||
| Penalties from the higher-level authorities for non-supervision by local governments when enterprises do not comply with the policy | ||
| The probability that the governments will be penalized by higher-level authorities for not fully supervising enterprises when enterprises are found not complying with the policies | ||
| The proportion of governments choosing a non-supervision strategy | ||
| Enterprise | Costs for an enterprise to comply with the policy, including the elimination of old and highly polluting equipment, industrial transformation, upgrading the talent pool, updating energy-saving equipment, etc. | |
| The penalty a government obtains from an enterprise when an enterprise chooses a non-compliance strategy and the government chooses a supervision strategy | ||
| Benefits of corporate compliance, including reputational benefits, preferential treatment from government policies, sales benefits from green consumption trends, etc. | ||
| The proportion of enterprises choosing a non-compliance strategy | ||
| The public | The benefits enjoyed when the public saves the trouble of changing habits and enjoys the convenience of using plastic bags because they chose a non-cooperation strategy and an enterprise chooses a non-compliance strategy | |
| The environmental rewards that the public can enjoy when an enterprise chooses a compliance strategy, including the improvement of environmental quality, the increase of happiness in life, etc. | ||
| The compensation obtained by the public from an enterprise when this enterprise does not choose a compliance strategy, the public chooses a cooperation strategy, and the government chooses a supervision strategy | ||
| The cost to the public for choosing a cooperation strategy, including the public’s time, energy, etc. | ||
| The loss of the public due to deterioration of the environment caused when an enterprise chooses a non-compliance strategy | ||
| The proportion of the public choosing a non-cooperation strategy |
| Strategy Combination | Payoffs of Enterprise, Government, and the Public |
|---|---|
| |
| |
| |
| |
| |
| |
| |
|
| Equilibrium Points | Eigenvalues | Eigenvalues | Eigenvalues |
|---|---|---|---|
| Cases | Discussion on the Benefits of Decision-Making | Balance Point | Strategic Combination of Government, Enterprise and the Public |
|---|---|---|---|
| 1-1 | , | (non-supervision, non-compliance, cooperation) | |
| 1-2 | , | (supervision, non-compliance, cooperation) | |
| 2-1 | , | (non-supervision, non-compliance, cooperation) | |
| 2-2 | , | —— | —— |
| 3-1 | , | (non-supervision, non-compliance, cooperation) | |
| 3-2 | , | —— | —— |
| 4-1 | , | (non-supervision, compliance, non-cooperation) | |
| 4-2 | , | (non-supervision, compliance, non-cooperation) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouyang, C.; Jiang, H.; Sheng, Q.; Liu, G.; Jiang, M. Tripartite Evolutionary Game Analysis for Plastic Pollution Prevention and Control under the Background of China’s Plastic Ban. Sustainability 2022, 14, 2179. https://doi.org/10.3390/su14042179
Ouyang C, Jiang H, Sheng Q, Liu G, Jiang M. Tripartite Evolutionary Game Analysis for Plastic Pollution Prevention and Control under the Background of China’s Plastic Ban. Sustainability. 2022; 14(4):2179. https://doi.org/10.3390/su14042179
Chicago/Turabian StyleOuyang, Chenlu, Huiqi Jiang, Qing Sheng, Guannan Liu, and Minghui Jiang. 2022. "Tripartite Evolutionary Game Analysis for Plastic Pollution Prevention and Control under the Background of China’s Plastic Ban" Sustainability 14, no. 4: 2179. https://doi.org/10.3390/su14042179
APA StyleOuyang, C., Jiang, H., Sheng, Q., Liu, G., & Jiang, M. (2022). Tripartite Evolutionary Game Analysis for Plastic Pollution Prevention and Control under the Background of China’s Plastic Ban. Sustainability, 14(4), 2179. https://doi.org/10.3390/su14042179






