Carbon Emission Efficiency Network: Evolutionary Game and Sensitivity Analysis between Differentiated Efficiency Groups and Local Governments
Abstract
:1. Introduction
2. Literature Review
2.1. Carbon Emission and Carbon Emission Efficiency
2.2. Carbon Emission Reduction
2.3. The Marketization of Energy Use Rights and Carbon Emission Rights
3. Methodology
3.1. Research Hypothesis
3.2. Model Derivation
4. Results and Discussion
4.1. Stability Strategy Analysis of the Trilateral Evolutionary Game
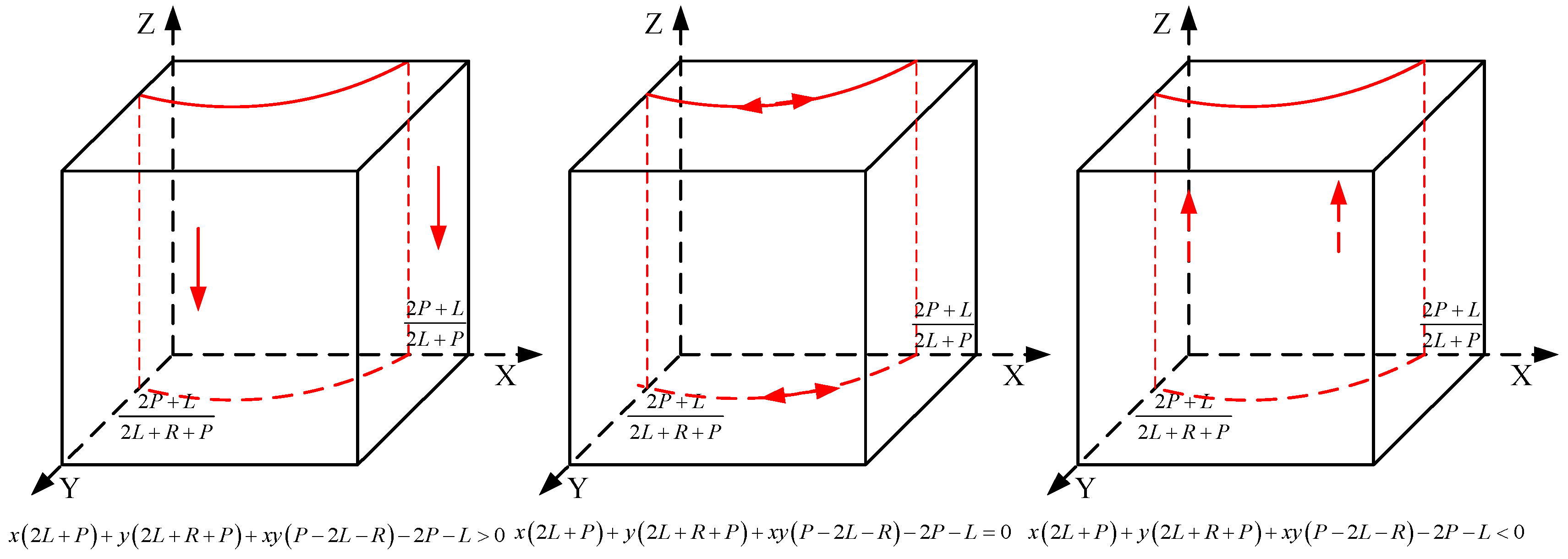
4.1.1. Stability Condition of the High-efficiency Group Strategy
4.1.2. Stability Condition of the Low-Efficiency Group Strategy
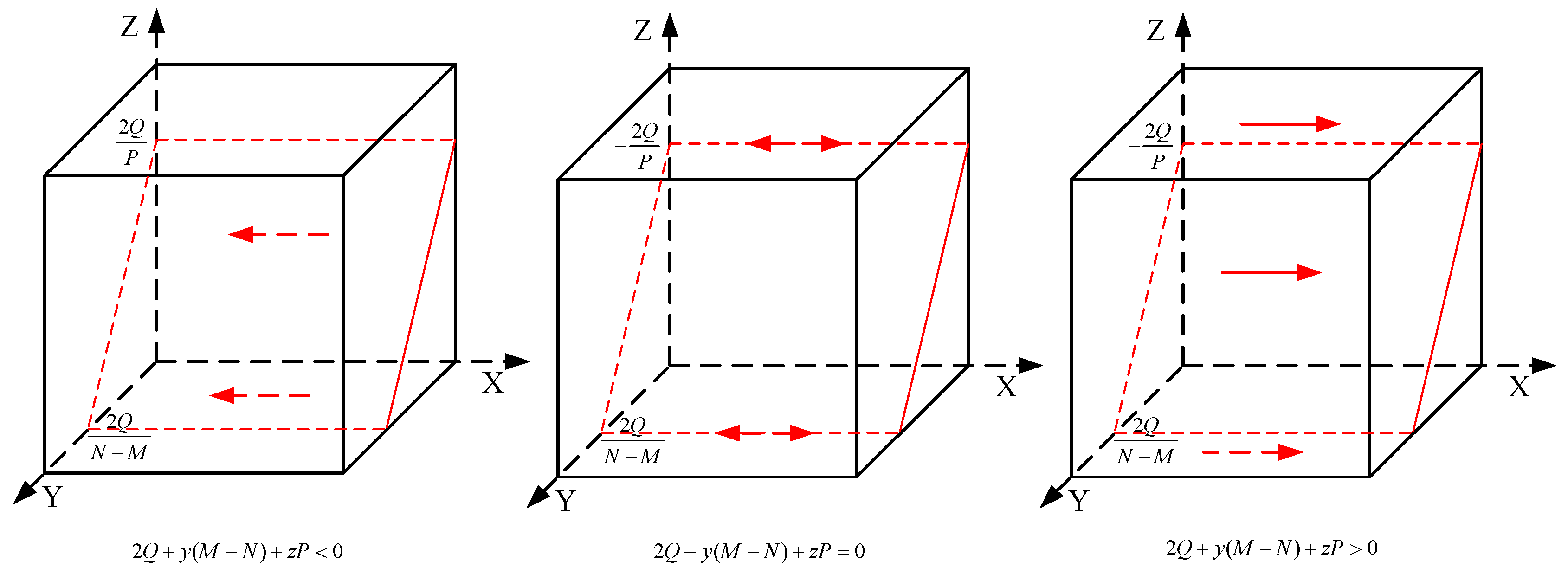
4.1.3. Stability Condition of the Local Government’s Strategy
4.1.4. Stability Conditions of the Trilateral Evolutionary Game
4.2. Evolutionary Simulation of the Tripartite Game
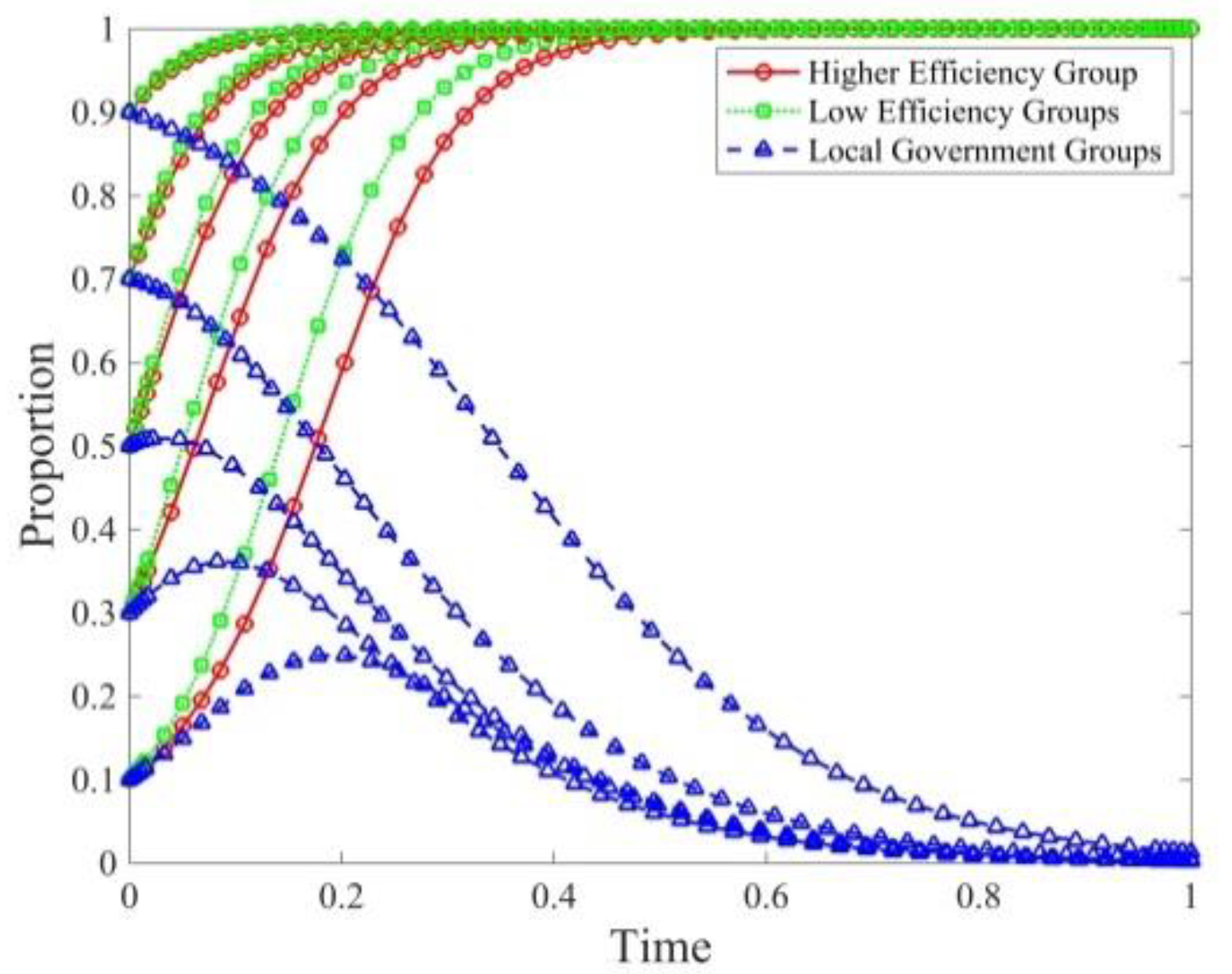
4.2.1. System Evolution under Different Initial Strategy Proportion Scenarios
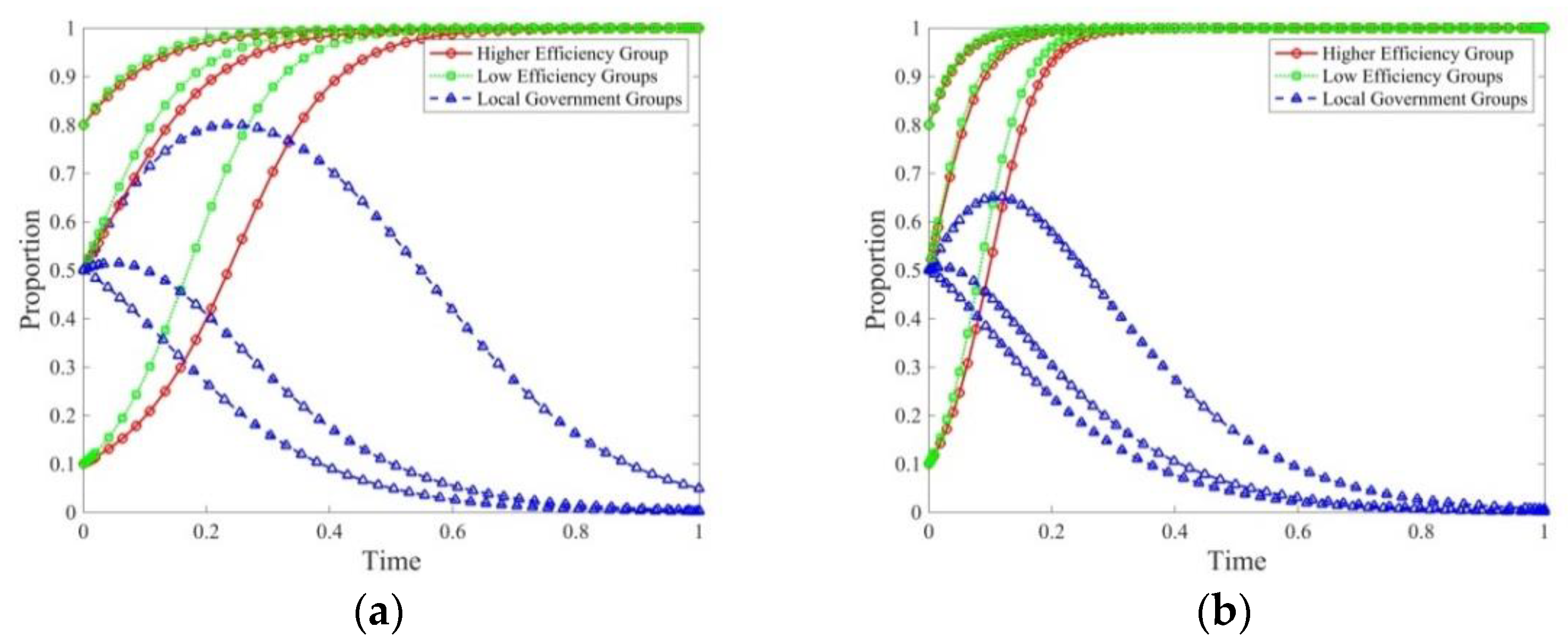
4.2.2. System Evolution under Different Transformation Cost Scenarios
4.2.3. System Evolution under Different Reward and Punishment Situations
4.2.4. System Evolution under Different Network Capitals
5. Conclusions and Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Variable | Simulation Data | Evolutionary Path | Curve Feature |
|---|---|---|---|
| initial strategy proportion () | 0.1 | unchanged | The higher the efficiency ratio of the group, the faster it converges to the stable strategy, but the opposite is true for local governments. |
| 0.3 | |||
| 0.5 | |||
| 0.7 | |||
| 0.9 | |||
| transformation cost () | 1.0 | unchanged | The transition cost will prolong the time for the inefficient group to reach the stable equilibrium strategy, while it has a weak influence on other game participants. |
| 20.0 | |||
| reward () | 2.0 | unchanged | The convergence speed of low-efficient groups is more sensitive to incentive policies, and local governments need to spend more time to achieve stable and balanced strategies when the initial proportion of other players is low. |
| 20.0 | |||
| punishment () | 2.0 | unchanged | Punishment policy has a stronger influence on low-efficient groups, and can reduce the time for local governments to reach the stable equilibrium strategy. |
| 20.0 | |||
| network capital () | 2.0 | unchanged | Network capital can shorten the time for all game participants to reach the stable equilibrium strategy. |
| 9.0 |
References
- Huang, Y.; Matsumoto, K. Drivers of the change in carbon dioxide emissions under the progress of urbanization in 30 provinces in China: A decomposition analysis. J. Clean. Prod. 2021, 322, 129000. [Google Scholar] [CrossRef]
- Wen, W.; Feng, C.; Zhou, H.; Zhang, L.; Wu, X.; Qi, J.; Yang, X.; Liang, Y. Critical provincial transmission sectors for carbon dioxide emissions in China. Renew. Sustain. Energy Rev. 2021, 149, 111415. [Google Scholar] [CrossRef]
- Qin, H.; Huang, Q.; Zhang, Z.; Lu, Y.; Li, M.; Xu, L.; Chen, Z. Carbon dioxide emission driving factors analysis and policy implications of Chinese cities: Combining geographically weighted regression with two-step cluster. Sci. Total Environ. 2019, 684, 413–424. [Google Scholar] [CrossRef]
- Lin, B.; Benjamin, N.I. Determinants of industrial carbon dioxide emissions growth in Shanghai: A quantile analysis. J. Clean. Prod. 2019, 217, 776–786. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Wang, J. Impact of COVID-19 pandemic on energy consumption and carbon dioxide emissions in China’s transportation sector. Case Stud. Therm. Eng. 2021, 26, 101091. [Google Scholar] [CrossRef]
- Rehman, A.; Ma, H.; Ahmad, M.; Irfan, M.; Traore, O.; Chandio, A.A. Towards environmental Sustainability: Devolving the influence of carbon dioxide emission to population growth, climate change, Forestry, livestock and crops production in Pakistan. Ecol. Indic. 2021, 125, 107460. [Google Scholar] [CrossRef]
- Leitão, J.; Ferreira, J.; Santibanez-González, E. New insights into decoupling economic growth, technological progress and carbon dioxide emissions: Evidence from 40 countries. Technol. Forecast. Soc. Chang. 2021, 174, 121250. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, H.; Sun, R. Effectiveness of China’s provincial industrial carbon emission reduction and optimization of carbon emission reduction paths in “lagging regions”: Efficiency-cost analysis. J. Environ. Manag. 2020, 275, 111221. [Google Scholar] [CrossRef]
- Yao, X.; Zhang, X.; Guo, Z. The tug of war between local government and enterprises in reducing China’s carbon dioxide emissions intensity. Sci. Total Environ. 2020, 710, 136140. [Google Scholar] [CrossRef]
- Adams, S.; Nsiah, C. Reducing carbon dioxide emissions; Does renewable energy matter? Sci. Total Environ. 2019, 693, 133288. [Google Scholar] [CrossRef]
- He, A.; Xue, Q.; Zhao, R.; Wang, D. Renewable energy technological innovation, market forces, and carbon emission efficiency. Sci. Total Environ. 2021, 796, 148908. [Google Scholar] [CrossRef]
- Jiang, M.; An, H.; Gao, X.; Liu, S.; Xi, X. Factors driving global carbon emissions: A complex network perspective. Resour. Conserv. Recycl. 2019, 146, 431–440. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Peng, S.; Ming, L.; Cui, C.; Niu, B. Interactions between households and industrial sectors in embodied carbon emission networks. J. Clean. Prod. 2020, 275, 123809. [Google Scholar] [CrossRef]
- Jiang, Q.; Ma, X. Spillovers of environmental regulation on carbon emissions network. Technol. Forecast. Soc. Chang. 2021, 169, 120825. [Google Scholar] [CrossRef]
- Wang, G.; Deng, X.; Wang, J.; Zhang, F.; Liang, S. Carbon emission efficiency in China: A spatial panel data analysis. China Econ. Rev. 2019, 56, 101313. [Google Scholar] [CrossRef]
- Li, S.; Zhou, C.; Wang, S. Does modernization affect carbon dioxide emissions? A panel data analysis. Sci. Total Environ. 2019, 663, 426–435. [Google Scholar] [CrossRef]
- Wu, D.; Geng, Y.; Pan, H. Whether natural gas consumption bring double dividends of economic growth and carbon dioxide emissions reduction in China? Renew. Sustain. Energy Rev. 2021, 137, 110635. [Google Scholar] [CrossRef]
- He, Y.; Fu, F.; Liao, N. Exploring the path of carbon emissions reduction in China’s industrial sector through energy efficiency enhancement induced by R&D investment. Energy 2021, 225, 120208. [Google Scholar] [CrossRef]
- Nam, E.; Jin, T. Mitigating carbon emissions by energy transition, energy efficiency, and electrification: Difference between regulation indicators and empirical data. J. Clean. Prod. 2021, 300, 126962. [Google Scholar] [CrossRef]
- Qiao, W.; Lu, H.; Zhou, G.; Azimi, M.; Yang, Q.; Tian, W. A hybrid algorithm for carbon dioxide emissions forecasting based on improved lion swarm optimizer. J. Clean. Prod. 2020, 244, 118612. [Google Scholar] [CrossRef]
- Cai, W.; Ye, P. Does Carbon Emission Trading Improve Low-carbon Technical Efficiency? Evidence from China. Sustain. Prod. Consum. 2021, 29, 46–56. [Google Scholar] [CrossRef]
- Zhao, D.; Ji, S.-F.; Wang, H.-P.; Jiang, L.-W. How do government subsidies promote new energy vehicle diffusion in the complex network context? A three-stage evolutionary game model. Energy 2021, 230, 120899. [Google Scholar] [CrossRef]
- Wen, W.; Wang, Q. Re-examining the realization of provincial carbon dioxide emission intensity reduction targets in China from a consumption-based accounting. J. Clean. Prod. 2020, 244, 118488. [Google Scholar] [CrossRef]
- Xie, Z.; Wu, R.; Wang, S. How technological progress affects the carbon emission efficiency? Evidence from national panel quantile regression. J. Clean. Prod. 2021, 307, 127133. [Google Scholar] [CrossRef]
- Zhang, X.; Nie, S.; He, M.; Wang, J. Charging system analysis, energy consumption, and carbon dioxide emissions of battery electric buses in Beijing. Case Stud. Therm. Eng. 2021, 26, 101197. [Google Scholar] [CrossRef]
- Mahapatra, B.; Irfan, M. Asymmetric impacts of energy efficiency on carbon emissions: A comparative analysis between developed and developing economies. Energy 2021, 227, 120485. [Google Scholar] [CrossRef]
- Chen, P.; Lu, Y.; Wan, Y.; Zhang, A. Assessing carbon dioxide emissions of high-speed rail: The case of Beijing-Shanghai corridor. Transp. Res. Part D Transp. Environ. 2021, 97, 102949. [Google Scholar] [CrossRef]
- Martins, T.; Barreto, A.C.; Souza, F.M.; Souza, A.M. Fossil fuels consumption and carbon dioxide emissions in G7 countries: Empirical evidence from ARDL bounds testing approach. Environ. Pollut. 2021, 291, 118093. [Google Scholar] [CrossRef]
- Yu, D.-J.; Li, J. Evaluating the employment effect of China’s carbon emission trading policy: Based on the perspective of spatial spillover. J. Clean. Prod. 2021, 292, 126052. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, T.; Pan, L. Operational Strategy and User Price Preference Analysis of China’s Microgrids: Based on An Evolutionary Game Model. Chem. Eng. Res. Des. 2021. [Google Scholar] [CrossRef]
- Guo, L.-Y.; Feng, C. Are there spillovers among China’s pilots for carbon emission allowances trading? Energy Econ. 2021, 103, 105574. [Google Scholar] [CrossRef]
- Zang, H.; Xu, Y.; Zhai, M.; Li, W.; Su, S. Development of carbon emission interactive network model: A case study of Northeast Industrial District. J. Environ. Manag. 2021, 300, 113618. [Google Scholar] [CrossRef] [PubMed]
- Jiang, M.; An, H.; Gao, X.; Jia, N.; Liu, S.; Zheng, H. Structural decomposition analysis of global carbon emissions: The contributions of domestic and international input changes. J. Environ. Manag. 2021, 294, 112942. [Google Scholar] [CrossRef] [PubMed]
- Al Sadawi, A.; Madani, B.; Saboor, S.; Ndiaye, M.; Abu-Lebdeh, G. A comprehensive hierarchical blockchain system for carbon emission trading utilizing blockchain of things and smart contract. Technol. Forecast. Soc. Chang. 2021, 173, 121124. [Google Scholar] [CrossRef]
- Ying, Z.; Xin-Gang, Z. The impact of Renewable Portfolio Standards on carbon emission trading under the background of China’s electricity marketization reform. Energy 2021, 226, 120322. [Google Scholar] [CrossRef]
- Chen, X.; Lin, B. Towards carbon neutrality by implementing carbon emissions trading scheme: Policy evaluation in China. Energy Policy 2021, 157, 112510. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, N. Low-carbon city pilot and carbon emission efficiency: Quasi-experimental evidence from China. Energy Econ. 2021, 96, 105125. [Google Scholar] [CrossRef]
- Zhanga, Y. Research on International Carbon Emissions Trading and Optimal Exports Scale of China Carbon Emissions. Procedia Environ. Sci. 2011, 10, 101–107. [Google Scholar] [CrossRef] [Green Version]
- Jiang, M.; Gao, X.; Guan, Q.; Hao, X.; An, F. The structural roles of sectors and their contributions to global carbon emissions: A complex network perspective. J. Clean. Prod. 2019, 208, 426–435. [Google Scholar] [CrossRef]
- Melgar-Dominguez, O.D.; Pourakbari-Kasmaei, M.; Lehtonen, M.; Mantovani, J.R.S. An economic-environmental asset planning in electric distribution networks considering carbon emission trading and demand response. Electr. Power Syst. Res. 2020, 181, 106202. [Google Scholar] [CrossRef]
- Shi, Y.; Wei, Z.; Shahbaz, M.; Zeng, Y. Exploring the dynamics of low-carbon technology diffusion among enterprises: An evolutionary game model on a two-level heterogeneous social network. Energy Econ. 2021, 101, 105399. [Google Scholar] [CrossRef]
- Liu, W.; Long, S.; Xie, D.; Liang, Y.; Wang, J. How to govern the big data discriminatory pricing behavior in the platform service supply chain? An examination with a three-party evolutionary game model. Int. J. Prod. Econ. 2021, 231, 107910. [Google Scholar] [CrossRef]




| Parameter | Parameter Interpretation |
|---|---|
| basic benefits of high-efficiency group | |
| basic benefits of low-efficiency group | |
| changes in network capital of efficiency groups; it reflects the degree of interaction between different efficiency groups. | |
| high-efficiency groups choose the benefits of efficiency spillovers | |
| the cost and opportunity cost of efficient group selection efficiency spillover, including technology transfer, capital investment, etc. | |
| government punishment for maintaining the status quo | |
| government incentives for carbon emission efficiency improvement or green transformation | |
| the cost of low-efficiency group choosing independent green transformation, including low-carbon technology development, project planning, etc. | |
| benefits from green transformation of inefficient groups | |
| low-efficiency groups are affected by the transformation cost of spillover efficiency spillover | |
| supervision cost of local government | |
| system construction cost of local government |
| Strategy Space | High-Efficiency Group | Low-Efficiency Group | Local Government |
|---|---|---|---|
| Equilibrium Strategy | Eigenvalue1 | Eigenvalue2 | Eigenvalue3 | Symbol |
|---|---|---|---|---|
| + + + | ||||
| * − + | ||||
| − + * | ||||
| + − + | ||||
| − − − | ||||
| * − + | ||||
| * + − | ||||
| + − − |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Tai, H.; Cheng, K.; Dong, H.; Liu, W.; Hou, J. Carbon Emission Efficiency Network: Evolutionary Game and Sensitivity Analysis between Differentiated Efficiency Groups and Local Governments. Sustainability 2022, 14, 2191. https://doi.org/10.3390/su14042191
Zhang R, Tai H, Cheng K, Dong H, Liu W, Hou J. Carbon Emission Efficiency Network: Evolutionary Game and Sensitivity Analysis between Differentiated Efficiency Groups and Local Governments. Sustainability. 2022; 14(4):2191. https://doi.org/10.3390/su14042191
Chicago/Turabian StyleZhang, Renjie, Hsingwei Tai, Kuotai Cheng, Huizhong Dong, Wenhui Liu, and Junjie Hou. 2022. "Carbon Emission Efficiency Network: Evolutionary Game and Sensitivity Analysis between Differentiated Efficiency Groups and Local Governments" Sustainability 14, no. 4: 2191. https://doi.org/10.3390/su14042191
APA StyleZhang, R., Tai, H., Cheng, K., Dong, H., Liu, W., & Hou, J. (2022). Carbon Emission Efficiency Network: Evolutionary Game and Sensitivity Analysis between Differentiated Efficiency Groups and Local Governments. Sustainability, 14(4), 2191. https://doi.org/10.3390/su14042191







