Exploration of Copula Models Use in Risk Assessment for Freezing and Snow Events: A Case Study in Southern China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sources and Factor Selection
2.3. Methods
2.3.1. Fitting Distribution Functions
2.3.2. Construction of the Copula Model
2.3.3. Calculations and Comparisons of Return Periods
3. Results
3.1. Spatial Distribution of Frequency and Duration
3.2. Construction of Distributions
3.2.1. Univariate Distributions
3.2.2. Bivariate Joint Distribution
3.3. Calculation of the Return Period
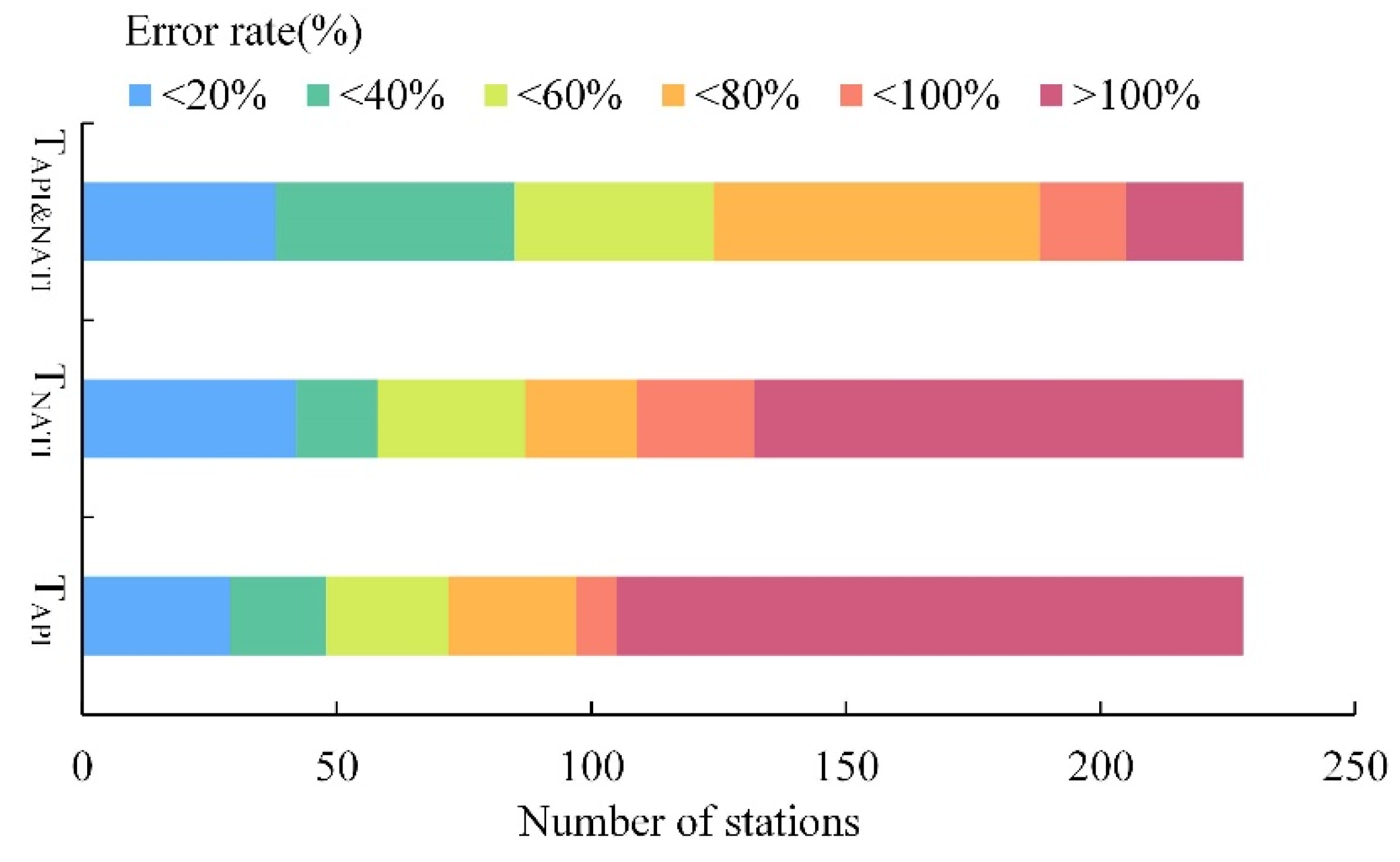
3.4. Comparison of Return Period Accuracies
3.5. Risk Analysis of Severe Freezing and Snow Events
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, S.; Zhu, C.; Liu, J. Combined Impacts of Warm Central Equatorial Pacific Sea Surface Temperatures and Anthropogenic Warming on the 2019 Severe Drought in East China. Adv. Atmos. Sci. 2020, 37, 1149–1163. [Google Scholar] [CrossRef]
- Cohen, J.; Agel, L.; Barlow, M.; Garfinkel, C.I.; White, I. Linking Arctic Variability and Change with Extreme Winter Weather in the United States. Science 2021, 373, 1116–1121. [Google Scholar] [CrossRef]
- Cohen, J.; Screen, J.A.; Furtado, J.C.; Barlow, M.; Whittleston, D.; Coumou, D.; Francis, J.; Dethloff, K.; Entekhabi, D.; Overland, J.; et al. Recent Arctic Amplification and Extreme Mid-Latitude Weather. Nat. Geosci. 2014, 7, 627–637. [Google Scholar] [CrossRef]
- Overland, J.; Francis, J.A.; Hall, R.; Hanna, E.; Kim, S.J.; Vihma, T. The Melting Arctic and Midlatitude Weather Patterns: Are They Connected? J. Clim. 2015, 28, 7917–7932. [Google Scholar] [CrossRef]
- Cohen, J.; Zhang, X.; Francis, J.; Jung, T.; Kwok, R.; Overland, J.; Ballinger, T.J.; Bhatt, U.S.; Chen, H.W.; Coumou, D.; et al. Divergent Consensuses on Arctic Amplification Influence on Midlatitude Severe Winter Weather. Nat. Clim. Change 2020, 10, 20–29. [Google Scholar] [CrossRef]
- Zheng, F.; Yuan, Y.; Ding, Y.; Li, K.; Fang, X.; Zhao, Y.; Sun, Y.; Zhu, J.; Ke, Z.; Wang, J.; et al. The 2020/21 Extremely Cold Winter in China Influenced by the Synergistic Effect of La Niña and Warm Arctic. Adv. Atmos. Sci. 2022, 39, 546–552. [Google Scholar] [CrossRef]
- Barnett, A.G.; Hajat, S.; Gasparrini, A.; Rocklöv, J. Cold and Heat Waves in the United States. Environ. Res. 2012, 112, 218–224. [Google Scholar] [CrossRef]
- Wang, C.; Yao, Y.; Wang, H.; Sun, X.; Zheng, J. The 2020 Summer Floods and 2020/21 Winter Extreme Cold Surges in China and the 2020 Typhoon Season in the Western North Pacific. Adv. Atmos. Sci. 2021, 38, 896–904. [Google Scholar] [CrossRef]
- Ye, Q. Building Resilient Power Grids from Integrated Risk Governance Perspective: A Lesson Learned from China’s 2008 Ice-Snow Storm Disaster. Eur. Phys. J. Spec. Top. 2014, 223, 2439–2449. [Google Scholar] [CrossRef]
- Feng, J.; Li, N.; Zhang, Z.; Chen, X. The Dual Effect of Vegetation Green-up Date and Strong Wind on the Return Period of Spring Dust Storms. Sci. Total Environ. 2017, 592, 729–737. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Gong, D.; Hu, M.; Guo, D.; He, X.; Lei, Y. Anomalous Winter Temperature and Precipitation Events in Southern China. J. Geogr. Sci. 2009, 19, 471–488. [Google Scholar] [CrossRef]
- Liao, Z.; Zhai, P.; Chen, Y.; Lu, H. Differing Mechanisms for the 2008 and 2016 Wintertime Cold Events in Southern China. Int. J. Climatol. 2020, 40, 4944–4955. [Google Scholar] [CrossRef]
- Zhang, H.; Qin, J.; Li, Y. Climatic Background of Cold and Wet Winter in Southern China: Part I Observational Analysis. Clim. Dyn. 2011, 37, 2335–2354. [Google Scholar] [CrossRef]
- de Silva, K.; Tanaka, N.; Yagisawa, J. Return Period of Flood Disturbance That Increases Diversity on Gravel Bars in Middle Stream of Rivers. Landsc. Ecol. Eng. 2015, 11, 1–18. [Google Scholar] [CrossRef]
- de Biagi, V.; Barbero, M.; Borri-Brunetto, M. A Reliability-Based Method for Taking into Account Snowfall Return Period in the Design of Buildings in Avalanche-Prone Areas. Nat. Hazards 2016, 81, 1901–1912. [Google Scholar] [CrossRef][Green Version]
- Shiau, J.T. Return Period of Bivariate Distributed Extreme Hydrological Events. Stoch. Environ. Res. Risk Assess. 2003, 17, 42–57. [Google Scholar] [CrossRef]
- Mochizuki, J.; Vitoontus, S.; Wickramarachchi, B.; Hochrainer-Stigler, S.; Williges, K.; Mechler, R.; Sovann, R. Operationalizing Iterative Risk Management under Limited Information: Fiscal and Economic Risks Due to Natural Disasters in Cambodia. Int. J. Disaster Risk Sci. 2015, 6, 321–334. [Google Scholar] [CrossRef]
- Kao, S.C.; Govindaraju, R.S. A Copula-Based Joint Deficit Index for Droughts. J. Hydrol. 2010, 380, 121–134. [Google Scholar] [CrossRef]
- Alam, M.A.; Emura, K.; Farnham, C.; Yuan, J. Best-Fit Probability Distributions and Return Periods for Maximum Monthly Rainfall in Bangladesh. Climate 2018, 6, 9. [Google Scholar] [CrossRef]
- Yue, S.; Ouarda, T.B.M.J.; Bobée, B. A Review of Bivariate Gamma Distributions for Hydrological Application. J. Hydrol. 2001, 246, 1–18. [Google Scholar] [CrossRef]
- Li, Y.; Gu, W.; Cui, W.; Chang, Z.; Xu, Y. Exploration of Copula Function Use in Crop Meteorological Drought Risk Analysis: A Case Study of Winter Wheat in Beijing, China. Nat. Hazards 2015, 77, 1289–1303. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Bivariate Rainfall Frequency Distributions Using Archimedean Copulas. J. Hydrol. 2007, 332, 93–109. [Google Scholar] [CrossRef]
- Huang, X.; Deng, J.; Ma, X.; Wang, Y.; Feng, Q.; Hao, X.; Liang, T. Spatiotemporal Dynamics of Snow Cover Based on Multi-Source Remote Sensing Data in China. Cryosphere 2016, 10, 2453–2463. [Google Scholar] [CrossRef]
- Wang, X.; Yang, F.; Gao, X.; Wang, W.; Zha, X. Evaluation of Forest Damaged Area and Severity Caused by Ice-Snow Frozen Disasters over Southern China with Remote Sensing. Chin. Geogr. Sci. 2019, 29, 405–416. [Google Scholar] [CrossRef]
- Hu, A.; Xie, W.; Li, N.; Xu, X.; Ji, Z.; Wu, J. Analyzing Regional Economic Impact and Resilience: A Case Study on Electricity Outages Caused by the 2008 Snowstorms in Southern China. Nat. Hazards 2014, 70, 1019–1030. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Jiang, Z.; Ceng, X.; Ma, Q.; Cheng, C.; Liu, Q. Assessment and Zoning of Low Temperature, Rain/Snow and Freezing Disasters in China. Meteorol. Mon. 2013, 39, 585–591. (In Chinese) [Google Scholar]
- Wang, L.; Gao, G.; Zhang, Q.; Sun, J.; Wang, Z.; Zhang, Y.; Zhao, S.; Chen, X.; Chen, Y.; Wang, Y. Analysis of the Severe Cold Surge, Ice Snow and Frozen Disasters in South China During January 2008: I. Climatic Features and Its Impact. Meteorol. Mon. 2008, 34, 95–100. (In Chinese) [Google Scholar]
- Sklar, A. Fonctions de Repartition a n Dimensions et Leurs Marges. Publ. L’institut Stat. L’université Paris 1959, 8, 229–231. [Google Scholar]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Aihaiti, A.; Jiang, Z.; Zhu, L.; Li, W.; You, Q. Risk Changes of Compound Temperature and Precipitation Extremes in China under 1.5 °C and 2 °C Global Warming. Atmos. Res. 2021, 264, 105838. [Google Scholar] [CrossRef]
- Gao, J. Analysis and Assessment of the Risk of Snow and Freezing Disaster in China. Int. J. Disaster Risk Reduct. 2016, 19, 334–340. [Google Scholar] [CrossRef]
- He, F.; Shao, B. Risk Regionalization of Meteorological Disasters Caused by Cryogenic Freezing Rain and Snow in Shanghai. Sci. Meteorol. Sin. 2011, 31, 33–39. (In Chinese) [Google Scholar]
- Hu, A.; Li, N.; Zhu, Y.; Wu, J.; Li, C. Integrated Risk Governance Paradigm for Meteorological Disasters: Thoughts on the Low-Temperature Freezing Rain and Snow Disaster in Southern China of 2008. Prog. Geogr. 2010, 29, 159–165. (In Chinese) [Google Scholar]
- Mao, S.J.; Li, D.L. Comprehensive Assessment of Low Temperature, Snow and Freezing Weather in Southern China Based on Meteorological Elements. J. Glaciol. Geocryol. 2015, 37, 14–26. (In Chinese) [Google Scholar]
- Wei, Y.; Wang, S.; Fang, Y.; Nawaz, Z. Integrated Assessment on the Vulnerability of Animal Husbandry to Snow Disasters under Climate Change in the Qinghai-Tibetan Plateau. Glob. Planet. Change 2017, 157, 139–152. [Google Scholar] [CrossRef]
- Han, S.; Guo, W.; Ke, C.; Zhao, J.; Ma, D. Comprehensive Assessment of Snow Disaster Risk in Northeast China. Gaojishu Tongxin/Chin. High Technol. Lett. 2020, 30, 91–100. (In Chinese) [Google Scholar] [CrossRef]





| Copula | Functions |
|---|---|
| Gaussian Copula | |
| t-Copula | |
| Clayton Copula | |
| Frank Copula | ) |
| Gumbel Copula |
| Variable | Station | Type | Distribution Function | Parameters |
|---|---|---|---|---|
| API | Weining | Generalized Extreme Value | k = 0.64 μ = 0.91 σ = 1.24 | |
| ATI | −0.20 1.29 4.91 | |||
| API | Puan | Lognormal | μ = 1.08 0.79 | |
| ATI | Generalized Extreme Value | −0.12 0.84 2.06 |
| Station | Copula | Parameter Estimation | RMSE | AIC | Selected Copula |
|---|---|---|---|---|---|
| Puan | Gaussian Copula | 0.2442 | 0.0211 | −458.822 | t-Copula |
| t-Copula | 0.2516 | 0.0210 | −459.668 | ||
| Clayton Copula | 0.2716 | 0.0221 | −455.337 | ||
| Frank Copula | 1.4752 | 0.0214 | −459.145 | ||
| Gumbel Copula | 1.1657 | 0.0233 | −449.345 |
| Univariate RP | Weining Station | Puan Station | Panxian Station | Joint RP | |||||
|---|---|---|---|---|---|---|---|---|---|
| API/mm | ATI/°C | API/mm | ATI/°C | API/mm | ATI/°C | TARI&ATI | TAPI | TATI | |
| 5 | 3.52 | 6.58 | 5.70 | 3.22 | 4.89 | 2.85 | 2.84 | 3.01 | 2.81 |
| 10 | 5.81 | 7.24 | 8.07 | 3.73 | 8.45 | 3.61 | 5.39 | 5.75 | 5.30 |
| 30 | 12.20 | 8.08 | 12.50 | 4.42 | 16.91 | 4.86 | 15.66 | 16.78 | 15.29 |
| 50 | 17.08 | 8.40 | 14.87 | 4.70 | 22.50 | 5.48 | 25.93 | 27.82 | 25.29 |
| Station | Extreme Event Threshold | Return Period | Error Rate/% | ||||||
|---|---|---|---|---|---|---|---|---|---|
| API/mm | ATI/°C | Real | TARI&ATI | TAPI | TATI | TARI&ATI | TAPI | TATI | |
| Badong | 4.13 | 1.58 | 7.20 | 6.75 | 35.35 | 12.86 | 6% | 391% | 79% |
| Jingzhou | 9.05 | 3.53 | 4.50 | 4.06 | 6.49 | 20.31 | 10% | 44% | 351% |
| Wuhan | 11.20 | 4.45 | 4.50 | 3.90 | 6.79 | 10.79 | 13% | 51% | 140% |
| Laifeng | 5.24 | 2.86 | 4.75 | 3.39 | 8.28 | 5.43 | 29% | 74% | 14% |
| Renhuai | 3.60 | 1.52 | 5.57 | 5.357 | 12.89 | 10.00 | 4% | 131% | 80% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Chen, L.; Yan, Z.; Xu, Y. Exploration of Copula Models Use in Risk Assessment for Freezing and Snow Events: A Case Study in Southern China. Sustainability 2022, 14, 2568. https://doi.org/10.3390/su14052568
Li Q, Chen L, Yan Z, Xu Y. Exploration of Copula Models Use in Risk Assessment for Freezing and Snow Events: A Case Study in Southern China. Sustainability. 2022; 14(5):2568. https://doi.org/10.3390/su14052568
Chicago/Turabian StyleLi, Qian, Liutong Chen, Zhengtao Yan, and Yingjun Xu. 2022. "Exploration of Copula Models Use in Risk Assessment for Freezing and Snow Events: A Case Study in Southern China" Sustainability 14, no. 5: 2568. https://doi.org/10.3390/su14052568
APA StyleLi, Q., Chen, L., Yan, Z., & Xu, Y. (2022). Exploration of Copula Models Use in Risk Assessment for Freezing and Snow Events: A Case Study in Southern China. Sustainability, 14(5), 2568. https://doi.org/10.3390/su14052568





