Risk Assessment and Prediction of Air Pollution Disasters in Four Chinese Regions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
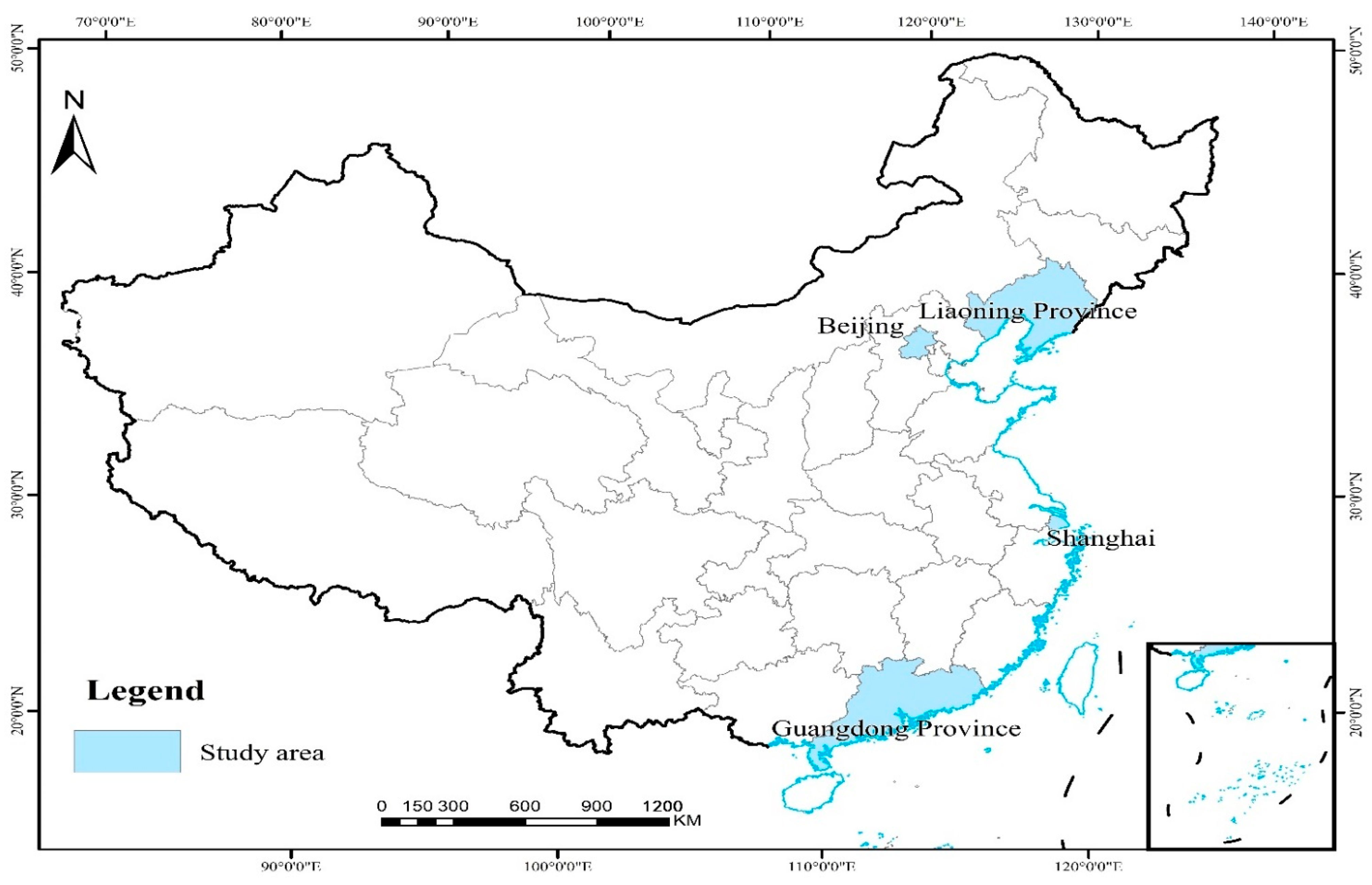
2.1.1. Overview of the Study Area
2.1.2. Details of the Data Sources
2.1.3. Construction of the Indicators System
2.2. The Principle of the PCA-GA-BP Neural Network
2.2.1. Data Standardization
2.2.2. PCA Principle
2.2.3. GA Principle
2.2.4. BP Neural Network Principle
3. Analytical Results of Air Pollution Disaster Risk
4. Discussion
4.1. Evaluation Indicators of the Prediction Model
4.2. Analysis Results Based on PCA-GA-BP Neural Network
5. Conclusions
- (1)
- From the indicator weighting represented by the indicator loading matrix, it can be seen that the annual average SO2 concentration, annual average NO2 concentration, annual average PM10 concentration, and annual average PM2.5 concentration comprised the most serious air pollutants in the region, which affected the natural ecology environment and residents’ health. The annual average temperature, average annual rainfall, regional GDP, the density of the economy, the proportion of secondary industry and building construction areas largely reflected the sensitivity of the regional hazard-laden environment from the points of view of the natural environment and economic development. The birth rate, the death rate from respiratory diseases, the death rate from heart disease, average annual residents’ medical treatment visits and average annual hospitalization rate reflected the sensitivity of the population to air pollution disasters from the point of view of residents’ health. The six indicators of regional resilience reflected the emergency response capacity of different regions to air pollution disasters.
- (2)
- Using GIS technology to classify the risk index of each region from 2010 to 2019, we identified that Guangdong Province, which has the largest population and the largest geographical area, has been subject to the greatest risk of air pollution disasters every year since the introduction of a number of policies in the Environmental Protection Law in 2010. The disaster risks of Liaoning Province, Beijing and Shanghai were small. Starting with each geographical location, the air pollution disaster risk index was generally increasing from the north, east and south directions year by year.
- (3)
- This research verified that the PCA-GA-BP neural network could be used as a method of air pollution disaster risk assessment. Regional air pollution disaster risk assessment is a basic way to effectively identify the influence of air pollution on the natural ecological environment and the residents’ health. Air pollution disaster risk prediction and management need long-term complex system engineering, and an air pollution disaster risk assessment indicator system and prediction model is needed for the various different regions to carry out more in-depth and advanced research.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Tangency Quantity of KMO Sampling | Bartlett Spherical Degree Test | ||
|---|---|---|---|
| Approximate Chi-Square | Degrees of Freedom | Significance (Sig) | |
| 0.662 | 3186.978 | 435 | 0.000 |
| Principal Components | Characteristic Values | Contribution Rates | Cumulative Contributions |
|---|---|---|---|
| 1 | 14.117 | 47.056 | 47.056 |
| 2 | 7.186 | 23.953 | 71.009 |
| 3 | 3.961 | 13.204 | 84.213 |
| 4 | 2.739 | 9.129 | 93.342 |
| 5 | 0.634 | 2.115 | 95.457 |
| 6 | 0.351 | 1.170 | 96.627 |
| 7 | 0.254 | 0.847 | 97.474 |
| 8 | 0.197 | 0.658 | 98.132 |
| 9 | 0.118 | 0.393 | 98.525 |
| 10 | 0.115 | 0.385 | 98.910 |
| 11 | 0.074 | 0.247 | 99.158 |
| 12 | 0.066 | 0.220 | 99.377 |
| 13 | 0.049 | 0.162 | 99.540 |
| 14 | 0.044 | 0.146 | 99.685 |
| 15 | 0.026 | 0.088 | 99.773 |
| 16 | 0.020 | 0.066 | 99.839 |
| 17 | 0.014 | 0.046 | 99.885 |
| 18 | 0.009 | 0.030 | 99.915 |
| 19 | 0.006 | 0.022 | 99.936 |
| 20 | 0.005 | 0.016 | 99.952 |
| 21 | 0.004 | 0.015 | 99.967 |
| 22 | 0.003 | 0.009 | 99.976 |
| 23 | 0.002 | 0.007 | 99.984 |
| 24 | 0.002 | 0.005 | 99.989 |
| 25 | 0.001 | 0.005 | 99.993 |
| 26 | 0.001 | 0.002 | 99.996 |
| 27 | 0.001 | 0.001 | 99.997 |
| 28 | 0.000 | 0.001 | 99.998 |
| 29 | 0.000 | 0.001 | 99.999 |
| 30 | 0.000 | 0.001 | 100.000 |
| Indicator Codes | ||||
|---|---|---|---|---|
| X1 | 0.497 | 0.770 | -0.112 | 0.083 |
| X2 | −0.043 | 0.243 | 0.885 | 0.118 |
| X3 | 0.734 | 0.565 | 0.250 | −0.120 |
| X4 | 0.671 | 0.344 | 0.503 | −0.245 |
| X5 | 0.301 | −0.599 | 0.391 | −0.502 |
| X6 | 0.679 | 0.329 | 0.605 | −0.094 |
| X7 | 0.833 | 0.053 | −0.408 | 0.238 |
| X8 | 0.790 | 0.140 | −0.554 | 0.133 |
| X9 | 0.876 | 0.266 | −0.308 | −0.207 |
| X10 | 0.782 | −0.260 | 0.145 | −0.469 |
| X11 | 0.908 | −0.086 | −0.057 | −0.243 |
| X12 | −0.940 | 0.107 | −0.023 | −0.266 |
| X13 | −0.835 | −0.271 | −0.175 | 0.274 |
| X14 | −0.383 | 0.814 | −0.235 | 0.340 |
| X15 | 0.515 | 0.251 | −0.775 | −0.069 |
| X16 | 0.776 | 0.418 | 0.306 | 0.137 |
| X17 | 0.776 | 0.017 | −0.337 | −0.477 |
| X18 | −0.050 | −0.926 | 0.312 | 0.141 |
| X19 | −0.130 | −0.467 | −0.785 | −0.323 |
| X20 | −0.836 | 0.454 | −0.024 | −0.291 |
| X21 | −0.863 | 0.463 | 0.022 | −0.160 |
| X22 | 0.292 | −0.853 | 0.311 | 0.259 |
| X23 | −0.634 | −0.211 | −0.062 | 0.701 |
| X24 | 0.943 | −0.306 | −0.028 | 0.000 |
| X25 | −0.042 | 0.952 | 0.110 | −0.002 |
| X26 | −0.040 | 0.976 | 0.093 | 0.029 |
| X27 | 0.858 | 0.090 | 0.063 | 0.399 |
| X28 | 0.665 | 0.253 | −0.049 | 0.572 |
| X29 | 0.914 | −0.283 | −0.014 | 0.230 |
| X30 | 0.866 | −0.323 | 0.007 | 0.378 |
| Region | Year | |||||
|---|---|---|---|---|---|---|
| Liaoning Province | 2010 | −15.330 | −15.265 | −0.362 | −1.171 | −11.811 |
| 2011 | −14.955 | −13.106 | 1.090 | −0.705 | −10.817 | |
| 2012 | −13.596 | −12.090 | 2.203 | −0.214 | −9.666 | |
| 2013 | −12.046 | −10.785 | 3.000 | 0.072 | −8.409 | |
| 2014 | −11.548 | −8.469 | 1.995 | 1.015 | −7.613 | |
| 2015 | −10.387 | −7.523 | 3.111 | 1.117 | −6.617 | |
| 2016 | −8.810 | −4.789 | 6.089 | 1.360 | −4.676 | |
| 2017 | −8.833 | −3.386 | 6.661 | 1.800 | −4.203 | |
| 2018 | −7.539 | −2.539 | 8.124 | 1.889 | −3.118 | |
| 2019 | −6.319 | −2.285 | 8.206 | 1.776 | −2.437 | |
| Beijing | 2010 | −16.058 | −0.080 | −7.089 | 1.222 | −8.999 |
| 2011 | −14.062 | 1.638 | −7.049 | 1.710 | −7.499 | |
| 2012 | −12.414 | 1.918 | −6.283 | 1.590 | −6.499 | |
| 2013 | −11.830 | 2.556 | −6.292 | 1.422 | −6.059 | |
| 2014 | −10.953 | 3.932 | −6.186 | 2.417 | −5.151 | |
| 2015 | −11.519 | 5.548 | −4.214 | 2.772 | −4.708 | |
| 2016 | −9.518 | 7.323 | −2.944 | 3.753 | −2.968 | |
| 2017 | −7.588 | 8.950 | −0.767 | 3.933 | −1.252 | |
| 2018 | −7.696 | 10.420 | 1.625 | 3.922 | −0.592 | |
| 2019 | −5.946 | 12.344 | 3.594 | 3.821 | 1.052 | |
| Shanghai | 2010 | −5.975 | 0.512 | −3.373 | −4.815 | −3.829 |
| 2011 | −4.743 | 1.035 | −1.896 | −5.231 | −2.905 | |
| 2012 | −3.069 | 2.421 | −2.296 | −4.482 | −1.689 | |
| 2013 | −2.963 | 3.733 | −0.958 | −4.517 | −1.113 | |
| 2014 | −1.036 | 5.387 | 0.717 | −4.578 | 0.514 | |
| 2015 | −1.259 | 6.273 | 0.709 | −4.400 | 0.645 | |
| 2016 | 2.417 | 8.834 | 1.755 | −3.368 | 3.405 | |
| 2017 | 2.349 | 10.705 | 2.755 | −2.369 | 4.089 | |
| 2018 | 3.145 | 11.383 | 4.708 | −2.791 | 4.900 | |
| 2019 | 4.256 | 12.583 | 5.973 | −2.924 | 5.933 | |
| Guangdong Province | 2010 | 13.714 | −8.315 | −3.931 | −2.072 | 4.021 |
| 2011 | 14.226 | −6.977 | −2.012 | −1.395 | 4.960 | |
| 2012 | 16.971 | −6.403 | −2.928 | −1.243 | 6.377 | |
| 2013 | 18.406 | −5.516 | −1.900 | −0.464 | 7.549 | |
| 2014 | 19.868 | −4.275 | −0.829 | 0.298 | 8.831 | |
| 2015 | 23.412 | −3.482 | −0.332 | 0.322 | 10.893 | |
| 2016 | 26.289 | −2.235 | 0.258 | 0.800 | 12.794 | |
| 2017 | 28.254 | −1.274 | −1.178 | 2.455 | 13.990 | |
| 2018 | 29.549 | 0.035 | −0.206 | 3.341 | 15.203 | |
| 2019 | 33.136 | 1.261 | 0.454 | 3.932 | 17.477 |
References
- Kumar, P.; Druckman, A.; Gallagher, J.; Gatersleben, B.; Allison, S.; Eisenman, T.S.; Hoang, U.; Hama, S.; Tiwari, A.; Sharma, A.; et al. The nexus between air pollution, green infrastructure and human health. Environ. Int. 2019, 133, 105181. [Google Scholar] [CrossRef] [PubMed]
- Li, X.L.; Zheng, W.F.; Yin, L.R.; Yin, Z.T.; Song, L.H.; Tian, X. Influence of Social-economic Activities on Air Pollutants in Beijing, China. Open Geosci. 2017, 9, 314–321. [Google Scholar] [CrossRef] [Green Version]
- Zheng, W.F.; Li, X.L.; Yin, L.R.; Wang, Y.L. Spatiotemporal heterogeneity of urban air pollution in China based on spatial analysis. Rend. Lincei 2016, 27, 351–356. [Google Scholar] [CrossRef]
- Chen, X.B.; Yin, L.R.; Fan, Y.L.; Song, L.H.; Ji, T.T.; Liu, Y.; Tian, J.W.; Zheng, W.F. Temporal evolution characteristics of PM2.5 concentration based on continuous wavelet transform. Sci. Total Environ. 2020, 699, 134244. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Xu, Y.; Zhang, S.Q. Will joint regional air pollution control be more cost-effective? An empirical study of China’s Beijing-Tianjin-Hebei region. Environ. Manag. 2015, 149, 27–36. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Warburton, D.E.R.; Bredin, S.S.D.; Shellington, E.M.; Cole, C.; de Faye, A.; Harris, J.; Kim, D.D.; Abelsohn, A. A Systematic Review of the Short-Term Health Effects of Air Pollution in Persons Living with Coronary Heart Disease. J. Clin. Med. 2019, 8, 274. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.H.; Kabir, E.; Kabir, S. A review on the human health impact of airborne particulate matter. Environ. Int. 2015, 74, 136–143. [Google Scholar] [CrossRef]
- Crouse, D.L.; Pinault, L.; Balram, A.; Brauer, M.; Burnett, R.T.; Martin, R.V.; van Donkelaar, A.; Villeneuve, P.J.; Weichenthal, S. Complex relationships between greenness, air pollution, and mortality in a population-based Canadian cohort. Environ. Int. 2019, 128, 292–300. [Google Scholar] [CrossRef]
- Pruss-Ustun, A.; Wolf, J.; Corvalan, C.; Neville, T.; Bos, R.; Neira, M. Diseases due to unhealthy environments: An updated estimate of the global burden of disease attributable to environmental determinants of health. J. Public Health 2017, 39, 464–475. [Google Scholar] [CrossRef]
- Zhang, N.N.; Ma, F.; Qin, C.B.; Li, Y.F. Spatiotemporal trends in PM2.5 levels from 2013 to 2017 and regional demarcations for joint prevention and control of atmospheric pollution in China. Chemosphere 2018, 210, 1176–1184. [Google Scholar] [CrossRef]
- GBD 2016 Risk Factors Collaborators. Global, regional, and national comparative risk assessment of 84 behavioural, environmental and occupational, and metabolic risks or clusters of risks, 1990–2016: A systematic analysis for the Global Burden of Disease Study 2016. Lancet 2017, 390, 1345–1422. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.J.; Kan, H.D.; Chen, B.H.; Huang, W.; Bai, Z.P.; Song, G.X.; Pan, G.W. Association of particulate air pollution with daily mortality: The China air pollution and health effects study. Epidemiology 2012, 175, 1173–1181. [Google Scholar] [CrossRef] [PubMed]
- Gostner, J.M.; Fuchs, D.; Felder, T.; Griesmacher, A.; Melichar, B.; Postolache, T.; Reibnegger, G.; Weiss, G.; Werner, E.R. 39th International Winter-Workshop Clinical, Chemical and Biochemical Aspects of Pteridines and Related Topics Innsbruck, February 25th–28th. Pteridines 2020, 31, 109–135. [Google Scholar] [CrossRef]
- Ragguett, R.M.; Cha, D.S.; Subramaniapillai, M.; Carmona, N.E.; Lee, Y.; Yuan, D.; Rong, C.; McIntyre, R.S. Air pollution, aeroallergens and suicidality: A review of the effects of air pollution and aeroallergens on suicidal behavior and an exploration of possible mechanisms. Rev. Environ. Health 2017, 32, 343–359. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brockmeyer, S.; D’Angiulli, A. How air pollution alters brain development: The role of neuroinflammation. Transl. Neurosci. 2016, 7, 24–30. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.H.; Wu, X.; Yazdi, M.D.; Braun, D.; Awad, Y.A.; Wei, Y.G.; Liu, P.F.; Di, Q.; Wang, Y.; Schwartz, J.; et al. Long-term effects of PM2.5 on neurological disorders in the American Medicare population: A longitudinal cohort study. Lancet Planet. Health 2020, 4, 557–565. [Google Scholar] [CrossRef]
- Luan, G.J.; Yin, P.; Zhou, M.G. Associations between ambient air pollution and years of life lost in Beijing. Atmos. Pollut. Res. 2021, 12, 200–205. [Google Scholar] [CrossRef]
- Khojasteh, D.N.; Goudarzi, G.; Taghizadeh-Mehrjardi, R.; Asumadu-Sakyi, A.B.; Fehresti-Sani, M. Long-term effects of outdoor air pollution on mortality and morbidity–prediction using nonlinear autoregressive and artificial neural networks model. Atmos. Pollut. Res. 2021, 12, 46–56. [Google Scholar] [CrossRef]
- Li, A.; Zhou, Q.; Xu, Q. Prospects for ozone pollution control in China: An epidemiological perspective. Environ. Pollut. 2021, 285, 117670. [Google Scholar] [CrossRef]
- Syed, N.; Ryu, M.H.; Dhillon, S.; Schaeffer, M.R.; Ramsook, A.H.; Leung, J.M.; Ryerson, C.J.; Carlsten, C.; Guenette, J.A. Effects of traffic-related air pollution on exercise endurance, dyspnea and cardiorespiratory physiology in health and COPD-A randomized, placebo-controlled crossover trial. Chest 2022, 161, 662–675. [Google Scholar] [CrossRef]
- Burkart, K.; Canário, P.; Breitner, S.; Schneider, A.; Scherber, K.; Andrade, H.; Alcoforado, M.J.; Endlicher, W. Interactive short-term effects of equivalent temperature and air pollution on human mortality in Berlin and Lisbon. Environ. Pollut. 2013, 183, 54–63. [Google Scholar] [CrossRef] [PubMed]
- Willers, S.M.; Jonker, M.F.; Klok, L.; Keuken, M.P.; Odink, J.; Elshout, S.V.D.; Sabel, C.E.; Mackenbach, J.P.; Burdorf, A. High resolution exposure modelling of heat and air pollution and the impact on mortality. Environ. Int. 2016, 89, 102–109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Requia, W.J.; Koutrakis, P. Mapping distance-decay of premature mortality attributable to PM2.5-related traffic congestion. Environ. Pollut. 2018, 243, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.Y.; Tesch, F.; Markevych, I.; Baumbach, C.; Janben, C.; Schmitt, J.; Romanos, M.; Nowak, D.; Heinrich, J. Depression and anxiety with exposure to ozone and particulate matter: An epidemiological claims data analysis. Int. J. Hyg. Environ. Health. 2020, 228, 113562. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.N.; Yan, Y.; Nazhalati, N.; Kuerban, A.; Li, J.; Huang, L. The effect of PM2.5 exposure and risk perception on the mental stress of Nanjing citizens in China. Chemosphere 2020, 254, 126797. [Google Scholar] [CrossRef]
- Yuan, L.; Shin, K.; Managi, S. Subjective Well-being and Environmental Quality: The Impact of Air Pollution and Green Coverage in China. Ecol. Econ. 2018, 153, 124–138. [Google Scholar] [CrossRef]
- Chen, X.G.; Ye, J.J. When the wind blows: Spatial spillover effects of urban air pollution in China. J. Environ. Plan. Manag. 2018, 62, 1359–1376. [Google Scholar] [CrossRef]
- Zhou, D.; Lin, Z.L.; Liu, L.M.; Qi, J.L. Spatial-temporal characteristics of urban air pollution in 337 Chinese cities and their influencing factors. Environ. Sci. Pollut. Res. Int. 2021, 28, 36234–36258. [Google Scholar] [CrossRef]
- Morelli, X.; Rieux, C.; Cyrys, J.; Forsberg, B.; Slama, R. Air pollution, health and social deprivation: A fine-scale risk assessment. Environ. Res. 2016, 147, 59–70. [Google Scholar] [CrossRef]
- Qiu, L.; Liu, F.; Zhang, X.; Gao, T. The reducing effect of green spaces with different vegetation structure on atmospheric particulate matter concentration in BaoJi City, China. Atmosphere 2018, 9, 332. [Google Scholar] [CrossRef] [Green Version]
- Guijarro, F.; Poyatos, J.A. Designing a Sustainable Development Goal Index through a Goal Programming Model: The Case of EU-28 Countries. Sustainability 2018, 10, 3167. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.S.; Yang, Y.G.; Li, H.H.; van Dijk, M.P. Measuring Urban Resilience to Climate Change in Three Chinese Cities. Sustainability 2020, 12, 9735. [Google Scholar] [CrossRef]
- Sun, Z.; Yang, L.Y.; Bai, X.X.; Du, W.; Shen, G.F.; Fei, J.; Wang, Y.H.; Chen, A.; Chen, Y.C.; Zhao, M.R. Maternal ambient air pollution exposure with spatial-temporal variations and preterm birth risk assessment during 2013–2017 in Zhejiang Province, China. Environ. Int. 2019, 133, 105242. [Google Scholar] [CrossRef] [PubMed]
- Du, W.; Chen, Y.C.; Zhu, X.; Zhong, Q.R.; Zhuo, S.J.; Liu, W.J.; Huang, Y.; Shen, G.F.; Tao, S. Wintertime air pollution and health risk assessment of inhalation exposure to polycyclic aromatic hydrocarbons in rural China. Atmos. Environ. 2018, 191, 1–8. [Google Scholar] [CrossRef]
- Zhang, H.; Ji, Y.Y.; Wu, Z.H.; Peng, L.; Bao, J.M.; Peng, Z.J.; Li, H. Atmospheric volatile halogenated hydrocarbons in air pollution episodes in an urban area of Beijing: Characterization, health risk assessment and sources apportionment. Sci. Total Environ. 2022, 806, 150283. [Google Scholar] [CrossRef] [PubMed]
- Bao, J.M.; Li, H.; Wu, Z.H.; Zhang, X.; Zhang, H.; Li, Y.F.; Qian, J.; Chen, J.H.; Deng, L.Q. Atmospheric carbonyls in a heavy ozone pollution episode at a metropolis in Southwest China: Characteristics, health risk assessment, sources analysis. J. Environ. Sci. 2022, 133, 40–54. [Google Scholar] [CrossRef] [PubMed]
- Meijering, J.; Tobi, H.; Kern, K. Defifining and measuring urban sustainability in Europe: A Delphi study on identifying its most relevant components. Ecol. Indic. 2018, 90, 38–46. [Google Scholar] [CrossRef]
- Guan, D.; Gao, W.; Su, W.; Li, H.; Hokao, K. Modeling and dynamic assessment of urban economy-resource-environment system with a coupled system dynamics—Geographic information system model. Ecol. Indic. 2011, 11, 1333–1344. [Google Scholar] [CrossRef]
- Wang, Q.; Yuan, X.; Cheng, X.; Mu, R.; Zuo, J. Coordinated development of energy, economy and environment subsystems—A case study. Ecol. Indic. 2014, 46, 514–523. [Google Scholar] [CrossRef]
- Duan, Y.; Mu, H.; Li, N.; Li, L.; Xue, Z. Research on comprehensive evaluation of low carbon economy development level based on AHP-entropy method: A case study of Dalian. Energy Procedia 2016, 104, 468–474. [Google Scholar] [CrossRef]
- Du, Z.J.; Heng, J.N.; Niu, M.F.; Sun, S.L. An innovative ensemble learning air pollution early-warning system for China based on incremental extreme learning machine. Atmos. Pollut. Res. 2021, 12, 101153. [Google Scholar] [CrossRef]
- Li, Y.Y.; Huang, S.; Yin, C.X.; Sun, G.H.; Ge, C. Construction and countermeasure discussion on government performance evaluation model of air pollution control: A case study from Beijing-Tianjin-Hebei region. J. Clean. Prod. 2020, 254, 120072. [Google Scholar] [CrossRef]
- Wang, L.; Bi, X.H. Risk assessment of knowledge fusion in an innovation ecosystem based on a GA-BP neural network. Cogn. Syst. Res. 2021, 66, 201–210. [Google Scholar] [CrossRef]
- Karim, B.; Blaise, N. Effect of atmospheric pollutants on the air quality in Tunisia. J. Sci. World 2012, 2012, 863528. [Google Scholar]
- Rupakheti, D.; Yin, X.F.; Rupakheti, M.; Zhang, Q.G.; Li, P.; Rai, M.; Kang, S.C. Spatio-temporal characteristics of air pollutants over Xinjiang, northwestern China. Environ. Pollut. 2021, 268, 115907. [Google Scholar] [CrossRef]
- Kim, Y.; Lee, I.; Farquhar, J.; Kang, J.; Villa, I.M.; Kim, H. Multi isotope systematics of precipitation to trace the sources of air pollutants in Seoul, Korea. Environ. Pollut. 2021, 286, 117548. [Google Scholar] [CrossRef]
- Zou, X.D.; Cai, F.; Wang, X.Y.; Li, K.P.; Zhang, Y.H.; Wang, H.Y.; Yang, H.B.; Liu, Y.C. Study on ozone mass concentration change in Liaoning Province. Ecol. Environ. Sci. 2020, 29, 1830–1838. [Google Scholar]
- Hao, W.S.; Zhu, X.S.; Li, X.F.; Turyagyenda, G. Prediction of cutting force for self-propelled rotary tool using artificial neural networks. J. Mater. Process. Technol. 2006, 180, 23–29. [Google Scholar] [CrossRef]
- Wang, H.Y.; Zhang, Z.X.; Liu, L.M. Prediction and fitting of weld morphology of Al alloy-CFRP welding-rivet hybrid bonding joint based on GA-BP neural network. J. Manuf. Process. 2021, 63, 109–120. [Google Scholar] [CrossRef]
- Polutchko, S.K.; Stewart, J.J.; Demmig-Adams, B.; Adams, W.W. Evaluating the link between photosynthetic capacity and leaf vascular organization with principal component analysis. Photosynthetica 2018, 56, 392–403. [Google Scholar] [CrossRef]
- Zhou, Z.; Du, N.; Xu, J.Y.; Li, Z.X.; Wang, P.L.; Zhang, J. Randomized Kernel Principal Component Analysis for Modeling and Monitoring of Nonlinear Industrial Processes with Massive Data. Ind. Eng. Chem. Res. 2019, 58, 10410–10417. [Google Scholar] [CrossRef]
- Chen, J.; Liao, C.M. Dynamic process fault monitoring based on neural network and PCA. J. Process Control 2002, 12, 277–289. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Ye, Z.F.; Tang, Y. Non-destructive identification for gender of chicken eggs based on GA-BPNN with double hidden layers. J. Appl. Poult. Res. 2021, 30, 100203. [Google Scholar] [CrossRef]
- He, F.; Zhang, L.Y. Prediction model of end-point phosphorus content in BOF steelmaking process based on PCA and BP neural network. J. Process Control 2018, 66, 51–58. [Google Scholar] [CrossRef]








| Region | SO2 (ug/m−3) | NO2 (ug/m−3) | PM10 (ug/m−3) | CO (ug/m−3) | O3 (mg/m−3) | PM2.5 (ug/m−3) |
|---|---|---|---|---|---|---|
| Liaoning Province | 27.786 | 5.075 | 26.429 | 0.757 | 12.452 | 16.248 |
| Beijing | 10.965 | 6.119 | 15.351 | 0.830 | 7.130 | 18.135 |
| Shanghai | 7.284 | 3.955 | 14.920 | 0.345 | 10.316 | 11.270 |
| Guangdong Province | 6.216 | 3.100 | 9.133 | 0.314 | 14.869 | 8.331 |
| Primary Indicators | Secondary Indicators | Reference Source | Impact Direction |
|---|---|---|---|
| Hazard factors | X1: Annual average SO2 (ug/m−3) | [1,6,7] | + |
| X2: Annual average NO2 (ug/m−3) | + | ||
| X3: Annual average PM10 (ug/m−3) | + | ||
| X4: Annual average CO (mg/m−3) | + | ||
| X5: Annual average O3 (ug/m−3) | + | ||
| X6: Annual average PM2.5 (ug/m−3) | + | ||
| Hazard-laden environment | X7: Birth rate (%) | [2,11,14,19,22] | − |
| X8: Natural growth rate (%) | − | ||
| X9: Average annual temperature (℃) | − | ||
| X10: Annual average relative humidity (%) | − | ||
| X11: Average annual rainfall (mm) | − | ||
| X12: Regional GDP (CNY 100 million) | + | ||
| X13: Density of economy (CNY 100 million/km2) | + | ||
| X14: Proportion of secondary industry (%) | + | ||
| X15: Building construction area (km2) | + | ||
| X16: Death rate (%) | + | ||
| X17: Death rate from respiratory diseases (%) | + | ||
| X18: Death rate from heart diseases (%) | + | ||
| X19: Average annual residents’ medical treatment visits (Times) | + | ||
| X20: Average annual hospitalization rate (%) | + | ||
| Hazard-bearing body | X21: Population (10,000 people) | [33,35] | + |
| X22: Proportion of urban population (%) | + | ||
| X23: Density of population (people/km2) | + | ||
| X24: Urban green space area (hm2) | − | ||
| Disaster resilience | X25: Per capita disposable income (CNY) | [12,16,32] | − |
| X26: Per capita consumption expenditure (CNY) | − | ||
| X27: Health expenditure (CNY 100 million) | − | ||
| X28: Energy conservation and environmental protection expenditure (CNY 100 million) | − | ||
| X29: Number of medical insurance participants (10,000 people) | − | ||
| X30: Number of health workers (people) | − |
| Region | Real Value | PCA-GA-BP Neural Network | PCA-BP Neural Network | ||
| Predicted Value | Absolute Error | Predicted Value | Absolute Error | ||
| Liaoning Province | −2.437 | −2.874 | 0.437 | −3.973 | 1.536 |
| Beijing | 1.052 | 1.519 | 0.467 | 1.351 | 0.299 |
| Shanghai | 5.933 | 5.036 | 0.897 | 7.585 | 1.652 |
| Guangdong Province | 17.477 | 16.852 | 0.625 | 18.903 | 1.426 |
| Region | Real Value | GA-BP Neural Network | BP Neural Network | ||
| Predicted Value | Absolute Error | Predicted Value | Absolute Error | ||
| Liaoning Province | −2.437 | −1.186 | 1.251 | −4.582 | 2.145 |
| Beijing | 1.052 | 1.907 | 0.855 | 1.727 | 0.675 |
| Shanghai | 5.933 | 6.852 | 0.919 | 7.692 | 1.759 |
| Guangdong Province | 17.477 | 14.932 | 2.545 | 19.971 | 2.494 |
| Prediction Model | MAE | RMSE | MAPE (%) |
|---|---|---|---|
| PCA-GA-BP Neural Network | 0.607 | 0.317 | 20.3 |
| PCA-BP Neural Network | 1.228 | 0.671 | 31.9 |
| GA-BP Neural Network | 1.393 | 0.775 | 40.6 |
| BP Neural Network | 1.768 | 0.948 | 49.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, G.; Chen, H.; Xie, B.; Wang, M. Risk Assessment and Prediction of Air Pollution Disasters in Four Chinese Regions. Sustainability 2022, 14, 3106. https://doi.org/10.3390/su14053106
Deng G, Chen H, Xie B, Wang M. Risk Assessment and Prediction of Air Pollution Disasters in Four Chinese Regions. Sustainability. 2022; 14(5):3106. https://doi.org/10.3390/su14053106
Chicago/Turabian StyleDeng, Guoqu, Hu Chen, Bo Xie, and Mengtian Wang. 2022. "Risk Assessment and Prediction of Air Pollution Disasters in Four Chinese Regions" Sustainability 14, no. 5: 3106. https://doi.org/10.3390/su14053106






