Abstract
The operation process of the Chinese provincial industrial system consists of four stages, namely the production (P) stage, wastewater treatment (WWT) stage, solid waste treatment (SWT) stage, and sulfur dioxide treatment (SDT) stage. Based on this structure, a four-stage data envelopment analysis (DEA) model is developed to evaluate the eco-efficiency, production efficiency, wastewater treatment efficiency, solid waste treatment efficiency, and sulfur dioxide treatment efficiency of provincial industrial systems in China, considering the undesirable output and variable returns to scale (VRS). Based on the objective data from 2011 to 2015, the following conclusions are drawn: Firstly, the eco-efficiency of the Chinese provincial industrial system has not been significantly improved during the study period, and the average eco-efficiency score is low, only 0.3805. Secondly, the reasons for the low eco-efficiency of the industrial system are different in the Eastern, Central, Western, and Northeastern regions. Thirdly, compared with the P stage, industrial WWT stage, and SWT stage, the efficiency of SDT stage is still relatively weak.
1. Introduction
Since its reform and opening up, and with the rapid development of industrialization, the Chinese economy has made remarkable achievements. However, behind this achievement, China has paid a huge energy and environmental price. The extensive economic development model with high energy consumption and high emissions has brought energy shortages and environmental pollution to China. As the world’s largest energy consumer and greenhouse gas emitter, China accounts for 23% of the world’s energy consumption, according to data released by the BP Statistical Yearbook of World Energy. Only 29.3% of China’s 338 major cities meet the air quality standards recommended by the Ministry of Ecology and Environment, according to the 2017 China Environmental Status Bulletin [1]. For this reason, the Chinese government has taken drastic measures to control air pollution. For example, The State Council issued the Air Pollution Prevention and Control Action Plan (2013) and the Three-year Action Plan to Win the Battle against Blue Skies (2017). Currently, air pollution in China has attracted widespread attention in policy making and industrial research.
The industrial sector is one of the high energy consuming sectors in China, which determines that the industrial sector plays an important role in reducing energy consumption and environmental pollution. Chinese industrial energy consumption accounted for 65.6% of the country’s total energy consumption in 2017, according to data released by the National Bureau of Statistics. The huge consumption of industrial fossil energy will discharge a large amount of industrial wastewater, solid waste, and sulfur dioxide, which is one of the main culprits of smog. According to the China Environmental Statistics Yearbook, industrial wastewater emissions accounted for 27.1% of total wastewater emissions in 2015, and industrial sulfur dioxide emissions accounted for 83.7% of total sulfur dioxide emissions. The discharge of a large number of industrial pollutants is not only harmful to human health, but also detrimental to sustainable development strategies.
Industrial eco-efficiency is defined as the efficiency level of ecological resources to meet the needs of industrial development, aiming at the unification of economic efficiency and environmental benefits to achieve sustainable development of industrial economy and society. The concept of eco-efficiency was developed by the World Business Council for Sustainable Development. Eco-efficiency can be defined as the ratio of economic value to environmental impact [2]. It involves producing more goods and services with fewer resources, with less impact on the environment [3]. Eco-efficiency is defined as the ratio of environmental performance measurement index to financial performance measurement index. From this perspective, the goal is to achieve the lowest negative environmental impact with the lowest consumption of economic resources [4]. One of the basic characteristics of previous studies on the efficiency of industrial systems is that the industrial system is regarded as a “black box” structure, in which resources such as energy, capital, and labor are invested to obtain industrial emissions and GDP output without considering its internal structure, which often results in exaggerated efficiency results [5]. Because processes of industrial operations are often accompanied by a variety of undesirable industrial pollutants, these pollutants are an important goal of emission reduction. However, many different industrial pollutants are generated, and the process for reducing these is not the same; therefore, to ignore these different characteristics, inhibits accurate exploration of the eco-efficiency of the industrial system, and limits the ability to provide valuable information for energy conservation and emissions reduction targets. According to the characteristics of different links of production and pollution control in the industrial system, the Chinese provincial industrial system includes P stage, WWT stage, SWT stage, and SDT stage, and its structure is shown in Figure 1. In Figure 1, the P stage inputs energy, capital, and labor, producing industrial added value, wastewater, solid waste, and sulfur dioxide. Among them, wastewater, solid waste, and sulfur dioxide need to be treated through various treatment stages and then discharged. Wastewater treatment, solid waste treatment, and sulfur dioxide treatment all require additional investment in treatment. Wastewater and sulfur dioxide are treated and then discharged, while solid waste is treated by recycling and comprehensive utilization to reduce environmental pollution. Therefore, to improve the eco-efficiency of the entire industrial system, the efficiency of these four interrelated sub-stages must be improved simultaneously. Based on the above considerations, this paper mainly discusses the following questions:
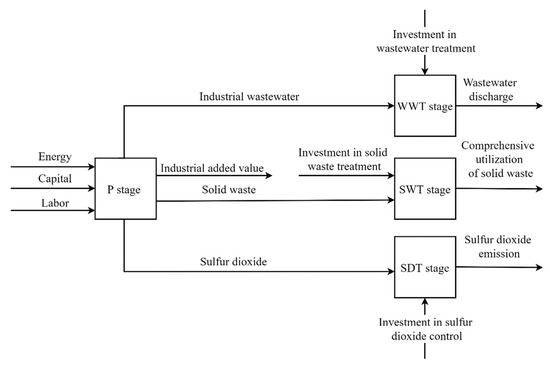
Figure 1.
Network structure of industrial systems.
- ➢
- Has the eco-efficiency of the Chinese provincial industrial system been improved from 2011 to 2015? How efficient are the sub-stages?
- ➢
- Which sub-stages are the causes of low efficiency?
- ➢
- What are the differences in efficiency among the four regions? What are the characteristics of efficiency at different stages in the same system and in different years? Therefore, this paper evaluates the efficiency of Chinese provincial industrial sectors from 2011 to 2015 by combining the network SBM-DEA model and efficiency decomposition method, in order to provide necessary guidance for policy making and sustainable development of industrial economy.
2. Literature Review
At present, the concepts of energy conservation and emission reduction, clear water and green mountains have become more and more common across society. As one of the representative sectors of high energy consumption and high emissions, how to improve the energy and environmental efficiency of industrial enterprises has attracted more and more attention from the industry and academia. Generally speaking, the efficiency evaluation of industrial sectors is mainly carried out at the regional and industry levels. For example, reference [6] used a DEA based method to evaluate the energy and environmental efficiency of 30 regions in China and found that the energy and environmental efficiency of Chinese industry was poor. Reference [7] applied the Malmquist index (MI) method to evaluate the performance of industrial energy conservation and emission reduction in more than 200 Cities in China. Reference [8] used DEA to evaluate provincial environmental efficiency in China from 2004 to 2012. Reference [9] used the input-oriented ZSG-DEA model to explore the carbon emission quota efficiency of 39 industries in China in 2020.
There are two main methods to study the efficiency of industrial sectors. The first is parametric method represented by stochastic frontier method (SFA). For example, reference [10] used SFA to evaluate the GHG efficiency of 26 industries in China at the industry level and analyzed its influencing factors. Reference [11] proposed a hybrid method using logarithmic average divided by index, symmetric component, and SFA to estimate the energy saving potential of industrial sectors. Reference [12] quantitatively measured the total factor carbon emission performance and carbon emission reduction potential of 39 industrial sectors in the Beijing–Tianjin–Hebei region from 2010 to 2016 by using SFA method. However, a great limitation of these studies lies in the fact that the functional form of industrial production technology must be given compulsorily in advance, that is, a certain functional relationship between input and output, and different functional forms may lead to different evaluation results, which is a deficiency of SFA method for industrial system efficiency evaluation. The other is the more widely used non-parametric method represented by DEA, which makes up for the shortcomings of the SFA method. It does not need to specify a certain functional relationship between input and output. This method was first proposed by [13] in 1978. Since then, more and more research on methods, model innovation, and different application scenarios based on this method have been carried out, including [14,15]. For the research on energy and environment using DEA method, please refer to the review of [16].
Research on efficiency evaluation of industrial systems using traditional DEA or its extended model mostly regard the evaluated system as a “black box” structure without considering its internal situation. Reference [17] used the super-efficiency DEA model to evaluate the eco-environmental benefits of cities in the Yellow River Basin from 2008 to 2017, and discussed the temporal and spatial evolution characteristics of regional economic benefits and the factors affecting regional economic benefits. Reference [18] used the data of 42 thermal power plants in China in 2020 to construct a multi-dimensional index evaluation system of carbon emission efficiency from three aspects: energy, economy, and environment. The super-efficiency slacks-based measure (SBM) model with undesirable output is used to identify and distinguish several efficient decision units and the efficiency improvement path of inefficient thermal power plant is discussed. Reference [19] used non-parametric DEA and fractional regression model to analyze the evolution of eco-efficiency in 27 countries of the European Union (EU) from 2008 to 2018, providing a high level of attention to the relationship between economic growth and environmental performance in the EU. Reference [20] extends the previous framework for efficiency analysis, introducing a new slacks-based measure of efficiency called the scale directional distance function (SDDF) approach, used to measure the eco-efficiency of Malaysia’s manufacturing industry. Reference [21] uses DEA methodology to calculate environmental efficiency across the 28 member states of the European Union (EU). For more studies in this field, please refer to [22,23,24,25,26,27,28]. To determine the causes of inefficiency in industrial systems, it is necessary to consider the internal structure of industrial systems. Therefore, reference [29] developed a network DEA model for evaluating organizational performance and its component performance. The proposed network DEA model has aroused the research interest of many scholars, and many new network DEA expansion models have been developed successively, such as network SBM model and dynamic network SBM model of [30,31], additive network DEA efficiency decomposition model of [32], and network DEA efficiency decomposition method of [33]. Reference [34] extended the traditional two-stage network DEA model to the uncertain two-stage network DEA model. Reference [35] proposed a common weight network DEA model when the production system contains multiple interrelated processes. The two-stage DEA model is a kind of network model. Reference [36] used two-stage DEA model to construct an index system to measure the mining technology innovation efficiency, mining eco-efficiency, and mining comprehensive efficiency of 30 provinces in China. Reference [37] simulated the operation process of the electric power industry through the network structure, introduced the dynamic slacks-based measure method, and evaluated the operation efficiency of the whole industry and each stage in each period. Reference [38] proposed a two-stage efficiency evaluation model of Chinese regional industrial system based on SBM-DEA. The model decomposed efficiency into production efficiency and emission reduction efficiency, which can simultaneously estimate the efficiency of the entire regional industrial system, production stage, and emission reduction stage. However, this study did not consider the differences in the treatment processes of different industrial pollutants in the treatment stage, and could not further find out the cause of low efficiency in the internal stage of the system. Reference [39] separated the energy production sector from the energy consumption sector and proposed an adjusted energy efficiency evaluation network DEA model, which was then applied to the energy efficiency evaluation of provincial industrial sectors in China. Reference [40] established a network SBM model to evaluate the environmental performance of the Chinese industrial system. Reference [41] proposed a two-stage game DEA method, using centralized and Stackelberg game models to measure the cost efficiency (CE) of Iran’s power grid. Reference [42] extended the existing two-stage network DEA model that distinguishes pure energy efficiency from economic efficiency to investigate whether energy efficiency has a positive relationship with corporate financial performance in South Korea. Reference [43] used a dynamic network DEA (DNDEA) model to evaluate the performance of Taiwan’s machine tool industry from 2010 to 2014. Using data from fiscal 2011 and 2017, reference [44] analyzed the efficiency of the Italian urban water sector using an extended parallel network DEA model. These studies considered the internal structure of the industrial system, but did not carry out a further analysis of the sub-stage, so they could not further find out the deeper reasons for the inefficiency of the system. In view of this, this paper reexamines the internal structure of the industrial system on the basis of these scholars’ research, proposes a new network SBM model according to the characteristics of the system structure, and evaluates the efficiency of the Chinese provincial industrial system. The research route is shown in Figure 2.
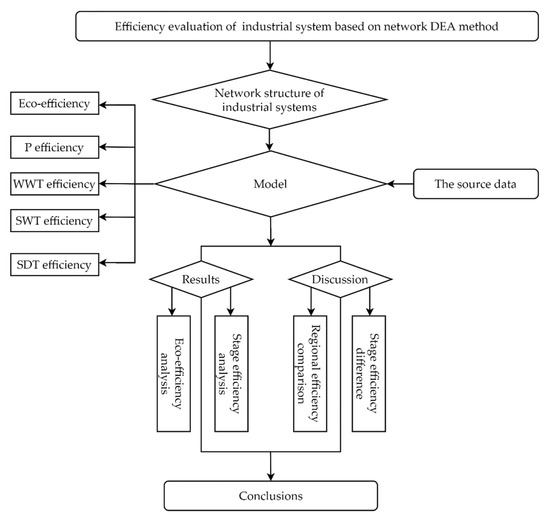
Figure 2.
The research flow chart.
3. Materials and Methods
3.1. Materials
This paper selects 30 provincial-level regions in mainland China as research objects (DMU). Tibet was excluded from the study due to a lack of data on industrial pollutants. The study covered the period from 2011 to 2015, China’s 12th Five-Year Plan period. The industrial system will be divided into four interconnected stages, which is different from previous studies, such as [45,46,47]. In order to study the efficiency of China’s provincial industrial systems, the input and output indicators and data sources selected in this paper are explained as follows based on previous research.
In the P stage, net fixed assets (NFA) indicator was selected to represent capital input, and the data came from China Industrial Statistics Yearbook or Economic Census Yearbook of provinces and autonomous regions. NFA is usually used as an input of regional efficiency evaluation [1,38,48]. As an indicator of energy input, total energy consumption (TEC) comes from China Energy Statistical Yearbook, Statistical Yearbook of Provinces and Autonomous Regions, and China Statistical Yearbook. In terms of labor input, the annual average number of all employees (Labor) is used, and the data are mainly from China Industrial Statistical Yearbook, Statistical Yearbook of Provinces and Autonomous Regions, and China Statistical Yearbook. The desirable output indicator in the P stage is industrial added value (IAV), and relevant data can be found in China Statistical Yearbook and Statistical Yearbook of Provinces and Autonomous Regions. Labor and TEC are used as the other two inputs in the P stage, and IVA is used as a desirable output in the stage. Similar literature can also be referred to [1,49,50,51,52,53]. Industrial wastewater production (WWP), solid waste production (SWP), and sulfur dioxide production (SDP) [47] are undesirable outputs in the P stage, but also intermediate outputs. They are both the output of the production stage and the input of the pollutant treatment stage, as shown in Figure 1. The data are obtained from China Environmental Statistics Annual Report, and a few missing data are obtained by calculating the mean value before and after two years.
In the WWT stage, the amount of WWP in the P stage and the investment in industrial wastewater treatment (WWTI) will be the input of this stage, whereas the output is the discharge of industrial wastewater (WWD). In the SWT stage, SWP and investment in solid waste treatment (SWTI) are the input factors, and the desirable output is the comprehensive utilization of solid waste (CUSW) [54]. In the SDT stage, the amount of SDP in the P stage and the investment in industrial sulfur dioxide treatment (SDTI) will be put into use, and the emission of sulfur dioxide (SDE) [49] will be taken as an undesirable output indicator. When measuring the performance of an industrial system, industrial waste gas, industrial wastewater, and solid waste are usually considered, as per [46,55]. In this paper, for the convenience of data acquisition, industrial sulfur dioxide will be used as a proxy variable of industrial waste gas. In the corresponding industrial waste treatment stage, the treatment investment of different pollutants is the main input variable in the treatment stage. Different from WWD and SDE in nature, CUSW belongs to the desirable output, and it is expected that its value should be as large as possible. The above data of WWTI, SWTI, and SDTI are all from China Statistical Yearbook, while the data of industrial WWD, industrial SDE, and CUSW are from China Environmental Statistical Yearbook. The input and output variables are summarized in Table 1. Descriptive statistics of the data are shown in Table 2.

Table 1.
Input and output variables.

Table 2.
Descriptive statistics of input–output variables.
3.2. Methods
According to the structure of industrial system, this paper refers to the study of [33] and expands its network SBM model to evaluate efficiency. Considering that it is impossible for all the pollutants produced in the production system to be purified and treated in each treatment system, the non-cooperative network SBM model is adopted in this paper, which assumes that the amount of pollutants treated in each treatment stage is less than or equal to the amount produced in the P stage. In the past, there were two main methods to deal with the modeling of undesirable outputs: one was the method of non-data transformation, which mainly includes the processing of undesirable outputs as input indicators [56] and the method of direction distance function (DDF) [57]; second, through the method of data transformation, the undesirable output is transformed to the desirable output for processing, mainly including linear transformation [58] and nonlinear transformation [59]. It is easy to use to treat the undesirable outputs as input factors, which is very helpful to study the operating efficiency of the system. This paper adopts this method to deal with the undesirable outputs. To facilitate modeling, the industrial system structure is generalized as shown in Figure 3. In this paper, 30 provincial regional industrial systems in China are taken as evaluation objects (DMU), and the network SBM model used to measure their efficiency is assumed as follows. The relevant modeling process can be referred to in the studies of [1,46,47].
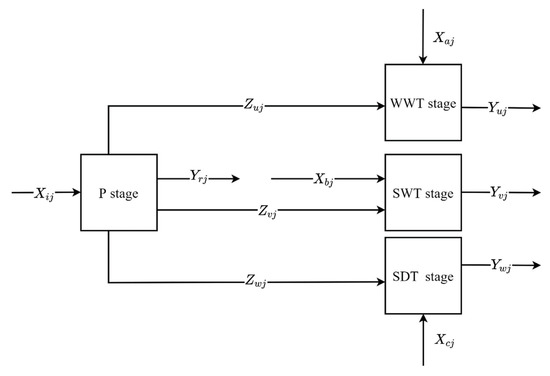
Figure 3.
Industrial system structure.
For In the P stage, input resource produces desirable output and undesirable intermediate output , , . In the WWT stage, input processes to produce an undesirable output . In the SWT stage, input will treat to obtain the desirable output . In the SDT stage, input with to produce an undesirable output . According to the measurement method of efficiency, DEA model can be divided into three types: input-oriented model, output-oriented model, and non-oriented model. Input-oriented focuses on reducing input factors as much as possible to achieve efficiency without reducing output, while output-oriented focuses on increasing output level as much as possible without increasing input factors to achieve efficiency [60]. To avoid bias, our model adopts a non-oriented form, attempting to measure efficiency from both input and output.
Based on the above assumptions, the efficiency evaluation model with VRS and undesirable outputs is
According to the efficiency decomposition method, the efficiency calculation formula of the four stages of the system is as follows
4. Results
4.1. Eco-Efficiency Analysis
By applying the collected data to the model and formula established in this paper, the industrial eco-efficiency and stage efficiency of Chinese provincial industrial system under non-cooperative conditions can be calculated. The results are shown in Table A1, Table A2, Table A3, Table A4 and Table A5.
According to the results of Table A1 and Table A2, it can be found that during the whole study period, only Hainan province has an eco-efficiency score of 1, while the industrial eco-efficiency of other provinces is less than 1. Hebei Province and Beijing rank second and third, respectively, with scores of 0.7715 and 0.6832. The industrial P efficiency, WWT efficiency, SWT efficiency, and SDT efficiency of Hainan province are all 1. During the 12th Five-Year Plan period, Hainan province, guided by the spirit of the CPC Central Committee, persisted in establishing an ecological province, focused on improving environmental quality, set a red line for ecological protection, and made solid progress in pollution reduction. The ecological and environmental quality of the province maintained a good momentum. On the basis of the plans of the CPC Central Committee and The State Council for ecological civilization construction, and based on the actual conditions of Hainan province, supporting laws and regulations for ecological civilization construction have been implemented, such as The Implementation Rules for Investigation of Responsibility for Ecological Environment Damage by Party and Government Officials in Hainan Province and the Construction Plan for Ecological Environment Monitoring Network in Hainan Province. The empirical results show that these policies and measures have achieved good results. During the 12th Five-Year Plan period, the production of industrial solid waste in Hainan province showed an overall upward trend. In 2015, the comprehensive utilization of industrial solid waste increased by 37.7% compared with 2010, a significant increase compared with 2010 [61]. In 2015, the total amount of wastewater discharged in Hainan province decreased by 2% from the previous year, which is inseparable from the implementation of environmental policies and increased investment in cleaner production and industrial wastewater treatment [62]. In addition, the environmental Kuznets curve shows that the environmental pollution degree of a country or region is relatively low when the level of economic development is low. During the 12th Five-Year Plan period, the industrial economic aggregate of Hainan province is still small and still in the stage of low industrialization level [63]. Therefore, according to the environmental Kuznets curve, the industrial environmental pollution degree of Hainan Province is relatively low, thus achieving a good ecological efficiency score. From 2011 to 2015, the industrial system of Hebei province operated efficiently in the stages of production, wastewater treatment, and solid waste treatment, but the average efficiency of sulfur dioxide treatment was relatively low, scoring only 0.2933. It can be seen that the main reason for ecological inefficiency of the industrial system in Hebei province during the 12th Five-Year Plan period is the low efficiency of the industrial sulfur dioxide treatment stage, which is similar to the research results of [47]. Beijing has a good level of economic development and technological innovation system, but at the same time, the degree of environmental pollution is relatively high, as can be seen from the northern sandstorms and severe smog in recent years. When the pollution control technology cannot keep up with the pollution degree of the environment or when economic development is too fast, it will lead to the decline of the efficiency of pollution control. The results also show that the whole industrial system is eco-efficient only when the P efficiency, WWT efficiency, SWT efficiency, and SDT efficiency are all 1. Yunnan and Ningxia were the two regions with the lowest eco-efficiency of the industrial system, with efficiency scores of 0.1707 and 0.1504, respectively. In Yunnan, for example, due to the low level of industrial enterprises in the region for science and technology, pollution source treatment and terminal treatment ability is limited, the main pollutant emissions continue to rise, leading to ethnic minority areas in Yunnan with an imbalance in the relationship among economy, resources, and environment. This led to a relatively low level of eco-efficiency during the evaluation period of the industrial enterprises in the region [64].
In addition, the average eco-efficiency of China’s provincial industrial systems from 2011 to 2015 was only 0.3805, and nearly 77% of provincial industrial systems had an average eco-efficiency score below 0.5. This result indicates that the eco-efficiency of China’s provincial industrial system is generally low, and there is still a great potential for improvement. The same result can also be found in the study of [65]. For a long period of time in the past, China’s economy adopted the economic development mode of high energy consumption and high emissions [66], which consumed a large amount of energy resources and caused a large number of industrial pollutant emissions. Therefore, the government should adopt more active policies and measures to promote the upgrading of industrial structures, improve the technological level of industrial development, reduce energy consumption, and strive to improve the eco-efficiency of industrial sectors.
4.2. Stage Efficiency Analysis
At the P stage, more than 80% of provincial industrial systems had a production efficiency score greater than 0.6 during the study period. Among them, Hainan, Hebei, and Zhejiang provinces are highly efficient in industrial production. The average industrial productivity score during the survey period was 0.7909. Fifteen provincial industrial systems had industrial productivity scores higher than the average productivity during the study period. According to the results of Table A1, the provincial-level regions with production efficiency less than 0.6 include Xinjiang, Guizhou, Yunnan, Ningxia, Gansu, and Inner Mongolia, all of which belong to the Western region. Western China has a large area with sparse population, relatively weak industrial base, single industrial industry, and backward industrial production technology, all of which lead to generally low industrial production efficiency in Western China [67]. Inner Mongolia Autonomous Region scored the lowest in production efficiency, with a production efficiency of 0.4949.
According to the results of Table A1 and Table A3, it can be found that the WWT of industrial systems in Hebei and Hainan operated efficiently during the study period. In the stage of industrial WWT, Hebei and Hainan are always at the forefront of WWT efficiency. Shaanxi had the lowest efficiency of industrial wastewater treatment, with a 5-year average score of 0.0355. Of the 30 provincial industrial systems, only four districts scored more than 0.5 for industrial WWT efficiency, while the rest averaged less than 0.5 for industrial WWT efficiency. It can be seen that during the research period, the efficiency of industrial WWT in many areas is still very low [68]. Taking Chongqing as an example, the industrial WWT efficiency from 2011 to 2015 was 0.1577, 0.4402, 0.3881, 0.1462, and 0.1045, respectively, and the average WWT efficiency was only 0.2473. The results in Table A1 and Table A4 show that the industrial systems in Hebei and Hainan have also been at the forefront of efficiency in SWT during the study period. Meanwhile, Tianjin and Shanxi also performed well in SWT, showing high efficiency in four out of five years. Chongqing has the worst performance in industrial SWT, with an average efficiency score of 0.0564 in five years, much lower than the average (0.3990), indicating that there is a huge room for improvement in industrial SWT. However, only the industrial system in Hainan province operated with the most efficient SDT during the study period, as shown in Table A1 and Table A5. Other provincial industrial systems are inefficient at the SDT stage. Average industrial SDT efficiency was higher than average in 11 districts (0.2899). The top three in efficiency were Hainan, Beijing, and Qinghai, with scores of 1.0000, 0.8387, and 0.6487, respectively. Inner Mongolia Autonomous Region had the lowest average efficiency of industrial sulfur dioxide control, with a score of 0.0429. Based on the above results, it can be seen that most of the Central and Western regions have low industrial eco-efficiency, most provinces have poor performance in industrial waste treatment, and industrial pollutant control policies fail to meet expectations, which is consistent with the research results of [69]. On the one hand, it may be due to the backward industrial waste treatment technology and equipment. On the other hand, the treatment of industrial pollutants is still mainly terminal treatment, not from the source of pollution to consider energy conservation and emission reduction, the lack of advanced technical support, and sufficient financial support.
5. Discussion
5.1. Regional Efficiency Comparison
According to the regional classification standards of the National Bureau of Statistics (2011), the 31 provincial-level administrative regions in mainland China are divided into four major regions, namely, Eastern, Central, Western, and Northeastern regions. See Table 3 for details.

Table 3.
Regional division in China.
According to the efficiency calculation results in the previous section and the regional division criteria in Table 3, the efficiency scores of each region are summarized and the Figure A1, Figure A2 and Figure A3 are drawn.
According to Figure A1, among the four regions, P stage efficiency was the highest throughout the study period. As can be seen from Figure A1a, the fluctuation of average industrial production efficiency in the Eastern region was not obvious from 2011 to 2015, whereas Figure A1b–d showed surprisingly similar trends of average industrial production efficiency in the Central, Western, and Northeastern regions during the study period. This indicates that the industrial production system in the Eastern and the other three regions have technological heterogeneity, while the industrial production system in the Central, Western, and Northeastern regions has technological homogeneity; the industrial production technology similarity between the Western region and the Northeastern region is particularly obvious. Similarities can also be found across the period of study, with the Eastern, Central, and Northeastern areas showing relatively similar change trends in the field of industrial WWT efficiency, whereas the Western region shows certain differences. Overall, however, the four major areas of industrial WWT efficiency demonstrated a certain decline during the study, which is probably due to the regional industrial production scale increasing. The industrial WWT technology has not made great progress on the basis of the expansion of production scale, therefore, the WWT capacity per unit scale output presents a downward trend. In terms of SWT, the efficiency of SWT is stable and rising in the Eastern region, while it is stable and decreasing in the Central and Northeastern regions, whereas the efficiency of SWT in the Western region shows a V-shaped change. This suggests that the Eastern region’s industrial system in SWT technology is mature and stable. Meanwhile, Central and Northeast industrial SWT technology could not keep up with the expansion of industrial production, showing signs of backward technology. In the Western region, the industrial SWT technology is not very mature or stable overall, its industrial production scale is relatively similar, and there was no technological breakthrough. From the perspective of industrial SDT, in the Eastern, Central, and Northeastern regions of China the efficiency of industrial SDT rose first and then declined, and the overall trend of industrial SDT efficiency in Western China is M-shaped, which shows general stability.
Figure A2 shows the efficiency of different industrial stages in different regions. As can be seen from Figure A2a, the variation trends of average P efficiency in the four regions are similar to some extent, especially in the Central, Western, and Northeastern regions. Figure A2b shows a similar trend of average WWT efficiency in Central China and Northeastern China, while the average SWT efficiency and SDT efficiency are significantly different among the four regions, as shown in Figure A2c,d. Figure A3 is the regional eco-efficiency over time and the change trend of average figure. You can see similarities in the ecological industrial system efficiency of Eastern and Central regions, and Western and Northeastern industrial eco-efficiency show the same change trend. Meanwhile, Eastern and Central ecological industrial system efficiency is generally higher than that of the Western and Northeastern regions. The most efficient of industrial ecology is found in the Eastern region, whereas the industrial eco-efficiency in Western China is generally low. The Eastern region is the Chinese economy’s most active region, where economic development level is higher, with greater capital, technology, and talent, more sound investment and financing systems, perfect technical innovation system, and abundant talent reserve system. Therefore, in the Eastern region, the industrial economy, industrial production, and industrial pollution treatment efficiency are the best of the four regions. Take 2015 as an example, the annual industrial output value of the Eastern region reached 13.6889 billion yuan, far higher than that of the Central region (5.9126 billion yuan), the Western region (4.7786 billion yuan), and the Northeastern region (2.0612 billion yuan). It is even higher than the IAV of the Central, Western, and Northeastern regions combined (12.7523 trillion yuan). According to the data collected in this paper, in 2015, under the situation that the total industrial economic aggregate and IAV of the Western region were in a weak position, the annual total industrial SDP of the Western region was 23.532 million tons, higher than the Eastern region of 19.4840 million tons and the Central region of 16.7390 million tons. The amount of industrial SWP in the Western region was also higher than that of the Eastern region (85.4688 million tons) and the Central region (85.2288 million tons). One possible reason is that some manufacturing industries eliminated from the Eastern region were transferred to the Central and Western regions, leading to more energy consumption and pollution emissions, thus resulting in lower eco-efficiency [47]. On the one hand, the Northeastern area, subject to the size of its industrial economy which is relatively small, only consists of three provincial industrial systems. On the other hand, the Northeastern area is characterized by old industrial bases, an unreasonable industrial structure, and backward production technology, which hinder efforts to improve efficiency. The results also reflect that the strategy to revitalize the Northeast’s old industrial bases has not reached the expected target. In addition, it can also be seen from Figure A3 that the eco-efficiency of China’s provincial industrial systems is generally low. The average industrial eco-efficiency of the Eastern region achieved the highest score of 0.5290, while that of the Western region had the lowest score at only 0.2602. For this purpose, the provincial government should make greater efforts to improve the industrial investment and financing system, more actively creating an atmosphere of industrial production technology innovation where industrial enterprises are encouraged to increase investment in industrial pollution treatment technology research and development, while at the same time providing a proactive fiscal policy and prudent monetary policy, establishing and improving the carbon tax system reform, and actively piloting “carbon trading” policy, to ensure industrial production efficiency and low emission of industrial pollutants.
5.2. Stage Efficiency Difference
As can be seen from the above results, the P efficiency of the provincial industrial system (0.7909) is much higher than the WWT efficiency (0.2510), SWT efficiency (0.3990), and SDT efficiency (0.2899). The same conclusions can be found in the studies of [47,52]. In recent years, the Chinese government has been emphasizing the importance of industrial pollution control. Although a large amount of money has been invested in energy conservation and emission reduction to relieve environmental pressure, the awareness and technology of industrial wastewater, solid waste, and sulfur dioxide control are still relatively backward, resulting in low efficiency of industrial pollution control. Therefore, it is urgent for governments at all levels to adopt stricter policies to enhance public awareness of environmental protection and encourage industrial enterprises to research and develop new pollution control technologies and equipment to improve the treatment efficiency of industrial pollutants. From the perspective of the whole industrial system, the low efficiency of industrial pollutant treatment is the main reason for the low eco-efficiency of the industrial system.
The differences in the treatment efficiency of industrial wastewater, solid waste, and sulfur dioxide can reflect the level of pollutant control in provincial industrial systems. Therefore, it is necessary to analyze the efficiency differences of the three pollutant treatment stages. According to Figure A4, from 2011–2015 Shanxi and Shandong province demonstrated greater solid waste treatment efficiency than wastewater and sulfur dioxide treatment efficiency, suggesting that the two provincial systems had higher levels of industrial SWT compared with the treatment of industrial wastewater and sulfur dioxide. At the same time, in order to improve the efficiency of the industrial ecology of the region, they should pay close attention to the treatment of industrial wastewater and sulfur dioxide. For example, investment and financing policies and technological research and development could be moderately inclined to WWT and SDT, so as to comprehensively improve the control level of regional industrial pollutants. In the Hebei province, of the three waste treatment types, SDT efficiency is the least efficient, with an average SDT efficiency of 0.2933. Hebei province should intensify efforts to improve the level of its industrial SDT, the government should provide policy support in this regard, and enterprises should increase research and development of industrial SDT technology and purchase new equipment. The industrial eco-efficiency of Hebei province will be greatly improved by making up the shortcomings of industrial SDT. The WWT efficiency of Qinghai province is the highest among the “three industrial wastes” in each year during the study period, and the SWT efficiency is the lowest. It can be seen that the main reason for the low industrial eco-efficiency of Qinghai province is the low level of SWT. In order to realize the strategy of “ecological province”, Qinghai province should make great efforts to improve the processing capacity of industrial solid waste and improve the comprehensive utilization rate of industrial solid waste. Therefore, increasing investment in industrial solid waste treatment is a feasible path. According to Figure A4, only the industrial system of Hainan province achieved an industrial SDT efficiency score of 1 every year. Fujian, Hunan, and Guangdong province demonstrated the highest levels of industrial SDT efficiency in each year of the study period except for 2012. These results show that these three areas of the industrial system have relatively good sulfur dioxide management, but the efficiency of SDT is still low across the whole country. This suggests that in addition to the Hainan province, which is a provincial industrial system that maintains a good industrial SDT level every year, China’s provincial industrial system’s industrial SDT is still insufficient. Therefore, in order to realize the desired quality of hills and green ecological environment, industrial air pollution problems must be solved. The above analysis can help some provincial industrial systems find “appropriate medicine” to improve their industrial eco-efficiency, so as to improve their industrial eco-efficiency in a targeted way and provide certain guidance and suggestions for relevant policy makers.
6. Conclusions
Under the framework of SBM method, a four-stage SBM model for eco-efficiency evaluation of the Chinese provincial industrial system is established in this paper. Generally speaking, the operation process of any industrial system includes the production stage and the pollutant treatment stage, which can be subdivided into WWT stage, SWT stage, and SDT stage, thus forming a four-stage network system. According to the model, the eco-efficiency and pollutant treatment efficiency of each stage can be obtained respectively. The proposed approach, which takes into account the internal structure of the industrial system and the differences between the pollutant treatment stages, can provide detailed information on the causes of inefficiency in provincial industrial systems. Based on the proposed method, an empirical study is conducted on the efficiency of 30 provincial industrial systems in China, and the following conclusions are drawn.
Firstly, the eco-efficiency of the provincial industrial system has not been significantly improved from 2011 to 2015, and the average eco-efficiency score is only 0.3805, which still has great potential for improvement. The main reason for this low efficiency is the low efficiency of pollutant treatment, especially the low efficiency of WWT and SDT.
Secondly, the reasons for the low eco-efficiency of the industrial system in the Eastern, Central, Western, and Northeastern regions are different. The low efficiency in the Eastern and Central regions is mainly caused by the low efficiency of WWT, while the low efficiency in the Western and Northeastern regions is mainly caused by the low efficiency of SWT.
Thirdly, compared with WWT and SWT, China’s provincial industrial system is still relatively weak in SDT. To achieve a high-quality ecological environment with clear water and green mountains, we must focus on solving the problem of industrial air pollution. For a long time in the past, China’s economy has adopted the economic development mode of high energy consumption and high emissions, which has consumed a large amount of energy resources and caused a large number of industrial pollutant emissions. On the one hand, this is a result of the industrial waste treatment technology and equipment being backward. On the other hand, industrial pollutant treatment is still given priority to, with little attention to terminal handling, pollution source, energy conservation and emissions reduction, as well as a lack of advanced technology support and abundant capital support. Efforts to attain eco-efficiency are therefore not obvious during the study period, and the average eco-efficiency score is low. The Eastern region is the most active region of China’s economy, with higher levels of economic development, capital, technology, and talent of the population. Meanwhile, the Western region does not have these advantages, and the Eastern region outsources some of its manufacturing industry to the Western region, leading to more energy consumption and pollution emissions, resulting in the Western region’s lower industrial eco-efficiency score. On the one hand, Northeastern China is restricted by its relatively small scale of industrial economy; on the other hand, Northeastern China is an old industrial base, and its unreasonable industrial structure and backward production technology hinder the improvement of efficiency. This result also reflects that the strategy of revitalizing the old industrial base in Northeastern China has not reached the expected goal. To this end, provincial governments should improve the industrial investment and financing system, encourage technological innovation in industrial production, and industrial enterprises should increase research and development investment in industrial pollutant treatment technology to ensure high efficiency of industrial production and low emissions of industrial pollutants.
To realize the sustainable development of the industrial sector, it is necessary for the industrial sector to pay attention to the improvement of eco-efficiency. In the whole industrial production system, the production process and pollutant treatment process are equally important. While improving the efficiency of industrial production and solid waste treatment, governments at all levels and industrial enterprises should pay more attention to improving the efficiency of industrial wastewater and sulfur dioxide treatment. Given that WWT and SDT efficiency in most provinces of China are much lower than P and SWT efficiency, the government should formulate flexible policy measures to encourage industrial enterprises to introduce new equipment and technology to improve pollution control efficiency, especially the treatment efficiency of industrial wastewater and sulfur dioxide.
To improve industrial eco-efficiency, industrial enterprises in different provinces can strengthen technological innovation cooperation and complement each other’s advantages. For example, Hebei has the best efficiency in P stage (1.0000), WWT stage (1.0000), and SWT stage (1.0000), but its SDT efficiency (0.2933) is not satisfactory (the results are similar to those of [47]). Therefore, in order to improve eco-efficiency, Hebei local government should pay more attention to the improvement of industrial sulfur dioxide treatment efficiency. Moreover, local governments in Hebei can introduce advanced waste gas treatment equipment and experience from SDT efficient provinces such as Beijing and Hainan.
This study did not consider the change trend of eco-efficiency and stage efficiency of each provincial industrial system with different periods during the study period, that is, it did not consider the system impact of dynamic effect, which is a limitation of this study. In addition, the linkage between the four internal stages of the industrial system has not been studied, nor has the situation of shared resources among the stages been considered, which is a possible research direction in the future. In addition, there may be technological differences among different DMU, and it is also worth studying to consider the efficiency level under the premise of technological heterogeneity.
Author Contributions
Conceptualization, K.H. and W.J.; methodology, N.Z.; software, C.Z.; validation, K.H., N.Z. and W.J.; formal analysis, K.H.; investigation, K.H.; resources, W.J.; data curation, K.H.; writing—original draft preparation, K.H.; writing—review and editing, W.J.; visualization, C.Z.; supervision, N.Z.; project administration, N.Z.; funding acquisition, N.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data available in a publicly accessible repository. The data presented in this study are openly available in China Industrial Statistics Yearbook, China Energy Statistical Yearbook, China Statistical Yearbook, China Environmental Statistics Yearbook, China Environmental Statistics Annual Report. http://www.stats.gov.cn/english/, accessed on 16 March 2022.
Acknowledgments
We thank to the editor and anonymous reviewers for their careful reading of our manuscript and their insightful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Average efficiency of provincial industrial systems from 2011 to 2015.
Table A1.
Average efficiency of provincial industrial systems from 2011 to 2015.
| Provinces | Eco | P | WWT | SWT | SDT |
|---|---|---|---|---|---|
| Beijing | 0.6832 | 0.9424 | 0.5305 | 0.5955 | 0.8387 |
| Tianjin | 0.5201 | 0.9515 | 0.1746 | 0.8024 | 0.4536 |
| Hebei | 0.7715 | 1.0000 | 1.0000 | 1.0000 | 0.2933 |
| Shanxi | 0.5516 | 0.8898 | 0.2530 | 0.8654 | 0.3951 |
| Inner Mongolia | 0.1870 | 0.4949 | 0.0801 | 0.2688 | 0.0429 |
| Liaoning | 0.3809 | 0.9217 | 0.2804 | 0.3299 | 0.1826 |
| Jilin | 0.2925 | 0.7926 | 0.2051 | 0.1432 | 0.1899 |
| Heilongjiang | 0.2603 | 0.6607 | 0.1648 | 0.2019 | 0.1576 |
| Shanghai | 0.5689 | 0.9674 | 0.4954 | 0.5287 | 0.4593 |
| Jiangsu | 0.4576 | 0.8937 | 0.1439 | 0.8338 | 0.2607 |
| Zhejiang | 0.3798 | 1.0000 | 0.0816 | 0.5854 | 0.1468 |
| Anhui | 0.4151 | 0.7663 | 0.1665 | 0.8110 | 0.1719 |
| Fujian | 0.2056 | 0.8110 | 0.0429 | 0.0643 | 0.1245 |
| Jiangxi | 0.3836 | 0.7787 | 0.1984 | 0.2138 | 0.5207 |
| Shandong | 0.3665 | 0.6980 | 0.1011 | 0.9369 | 0.0848 |
| Henan | 0.4468 | 0.9000 | 0.1582 | 0.6360 | 0.3677 |
| Hubei | 0.2526 | 0.7575 | 0.1585 | 0.0812 | 0.1565 |
| Hunan | 0.2808 | 0.8319 | 0.1493 | 0.0854 | 0.2151 |
| Guangdong | 0.3369 | 0.9314 | 0.1803 | 0.0692 | 0.3459 |
| Guangxi | 0.2726 | 0.7623 | 0.1152 | 0.0894 | 0.2786 |
| Hainan | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Chongqing | 0.2971 | 0.7648 | 0.2473 | 0.0564 | 0.5089 |
| Sichuan | 0.2583 | 0.6527 | 0.0928 | 0.2939 | 0.1832 |
| Guizhou | 0.2056 | 0.5866 | 0.1970 | 0.1194 | 0.0911 |
| Yunnan | 0.1707 | 0.5817 | 0.0429 | 0.0894 | 0.1057 |
| Shaanxi | 0.2001 | 0.7562 | 0.0355 | 0.0990 | 0.1038 |
| Gansu | 0.2308 | 0.5291 | 0.0948 | 0.3894 | 0.1423 |
| Qinghai | 0.6417 | 0.9753 | 0.9791 | 0.1972 | 0.6487 |
| Ningxia | 0.1514 | 0.5396 | 0.1067 | 0.0811 | 0.1248 |
| Xinjiang | 0.2464 | 0.5897 | 0.0528 | 0.5035 | 0.1013 |
| Mean | 0.3805 | 0.7909 | 0.2510 | 0.3990 | 0.2899 |

Table A2.
Provincial industrial eco-efficiency and production efficiency from 2011 to 2015.
Table A2.
Provincial industrial eco-efficiency and production efficiency from 2011 to 2015.
| Province | Eco-Efficiency | P Efficiency | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2014 | 2015 | 2011 | 2012 | 2013 | 2014 | 2015 | |
| Beijing | 1.0000 | 0.7079 | 0.6044 | 0.3031 | 0.8006 | 1.0000 | 1.0000 | 1.0000 | 0.7120 | 1.0000 |
| Tianjin | 0.1386 | 0.6930 | 0.7513 | 0.5757 | 0.4419 | 0.7575 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Hebei | 0.8499 | 0.8092 | 0.8019 | 0.6950 | 0.7014 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Shanxi | 0.4743 | 0.6531 | 0.6272 | 0.7155 | 0.2880 | 0.8485 | 0.9520 | 1.0000 | 1.0000 | 0.6483 |
| Inner Mongolia | 0.3933 | 0.1856 | 0.1234 | 0.0939 | 0.1390 | 0.6725 | 0.5555 | 0.5213 | 0.1464 | 0.5787 |
| Liaoning | 0.5757 | 0.4381 | 0.4235 | 0.2129 | 0.2541 | 1.0000 | 1.0000 | 1.0000 | 0.6083 | 1.0000 |
| Jilin | 0.2652 | 0.3944 | 0.3460 | 0.1602 | 0.2967 | 0.6336 | 0.9950 | 1.0000 | 0.3344 | 1.0000 |
| Heilongjiang | 0.3393 | 0.4562 | 0.2237 | 0.1280 | 0.1541 | 0.5963 | 0.9093 | 0.8707 | 0.2734 | 0.6539 |
| Shanghai | 0.7293 | 0.7223 | 0.6245 | 0.4868 | 0.2816 | 1.0000 | 0.9760 | 1.0000 | 0.9980 | 0.8630 |
| Jiangsu | 0.2296 | 0.5318 | 0.5471 | 0.5359 | 0.4436 | 0.4686 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Zhejiang | 0.5181 | 0.4631 | 0.4075 | 0.2608 | 0.2497 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Anhui | 0.4068 | 0.5041 | 0.5663 | 0.1814 | 0.4168 | 0.5853 | 0.9304 | 1.0000 | 0.4130 | 0.9030 |
| Fujian | 0.1503 | 0.3008 | 0.2555 | 0.1236 | 0.1977 | 0.6428 | 0.9960 | 1.0000 | 0.5176 | 0.8987 |
| Jiangxi | 0.2891 | 0.7147 | 0.5082 | 0.1639 | 0.2420 | 0.6904 | 1.0000 | 1.0000 | 0.3222 | 0.8808 |
| Shandong | 0.3155 | 0.3599 | 0.4011 | 0.4048 | 0.3511 | 0.4271 | 0.7883 | 0.7556 | 0.7634 | 0.7557 |
| Henan | 0.5890 | 0.6711 | 0.3738 | 0.4174 | 0.1830 | 1.0000 | 1.0000 | 1.0000 | 0.7988 | 0.7013 |
| Hubei | 0.1878 | 0.3186 | 0.3310 | 0.1616 | 0.2639 | 0.4920 | 0.9239 | 0.9393 | 0.5013 | 0.9312 |
| Hunan | 0.1942 | 0.3804 | 0.3769 | 0.1776 | 0.2748 | 0.5451 | 1.0000 | 1.0000 | 0.6145 | 1.0000 |
| Guangdong | 0.3486 | 0.3146 | 0.4126 | 0.3604 | 0.2482 | 0.6571 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Guangxi | 0.2158 | 0.3453 | 0.4309 | 0.1275 | 0.2432 | 0.6615 | 0.8568 | 1.0000 | 0.2932 | 1.0000 |
| Hainan | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Chongqing | 0.2220 | 0.5133 | 0.3183 | 0.2432 | 0.1884 | 0.6755 | 0.9060 | 0.8930 | 0.4856 | 0.8639 |
| Sichuan | 0.1727 | 0.2746 | 0.2731 | 0.1442 | 0.4271 | 0.4330 | 0.7572 | 0.8444 | 0.4400 | 0.7888 |
| Guizhou | 0.2032 | 0.2698 | 0.2095 | 0.1209 | 0.2245 | 0.4660 | 0.7201 | 0.7137 | 0.1803 | 0.8529 |
| Yunnan | 0.1687 | 0.2529 | 0.1738 | 0.1028 | 0.1553 | 0.5417 | 0.8140 | 0.7176 | 0.1491 | 0.6860 |
| Shaanxi | 0.1630 | 0.2486 | 0.2556 | 0.0899 | 0.2433 | 0.6149 | 1.0000 | 1.0000 | 0.2760 | 0.8904 |
| Gansu | 0.2820 | 0.1651 | 0.1707 | 0.1339 | 0.4021 | 0.5093 | 0.7408 | 0.7271 | 0.1244 | 0.5437 |
| Qinghai | 0.5520 | 0.8882 | 0.5976 | 0.6758 | 0.4950 | 0.8766 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Ningxia | 0.2507 | 0.1944 | 0.1212 | 0.0703 | 0.1203 | 0.4662 | 0.6830 | 0.7307 | 0.0930 | 0.7251 |
| Xinjiang | 0.3309 | 0.3540 | 0.1406 | 0.2261 | 0.1805 | 0.5613 | 1.0000 | 0.6728 | 0.1789 | 0.5354 |
| Mean | 0.3852 | 0.4708 | 0.4132 | 0.3031 | 0.3303 | 0.6941 | 0.9168 | 0.9129 | 0.5741 | 0.8567 |

Table A3.
Provincial industrial WWT efficiency from 2011 to 2015.
Table A3.
Provincial industrial WWT efficiency from 2011 to 2015.
| Province | 2011 | 2012 | 2013 | 2014 | 2015 |
|---|---|---|---|---|---|
| Beijing | 1.0000 | 1.0000 | 0.0848 | 0.2754 | 0.2922 |
| Tianjin | 0.1666 | 0.2968 | 0.2456 | 0.1136 | 0.0505 |
| Hebei | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Shanxi | 0.2406 | 0.6592 | 0.1509 | 0.1629 | 0.0517 |
| Inner Mongolia | 0.1946 | 0.0915 | 0.0415 | 0.0446 | 0.0283 |
| Liaoning | 0.2906 | 0.4065 | 0.4187 | 0.1350 | 0.1510 |
| Jilin | 0.1562 | 0.2880 | 0.3081 | 0.1846 | 0.0887 |
| Heilongjiang | 0.2070 | 0.3917 | 0.1382 | 0.0651 | 0.0219 |
| Shanghai | 1.0000 | 1.0000 | 0.3909 | 0.0419 | 0.0444 |
| Jiangsu | 0.0569 | 0.2234 | 0.1739 | 0.2364 | 0.0287 |
| Zhejiang | 0.1504 | 0.1045 | 0.0759 | 0.0627 | 0.0144 |
| Anhui | 0.1466 | 0.2396 | 0.3250 | 0.0593 | 0.0622 |
| Fujian | 0.0524 | 0.0755 | 0.0546 | 0.0177 | 0.0143 |
| Jiangxi | 0.1518 | 0.5274 | 0.2558 | 0.0278 | 0.0290 |
| Shandong | 0.0427 | 0.0889 | 0.1382 | 0.1917 | 0.0441 |
| Henan | 0.1782 | 0.2497 | 0.1582 | 0.1566 | 0.0482 |
| Hubei | 0.0894 | 0.1629 | 0.3581 | 0.1120 | 0.0700 |
| Hunan | 0.0776 | 0.2641 | 0.2501 | 0.0866 | 0.0683 |
| Guangdong | 0.1545 | 0.2049 | 0.3003 | 0.2320 | 0.0095 |
| Guangxi | 0.0766 | 0.1267 | 0.2437 | 0.0182 | 0.1108 |
| Hainan | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Chongqing | 0.1577 | 0.4402 | 0.3881 | 0.1462 | 0.1045 |
| Sichuan | 0.0610 | 0.1061 | 0.2159 | 0.0488 | 0.0319 |
| Guizhou | 0.5956 | 0.2036 | 0.0490 | 0.0526 | 0.0842 |
| Yunnan | 0.0876 | 0.0298 | 0.0587 | 0.0210 | 0.0173 |
| Shaanxi | 0.0258 | 0.0342 | 0.0487 | 0.0283 | 0.0403 |
| Gansu | 0.1404 | 0.0907 | 0.0764 | 0.0511 | 0.1156 |
| Qinghai | 0.8957 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Ningxia | 0.2201 | 0.1562 | 0.0738 | 0.0349 | 0.0486 |
| Xinjiang | 0.0893 | 0.0865 | 0.0484 | 0.0100 | 0.0300 |
| Mean | 0.2902 | 0.3516 | 0.2690 | 0.1872 | 0.1567 |

Table A4.
Provincial industrial SWT efficiency from 2011 to 2015.
Table A4.
Provincial industrial SWT efficiency from 2011 to 2015.
| Province | 2011 | 2012 | 2013 | 2014 | 2015 |
|---|---|---|---|---|---|
| Beijing | 1.0000 | 0.2435 | 0.7194 | 0.0148 | 1.0000 |
| Tianjin | 0.0122 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Hebei | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Shanxi | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0.3270 |
| Inner Mongolia | 0.9016 | 0.1723 | 0.0036 | 0.1774 | 0.0893 |
| Liaoning | 1.0000 | 0.2642 | 0.1719 | 0.1656 | 0.0476 |
| Jilin | 0.2730 | 0.1089 | 0.0402 | 0.0395 | 0.2543 |
| Heilongjiang | 0.7375 | 0.1500 | 0.0356 | 0.0303 | 0.0560 |
| Shanghai | 1.0000 | 0.3925 | 0.2652 | 0.7455 | 0.2403 |
| Jiangsu | 0.1765 | 0.9926 | 1.0000 | 1.0000 | 1.0000 |
| Zhejiang | 0.9141 | 1.0000 | 0.7477 | 0.0395 | 0.2256 |
| Anhui | 1.0000 | 0.9176 | 1.0000 | 0.1376 | 1.0000 |
| Fujian | 0.0639 | 0.2038 | 0.0104 | 0.0166 | 0.0271 |
| Jiangxi | 0.2517 | 0.4296 | 0.1360 | 0.0876 | 0.1643 |
| Shandong | 1.0000 | 0.7167 | 1.0000 | 1.0000 | 0.9677 |
| Henan | 1.0000 | 1.0000 | 0.0735 | 1.0000 | 0.1064 |
| Hubei | 0.1099 | 0.1015 | 0.0355 | 0.0241 | 0.1348 |
| Hunan | 0.1146 | 0.1916 | 0.0134 | 0.0132 | 0.0942 |
| Guangdong | 0.1422 | 0.0662 | 0.0191 | 0.0342 | 0.0843 |
| Guangxi | 0.1899 | 0.1353 | 0.1013 | 0.0087 | 0.0116 |
| Hainan | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Chongqing | 0.0401 | 0.1452 | 0.0102 | 0.0239 | 0.0626 |
| Sichuan | 0.2923 | 0.0971 | 0.0402 | 0.0396 | 1.0000 |
| Guizhou | 0.0159 | 0.1569 | 0.2248 | 0.0711 | 0.1281 |
| Yunnan | 0.1573 | 0.2132 | 0.0095 | 0.0064 | 0.0605 |
| Shaanxi | 0.1090 | 0.0865 | 0.0209 | 0.0260 | 0.2524 |
| Gansu | 0.7034 | 0.0153 | 0.0806 | 0.1478 | 1.0000 |
| Qinghai | 0.2335 | 0.5527 | 0.0286 | 0.0625 | 0.1089 |
| Ningxia | 0.3139 | 0.0351 | 0.0045 | 0.0063 | 0.0454 |
| Xinjiang | 1.0000 | 0.2849 | 0.0058 | 0.8929 | 0.3337 |
| Mean | 0.5251 | 0.4224 | 0.3266 | 0.3270 | 0.3941 |

Table A5.
Provincial industrial SDT efficiency from 2011 to 2015.
Table A5.
Provincial industrial SDT efficiency from 2011 to 2015.
| Province | 2011 | 2012 | 2013 | 2014 | 2015 |
|---|---|---|---|---|---|
| Beijing | 1.0000 | 0.6643 | 0.6954 | 0.8340 | 1.0000 |
| Tianjin | 0.1802 | 0.6220 | 1.0000 | 0.4227 | 0.0433 |
| Hebei | 0.5096 | 0.3467 | 0.4071 | 0.1189 | 0.0841 |
| Shanxi | 0.0813 | 0.1828 | 0.6110 | 1.0000 | 0.1003 |
| Inner Mongolia | 0.0465 | 0.0690 | 0.0446 | 0.0349 | 0.0197 |
| Liaoning | 0.2765 | 0.2080 | 0.2470 | 0.0750 | 0.1064 |
| Jilin | 0.1231 | 0.3578 | 0.1753 | 0.1940 | 0.0995 |
| Heilongjiang | 0.0644 | 0.4189 | 0.0684 | 0.1842 | 0.0520 |
| Shanghai | 0.1579 | 0.5206 | 1.0000 | 0.4643 | 0.1538 |
| Jiangsu | 0.3395 | 0.1862 | 0.3652 | 0.2583 | 0.1545 |
| Zhejiang | 0.3060 | 0.1053 | 0.1734 | 0.1164 | 0.0331 |
| Anhui | 0.1722 | 0.1608 | 0.2523 | 0.1935 | 0.0809 |
| Fujian | 0.1020 | 0.1200 | 0.1500 | 0.1768 | 0.0738 |
| Jiangxi | 0.2143 | 1.0000 | 1.0000 | 0.2713 | 0.1181 |
| Shandong | 0.1163 | 0.1139 | 0.0951 | 0.0615 | 0.0371 |
| Henan | 0.5133 | 0.7418 | 0.4526 | 0.0801 | 0.0505 |
| Hubei | 0.1348 | 0.2095 | 0.2127 | 0.1237 | 0.1020 |
| Hunan | 0.1539 | 0.1742 | 0.4363 | 0.2091 | 0.1022 |
| Guangdong | 0.7427 | 0.1137 | 0.4291 | 0.3202 | 0.1238 |
| Guangxi | 0.1116 | 0.4051 | 0.5371 | 0.2664 | 0.0726 |
| Hainan | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Chongqing | 0.4123 | 0.7945 | 0.1607 | 1.0000 | 0.1770 |
| Sichuan | 0.0550 | 0.2569 | 0.2182 | 0.1593 | 0.2263 |
| Guizhou | 0.0415 | 0.1275 | 0.0629 | 0.1574 | 0.0665 |
| Yunnan | 0.0443 | 0.1640 | 0.0678 | 0.2024 | 0.0501 |
| Shaanxi | 0.0613 | 0.1142 | 0.1923 | 0.1044 | 0.0467 |
| Gansu | 0.0389 | 0.1413 | 0.0843 | 0.2017 | 0.2453 |
| Qinghai | 0.3125 | 1.0000 | 0.6523 | 1.0000 | 0.2787 |
| Ningxia | 0.1197 | 0.1950 | 0.1029 | 0.1341 | 0.0721 |
| Xinjiang | 0.0467 | 0.2501 | 0.0653 | 0.0994 | 0.0450 |
| Mean | 0.2493 | 0.3588 | 0.3653 | 0.3155 | 0.1605 |
Appendix B
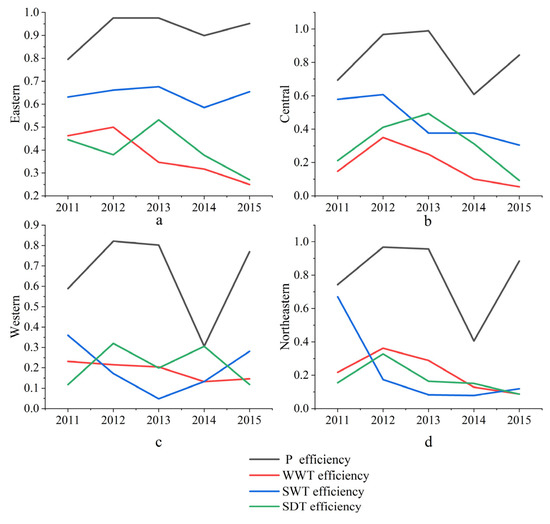
Figure A1.
Regional stage efficiency. (a) shows the change trend of efficiency in each stage with time in the Eastern region. Similarly, (b–d) show the change trend of efficiency with time in the Central, Western and Northeast regions respectively.
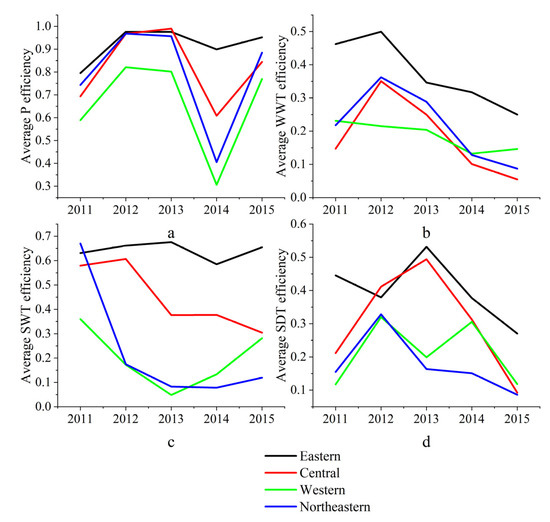
Figure A2.
Stage region efficiency. (a) shows the change trend of average P efficiency of each region over time during the study period. Similarly, (b–d) respectively show the change trend of average WWT efficiency, average SWT efficiency and average SDT efficiency over time in each region during the study period.
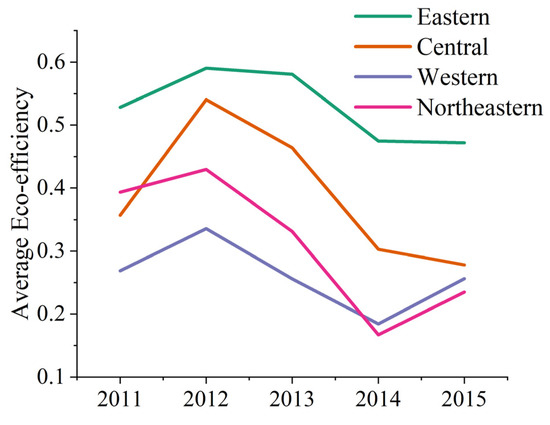
Figure A3.
Regional eco-efficiency.
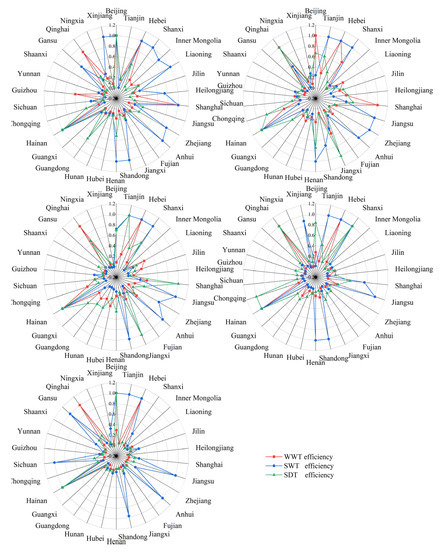
Figure A4.
Treatment efficiency of industrial wastewater, solid waste, and sulfur dioxide at provincial level from 2011 to 2015.
References
- Zhang, L.; Zhao, L.L.; Zha, Y. Efficiency evaluation of Chinese regional industrial systems using a dynamic two-stage DEA approach. Socio-Econ. Plan. Sci 2021, 77, 101031. [Google Scholar] [CrossRef]
- Díaz-Villavicencio, G.; Didonet, S.R.; Dodd, A. Influencing factors of eco-efficient urban waste management: Evidence from Spanish municipalities. J. Clean. Prod. 2017, 164, 1486–1496. [Google Scholar] [CrossRef]
- Delgado-Antequera, L.; Gémar, G.; Molinos-Senante, M.; Gómez, T.; Caballero, R.; Sala-Garrido, R. Eco-efficiency assessment of municipal solid waste services: Influence of exogenous variables. Waste Manag. 2021, 130, 136–146. [Google Scholar] [CrossRef]
- Lo Storto, C. Eco-Productivity Analysis of the Municipal Solid Waste Service in the Apulia Region from 2010 to 2017. Sustainability 2021, 13, 12008. [Google Scholar] [CrossRef]
- Li, R.; Sun, T. Research on Impact of Different Environmental Regulation Tools on Energy Efficiency in China. Pol. J. Environ. Stud. 2020, 29, 4151–4160. [Google Scholar] [CrossRef]
- Wu, J.; Zhu, Q.; Liang, L. CO2 emissions and energy intensity reduction allocation over provincial industrial sectors in China. Appl. Energy 2016, 166, 282–291. [Google Scholar] [CrossRef]
- Zhou, D.Q.; Wang, Q.; Su, B.; Zhou, P.; Yao, L.X. Industrial energy conservation and emission reduction performance in China: A city-level nonparametric analysis. Appl. Energy 2016, 166, 201–209. [Google Scholar] [CrossRef]
- Song, M.L.; Peng, J.; Wang, J.L.; Zhao, J.J. Environmental efficiency and economic growth of China: A Ray slack-based model analysis. Eur. J. Oper. Res. 2018, 269, 51–63. [Google Scholar] [CrossRef]
- Zhang, Y.-J.; Hao, J.-F. Carbon emission quota allocation among China’s industrial sectors based on the equity and efficiency principles. Ann. Oper. Res. 2016, 255, 117–140. [Google Scholar] [CrossRef]
- Sun, J.; Du, T.; Sun, W.; Na, H.; He, J.; Qiu, Z.; Yuan, Y.; Li, Y. An evaluation of greenhouse gas emission efficiency in China’s industry based on SFA. Sci. Total Environ. 2019, 690, 1190–1202. [Google Scholar] [CrossRef]
- Fetanat, A.; Shafipour, G. A hybrid method of LMDI, symmetrical components, and SFA to estimate the distribution of energy-saving potential with consideration of unbalanced components in decomposition analysis. Energ Effic. 2017, 10, 1041–1059. [Google Scholar] [CrossRef]
- Wang, C.; Zhan, J.; Bai, Y.; Chu, X.; Zhang, F. Measuring carbon emission performance of industrial sectors in the Beijing-Tianjin-Hebei region, China: A stochastic frontier approach. Sci. Total Environ. 2019, 685, 786–794. [Google Scholar] [CrossRef] [PubMed]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Chen, L.; Jia, G. Environmental efficiency analysis of China’s regional industry: A data envelopment analysis (DEA) based approach. J. Clean. Prod. 2017, 142, 846–853. [Google Scholar] [CrossRef]
- Zhou, H.; Yang, Y.; Chen, Y.; Zhu, J. Data envelopment analysis application in sustainability: The origins, development and future directions. Eur. J. Oper. Res. 2018, 264, 1–16. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Yuan, Y.; Goto, M. A literature study for DEA applied to energy and environment. Energy Econ. 2017, 62, 104–124. [Google Scholar] [CrossRef]
- Song, C.; Yin, G.; Lu, Z.; Chen, Y. Industrial ecological efficiency of cities in the Yellow River Basin in the background of China’s economic transformation: Spatial-temporal characteristics and influencing factors. Environ. Sci. Pollut. Res. Int. 2022, 29, 4334–4349. [Google Scholar] [CrossRef] [PubMed]
- Fang, T.; Fang, D.; Yu, B. Carbon emission efficiency of thermal power generation in China: Empirical evidence from the micro-perspective of power plants. Energ Policy 2022, 165, 112955. [Google Scholar] [CrossRef]
- Moutinho, V.; Madaleno, M. A Two-Stage DEA Model to Evaluate the Technical Eco-Efficiency Indicator in the EU Countries. Int. J. Environ. Res. Public Health 2021, 18, 3038. [Google Scholar] [CrossRef]
- Ramli, N.A.; Munisamy, S.; Arabi, B. Scale directional distance function and its application to the measurement of eco-efficiency in the manufacturing sector. Ann. Oper. Res. 2013, 211, 381–398. [Google Scholar] [CrossRef]
- Hermoso-Orzáez, M.J.; García-Alguacil, M.; Terrados-Cepeda, J.; Brito, P. Measurement of Environmental Efficiency in the Countries of the European Union with the Enhanced Data Envelopment Analysis Method (DEA) during the Period 2005–2012. In Proceedings of the 5th Ibero-American Congress on Entrepreneurship, Energy, Environment and Technology—CIEEMAT, Portalegre, Portugal, 11–13 September 2019. [Google Scholar]
- Wang, K.; Wei, Y.-M. China’s regional industrial energy efficiency and carbon emissions abatement costs. Appl. Energy 2014, 130, 617–631. [Google Scholar] [CrossRef]
- Nguyen, N.T. Integrating two stages of Malmquist index and Grey forecasting to access industrial performance: A case of Vietnamese steel industry. J. Grey Syst. 2021, 33, 43–58. [Google Scholar]
- Bi, G.-B.; Song, W.; Zhou, P.; Liang, L. Does environmental regulation affect energy efficiency in China’s thermal power generation? Empirical evidence from a slacks-based DEA model. Energ Policy 2014, 66, 537–546. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, Q.; Lv, L.; Chu, J.; Wu, J. Efficiency evaluation of regional energy saving and emission reduction in China: A modified slacks-based measure approach. J. Clean. Prod. 2017, 140, 1313–1321. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Goto, M. Undesirable congestion under natural disposability and desirable congestion under managerial disposability in U.S. electric power industry measured by DEA environmental assessment. Energy Econ. 2016, 55, 173–188. [Google Scholar] [CrossRef]
- Zhu, N.; He, K. The efficiency of major industrial enterprises in Sichuan province of China: A super slacks-based measure analysis. J. Ind. Manag. Optim. 2022. [Google Scholar] [CrossRef]
- Wu, J.; Li, M.J.; Zhu, Q.Y.; Zhou, Z.X.; Liang, L. Energy and environmental efficiency measurement of China’s industrial sectors: A DEA model with non-homogeneous inputs and outputs. Energy Econ. 2019, 78, 468–480. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S. Network DEA. Socio-Econ. Plan. Sci. 2000, 34, 35–49. [Google Scholar] [CrossRef]
- Tone, K.; Tsutsui, M. Network DEA: A slacks-based measure approach. Eur. J. Oper. Res. 2009, 197, 243–252. [Google Scholar] [CrossRef] [Green Version]
- Tone, K.; Tsutsui, M. Dynamic DEA with network structure: A slacks-based measure approach. Omega-Int. J. Manag. Sci. 2014, 42, 124–131. [Google Scholar] [CrossRef] [Green Version]
- Cook, W.D.; Zhu, J.; Bi, G.B.; Yang, F. Network DEA: Additive efficiency decomposition. Eur. J. Oper. Res. 2010, 207, 1122–1129. [Google Scholar] [CrossRef]
- Kao, C. Decomposition of slacks-based efficiency measures in network data envelopment analysis. Eur. J. Oper. Res. 2020, 283, 588–600. [Google Scholar] [CrossRef]
- Jiang, B.; Chen, H.; Li, J.; Lio, W.C. The uncertain two-stage network DEA models. Soft Comput. 2020, 25, 421–429. [Google Scholar] [CrossRef]
- Hatami-Marbini, A.; Saati, S. Measuring performance with common weights: Network DEA. Neural Comput. Appl. 2020, 32, 3599–3617. [Google Scholar] [CrossRef]
- Zuo, Z.; Guo, H.; Li, Y.; Cheng, J. A two-stage DEA evaluation of Chinese mining industry technological innovation efficiency and eco-efficiency. Environ. Impact Assess. Rev. 2022, 94, 106762. [Google Scholar] [CrossRef]
- Meng, M.; Pang, T. Operational efficiency analysis of China’s electric power industry using a dynamic network slack-based measure model. Energy 2022, 251, 123898. [Google Scholar] [CrossRef]
- Bian, Y.; Liang, N.; Xu, H. Efficiency evaluation of Chinese regional industrial systems with undesirable factors using a two-stage slacks-based measure approach. J. Clean. Prod. 2015, 87, 348–356. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, K. Energy efficiency of China’s industry sector: An adjusted network DEA (data envelopment analysis)-based decomposition analysis. Energy 2015, 93, 1328–1337. [Google Scholar] [CrossRef]
- Li, Y.J.; Shi, X.; Emrouznejad, A.; Liang, L. Environmental performance evaluation of Chinese industrial systems: A network SBM approach. J. Oper. Res. Soc. 2018, 69, 825–839. [Google Scholar] [CrossRef]
- Mousavizadeh, R.; Navabakhsh, M.; Hafezalkotob, A. Cost-efficiency measurement for two-stage DEA network using game approach: An application to electrical network in Iran. Sadhana-Acad. Proc. Eng. Sci. 2020, 45, 1–16. [Google Scholar] [CrossRef]
- Moon, H.; Min, D. A DEA approach for evaluating the relationship between energy efficiency and financial performance for energy-intensive firms in Korea. J. Clean. Prod. 2020, 255, 120283. [Google Scholar] [CrossRef]
- Lu, C.C.; Dan, W.; Chen, X.; Tseng, C.K.; Chou, K.W. Evaluation of the operating performance of Taiwanese machine tool industry with the dynamic network DEA model. Enterp. Inf. Syst. 2020, 15, 87–104. [Google Scholar] [CrossRef]
- Lo Storto, C. Measuring the efficiency of the urban integrated water service by parallel network DEA: The case of Italy. J. Clean. Prod. 2020, 276. [Google Scholar] [CrossRef]
- Wu, J.; Lv, L.; Sun, J.S.; Ji, X. A comprehensive analysis of China’s regional energy saving and emission reduction efficiency: From production and treatment perspectives. Energ Policy 2015, 84, 166–176. [Google Scholar] [CrossRef]
- Wu, J.; Xiong, B.B.; An, Q.X.; Sun, J.S.; Wu, H.Q. Total-factor energy efficiency evaluation of Chinese industry by using two-stage DEA model with shared inputs. Ann. Oper. Res. 2017, 255, 257–276. [Google Scholar] [CrossRef]
- Xu, C.Z.; Wang, S.X. Industrial three-division network system in China: Efficiencies and their impact factors. Environ. Sci. Pollut. Res. 2021, 28, 47375–47394. [Google Scholar] [CrossRef]
- Bian, Y.; Yang, F. Resource and environment efficiency analysis of provinces in China: A DEA approach based on Shannon’s entropy. Energ Policy 2010, 38, 1909–1917. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, J.; Choi, G. A two-stage eco-efficiency evaluation of China’s industrial sectors: A dynamic network data envelopment analysis (DNDEA) approach. Process. Saf. Environ. Prot. 2021, 148, 879–892. [Google Scholar] [CrossRef]
- Xiong, S.; Ma, X.; Ji, J. The impact of industrial structure efficiency on provincial industrial energy efficiency in China. J. Clean. Prod. 2019, 215, 952–962. [Google Scholar] [CrossRef]
- Wu, J.; Yin, P.; Sun, J.; Chu, J.; Liang, L. Evaluating the environmental efficiency of a two-stage system with undesired outputs by a DEA approach: An interest preference perspective. Eur. J. Oper. Res. 2016, 254, 1047–1062. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, H.; Zhang, Y.-J.; Zhu, T.-T. How does industrial policy affect the eco-efficiency of industrial sector? Evidence from China. Appl. Energy 2020, 272, 115206. [Google Scholar] [CrossRef]
- Shao, L.; Yu, X.; Feng, C. Evaluating the eco-efficiency of China’s industrial sectors: A two-stage network data envelopment analysis. J. Environ. Manag. 2019, 247, 551–560. [Google Scholar] [CrossRef]
- Tang, J.X.; Wang, Q.W.; Choi, G. Efficiency assessment of industrial solid waste generation and treatment processes with carry-over in China. Sci. Total Environ. 2020, 726, 138274. [Google Scholar] [CrossRef]
- Zhao, L.; Zha, Y.; Zhuang, Y.; Liang, L. Data envelopment analysis for sustainability evaluation in China: Tackling the economic, environmental, and social dimensions. Eur. J. Oper. Res. 2019, 275, 1083–1095. [Google Scholar] [CrossRef]
- Liu, W.; Sharp, J. DEA Models via Goal Programming. In Data Envelopment Analysis in the Service Sector; Westermann, G., Ed.; Deutscher Universitätsverlag: Wiesbaden, Germany, 1999; pp. 79–101. [Google Scholar]
- Färe, R.; Grosskopf, S. Modeling undesirable factors in efficiency evaluation: Comment. Eur. J. Oper. Res. 2004, 157, 242–245. [Google Scholar] [CrossRef]
- Iqbal Ali, A.; Seiford, L.M. Translation invariance in data envelopment analysis. Oper. Res. Lett. 1990, 9, 403–405. [Google Scholar] [CrossRef]
- Lovell, K.C.A.; Pastor, J.T.; Turner, J.A. Measuring macroeconomic performance in the OECD: A comparison of European and non-European countries. Eur. J. Oper. Res. 1995, 87, 507–518. [Google Scholar] [CrossRef]
- GanG, C. Data Envelopment Analysis: Methods and MaxDEA Software; Intellectual Property Publishing House: Beijing, China, 2014. [Google Scholar]
- Chun, H.; Wei, H.; Hui, C.Y. Analysis of production, disposal and utilization of industrial solid Waste in Hainan Province. Resour. Conserv. Environ. Prot. 2020, 1, 117–118. [Google Scholar] [CrossRef]
- Yanfei, Z.; Jun, G.; Hui, D.; Mei, Y.; Dan, F. Analysis of environmental Kuznets characteristics of industrial waste discharge in Hainan Province. Spec. Zone Econ. 2015, 4, 26–29. [Google Scholar]
- Sheng, H. Study on the development Strategy of industrial structure upgrading in Hainan Province. Hainan Financ. 2012, 7, 33–37. [Google Scholar]
- Zhang, C. Study on ecological Efficiency of industrial Enterprises in Yunnan minority Areas. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2018. [Google Scholar]
- Hasanbeigi, A.; Morrow, W.; Sathaye, J.; Masanet, E.; Xu, T. A bottom-up model to estimate the energy efficiency improvement and CO2 emission reduction potentials in the Chinese iron and steel industry. Energy 2013, 50, 315–325. [Google Scholar] [CrossRef]
- Wang, R.; Wu, Y.; Wang, Y.; Feng, X. An industrial area layout design methodology considering piping and safety using genetic algorithm. J. Clean. Prod. 2017, 167, 23–31. [Google Scholar] [CrossRef]
- Xiao, Z.; Zeng, W.; Ma, Z. Regional differences and pattern evolution of Industrial production efficiency in China. Mod. Manag. Sci. 2021, 2, 3–12. [Google Scholar]
- Feng, Y.; Chiu, Y.-H.; Liu, F.-P. Measuring the Performance of Wastewater Treatment in China. Appl. Sci. 2019, 9, 153. [Google Scholar] [CrossRef] [Green Version]
- Ding, T.; Wu, H.; Jia, J.; Wei, Y.; Liang, L. Regional assessment of water-energy nexus in China’s industrial sector: An interactive meta-frontier DEA approach. J. Clean. Prod. 2020, 244, 118797. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).