Understanding Housing Prices Using Geographic Big Data: A Case Study in Shenzhen
Abstract
:1. Introduction
2. Literature Review
2.1. The Law of Temporal and Spatial Evolution of Housing Prices
2.2. Factors Affecting Housing Prices
2.3. Housing Price Model
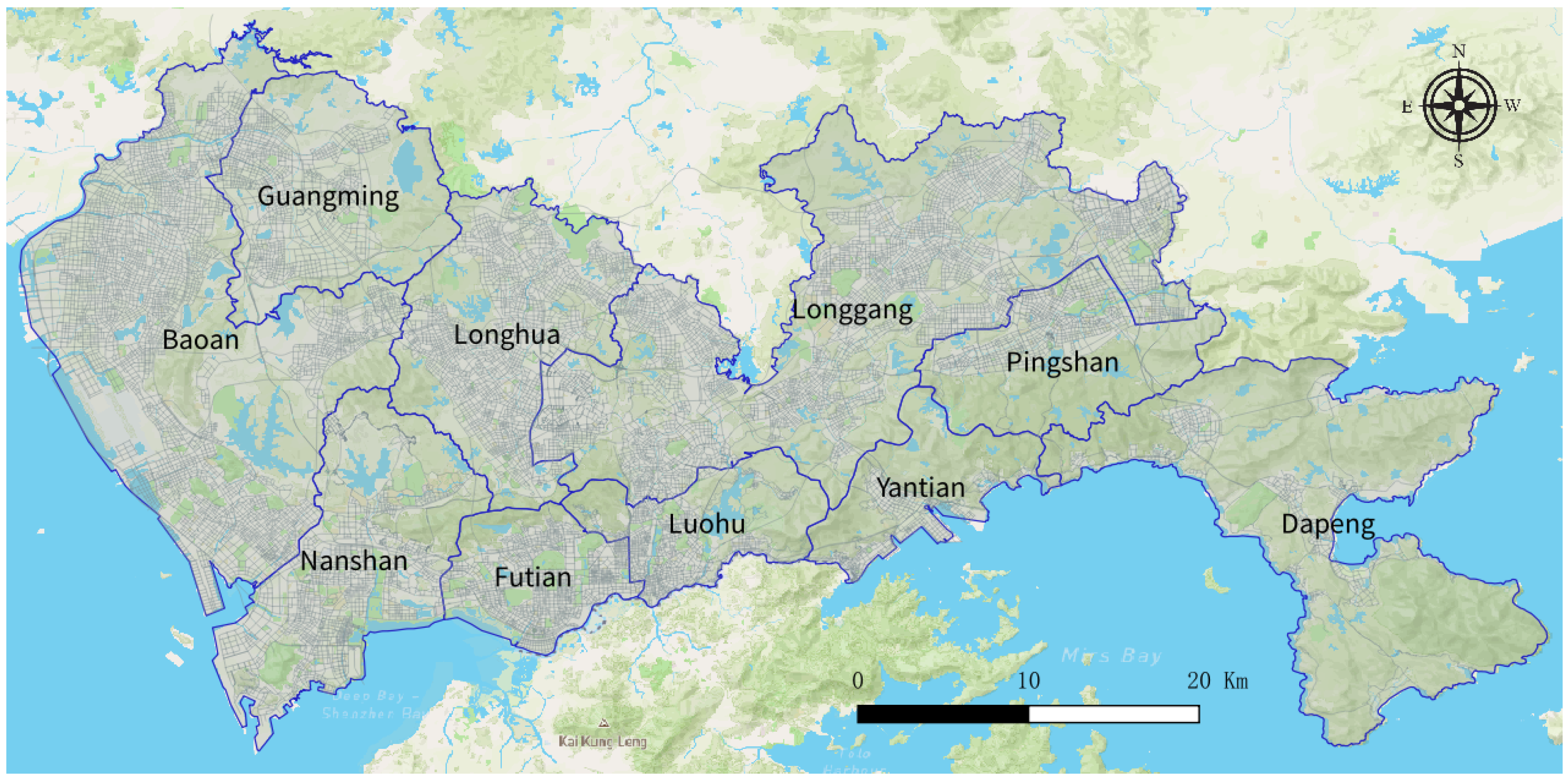
3. Study Area
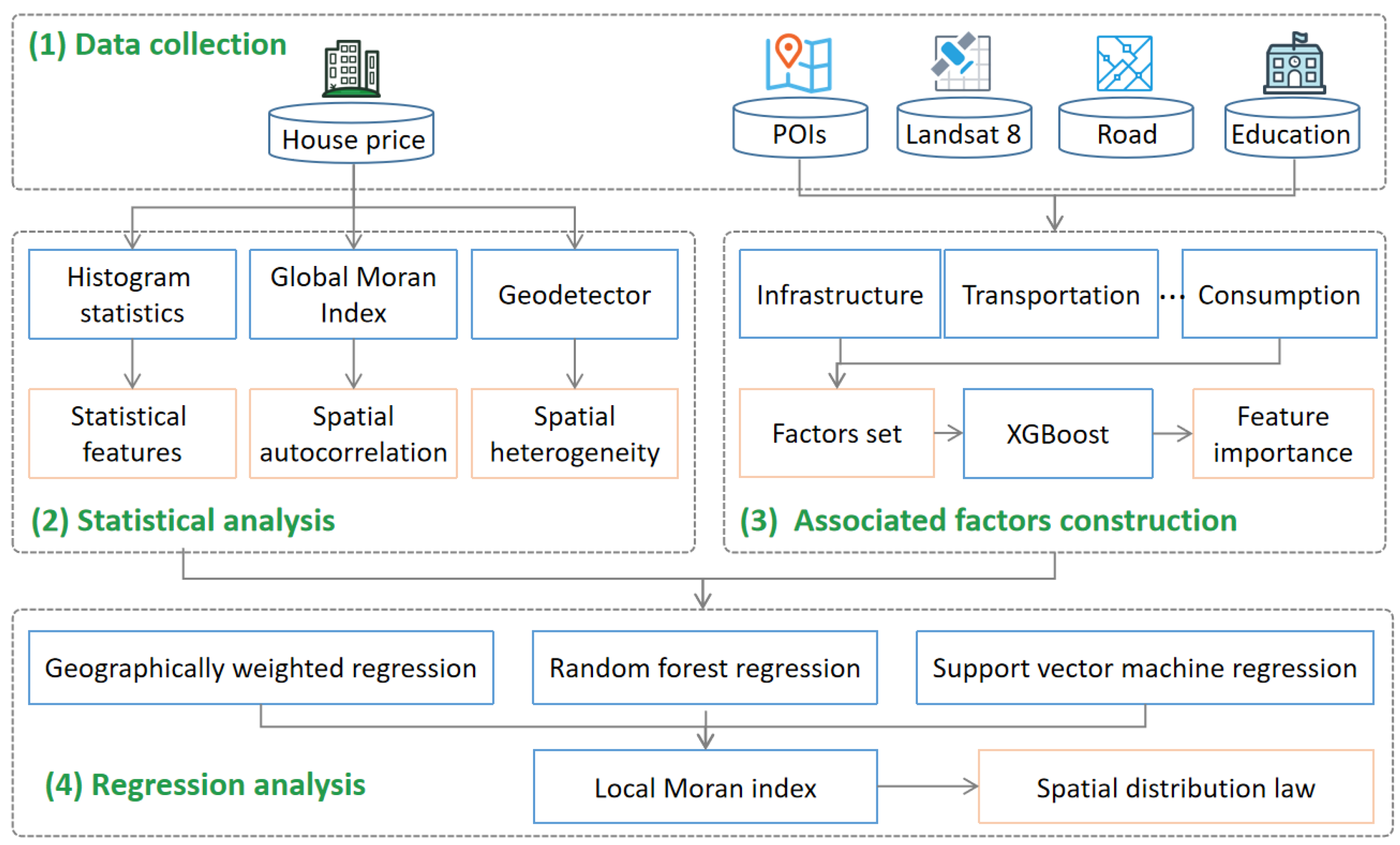
4. Methodology
4.1. Data Collection
4.1.1. House Price Data
4.1.2. Point of Interest Data
4.1.3. Remote Sensing Data
4.1.4. Road Network Data
4.2. Statistical Analysis
4.2.1. Global Moran Index
4.2.2. Geodetector
4.3. Associated Factors Construction
4.3.1. Associated Factor Indicator
4.3.2. Factor Importance Analysis
4.4. Regression Analysis
4.4.1. Random Forest Regression
4.4.2. Support Vector Machine Regression
4.4.3. Geographically Weighted Regression
5. Result and Analysis
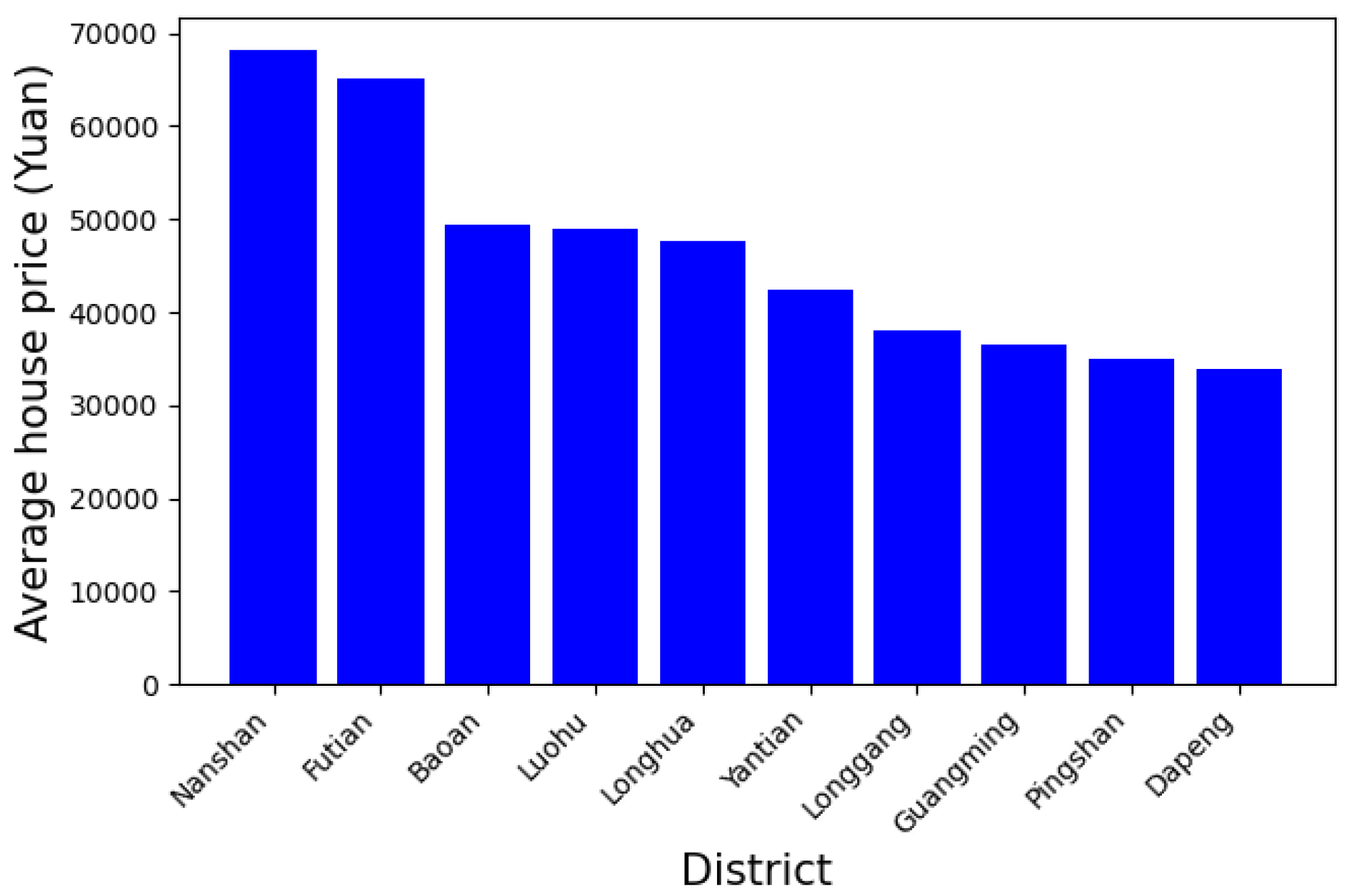
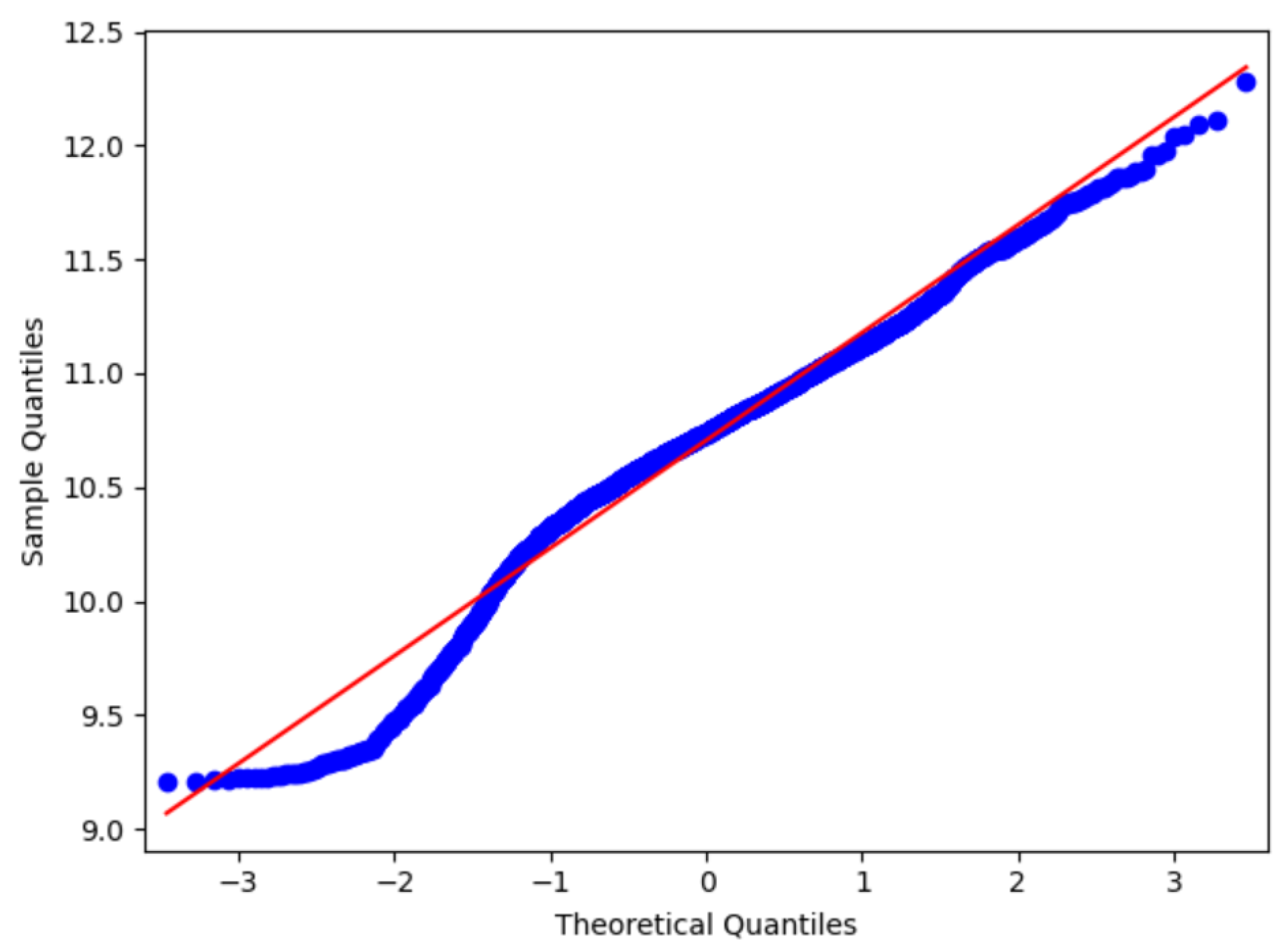
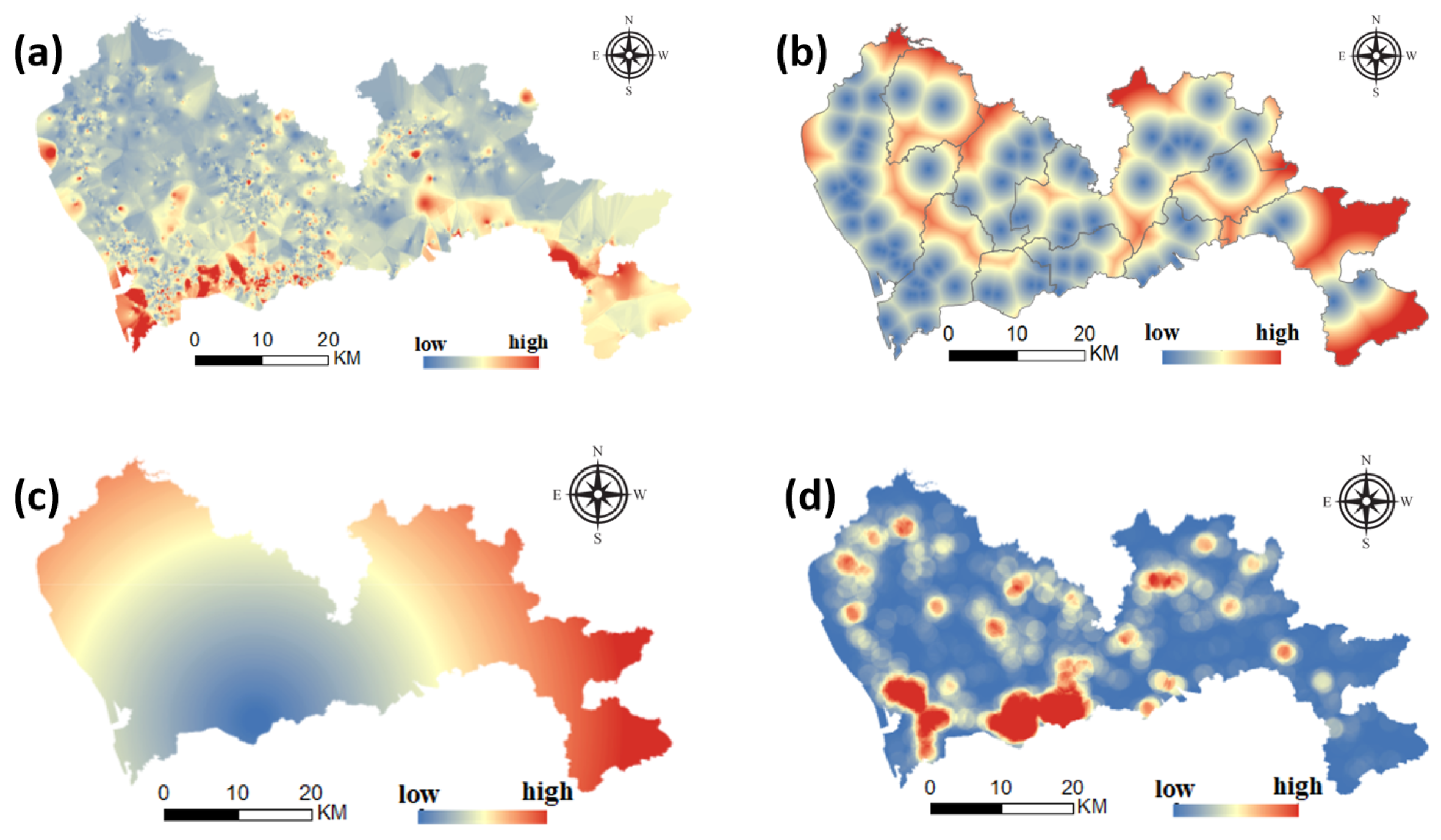
5.1. Statistical Law of Housing Prices
5.2. The Spatial Distribution and Importance of Associated Factors
5.3. Regression Analysis Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jeanty, P.W.; Partridge, M.; Irwin, E. Estimation of a spatial simultaneous equation model of population migration and housing price dynamics. Reg. Sci. Urban Econ. 2010, 40, 343–352. [Google Scholar] [CrossRef]
- Shen, Y.; Karimi, K. The economic value of streets: Mix-scale spatio-functional interaction and housing price patterns. Appl. Geogr. 2017, 79, 187–202. [Google Scholar] [CrossRef]
- Rahadi, R.A.; Wiryono, S.K.; Koesrindartoto, D.P.; Syamwil, I.B. Factors influencing the price of housing in Indonesia. Int. J. Hous. Mark. Anal. 2015, 8, 169–188. [Google Scholar] [CrossRef]
- Gurran, N.; Bramley, G. Urban Planning and the Housing Market; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Archer, W.R.; Gatzlaff, D.H.; Ling, D.C. Measuring the importance of location in house price appreciation. J. Urban Econ. 1996, 40, 334–353. [Google Scholar] [CrossRef]
- Cao, K.; Diao, M.; Wu, B. A big data–based geographically weighted regression model for public housing prices: A case study in Singapore. Ann. Am. Assoc. Geogr. 2019, 109, 173–186. [Google Scholar] [CrossRef]
- Hu, L.; He, S.; Han, Z.; Xiao, H.; Su, S.; Weng, M.; Cai, Z. Monitoring housing rental prices based on social media: An integrated approach of machine-learning algorithms and hedonic modeling to inform equitable housing policies. Land Use Policy 2019, 82, 657–673. [Google Scholar] [CrossRef]
- Alonso, W. A Theory of the Urban Land Market; Bobbs-Merrill Company, College Division: Indianapolis, India, 1960. [Google Scholar]
- Gillen, K.; Thibodeau, T.; Wachter, S. Anisotropic autocorrelation in house prices. J. Real Estate Financ. Econ. 2001, 23, 5–30. [Google Scholar] [CrossRef]
- Wang, W.C.; Chang, Y.J.; Wang, H.C. An application of the spatial autocorrelation method on the change of real estate prices in Taitung City. ISPRS Int. J. Geo-Inf. 2019, 8, 249. [Google Scholar] [CrossRef] [Green Version]
- Lu, B.; Charlton, M.; Harris, P.; Fotheringham, A.S. Geographically weighted regression with a non-Euclidean distance metric: A case study using hedonic house price data. Int. J. Geogr. Inf. Sci. 2014, 28, 660–681. [Google Scholar] [CrossRef]
- Helbich, M.; Brunauer, W.; Vaz, E.; Nijkamp, P. Spatial heterogeneity in hedonic house price models: The case of Austria. Urban Stud. 2014, 51, 390–411. [Google Scholar] [CrossRef] [Green Version]
- Clapp, J.; Giaccotto, C. Evaluating house price forecasts. J. Real Estate Res. 2002, 24, 1–26. [Google Scholar] [CrossRef]
- Cunningham, C.R. House price uncertainty, timing of development, and vacant land prices: Evidence for real options in Seattle. J. Urban Econ. 2006, 59, 1–31. [Google Scholar] [CrossRef]
- Bogin, A.; Doerner, W.; Larson, W. Local house price dynamics: New indices and stylized facts. Real Estate Econ. 2019, 47, 365–398. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Y.; Webster, C.; Orford, S. Identifying house price effects of changes in urban street configuration: An empirical study in Nanjing, China. Urban Stud. 2016, 53, 112–131. [Google Scholar] [CrossRef] [Green Version]
- Landier, A.; Sraer, D.; Thesmar, D. Banking integration and house price co-movement. J. Financ. Econ. 2017, 125, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Bourassa, S.C.; Hoesli, M.; Oikarinen, E. Measuring house price bubbles. Real Estate Econ. 2019, 47, 534–563. [Google Scholar] [CrossRef]
- Shao, A.W.; Hanewald, K.; Sherris, M. Reverse mortgage pricing and risk analysis allowing for idiosyncratic house price risk and longevity risk. Insur. Math. Econ. 2015, 63, 76–90. [Google Scholar] [CrossRef]
- Head, A.; Lloyd-Ellis, H. Has Canadian house price growth been excessive? Can. J. Econ./Revue Canadienne d’Économique 2016, 49, 1367–1400. [Google Scholar] [CrossRef] [Green Version]
- Capozza, D.R.; Hendershott, P.H.; Mack, C.; Mayer, C.J. Determinants of Real House Price Dynamics; National Bureau of Economic Research: Cambridge, MA, USA, 2002. [Google Scholar]
- Hilber, C.A. The economic implications of house price capitalization: A synthesis. Real Estate Econ. 2017, 45, 301–339. [Google Scholar] [CrossRef] [Green Version]
- Harter-Dreiman, M. Drawing inferences about housing supply elasticity from house price responses to income shocks. J. Urban Econ. 2004, 55, 316–337. [Google Scholar] [CrossRef] [Green Version]
- Gao, G.; Bao, Z.; Cao, J.; Qin, A.K.; Sellis, T. Location-centered house price prediction: A multi-task learning approach. ACM Trans. Intell. Syst. Technol. (TIST) 2022, 13, 1–25. [Google Scholar] [CrossRef]
- Tu, Y.; Zhou, C. Exploring house price volatility in major Canadian cities. J. Econ. Lit. Classif. 2015, 1–25. Available online: www.econ.queensu.ca/files/other/tu_zhou_20150118.pdf (accessed on 31 March 2022).
- Watson, M. House price Keynesianism and the contradictions of the modern investor subject. Hous. Stud. 2010, 25, 413–426. [Google Scholar] [CrossRef]
- Deng, C.; Ma, Y. Price Discovery Between Chinese House and Land Market Under Different Land Policy. In Proceedings of the 2008 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, China, 12–14 October 2008; pp. 1–4. [Google Scholar]
- Luttik, J. The value of trees, water and open space as reflected by house prices in the Netherlands. Landsc. Urban Plan. 2000, 48, 161–167. [Google Scholar] [CrossRef]
- Boyle, M.; Kiel, K. A survey of house price hedonic studies of the impact of environmental externalities. J. Real Estate Lit. 2001, 9, 117–144. [Google Scholar] [CrossRef]
- Geoghegan, J. The value of open spaces in residential land use. Land Use Policy 2002, 19, 91–98. [Google Scholar] [CrossRef]
- Yamagata, Y.; Murakami, D.; Yoshida, T.; Seya, H.; Kuroda, S. Value of urban views in a bay city: Hedonic analysis with the spatial multilevel additive regression (SMAR) model. Landsc. Urban Plan. 2016, 151, 89–102. [Google Scholar] [CrossRef]
- Ramirez, M.D. Marx’s theory of ground rent: A critical assessment. Contrib. Political Econ. 2009, 28, 71–91. [Google Scholar] [CrossRef]
- Goodchild, M.F. Citizens as sensors: The world of volunteered geography. GeoJournal 2007, 69, 211–221. [Google Scholar] [CrossRef] [Green Version]
- Gao, S.; Li, L.; Li, W.; Janowicz, K.; Zhang, Y. Constructing gazetteers from volunteered big geo-data based on Hadoop. Comput. Environ. Urban Syst. 2017, 61, 172–186. [Google Scholar] [CrossRef] [Green Version]
- Jackson, L.E.; Kose, M.A.; Otrok, C.; Owyang, M.T. Specification and Estimation of Bayesian Dynamic Factor Models: A Monte Carlo Analysis with an Application to Global House Price Comovement; Emerald Group Publishing Limited: Bingley, UK, 2016. [Google Scholar]
- Meese, R.; Wallace, N. House price dynamics and market fundamentals: The Parisian housing market. Urban Stud. 2003, 40, 1027–1045. [Google Scholar] [CrossRef]
- Bin, O. A prediction comparison of housing sales prices by parametric versus semi-parametric regressions. J. Hous. Econ. 2004, 13, 68–84. [Google Scholar] [CrossRef]
- Gu, J.; Zhu, M.; Jiang, L. Housing price forecasting based on genetic algorithm and support vector machine. Expert Syst. Appl. 2011, 38, 3383–3386. [Google Scholar] [CrossRef]
- Selim, H. Determinants of house prices in Turkey: Hedonic regression versus artificial neural network. Expert Syst. Appl. 2009, 36, 2843–2852. [Google Scholar] [CrossRef]
- Fan, G.Z.; Ong, S.E.; Koh, H.C. Determinants of house price: A decision tree approach. Urban Stud. 2006, 43, 2301–2315. [Google Scholar] [CrossRef]
- Wang, X.; Wen, J.; Zhang, Y.; Wang, Y. Real estate price forecasting based on SVM optimized by PSO. Optik 2014, 125, 1439–1443. [Google Scholar] [CrossRef]
- Tse, R.Y. Estimating neighbourhood effects in house prices: Towards a new hedonic model approach. Urban Stud. 2002, 39, 1165–1180. [Google Scholar] [CrossRef]
- Shao, Q.; Zhang, W.; Cao, X.; Yang, J.; Yin, J. Threshold and moderating effects of land use on metro ridership in Shenzhen: Implications for TOD planning. J. Transp. Geogr. 2020, 89, 102878. [Google Scholar] [CrossRef]
- Zhang, W.; Lu, D.; Zhao, Y.; Luo, X.; Yin, J. Incorporating polycentric development and neighborhood life-circle planning for reducing driving in Beijing: Nonlinear and threshold analysis. Cities 2022, 121, 103488. [Google Scholar] [CrossRef]
- Shi, X.; Wong, Y.D.; Li, M.Z.F.; Palanisamy, C.; Chai, C. A feature learning approach based on XGBoost for driving assessment and risk prediction. Accid. Anal. Prev. 2019, 129, 170–179. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, X.S. A XGBoost risk model via feature selection and Bayesian hyper-parameter optimization. arXiv 2019, arXiv:1901.08433. [Google Scholar] [CrossRef]
- Ming, Y.; Zhang, J.; Qi, J.; Liao, T.; Wang, M.; Zhang, L. Prediction and Analysis of Chengdu Housing Rent Based on XGBoost Algorithm. In Proceedings of the 2020 3rd International Conference on Big Data Technologies, Qingdao, China, 18–20 September 2020; pp. 1–5. [Google Scholar]
- Hong, J.; Choi, H.; Kim, W.S. A house price valuation based on the random forest approach: The mass appraisal of residential property in south korea. Int. J. Strateg. Prop. Manag. 2020, 24, 140–152. [Google Scholar] [CrossRef]
- Ruan, Y.; Zou, Y.; Chen, M.; Shen, J. Monitoring the Spatiotemporal Trajectory of Urban Area Hotspots Using the SVM Regression Method Based on NPP-VIIRS Imagery. ISPRS Int. J. Geo-Inf. 2021, 10, 415. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically weighted regression. J. R. Stat. Soc. Ser. D 1998, 47, 431–443. [Google Scholar] [CrossRef]




| Feature Type | Feature Quantification |
|---|---|
| Infrastructure factors | Density of POIs for shopping, food, entertainment, finance, enterprise, |
| life service, and distance to medical POIs | |
| Traffic factors | Distance to POIs of transportation facilities, distance to all levels of road network |
| Location factors | Distance to CBD, distance to government agency POIs |
| Educational factors | Average secondary school enrollment rate by housing location |
| Environmental factors | Normalized vegetation index, corrected normalized water index |
| Consumption level factors | Per capita consumption of catering POIs |
| Nanshan | Fotian | Luohu | Yantian | Baoan | Longgang | Pingshan | Guangming | Longhua | |
|---|---|---|---|---|---|---|---|---|---|
| Fotian | Y | ||||||||
| Luohu | Y | N | |||||||
| Yantian | Y | Y | Y | ||||||
| Baoan | Y | Y | Y | Y | |||||
| Longgang | Y | Y | Y | Y | Y | ||||
| Pingshan | Y | Y | Y | Y | Y | Y | |||
| Guangming | Y | Y | Y | Y | Y | Y | Y | ||
| Longhua | Y | Y | Y | Y | Y | Y | Y | Y | |
| Dapeng | Y | Y | Y | Y | Y | Y | Y | Y | Y |
| Feature Type | Feature Quantification | Importance Index |
|---|---|---|
| Infrastructure factors | Density of shopping POIs | 3.95 × |
| Distance to medical POIs | 3.88 × | |
| Density of food POIs | 4.08 × | |
| Density of entertainment POIs | 4.20 × | |
| Density of financial POIs | 4.16 × | |
| Density of enterprise POIs | 4.13 × | |
| Density of life services POIs | 4.15 × | |
| Transportation factors | Distance to transportation facilities POIs | 3.95 × |
| Distance to national highway | 4.42 × | |
| Distance to provincial road | 4.35 × | |
| Distance to high speed | 4.51 × | |
| Distance to the main road | 4.75 × | |
| Distance to secondary arterial road | 4.57 × | |
| Distance to city branch road | 4.88 × | |
| Distance to miscellaneous road | 5.51 × | |
| Distance to country road | 4.85 × | |
| Location factors | Distance to CBD | 5.07 × |
| Government POI point density | 4.22 × | |
| Educational factors | Secondary school enrollment rate | 5.58 × |
| Environmental factors | NDVI | 3.57 × |
| MNDWI | 3.96 × | |
| Consumption level | Per capita consumption of catering POIs | 5.08 × |
| Modle | RMSE | |
|---|---|---|
| SVM_RBF | 10,651.342 | 0.362 |
| SVM_LINEAR | 10,979.052 | 0.346 |
| RFA | 12,888.228 | 0.278 |
| LINEAR | 17,502.941 | 0.296 |
| GWR | 15,748.661 | 0.446 |
| Nanshan and Futian | Others | |||
|---|---|---|---|---|
| RMSE | RMSE | |||
| SVM_RBF | 9433.347 | 0.529 | 7906.373 | 0.582 |
| SVM_LINEAR | 10,997.567 | 0.376 | 8329.878 | 0.504 |
| RFA | 9687.463 | 0.481 | 7580.123 | 0.627 |
| LINEAR | 18,546.651 | 0.212 | 15,974.682 | 0.336 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Jia, Z.; Li, L.; Zhao, T. Understanding Housing Prices Using Geographic Big Data: A Case Study in Shenzhen. Sustainability 2022, 14, 5307. https://doi.org/10.3390/su14095307
Jiang X, Jia Z, Li L, Zhao T. Understanding Housing Prices Using Geographic Big Data: A Case Study in Shenzhen. Sustainability. 2022; 14(9):5307. https://doi.org/10.3390/su14095307
Chicago/Turabian StyleJiang, Xufeng, Zelu Jia, Lefei Li, and Tianhong Zhao. 2022. "Understanding Housing Prices Using Geographic Big Data: A Case Study in Shenzhen" Sustainability 14, no. 9: 5307. https://doi.org/10.3390/su14095307
APA StyleJiang, X., Jia, Z., Li, L., & Zhao, T. (2022). Understanding Housing Prices Using Geographic Big Data: A Case Study in Shenzhen. Sustainability, 14(9), 5307. https://doi.org/10.3390/su14095307






