Seismic Resilience Assessment of Curved Reinforced Concrete Bridge Piers through Seismic Fragility Curves Considering Short- and Long-Period Earthquakes
Abstract
1. Introduction
2. Seismic Resilience and Fragility Assessment
2.1. Seismic Fragility Curves and Damage Indices
2.2. Seismic Resilience
3. Modeling of Bridge and Ground Motion Selection
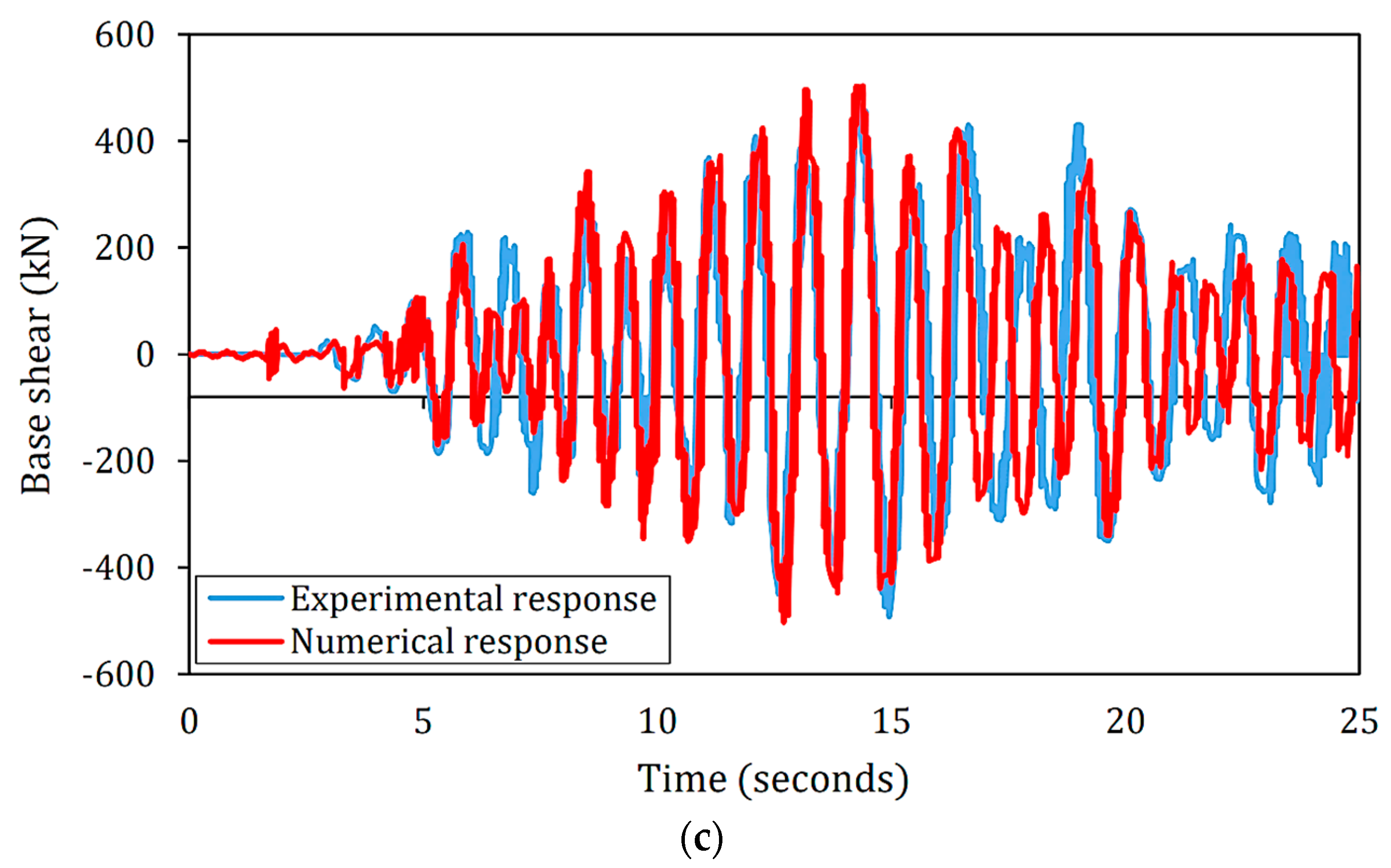
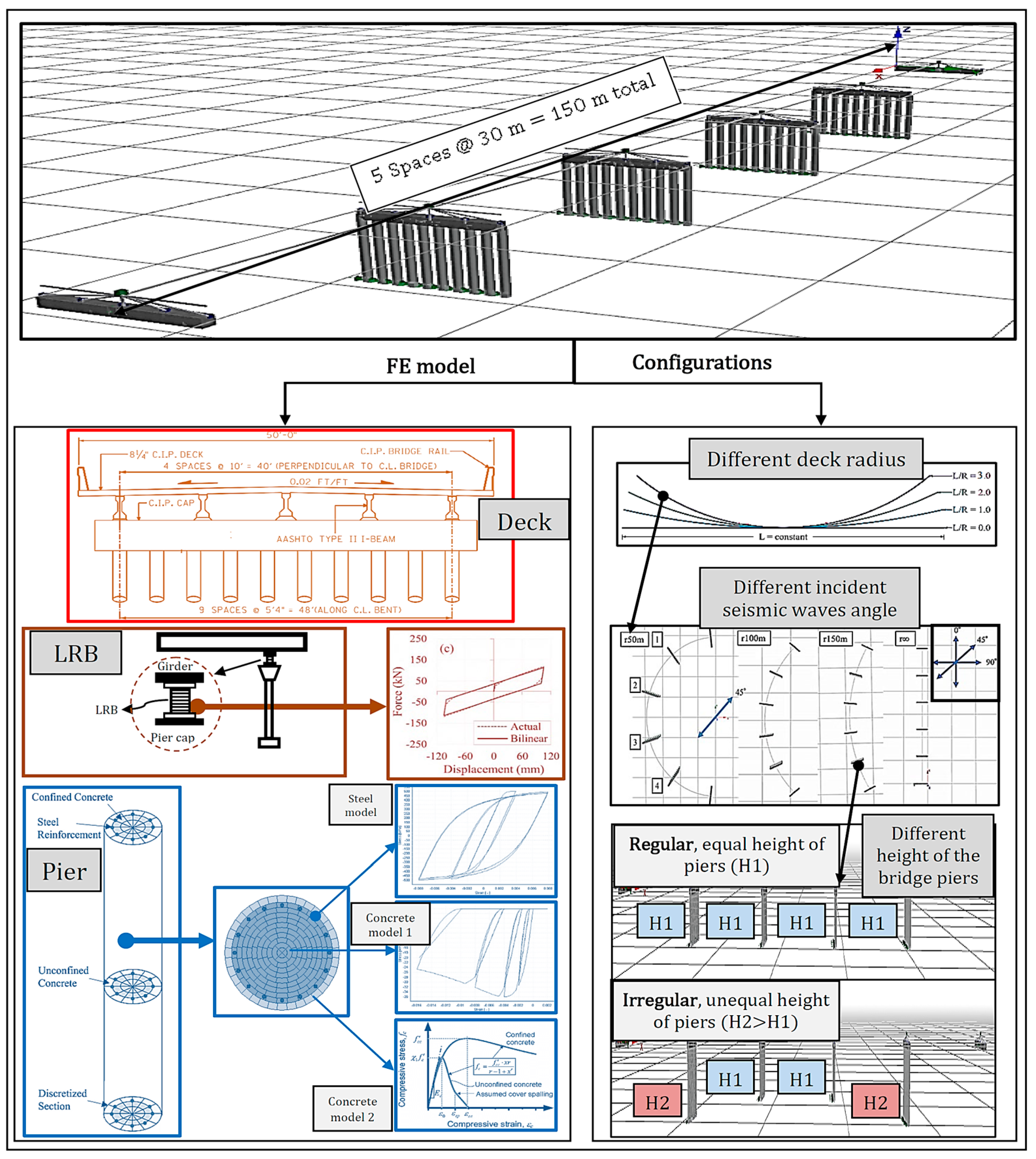
3.1. Bridge Model
3.2. Parameter Consideration
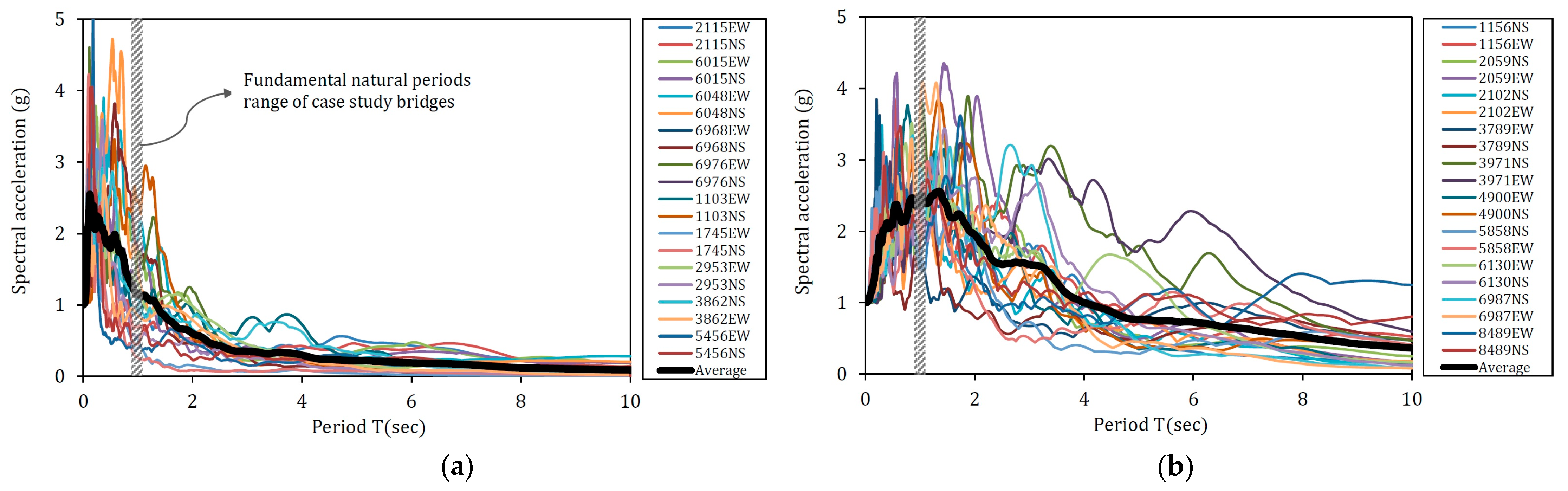
3.3. Strong Ground Motion Selection
4. Probabilistic Seismic Performance Assessments
4.1. Eigenvalue Analysis and Fundamental Vibration Characteristics
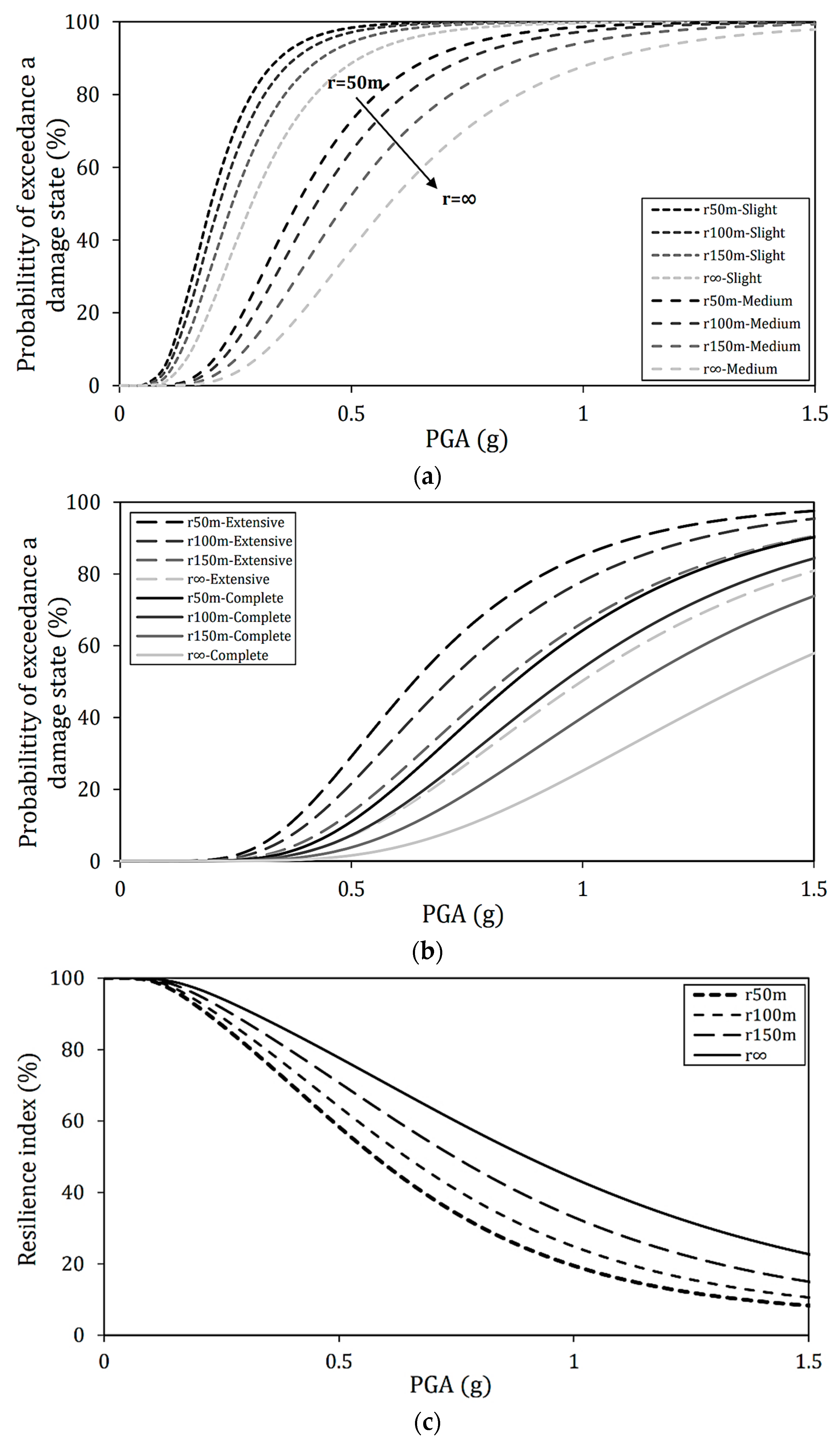
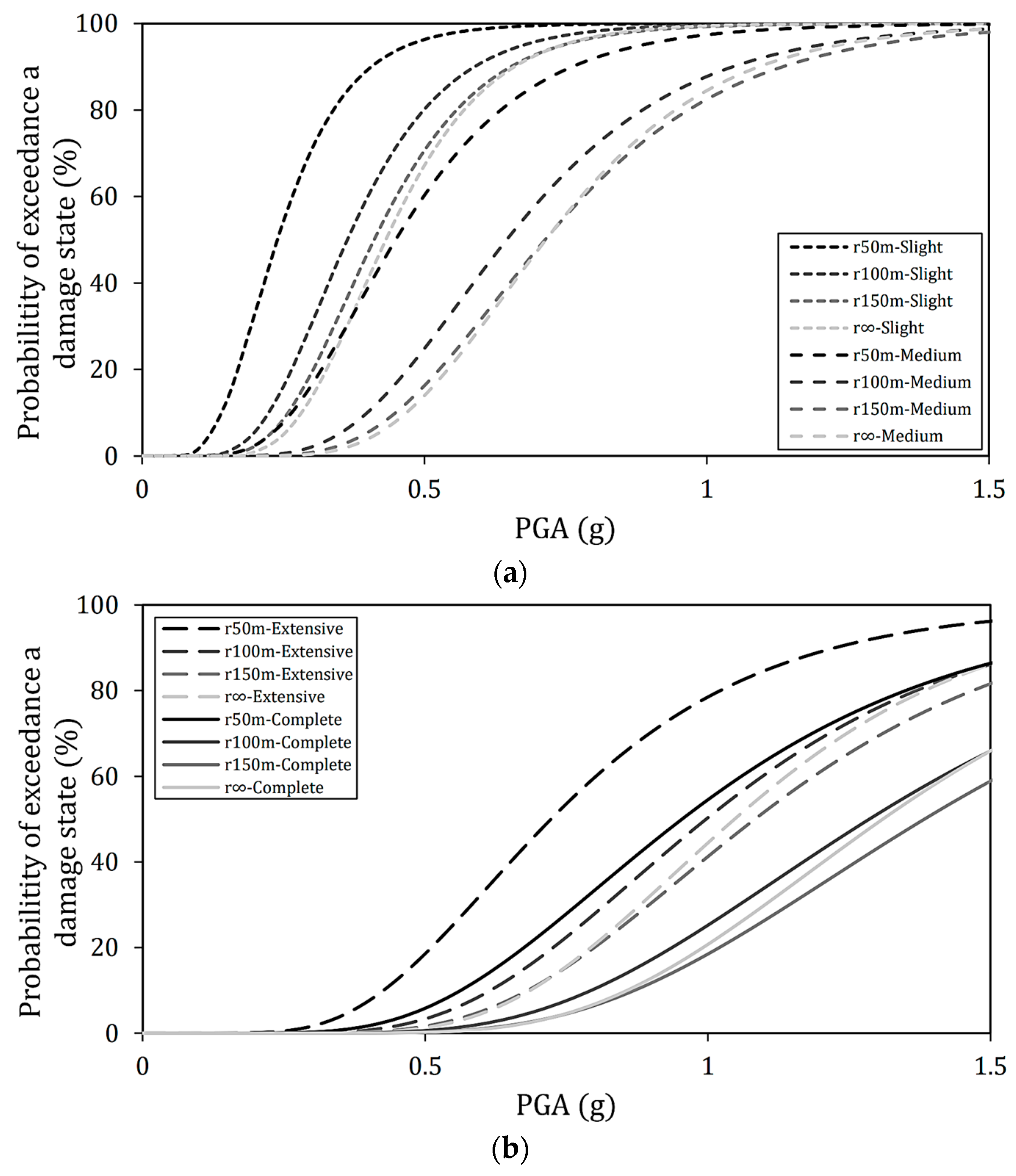
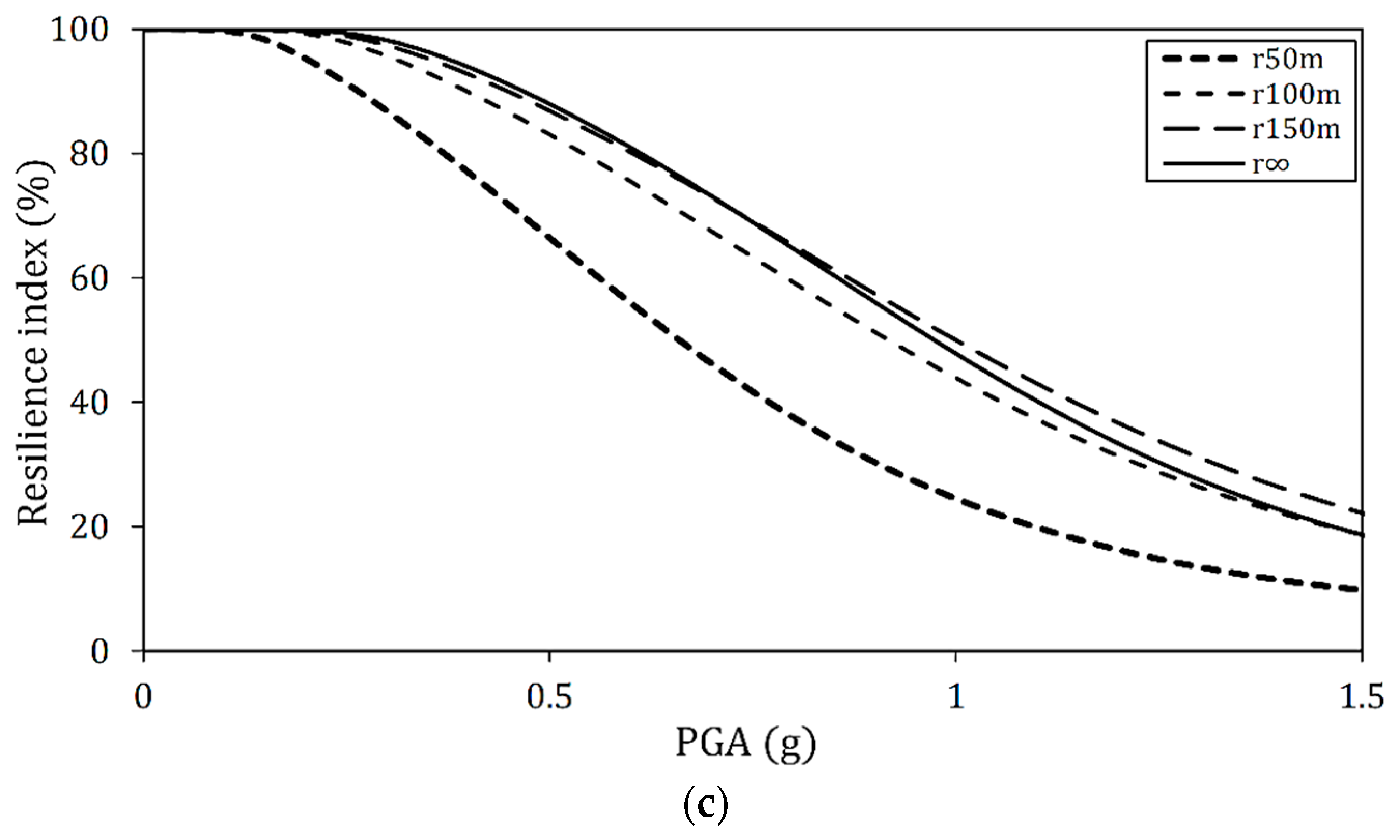
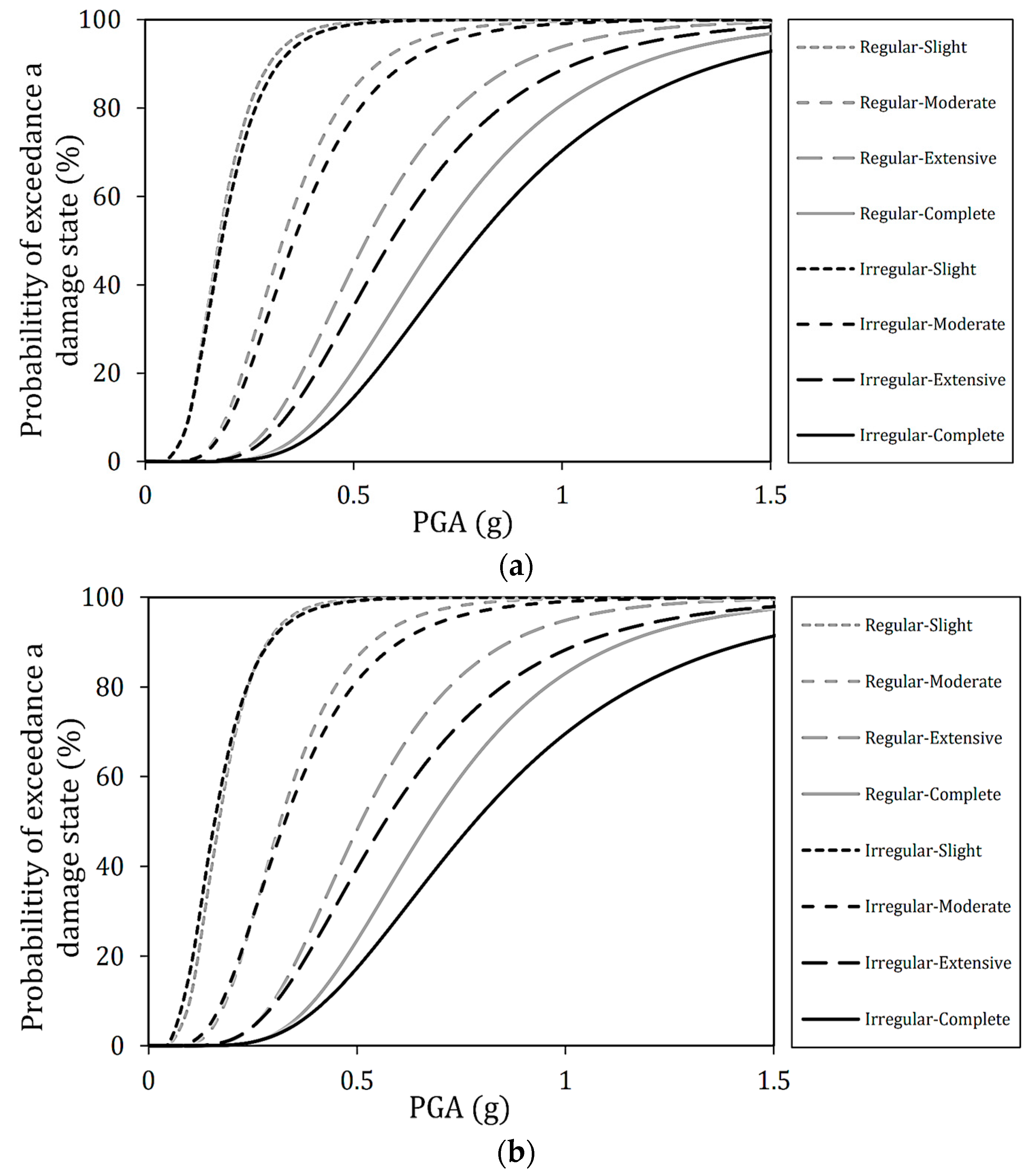
4.2. Effect of Deck Radius on Seismic Resilience Assessment
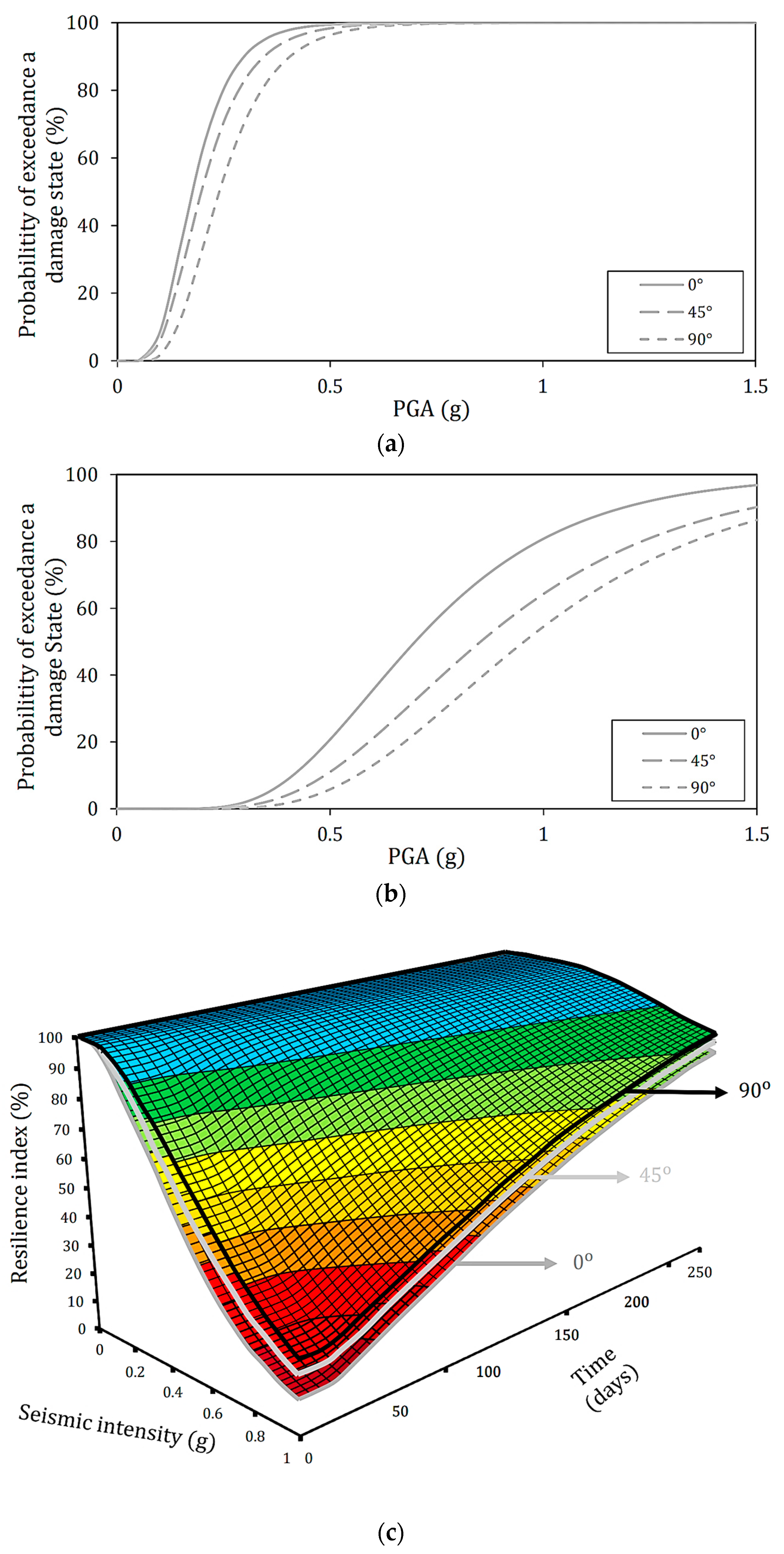
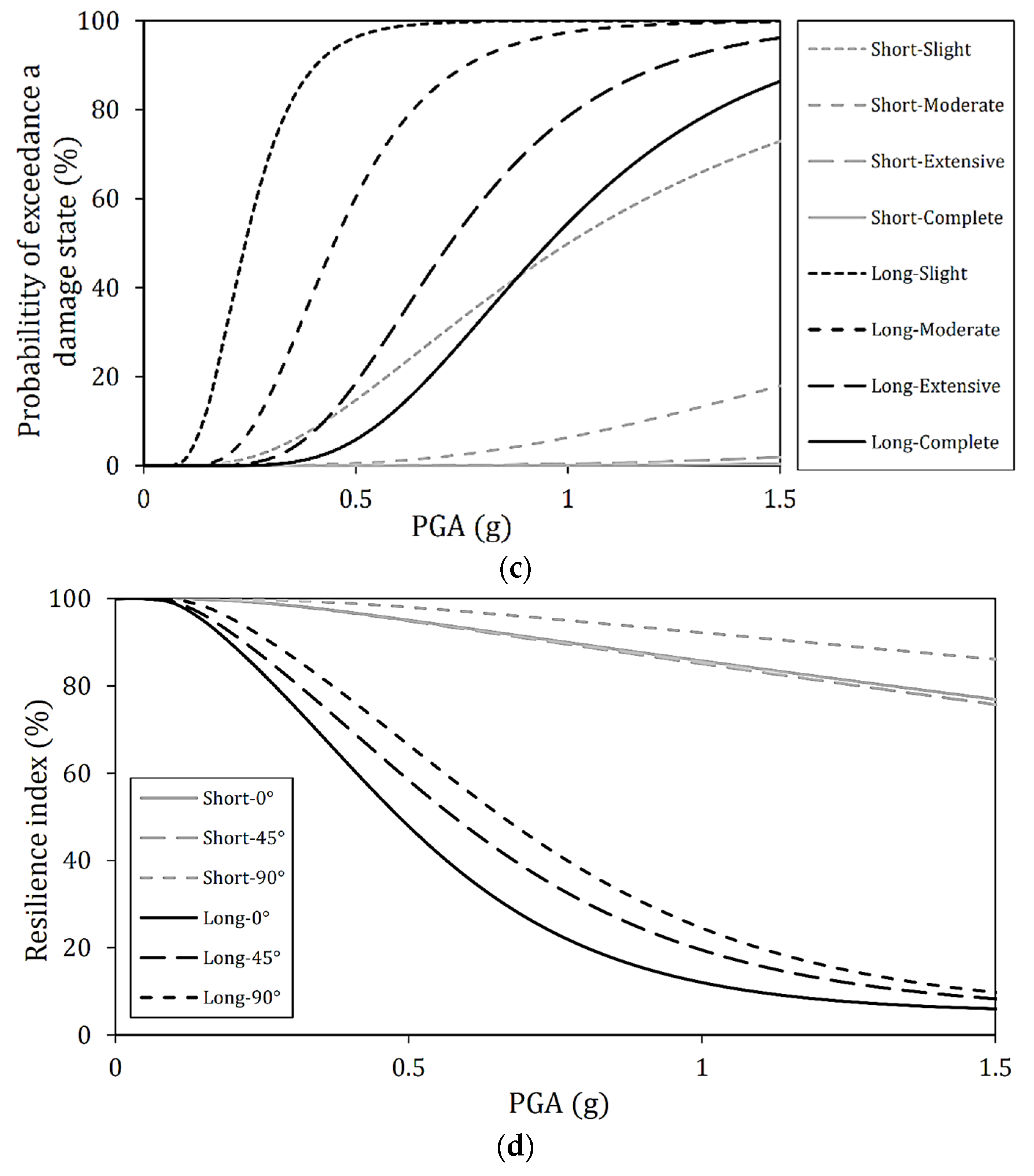
4.3. Effect of Incident Angle on Seismic Resilience Assessment
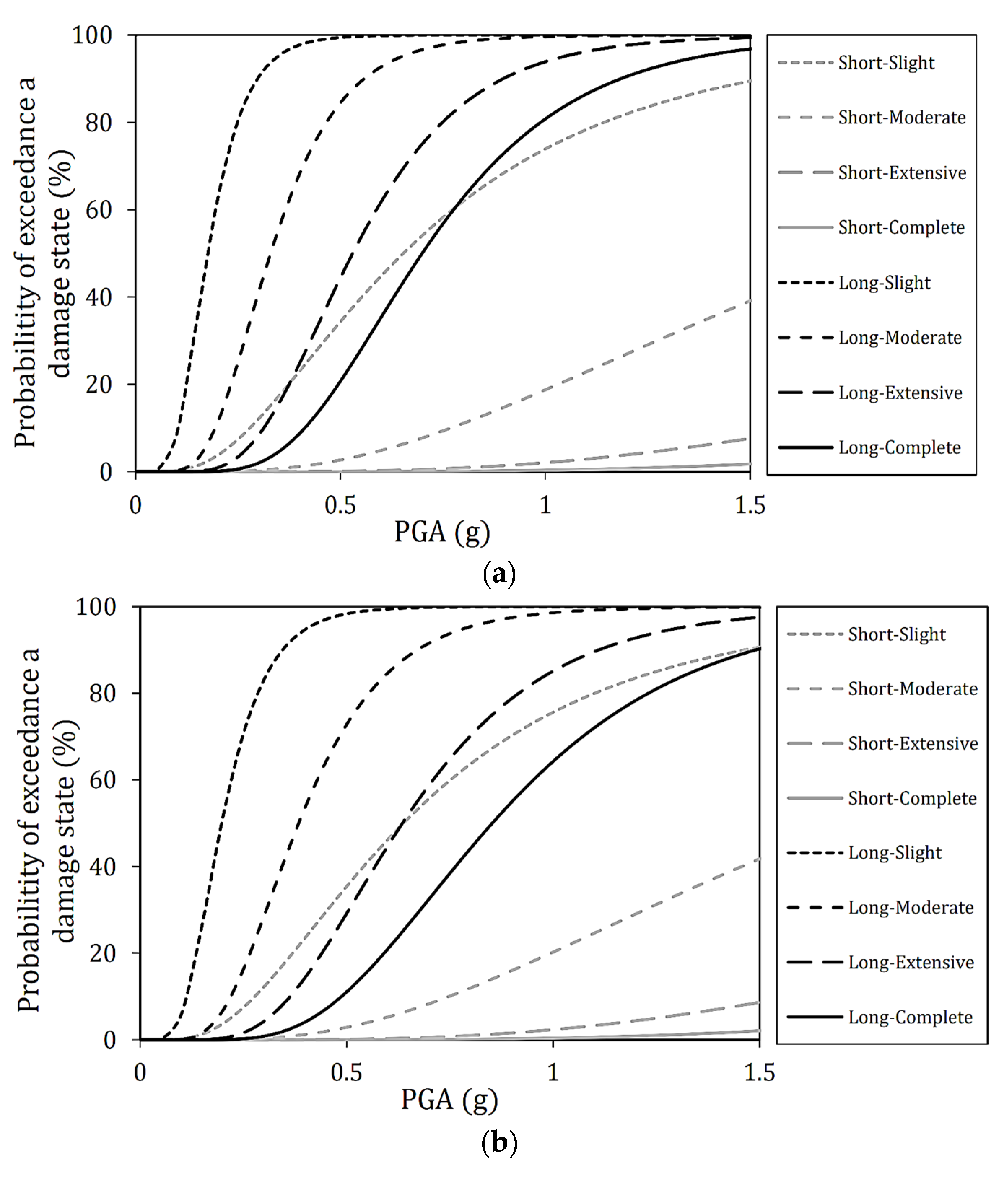
4.4. Effect of Earthquake Period on Seismic Resilience Assessment
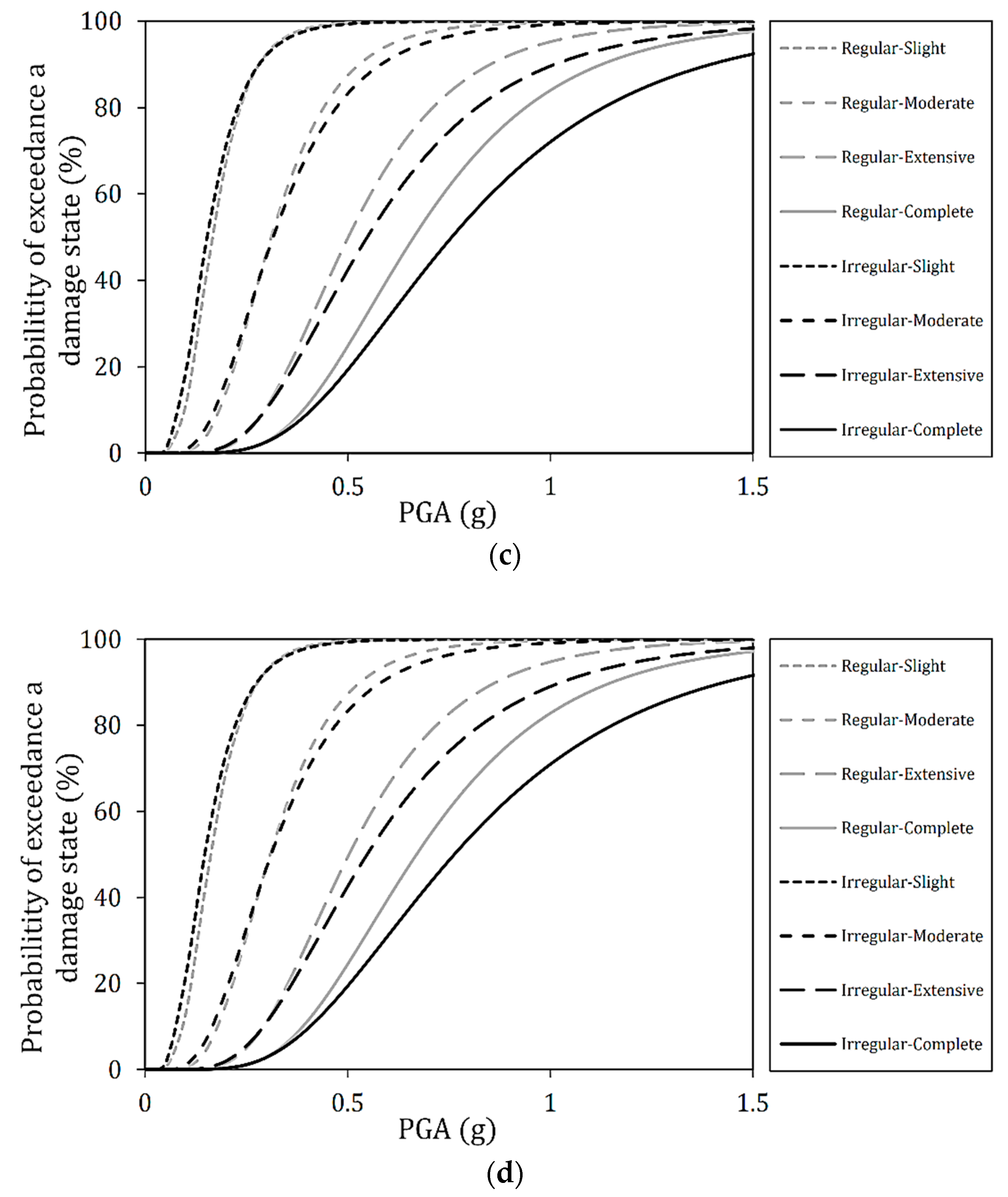
4.5. Effect of Pier Height Irregularity on Seismic Resilience Assessment
5. Conclusions
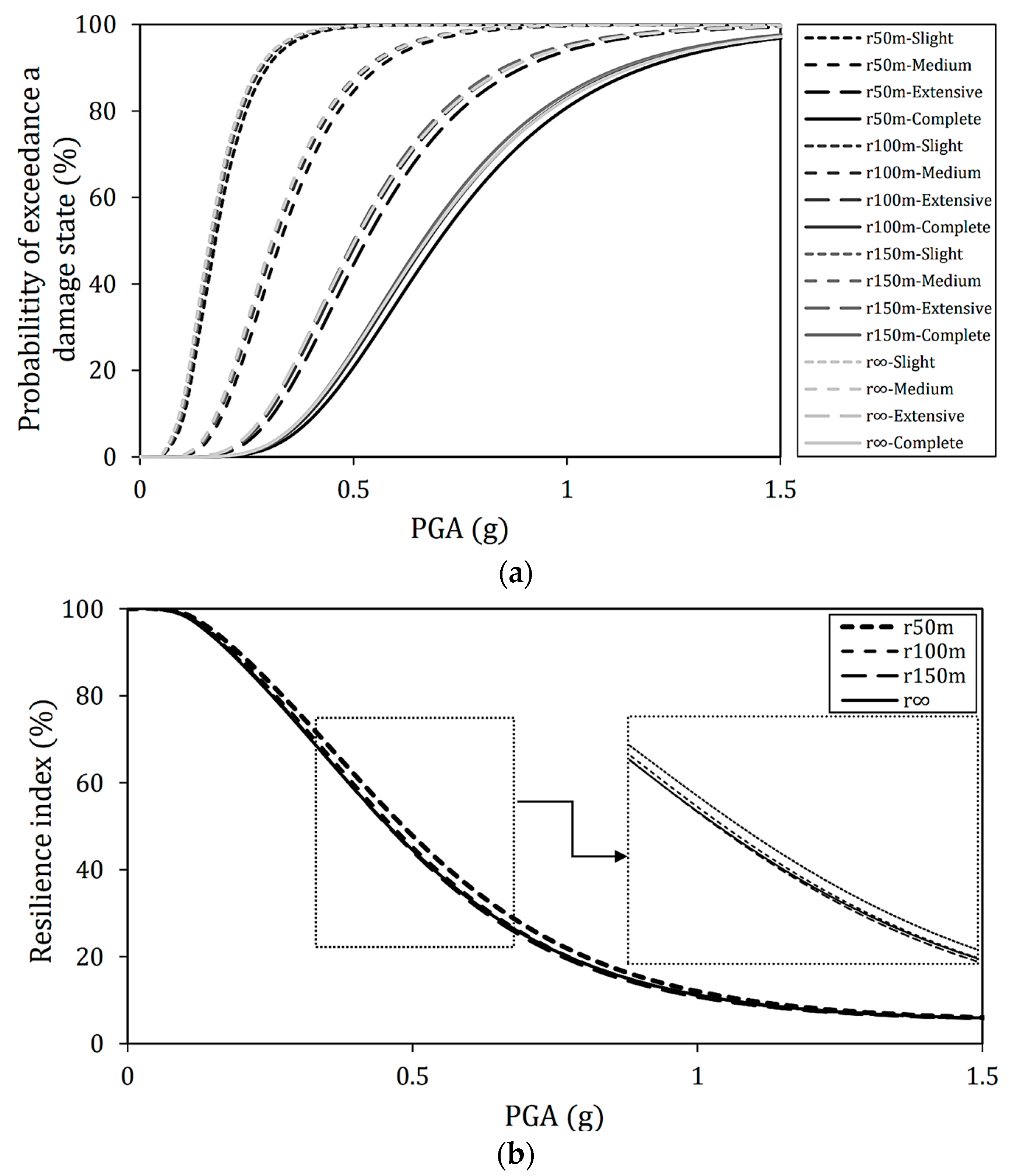
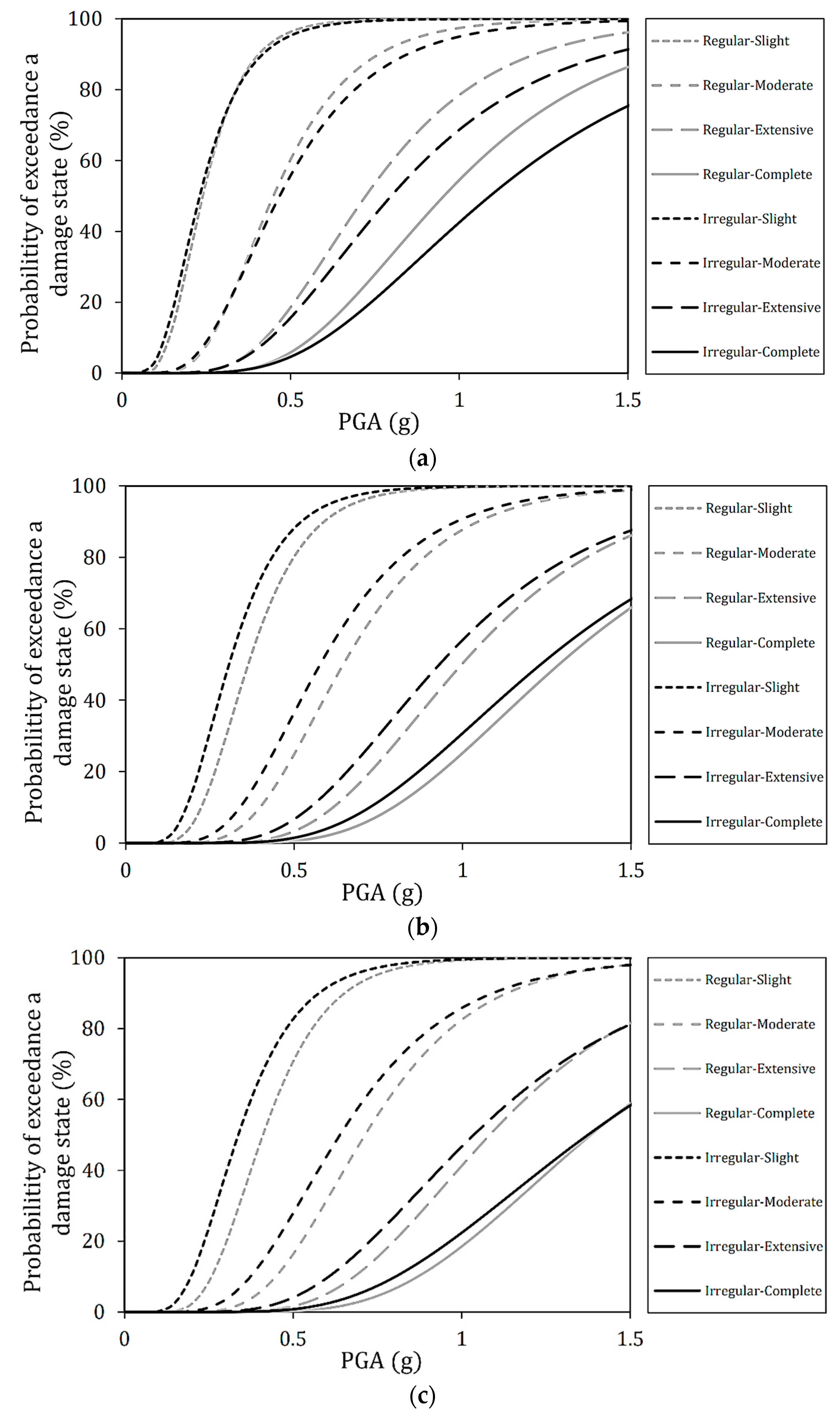
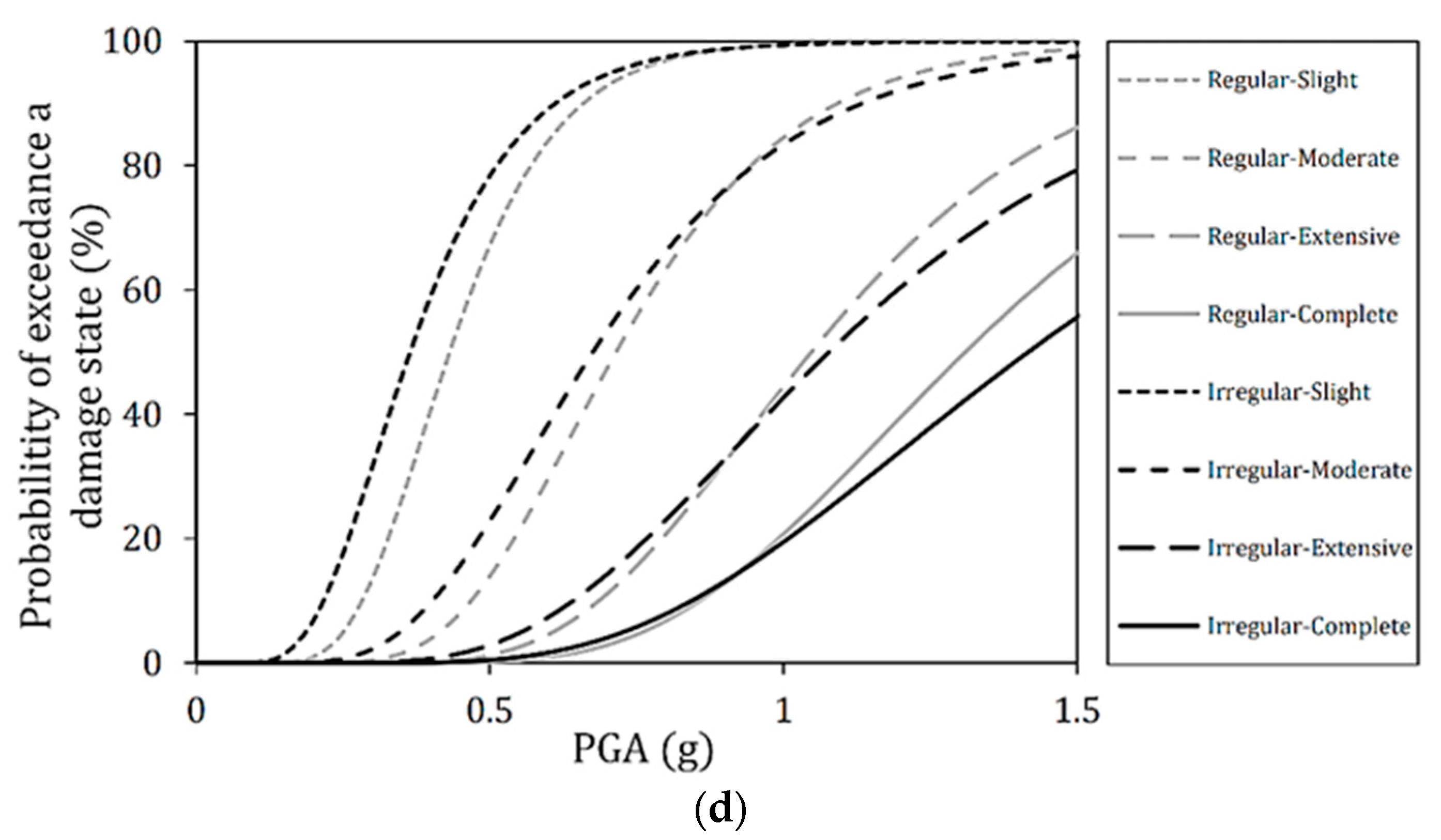
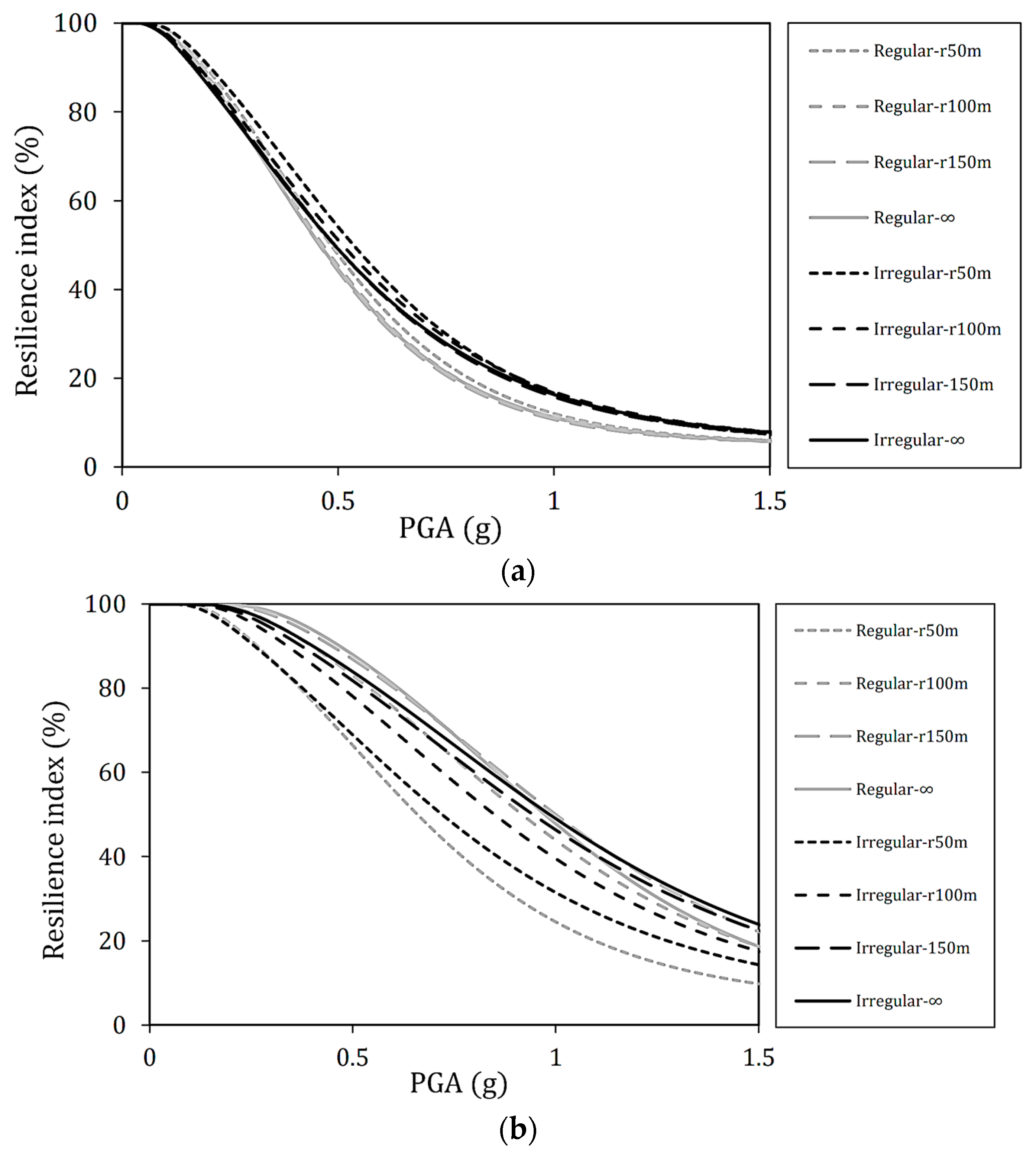
- Effect of deck radius on seismic vulnerability: under long-period ground motions with an incident angle of 0°, the first mode excited in the earthquake motion’s direction is the main mode. Therefore, since the natural periods of straight and curved bridges are almost the same, the behavior during earthquakes is nearly equivalent. However, as the radius becomes smaller, the fragility decreases slightly, and displacement may differ depending on the magnitude of the effective mass. In addition, when the incident angle becomes more significant, such as 45° and 90°, the main mode transforms to the secondary or third modes; hence, the effective mass ratio and the main mode vary. For this reason, it is considered that the fragility was reduced compared to the incident angle of 0°, and the effect of the deck radius on the seismic vulnerability and resilience index became more remarkable. Furthermore, it is confirmed that the fragility may increase when ground motion is incident perpendicular to the longitudinal direction of the piers.
- Effect of pier height irregularity on seismic vulnerability: the results indicate that Irregular bridges are less likely to become vulnerable as the intensity measurements increase compared to Regular bridges. This is thought to be due to the nature of seismic energy being dissipated by short piers, similar to previous studies on short-period ground motion. Unlike Regular bridges, which consist only of short piers, Irregular bridges may be less vulnerable or more resilient because the shorter piers restrict the displacement of the higher piers.
- Effect of ground motion period on seismic vulnerability, deck radius, and angle of incidence: reinforced concrete bridges generally have a natural period of 0.5 to 1.5 s. In this respect, the results show that even if the seismic intensity level is such that slight damage occurs under short-period ground motions, more severe damage may occur under long-period ground motions. In addition, when long-period ground motions are applied compared to short-period ground motions, the vulnerability of the bridge under study increased due to the difference in deck radius and incident angle. Since the natural period of the target bridge is within the range where the long-period ground motion is predominant, it is possible that it responds more sensitively to changes in parameters. In addition, irregularities tend to differ between long-period ground motion and short-period ground motion.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Mehrjoo, M.; Khaji, N.; Moharrami, H.; Bahreininejad, A. Damage detection of truss bridge joints using artificial neural networks. Expert Syst. Appl. 2008, 35, 1122–1131. [Google Scholar] [CrossRef]
- Ahmadi, H.R.; Daneshjoo, F.; Khaji, N. New damage indices and algorithm based on square time–frequency distribution for damage detection in concrete piers of railroad bridges. Struct. Control Health Monit. 2015, 22, 91–106. [Google Scholar] [CrossRef]
- Naghshineh, A.; Tehrani, F.M.; Fischer, O. Application of sustainable concrete in the seismic evaluation of an innovative type of buckling restrained brace. Sustainability 2022, 14, 16344. [Google Scholar] [CrossRef]
- An, W.; Zhou, L.; Kang, M.; Yang, H.; Mo, L. Failure mode analysis of bridge pier due to eccentric impact based on separation of pier and beam. Sustainability 2023, 15, 1435. [Google Scholar] [CrossRef]
- Fu, Z.; Wu, D.; Fang, L.; Chen, D.; Ji, B. Influence factors and repair effects of seismic damage to a box section steel pier. J. Earthq. Tsunami 2019, 13, 1940001. [Google Scholar] [CrossRef]
- Shekari, M.R.; Khaji, N.; Ahmadi, M.T. On the seismic behavior of cylindrical base-isolated liquid storage tanks excited by long-period ground motions. Soil Dyn. Earthq. Eng. 2010, 30, 968–980. [Google Scholar] [CrossRef]
- Liu, L.; Yang, X.; Yan, B.; Miao, S. Dynamic responses of RC girder bridge under heavy truck and seismic loads combined. Sustainability 2022, 14, 9263. [Google Scholar] [CrossRef]
- Kanamori, H. A semi-empirical approach to prediction of long-period ground motions from great earthquakes. Bull. Seismol. Soc. Am. 1979, 69, 1645–1670. [Google Scholar] [CrossRef]
- Guo, W.; Li, J.; Xiang, N. Seismic performance of the buckling-restrained brace central buckle for long-span suspension bridges. J. Earthq. Tsunami 2018, 12, 1850015. [Google Scholar] [CrossRef]
- Mahmood, K.; Rehman, Z.; Farooq, K.; Memon, S.A. One dimensional equivalent linear ground response analysis—A case study of collapsed Margalla Tower in Islamabad during 2005 Muzaffarabad Earthquake. J. Appl. Geophys. 2016, 130, 110–117. [Google Scholar] [CrossRef]
- Mahmood, K.; Zamin, B.; Igbal, S.; Rehman, Z.; Afzal, S.; Safdar, M.; Igbal, Q.; Ali, A. Local site effect on seismic hazard of the relocated new Balakot town. Soil Dyn. Earthq. Eng. 2022, 162, 107451. [Google Scholar] [CrossRef]
- Koketsu, K.; Miyake, H. A seismological overview of long-period ground motion. J. Seismol. 2008, 12, 133–143. [Google Scholar] [CrossRef]
- Choi, E.; DesRoches, R.; Nielson, B. Seismic fragility of typical bridges in moderate seismic zones. Eng. Struct. 2004, 26, 187–199. [Google Scholar] [CrossRef]
- Yi, J.; Li, J.; Guan, Z. Shake table studies on viscous dampers in seismic control of a single-tower cable-stayed bridge model under near-field ground motions. J. Earthq. Tsunami 2018, 12, 1850011. [Google Scholar] [CrossRef]
- Ma, H.B.; Zhuo, W.D.; Lavorato, D.; Nuti, C.; Fiorentino, G.; Marano, G.C.; Greco, R.; Briseghella, B. Probabilistic seismic response and uncertainty analysis of continuous bridges under near-fault ground motions. Front. Struct. Civ. Eng. 2019, 13, 1510–1519. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, H.; Bai, L.; Tang, M.; Chen, H.; Su, D. Fragility analyses of bridge structures using the logarithmic piecewise function-Based probabilistic seismic demand model. Sustainability 2021, 13, 7814. [Google Scholar] [CrossRef]
- Gong, C.; Kang, L.; Liu, L.; Lei, M.; Ding, W.; Yang, Z. A novel prediction model of packing density for single and hybrid steel fiber-aggregate mixtures. Powder Technol. 2023, 418, 118295. [Google Scholar] [CrossRef]
- Okazawa, S.; Tsumori, T.; Yamashita, T.; Tanaka, S. Finite element seismic response analysis of a reinforced concrete pier with a fractured fine tetrahedron mesh. J. Earthq. Tsunami 2016, 10, 1640013. [Google Scholar] [CrossRef]
- Dezfuli, F.H.; Alam, M.S. Effect of different steel-reinforced elastomeric isolators on the seismic fragility of a highway bridge. Struct. Control Health Monit. 2017, 24, e1866. [Google Scholar] [CrossRef]
- Mao, J.; Jia, D.; Yang, Z.; Xiang, N. Seismic performance of concrete bridge piers reinforced with hybrid shape memory alloy (SMA) and steel bars. J. Earthq. Tsunami 2020, 14, 2050001. [Google Scholar] [CrossRef]
- Román, Á.F.G.; Khan, M.S.A.; Kabir, G.; Billah, M.; Dutta, S. Evaluation of interaction between bridge infrastructure resilience factors against seismic hazard. Sustainability 2022, 14, 10277. [Google Scholar] [CrossRef]
- Tondini, N.; Stojadinovic, B. Probabilistic seismic demand model for curved reinforced concrete bridges. Bull. Earthq. Eng. 2012, 10, 1455–1479. [Google Scholar] [CrossRef]
- Amirihormozaki, E.; Pekcan, G.; Itani, A. Analytical fragility functions for horizontally curved steel I-girder highway bridges. Earthq. Spectra 2015, 31, 2235–2254. [Google Scholar] [CrossRef]
- Gupta, T.; Sandhu, D. Seismic response of horizontally curved bridges in combination with skewed abutments. Structures 2022, 36, 846–878. [Google Scholar] [CrossRef]
- Liu, X.; Li, J.; Tsang, H.H.; Wilson, J.L. Evaluating self-centering behavior of unbonded prestressed bridge columns using a new performance index based on quasi-static analysis. J. Earthq. Tsunami 2018, 12, 1850001. [Google Scholar] [CrossRef]
- Tehrani, F.M. Deploying and rating sustainable practices for resilient bridge infrastructure. In Proceedings of the Fifth International Conference on Bridges, Tehran, Iran, 17–18 December 2019; AUT: Tehran, Iran, 2019. Paper MS05. [Google Scholar]
- Liu, J.; Cheng, H.; Liu, Q.; Wang, H.; Bu, J. Research on the damage diagnosis model algorithm of cable-stayed bridges based on data mining. Sustainability 2023, 15, 2347. [Google Scholar] [CrossRef]
- Abbasi, M.; Zakeri, B.; Amiri, G.G. Probabilistic seismic assessment of multiframe concrete box-girder bridges with unequal-height piers. J. Perform. Constr. Facil. 2015, 30, 04015016. [Google Scholar] [CrossRef]
- Tamaddon, S.; Hosseini, M.; Vasseghi, A. The effect of curvature angle of curved RC box-girder continuous bridges on their transient response and vertical pounding subjected to near-source earthquakes. Structures 2020, 28, 1019–1034. [Google Scholar] [CrossRef]
- Yamamoto, H.; Shimizu, T.; Iwamoto, M.; Umehara, H. Effect of long-period ground motion on long-period concrete structures. Annu. Proc. Concr. Eng. 2007, 29, 829–834. (In Japanese) [Google Scholar]
- Tomi, K.; Fujita, K.; Itoyama, Y.; Umehara, H. Seismic response analysis of multi-span continuous viaduct under long-period seismic motion. Annu. Proc. Concr. Eng. 2007, 29, 817–822. (In Japanese) [Google Scholar]
- Todorov, B.; Billah, A.H.M.M. Seismic fragility and damage assessment of reinforced concrete bridge pier under long-duration, near-fault, and far-field ground motions. Structures 2021, 31, 671–685. [Google Scholar] [CrossRef]
- Peng, T.; Guan, J.; Wu, Y. Numerical and experimental investigation of the seismic effect of a two-stage seismic isolation method. Sustainability 2023, 15, 4883. [Google Scholar] [CrossRef]
- Omidian, P.; Khaji, N. A multi-objective optimization framework for seismic resilience enhancement of typical existing RC buildings. J. Build. Eng. 2022, 52, 104361. [Google Scholar] [CrossRef]
- Padgett, J.E.; DesRoches, R. Methodology for the development of analytical fragility curves for retrofitted bridges. Earthq. Eng. Struct. Dyn. 2008, 37, 1157–1174. [Google Scholar] [CrossRef]
- Billah, A.H.M.M.; Alam, M.S.; Bhuiyan, M.A.R. Fragility analysis of retrofitted multicolumn bridge bent subjected to near-fault and far-field ground motion. J. Bridge Eng. 2013, 18, 992–1004. [Google Scholar] [CrossRef]
- Billah, A.H.M.M.; Alam, M.S. Seismic fragility assessment of highway bridges: A state-of-the-art review. Struct. Infrastruct. Eng. 2015, 11, 804–832. [Google Scholar] [CrossRef]
- Kia, M.; Amini, A.; Bayat, M.; Ziehl, P. Probabilistic seismic demand analysis of structures using reliability approaches. J. Earthq. Tsunami 2021, 15, 2150011. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Soleimani, F.; Hajializadeh, D. State-of-the-art review on probabilistic seismic demand models of bridges: Machine-learning application. Infrastructures 2022, 7, 64. [Google Scholar] [CrossRef]
- HAZUS–MH MR5. Multi-Hazard Loss Estimation Methodology–Earthquake Model; Department of Homeland Security: Washington, DC, USA, 2014.
- Tehrani, F.M.; Nazari, M.; Naghshineh, A. Role of seismic isolation and protection devices in enhancing structural resilience. In Objective Resilience, Book 3: Technology; ASCE Press: Reston, VA, USA, 2022. [Google Scholar]
- Tehrani, F.M.; Nelson, D. From sustainability to resilience: A practical guide to ENVISION®. In Objective Resilience, Book 2: Objective Processes; Ettouney, M., Ed.; ASCE Press: Reston, VA, USA, 2022. [Google Scholar]
- Cimellaro, G.P.; Reinhorn, A.M.; Bruneau, M. Framework for analytical quantification of disaster resilience. Eng. Struct. 2010, 32, 3639–3649. [Google Scholar] [CrossRef]
- Huff, T. Partial isolation as a design alternative for pile bent bridges in the New Madrid seismic zone. Pract. Period. Struct. Des. 2016, 21, 04015018. [Google Scholar] [CrossRef]
- AASHTO. American Association of State Highway and Transportation Officials (AASHTO) Guide Specifications for LRFD Seismic Bridge Design; AASHTO: Washington, DC, USA, 2011. [Google Scholar]
- SeismoStruct. SeismoSoft, a Computer Program for Static and Dynamic Nonlinear Analysis of Framed Structures; SeismoStruct: Miki, Japan, 2023. [Google Scholar]
- Madas, P.; Elnashai, A.S. A new passive confinement model for transient analysis of reinforced concrete structures. Earthq. Eng. Struct. Dyn. 1992, 21, 409–431. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress–strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Martinez-Rueda, J.E.; Elnashai, A.S. Confined concrete model under cyclic load. Mater Struct. 1997, 30, 139–147. [Google Scholar] [CrossRef]
- Yassin, M.H.N. Nonlinear Analysis of Prestressed Concrete Structures under Monotonic and Cyclic Loads. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1994. [Google Scholar]
- Menegotto, M.; Pinto, P.E. Method of Analysis for Cyclically Loaded R.C. Plane Frames including Changes in Geometry and Non-Elastic Behaviour of Elements under Combined Normal Force and Bending, Symposium on the Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads; International Association for Bridge and Structural Engineering: Zurich, Switzerland, 1973; pp. 15–22. [Google Scholar]
- Filippou, F.C.; Popov, E.P.; Bertero, V.V. Effects of Bond Deterioration on Hysteretic Behaviour of Reinforced Concrete Joints; Report EERC 83-19; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1983. [Google Scholar]
- Monti, G.; Nuti, C.; Santini, S. CYRUS—Cyclic Response of Upgraded Sections; Report No. 96-2; University of Chieti: Chieti, Italy, 1996. [Google Scholar]
- Fragiadakis, M.; Pinho, R.; Antoniou, S. Modelling Inelastic Buckling of Reinforcing Bars under Earthquake Loading, in Progress in Computational Dynamics and Earthquake Engineering; Papadrakakis, M., Charmpis, D., Lagaros, N., Tsompanakis, Y., Balkema, A., Eds.; Taylor & Francis: Leiden, The Netherlands, 2008. [Google Scholar]
- Abdel Raheem, E.A. Exploring seismic response of bridges with bidirectional coupled modelling of base isolation bearings system. Arab. J. Sci. Eng. 2014, 39, 8669–8679. [Google Scholar] [CrossRef]
- Shome, N.; Cornel, C.A. Probabilistic Seismic Demand Analysis of Nonlinear Structures, Reliability of Marine Structures Program Technical Report RMS-35; Stanford Digital Repository: Tokyo, Japan, 1999. [Google Scholar]
- PEER. Pacific Earthquake Engineering Research Center (PEER) Online Strong Motion Database; PEER: Berkeley, CA, USA, 2023. [Google Scholar]
- Zhou, Y.; Ping, T.; Gong, S.; Zhu, Y. An improved defining parameter for long-period ground motions with application of a super-tall building. Soil Dyn. Earthq. Eng. 2018, 113, 462–472. [Google Scholar] [CrossRef]
- Bianchi, F.; Sousa, R.; Pinho, R. Blind prediction of a full-scale RC bridge column tested under dynamic conditions. In Proceedings of the 3rd International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, COMPDYN, Corfu, Greece, 25–28 May 2011. Paper no. 294. [Google Scholar]

| Abbreviations/Symbols | Definition |
|---|---|
| DI | Damage Index |
| DS/LS | Damage State/Limit State |
| TRE | Elapsed time to recover the infrastructure |
| EDP | Engineering Demand Parameter |
| E | Event |
| Exceedance probability for a damage/limit state | |
| Heaviside step functions | |
| IDA | Incremental Dynamic Analysis |
| IM | Intensity Measurement |
| Ti | i-th period value of record response spectrum |
| LRB | Laminated Rubber Bearing |
| Log-normal standard deviation | |
| Loss function | |
| Median log-normal | |
| PGA | Peak Ground Acceleration |
| Post-event recovery path | |
| PSDM | Probabilistic Seismic Demand Model |
| Resilience index | |
| System performance function |
| Damage States | Description | Fragility Curves in Drift 1 | Restoration Curves in Days, |
|---|---|---|---|
| Slight | Small cracks and peels on the abutment, cracks in the shear keys on the abutment, small peels on the hinges, small peels on the columns, or small cracks on the deck, etc. | 0.01 | 0.6 (0.6) |
| Moderate | Moderate shear cracking and peeling (structurally sound as a column), widespread cracking and peeling of shear keys, etc. | 0.025 | 2.5 (2.7) |
| Extensive | Shear failure of columns (structurally unsafe condition), large residual displacement at connections, breakage of shear keys at abutments, etc. | 0.05 | 75 (42) |
| Complete | Defined by the collapse of columns and loss of bearing support, the collapse of decks, and the tilting of substructures due to foundation breakage. | 0.075 | 230 (110) |
| Material | Mechanical Property | Value |
|---|---|---|
| Concrete | Compressive strength (MPa) | 30 |
| Tensile strength (MPa) | 3 | |
| Strain at peak stress (%) | 0.2 | |
| Modulus of elasticity (GPa) | 25.7 | |
| Specific weight (kN/m3) | 24 | |
| Steel (bar) | Modulus of elasticity (GPa) | 200 |
| Yield strength (MPa) | 525 | |
| Strain hardening parameters (%) | 0.5 | |
| Specific weight (kN/m3) | 78 |
| Start Data base input: Pacific Seismic Engineering Research Center (PEER) database. While () do ( is the number of considered (20) short- or long-period ground motions) Step 1—Set main formulation: Step 2—The response spectrum must first be scaled: This means that the PGA of the original record must be scaled to 1 g, and then response spectrum obtained. Step 3—Calculate^0.6: is the i-th period point (within the period range of [0, 10] s with interval of 0.01 s). Step 4—Calculate: is the normalized acceleration response spectrum value of the ground motions. Step 5—Calculate : Calculate the summations using the main formula (Step 1) to obtain . Step 6—Check main conditions: |
| End while Return the best set of records (short- or long-period ground motion) End |
| No. | RSN | Direction | Epicenter (km) | Year | Earthquake Name | |
|---|---|---|---|---|---|---|
| 1 | 2115 | EW | 190.09 | 2002 | Denali, Alaska | 0.3741 |
| 2 | 2115 | NS | 190.09 | 2002 | Denali, Alaska | 0.3614 |
| 3 | 6015 | EW | 197.73 | 2010 | El Mayor-Cucapah | 0.3956 |
| 4 | 6015 | NS | 197.73 | 2010 | El Mayor-Cucapah | 0.3377 |
| 5 | 6048 | EW | 278.58 | 2010 | El Mayor-Cucapah | 0.3837 |
| 6 | 6048 | NS | 278.58 | 2010 | El Mayor-Cucapah | 0.2990 |
| 7 | 6968 | EW | 281.89 | 2010 | Darfield, New Zealand | 0.1784 |
| 8 | 6968 | NS | 281.89 | 2010 | Darfield, New Zealand | 0.1935 |
| 9 | 6976 | EW | 108.93 | 2010 | Darfield, New Zealand | 0.3406 |
| 10 | 6976 | NS | 108.93 | 2010 | Darfield, New Zealand | 0.2921 |
| 11 | 1103 | EW | 196.18 | 1995 | Kobe, Japan | 0.2479 |
| 12 | 1103 | NS | 196.18 | 1995 | Kobe, Japan | 0.2455 |
| 13 | 1745 | EW | 101.42 | 1992 | Little Skull Mtn, NV | 0.0629 |
| 14 | 1745 | NS | 101.42 | 1992 | Little Skull Mtn, NV | 0.0752 |
| 15 | 2953 | EW | 104.84 | 1999 | Chi-Chi, Taiwan-05 | 0.2573 |
| 16 | 2953 | NS | 104.84 | 1999 | Chi-Chi, Taiwan-05 | 0.1482 |
| 17 | 3862 | EW | 108.50 | 1999 | Chi-Chi (aftershock 4), Taiwan | 0.1936 |
| 18 | 3862 | NS | 108.50 | 1999 | Chi-Chi (aftershock 4), Taiwan | 0.3073 |
| 19 | 5456 | EW | 145.22 | 2008 | Iwate | 0.2009 |
| 20 | 5456 | NS | 145.22 | 2008 | Iwate | 0.2268 |
| No. | RSN | Direction | Epicenter (km) | Year | Earthquake Name | |
|---|---|---|---|---|---|---|
| 1 | 1156 | EW | 311.50 | 1999 | Kocaeli, Turkey | 0.8970 |
| 2 | 1156 | NS | 311.50 | 1999 | Kocaeli, Turkey | 0.6124 |
| 3 | 2102 | EW | 296.11 | 2002 | Denali, Alaska | 0.6373 |
| 4 | 2102 | NS | 296.11 | 2002 | Denali, Alaska | 0.6185 |
| 5 | 3789 | EW | 183.89 | 1999 | Hector Mine | 0.7819 |
| 6 | 3789 | NS | 183.89 | 1999 | Hector Mine | 0.7074 |
| 7 | 5858 | EW | 176.89 | 2008 | El Mayor-Cucapah | 0.8067 |
| 8 | 5858 | NS | 176.89 | 2008 | El Mayor-Cucapah | 0.6276 |
| 9 | 6987 | EW | 261.39 | 2010 | Darfield, New Zealand | 0.6177 |
| 10 | 6987 | NS | 261.39 | 2010 | Darfield, New Zealand | 0.7137 |
| 11 | 2059 | EW | 275.02 | 2002 | Nenana Mountain, Alaska | 0.8345 |
| 12 | 2059 | NS | 275.02 | 2002 | Nenana Mountain, Alaska | 0.7218 |
| 13 | 3791 | EW | 304.73 | 2003 | San Simeon, CA | 1.6710 |
| 14 | 3791 | NS | 304.73 | 2003 | San Simeon, CA | 1.4591 |
| 15 | 4900 | EW | 300.23 | 2007 | Chuetsu-oki | 0.6506 |
| 16 | 4900 | NS | 300.23 | 2007 | Chuetsu-oki | 0.7369 |
| 17 | 6130 | EW | 308.51 | 2000 | Tottori, Japan | 0.8772 |
| 18 | 6130 | NS | 308.51 | 2000 | Tottori, Japan | 0.8422 |
| 19 | 8489 | EW | 332.00 | 2010 | El Mayor-Cucapah | 1.1992 |
| 20 | 8489 | NS | 332.00 | 2010 | El Mayor-Cucapah | 1.0083 |
| Bridge Type | Mode | r 50m | r 100m | r 150m | r ∞ | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Period (s) | Effective Modal Mass (%) | Period (s) | Effective Modal Mass (%) | Period (s) | Effective Modal Mass (%) | Period (s) | Effective Modal Mass (%) | ||||||||||
| 0° | 45° | 90° | 0° | 45° | 90° | 0° | 45° | 90° | 0° | 45° | 90° | ||||||
| Regular bridge | 1 | 0.931 | 59.96 | 29.97 | 0.00 | 0.923 | 87.32 | 43.29 | 0.00 | 0.921 | 93.50 | 46.75 | 0.00 | 0.919 | 98.72 | 49.36 | 0.00 |
| 2 | 0.699 | 0.00 | 44.37 | 88.73 | 0.652 | 0.00 | 40.53 | 26.51 | 0.646 | 0.00 | 3.91 | 7.59 | 0.641 | 0.00 | 0.00 | 0.00 | |
| 3 | 0.670 | 0.00 | 3.91 | 7.81 | 0.638 | 0.00 | 9.35 | 69.48 | 0.629 | 0.00 | 44.26 | 88.40 | 0.620 | 0.00 | 47.97 | 95.94 | |
| 4 | 0.638 | 32.21 | 16.11 | 0.00 | 0.620 | 11.04 | 3.67 | 0.00 | 0.617 | 5.22 | 2.44 | 0.00 | 0.615 | 0.00 | 0.00 | 0.00 | |
| 5 | 0.597 | 5.62 | 2.80 | 0.00 | 0.583 | 0.19 | 0.08 | 0.00 | 0.580 | 0.00 | 0.00 | 0.00 | 0.578 | 0.14 | 0.07 | 0.00 | |
| Irregular bridge | 1 | 1.056 | 63.56 | 31.78 | 0.00 | 1.042 | 88.67 | 43.84 | 0.00 | 1.038 | 94.21 | 47.10 | 0.00 | 1.035 | 98.86 | 49.43 | 0.00 |
| 2 | 0.778 | 0.00 | 47.31 | 94.59 | 0.728 | 0.00 | 51.53 | 95.24 | 0.716 | 0.00 | 48.39 | 96.05 | 0.706 | 0.00 | 48.60 | 97.20 | |
| 3 | 0.734 | 34.81 | 17.40 | 0.00 | 0.713 | 10.33 | 2.06 | 0.00 | 0.709 | 4.75 | 2.02 | 0.00 | 0.705 | 0.00 | 0.00 | 0.00 | |
| 4 | 0.671 | 0.00 | 1.45 | 2.90 | 0.648 | 0.00 | 0.67 | 2.06 | 0.645 | 0.00 | 0.60 | 1.20 | 0.642 | 0.00 | 0.00 | 0.00 | |
| 5 | 0.602 | 0.33 | 0.16 | 0.00 | 0.585 | 0.058 | 0.02 | 0.00 | 0.581 | 0.18 | 0.09 | 0.00 | 0.579 | 0.33 | 0.16 | 0.00 | |
| Radius | 50 m | 100 m | 150 m | ∞ | |
|---|---|---|---|---|---|
| Situation | |||||
| Long-period | Regular | 1 | |||
| Irregular | |||||
| Short-period | Regular | ||||
| Irregular |
| Situation | Ratio 1 | 50 m | 100 m | 150 m | ∞ |
|---|---|---|---|---|---|
| Regular | |||||
| Irregular |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uenaga, T.; Omidian, P.; George, R.C.; Mirzajani, M.; Khaji, N. Seismic Resilience Assessment of Curved Reinforced Concrete Bridge Piers through Seismic Fragility Curves Considering Short- and Long-Period Earthquakes. Sustainability 2023, 15, 7764. https://doi.org/10.3390/su15107764
Uenaga T, Omidian P, George RC, Mirzajani M, Khaji N. Seismic Resilience Assessment of Curved Reinforced Concrete Bridge Piers through Seismic Fragility Curves Considering Short- and Long-Period Earthquakes. Sustainability. 2023; 15(10):7764. https://doi.org/10.3390/su15107764
Chicago/Turabian StyleUenaga, Tomoya, Pedram Omidian, Riya Catherine George, Mohsen Mirzajani, and Naser Khaji. 2023. "Seismic Resilience Assessment of Curved Reinforced Concrete Bridge Piers through Seismic Fragility Curves Considering Short- and Long-Period Earthquakes" Sustainability 15, no. 10: 7764. https://doi.org/10.3390/su15107764
APA StyleUenaga, T., Omidian, P., George, R. C., Mirzajani, M., & Khaji, N. (2023). Seismic Resilience Assessment of Curved Reinforced Concrete Bridge Piers through Seismic Fragility Curves Considering Short- and Long-Period Earthquakes. Sustainability, 15(10), 7764. https://doi.org/10.3390/su15107764