Experimental Study on the Seismic Performance of a Steel Slag CFDST T-Joint
Abstract
:1. Introduction
2. Experimental Program
2.1. Specimen Design
2.2. Mechanical Properties of Materials
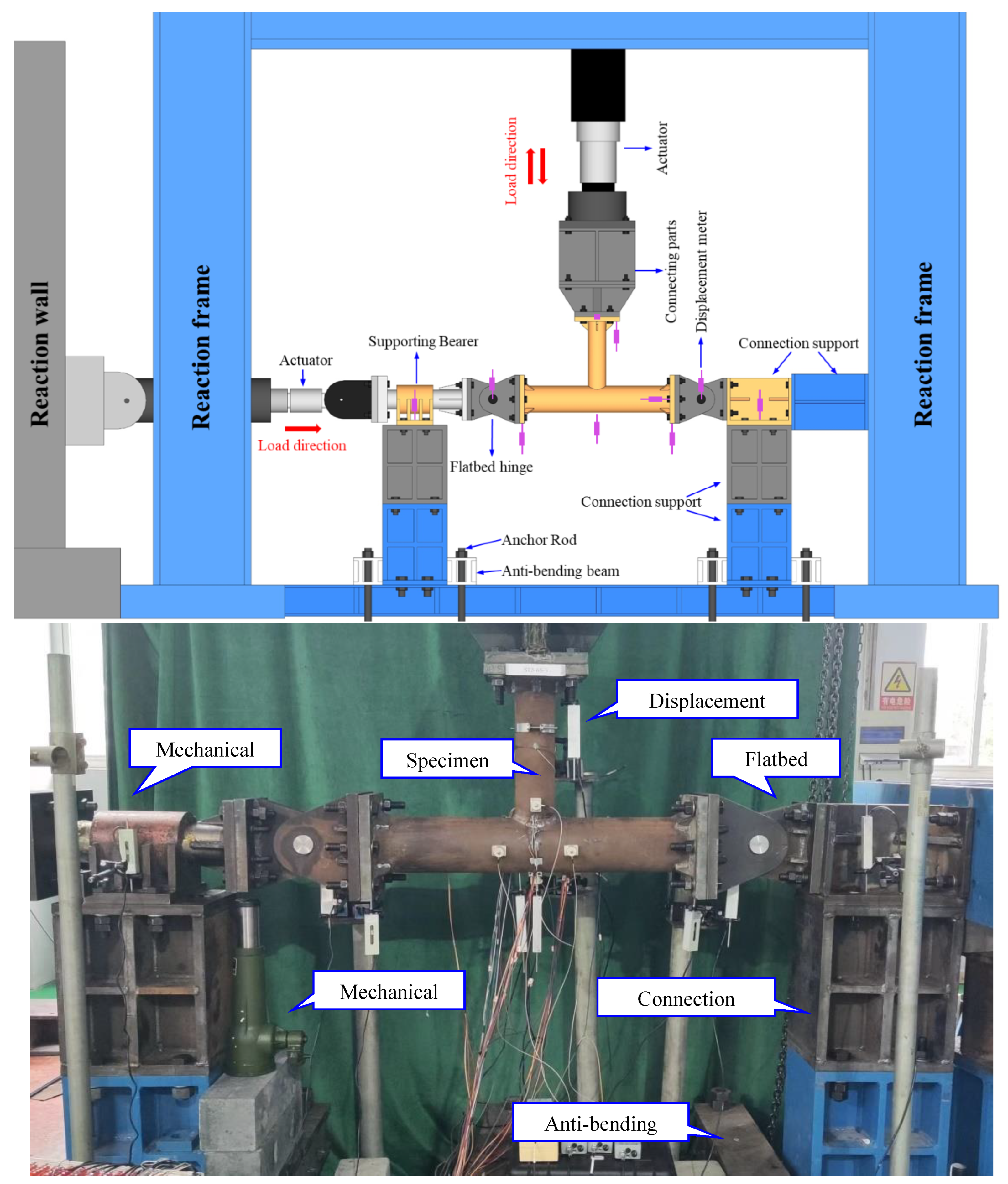
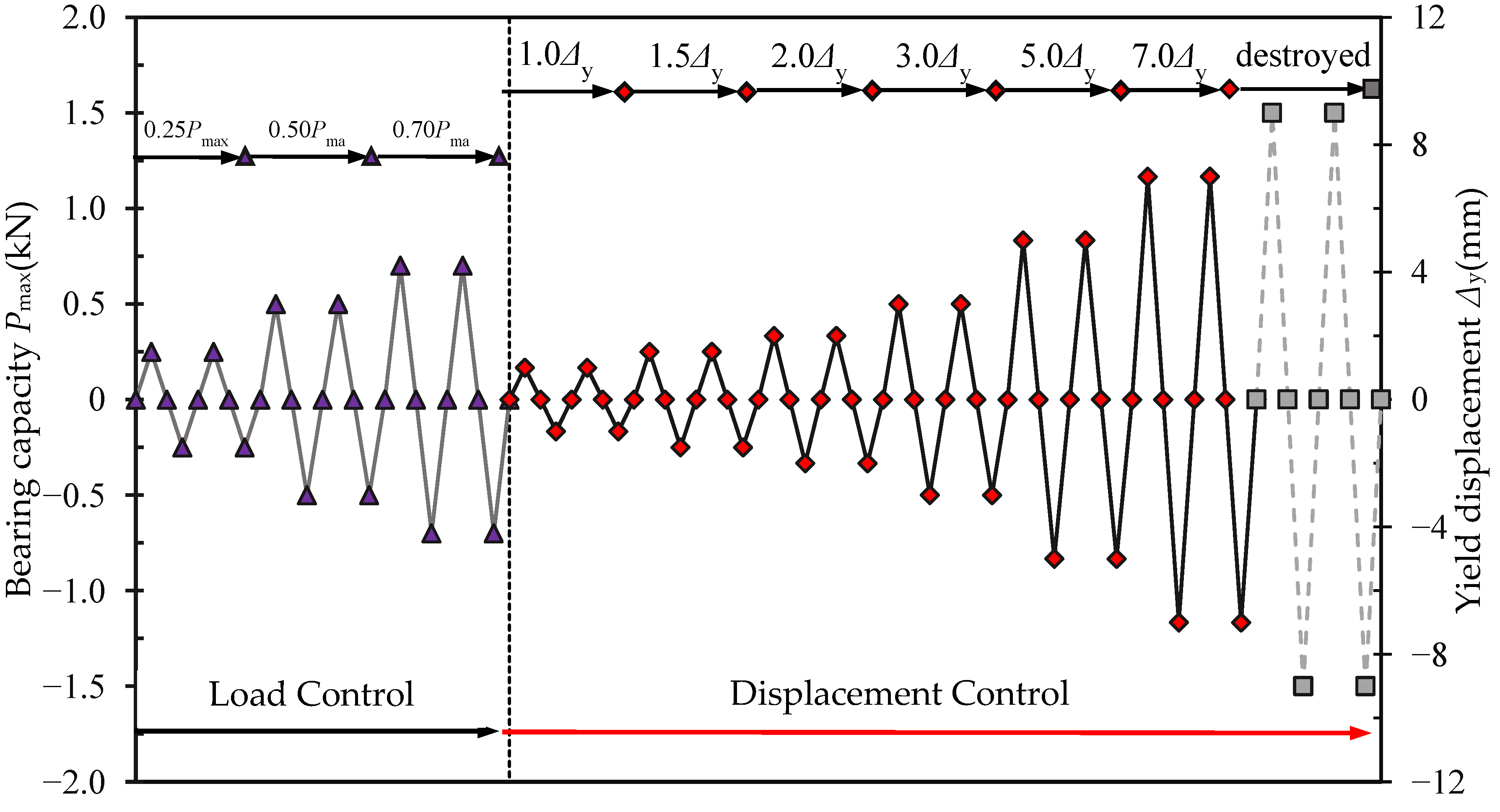
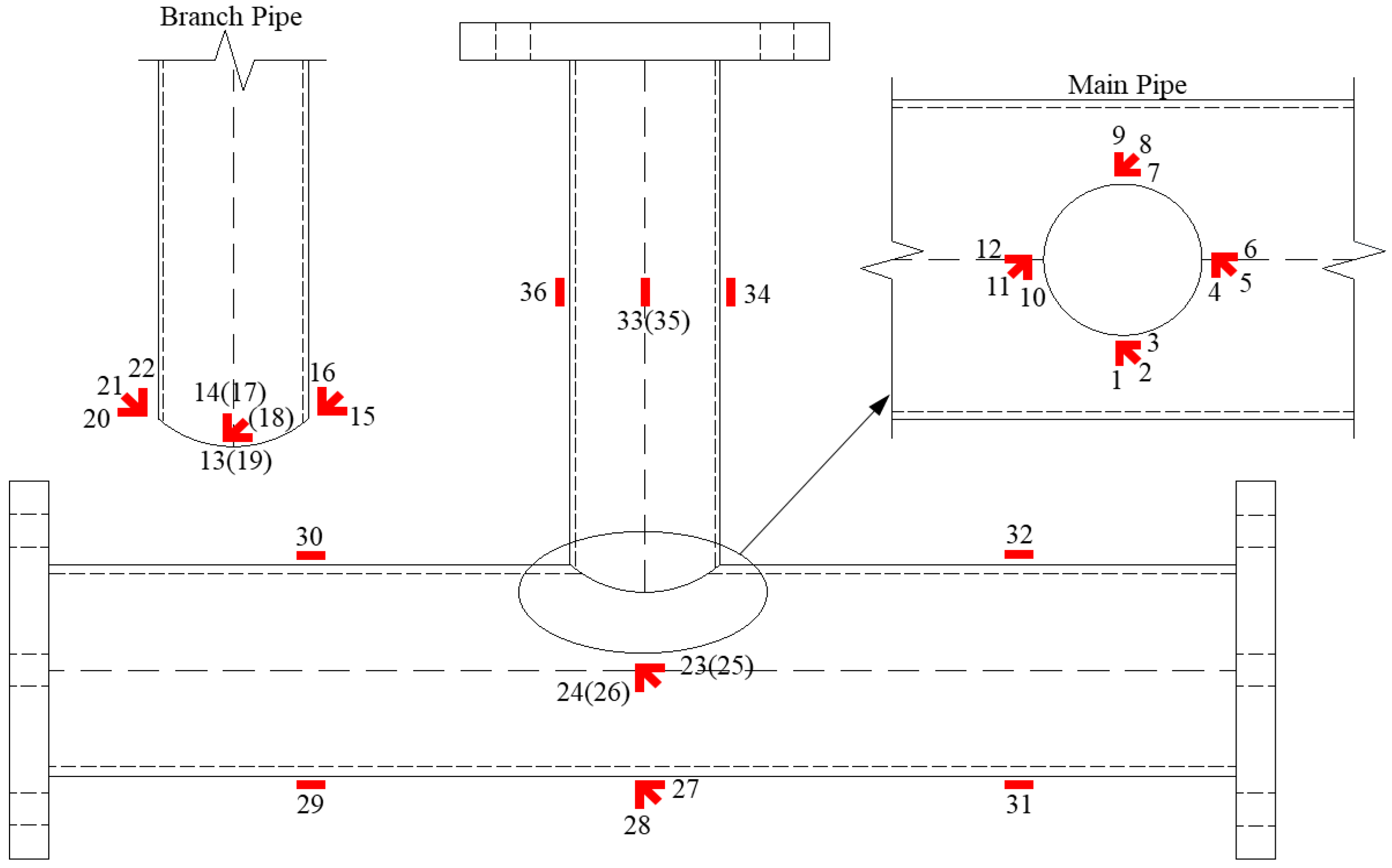
2.3. Experiment Setup and Loading Scheme
3. Results
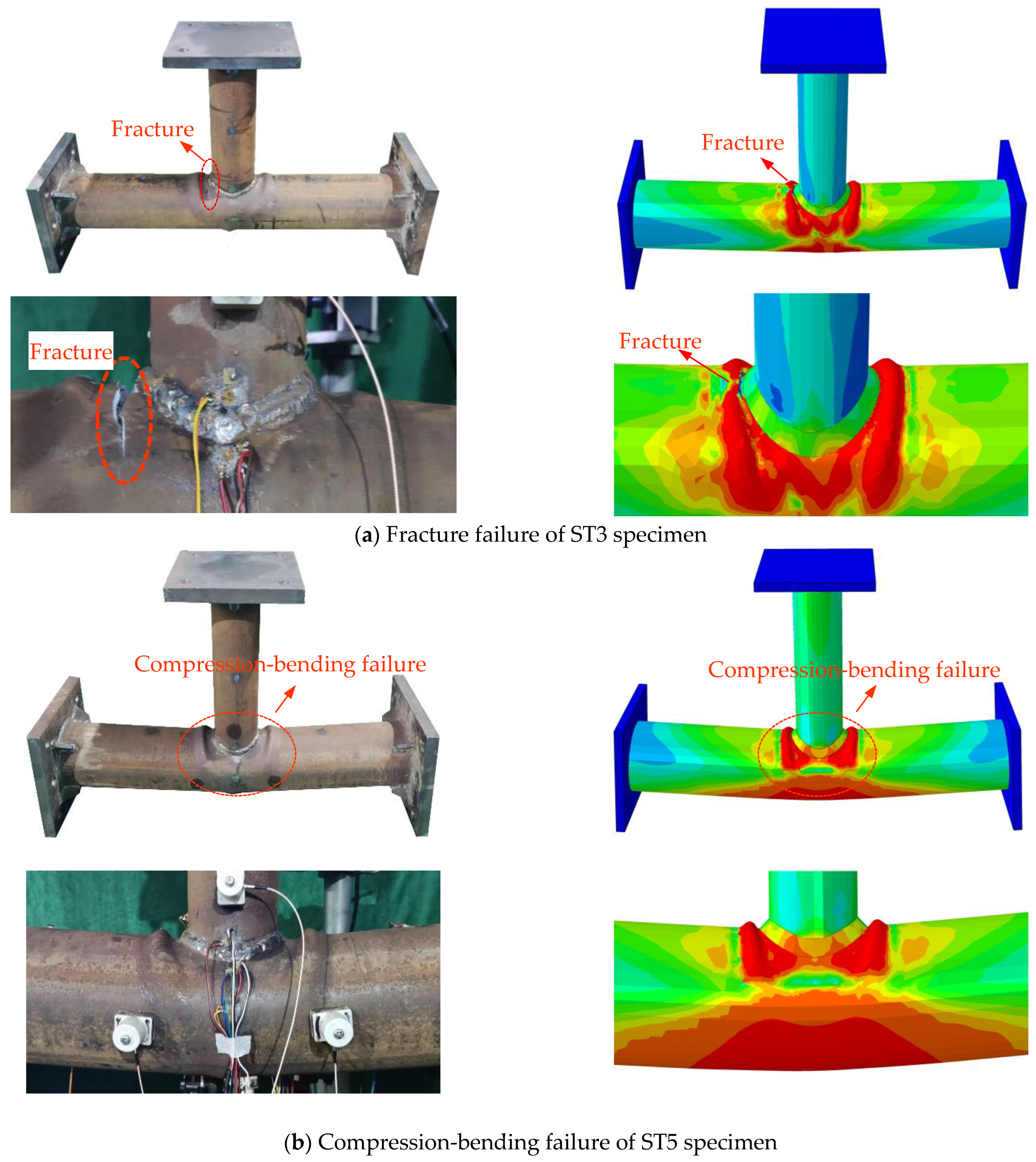
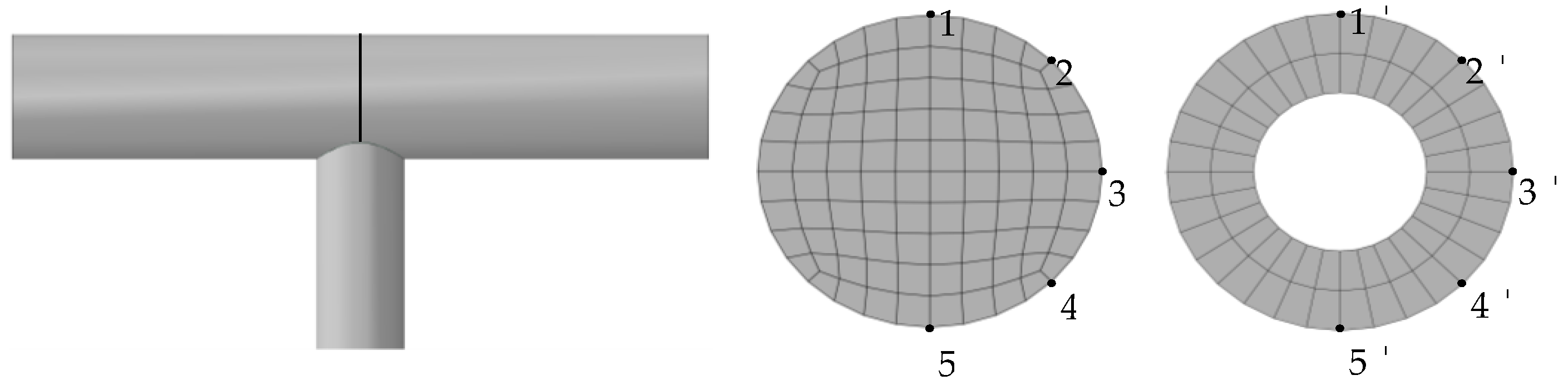
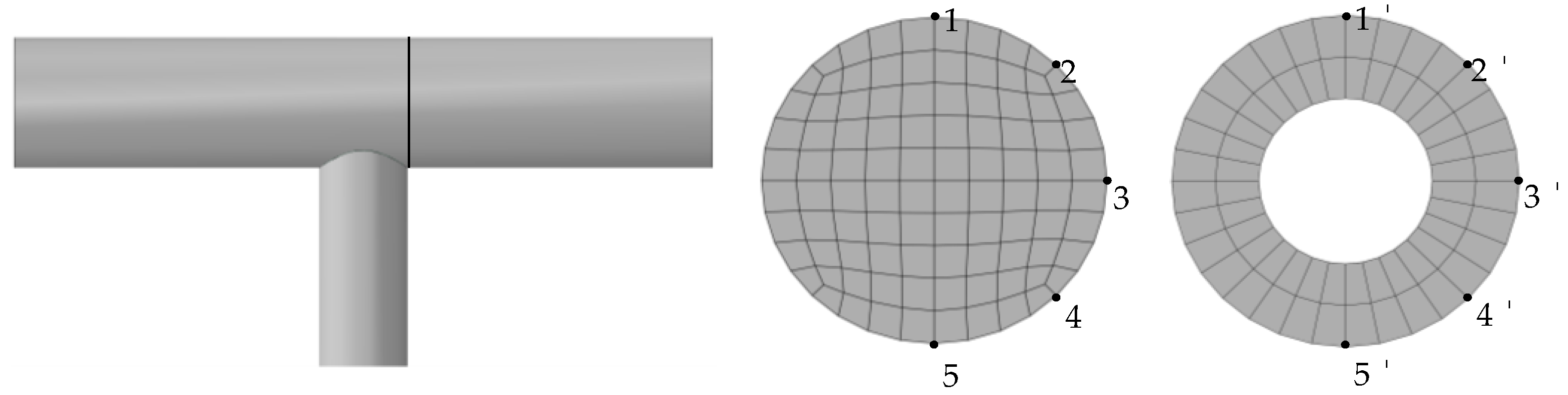
3.1. Failure Modes of Specimens
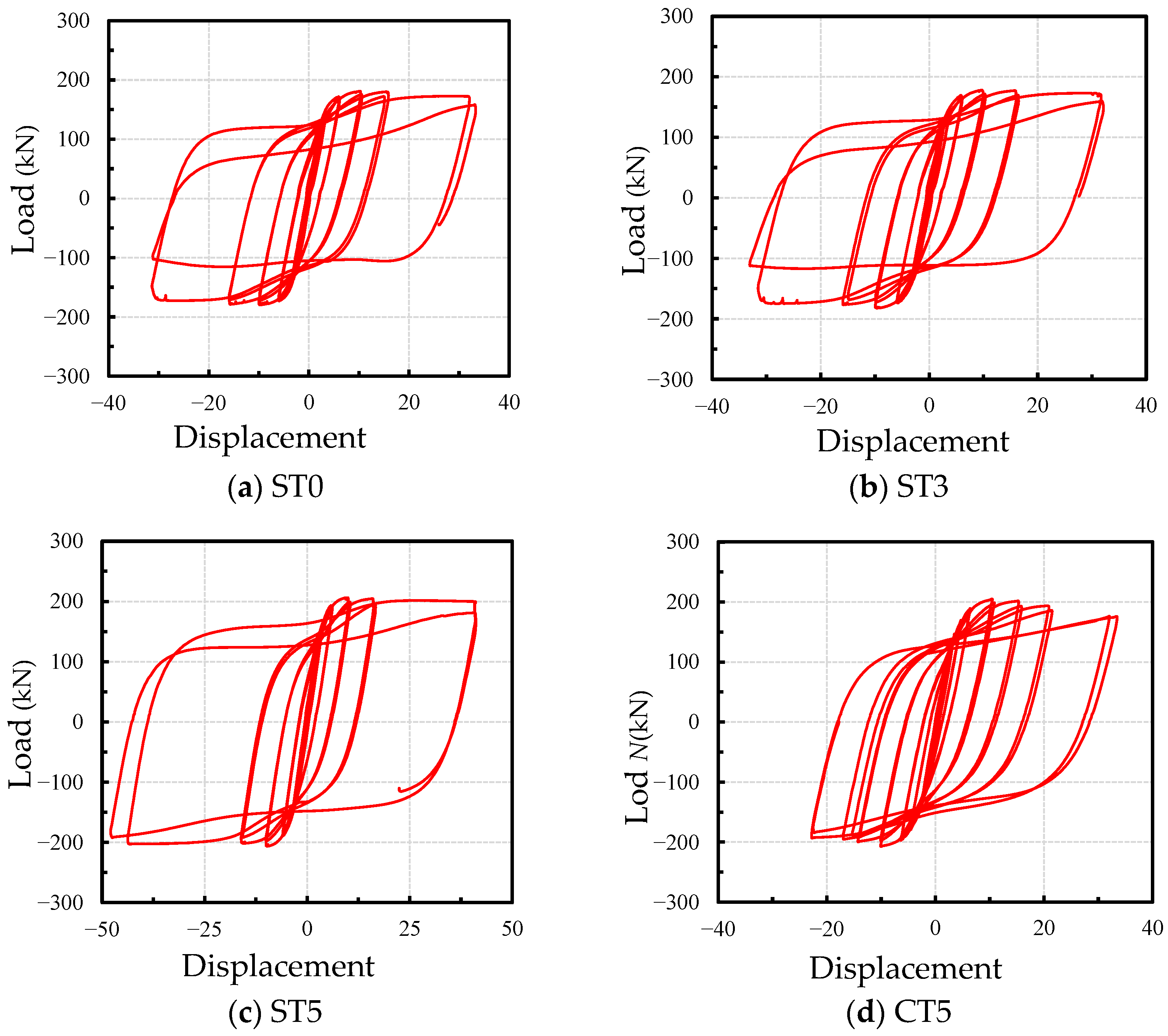
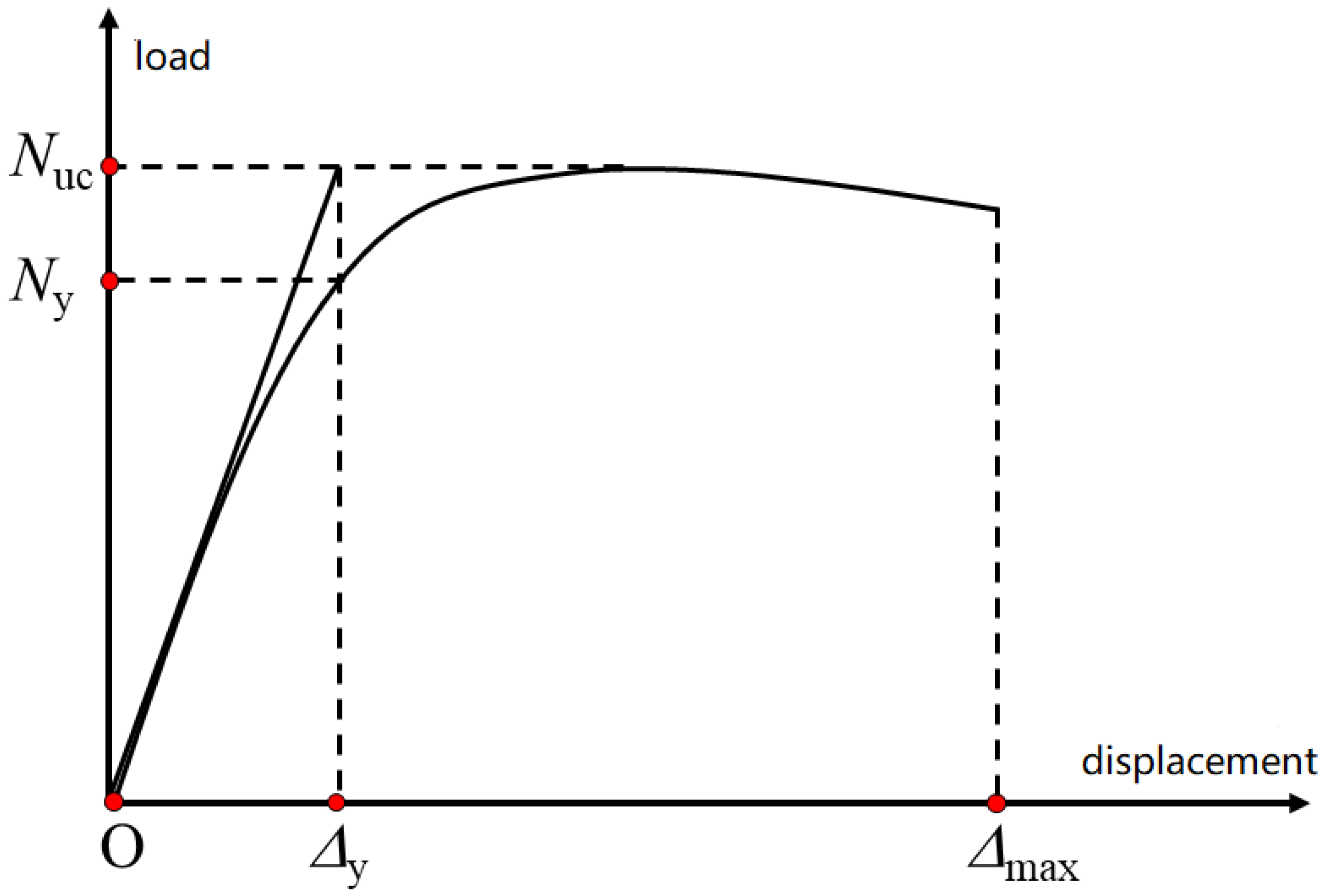
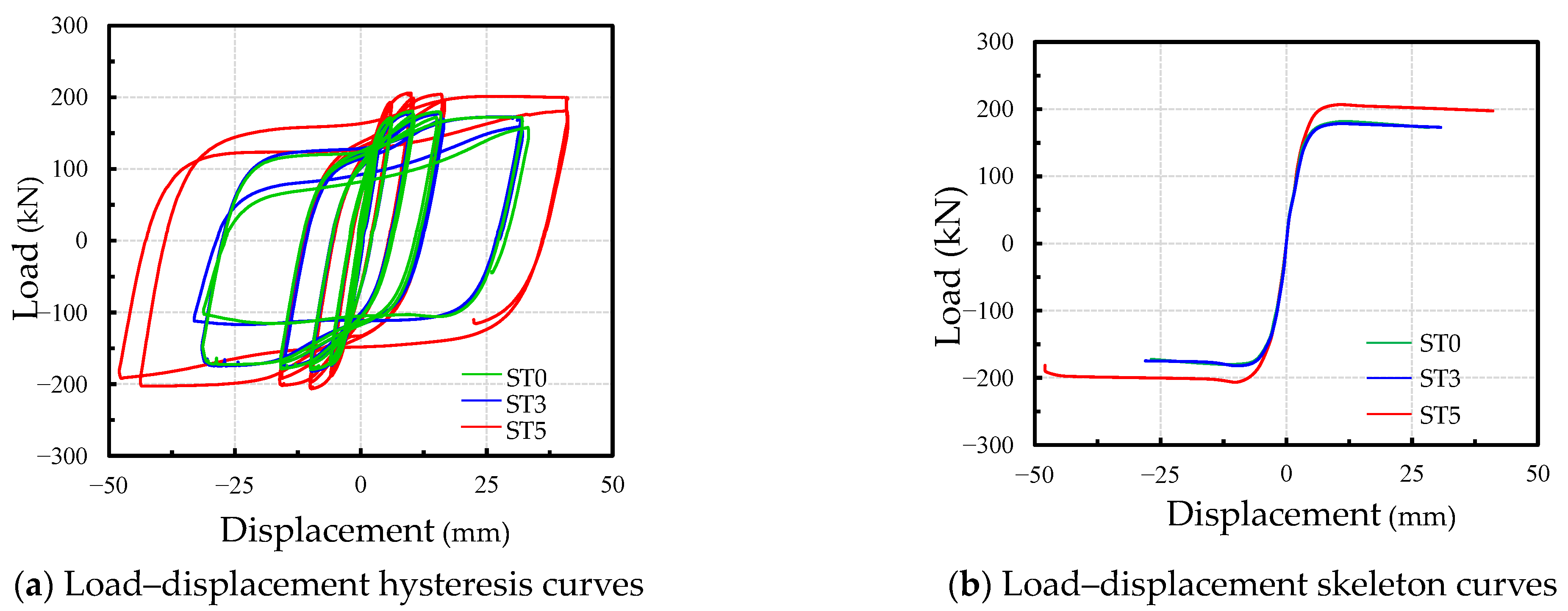
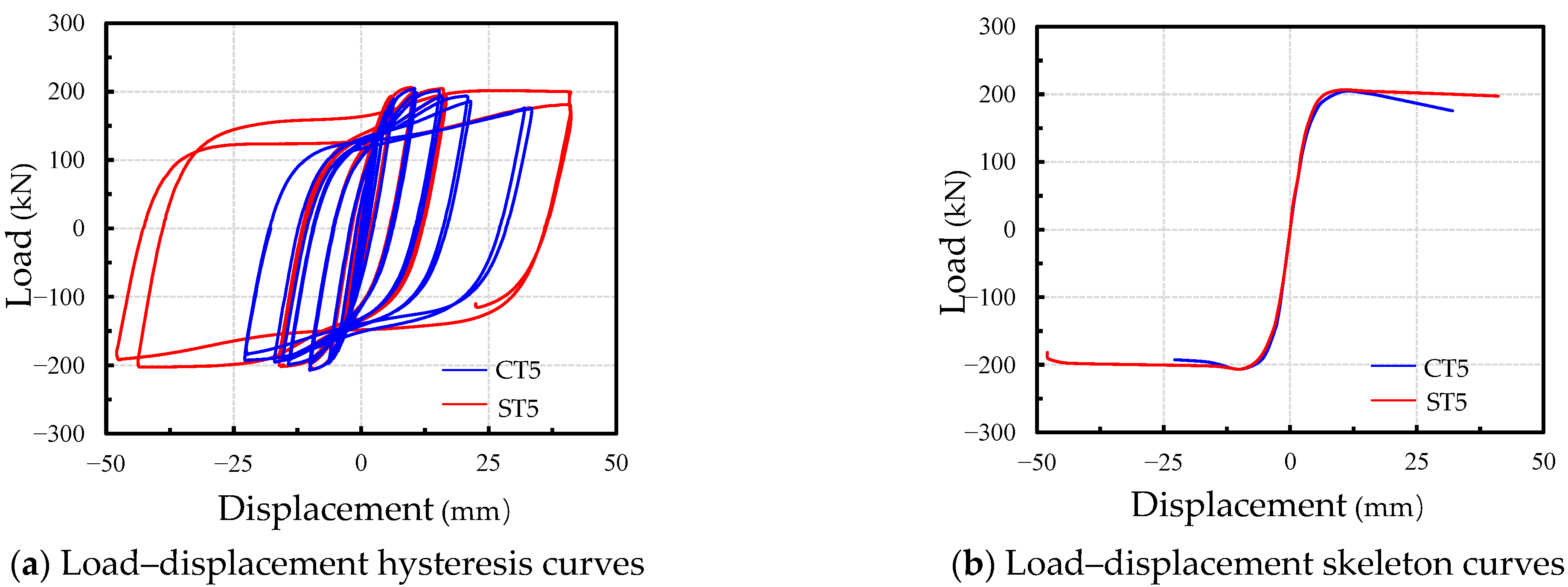
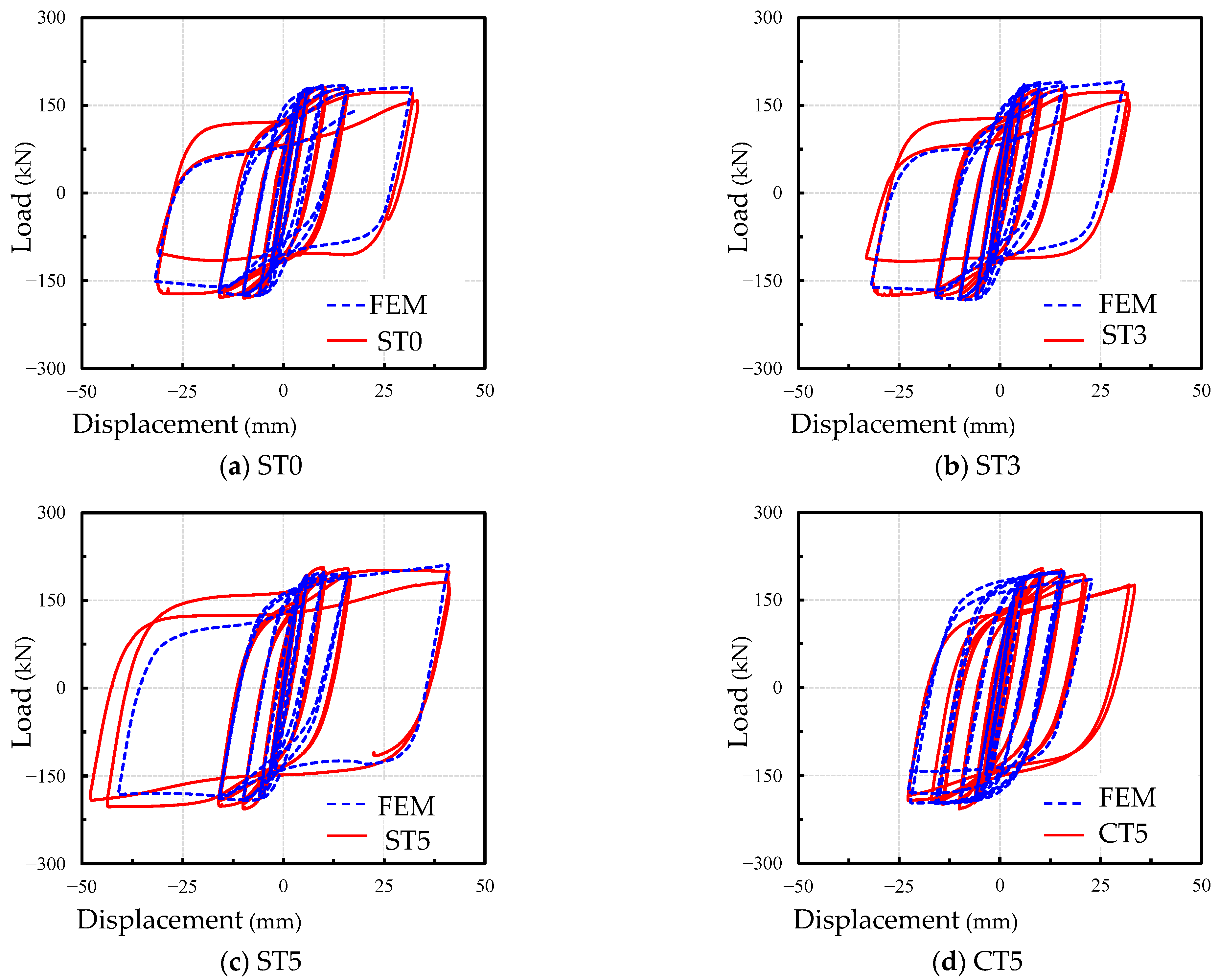
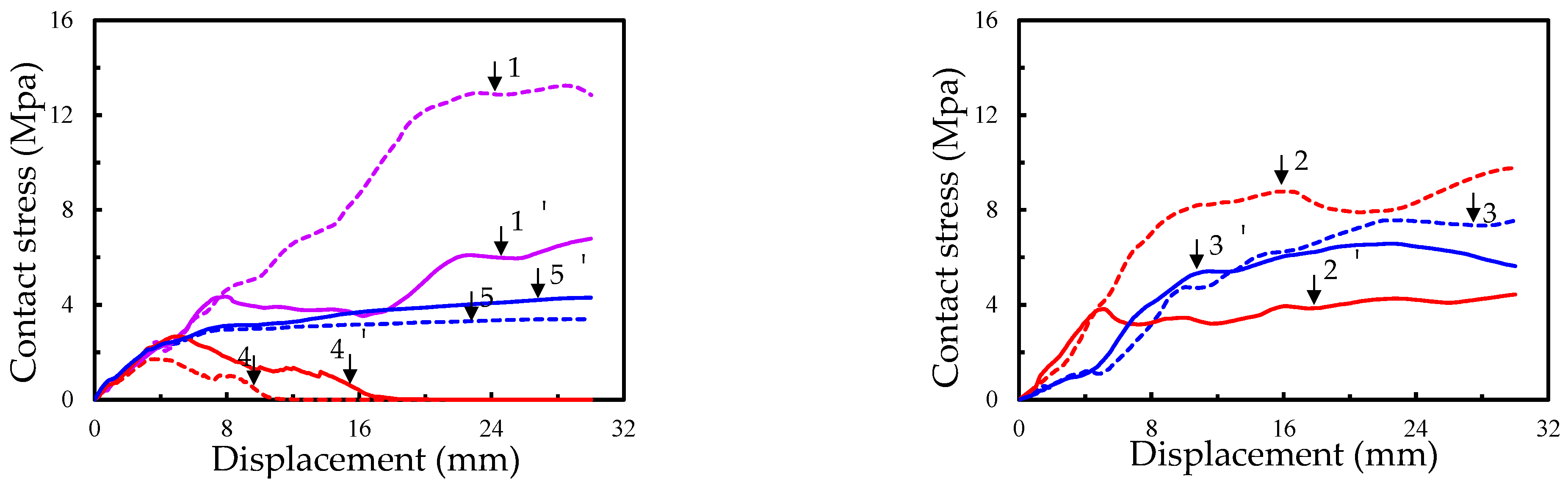
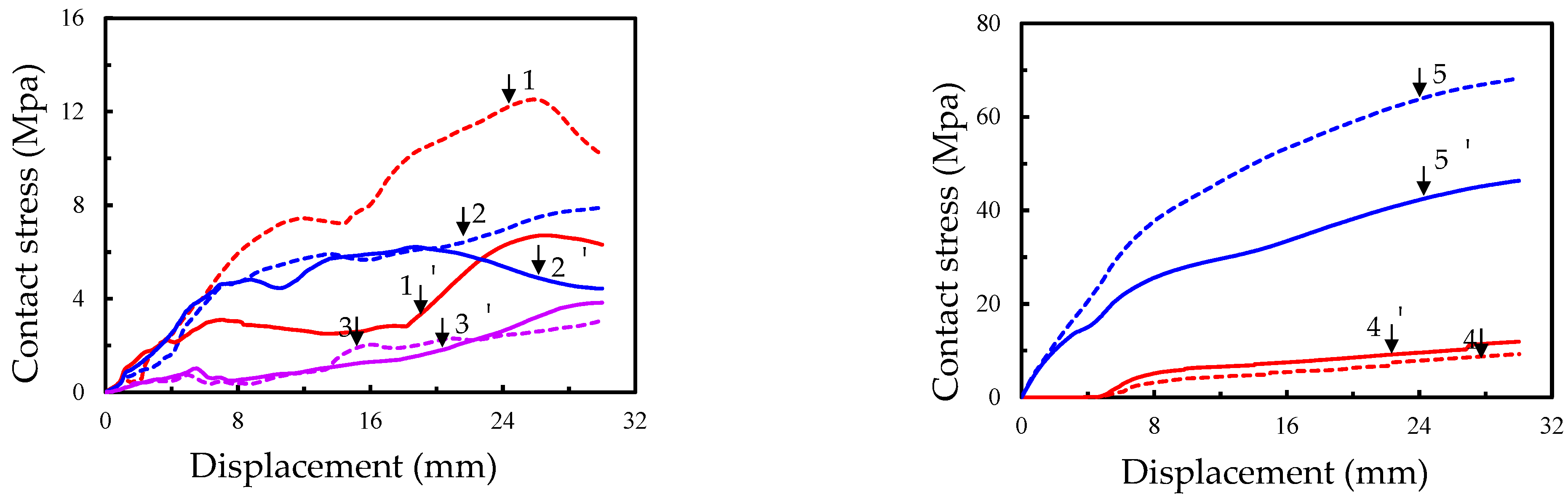
3.2. Load–Displacement Curves
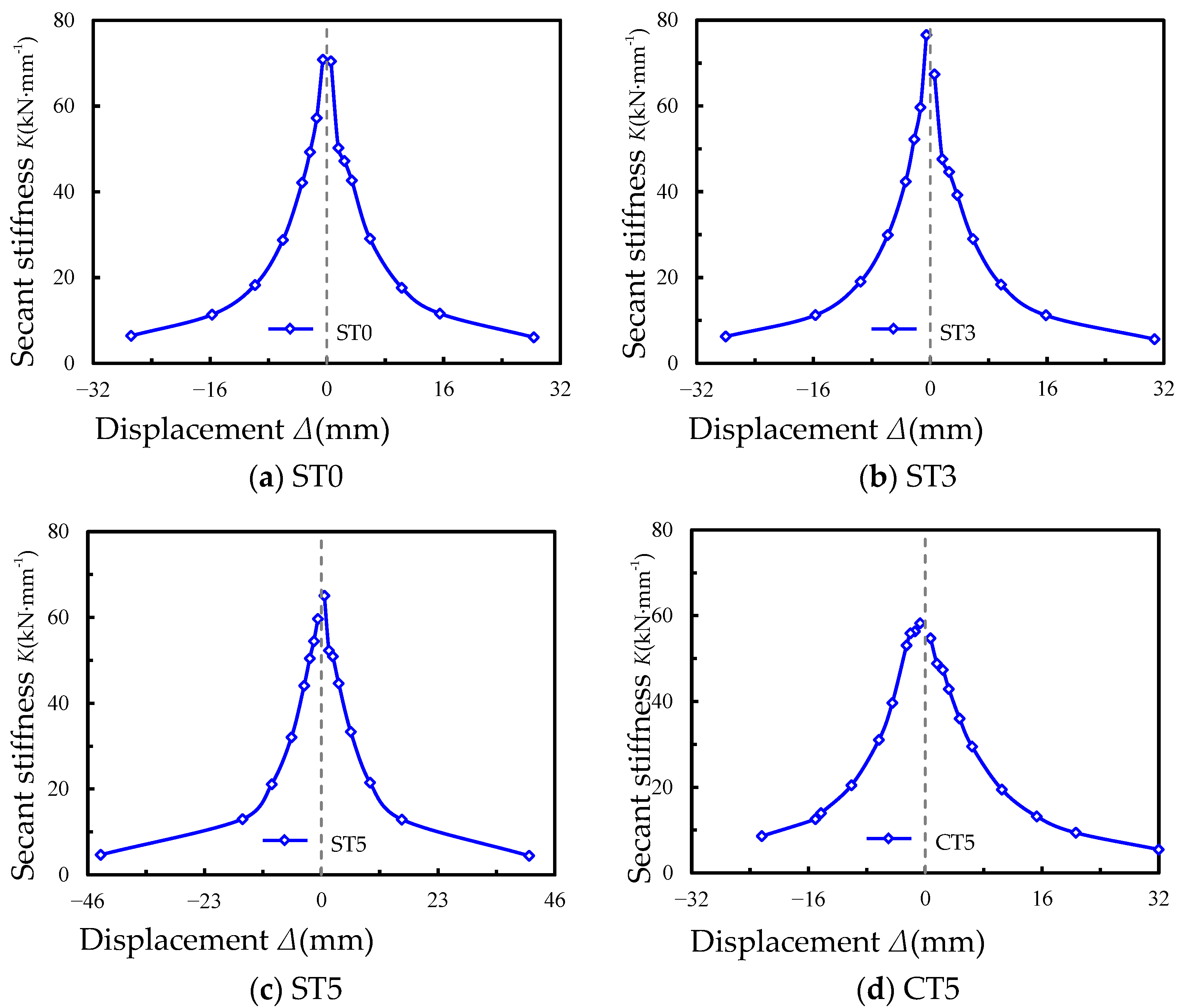
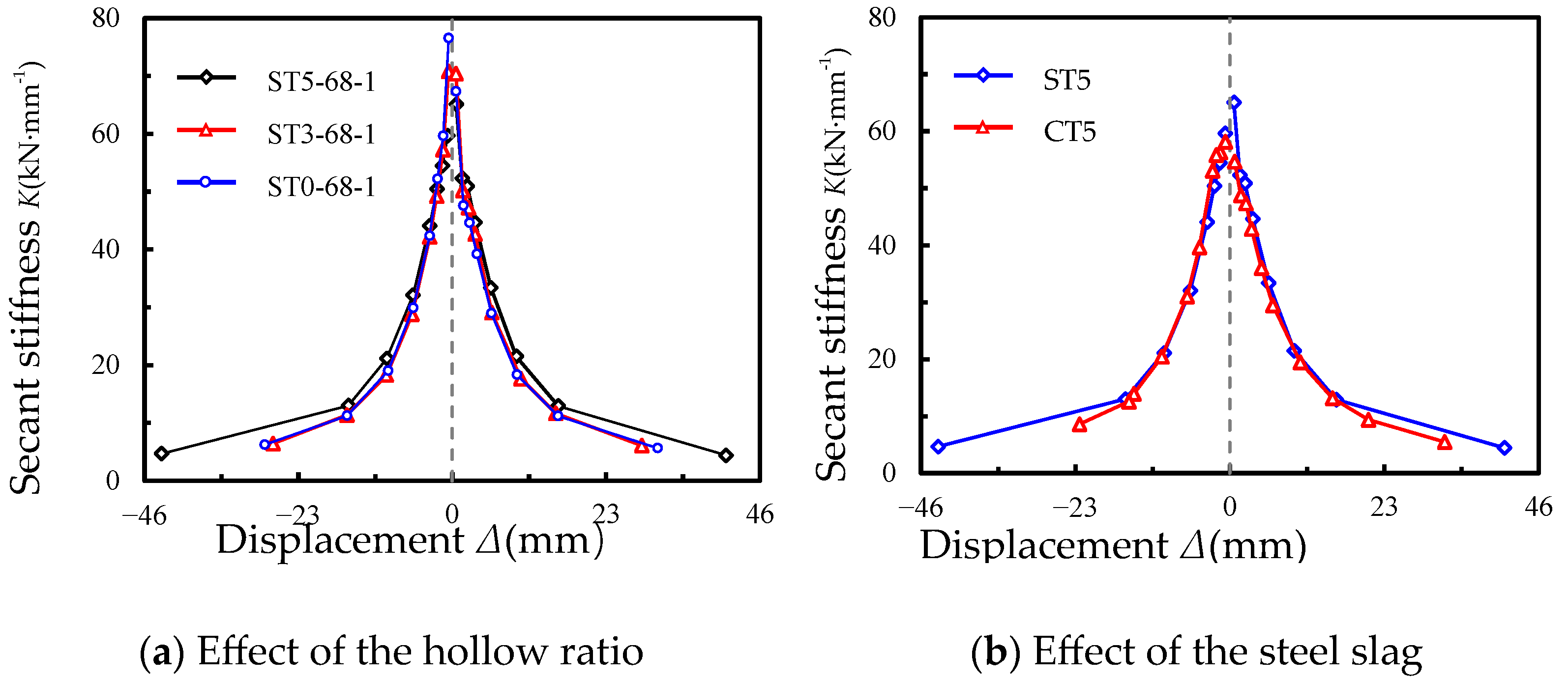
3.3. Stiffness Degradation
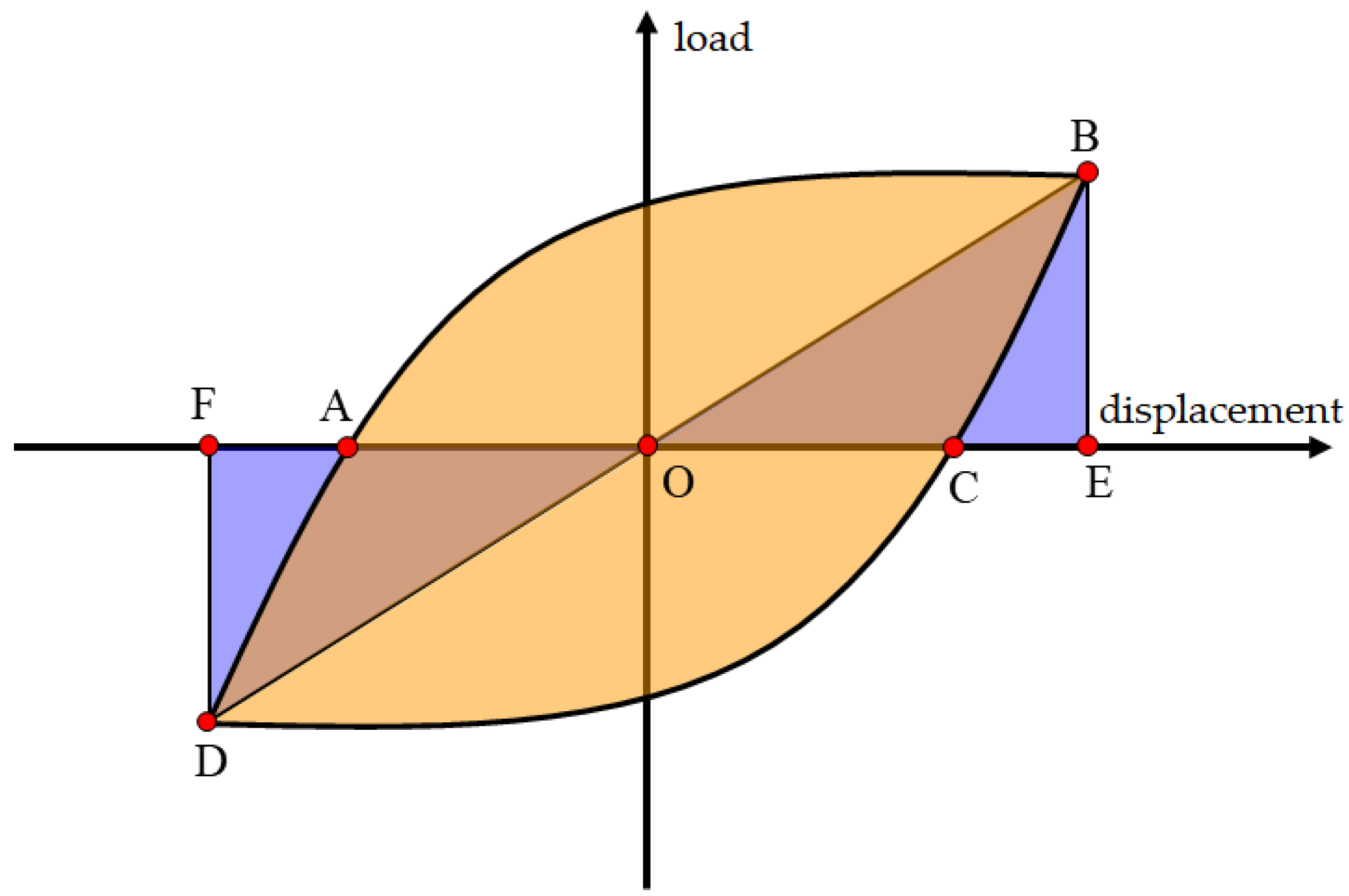
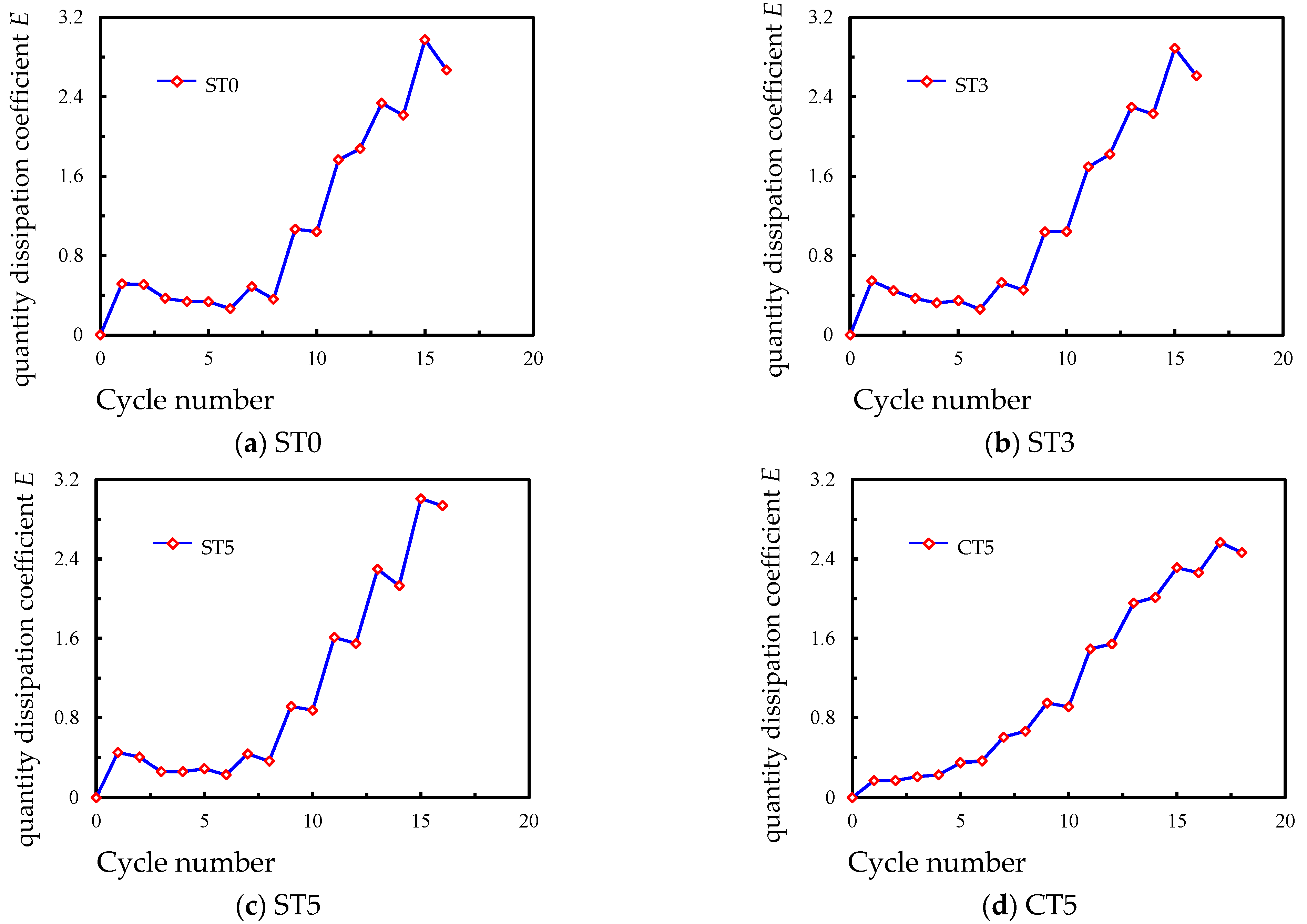
3.4. Energy Dissipation
3.5. Ductility
4. Finite Element Analysis
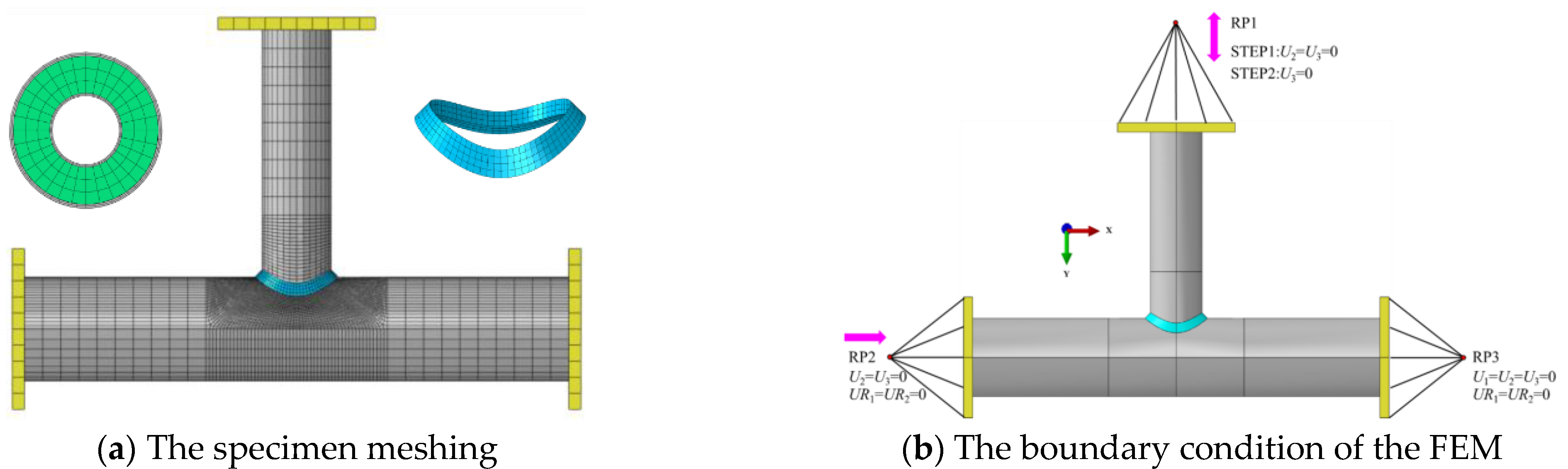
4.1. Finite Element Model
4.2. Verification of the Finite Element Model
4.3. Failure Mechanism Analysis
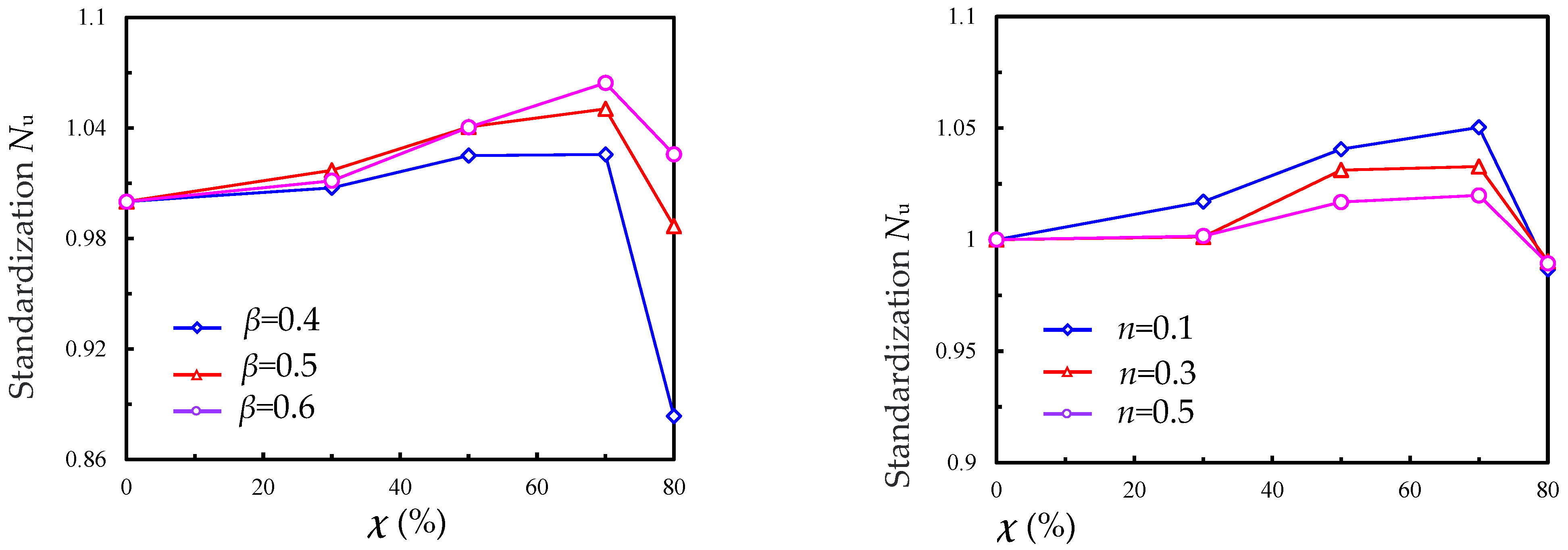
4.4. Parameter Analysis
5. Conclusions
- (1)
- The analysis shows that the ultimate capacity of the specimens could be improved with 54% displacement by filling steel slag concrete with a 0.5 hollow ratio of the CFDST main pipe.
- (2)
- There are two failure modes for the CFDST T-joint specimens, with those being the main pipe fracture and joint area compression-bending failure. The hysteresis curves of all specimens have a full fusiform shape and good energy dissipation capacity.
- (3)
- The steel slag CFDST T-joint provided in this paper that generated the displacement ductility coefficient results is strongly encouraged. The steel slag used in the structure can promote the reuse of solid waste and reduce project costs.
- (4)
- The bearing capacity of CFDST T-joint specimens with different parameters calculated by the finite element models shows that the optimal hollow ratio is 70%. Further research should be conducted on the effect of different parameters, including the strength of materials and so on.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rashad, A. A synopsis manual about recycling steel slag as a cementitious material. J. Mater. Res. Technol. 2019, 8, 4940–4955. [Google Scholar] [CrossRef]
- Song, Q.; Guo, M.Z.; Wang, L.; Ling, T.C. Use of steel slag as sustainable construction materials: A review of accelerated carbonation treatment. Resour. Conserv. Recycl. 2021, 173, 105740. [Google Scholar] [CrossRef]
- Tian, E.; Liu, Y.; Cheng, X.; Zeng, W. Characteristics of Pavement Cement Concrete Incorporating Steel Slag Powder. Adv. Mater. Sci. Eng. 2022, 2022, 6360301. [Google Scholar] [CrossRef]
- Li, L.; Ling, T.C.; Pan, S.Y. Environmental benefit assessment of steel slag utilization and carbonation: A systematic review. Sci. Total Environ. 2022, 806, 150280. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Kang, Q.; Cao, P. Flexural Strength for Negative Bending and Vertical Shear Strength of Composite Steel Slag-Concrete Beams. Adv. Steel Struct. 1999, 1, 385–389. [Google Scholar]
- Qasrawi, H.; Shalabi, F.; Asi, I. Use of low CaO unprocessed steel slag in concrete as fine aggregate. Constr. Build. Mater. 2009, 23, 1118–1125. [Google Scholar] [CrossRef]
- Hai, Y.; Zhan, Q.; Xiao, Y. Optimization of Mineralization Curing System for Efficient and Safe Utilization of Steel Slag Wastes. J. Wuhan Univ. Technol. Mater 2022, 37, 595–602. [Google Scholar]
- Calmon, J. Effects of BOF steel slag and other cementitious materials on the rheological properties of self-compacting cement pastes. Constr. Build. Mater. 2013, 40, 1046–1053. [Google Scholar] [CrossRef]
- Han, L.; Li, W.; Bjorhovde, R. Developments and advanced applications of concrete-filled steel tubular (CFST) structures: Members. J. Constr. Steel Res. 2014, 100, 211–228. [Google Scholar] [CrossRef]
- Han, L.; Lam, D.; Nethercot, D. Design Guide for Concrete-Filled Double Skin Steel Tubular Structures; CRC Press: Boca Raton, FL, USA, 2018; pp. 1–7. [Google Scholar]
- Yang, Y.; Shi, C.; Hou, C. Experimental and numerical study on static behaviour of uniplanar cfdst-chs t-joints. J. Constr. Steel Res. 2020, 173, 106250. [Google Scholar] [CrossRef]
- Li, W.; Cheng, Y.; Wang, D.; Han, L.; Zhao, X. Behaviour of high-strength cfdst chord to chs brace t-joint: Experiment. Eng. Struct. 2020, 219, 110780. [Google Scholar] [CrossRef]
- Wang, D. Fatigue Performance of High-Strength Steel CFDST Chord to CHS Brace T-Joints; Tsinghua University: Beijing, China, 2017. [Google Scholar]
- Gao, D. Experimental Study on Hysteretic Behavior of Concrete-Filled Double Skin Tube Overlapped K-Joints; Ningxia University: Ningxia, China, 2018. [Google Scholar]
- Ma, Y. Static Behavior of Square Concrete-Filled Double-Skin Steel Tube T-Joints; Dalian University of Technology: Dalian, China, 2018. [Google Scholar]
- Shi, C. Static Behavior of Concrete-Filled Double-Skin Steel Tube T-Joints; Dalian University of Technology: Dalian, China, 2019. [Google Scholar]
- Yang, Y.; Bie, X.; Fu, F. Static performance of square CFDST chord to steel SHS brace T-joints. J. Constr. Steel Res. 2021, 183, 1–20. [Google Scholar] [CrossRef]
- Fang, Y.; Yu, F.; Zhang, Y. Mechanical behavior and bearing capacity calculation of self-stressing steel slag aggregate reinforced concrete filled circular steel tube columns. Acta Mater. Compos. Sin. 2020, 37, 1211–1220. [Google Scholar]
- Shen, Q.; Gao, B.; Wang, J. Experimental study on performance of steel slag concrete filled elliptical steel tubular stub columns under axial load. J. Build. Struct. 2021, 42, 197–203. [Google Scholar]
- Yu, F.; Cao, Y.; Fang, Y.; Zhang, Y.; Niu, K. Mechanical behavior of self-stressing steel slag aggregate concrete filled steel tubular short columns with different loading modes. Structures 2020, 26, 947–957. [Google Scholar] [CrossRef]
- Yu, F.; Qin, Y.; Yao, C.; Bu, S.; Fang, Y. Experimental investigation on the seismic behavior of self-stressing steel slag CFST column. Struct. Concr. 2022, 23, 1492–1507. [Google Scholar] [CrossRef]
- GB/T228. 1-2021; Metallic Materials-Tensile Testing-Part 1: Method of Test at Room Temperature. China Standard Press: Beijing, China, 2021.
- JGJ55-2011; Specification for Mix Proportion Design of Ordinary Concrete. Architecture and Building Press: Beijing, China, 2011.
- GB/T 50081-2019; Standard Test Method for Physical and Mechanical Properties of Concrete. China Standard Press: Beijing, China, 2019.
- JGJ/T 101-201; Specification for Seismic Test of Buildings. China Architecture & Building Press: Beijing, China, 2015.
- Han, L. Concrete-Filled Steel Tube Structures—Theory and Practice, 3rd ed.; Science Press: Beijing, China, 2016. [Google Scholar]

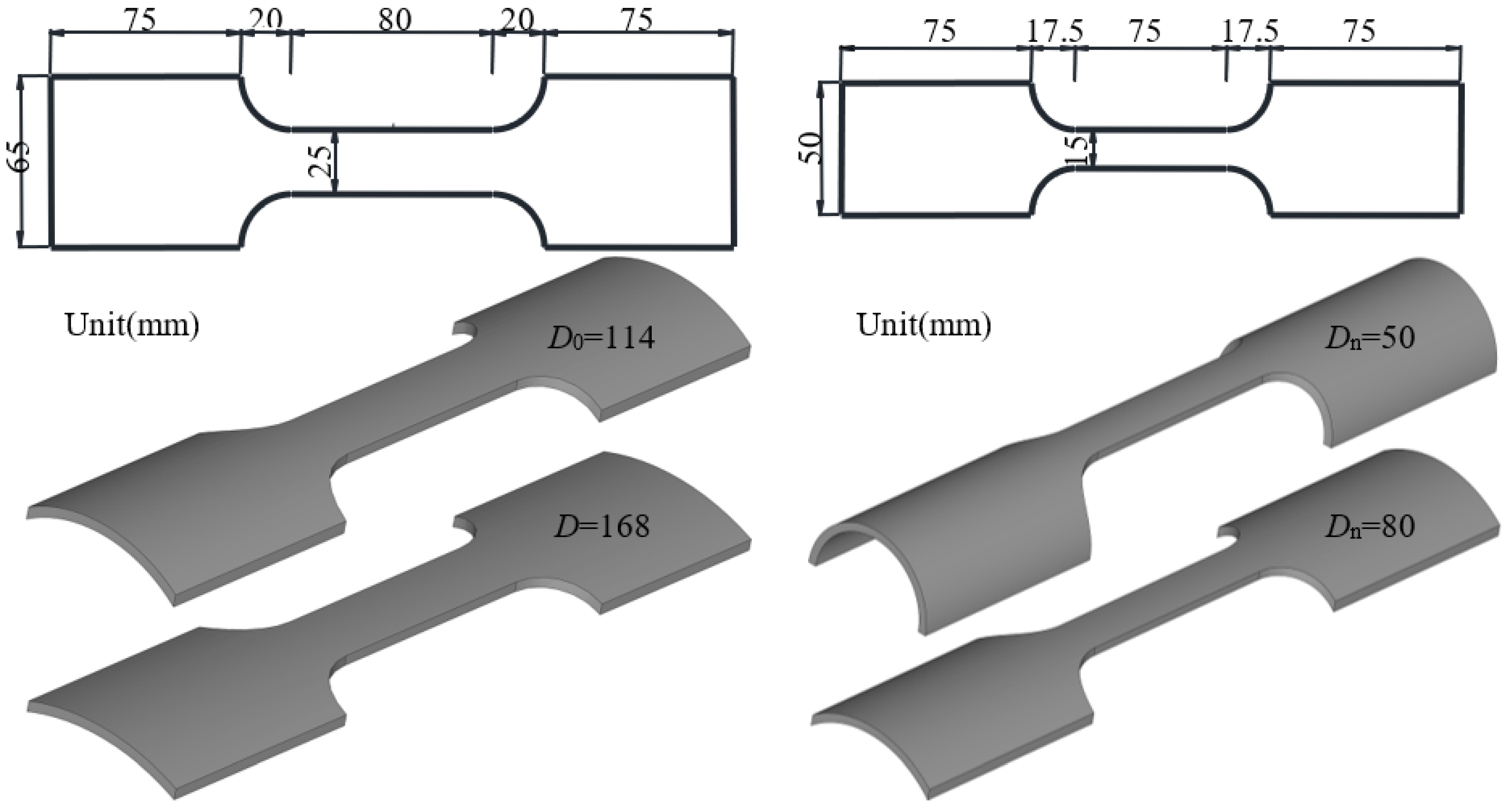

| Number | D × L × T (mm × mm × mm) | Dn × L × Tn (mm × mm × mm) | D0 × L0 × t (mm × mm × mm) | χ (Dn/D) | β (D0/D) | n |
|---|---|---|---|---|---|---|
| ST0 | 168 × 900 × 4 | 0 × 900 × 3 | 114 × 400 × 4 | 0.0 | 0.68 | 0.1 |
| ST3 | 168 × 900 × 4 | 50 × 900 × 3 | 114 × 400 × 4 | 0.3 | 0.68 | 0.1 |
| ST5 | 168 × 900 × 4 | 80 × 900 × 3 | 114 × 400 × 4 | 0.5 | 0.68 | 0.1 |
| CT5 | 168 × 900 × 4 | 80 × 900 × 3 | 114 × 400 × 4 | 0.5 | 0.68 | 0.1 |
| Dimension of Steel Tube D × t (mm × mm) | Yield Strength fy (MPa) | Ultimate Strength fu (MPa) |
|---|---|---|
| 168 × 4 | 280 | 355 |
| 114 × 4 | 328 | 494 |
| 80 × 3 | 283 | 386 |
| 50 × 3 | 372 | 507 |
| Type | CaO | SiO2 | Al2O3 | Fe2O3 | MgO | MnO | P2O5 | SO3 | Na2Oeq | Loss |
|---|---|---|---|---|---|---|---|---|---|---|
| Commercial Portland cement | 56.11 | 23.46 | 7.93 | 3.46 | 3.15 | - | - | 3.49 | 0.72 | 2.31 |
| Steel slag powder | 44.57 | 18.11 | 7.26 | 19.01 | 4.17 | 2.55 | 1.87 | - | 0.29 | 1.38 |
| Type | Water (kg/m3) | Cement (kg/m3) | Steel Slag (kg/m3) | Flyash (kg/m3) | Sand (kg/m3) | Stone (kg/m3) | Superplasticizer (kg/m3) |
|---|---|---|---|---|---|---|---|
| Commercial Portland concrete | 181 | 450 | 0 | 170 | 815 | 815 | 6.3 |
| Steel slag concrete | 181 | 405 | 63 | 153 | 815 | 815 | 6.3 |
| Number | Slump (mm) | Spread (mm) | Ec (GPa) | fcu (MPa) |
|---|---|---|---|---|
| ST0 | 280 | 600–610 | 31.1 | 55.7 |
| ST3 | 280 | 600–610 | 31.1 | 53.7 |
| ST5 | 280 | 600–610 | 31.1 | 55.4 |
| CT5 | 285 | 600–610 | 30.6 | 51.2 |
| Number | Yield Load | Yield Displacement | Ultimate Load | Ultimate Displacement | ||||
|---|---|---|---|---|---|---|---|---|
| Ny+ (kN) | Ny− (kN) | Δy+ (mm) | Δy− (mm) | Nu+ (kN) | Nu− (kN) | Δu+ (mm) | Δu− (mm) | |
| ST0 | 119.2 | −124.7 | 2.57 | −2.75 | 181.2 | −179.8 | 28.3 | −26.8 |
| ST3 | 120.7 | −120.1 | 2.74 | −2.38 | 178.1 | −182.2 | 30.7 | −28.0 |
| ST5 | 144.9 | −144.1 | 3.27 | −3.46 | 206.2 | −206.6 | 40.9 | −43.7 |
| CT5 | 151.2 | −152 | 3.73 | −3.69 | 204.3 | −206.7 | 32.1 | −22.8 |
| Number | Yield Load | Yield Displacement | Ultimate Load | Ultimate Displacement |
|---|---|---|---|---|
| ST0 | 80% | 72% | 88% | 100% |
| ST3 | 79% | 69% | 88% | 107% |
| ST5 | 95% | 91% | 100% | 154% |
| CT5 | 100% | 100% | 100% | 100% |
| Number | Yield Displacement | Ultimate Displacement | Ductility Coefficient | |||
|---|---|---|---|---|---|---|
| Δy+ (mm) | Δy− (mm) | Δu+ (mm) | Δu− (mm) | μ+ | μ− | |
| ST0 | 2.57 | −2.75 | 28.3 | −26.8 | 11.01 | 9.75 |
| ST3 | 2.74 | −2.38 | 30.7 | −28.0 | 11.20 | 11.76 |
| ST5 | 3.27 | −3.46 | 40.9 | −43.7 | 12.51 | 12.63 |
| CT5 | 3.73 | −3.69 | 32.1 | −22.8 | 8.61 | 6.18 |
| Parameter | D × T × L (mm × mm × mm) | D0 × T0 × L0 (mm × mm × mm) | n | β | χ (%) | Nu (KN) |
|---|---|---|---|---|---|---|
| Benchmark | 300 × 6 × 2000 | 150 × 4 × 400 | 0.1 | 0.5 | 0 | 500.8 |
| 300 × 6 ×2000 | 150 × 4 × 400 | 0.1 | 0.5 | 30 | 509.3 | |
| 300 × 6 ×2000 | 150 × 4 × 400 | 0.1 | 0.5 | 50 | 521.1 | |
| 300 × 6 ×2000 | 150 × 4 × 400 | 0.1 | 0.5 | 70 | 526.0 | |
| 300 × 6 ×2000 | 150 × 4 × 400 | 0.1 | 0.5 | 80 | 494.1 | |
| β | 300 × 6 × 2000 | 120 × 4 × 400 | 0.1 | 0.4 | 0 | 495.7 |
| 300 ×6 × 2000 | 120 × 4 × 400 | 0.1 | 0.4 | 30 | 499.4 | |
| 300 × 6 ×2000 | 120 × 4 × 400 | 0.1 | 0.4 | 50 | 508.1 | |
| 300 × 6 × 2000 | 120 × 4 × 400 | 0.1 | 0.4 | 70 | 508.4 | |
| 300 × 6 × 2000 | 120 × 4 × 400 | 0.1 | 0.4 | 80 | 438 | |
| 300 × 6 × 2000 | 180 × 4 × 400 | 0.1 | 0.6 | 0 | 503.1 | |
| 300 × 6 × 2000 | 180 × 4 × 400 | 0.1 | 0.6 | 30 | 508.8 | |
| 300 × 6 × 2000 | 180 × 4 × 400 | 0.1 | 0.6 | 50 | 523.4 | |
| 300 × 6 × 2000 | 180 × 4 × 400 | 0.1 | 0.6 | 70 | 535.5 | |
| 300 × 6 × 2000 | 180 × 4 × 400 | 0.1 | 0.6 | 80 | 516.0 | |
| n | 300 × 6 × 2000 | 150 × 4 × 400 | 0.3 | 0.5 | 0 | 500.7 |
| 300 × 6 × 2000 | 150 × 4 × 400 | 0.3 | 0.5 | 30 | 501.3 | |
| 300 × 6 × 2000 | 150 × 4 × 400 | 0.3 | 0.5 | 50 | 516.3 | |
| 300 ×6 × 2000 | 150 × 4 × 400 | 0.3 | 0.5 | 70 | 517.1 | |
| 300 × 6 × 2000 | 150 × 4 × 400 | 0.3 | 0.5 | 80 | 495.8 | |
| 300 × 6 × 2000 | 150 × 4 × 400 | 0.5 | 0.5 | 0 | 499.1 | |
| 300 × 6 × 2000 | 150 × 4 × 400 | 0.5 | 0.5 | 30 | 499.9 | |
| 300 × 6 × 2000 | 150 × 4 × 400 | 0.5 | 0.5 | 50 | 507.5 | |
| 300 × 6 × 2000 | 150 × 4 × 400 | 0.5 | 0.5 | 70 | 509.0 | |
| 300 × 6 × 2000 | 150 × 4 × 400 | 0.5 | 0.5 | 80 | 493.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, W.; Fu, M.; Lian, Y.; Zhong, H.; Wang, W. Experimental Study on the Seismic Performance of a Steel Slag CFDST T-Joint. Sustainability 2023, 15, 7991. https://doi.org/10.3390/su15107991
Zeng W, Fu M, Lian Y, Zhong H, Wang W. Experimental Study on the Seismic Performance of a Steel Slag CFDST T-Joint. Sustainability. 2023; 15(10):7991. https://doi.org/10.3390/su15107991
Chicago/Turabian StyleZeng, Wuhua, Mingliang Fu, Yuezong Lian, Hai Zhong, and Wei Wang. 2023. "Experimental Study on the Seismic Performance of a Steel Slag CFDST T-Joint" Sustainability 15, no. 10: 7991. https://doi.org/10.3390/su15107991
APA StyleZeng, W., Fu, M., Lian, Y., Zhong, H., & Wang, W. (2023). Experimental Study on the Seismic Performance of a Steel Slag CFDST T-Joint. Sustainability, 15(10), 7991. https://doi.org/10.3390/su15107991







