Cross-Scale Analysis on the Working Performance of Micropile Group and Talus Slope System
Abstract
:1. Introduction
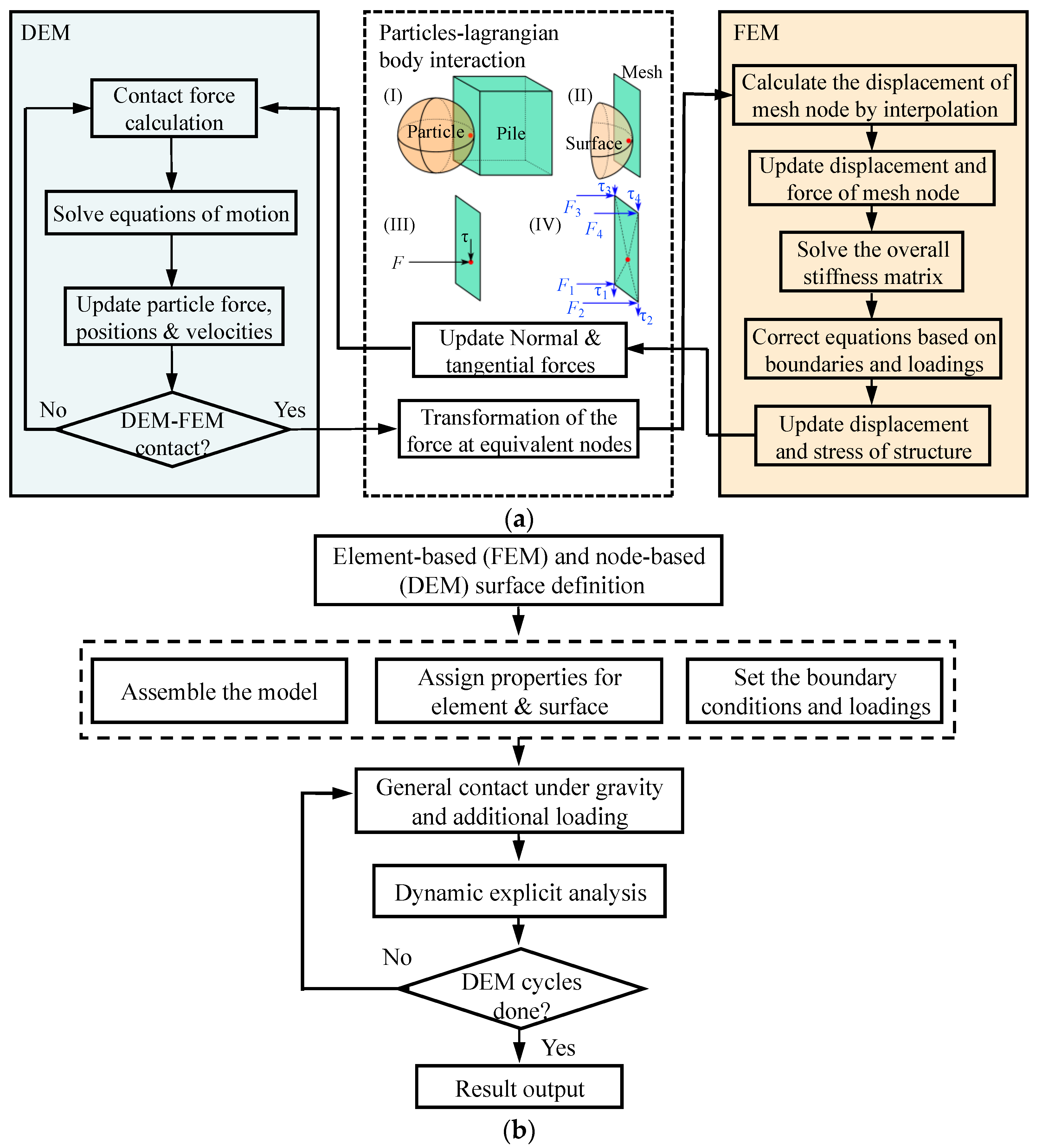
2. Cross-Scale Analysis Based on Coupled DEM-FEM Method
2.1. Discrete Element Model
2.2. MPG-Soil Interaction Modelling
2.3. Cross-Scale Analysis Based on Coupled DEM-FEM Method
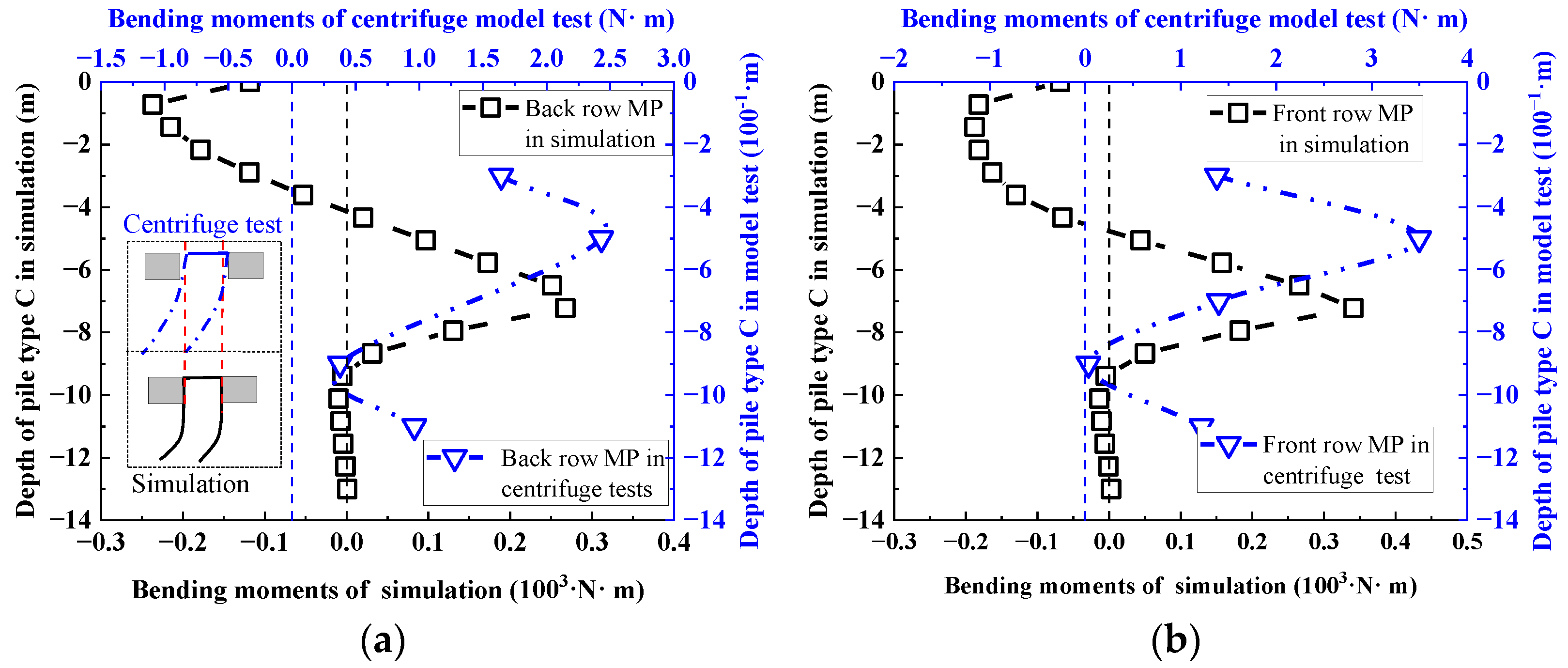
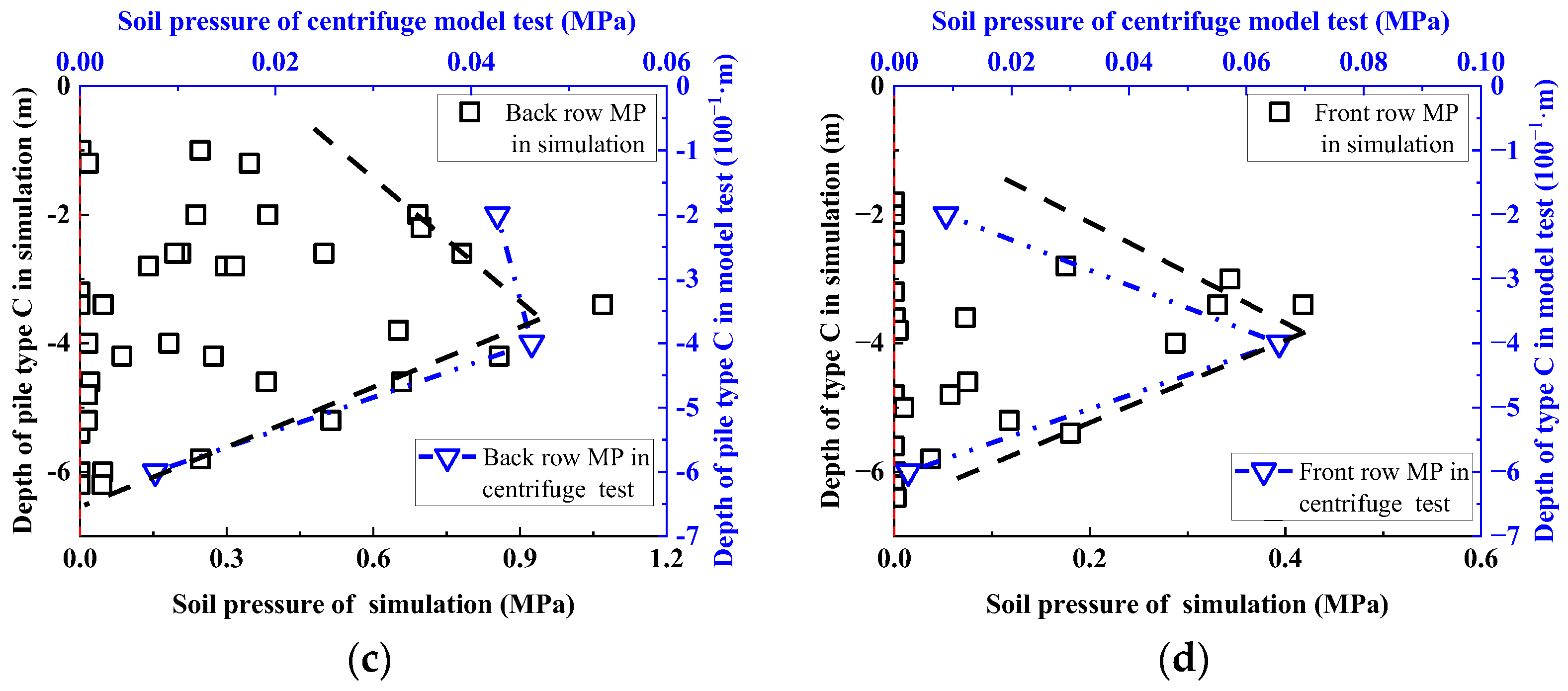
3. Validation of the Cross-Scale Analysis Based on the Coupled DEM-FEM Method
3.1. Example of the Talus Slope with Micropiles
3.2. Numerical Simulation Settings
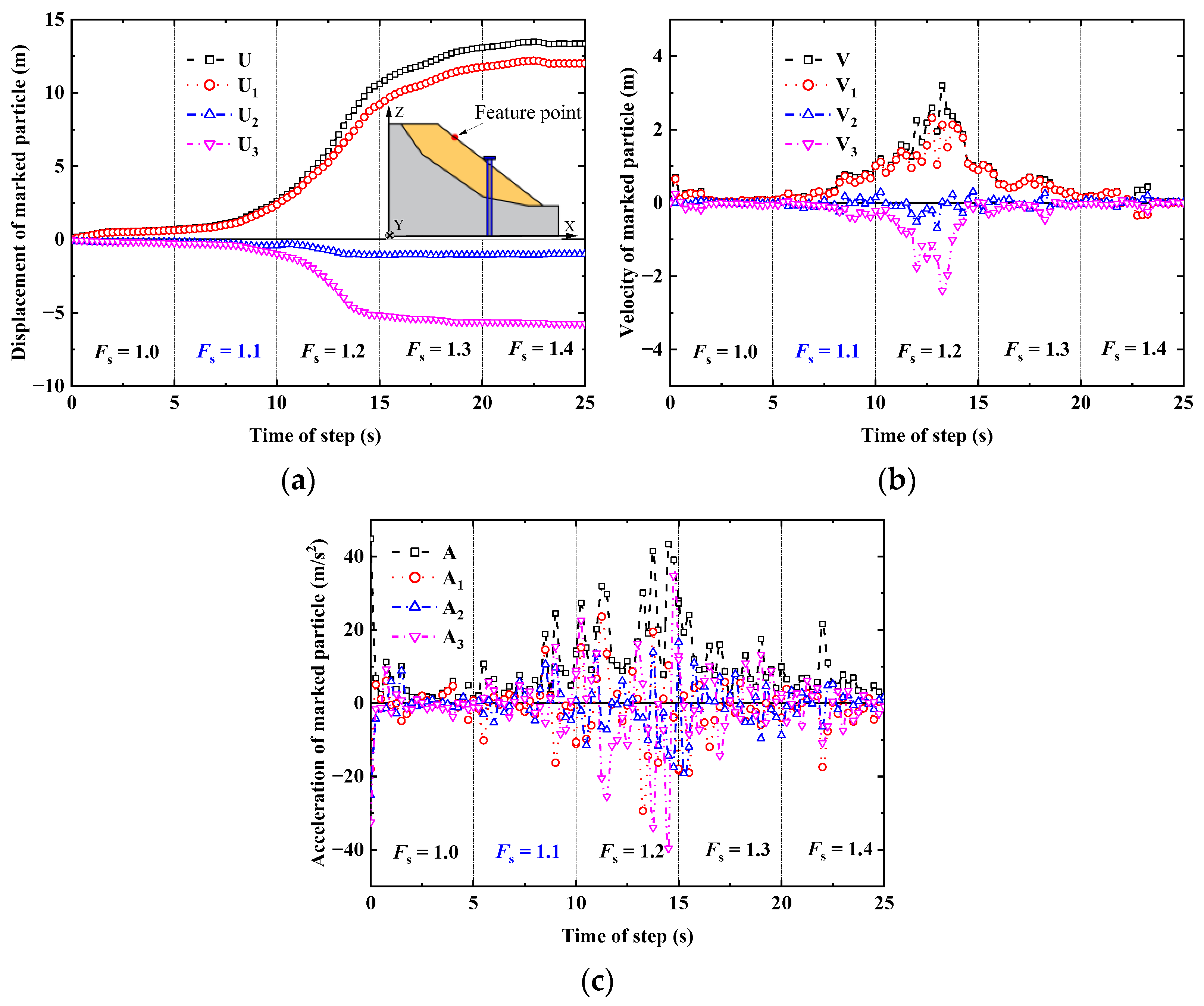
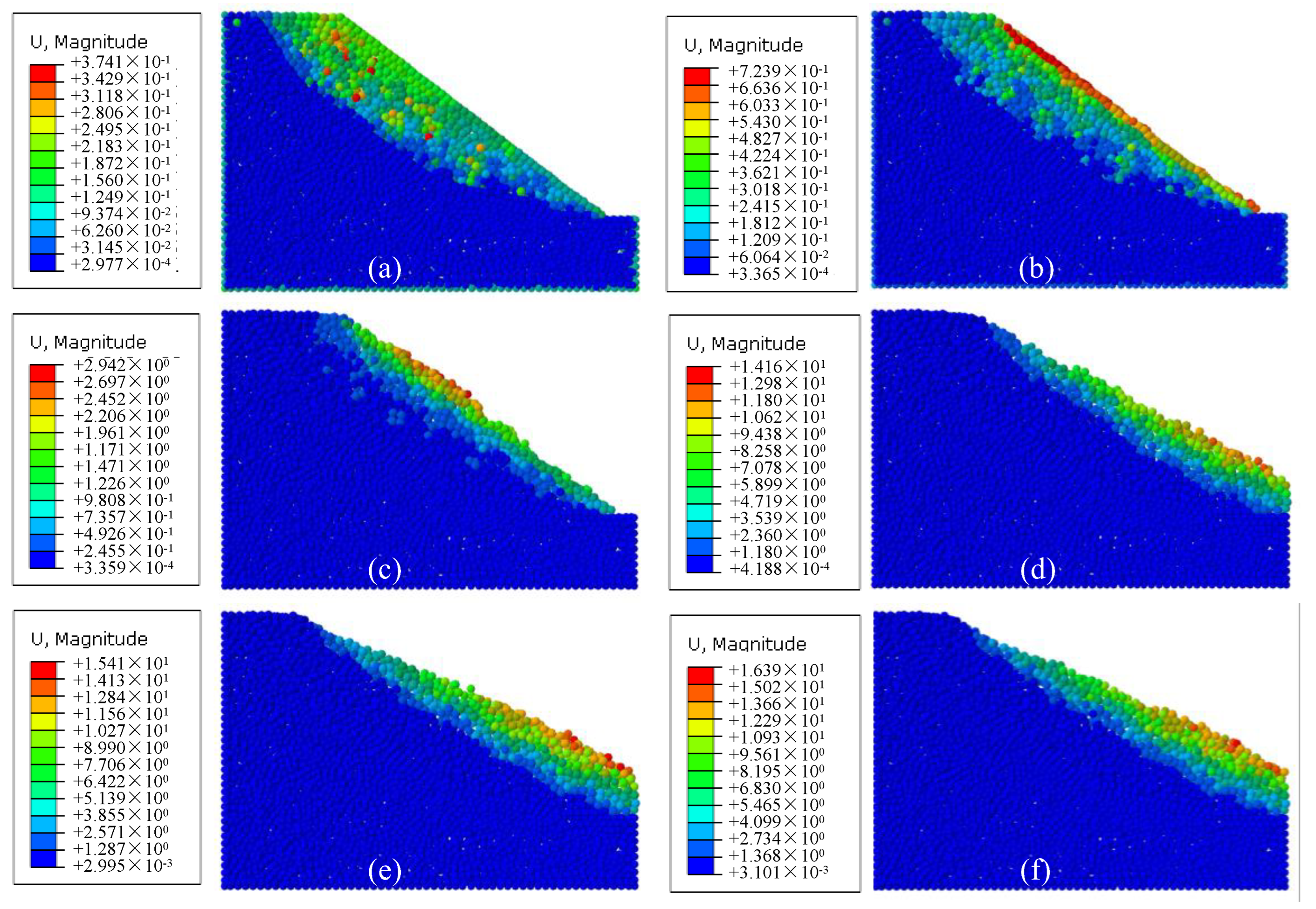
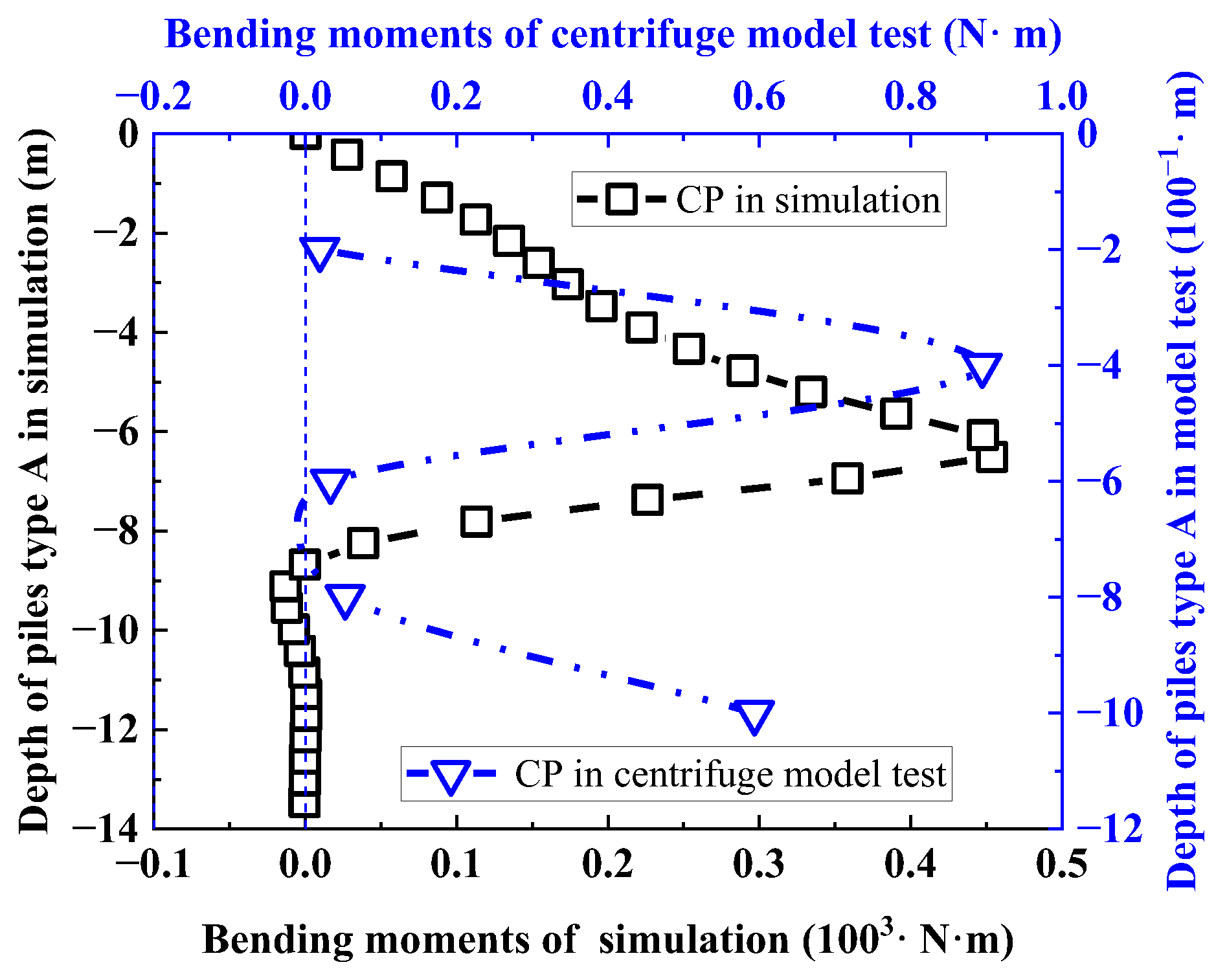
3.3. Validation of the Numerical Simulation
3.3.1. Calibration of Contact Parameters Adopted in Cross-Scale Analysis
3.3.2. Talus Slope Reinforced by Pile Type A
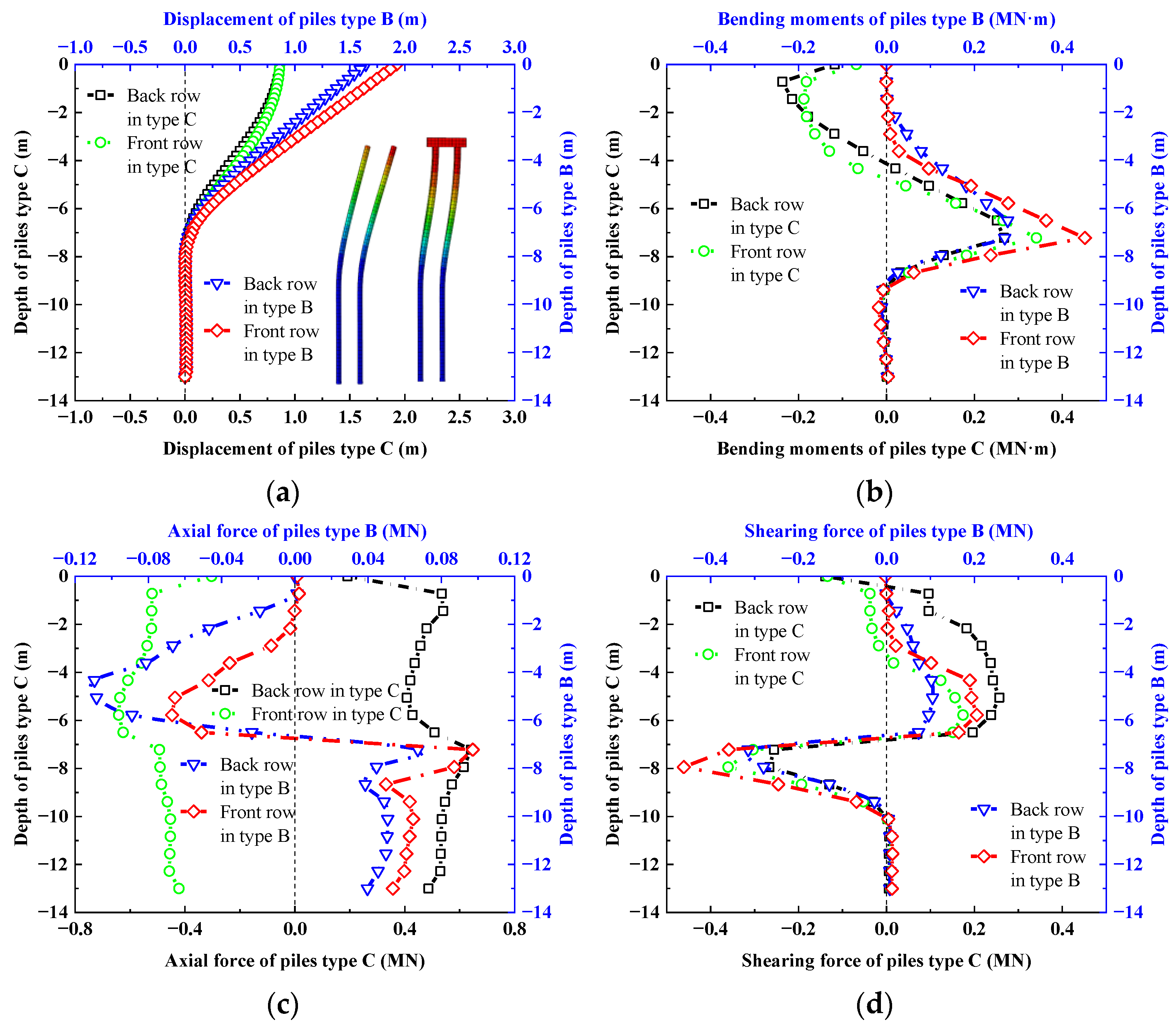
3.3.3. Talus Slope Reinforced by Pile Type B
3.3.4. Talus Slope Reinforced by Pile Type C
4. Performance of MPGs under Various Conditions
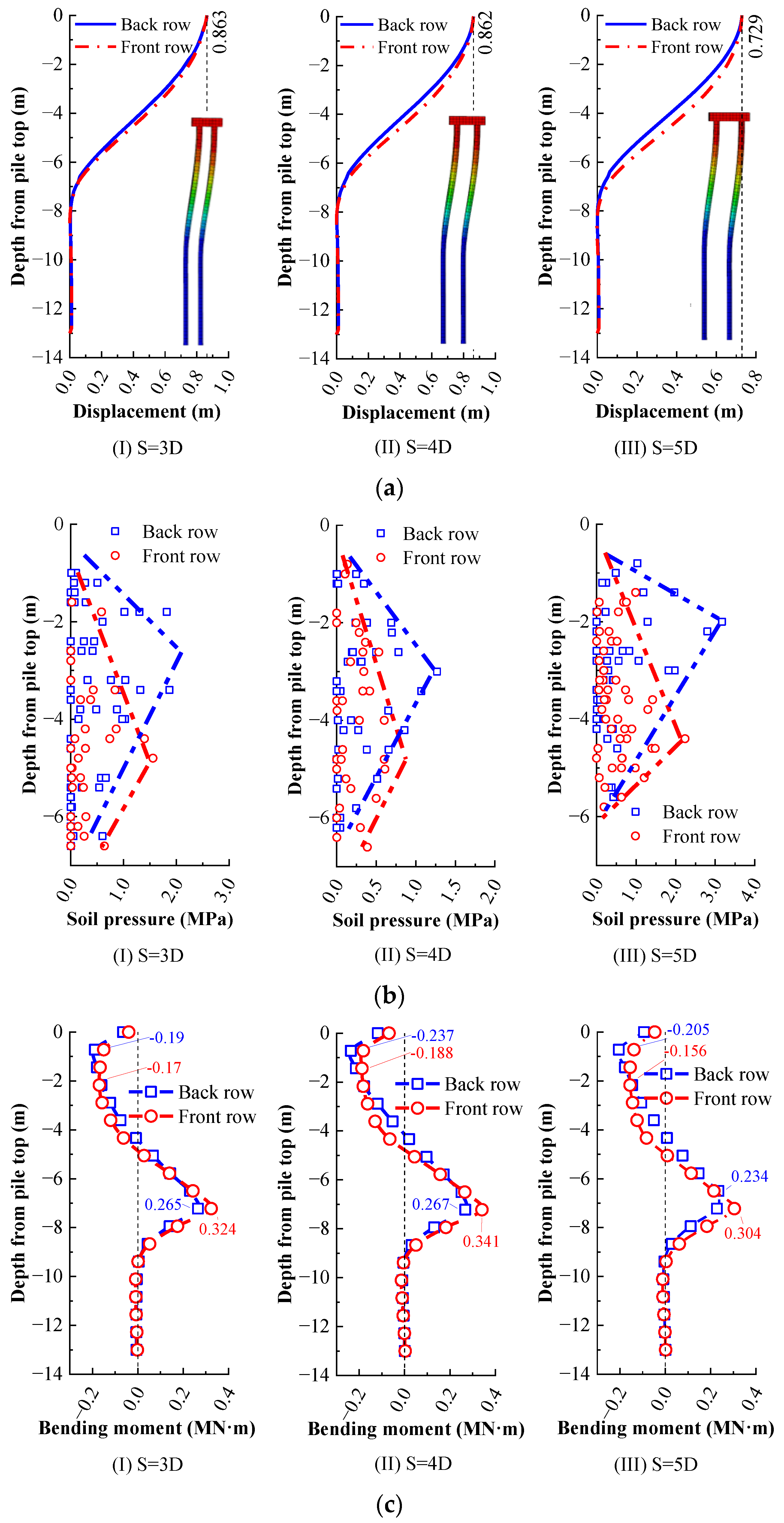
4.1. Performance of MPGs with Different Pile Spacing
4.1.1. Displacement Distribution for MPGs
4.1.2. Soil Pressure Distribution for MPGs
4.1.3. Bending Moment Distribution for MPGs
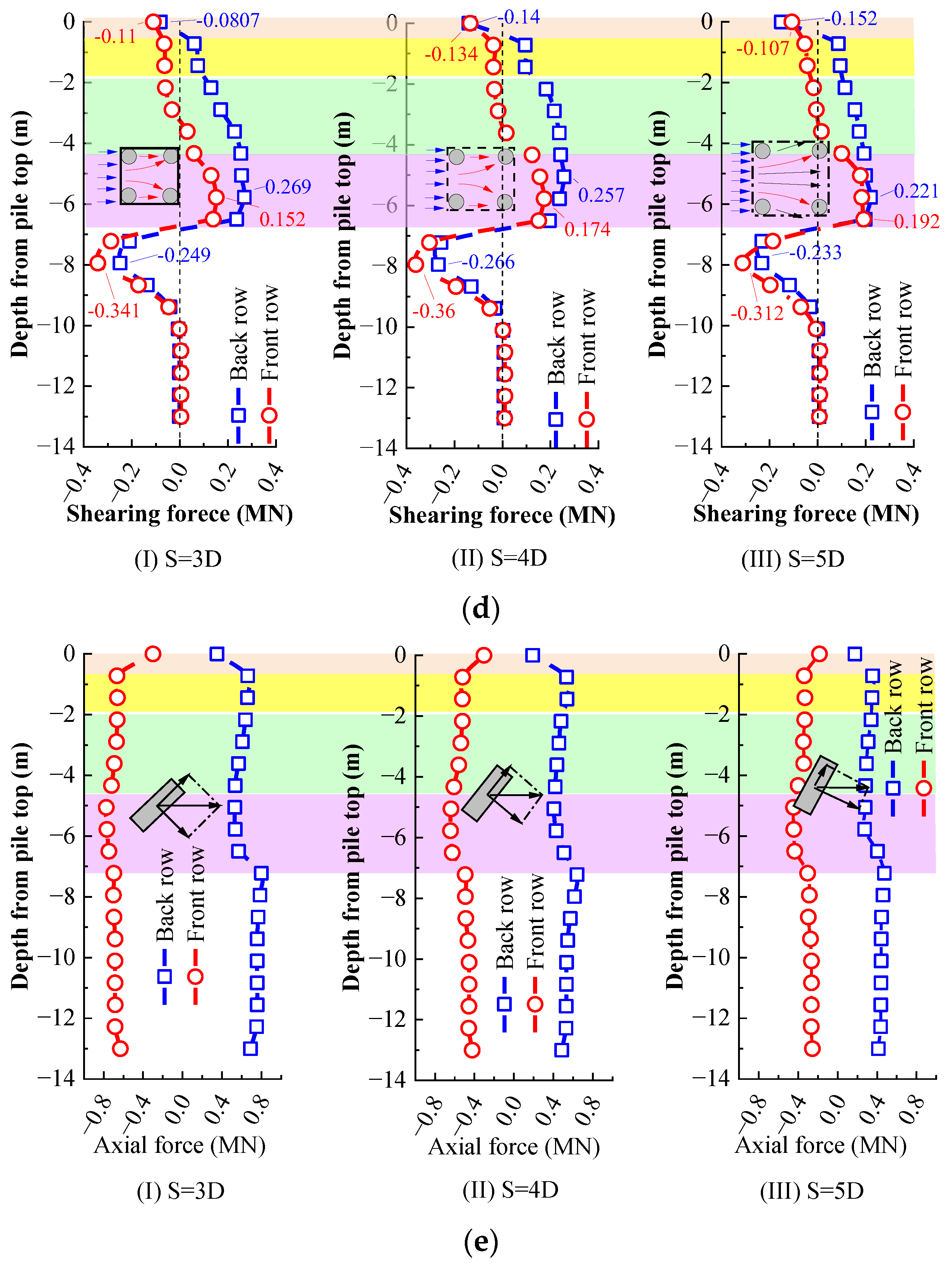
4.1.4. Shearing Force Distribution for MPGs
4.1.5. Axial Force Distribution for MPGs
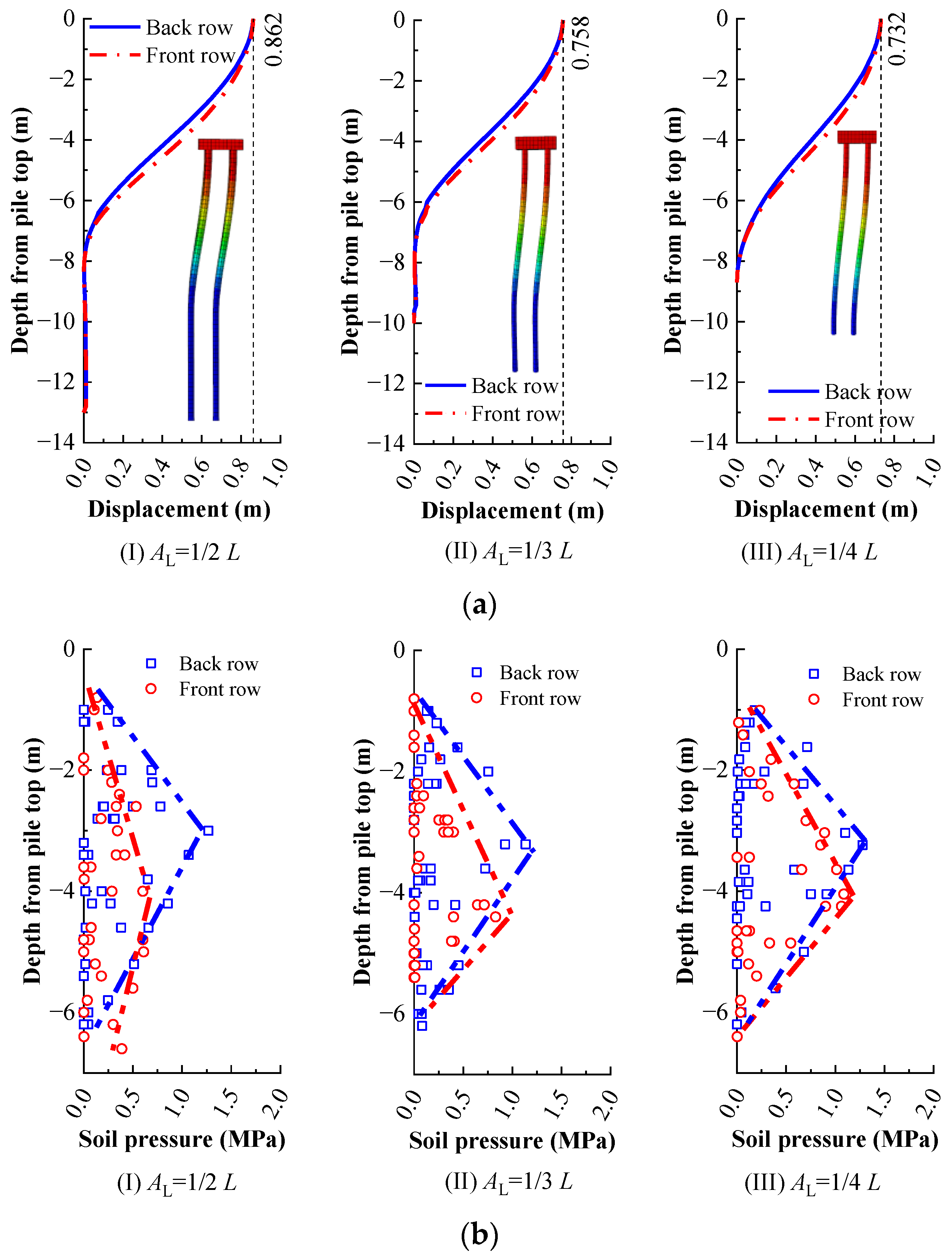
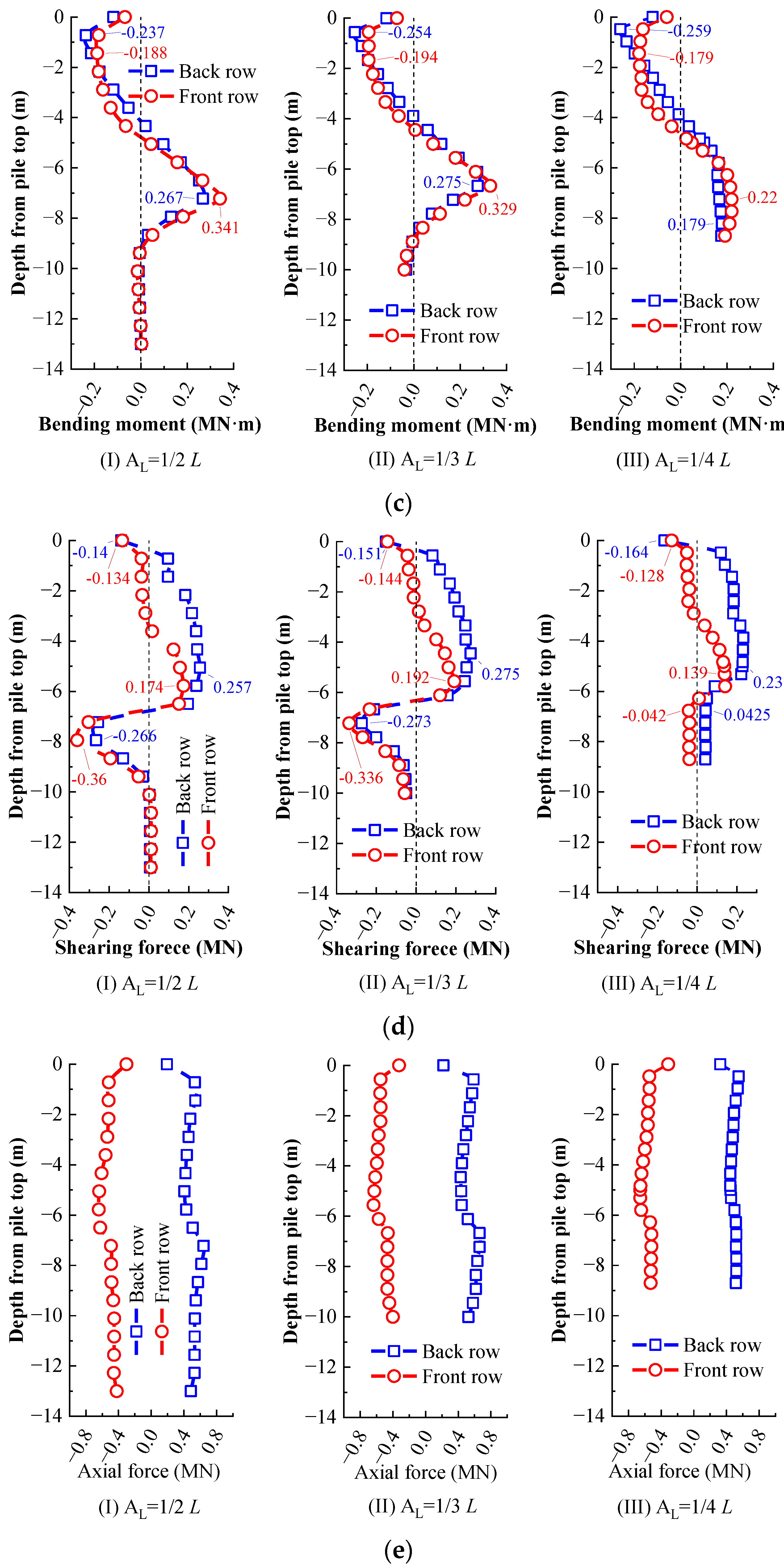
4.2. Performance of MPGs with Different Anchorage Lengths
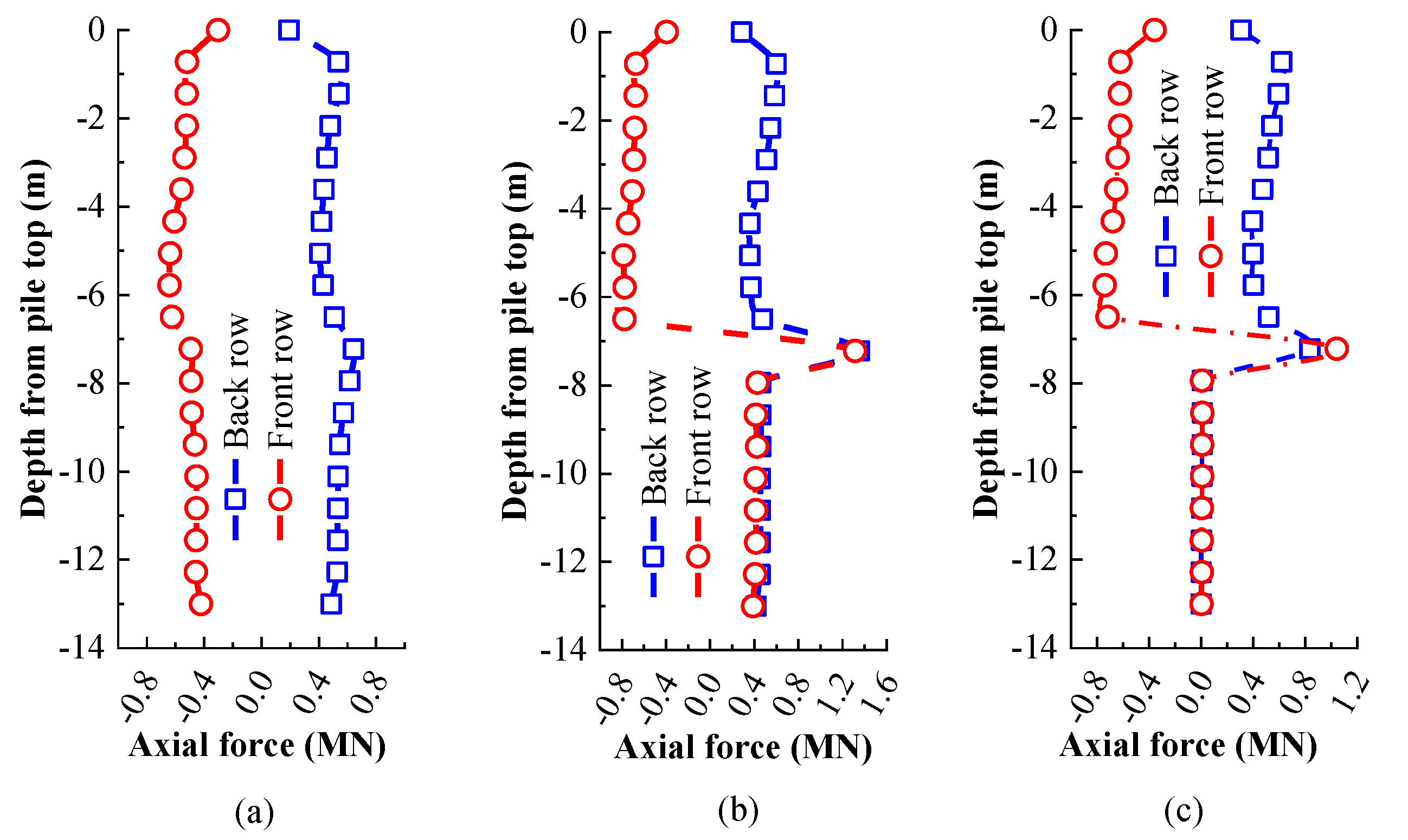
4.3. Performance of MPGs with Different Pile Bottom Constraints and Contact Mode
5. Discussions
5.1. Anti-Slip Mechanism of the MPG
5.2. Limitations and Further Works
6. Conclusions
- (1)
- The coupled numerical method can reproduce the results of the centrifuge model tests, indicating the applicability of the presented DEM-FEM coupling method in large deformation problems.
- (2)
- The forces and deformations of MPG with different pile spacing are essentially the same in the numerical simulations, i.e., the tensile S-shaped deformation and the opposite directional axial force in the front and back row piles within the anti-slip section. The MPG with a spacing of 4D, in particular, exhibits the best performance.
- (3)
- The effective anchorage length of the MPG needs to exceed 1/3 of the pile length. The end constraints of the pile bottom and the tangential pile–bedrock contact significantly affect the distribution of the internal forces in the piles, which cannot be ignored in the design of the MPG.
- (4)
- The anti-slip mechanism of the MPG with a platform is mainly attributed to the bidirectional anchoring effect of the bedrock and the platform, which allows the MPG to have a smaller displacement at the comparable stress level, contributing to a more integral pile–soil composite with a better anti-slip performance.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, X.Z.; Kong, J.M. Types and characteristics of typical landslides triggered by “5.12” Wenchuan Earthquake. J. Mt. Sci. 2011, 29, 598–607. (In Chinese) [Google Scholar]
- Zhi-liang, S.; Ling-wei, K.; Ai-guo, G.; Hai, T. Surface deformation and failure mechanisms of deposit slope under seismic excitation. Rock Soil Mech. 2015, 36, 3465–3472+3481. (In Chinese) [Google Scholar]
- Ding, P.P.; Yang, Z.Z.; Qiao, J.P.; Chen, X.Q.; Nie, Y.; Zhang, W.F. Fractal characteristic analysis on slope disasters along the KKH of China-Pakistan Economic Corridor. China Sci. 2018, 13, 1685–1689. (In Chinese) [Google Scholar]
- Kumar, J.S.; Nusari, M.S.; Purushotam, D.; Prasad, A.I.; Rajyaswori, S. Effectiveness of geocell wall, geogrid and micropile anchors for mitigation of unstable slopes. Geoenviron. Disasters 2021, 8, 11. [Google Scholar] [CrossRef]
- Jang, Y.-E.; Han, J.-T. Analysis of the shape effect on the axial performance of a waveform micropile by centrifuge model tests. Acta Geotech. 2018, 14, 505–518. [Google Scholar] [CrossRef]
- Guan, W.; Wu, H.; Wu, D.; Tang, L.; Wei, H. Study on Interaction Mechanism of Natural Gas Pipe-Landslide System Reinforced by Micropile Groups Based on Model Test. Geofluids 2022, 2022, 8436297. [Google Scholar] [CrossRef]
- Wang, R.H.; Zhou, H.Q.; Peng, G.Y. Discrete Element Simulation Analysis of Sudden Instability of Stacked Slope. J. Ordnance Equip. Eng. 2018, 39, 192–196. (In Chinese) [Google Scholar]
- Gupta, R.K.; Chawla, S. Finite element analysis of micropile reinforced subgrade in railway tracks. Lect. Notes Civ. Eng. 2020, 85, 751–761. [Google Scholar] [CrossRef]
- Ghorbani, A.; Hasanzadehshooiili, H.; Ghamari, E. 3D finite element analysis of seismic soil-micropile-structure interaction. In Advances in Civil Engineering and Building Materials; CRC Press: Boca Raton, FL, USA, 2012; pp. 265–269. [Google Scholar]
- Ghorbani, A.; Hasanzadehshooiili, H.; Ghamari, E.; Medzvieckas, J. Comprehensive three dimensional finite element analysis, parametric study and sensitivity analysis on the seismic performance of soil–micropile-superstructure interaction. Soil Dyn. Earthq. Eng. 2014, 58, 21–36. [Google Scholar] [CrossRef]
- Elaziz, A.Y.A.; El Naggar, M.H. Group behaviour of hollow-bar micropiles in cohesive soils. Can. Geotech. J. 2014, 51, 1139–1150. [Google Scholar] [CrossRef]
- Alnuaim, A.M.; El Naggar, M.H.; El Naggar, H. Numerical investigation of the performance of micropiled rafts in sand. Comput. Geotech. 2016, 77, 91–105. [Google Scholar] [CrossRef]
- Wang, Z.; Mei, G. Numerical Analysis of Seismic Performance of Embankment Supported by Micropiles. Mar. Georesour. Geotechnol. 2012, 30, 52–62. [Google Scholar] [CrossRef]
- Zeng, J.; Xiao, S. A Simplified Analytical Method for Stabilizing Micropile Groups in Slope Engineering. Int. J. Civ. Eng. 2020, 18, 199–214. [Google Scholar] [CrossRef]
- Wang, W.; Yin, Y.; Li, D.; Meng, M.; Luo, G.; Zhang, Z. Numerical Simulation Study of the Load Sharing of an Arched Micropile Group in the Tizicao High-Position Landslide, China. IOP Conf. Ser. Earth Environ. Sci. 2020, 570, 62001. [Google Scholar] [CrossRef]
- Sun, S.W.; Zhu, B.Z. Numerical simulation study of the ultimate resistance of micropiles in earth slope stabilization. J. Railw. Eng. Soc. 2018, 35, 1–5+83. (In Chinese) [Google Scholar]
- Hussain, Z.; Sharma, B.; Rahman, T. Micropile group behaviour subjected to lateral loading. Innov. Infrastruct. Solut. 2019, 4, 22. [Google Scholar] [CrossRef]
- Alnuaim, A.; El Naggar, M. Performance of micropiled rafts in clay: Numerical investigation. Comput. Geotech. 2018, 99, 42–54. [Google Scholar] [CrossRef]
- Hassan, S.; El Shamy, U. DEM simulations of the seismic response of granular slopes. Comput. Geotech. 2019, 112, 230–244. [Google Scholar] [CrossRef]
- Pei, Z.-W.; Zhang, Y.-J.; Nian, T.-K.; Song, X.-L.; Zhao, W. Performance investigation of micropile groups in stabilizing unstable talus slopes via centrifuge model tests. Can. Geotech. J. 2023, 60, 3. [Google Scholar] [CrossRef]
- Ma, Z.; Shirvan, K.; Wu, Y.; Su, G. A three-dimensional axial fuel relocation framework with discrete element method to support burnup extension. J. Nucl. Mater. 2020, 541, 152408. [Google Scholar] [CrossRef]
- Chen, X.; Elliott, J.A. On the scaling law of JKR contact model for coarse-grained cohesive particles. Chem. Eng. Sci. 2020, 227, 115906. [Google Scholar] [CrossRef]
- Li, D.; Nian, T.; Wu, H.; Wang, F.; Zheng, L. A predictive model for the geometry of landslide dams in V-shaped valleys. Bull. Eng. Geol. Environ. 2020, 79, 4595–4608. [Google Scholar] [CrossRef]
- Nian, T.; Li, D.; Liang, Q.; Wu, H.; Guo, X. Multi-phase flow simulation of landslide dam formation process based on extended coupled DEM-CFD method. Comput. Geotech. 2021, 140, 104438. [Google Scholar] [CrossRef]
- Jiang, M.; Murakami, A. Distinct element method analyses of idealized bonded-granulate cut slope. Granul. Matter 2012, 14, 393–410. [Google Scholar] [CrossRef]
- Liu, H.S.; Wang, G.L.; Bao, J.S. Report of Landslide of Beihou Mountain in Hanyuan County in Wenchuan 8.0 Magnitude Earthquake; Institute of Engineering Mechanics, China Earthquake Administration: Harbin, China, 2008. (In Chinese) [Google Scholar]
- Pissinatti, C.; Poncetti, B.L.; Buchaim, R.; Vanderlei, R.D. The influence of the reinforced concrete deformability in the design of slender columns. Eng. Struct. 2021, 245, 112882. [Google Scholar] [CrossRef]
- Nian, T.K.; Chen, G.Q.; Luan, M.T.; Yang, Q.; Zheng, D.F. Limit analysis of the stability of slopes reinforced with piles against landslide in nonhomogeneous and anisotropic soils. Can. Geotech. J. 2008, 45, 1092–1103. [Google Scholar] [CrossRef]
- Fang, K.; Tang, H.; Li, C.; Su, X.; An, P.; Sun, S. Centrifuge modelling of landslides and landslide hazard mitigation: A review. Geosci. Front. 2023, 14, 101493. [Google Scholar] [CrossRef]
- Chen, M.-L.; Lv, P.-F.; Zhang, S.-L.; Chen, X.-Z.; Zhou, J.-W. Time evolution and spatial accumulation of progressive failure for Xinhua slope in the Dagangshan reservoir, Southwest China. Landslides 2018, 15, 565–580. [Google Scholar] [CrossRef]
- Wu, H.; Nian, T.-K.; Shan, Z.-G.; Li, D.-Y.; Guo, X.-S.; Jiang, X.-G. Rapid prediction models for 3D geometry of landslide dam considering the damming process. J. Mt. Sci. 2023, 20, 928–942. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, J.Q.; Zeng, Y.; Jia, M. Slope safety factor by methods of particle flow code strength reduction and gravity increase. Rock Soil Mech. 2009, 30, 1549–1554. (In Chinese) [Google Scholar] [CrossRef]
- Fang, K.; Miao, M.; Tang, H.; Jia, S.; Dong, A.; An, P.; Zhang, B. Insights into the deformation and failure characteristic of a slope due to excavation through multi-field monitoring: A model test. Acta Geotech. 2023, 18, 1001–1024. [Google Scholar] [CrossRef]
- Nian, T.-K.; Zhang, Y.-J.; Wu, H.; Chen, G.-Q.; Zheng, L. Runout simulation of seismic landslides using discontinuous deformation analysis (DDA) with state-dependent shear strength model. Can. Geotech. J. 2020, 57, 1183–1196. [Google Scholar] [CrossRef]
- Ng, C.W.W. The state-of-the-art centrifuge modelling of geotechnical problems at HKUST. J. Zhejiang Univ. A 2014, 15, 1300217. [Google Scholar] [CrossRef]
- Zhang, C.; Yin, Y.; Yan, H.; Zhu, S.; Li, B.; Hou, X.; Yang, Y. Centrifuge modeling of multi-row stabilizing piles reinforced reservoir landslide with different row spacings. Landslides 2022, 20, 559–577. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, Y. Numerical method for retaining structures based on coupled finite difference method and discrete element method. Chin. J. Geotech. Eng. 2009, 31, 1402–1407. (In Chinese) [Google Scholar]
- Guo, P.H.; Zou, X.J. Bearing capacity of a single pile in sand under combined vertical force-horizontal force-torque load. Chin. J. Rock Mech. Eng. 2018, 37, 2593–2600. (In Chinese) [Google Scholar] [CrossRef]
- Nian, T.-K.; Jiang, J.-C.; Wang, F.-W.; Yang, Q.; Luan, M.-T. Seismic stability analysis of slope reinforced with a row of piles. Soil Dyn. Earthq. Eng. 2016, 84, 83–93. [Google Scholar] [CrossRef]
- Fang, K.; An, P.; Tang, H.; Tu, J.; Jia, S.; Miao, M.; Dong, A. Application of a multi-smartphone measurement system in slope model tests. Eng. Geol. 2021, 295, 106424. [Google Scholar] [CrossRef]
- Zheng, J.; Xie, M.; Cao, W.; Zhang, J. Analyzing stability of embankment considering failure mode of soil between piles. J. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 2012, 40, 99–102. (In Chinese) [Google Scholar]
- Xu, C.; Xue, L.; Cui, Y.; Guo, S.; Zhai, M.; Bu, F. A New Multi-Objective Comprehensive Optimization Model for Homogeneous Slope Reinforced by Anti-Slide Piles: Insights from Numerical Simulation. Lithosphere 2022, 2022, 6499724. [Google Scholar] [CrossRef]
- Chen, G.; Yang, J.; Liu, Y.; Kitahara, T.; Beer, M. An energy-frequency parameter for earthquake ground motion intensity measure. Earthq. Eng. Struct. Dyn. 2023, 52, 271–284. [Google Scholar] [CrossRef]
- Chen, G.; Beer, M.; Liu, Y. Modeling response spectrum compatible pulse-like ground motion. Mech. Syst. Signal Process. 2022, 177, 109177. [Google Scholar] [CrossRef]


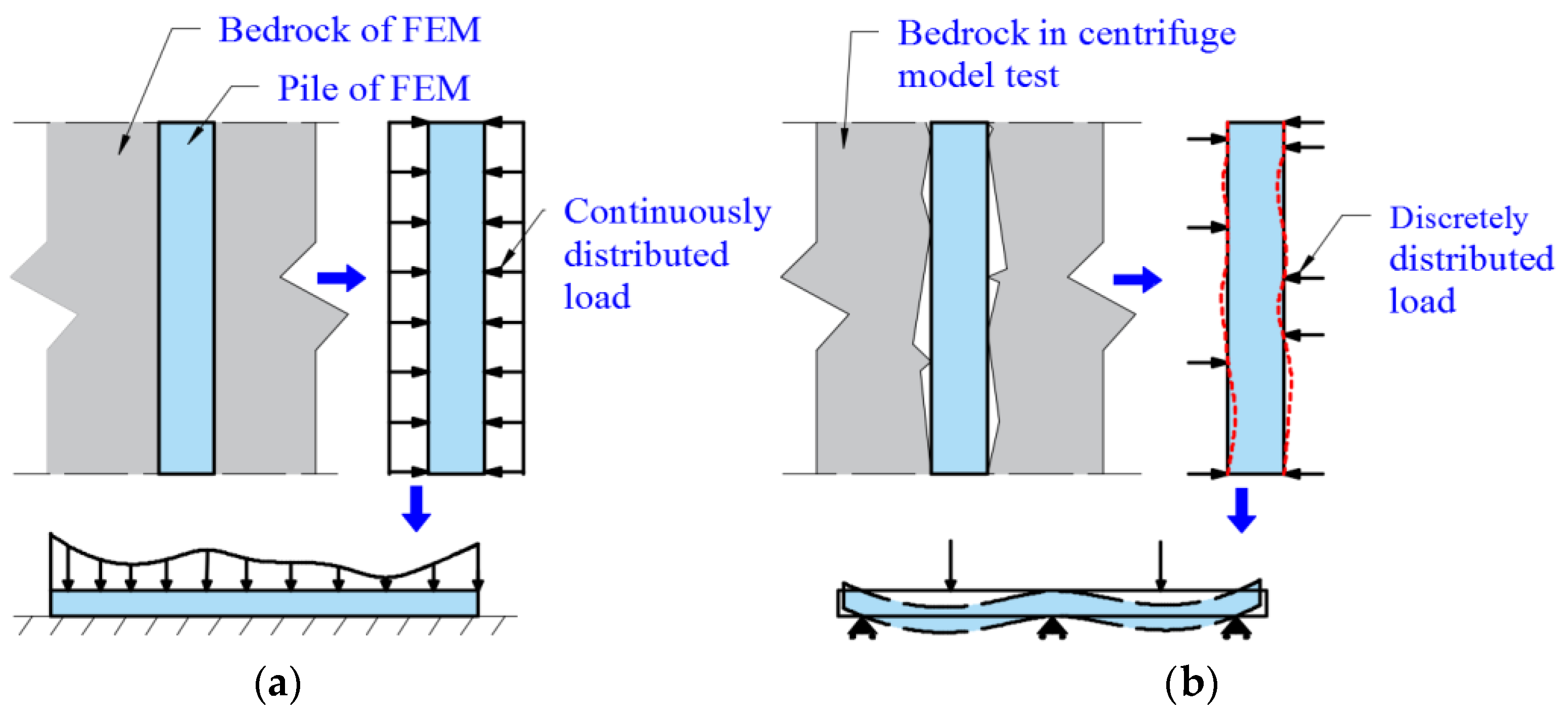
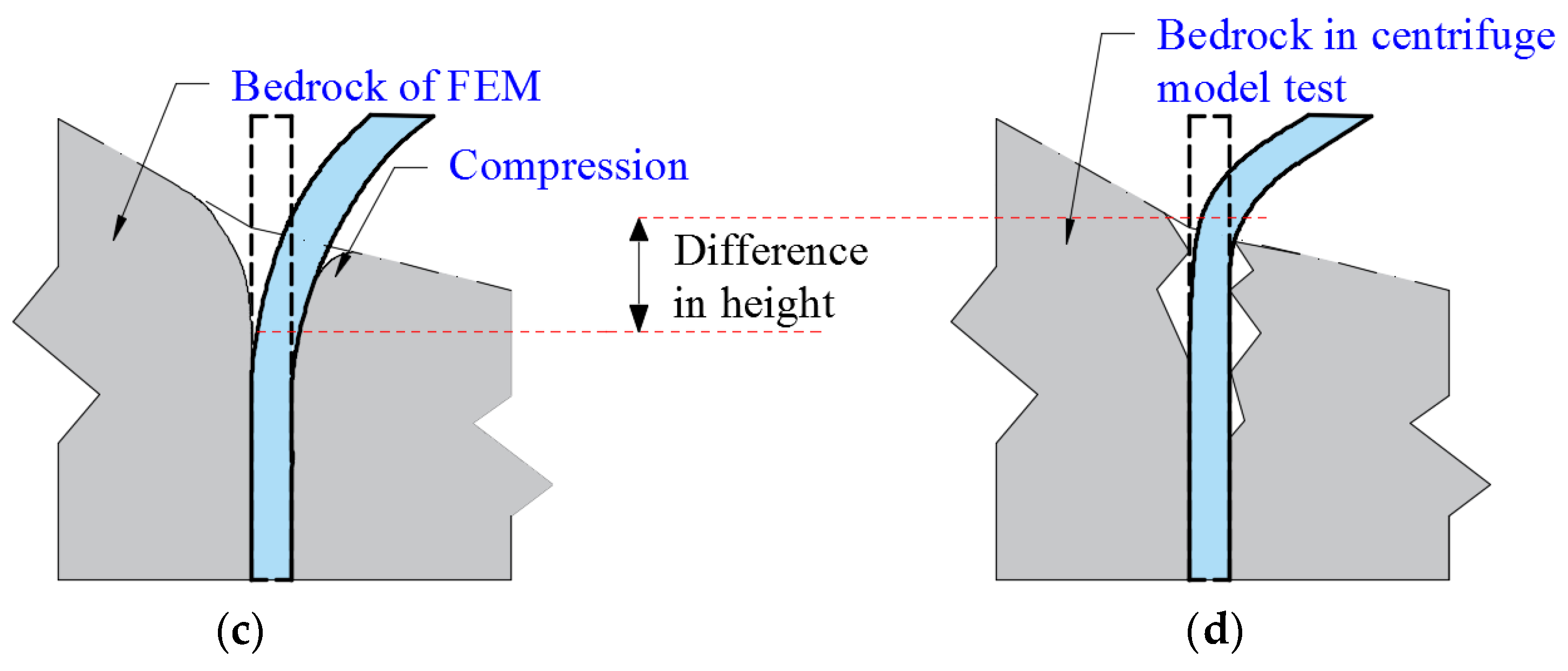

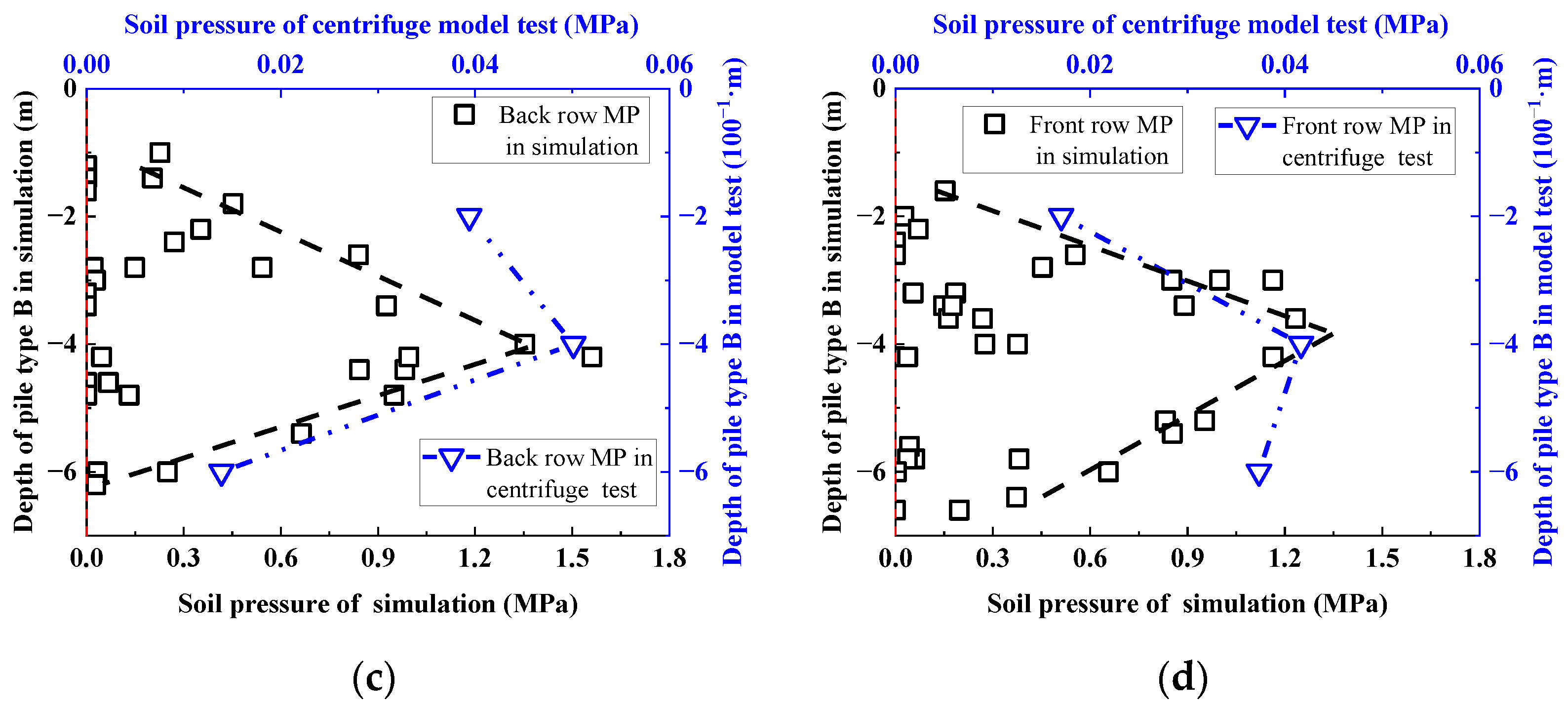
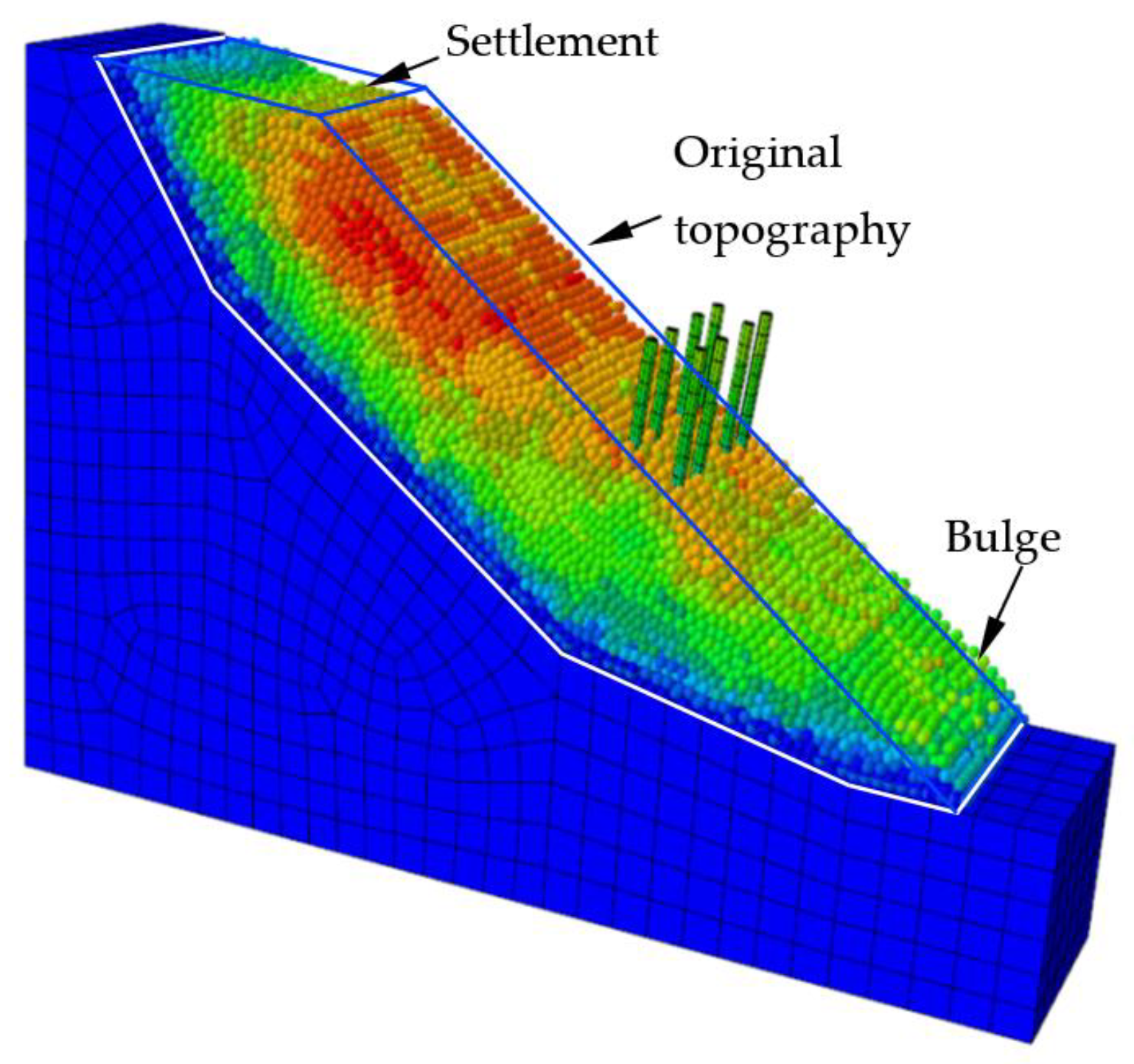

| Pile Type | Conventional Pile (CP) | Micropile Group (MPG) | |
|---|---|---|---|
| Type A | Type B | Type C | |
| Sketch |  | 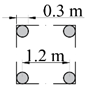 | 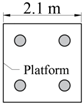 |
| Parameter | Loose Deposit/Slide | Pile | Bedrock |
|---|---|---|---|
| Elasticity modulus E (GPa) | 0.2 | 30 | 30 |
| Poisson’s ratio μ | 0.35 | 0.2 | 0.2 |
| Density ρ (kg/m3) | 1900 | 2600 | 3000 |
| Type of element | PD3D | C3D8R | |
| Alpha damping α | 0.4 | - | |
| Diameter/Mesh size (m) | 0.3 | 0.2 | 0.2 |
| Name | Type | Friction Coefficient | Stiffness (N/M) | Shearing Force Slope | Surface Energy (J/m2) | |
|---|---|---|---|---|---|---|
| P–P | P11 | JKR | 0.54 | 1 × 108 | 1 × 108 | 6000 |
| P–F | P1B | LINEAR | 0.4 | 1 × 108 | - | |
| P–B | P1F | HERTZ | 0 | 1 × 108 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, Z.; Zhang, Y.; Nian, T.; Xiao, S.; Liu, H. Cross-Scale Analysis on the Working Performance of Micropile Group and Talus Slope System. Sustainability 2023, 15, 8154. https://doi.org/10.3390/su15108154
Pei Z, Zhang Y, Nian T, Xiao S, Liu H. Cross-Scale Analysis on the Working Performance of Micropile Group and Talus Slope System. Sustainability. 2023; 15(10):8154. https://doi.org/10.3390/su15108154
Chicago/Turabian StylePei, Zhenwei, Yanjun Zhang, Tingkai Nian, Shiguo Xiao, and Hongshuai Liu. 2023. "Cross-Scale Analysis on the Working Performance of Micropile Group and Talus Slope System" Sustainability 15, no. 10: 8154. https://doi.org/10.3390/su15108154








