Modeling and Dynamic Impact Analysis of Prismatic Lithium-Ion Battery
Abstract
:1. Introduction
2. Experiments
2.1. Experimental Specimen
2.2. Experimental Setups
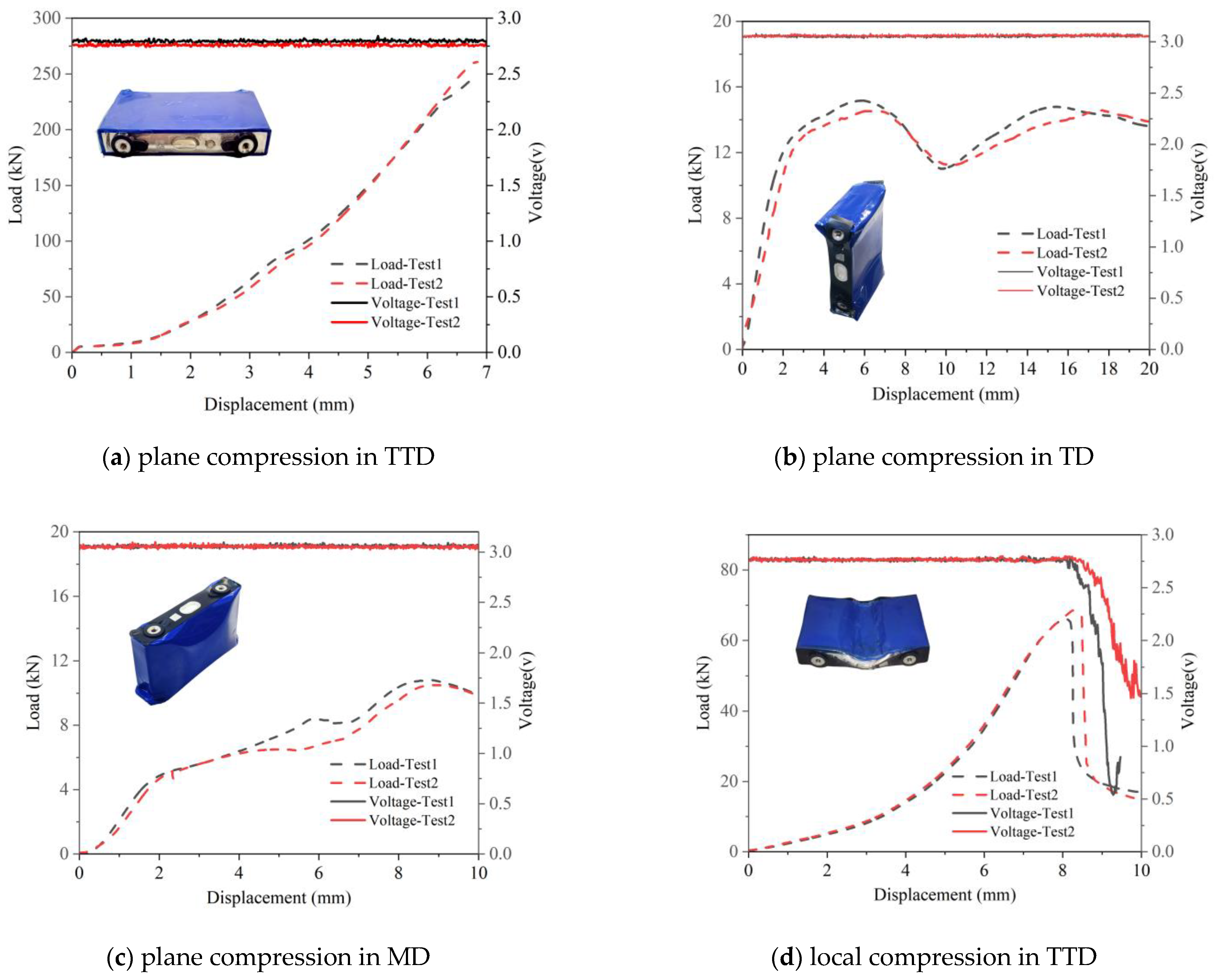
2.3. Quasi-Static Compression Experiment and Result Analysis
3. Numerical Simulation
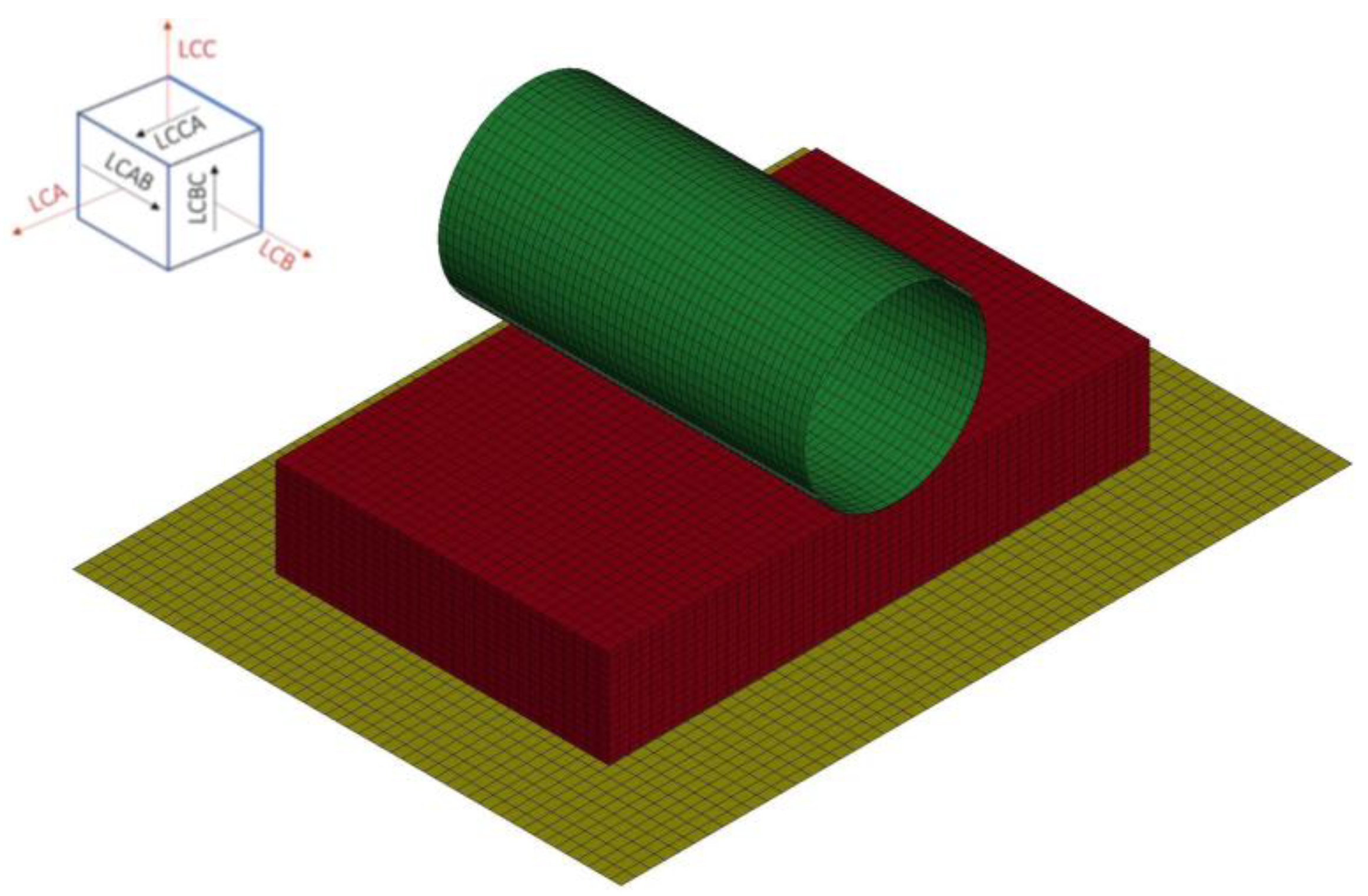
3.1. Establishment of a Computational Model
3.2. Model Validation
4. Discussion
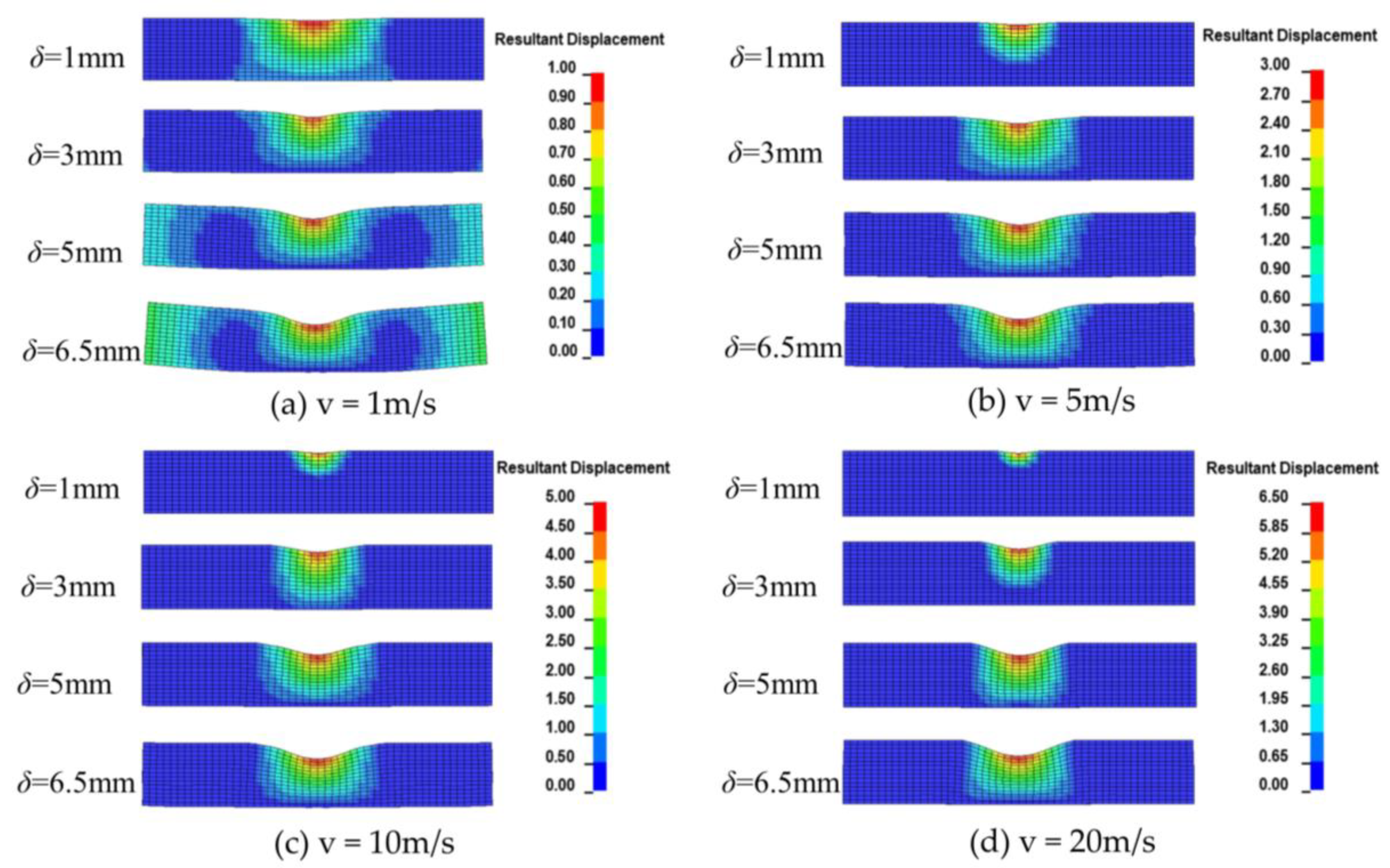
4.1. Deformation Feature of PLIB at Different Loading Velocities
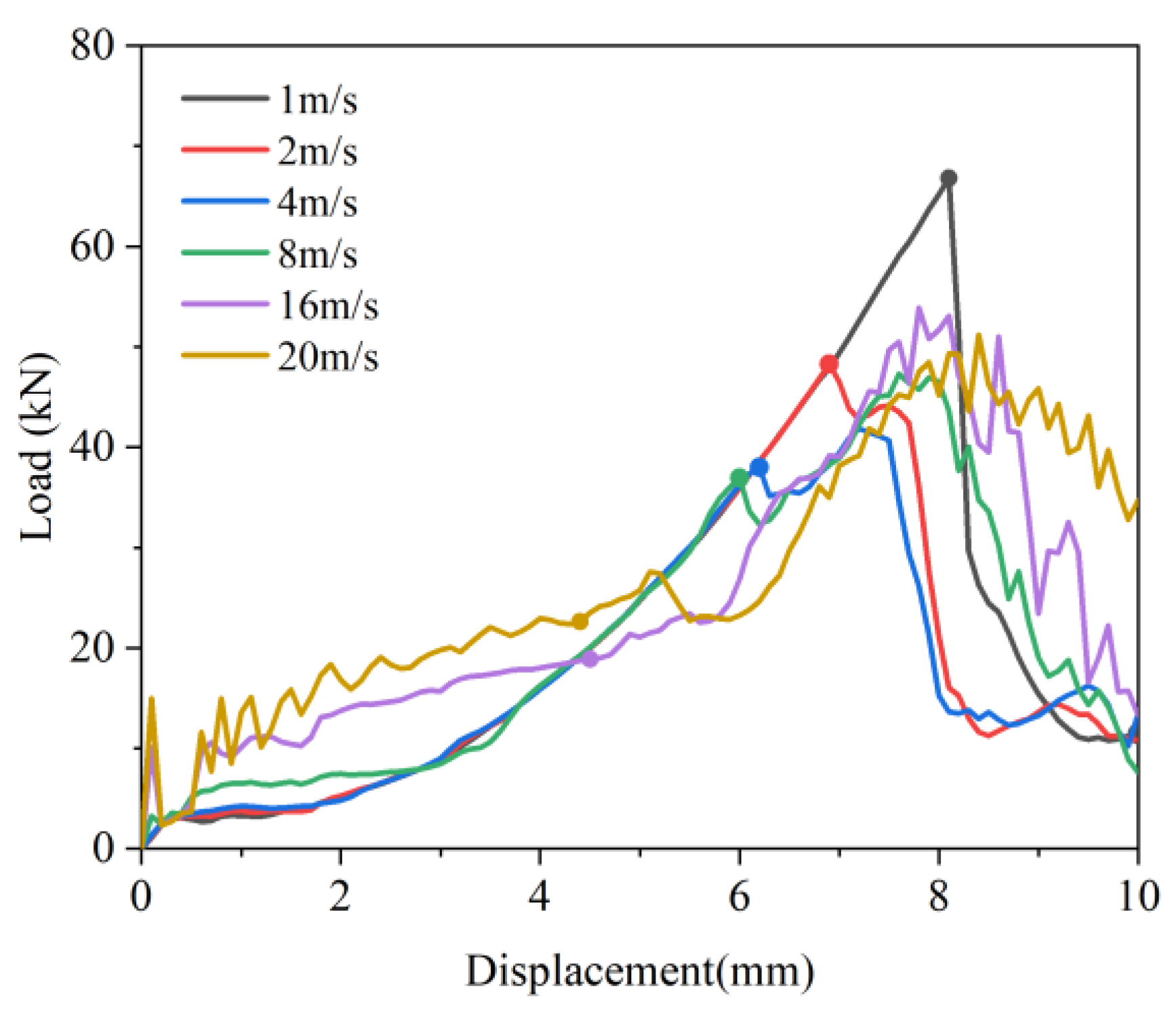
4.2. Dynamic Response of PLIB at Different Loading Velocities
4.3. Failure Analysis of PLIB at Different Loading Velocities
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rangarajan, S.S.; Sunddararaj, S.P.; Sudhakar, A.V.V.; Shiva, C.K.; Subramaniam, U.; Collins, E.R.; Senjyu, T. Lithium-ion batteries—The crux of electric vehicles with opportunities and challenges. Clean Technol. 2022, 4, 908–930. [Google Scholar] [CrossRef]
- Li, S.Q.; Wang, K.; Zhang, G.; Li, S.N.; Xu, Y.A.; Zhang, X.D.; Zhang, X.; Zheng, S.H.; Sun, X.Z.; Ma, Y.W. Fast Charging Anode Materials for Lithium-Ion Batteries: Current Status and Perspectives. Adv. Funct. Mater. 2022, 32, 2200796. [Google Scholar] [CrossRef]
- Javia, D.; Tewari, K.; Budarapu, P.R.; Natarajan, S. Design of lithium-ion battery packs for two-wheeled electric vehicles. Energy Storage 2023, e458. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, X.; Wierzbicki, T.; Xia, Y.; Chen, G. Structural Designs for Electric Vehicle Battery Pack against Ground Impact. In Proceedings of the WCX World Congress Experience, Detroit, MI, USA, 10–12 April 2018. [Google Scholar] [CrossRef]
- Tran, M.K.; Mevawalla, A.; Aziz, A.; Panchal, S.; Xie, Y.; Fowler, M. A Review of Lithium-Ion Battery Thermal Runaway Modeling and Diagnosis Approaches. Processes 2022, 10, 1192. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Xiong, R.; Sun, F.C. Research Status and Analysis for Battery Safety Accidents in Electric Vehicles. J. Mech. Eng. 2019, 55, 93–104. [Google Scholar] [CrossRef]
- Huang, W.S.; Feng, X.N.; Han, X.B.; Zhang, W.F. Questions and Answers Relating to Lithium-Ion Battery Safety Issues. Cell Rep. Phys. Sci. 2021, 2, 100285. [Google Scholar] [CrossRef]
- Sun, P.Y.; Bisschop, R.; Niu, H.H.; Huang, X.Y. A Review of Battery Fires in Electric Vehicles. Fire Technol. 2020, 56, 1361–1410. [Google Scholar] [CrossRef]
- Sahraei, E.; Kahn, M.; Meier, J.; Wierzbicki, T. Modelling of cracks developed in lithium-ion cells under mechanical loading. RSC Adv. 2015, 5, 80369–80380. [Google Scholar] [CrossRef]
- Sahraei, E.; Bosco, E.; Dixon, B.; Lai, B. Microscale failure mechanisms leading to internal short circuit in li-ion batteries under complex loading scenarios. J. Power Sources 2016, 319, 56–65. [Google Scholar] [CrossRef]
- Sahraei, E.; Hill, R.; Wierzbicki, T. Calibration and finite element simulation of pouch lithium-ion batteries for mechanical integrity. J. Power Sources 2012, 201, 307–321. [Google Scholar] [CrossRef]
- Sahraei, E.; Campbell, J.; Wierzbicki, T. Modeling and short circuit detection of 18650 Li-ion cells under mechanical abuse conditions. J. Power Sources 2012, 220, 360–372. [Google Scholar] [CrossRef]
- Wierzbicki, T.; Sahraei, E. Homogenized mechanical properties for the jellyroll of cylindrical Lithium-ion cells. J. Power Sources 2013, 241, 467–476. [Google Scholar] [CrossRef]
- Sahraei, E.; Meier, J.; Wierzbicki, T. Characterizing and modeling mechanical properties and onset of short circuit for three types of lithium-ion pouch cells. J. Power Sources 2014, 247, 503–516. [Google Scholar] [CrossRef]
- Li, W.; Xia, Y.; Zhu, J.E.; Luo, H.L. State-of-charge dependence of mechanical response of lithium-ion batteries: A result of internal stress. J. Electrochem. Soc. 2018, 165, A1537–A1546. [Google Scholar] [CrossRef]
- Li, W.; Xia, Y.; Chen, G.H.; Sahraei, E. Comparative study of mechanical-electrical-thermal responses of pouch, cylindrical, and prismatic lithium-ion cells under mechanical abuse. Sci. China Technol. Sci. 2018, 61, 1472–1482. [Google Scholar] [CrossRef]
- Zhu, J.E.; Li, W.; Xia, Y.; Sahraei, E. Testing and modeling the mechanical properties of the granular materials of graphite anode. J. Electrochem. Soc. 2018, 165, A1160–A1168. [Google Scholar] [CrossRef]
- Wang, L.B.; Yin, S.; Xu, J. A detailed computational model for cylindrical lithium-ion batteries under mechanical loading: From cell deformation to short-circuit onset. J. Power Sources 2019, 413, 284–292. [Google Scholar] [CrossRef]
- Wang, L.B.; Yin, S.; Xu, J. A Finite Element Model of 18650 Lithium-Ion Battery for Explosion Caused by Internal Short Circuit. In Proceedings of the 35th ASME International Conference on Ocean, Busan, Republic of Korea, 19–24 June 2016. [Google Scholar]
- Xu, J.; Liu, B.H.; Wang, X.Y.; Hu, D.Y. Computational model of 18650 lithium-ion battery with coupled strain rate and SOC dependencies. Appl. Energy 2016, 172, 180–189. [Google Scholar] [CrossRef]
- Wang, T.; Chen, X.P.; Chen, G.; Ji, H.B.; Li, L.; Yuan, Q.; Liu, Y.Z.; Ji, Y.P. Investigation of Mechanical Integrity of Prismatic Lithium-Ion Batteries With Various State of Charge. J. Electrochem. Energy 2021, 18, 031002. [Google Scholar] [CrossRef]
- Vusa, V.R.; Budarapu, P.R.; Rabczuk, T. Crash-worthiness studies on multistage stiffened honeycomb core sandwich structures under dynamic loads. Int. J. Crashworthines 2022, 2121196. [Google Scholar] [CrossRef]
- Liu, Y.J.; Xia, Y.; Xing, B.B.; Zhou, Q. Mechanical-electrical-thermal responses of lithium-ion pouch cells under dynamic loading: A comparative study between fresh cells and aged ones. Int. J. Impact Eng. 2022, 166, 104237. [Google Scholar] [CrossRef]
- Yu, D.; Ren, D.S.; Dai, K.R.; Zhang, H.; Yang, B.Q.; Zhang, J.M.; Ma, S.J.; Wang, X.F.; You, Z. Failure mechanism and predictive model of lithium-ion batteries under extremely high transient impact. J. Energy Storage 2021, 43, 103191. [Google Scholar] [CrossRef]
- Zhou, M.Z.; Hu, L.L.; Chen, S.R.; Zhao, X. Different mechanical-electrochemical coupled failure mechanism and safety evaluation of lithium-ion pouch cells under dynamic and quasi-static mechanical abuse. J. Power Sources 2021, 497, 229897. [Google Scholar] [CrossRef]
- Logakannan, K.P.; Zhu, F.; Sypeck, D.; Deng, J.; Kim, S. Impact response of prismatic Li-ion battery jellyrolls and cells. Int. J. Impact Eng. 2022, 170, 104352. [Google Scholar] [CrossRef]
- Kermani, G.; Sahraei, E. Dynamic impact response of lithium-ion batteries, constitutive properties and failure model. RSC Adv. 2019, 9, 2464–2473. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.P.; Wang, T.; Zhang, Y.; Ji, H.B.; Ji, Y.P.; Yuan, Q.; Li, L. Dynamic behavior and modeling of prismatic lithium-ion battery. Int. J. Energy Res. 2020, 44, 2984–2997. [Google Scholar] [CrossRef]
- Chen, X.P.; Wang, T.; Zhang, Y.; Ji, H.B.; Ji, Y.P.; Yuan, Q. Dynamic mechanical behavior of prismatic lithium-ion battery upon impact. Int. J. Energy Res. 2019, 43, 7421–7432. [Google Scholar] [CrossRef]
- Pan, Z.X.; Li, W.; Xia, Y. Experiments and 3D detailed modeling for a pouch battery cell under impact loading. J. Energy Storage 2020, 27, 101016. [Google Scholar] [CrossRef]
- Zhu, J.E.; Luo, H.L.; Li, W.; Gao, T.; Xia, Y.; Wierzbicki, T. Mechanism of strengthening of battery resistance under dynamic loading. Int. J. Impact Eng. 2019, 131, 78–84. [Google Scholar] [CrossRef]
- Jia, Y.K.; Yin, S.; Liu, B.H.; Zhao, H.; Yu, H.L.; Li, J.; Xu, J. Unlocking the coupling mechanical -electrochemical behavior of lithium-ion battery upon dynamic mechanical loading. Energy 2019, 166, 951–960. [Google Scholar] [CrossRef]
- Xu, J.; Liu, B.H.; Wang, L.B.; Shang, S. Dynamic mechanical integrity of cylindrical lithium-ion battery cell upon crushing. Eng. Fail. Anal. 2015, 53, 97–110. [Google Scholar] [CrossRef]
- Wang, L.B.; Chen, J.Y.; Li, J.P.; Li, B.Q.; Wang, T. A novel anisotropic model for multi-stage failure threshold of lithium-ion battery subjected to impact loading. Int. J. Mech. Sci. 2022, 236, 107757. [Google Scholar] [CrossRef]
- Keshavarzi, M.M.; Gilaki, M.; Sahraei, E. Characterization of in-situ material properties of pouch lithium-ion batteries in tension from three-point bending tests. Int. J. Mech. Sci. 2022, 219, 107090. [Google Scholar] [CrossRef]
- Zhang, H.J.; Zhou, M.Z.; Hu, L.L.; Zhang, Z.W. Mechanism of the dynamic behaviors and failure analysis of lithium-ion batteries under crushing based on stress wave theory. Eng. Fail. Anal. 2019, 108, 104290. [Google Scholar] [CrossRef]
- Xi, S.J.; Zhao, Q.C.; Chang, L.J.; Huang, X.Y.; Cai, Z.H. The dynamic failure mechanism of a lithium-ion battery at different impact velocity. Eng. Fail. Anal. 2020, 116, 104747. [Google Scholar] [CrossRef]






| Objects | Parameters |
|---|---|
| Anode | Graphite |
| Cathode | LiFePO4 |
| Nominal capacity | 20 Ah |
| Nominal voltage | 3.2 V |
| Cut off voltage | 2.5~3.65 V |
| Continuous discharging current (max) | 5 C |
| Charging current (max) | 3 C |
| Weight | 654 g |
| Size | 148 × 91 × 26.5 mm |
| Component | Material | Elastic Modulus (MPa) | Poisson Ratio | Density (kg/m3) | Type of Elements | Number of Elements |
|---|---|---|---|---|---|---|
| Aluminum Shell | MAT_24 | 70,000 | 0.33 | 2700 | Shell | 5400 |
| Jellyroll | MAT_126 | 800 | 0.01 | 2080 | Solid | 22,500 |
| flat indenter | MAT_20 | 210,000 | 0.3 | 7800 | Shell | 2500 |
| cylinder indenter | MAT_20 | 210,000 | 0.3 | 7800 | Shell | 2000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, D.; Wang, P.; Wang, T.; Chen, J. Modeling and Dynamic Impact Analysis of Prismatic Lithium-Ion Battery. Sustainability 2023, 15, 8414. https://doi.org/10.3390/su15108414
Qin D, Wang P, Wang T, Chen J. Modeling and Dynamic Impact Analysis of Prismatic Lithium-Ion Battery. Sustainability. 2023; 15(10):8414. https://doi.org/10.3390/su15108414
Chicago/Turabian StyleQin, Dongchen, Peizhuo Wang, Tingting Wang, and Jiangyi Chen. 2023. "Modeling and Dynamic Impact Analysis of Prismatic Lithium-Ion Battery" Sustainability 15, no. 10: 8414. https://doi.org/10.3390/su15108414
APA StyleQin, D., Wang, P., Wang, T., & Chen, J. (2023). Modeling and Dynamic Impact Analysis of Prismatic Lithium-Ion Battery. Sustainability, 15(10), 8414. https://doi.org/10.3390/su15108414










