The Impact of Digital Enterprise Agglomeration on Carbon Intensity: A Study Based on the Extended Spatial STIRPAT Model

Abstract

The digital economy has broken the physical space limit, reshaped factor input ratios, and accelerated factor mobility, which drives carbon reduction and social sustainability. Digital enterprise agglomeration is becoming the new tendency and a significant spatial feature for digital economy development. This work aimed to study the impact of digital enterprise agglomeration on carbon intensity. This study first proposed an extended spatial stochastic IPAT (STIRPAT) theoretical framework and regarded digital enterprise agglomeration as a technology factor. Secondly, by building a dataset with 7,902,050 digital enterprises and using the distance-based Duranton and Overman index, this study evaluated the digital enterprise agglomeration of 278 cities from 2007 to 2017 in China. Thirdly, by matching micro digital enterprise data and macro city data, this study employed spatial Durbin, mediating, and moderating effects models to test the impact and mechanism of digital enterprise agglomeration on carbon intensity. There are four main findings: (1) There is a negative “U-shaped” correlation between digital enterprise agglomeration and local and neighboring cities’ carbon intensities, and the impact of neighboring digital enterprise agglomeration on local carbon intensity is more significant than the effect of regional digital enterprise agglomeration on local carbon intensity. (2) The impact of digital enterprise agglomeration on carbon intensity shows great differences under spatial, resource, industrial, and financial heterogeneity. (3) Digital enterprise agglomeration indirectly impacts carbon intensity in two ways: the green technology innovation effect and the industry structure rationalization effect. (4) Human capital enhances the role of digital enterprise agglomeration in reducing carbon intensity, whereas government intervention weakens the effect of digital enterprise agglomeration in decreasing carbon intensity. This paper suggests that digital enterprise agglomeration strategies should be dynamically adjusted based on local digital economy development and resource conditions.

1. Introduction

Global climate change poses a huge threat to the ecological environment and human well-being, negatively impacting sustainable social development [1,2]. Carbon dioxide (CO₂) emission is the main source affecting climate change [3,4], so it is vital to reduce CO₂. How to effectively reduce CO₂ has become a common concern and a pressing issue worldwide. To reduce CO₂ and promote environmental sustainability, the international community has conducted several rounds of climate negotiations and signed a series of international treaties, such as the Kyoto Protocol and the Paris Agreement, but CO₂ has continued to increase [5]. China produced approximately 1 billion tons of CO₂ in 2020, accounting for roughly 30% of worldwide emissions [6]. China has pledged to reach carbon neutrality by 2060 to fulfill global carbon emission reduction objectives and assume leadership [4,6,7]. China’s management of CO₂ emissions may help other emerging economies decrease carbon emissions while simultaneously enhancing sustainable social development and addressing the ecological issue on a global scale.

Due to the different development stages and income levels, CO₂ emission reduction paths vary across countries [8]. Some industrialized economies have achieved significant results in CO₂ emission reduction through various means, such as the phasing out of coal power in Germany and the promotion of electric bicycles in Denmark. However, China, the greatest rising economy, is important to global economic development. Therefore, China’s CO₂ reduction approach cannot compromise economic development, and the path to China’s “dual carbon” goals may differ from that of industrialized economies. Recently, the international community has reached a consensus on inclusive growth, that is, the pursuit of harmonious social development and economic growth [9]. To better integrate social and economic sustainability, some scholars have proposed carbon intensity (CI) that takes into account both environmental protection and economic growth using the ratio of total CO₂ emissions divided by real GDP as a measure of CI [6,10,11]. Faced with the dual pressures of economic development and limiting CO₂, reducing CI is an essential means to alleviate the prominent problem of resource constraints and ensure sustainable development in China.

The digital economy is becoming a core element of production in modern society and an important pillar of promoting sustainable production methods [12,13,14]. Digital technologies are continuing to break spatial constraints, guide factor flow, and reorganize factors’ input ratio [5,12,15,16], providing a valuable opportunity to reduce CI and promote green development. Many scholars investigated the effect of the digital economy on air pollution and social sustainability, and their views differed from each other. The various effects included the energy-savings effect [10,13], energy rebound effect [17,18], technical effect [9], and industry structure effect [4,9]. In addition, digitalization is reshaping cities’ spatial patterns, and the debate on whether it is decentralizing never ends [19]. Some early scholars argue that digitalization decentralizes economic activities, eliminating geographical disparities and preventing digital economy agglomeration [20,21]. However, some scholars take opposing views, and a growing number of studies argue that the digital economy does not lead to the death of distance [15,22,23] and that digital economy agglomeration is a distinctly spatial geographical phenomenon. For example, Forman et al. [24] showed that information and communication technology (ICT) continued to agglomerate in the American Bay Area from 1976 to 2008.

According to location theory [25], digital enterprise agglomeration (DIGA) refers to the concentration of digital firms in a certain region due to the lower cost. Enterprise agglomeration or industrial agglomeration is a key factor affecting CI [26,27,28], but the relationship between DIGA and CI has rarely been investigated. The correlation between traditional economic agglomeration and CI has been discussed in depth, but scholars have yet to reach a final answer. First, theoretical studies suggest that economic agglomeration’s effect on CI includes positive agglomeration economic effects and negative congestion effects [29]. Second, empirical research results indicate the correlation between economic agglomeration and CI is varied: positive [26], negative [6,30], and “U-shaped” [28]. Third, economic agglomeration’s impact on CI is decided by many factors, such as environmental regulation (ER) [31] and geographical location [28]. Accordingly, a higher DIGA does not necessarily lead to lower CI, and the relationship between DIGA and CI is intricate. Unfortunately, few scholars have focused on the impact of DIGA on CI. Past studies mainly focused on the impact of digital changes or agglomeration on CI. Moreover, compared with other traditional industries, the digital industry is knowledge- and technology-intensive [9], which means that the concentration of digital enterprises may have distinct features and effects. Therefore, the first question studied in this research is the link between DIGA and CI in China. In addition, this paper investigated how DIGA affects CI. Finally, the factors that affect the relationship between DIGA and CI are also the focus of this study. Resolving these questions has significant practical implications for digital enterprise clustering and regional green synergy development.

This paper makes three key contributions. First, based on the stochastic IPAT (STIRPAT) framework proposed by Dietz and Rosa [32], we offer an extended spatial STIRPAT model by considering DIGA and spatial effects. We regard DIGA as a technology factor, providing expansion and a supplement to investigate factors impacting CI. Second, previous studies mainly used macro data and discrete agglomeration measures to measure digital agglomeration, but our study employed a dataset including 7,902,050 digital enterprises and the continuous Duranton and Overman (DO) index [33] to measure DIGA, effectively eliminating the modifiable areal unit problem (MAUP) caused by administrative subdivision. Finally, by matching the micro digital enterprise data and macro city data, we examined the nonlinear and spatial impact of DIGA on CI. The study also discusses the spatial mediating and moderating effects of DIGA on CI, providing insightful and applicable policies for digital economy cluster construction and regional CO₂ reduction.

2. Literature Review

2.1. Digital Economy and Carbon Intensity

Increased temperature poses a significant threat to sustainable human development; CO₂ reduction is becoming an imminent worldwide issue, and many scholars have investigated the digital economy’s influence on CO₂ emission [5,11,34]. Using various theories and empirical models, scholars discussed the correlation between CI and the digital economy and came to three different conclusions.

Some investigators contended that the digital economy is negatively related to CI. Moyer and Hughes [34] suggested that information and communication technologies (ICTs) negatively impact CO₂ by building an integrated evaluation model including energy, environment, population, and economic impacts. Awan, Abbasi, Rej, Bandyopadhyay, and Lv [13] found that internet penetration reduces CO₂ emissions and mitigates environmental degradation based on empirical analysis. Finance plays a key role in economic development, so some scholars studied the impact of digital finance on CI. Zhao et al. [35] found that digital finance is negatively correlated to carbon emission using nonspatial econometric models. Lee and Wang [11] pointed out that the paper by Zhao et al. [35] ignores the spatial effect of digital finance. Using spatial econometric methods, Lee and Wang [11] asserted that digital finance decreases local and surrounding cities’ CI, with the spatial spillover effect ranging from 350 km to 400 km.

Despite this, many scholars argued that the emergence and spread of the digital economy raised CI. Some scholars contended that digital technologies may lead to potential rebound effects; that is, the new demand for energy from digital technology advances outweighs their saving energy. For example, Lange, Pohl, and Santarius [17] found that although ICTs reduce energy consumption through energy efficiency gains, ICTs also increase energy consumption due to the fact of economic development and ICT sector expansion, and their results showed that the energy growth effects of ICTs outweigh their energy-saving effects. Similarly, Haldar, Sucharita, Dash, Sethi, and Padhan [14] confirmed the positive effect of internet use on electricity consumption using data from 16 emerging economies. Zhou et al. [36] pointed out that the household sector is energy-intensive, and a significant amount of CO₂ emissions come from the household sector. Many scholars investigated the digital economy’s impact on CO₂ from the perspective of the household sector. Yue et al. [37] contended that digital finance increases financial inclusion through the digital credit platform. In addition, Le et al. [38] found that improving financial inclusion leads to more CO₂ emissions due to an increase in energy-intensive products, such as refrigerators and fuel vehicles. Similarly, Zhou, Yin, and Yue [36] found that the availability of household credit increases household carbon emissions.

Based on these two different effects, the digital economy’s impact on CO₂ may be nonlinear. Berkhout and Hertin [39] suggested that the application and diffusion of ICTs have both positive and negative impacts on environmental sustainability based on a theoretical study. In addition, many researchers have empirically found a nonlinear correlation between the digital economy and CO₂. Cheng, Zhang, Wang, and Jiang [10] found that digital economy development has an inverted “U-shaped” correlation with CI. There is a great difference in ICT penetration between developed and developing economies. According to Asongu and Nwachukwu [40], the saturation point of mobile telecommunications has been achieved in industrialized countries, but penetration in emerging economies remains low. The digital economy boom has highlighted the digital divide, resulting in the heterogeneity of the digital economy’s CO₂ reduction impact among nations with varying incomes. Ndri, Islam, and Kakinaka [5] found that ICT usage is positively correlated to CO₂ in relatively low-income nations, while ICT use has no impact on CO₂ in relatively high-income developing nations.

2.2. Economic Agglomeration and Carbon Intensity

Economic agglomeration is an evident economic geographical feature. Many scholars have studied the role of enterprise agglomeration or industrial agglomeration on CI, and past studies indicated that there is an uncertain correlation between economic agglomeration and CI.

Many scholars contended that economic agglomeration reduces CI. Zhao, Dong, and Dong [30] found that productive service agglomeration increases CO₂ emissions via increased economic scale, technological spillover, and knowledge spillover, while industrial structure optimization decreases them. In general, productive service agglomeration will speed up China’s carbon neutrality. Chen et al. [41] discussed the industry agglomeration’s effect on CO₂ emissions and carbon intensity, and the results indicated that industrial agglomeration increases carbon emissions but decreases CI. In addition, Yu et al. [42] empirically found that digital economy agglomeration is negatively related to local CI.

However, a small number of scholars provided the opposite answer, arguing that economic agglomeration is negatively correlated to CI. Gaigné et al. [43] found that compact cities with higher population agglomeration caused more greenhouse gases and environmental unsustainability. Based on the output density model, Ciccone [29] theoretically contended that while economic agglomeration has good agglomeration effects, it also causes bad congestion effects, leading to environmental pollution. Higgins et al. [44] pointed out that the benefits of agglomeration are impacted by the spatial structure of cities and that agglomeration is more likely to cause congestion effects and air pollution in areas with good access and high exposure to air pollution. Wang, Dong, and Dong [27] suggested that the construction of the 5G network and data center consumes large amounts of energy, and their study showed that ICT enterprise agglomeration in the Yangtze River Delta increases CO₂ emissions.

Some investigators contended that economic agglomeration is not just positively or negatively related to CI. Seto et al. [45] argued that the impact of economic agglomeration on environmental sustainability is decided by many other factors, such as urban governance and the positioning of urban functions. In addition, using Chinese data, Yu, Li, Li, Wang, and Chen [28] found that the association between economic agglomeration and CI varies in different development stages; for example, the relationship between economic agglomeration and CI in the middle Yangtze River urban agglomeration is an inverted “U-shape” in the early stage of development and becomes negative in the middle and late stages of development. Hashmi et al. [46] studied the relationship between urban agglomeration and CO₂ emissions using cross-country data, and their results indicated that the correlation between urban agglomeration and CO₂ emissions is significantly positive in most countries and significantly negative in a few countries, such as Israel and Paraguay.

In conclusion, existing studies mainly focus on the digital economy’s or economy agglomeration’s effect on CI. Though few studies have discussed the impact of digital economy agglomeration on CI, they used macro city data to measure digital economy agglomeration. Unlike past research, we used micro digital firm data to evaluate DIGA and investigate DIGA’s effect on CI. In addition, existing studies indicate that the relationship between DIGA and CI may be intricate, so we employed nonlinear spatial econometric models to identify DIGA’s spatial spillover and nonlinear effects on CI.

3. Theoretical Analysis and Hypothesis Development

3.1. The Direct Impact of Digital Enterprise Agglomeration on Carbon Intensity

The impact of DIGA on CI is multiple, and DIGA may increase CI or decrease CI. Figure 1 shows the direct path for DIGA to impact CI.

On the one hand, DIGA may increase CI at an early stage of digital economy development. First, DIGA may produce energy rebound effects. Due to the integration of digital technologies with other sectors and the explosive growth of digital enterprises, social production and personal consumption are heavily dependent on digital technology and digital devices [47], and digital technologies, such as smartphones and laptops, are addictive [48]. The construction of digital infrastructure and the popularity of digital devices increase energy consumption, and such rebound effects may increase CI [17]. Second, enterprise agglomeration may cause congestion effects. The limited area and natural resources in agglomeration clusters cannot support too many digital enterprises, and an excessive concentration of digital enterprises may lead to road congestion and air pollution [29]. Third, DIGA may generate economic expansion effects [17,27]. Data have become a key production factor [12], empowering the real economy and driving the growth of other enterprises. At the same time, DIGA may also impose competitive pressure on enterprises in other industries [49], promoting the expansion of investment in other enterprises. Therefore, DIGA may cause blind economic expansion and extensive economic growth, and such effects of economic expansion may increase CI.

On the other hand, DIGA may decrease CI at a later stage of digital economy development. First, the scale economy effects of DIGA help to reduce CI. According to the theory of agglomeration economy [29,50], DIGA may decrease the energy consumption per unit of production via economies of scale, improving energy efficiency and environmental quality. Second, the various spillover effects of DIGA may reduce CI. Based on Marshall’s theory of agglomeration’s externality [50], DIGA has knowledge and technology spillover effects, encouraging the dissemination of environmental knowledge and green technical information, which may help people increase their understanding of environmental protection and businesses increase their green innovation, hence lowering CI. Third, the diffusion effects of DIGA may reduce CI. The digital economy breaks the geographical space limitation [9,15], making technological innovation spread faster. Such diffusion effects positively impact the technological progress in less developed regions, improving their clean production and pollution control abilities to a large extent. Hence, DIGA may improve the pollution treatment capacity of less developed regions and reduce CI through diffusion effects.

Hence, we propose the first hypothesis:

 Hypothesis 1. 

The correlation between DIGA and CI is a negative “U-shape”.

3.2. The Mediating Mechanism of Green Technology Innovation

This study contends that green technology innovation (GTI), industrial structure rationalization (ISR), and industrial structure advancement (ISA) may play mediating roles between DIGA and CI. Figure 2 depicts the indirect path by which DIGA impacts CI.

GTI refers to technological innovation that is beneficial to environmental protection and low-carbon development [7]. DIGA may reduce CI through GTI. The first path is that DIGA is conducive to the improvement in GTI capabilities. According to the agglomeration externality theory [50], the concentration of digital enterprises may generate positive externalities by forming labor pools. Meanwhile, the formation of a professional digital labor market has a positive effect on talent flow and talent exchange in the agglomeration areas. Hence, labor pooling effects may promote the rational allocation of digital talents, making full use of green innovation resources and advanced digital equipment to improve GTI. In addition, the knowledge spillover effects [40] and technology diffusion effects [9] of DIGA may improve individual knowledge levels and technological abilities via knowledge exchange and technological information sharing, facilitating the large-scale improvement and application of green technologies.

The second path is that GTI may reduce CI. GTI may decrease CI in two ways: cleaner production and improved carbon treatment technologies [51]. First, improved GTI capabilities provide companies with cleaner production technologies at the production end of the company, assisting in the reduction of the CI of enterprises. Second, some CO₂ emissions are unavoidable, such as refrigerators and air conditioners, so it is necessary to reduce CO₂ at the disposal stage. GTI may reduce CO₂ emissions by improving carbon disposal technologies, such as carbon capture and storage. In conclusion, GTI may reduce CI by controlling CO₂ at both the formation and disposal stages.

Hence, we propose the second hypothesis:

 Hypothesis 2. 

Green technology innovation plays a mediating role between digital enterprise agglomeration and carbon intensity.

3.3. The Mediating Mechanism of Industrial Structure Rationalization

ISR refers to the process in which the economic and technical links and quantitative proportional relationships among industries constantly tend to balance [52]. DIGA may reduce CI through ISR. The first path is that DIGA promotes ISR. Due to the fact of innovations in digital technology, new products, services, and business models are emerging [53]; for example, the internet-based platform economy has created a large number of odd jobs and knowledge payment projects [54]. As the digital economy and real economy rapidly integrate, companies rely more on digital resources in the digital economy era [15], and DIGA based on digital technology improves industry coordination and association, increasing ISR.

The second path is that ISR decreases CI. A reduction in CI emphasizes the reduction in total energy consumption and better resource utilization [8,55]. First, ISR may slow down industrial homogenization, allowing cities to develop distinctive and advantageous industries based on local resource endowments and geographical conditions, avoiding vicious competition and waste of resources. The energy waste caused by the extensive development mode is the root cause of China’s high CI [56]. Accordingly, ISR may reduce CI through decreased energy and resource waste. Second, ISR is conducive to coordinated development among industries, promoting the integration of industrialization and digitalization, facilitating industry transformation from being energy intensive into energy efficient, and improving the energy use efficiency of cities [4]. As a result, industrial rationalization may lower a city’s CI by increasing energy efficiency and reducing energy waste.

Hence, we propose the third hypothesis:

 Hypothesis 3. 

Industrial structure rationalization plays a mediating role between digital enterprise agglomeration and carbon intensity.

3.4. The Mediating Mechanism of Industrial Structure Advancement

ISA refers to the process of transforming an industrial structure from a low-level to a high-level state [52]. DIGA may reduce CI through ISA. First, DIGA may promote ISA. Digital technologies such as blockchain and the Internet of Things enhance cooperation between industries and communication frequency and efficiency between businesses [15], and these new-generation digital technologies are critical for the growth of service-based manufacturing and the transformation of conventional production, contributing to the increase of the share of tertiary industries. In addition, advancement in digital technologies has accelerated the pace of digital innovation and industrial differentiation [57]. At the same time, DIGA has technology spillover and technology diffusion effects [9], so DIGA may lead to more intense industrial competition by accelerating the adoption of digital technologies. Accordingly, emerging sectors powered by digital components may progressively displace existing backward industries, which is beneficial to ISA.

Second, ISA has a positive effect on CI. The essence of high-end industry transformation is the process of transitioning from agriculture and manufacturing to the service industry [8]. Firstly, manufacturing is an energy-intensive industry with more CO₂ emissions than services [7,58], so the sharing of services is negatively related to CI. Secondly, energy efficiency differs greatly between the service and industrial sectors [8], and advanced industrial structure indicates that energy will move from manufacturing to the service sector. Hence, ISA may boost energy efficiency, lowering CI.

Hence, we propose the fourth hypothesis:

 Hypothesis 4. 

Industrial structure advancement plays a mediating role between digital enterprise agglomeration and carbon intensity.

3.5. The Moderating Impact of Human Capital

Human capital (EDU) is a vital production factor and essential to support and guarantee low-carbon development and high-efficiency production [9,29]. The concentration of digital talents is the driving force behind the formation of DIGA [59]. Based on the theory of agglomeration externalities [50], DIGA has knowledge and technology spillover effects through labor pooling effects. Meanwhile, human capital has positive externalities, so the knowledge and spillover effects are highly correlated to the quality of the agglomerated human capital [9]. Additionally, the positive effect of human capital on CO₂ reduction is long-term. The accumulation of knowledge and technology will amplify the carbon-reduction effectiveness of high-quality human capital. Therefore, high-quality human capital agglomeration boosts DIGA’s spillover effects to promote company digital resource utilization and individual environmental consciousness [27], thus reducing CI.

In addition, from the aspect of the industry’s own features, knowledge and technology drive digital economy development, and digital technologies are more complex than ordinary technologies, as they have demanding requirements for workers’ digital skills [14]. Li [60] contended that improving human capital and mastering digital skills depend on good education. It is easier for better-educated workers to master and apply digital technologies proficiently [61]. At the same time, the adoption of digital technologies in company production and household consumption may decrease CI. Hence, higher human capital facilitates the release of the economic and environmental effects of DIGA.

Hence, we propose the fifth hypothesis:

 Hypothesis 5. 

Human capital is a moderator of the relationship between digital enterprise agglomeration and carbon intensity.

3.6. The Moderating Impact of Government Intervention

Enterprise agglomeration is formed and developed under the action of market mechanisms, and it is a spontaneous concentration of firms in a certain area due to the decreased unit cost [49,59]. In the process of economic development, markets may be imperfect [62], and resources such as financial subsidies and cheap loans are scarce. To intervene and control the flow of digital firms, governments may use administrative means to influence DIGA. On the one hand, moderate government intervention (GI) compensates for the inadequacy of market mechanisms [63]. Since CO₂ emissions have externalities, the impact of such externalities cannot be fully addressed by the market. The government may supply more public services to areas where the digital economy is concentrated to alleviate congestion and mitigate the pollution problems caused by excessive DIGA. In addition, government guidance plays a signaling role in the market, reducing market information asymmetry [62]. The decrease in market friction improves resource allocation through price correction [62]. Decreased resource misallocation improves energy efficiency and CI. Hence, minimizing crowding effects and asymmetry problems may promote the environmental governance effects of DIGA, thus reducing urban CI.

On the other hand, excessive GI may lead to stronger government power than market power, causing firms to pursue the establishment of political connections rather than technological innovation [6,62]. At the same time, GI may also lead to capital mismatch [63], resulting in small- and medium-sized enterprises with stronger GTI capacity not having access to low-price credit, while large stability-seeking capacity enterprises with weaker GTI have excess cheap credit. Thus, both inefficient resource allocation and political connections may weaken DIGA’s CO₂ reduction impact, which will negatively affect CI.

Hence, we propose the sixth hypothesis:

 Hypothesis 6. 

Government intervention is a moderator of the relationship between digital enterprise agglomeration and carbon intensity.

4. Model and Data

4.1. Model Specification

4.1.1. STIRPAT Model

Regarding the factors influencing environmental quality, Ehrlich and Holdren [64] proposed the IPAT analytical framework, arguing that the environment was decided by the population, affluence, and technology. The IPAT model is set as:

$$I=P\times A\times T$$

(1)

where $I$ is the environmental performance; $P, A,\mathrm{and} T$ are the population, affluence, and technical effects, respectively.

Although the IPAT framework allows for a simple and systematic study of environmental quality impacts, it is limited to conducting qualitative evaluations [32]. To carry out quantitative studies accurately, Dietz and Rosa [32] proposed STIRPAT based on the IPAT framework. The STIRPAT model takes the form of:

$$I_i={\alpha }_1{P}_i^{{\beta }_1}{A}_i^{{\beta }_2}{T}_i^{{\beta }_3}{e}_i$$

(2)

where ${\mathrm{I}}_{\mathrm{i}}$ is the environmental performance of observation unit $\mathrm{I}$; ${\mathsf{\alpha }}_1$ is a constant; ${\mathrm{P}}_{\mathrm{i}},{\mathrm{A}}_{\mathrm{i}},{\mathrm{and}\mathrm{T}}_{\mathrm{i}}$ are the population, affluence, and technical performances of observation unit $\mathrm{i},$ respectively. ${\beta }_1, {\beta }_2,\mathrm{and} {\beta }_3$ are the impacts of the population, affluence, and technical factors on environmental quality, respectively, and $e_i$ is an error term. As Equation (2) is of a multiplicative form, it is hard to estimate through the regression technique. To facilitate the estimation of parameters, we logarithmically treat Equation (2):

$$ln{I}_i=ln{\alpha }_1+{\beta }_{1}ln{P}_i+{\beta }_{2}ln{A}_i+{\beta }_{3}ln{T}_i+ln{e}_i$$

(3)

where $\ln (·)$ denotes natural logarithms; ${\mathsf{\beta }}_1,{\mathsf{\beta }}_2,{\mathrm{and}\mathsf{\beta }}_3$ are the corresponding estimated coefficients; $\ln \mathsf{\alpha }$ is the intercept term; and ${\mathrm{lne}}_{\mathrm{i}}$ is the error term.

4.1.2. Extended Spatial STIRPAT Model

The STIRPAT model is flexible in practical applications, allowing for the inclusion of additional factors affecting the environment. Based on theoretical research, this study contends that DIGA may have a significant impact on the environment. Meanwhile, both DIGA and CO₂ emissions have serious spatial characteristics [11,28,65], so this study proposes an extended STIRPAT model. Referring to Dietz and Rosa [32], we used CI to represent environmental performance. We used population density to characterize the population’s impact, GDP per capita to characterize the impact of affluence, and DIGA to characterize the technical effect. Hence, the extended spatial STIRPAT model is set as:

$$\begin{gathered} lnC{I}_{it}=a_1+{\rho }_{1}WlnC{I}_{it}+{\beta }_{1}DIG{A}_{it}+{\rho }_{2}WDIG{A}_{it}+{\beta }_{2}SDIG{A}_{it} \\ +{\rho }_{3}WSDIG{A}_{it}+\beta X_{it}+\rho W{X}_{it}+u_{1i}+{\nu }_{1t}+{\epsilon }_{1it} \end{gathered}$$

(4)

where $lnC{I}_{it}$ is the natural logarithm of CI of city $i$ in year $t$; $W$ is the spatial weighted matrix; $X_{it}$ is a set of control variables; $W{X}_{it}$ is the interaction term of $W$ and $X_{it}$; $DIG{A}_{it}\mathrm{and}SDIG{A}_{it}$ are the primary and squared term of the DIGA of city $i$ in year $t$;$u_{1i}\mathrm{and}{u}_{2i}$ are individual-fixed and time-fixed terms, respectively; ${\epsilon }_{1it}$ is the error term; $a_1$ is the intercept term; and $\rho \mathrm{and}\beta$ are the estimated parameters of the corresponding variables.

4.1.3. Mediating Effect Model

Theoretical analysis indicates that DIGA may indirectly affect CI through technology effects and industrial structure effects. Specifically, GTI, ISR, and ISA may be the channels through which DIGA affects CI. To test Hypotheses 2, 3, and 4, following Baron and Kenny [66], we deployed a mediating effects model, which was set as:

$$\begin{gathered} lnC{I}_{it}=a_1+{\rho }_{1}WlnC{I}_{it}+{\beta }_{1}DIG{A}_{it}+{\rho }_{2}WDIG{A}_{it}+{\beta }_{2}SDIG{A}_{it} \\ +{\rho }_{3}WSDIG{A}_{it}+\beta X_{it}+\rho W{X}_{it}+u_{1i}+{\nu }_{1t}+{\epsilon }_{1it} \end{gathered}$$

(5)

$$\begin{gathered} Me{d}_{it}=a_2+{\phi }_1\mathit{W}Me{d}_{it}+{\gamma }_{1}DIG{A}_{it}+{\phi }_2\mathit{W}DIG{A}_{it}+{\gamma }_{2}SDIG{A}_{it} \\ +{\phi }_{3}WSDIG{A}_{it}+\gamma X_{it}+\phi W{X}_{it}+u_{2i}+{\nu }_{2t}+{\epsilon }_{2it} \end{gathered}$$

(6)

$$\begin{gathered} lnC{I}_{it}=a_3+{\chi }_1\mathit{W}lnC{I}_{it}+{\delta }_{1}DIG{A}_{it}+{\chi }_2\mathit{W}DIG{A}_{it}+{\delta }_{2}SDIG{A}_{it} \\ +{\chi }_3\mathit{W}SDIG{A}_{it}+{\delta }_{3}Me{d}_{it}+{\chi }_4\mathit{W}Me{d}_{it}+\mathsf{\delta }{\mathit{X}}_{\mathit{i}\mathit{t}}+\mathsf{\chi }\mathit{W}{\mathit{X}}_{\mathit{i}\mathit{t}} \\ +u_{3i}+{\nu }_{3t}+{\epsilon }_{3it} \end{gathered}$$

(7)

where $Me{d}_{it}$ is the mediator, defined as the GTI, ISR, or ISA of city $i$ in year $t$; $\rho , \beta , \phi , \gamma , \chi , \mathrm{and} \delta$ are the estimated parameters of the corresponding variables; $a_1, a_2, \mathrm{and} a_3$ are the intercept terms of Models (5), (6), and (7), respectively; $u_{1i},u_{2i}, \mathrm{and} u_{3i}$ are the individual-fixed terms of Models (5), (6), and (7), respectively; $v_{1t}, v_{2t}, \mathrm{and} v_{33}$ are the time-fixed terms of Models (5), (6), and (7), respectively; ${\epsilon }_{1it}, {\epsilon }_{2it},\mathrm{and}{\epsilon }_{3it}$ are the error terms of Models (5), (6), and (7), respectively.

4.1.4. Moderating Models

Based on theoretical research, this study contends that the EDU and GI are important moderators of the process of DIGA in influencing CI. To test Hypotheses 5 and 6, following Baron and Kenny [66], we deployed a moderating effects model, which was set as:

$$\begin{gathered} lnC{I}_{it}=a_1+{\rho }_{1}WlnC{I}_{it}+{\beta }_{1}DIG{A}_{it}+{\rho }_{2}WDIG{A}_{it}+{\beta }_{2}SDIG{A}_{it}+{\rho }_3 \\ WSDIG{A}_{it}+\beta X_{it}+\rho W{X}_{it}+u_{1i}+{\nu }_{1t}+{\epsilon }_{1it} \end{gathered}$$

(8)

$$\begin{gathered} lnC{I}_{it}=a_4+{\sigma }_1\mathit{W}lnC{I}_{it}+{\eta }_{1}DIG{A}_{it}\times Mo{d}_{it}+{\sigma }_2\mathit{W}DIG{A}_{it}\times Mo{d}_{it} \\ +{\eta }_{2}SDIG{A}_{it}\times Mo{d}_{it}+{\sigma }_3\mathit{W}SDIG{A}_{it}\times Mo{d}_{it}+\mathsf{\eta }{\mathit{X}}_{\mathit{i}\mathit{t}} \\ +\mathsf{\sigma }\mathit{W}{\mathit{X}}_{\mathit{i}\mathit{t}}+u_{4i}+{\nu }_{4t}+{\epsilon }_{4it} \end{gathered}$$

(9)

where $Mo{d}_{it}$ is the moderator defined as the EDU or GI of city $i$ in year $t$; $DIG{A}_{it}\times Mo{d}_{it}$ is the intersection term of $DIG{A}_{it}$ and $Mo{d}_{it}; SDIG{A}_{it}\times Mo{d}_{it}$ is the intersection term of $SDIG{A}_{it}$ and $Mo{d}_{it}$; $u_{4i} \mathrm{and} u_{4i}$ are the individual-fixed and time-fixed terms, respectively; ${\epsilon }_{4it}$ is an error term; $a_4$ is the intercept term; and $\sigma \mathrm{and} \eta$ are parameters to be estimated.

4.2. Data

4.2.1. Measure of Digital Enterprise Agglomeration

Economic agglomeration is a key geographical feature in economic activities, and its measurement methods have been widely studied [24,29,59,65]. The division of spatial units is a key factor affecting the accuracy of measurement results. According to whether the space of the measurement object is divided into units, the measures are summarized into two types: the economic agglomeration index of discrete distance and the economic agglomeration index of continuous space. These two types of methods have some differences in terms of data requirements, measurement results, and spatial attributes. Discrete economic agglomeration measures, such as the location entropy index [27] and Herfindahl–Hirschman index [56], mainly assess the intensity of the economic agglomeration in a single geographical unit, suffering from the MAUP caused by the division of administrative units. In addition, these measures fragment the economic agglomeration areas near the administrative boundary, leading to the underestimation of economic agglomeration. Continuous economic agglomeration measures, such as the Duranton and Overman (DO) index [33], focus on the spatial extent of enterprise agglomeration and effectively avoid the MAUP. Discrete economic agglomeration measurement methods mainly employ macro data of firm output and employment, ignoring the spatial distribution characteristics of enterprises and business activities. The calculation of the continuous spatial enterprise agglomeration index relies on geographical distance data, such as latitude and longitude, which more effectively reflect the spatial distribution of enterprises. Therefore, we used the DO index to measure DIGA.

Measuring DIGA consists of four steps. First is the identification of digital economy enterprises, obtaining their latitude and longitude. We first compiled a set of keywords based on the connotation, formation elements, and scope of the digital economy. Then, we screened the enterprises whose business scope included keywords from Qichahca (https://www.qcc.com). Qichahca is a national enterprise credit agency officially filed with the Chinese government that provides various types of business, financial, and court judgment information, such as enterprise name, address, business scope, industry, registered capital, registration time, cancellation time, and business registration number. At the same time, we combined the industry classification standards of The International Standard Industrial Classification of All Economic Activities Revision 4 and Industrial Classification for National Economic Activities Revision 2017 to further control the industries to which the enterprises belong in order to determine the digital enterprises. Finally, we applied the AutoNavi Map API to process the name and address of the enterprise to obtain the specific longitude and latitude of the enterprise.

Second, the kernel density function needs to be estimated. Assuming that subsector $I$ in the digital economy industry has $n$ digital firms, then $\frac{n\left(n+1\right)}{2}$ bilateral Euclidean distances can be calculated via the longitude and latitude of digital enterprises. The real world is intricate, and the direct application of Euclidean distances to measure the distance between enterprise $i$ and $j$ causes underestimated results [33]. Hence, we used the kernel function to estimate the density of bilateral distances at any distance $d$:

$$\widehat{K_I}\left(d\right)=\frac{1}{n\left(n-1\right)h}{{\displaystyle \sum }}_{i=1}^{n-1}{\displaystyle \sum }_{j=i+1}^{n}f\left(\frac{d-d_{ij}}{h}\right)$$

(10)

where $d$ denotes the distance of enterprises; $h$ represents bandwidth; $d_{ij}$ is the Euclidean distance between enterprise $i$ and $j$; $f( )$ is the Gaussian kernel function in this study.

In addition, considering the effect of the size of digital firms on the calculation results, this study recalculated Equation (10) by adding weights of size. The size of digital firms is reflected by the registered capital in our study. Then, we introduced the weighted density of the bilateral distances at any distance, $d$, based on a measure by Duranton and Overman [33]:

$$\widehat{K_I^W}\left(d\right)=\frac{1}{n\left(n-1\right)h}{{\displaystyle \sum }}_{i=1}^{n-1}{\displaystyle \sum }_{j=i+1}^{n}f\left(\frac{d-d_{ij}}{h}\right)\frac{\left(e_i+e_j\right)}{{{\displaystyle \sum }}_{i=1}^{n-1}{{\displaystyle \sum }}_{j=i+1}^n\left(e_i+e_j\right)}$$

(11)

where $e_i$ and $e_j$ are the registered capital of enterprises $i$ and $j$, respectively.

Third, counterfactuals need to be built. Comparing the actual distribution of firms with the random distribution can determine whether subsector $I$ is localized or dispersed. Assuming that the location of digital economy enterprises in subsector $I$ forms a location set, simulated digital economy enterprises can select any one location from the set. Hence, we randomly drew $n$ data from the location set without put-back as a distribution of $n$ simulated firms, consisting of the random distribution. Finally, we estimate the kernel density of random distribution. The time of random experiments is 1000.

Fourth, global confidence intervals need to be built. For a given distance $d$, the 1000 kernel density values are obtained. We treat the quintiles 5 and 95 as the lower and upper limits of the confidence bands, respectively, and denote them as $\underset{\_}{\underset{\_}{K_I^W}}\left(d\right)$ and $\overline{\overline{K_I^W}}\left(d\right)$. Referring to Duranton and Overman [33], the global agglomeration index for the subsector $I$ (${}_A^W\left(d\right)$) is defined as:

$${\lceil }_I^W\left(d\right)=\max \left\{\widehat{{\mathrm{K}}_I^W}\left(d\right)-\overline{\overline{K_I^W}}\left(d\right),0\right\}$$

(12)

To further measure the $DIGA$ index of industry $I$ at the city level, we measured the agglomeration degree of industry $A$ within any distance ($D$) by cumulating ${\lceil }_I^W\left(d\right)$:

$$DIG{A}_{I,c}={{\displaystyle \sum }}_{d=0}^D{\lceil }_I^W\left(d\right)$$

(13)

As the volume of digital firms greatly impacts the agglomeration level, we considered the number of digital economy enterprises in industry $A$ in city $c$:

$$DIG{A}_c={{\displaystyle \sum }}_{I}DIG{A}_{I,c}\frac{Coun{t}_{I,c}}{{{\displaystyle \sum }}_{I}Coun{t}_{I,c}}$$

(14)

where $Coun{t}_{I,c}$ represents the volume of digital firms in industry $I$ in city $c$.

4.2.2. Carbon Intensity

CI is the core independent variable. There are no official Chinese data on CO₂ emissions at the prefecture-level city level that have been publicly issued [41]. Commonly used data on city CO₂ emissions are calculated using two methods. Some scholars have used the Intergovernmental Panel on Climate Change formula and energy consumption data from large industrial enterprises to measure CO₂ emissions [8]. This measure only takes into account the energy consumption of large industrial enterprises, which suffer from the problem of incomplete types of energy consumption. To improve the accuracy of the measurement and provide data with broader coverage, Chen et al. [67] calculated the CO₂ emissions of 2735 counties using machine learning techniques, and the data are publicly available through the Carbon Emission Accounts and Datasets (CEADs, https://www.ceads.net ( accessed on 22 January 2023). To obtain the carbon emissions at the city level, we cumulated the data for each county in the city:

$$CO{2}_{it}={{\displaystyle \sum }}_{j=1}^{n}CO{2}_{ijt}$$

(15)

where $CO{2}_{it}$ denotes the CO₂ of city $i$ in year $t$; $CO{2}_{ijt}$ is the CO₂ of county $j$ of city $i$ in year $t$; and $n$ is the number of counties of city $i$.

This study used the ratio of carbon emissions scaled by real GDP to calculate the CI:

$$C{I}_{it}=\frac{CO{2}_{it}}{GD{P}_{it}}$$

(16)

where $GD{P}_{it}$ is the real GDP of city $i$ in year $t$.

4.2.3. Control Variable

We controlled for five variables to mitigate the endogeneity problems associated with omitting important variables.

(1) Population density (PD): Based on Marshall’s theories of economic agglomeration [50], an increased population density results in the concentration of population, creating a specialized division of labor, which may significantly reduce CI through economies of scale. Following Yan and Huang [6], we used the logarithm of population per square kilometer to measure PD.

(2) Per capita GDP (PGDP): There is an essential link between environmental quality and economic development [68]. Per capita income can well reflect a city’s economic level. Following Grossman and Krueger [68], we employed the logarithm of urban GDP per capita to measure PGDP.

(3) Infrastructure (INFRA): The economic development potential of a city and the selection of businesses are greatly impacted by transportation conditions [69]. Lin and Chen [58] contended that land transport infrastructure is strongly related to carbon emission efficiency. Referring to Xu, Fan, Yang, and Shao [7], the study measured INFRA using the logarithm of the ratio of the total length of roads to the administrative area at the end of the year in each city.

(4) Openness (OPEN): Openings help attract foreign enterprises with better eco-friendly and carbon-reduction technologies [7,13] and lead to cleaner production and efficient pollution treatment by local enterprises through technology spillover effects, contributing to carbon reduction. However, the adoption of foreign technologies may inhibit green innovation by local enterprises [7] which in turn is detrimental to the reduction of CI. Referring to Xu, Fan, Yang, and Shao [7], we deployed the proportion of foreign investment in GDP to identify OPEN.

(5) Environmental regulation (ER): Some studies suggest that moderate ER reduces CO₂ [70,71]. However, overly stringent ER may force companies to relocate and move to areas with fewer ERs. Following Yang et al. [72], we employed the frequency of environmental protection-related words in local government work reports to assess ER.

4.2.4. Mediator and Moderator

(1) Green technology innovation

Green patents are one of the most commonly used indicators to measure a company’s green innovation ability [7]. According to the Chinese Research Data Services (CNRDS, https://www.cnrds.com (accessed on 22 January 2023)) database, green patent data include the number of green patent applications and green patents granted. Zhao, Nakonieczny, Jabeen, Shahzad, and Jia [63] and Xu, Fan, Yang, and Shao [7] argued that granting green patents has time lag effects. The number of green patents granted cannot accurately measure green GTI. Therefore, using data on green patent applications is a better measure of GTI than data on green patents granted. In addition, large cities usually have more green patent applications due to the fact of their greater economies and population size. As a result, following Xu, Fan, Yang, and Shao [7], we used the number of green patent applications per 10,000 people to measure urban GTI.

(2) Industrial structure rationalization

According to resource allocation theory, ISR reflects the efficiency of the allocation, coordination, and adoption of production factors among industries. Most empirical studies measure ISR based on resource allocation theory, defining ISR as an indicator to measure the coupling degree between factor input structure and output structure [52,71]. To assess this degree of coupling, the structural deviation was proposed [71]:

$$E={{\displaystyle \sum }}_{i=1}^n\left|\frac{\raisebox{1ex}{$Y_i$}\!\left/ \!\raisebox{-1ex}{$Y$}\right.}{\raisebox{1ex}{$L_i$}\!\left/ \!\raisebox{-1ex}{$L$}\right.}-1\right|$$

(17)

where $\raisebox{1ex}{$Y_i$}\!\left/ \!\raisebox{-1ex}{$Y$}\right.$ is the output structure; $\raisebox{1ex}{$L_i$}\!\left/ \!\raisebox{-1ex}{$L$}\right.$ is the labor input structure; $Y_i \mathrm{and} L_i$are GDP and labor in city $i$.

As the structural deviation index does not reflect the importance of each industry, and a calculation with absolute values is inconvenient, the Theil index with structure deviation was developed [71]:

$$IS{R}_{it}={{\displaystyle \sum }}_{j=1}^n\left(\frac{Y_{ijt}}{Y_{it}}\right)ln\left(\frac{\raisebox{1ex}{$Y_{ijt}$}\!\left/ \!\raisebox{-1ex}{$L_{ijt}$}\right.}{\raisebox{1ex}{$Y_{it}$}\!\left/ \!\raisebox{-1ex}{$L_{it}$}\right.}\right)$$

(18)

where $Y_{ijt} \mathrm{and} L_{ijt}$ are the GDP output and labor input of industry $j$ of city $i$ in year $t$, respectively; $Y_{it} \mathrm{and} L_{it}$ are the total GDP and labor of city $i$ in year $t$; and $n=3$, indicating the three different industries. The smaller the ISR, the more the economy deviates from the equilibrium and the more irrational the industrial structure.

(3) Industrial structure advancement (ISA)

The service sector is mostly knowledge and technology-intensive [9], and its technical complexity and added value are usually high. Therefore, the transformation of a city’s industries into service industries indicates that the industrial structure is being upgraded to a high degree. Following Zhu, Zhang, Zhou, Wang, Sheng, He, Wei, and Xie [52], ISA was determined by the ratio of third- to second-sector added value.

(4) Human capital (EDU)

Human capital refers to a person’s degree of knowledge and personal competence, reflecting their production skills [61]. Higher education is an important means of accumulating human capital in the process of human capital development, so human capital is positively related to the level of education [73]. Taking into account the influence of city size and referring to Zhu, Zhang, Zhou, Wang, Sheng, He, Wei, and Xie [52] and Yuan, Zou, Luo, and Feng [56], we used college and university enrollment per 10,000 people to quantify urban human capital.

(5) Government intervention (GI)

Government intervention refers to the actions by the government to intervene in the market economy through policy instruments. Government interventions include central and local government interventions. Due to the availability of data, only local government intervention is of interest in this study. Following Lee and Wang [11] and Zhao, Nakonieczny, Jabeen, Shahzad, and Jia [63], the ratio of local general public budget expenditures in GDP was used to calculate GI.

4.3. Research Sample and Data Source

This paper used 2007 as the starting year since the volume of China’s digital economy was small before that year and many cities lacked a significant agglomeration of digital enterprises. The data on carbon emissions at the county level from CEADs were updated in 2017. Accordingly, our research period was from 2007–2017. As the data on Chinese cities at the prefecture level were the most complete, our basic research unit was the prefecture-level city. Due to the absence of data records in several cities, such as Longnan and Lhasa, this study selected 278 prefecture-level or above cities as the research area, as shown in Figure 3. The raw map is from China’s National Basic Geographic Information Database.

The data on digital economy enterprises were obtained from Qichacha. The data on CO₂ were from CEADS. The data regarding green patents came from CNRDS. The data measuring governmental regulation were from government work reports. Other data mainly came from the Easy Professional Superior database.

5. Empirical Analysis

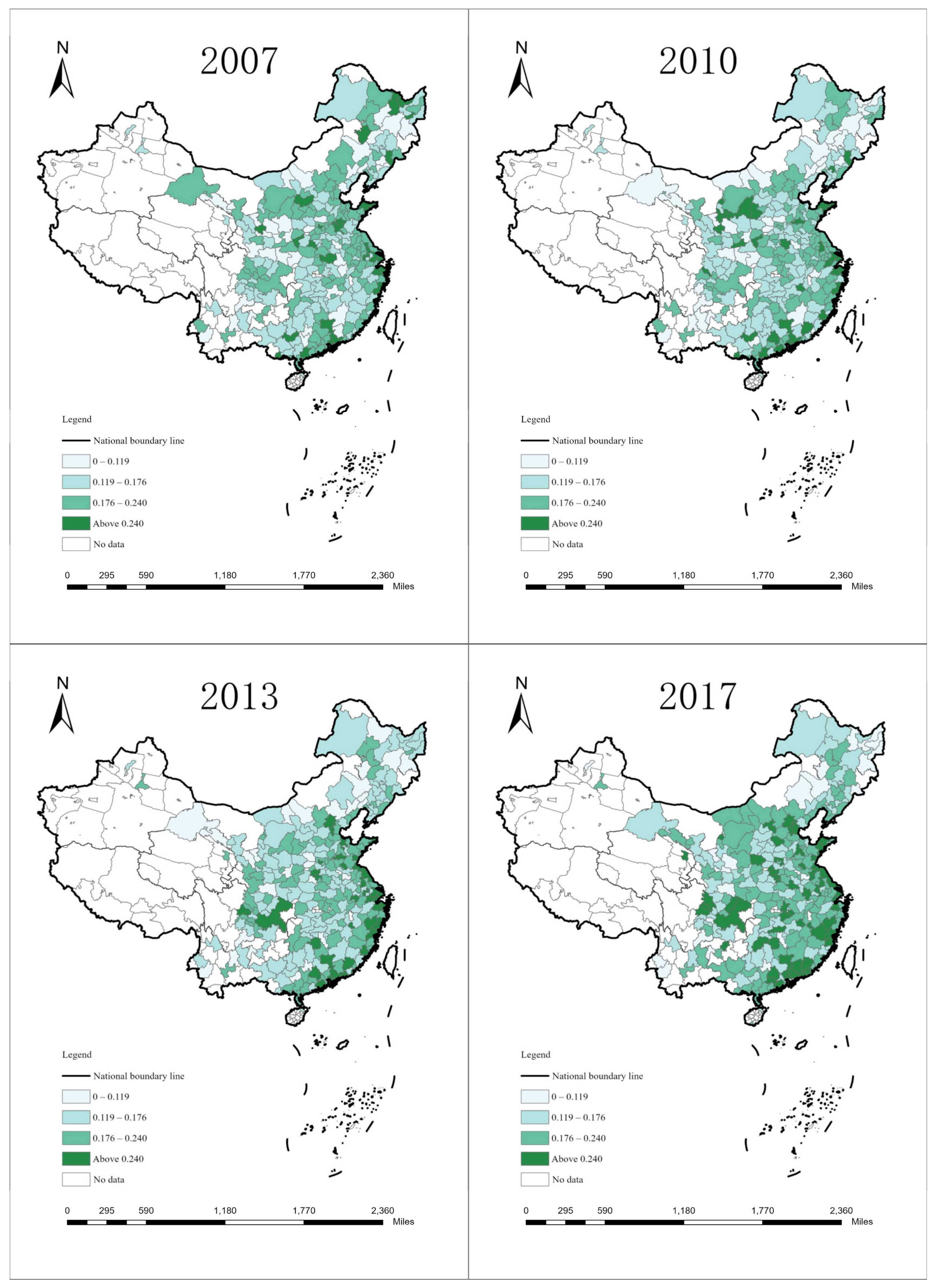
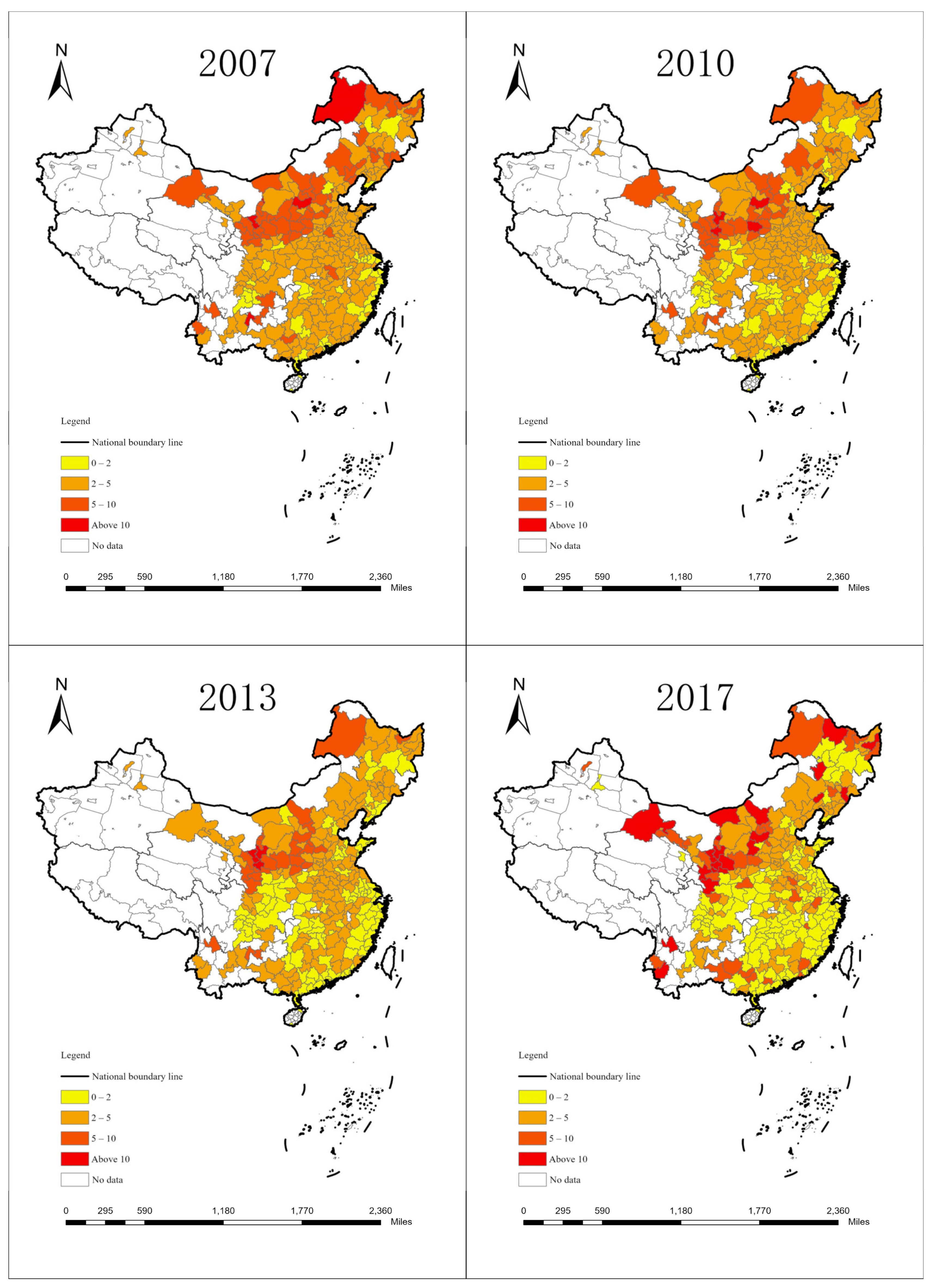
5.1. Temporal–Spatial Distribution Characteristics of Digital Enterprise Agglomeration and Carbon Intensity

Figure 4 and Figure 5 demonstrate the spatial and temporal changes in DIGA and CI between 2007 and 2017.

First, as can be seen in Figure 4, coastal cities had higher levels of DIGA than inland cities. Cities in the south had significantly higher levels of DIGA than those in the north. These geospatial distribution characteristics are consistent with the fact that development is uneven among different regions of China [56]. Second, the development phenomenon of DIGA was not evident before 2013. Compared to 2013, there were significantly more cities with DIGA over 0.176 in 2017. Third, we found an interesting phenomenon in that DIGA in northeast China showed a decreasing level from 2007 to 2017, which is contrary to the digital economy boom in China over the last decade. We contend that this is mainly related to the brain drain and extreme climate in the northeast. Historically in China, the northeast experienced a longer period of planned economy and missed an opportunity to reform the economic system [74]. Influenced by the planned economy, the poor social service system and outdated management style of private enterprises in the northeast have constrained the growth of the private economy, as well as the agglomeration of digital firms.

When it comes to CI, as can be seen in Figure 5, it was high throughout China in 2007 and 2010. However, in 2013 and 2017, the CI of cities in southern China decreased significantly but remained high in the north, indicating that southern cities had a better performance than the north in terms of green transformation. Therefore, China should focus on guiding the northern regions to reduce CI in the process of achieving the carbon neutrality target, in particular, the Inner Mongolia Autonomous Region, located on the northern border of China, the Ningxia Hui Autonomous Region and Gansu Province in the northwest, and Heilongjiang Province in the far northeast of China. In addition, the Yangtze River Delta and the Pearl River Delta, two of China’s most economically developed regions, are leading the way in high-quality economic growth [75]. Comparing the two economic zones, the proportion of cities with a CI greater than 10 in the Yangtze River Delta Economic Zone is significantly lower than that in the Pearl River Delta, implying that the environment of synergistic governance in the Pearl River Delta Economic Zone needs to be enhanced and that CO₂ emissions cannot be reduced simply by transferring heavy polluting enterprises.

5.2. The Direct Impact of Digital Enterprise Agglomeration on Carbon Intensity

5.2.1. Panel Unit Root Test

Pseudo-regression problems may stem from the parameter estimation of nonstationary data, so we first identified whether our data were stationary through panel unit root tests. As our data were in a short panel, we employed the Harris–Tzavalis (HT) test. From

Table 1. Panel unit root tests of variables.

Variable	HT
	No Constant	Intercept Term	Intercept Term and Time Trend
lnCI	1.012	0.423 ***	0.071 ***
DIGA	0.912 ***	0.679 ***	0.342 ***
SDIGA	0.928 ***	0.704 ***	0.371 ***
lnPD	0.897 ***	0.609 ***	0.235 ***
lnPGDP	0.976 ***	0.763	0.370 ***
lnINFRA	0.922 ***	0.561 ***	0.300 ***
OPEN	0.8723 **	0.647 ***	0.335 ***
ER	0.543 ***	0.224 ***	−0.023 ***

***, **, and * indicate a significance level of 1%, 5%, and 10%, respectively.

, all variables passed the panel unit root test, indicating that the variables were stationary, and the regression results did not have pseudo-regression problems.

5.2.2. Spatial Autocorrelation Test

To determine whether the variables were spatially autocorrelated and whether the spatial econometric models were suitable for our study, we performed a spatial autocorrelation test. In general, the global Moran’s I is used to measure the degree of the spatial autocorrelation of variables [28,62,65]. The specific formula is:

$$I=\frac{{{\displaystyle \sum }}_{i=1}^n{{\displaystyle \sum }}_{j=1}^n{w}_{ij}\left(x_i-\overline{x}\right)\left(x_j-\overline{x}\right)}{{{\displaystyle \sum }}_{i=1}^n{\left(x_i-\overline{x}\right)}^2}$$

(19)

where $w_{ij}$ is the distance between city $i$ and $j$ in the spatial weighted matrix; $x_i$ and $x_j$ represent the value of variable $x$ of city $i$ and $j$, respectively; and $\overline{x}$ represents the mean of variable $x$.

We use the global Moran’s I index to examine the spatial autocorrelation. When performing the spatial autocorrelation test, the construction of suitable spatial weighted matrices is the first step. Most studies use 0–1 matrices [28] or geographical distance matrices [11,63] to construct the spatial weighted matrices based on the perspective of geographical distance. However, spatial weighted matrices that ignore socioeconomic distances cannot fully measure the spatial correlation among variables. At the same time, spatial units have different strengths in terms of influence on each other [76]; for example, Beijing’s impact on Baoding is greater than Baoding’s impact on Beijing. Therefore, we constructed an asymmetrical economic–geographic spatial weighted matrix $(W_1)$ and asymmetrical technical–geographic spatial weighted matrix $(W_2)$ for the spatial econometric analysis.

$$W_1=W_g\times diag\left(\frac{\overline{E_1}}{\overline{E}},\frac{\overline{E_2}}{\overline{E}},L,\frac{\overline{E_n}}{\overline{E}}\right)$$

(20)

$$\overline{E_i}=\frac{{{\displaystyle \sum }}_{t_0}^{t_1}{E}_{it}}{\left(t_1-t_0+1\right)},i=1,2,\dots ,n$$

(21)

$$\overline{E}=\frac{{{\displaystyle \sum }}_{k=1}^n{{\displaystyle \sum }}_{t_0}^{t_1}{E}_{it}}{n\left(t_1-t_0+1\right)},i=1,2,\dots ,n$$

(22)

$$W_2=W_g\times diag\left(\frac{\overline{IC{T}_1}}{\overline{ICT}},\frac{\overline{IC{T}_2}}{\overline{ICT}},L,\frac{\overline{IC{T}_n}}{\overline{ICT}}\right)$$

(23)

$$\overline{IC{T}_i}=\frac{{{\displaystyle \sum }}_{t_0}^{t_1}IC{T}_{it}}{\left(t_1-t_0+1\right)},i=1,2,\dots ,n$$

(24)

$$\overline{ICT}=\frac{{{\displaystyle \sum }}_{k=1}^n{{\displaystyle \sum }}_{t_0}^{t_1}IC{T}_{it}}{n\left(t_1-t_0+1\right)},i=1,2,\dots ,n$$

(25)

where $W_g$ indicates the spatial weighted matrix of the geographic distance based on latitude and longitude; $\overline{E_{it}} \mathrm{and} \overline{IC{T}_{it}}$ are the GDP per capita and IT development per capita of city $i$ in time $t$; $\overline{E_i} \mathrm{and} \overline{IC{T}_i}$ are the GDP per capita and IT development per capita for city $i$ from $t_0$ to $t_1$; and $\overline{E} \mathrm{and} \overline{ICT}$ are the GDP per capita and IT development per capita of all cities during the study period. All spatial weighted matrices have been normalized.

We performed spatial autocorrelation tests using $W_1$ and $W_2$ year by year.

Table 2. Spatial autocorrelation tests results.

Economy–Geographical Weighted Matrix (W1)
Year	lnCI	DIGA	SDIGA	lnPD	lnPGDP	lnINFRA	OPEN	ER
2007	0.161 ***	0.049 **	0.050 ***	0.029 ***	0.093 ***	0.061 ***	0.129 ***	0.072 ***
2008	0.158 ***	0.048 *	0.051 ***	0.036 ***	0.091 ***	0.068 ***	0.116 ***	0.037 ***
2009	0.150 ***	0.061 ***	0.065 ***	0.032 ***	0.087 ***	0.070 ***	0.124 ***	0.025 ***
2010	0.150 ***	0.072 ***	0.079 ***	0.033 ***	0.086 ***	0.063 ***	0.109 ***	0.030 ***
2011	0.146 ***	0.082 **	0.090 ***	0.038 ***	0.082 ***	0.060 ***	0.092 ***	0.034 ***
2012	0.146 ***	0.096 ***	0.103 ***	0.040 ***	0.078 ***	0.066 ***	0.097 ***	0.024 ***
2013	0.150 ***	0.096 ***	0.103 ***	0.041 ***	0.076 ***	0.059 ***	0.086 ***	0.010 **
2014	0.154 ***	0.082 ***	0.088 ***	0.042 ***	0.078 ***	0.055 ***	0.062 ***	0.016 ***
2015	0.125 ***	0.052 ***	0.044 ***	0.041 ***	0.077 ***	0.058 ***	0.053 ***	0.010 **
2016	0.171 ***	0.043 ***	0.037 ***	0.041 ***	0.087 ***	0.057 ***	0.054 ***	0.012 ***
2017	0.115 ***	0.032 ***	0.024 ***	0.035 ***	0.090***	0.054 ***	0.038 ***	0.008 ***
ICT–Geographical Weighted Matrix (W2)
2007	0.127 ***	0.051 **	0.054 ***	0.024 ***	0.107 ***	0.044 ***	0.109 ***	0.058 ***
2008	0.127 ***	0.054 *	0.060 ***	0.030 ***	0.102 ***	0.046 ***	0.090 ***	0.037 ***
2009	0.124 ***	0.068 ***	0.075 ***	0.029 ***	0.097 ***	0.047 ***	0.092 ***	0.028 ***
2010	0.124 ***	0.073 ***	0.079 ***	0.033 ***	0.097 ***	0.043 ***	0.068 ***	0.023 ***
2011	0.117 ***	0.085 **	0.094 ***	0.038 ***	0.094 ***	0.041 ***	0.045 ***	0.030 ***
2012	0.118 ***	0.094 ***	0.103 ***	0.037 ***	0.088 ***	0.046 ***	0.051 ***	0.022 ***
2013	0.115 ***	0.091 ***	0.101 ***	0.038 ***	0.086 ***	0.039 ***	0.040 ***	0.008 **
2014	0.116 ***	0.077 ***	0.085 ***	0.037 ***	0.087***	0.034 ***	0.035 ***	0.017 ***
2015	0.091 ***	0.047 ***	0.039 ***	0.035 ***	0.085 ***	0.035 ***	0.022 ***	0.007 *
2016	0.121 ***	0.032 ***	0.026 ***	0.033 ***	0.093 ***	0.034 ***	0.033 ***	0.017 ***
2017	0.074 ***	0.022 ***	0.015 ***	0.028 ***	0.092 ***	0.031 ***	0.023 ***	0.007

***, **, and * indicate a significance level of 1%, 5%, and 10%, respectively.

shows the results, which reveal that all variables passed the 1% significance test except for ER under both $W_1$ and $W_2$. Regarding ER, all were statistically significant for $W_1$. ER is only statistically insignificant for $W_2$ in 2017. Referring to Yuan, Feng, Lee, and Cen [76], we can still consider that ER is spatially correlated. In conclusion, this study is applicable to the spatial econometric model.

5.2.3. Model Selection

Spatial econometric models take many forms, and inappropriate spatial econometric models cannot accurately estimate parameters. Before performing spatial econometric regression, it is essential to select the most suitable model to study DIGA’s impact. The model selection tests consisted of four steps. First, we performed the Hausman test. The results of the Hausman test, as shown in

Table 3. Model selection tests.

Test	Chi-Square Statistic
	W1	W2
Hausman test	41.21 ***	41.21 ***
LR test (ind. vs. both)	59.15 ***	59.15 ***
LR test (time vs. both)	5079.95 ***	5079.95 ***
LM test (error)	3228.707 ***	1208.063 ***
Robust LM test (error)	1418.847 ***	360.598 ***
LM test (lag)	1931.322 ***	984.134 ***
Robust LM test (lag)	121.461 ***	136.669 ***
Wald test (lag)	51.40 ***	40.05 ***
Wald test (error)	59.74 ***	41.51 ***
LR test (lag)	54.03 ***	40.38 ***
LR test (error)	59.97 ***	25.22 ***

***, **, and * indicate a significance level of 1%, 5%, and 10%, respectively.

, indicate that we should use a fixed effects model. Second, we performed LR tests. Based on the results of the LR test (ind./time vs. both), as shown in Table 3, we should use a fixed effects model with both individual- and time-fixed effects. Third, we performed LM tests. From Table 3, the LM and robust LM test results indicate that the SDM, SAR, and SEM are all applicable to this study. Finally, we performed Wald and LR tests. The Wald test and LR tests, as shown in Table 3, indicate that SDM cannot be reduced to SAR or SEM. As a result, this study is more applicable to the SDM. In all subsequent model estimations, we employed the SDM and controlled individual and time effects for the parameter estimation.

5.2.4. Spatial Econometric Regression Results

We performed SDM estimation using $W_1$ and $W_2$, respectively. Model 1 shows the results of the SDM with the individual- and time-fixed effects under $W_1$; Model 2 shows the results of the SDM with the individual- and time-fixed effects under $W_2$. To facilitate the subsequent analysis, Model 1 is defined as the baseline model in this study.

According to Model 1, in

Table 4. Baseline model results.

	Spatial
	SDM_W1	SDM_W2
Model	1	2
DIGA	0.973 ** (2.21)	0.976 ** (2.18)
SDIGA	−2.878 *** (−2.68)	−2.967 *** (−2.72)
lnPD	0.000 (0.03)	0.005 (0.50)
lnPGDP	−0.231 *** (−9.68)	−0.256 *** (−10.56)
lnINFRA	0.069 *** (3.72)	0.078 *** (4.15)
OPEN	0.785 ** (2.18)	0.292 (0.82)
ER	−1.600 (−0.51)	−0.583 (−0.18)
W*DIGA	16.307 *** (3.22)	11.651 ** (2.20)
W*SDIGA	−41.865 *** (−3.67)	−27.016 ** (−2.48)
W*lnPD	0.162 (1.29)	−0.564 *** (−2.90)
W*lnPGDP	0.118 (0.69)	0.092 (0.41)
W*lnINFRA	1.017 *** (3.77)	−0.153 (−0.52)
W*OPEN	−9.035 *** (−3.64)	−1.060 (−0.41)
W*ER	149.400 *** (3.66)	125.826 *** −3.26
Constant
rho	0.587 ***	0.3 ***
Time-fixed effect	YES	YES
City-fixed effect	YES	YES
N	3058	3058

The values in brackets are t-values or z-values with ***, **, and * indicating significance levels of 1%, 5%, and 10%, respectively.

, the coefficients of SDIGA are −2.878 and −2.967, significant at the 1% level, showing that DIGA had an inverted “U-shaped” effect on CI. Specifically, between 2007 and 2017, as DIGA increased, local CI decreased and then increased. This might be cause for many reasons. The 2008 global financial crisis hampered China’s economic development. Chinese cities developed significant digital infrastructure to boost economic growth during the financial crisis. China’s production technology level at this stage was low, and economic development was mainly driven by factor inputs rather than by technological progress and productivity improvement. Therefore, DIGA in Chinese cities at this stage contributes to local CI. When DIGA crosses a certain inflection point, the positive impact of DIGA outweighs the negative impact, and DIGA reduces CI. The possible causes are proposed as follows. First, DIGA may improve enterprise productivity and resource utilization efficiency through economies of scale and network economy, reducing local CI. Second, DIGA forms a specialized labor market through digital talent agglomeration. The improvements in the frequency of talent exchange and efficiency in talent matching may promote knowledge spillovers and reduce human capital mismatch to improve labor productivity [9], decreasing local CI. Third, the modern economy relies heavily on data for its production. DIGA boosts the platform economy. Algorithm optimization reduces enterprise computing’s consumption of power energy, and data-driven smart crating dampens local CI via improved logistics.

As can be seen in the coefficient of W*SDIGA in Model 3, there is a spatial spillover effect of DIGA on CI. The possible causes are as follows: Ren, Li, Han, Hao, and Wu [9] contend that technology and knowledge drive the digital economy. The knowledge and technology spillover effects may impact surrounding cities’ CI by improving enterprises’ clean production technologies and residents’ digital literacy. In addition, the digital economy’s penetration and diffusion effects will rapidly spread digital technology innovation [39], impacting neighboring cities’ CI.

5.3. Spatial Spillover Effect Analysis

To analyze the marginal effects of each variable on the local CI and nearby CI, following Cheng, Zhang, Wang, and Jiang [10], we performed a spatial effect decomposition analysis. The total effect is the average effect of the independent variable on the CI of all regions, which is the sum of the direct and indirect effects; the direct effect is the impact of the independent variable on local CI, and the indirect effect is the effect of the independent variable on the CI of the neighboring cities.

Table 5. Spatial spillover effect results.

	Effect	DIGA	SDIGA	lnPD	lnPGDP	lnINFRA	OPEN	ER
W1	Total effect	42.613 *** (2.78)	−110.322 *** (−2.92)	0.420 (1.25)	−0.280 (−0.70)	2.732 *** (3.03)	−21.106 *** (−2.58)	375.386 *** (2.62)
	Direct effect	1.127 ** (2.48)	−3.282 *** (−2.95)	0.003 (0.29)	−0.232 *** (−10.18)	0.078 *** (4.23)	0.730 ** (2.06)	−0.355 (−0.11)
	Indirect effect	41.486 *** (2.72)	−107.040 *** (−2.85)	0.417 (1.25)	−0.048 (−0.12)	2.654 *** (2.96)	−21.836 *** (−2.67)	375.741 *** (2.63)
W2	Total effect	18.077 ** (2.30)	−42.867 ** (−2.51)	−0.813 ** (−2.40)	−0.244 (−0.77)	−0.092 (−0.20)	−1.288 (−0.35)	186.157 *** (2.61)
	Direct effect	1.025 ** (2.23)	−3.095 *** (−2.76)	0.004 (0.46)	−0.256 *** (−11.01)	0.078 *** (4.26)	0.306 (0.87)	−0.217 (−0.07)
	Indirect effect	17.052 ** (2.18)	−39.772 ** (−2.34)	−0.818 ** (−2.42)	0.012 (0.40)	−0.170 (−0.37)	−1.594 (−0.43)	186.374 *** (2.63)

The values in brackets are z-values with ***, **, and * indicating significance levels of 1%, 5%, and 10%, respectively.

reports the model’s estimation results.

Table 5 indicates that SDIGA’s direct and indirect effects on CI were both significantly negative under the two spatial weighted matrices, implying that DIGA has an inverted “U-shaped” link on both local and neighboring cities’ CI. Compared with the direct effect coefficient of SDIGA under the two spatial weighted matrices, the indirect effect coefficient is greater, indicating that the native CI is more impacted by DIGA in neighboring areas. Our result is the opposite of that of the impact of the digital economy on CI [10]. The first possible reason is related to our matrix settings. This study used an asymmetrical matrix and considered the impact of large cities on small cities to be greater than the impact of small cities on large cities. Another reason is the higher DIGA in large cities. Since large cities have a higher degree of DIGA, they are able to effectively drive small cities to reduce CI through the positive externalities of the agglomeration economy.

We used $W_1$ as an example for the analysis of the effect of the control variables on CI. (1) The effects of population density on CI were not statistically significant in both local and neighboring cities, which is different from the negative impact of population density on CI found by Lee and Wang [11]. (2) Economic development was negatively related to local CI, which is in line with the results of Zheng, Yang, Huang, Cui, and Zhan [65]. According to the actual situation in China, in recent years, it has no longer been pursuing high-speed economic expansion but is seeking high-quality economic growth [9]. In addition, such findings also suggest that China has successfully shifted from extensive to intense economic expansion, achieving the CO₂ reduction target. (3) Infrastructure development contributes to the CI of local and neighboring cities, lending support to the conclusion of Yuan, Zou, Luo, and Feng [56], indicating that China has paid a serious environmental cost in the past during infrastructure development. (4) Openness boosts local CI and suppresses neighboring CI, which is in line with the result of Yan, Yang, Nie, Su, Zhao, and Ran [62]. Since the cities that introduce foreign investment are mainly those with higher economic development, opening up these cities to the outside world may reduce nearby CI through technology spillover. However, the introduction and use of foreign technologies may inhibit the green innovation of local enterprises and transfer energy industries [62], raising local CI. (5) Environmental regulations did not affect local or neighboring CI, which is different from the findings of Yuan, Zou, Luo, and Feng [56]. The study contended that when the environmental regulations in a region tighten, heavy polluters may consider moving to a region with looser environmental regulations.

5.4. Robustness Test

5.4.1. Replacing Spatial Weighted Matrix

Table 6. Robustness test results.

	SDM_W1	SDM_M3	SDM_M4	Removing Municipalities	Adding Control Variables
Model	1	2	3	4	5
DIGA	0.973 ** (2.21)	0.985 ** (2.23)	0.998 ** (2.31)	0.784 * (1.77)	0.835 * (1.93)
SDIGA	−2.878 *** (−2.68)	−2.899 *** (−2.70)	−2.901 *** (−2.76)	−2.332 ** (−2.15)	−2.408 ** (−2.29)
W*DIGA	16.307 *** (3.22)	21.180 *** (3.61)	22.546 *** (3.52)	15.221 *** (3.07)	12.060 ** (2.32)
W*SDIGA	−41.865 *** (−3.67)	−55.681 *** (−4.15)	−64.781 *** (−4.29)	−39.112 *** (−3.51)	−29.568 ** (−2.55)
Control variables	Yes	Yes	Yes	Yes	Yes
Time-fixed effect	Yes	Yes	Yes	Yes	Yes
City-fixed effect	Yes	Yes	Yes	Yes	Yes
N	3058	3058	3058	3058	3058

The values in brackets are Z-values with ***, **, and * indicating significance levels of 1%, 5%, and 10%, respectively.

reports the robustness test results. The spatial weighted matrix settings significantly affected the model estimation results in the spatial econometric analysis. We constructed one new asymmetrical economic–geographic spatial weighted matrix $(W_3)$ using the square of the per capita GDP and geographical distance. In addition, following Yuan, Feng, Lee, and Cen [76], we built one inverse distance matrix $(W_4)$. We performed the robustness test by replacing $W_1$ with $W_3$ and $W_4$. Table 6 reports the results. Compared with Model 1, the values of DIGA, SDIGA, W*DIGA, and W*SDIGA in Models 2 and 3 did not change in terms of positive or negative values, and they passed the 5% significance test. Additionally, the coefficients of the DIGA, SDIGA, W*DIGA, and W*SDIGA in Models 2 and 3 changed slightly, indicating that the impact intensity of DIGA on the local and adjacent CI hardly changed after replacing the spatial weighted matrices. Hence, the relationship between DIGA and CI does not change because of different matrices.

5.4.2. Removing Municipalities

China’s DIGA has been heavily impacted by policies. The administrative level is an important basis for cities to obtain policy support, and China’s central government usually provides more policy support to cities with higher administrative levels [7]. We excluded Beijing, Shanghai, Chongqing, and Tianjin from the sample to eliminate administrative-level effects on the empirical findings. Compared with Model 1, as shown in Table 6, the linear and quadratic coefficients of DIGA and W*DIGA in Model 4 are significantly smaller, implying that the administrative level has an impact on the intensity of DIGA affecting CI. Nevertheless, the linear and quadratic signs of DIGA and W*DIGA in Model 4 did not change. Therefore, the core conclusion of this study is robust.

5.4.3. Adding Control Variables

Yan, Yang, Nie, Su, Zhao, and Ran [62] contended that financial development, government intervention, and human capital may be crucial factors affecting CI. To avoid omitted variables, the three variables were further controlled in Model 5, as shown in Table 6. Compared with Model 1, the linear and quadratic signs of DIGA and W*DIGA in Model 5 did not change. Therefore, the core findings of our model are still reliable after controlling for more variables.

5.5. Heterogeneity Analysis

5.5.1. Spatial Heterogeneity

Geographic location [58], natural resource endowment [76], industrial structure [8], and capitalization [37] may enable cities to develop a low-carbon economy differently according to their competitive advantages, resulting in varied degrees of heterogeneity in DIGA’s impact on CI under different city samples. In this regard, this study analyzed heterogeneity from four perspectives: spatial, resource, industrial, and financial differences.

China has a vast territorial area. Varied regions differ greatly in terms of natural resources, climatic conditions, cultural practices, and policies. Referring to Yan, Yang, Nie, Su, Zhao, and Ran [62], we separated sample cities into eastern, central, and western areas. We constructed cross-terms for parameter estimations by generating dummy variables, effectively avoiding the problem of missing information caused by grouped regression.

As can be seen from Model 2 shown in

Table 7. Heterogeneity results from spatial differences.

	Eastern Regions	Middle Regions	Western Regions
Model	1	2	3
DIGA	2.241 *** (2.79)	−1.133 * (−1.67)	4.215 *** (4.30)
SDIGA	−5.219 *** (−2.90)	2.443 (1.48)	−12.570 *** (−4.61)
W*DIGA	12.713 ** (2.09)	−29.769 ** (−2.53)	115.876 *** (6.69)
W*SDIGA	−40.739 *** (−2.93)	66.074 *** (2.57)	−234.847 *** (−5.39)
Control variables	Yes	Yes	Yes
Time-fixed effect	Yes	Yes	Yes
City-fixed effect	Yes	Yes	Yes
N	3058	3058	3058

The values in brackets are z-values with ***, **, and * indicating significance levels of 1%, 5%, and 10%, respectively.

, the corresponding coefficients of DIGA and SDIGA are −1.133 and 2.433, but only DIGA is statistically significant at the 10% level, so DIGA in the middle regions has a dampening effect on local CI. The middle regions have complete industrial chains, reasonable house prices, and moderate population size, so DIGA shows the effect of reducing local CI in the central regions rather than a “U-shaped” impact. In addition, the coefficients of SDIGA and W*SDIGA in Models 1 and 3 are all significantly negative at the 1% level, which means that DIGEA’s impact on local and nearby cities’ CI is negatively “U-shaped” in the eastern and western regions, which is in line with the full sample. Meanwhile, the absolute values of the coefficients of DIGA, SDIGA, W*DIGA, and W*SDIGA in Model 1 are less than those in Model 3, implying that western areas experience a greater influence of DIGA on CI than eastern regions. We contend that compared with the eastern areas, western regions have remarkable advantages in data storage capacity and computing power resources due to the fact of low land and labor costs; thus, the economies of scale effects of DIGA are more obvious in the western regions. In addition, China’s “East Data, West Computing” project also strongly indicates that the western regions have unique advantages in digitally empowering high-quality economic development.

5.5.2. Resource Heterogeneity

We categorized the study sample into resource-based and non-resource-based cities based on the State Council of China’s list of resource-based cities. Cities that rely heavily on the extraction and processing of local natural resources, such as minerals, are known as resource-based cities. Resource-based cities are vital strategic hubs for safeguarding China’s energy resources and are key areas for speeding the country’s economic transition to a greener one and realizing the “beautiful China” goal. We deployed the same method in Section 5.5.1 to study the effect of DIGA on CI in resource heterogeneity.

From Models 1 and 2 shown in

Table 8. Heterogeneity results from resource differences.

	Non-Resource-Based Cities	Resource-Based Cities
Model	1	2
DIGA	0.809 (1.44)	1.511 * (1.82)
SDIGA	−2.459 * (−1.91)	−4.474 ** (−1.99)
W*DIGA	12.774 ** (2.20)	9.171 (0.61)
W*SDIGA	−38.711 *** (−3.03)	2.662 (0.07)
Control variables	Yes	Yes
Time-fixed effect	Yes	Yes
City-fixed effect	Yes	Yes
N	3058	3058

The values in brackets are z-values with ***, **, and * indicating significance levels of 1%, 5%, and 10%, respectively.

, the coefficients of SDIGA are both negative at the 10% significance level. From the perspective of spatial spillover effects, it can be seen in Table 8 that DIGA had no spatial spillover effects on CI in resource-based cities. However, the DIGA of non-resource-based cities still had spatial spillover effects on CI. In addition, the resource-based sample’s SDIGA coefficients had a higher absolute value than the non-resource-based sample, which is in line with the findings of Yuan, Zou, Luo, and Feng [56], implying that resource-based cities see a greater effect of DIGA on CI than non-resource-based cities. Such results may be caused by the policy intensity and industrial base. First, boosting resource-based cities’ green transformation and energy-efficient manufacturing is a primary goal for the Chinese government in order to minimize CI since these cities are crucial to guaranteeing China’s energy security. The government has provided more resources and policy support to guide resource-based cities in developing the digital economy. Second, resource-based cities have better economic conditions and industrial bases due to the fact of their richer natural resources [56], which provides them with great advantages in attracting digital talent and advanced digital technologies. Such advantages facilitate the timely digital transformation of local companies and the formation of digital economy clusters.

5.5.3. Industry Heterogeneity

Manufacturing is the pillar of China’s national economy [16,76]. It is the basis for industrial transformation and upgrading, as well as the focus of China’s digitalization [16]. Due to the different comparative advantages, each city in China has its featured industry. For example, the Yangtze River Delta economic belt has formed obvious advantages in industrial agglomeration because of its superior geographical location and perfect industrial chain, and most of the cities in this region are highly industrialized because the Yangtze River Delta is in the late stage of industrialization. However, most cities in western China mainly develop tourism and agriculture because of their special geographical features, customs, and culture. Based on the degree of manufacturing development, we divided the research sample into industrialized and nonindustrialized cities. This study used the same method as in Section 5.5.1 to study the effect of DIGA on CI in industry heterogeneity.

From

Table 9. Heterogeneity results from industrial differences.

	Nonindustrialized Cities	Industrialized Cities
Model	1	2
DIGA	1.898 *** (3.21)	−0.572 (−0.87)
SDIGA	−4.858 *** (−3.38)	0.726 (0.45)
W*DIGA	−15.131 ** (−2.34)	7.274 (1.14)
W*SDIGA	32.671 ** (2.47)	−20.997 (−1.49)
Control variables	Yes	Yes
Time-fixed effect	Yes	Yes
City-fixed effect	Yes	Yes
N	3058	3058

The values in brackets are z-values with ***, **, and * indicating significance levels of 1%, 5%, and 10%, respectively.

, DIGA significantly impacted local and neighboring cities’ CI in nonindustrialized cities. Compared with the effect in the nonindustrialized sample, DIGA had no effect on CI in industrialized cities. China’s manufacturing quality may explain the gap between the two types of cities. China is the world’s factory but not a manufacturing superpower [31,56], so the digitalization and intelligent transformation of China’s manufacturing industry were not of high quality. Due to the low level of independent innovation, Chinese manufacturing products have low added value. The development of China’s manufacturing industry promotes economic growth at serious environmental costs [76]. However, e-commerce, represented by “Rural Taobao”, supports the green transformation of nonindustrialized cities, and digital technologies accelerate the development of green and smart agriculture. Therefore, the DIGA of nonindustrialized cities significantly impacts CI, but such effects are not manifested in industrialized cities.

5.5.4. Finance Heterogeneity

In the course of economic growth, finance is essential. Financial development is intricately tied to the development of the digital economy and energy use [11,37]. Yue, Korkmaz, Yin, and Zhou [37] contended that a well-developed financial sector helps to address information asymmetries and resource misallocation. Based on the total deposit and loan balance as a percentage of GDP, we divided the research sample into financially undeveloped cities and financially developed cities. The study employed the same method as in Section 5.5.1 to study the effect of DIGA on CI in finance heterogeneity.

According to Model 1, as shown in

Table 10. Heterogeneity results from financial differences.

	Financially Undeveloped Cities	Financially Developed Cities
Model	1	2
DIGA	−0.302 (−0.49)	1.605 ** (2.53)
SDIGA	0.922 (0.60)	−4.968 *** (−3.30)
W*DIGA	6.535 * (1.09)	−10.136 * (−1.76)
W*SDIGA	−25.915 (−1.85)	25.453 ** (2.05)
Control variables	Yes	Yes
Time-fixed effect	Yes	Yes
City-fixed effect	Yes	Yes
N	3058	3058

The values in brackets are z-values with ***, **, and * indicating significance levels of 1%, 5%, and 10%, respectively.

, DIGA and SDIGA are both statistically insignificant, showing that DIGA had no relationship with CI in financially undeveloped cities. Additionally, the coefficients of W*DIGA and W*SDIGA are 6.535 and −25.915, respectively, and only W*DIGA is significant, implying that DIGA promoted the neighboring CI in the financially undeveloped sample.

As can be seen in Model 2, as shown in Table 10, the coefficient of SDIGA is statistically negative, which is in line with the result of the full sample. In addition, the coefficient of W*SDIGA is statistically positive, showing a positive “U-shaped” correlation between DIGA and neighboring CI. This result contradicts the baseline model including the total sample.

Based on the different impacts of DIGA on CI in financially developed and undeveloped cities, this study contends that digital economy development and agglomeration have a high demand for credits. Improved finance development allows firms to undergo digital transformation and households to buy energy-saving appliances via convenient and affordable credit [35].

6. Mechanism Identification

6.1. Mediating Effect Identification

Based on Hypotheses 2, 3, and 4, this study contends that DIGA may indirectly affect CI through technology effects and industrial structure effects. To test whether GTI, ISR, and ISA are mediators for the impact of DIGA on CI, we deployed a mediating effects model. The estimation results are presented in

Table 11. Identification of the mediating effect based on GTI, ISR, and ISA.

Variable	Total Effect	Green Technology Innovation Effect		Industrial Structure Rationalization Effect		Industrial Structure Advancement Effect
	lnCI	GTI	lnCI	ISR	lnCI	ISA	lnCI
Model	1	2	3	4	5	6	7
DIGA	0.973 ** (2.21)	−18.253 *** (−4.67)	0.628 (1.44)	−0.671 *** (−2.94)	0.910 ** (2.07)	−1.338 *** (−4.04)	1.071 ** (2.43)
SDIGA	−2.878 *** (−2.68)	40.865 *** (4.30)	−2.154 ** (−2.03)	1.246 ** (2.24)	−2.771*** (−2.59)	3.345 *** (4.15)	−3.121 *** (−2.91)
GTI			−0.014 *** (−6.13)
ISR					−0.095 *** (−2.74)
ISA							0.068 *** (2.78)
rho	0.587 ***	0.345 ***	0.351 ***	−0.007	0.559 ***	0.436 ***	0.585 ***
Control variables	Yes	Yes	YES	YES	YES	YES	YES
Time-fixed effect	YES	YES	YES	YES	YES	YES	YES
City-fixed effect	YES	YES	YES	YES	YES	YES	YES
Sobel test		0.052 **		0.019 **		−0.008
N	3058	3058	3058	3058	3058	3058	3058

The values in brackets are z-values with ***, **, and * indicating significance levels of 1%, 5%, and 10%, respectively.

. We focused only on the mechanisms by which DIGA affects local CI in the mediating effect analysis.

First, we analyzed the mediating effect of GTI. According to Model 1, SGIGA is negative and passed the 1% significance test, showing that DIGA has a negative “U-shaped” impact on CI. According to Model 2, SDIGA is positive and passed the 1% significance test, demonstrating a significant positive “U-shaped” association between DIGA and GTI. From Model 3, SDIGA is negative and passed the 5% significance test, and the inverse “U-shaped” correlation between DIGA and CI still existed after adding GTI based on Model 1. Meanwhile, GTI had a negative sign and passed the 1% significance test, implying that GTI reduces CI. In addition, the absolute value of the coefficient of SDIGA in Model 3 is smaller than that in Model 1. As a result, GTI is a significant mediator. We also performed the Sobel test. The result shows that DIGA indirectly affects CI through GTI.

Second, we analyzed the ISR’s mediating impact. From Model 4, SDIGA is positive and passed the 5% significance test, indicating that DIGA has a positive “U-shaped” impact on ISR. According to Model 5, SDIGA is negative, passing the 1% significance test. Meanwhile, ISR is negative and passed the 1% significance test. In addition, compared with Model 1, the absolute values of the coefficients of DIGA and SDIGA in Model 5 are smaller. Therefore, ISR is also a significant mediator. We also performed the Sobel test. The result indicates that DIGA indirectly affects CI through ISR.

Finally, we analyzed the mediating effect of ISA. According to Model 6, SDIGA is positive and passed the 1% significance test, showing a significant positive “U-shaped” link between DIGA and ISA. According to Model 7, SDIGA and ISA are both statistically significant. However, the absolute value of the coefficients of both DIGA and SDIGA in Model 7 is greater than in Model 1, indicating that ISA has a suppressing effect on the relationship between DIGA and CI. Hence, ISA is not a channel through which DIGA indirectly affects CI. We also performed the Sobel test. The result of the Sobel test further confirms that ISA is not a mediator between DIGA and CI.

6.2. Moderating Effect Identification

Based on Hypotheses 5 and 6, we contend that the strength with which DIGA affects CI may depend on human capital and GI. To test whether EDU and GI are moderators, we employed the moderating effects model for estimation. The estimation results are presented in

Table 12. Identification of the moderating effect based on EDU and GI.

Variable	EDU	GI
	lnCI	lnCI
	1	2
DIGA	2.255 *** (4.11)	0.396 (0.83)
SDIGA	−2.242 ** (−2.10)	−2.596 ** (−2.42)
lnEDU	0.123 *** (7.04)
GI		−0.445 *** (−3.17)
DIGA* lnEDU	−0.256 *** (−3.41)
DIGA * GI		2.791 *** (3.01)
rho	0.323 **	0.568 ***
Control variables	Yes	Yes
Time-fixed effect	Yes	Yes
City-fixed effect	Yes	Yes
N	3058	3058

The values in brackets are z-values with ***, **, and * indicating significance levels of 1%, 5%, and 10%, respectively.

. The moderating effects analysis in this study focused only on the mechanisms by which DIGA affects local CI.

According to Model 1, the interaction term of DIGA and lnEDU has a negative coefficient and passed the 1% significance test, showing that human capital complements DIGA to impact CI. Hence, human capital moderates DIGA to reduce CI. The explanations are as follows: The digital economy industry is knowledge intensive [9]. Compared to other technologies, digital technology is more complex and requires a more educated workforce [61], so the role of DIGA in reducing CI may be enhanced by human capital.

Additionally, according to Model 2, the interaction term of DIGA and GI has a positive coefficient, passing the significance test at the 1% level, demonstrating that the effect of DIGA in reducing CI is significantly weaker due to the higher GI. In other words, there are areas with a high GI, such as the cities of Sanya and Huangshan, where DIGA reduces CI less effectively than in cities with a low GI, such as Dongguan and Foshan. Thus, GI is a key moderator between DIGA and CI. This study argues that digitalization in cities with a high GI is heavily impacted by policies, and the formation of DIGA cannot follow the laws of market economic development. Such policy effects may cause resource misallocation [62] and dysfunctional economies of scale [29], weakening the role of DIGA in reducing CI.

7. Conclusions and Further Discussions

7.1. Conclusions

First, this study expanded the STIRPAT framework put forward by Dietz and Rosa [32] and proposed the extended spatial STIRPAT model by considering the DIGA and spatial effect. Based on the extended spatial STIRPAT framework and several agglomeration theories, such as the theory of agglomeration externalities [50] and locational theory [25], this work theoretically analyzed DIGA’s impact on CI and the mechanism by which this occurs. Second, this study constructed a unique dataset containing 7,902,050 Chinese digital enterprises and employed their latitude and longitude to measure DIGA at the city level using the DO index. The used metric of enterprise agglomeration avoids the MAUP of discrete enterprise agglomeration measures. Third, by matching micro digital enterprise data with macro city data, this study deployed SDM and the asymmetrical economic–geographic spatial weighted matrix and asymmetrical technical–geographic spatial weighted matrix to empirically investigate the nonlinear relationship between DIGA and CI and the inner mechanism for how DIGA affects CI. We drew the following conclusions:

(1) There is a serious imbalance in China’s DIGA and CI from a spatial perspective, which is in line with China’s imbalanced development. Overall, coastal regions have higher DIGA than inland regions, and southern regions have higher DIGA than northern regions. Meanwhile, the brain drain and extreme climate have negatively affected the DIGA in the northeast. There is a downward tendency in the DIGA of northeast China from 2007 to 2017, which contradicts the trend of fast digital economy expansion and agglomeration. In addition, cities in southern China have performed better than the north in reducing CI. Finally, the Pearl River Delta economic belt has a significant CO₂ emission transfer phenomenon and performs less well than the Yangtze Delta economic belt in terms of regional synergy in reducing CI.

(2) DIGA has a significant nonlinear and spatial spillover effect on CI. First, DIGA has a negative “U-shaped” impact on local cities’ CI. That is, in the early stages of DIGA, DIGA increases local CI, and when DIGA crosses a certain inflection point, the positive impact of DIGA outweighs its negative impact, and DIGA reduces local CI. Second, DIGA’s effect on neighboring cities’ CI is also negatively “U-shaped”. The impact of neighboring DIGA on local CI is more significant than the effect of native DIGA on local CI.

(3) There may be heterogeneity among regions, resource endowment, industrialization degree, and financialization level across Chinese cities, so the influence of DIGA on CI shows great differences. Regarding spatial heterogeneity, the relationships between DIGA and local CI and nearby CI are both negatively “U-shaped” in the eastern and western regions. However, the correlations between DIGA and local CI and nearby CI are negatively and positively “U-shaped”, respectively, in the middle regions. In terms of resource heterogeneity, DIGA has no spatial spillover effect on CI in resource-based cities. However, DIGA demonstrates a significant spatial spillover impact on CI in non-resource-based cities. Regarding industrial heterogeneity, DIGA in nonindustrialized cities significantly impacts local and neighboring cities’ CI, whereas DIGA in industrialized cities has no effect on local and neighboring cities’ CI. In terms of financial heterogeneity, the correlation between DIGA and local CI is an inverted “U-shape” in financially undeveloped cities; however, no significant association was found between DIGA and local CI in financially developed cities.

(4) DIGA indirectly impacts CI through GTI and ISR; however, DIGA does not indirectly influence CI via ISA. In addition, human capital enhances the role of DIGA in reducing CI, whereas government intervention weakens the effect of DIGA in decreasing CI.

7.2. Theoretical Implications

Based on our study, we can conclude two theoretical implications. First, we proposed an extended spatial STIRPAT theoretical framework based on the STIRPAT developed by Dietz and Rosa [32]. Future research could replace DIGA with other variables of interest, such as digital finance, to investigate the spatial impact of digital finance on carbon intensity. Second, the extended spatial STIRPAT theoretical framework can also be used to study other environmental variables of interest, such as CO₂ emission performance [58] and renewable energy [55]. Thirdly, this study focused on the mechanism of the role of digital enterprise agglomeration on carbon intensity in terms of the industrial structure effect and green innovation effect. Future theoretical mechanisms may consider resource allocation and knowledge spillover theories.

7.3. Policy Recommendations

The findings and conclusions indicate that DIGA is an effective means of reducing CI in China. According to the empirical findings and conclusions, we provide four policy recommendations on how China can promote sustainable green development in the clustering process of digital firms.

(1) Based on the agglomeration theory, DIGA has both a positive agglomeration effect [59] and a negative congestion effect [44,56]. The formulation of DIGA policies needs to be dynamically adjusted to the stage of digital economy development. First, for cities with insufficient DIGA, developing digital economy industrial park programs and accelerating DIGA are vital. Meanwhile, the government should try its best to reduce the CO₂ emissions of digital infrastructure construction at this stage. Second, for cities with a moderate level of DIGA, the government should increase public service provision to mitigate negative externalities, such as traffic congestion and environmental damage. In addition, the policy-driven agglomeration effects of digital firms may lead to policy failures and inadequate agglomeration effects [77]. The government should gradually transform policy-driven DIGA to market-driven DIGA, eliminating and cleaning up backward digital enterprises or zombie enterprises and attracting more digital firms with advanced carbon-emission technologies.

(2) DIGA has knowledge and technology spillover effects [9]. Due to the spatial effects of DIGA, the reduction in CI in China needs to follow a regional synergistic carbon reduction principle. First, breaking the boundary restrictions of cities’ administrative districts is significant, and the government should strengthen joint regional CO₂ emissions governance, build a regional-level CO₂ emissions monitoring platform, and realize regional CO₂ emissions information sharing and joint early warning, avoiding the emergence of shifting high-carbon industries in large cities. Second, it is necessary to develop regional digital economy development programs, strengthen inter-regional digital economy synergistic development and cooperation, accelerate inter-regional digital factor flow, and use DIGA’s spatial spillover effect to lower the CI of small cities.

(3) In the future, regarding the digitalization process, the Chinese government should, in addition to simply pursuing the upgrading of industrial structure [9], focus more on industrial restructuring [8,52] and green innovation [7] to enhance the coordinated development of various industries and green technological progress.

(4) It is vital for the Chinese government to improve EDU and weaken GI in the process of DIGA. First, the government should use the internet to promote online education on a large scale to break the uneven distribution of educational resources and promote overall educational attainment in China. Meanwhile, the government should popularize digital skills training to improve the digital literacy of all Chinese citizens, promoting the full use of digital technologies and data elements. Second, the government should reduce direct policy interventions in the process of DIGA and play more of a service and guidance role [62]. It is necessary to allow the market to determine the geographical location of digital economy enterprises.

7.4. Critical Analysis and Further Research

This study requires future work for its completion.

(1) Though this study investigated DIGA’s impact on CI at the theoretical and empirical levels, the focus was on digital firms. The agglomeration of other enterprises in other industries can be discussed in the future [27,56]. For example, future scholars may collect the latitude and longitude of financial institutions to assess financial enterprise agglomeration and investigate the relationship and inner mechanism between financial enterprise agglomeration and CI. It is beneficial to provide new perspectives in terms of the factors impacting CI.

(2) Due to the limitations of the data on cities at the county level in China, this study’s basic unit was the city at the prefecture level. If Chinese officials can establish a macro database at the county level, future research can, subsequently, explore the impact on CI at the county level [67] so that more detailed findings can be mined, making the planning of digital economy development and CO₂ reduction policies more accurate and scientific.