Triaxial Creep Damage Model for Salt Rock Based on Fractional Derivative
Abstract
:1. Introduction
2. Creep Model of Salt Rock Based on Fractional Derivative
2.1. Fractional-Order Maxwell Model
2.2. Viscoplastic Damage Model
2.3. Fractional Creep Damage Model
3. Creep Test of Salt Rock
3.1. Specimens and Test Equipment
3.2. Test Protocol and Steps
- Specimen installation: the prepared rock specimen was placed onto the TATW-2000 rock triaxial shear testing machine, with the position of the indenter adjusted to make contact with the rock.
- Load application: according to the test scheme, the confining pressure was first applied, and once stabilized, the axial pressure was applied.
- Data recording and analysis: The computer automatically records the deformation values and plots the change in strain over time. After completion of a test, the specimen was replaced, the above steps were repeated until all tests were completed, and the collected data were sorted and analyzed, ultimately resulting in a strain–time curve under different stress conditions.
3.3. Test Results and Analysis
3.3.1. Creep Curves at Different Deviatoric Stresses
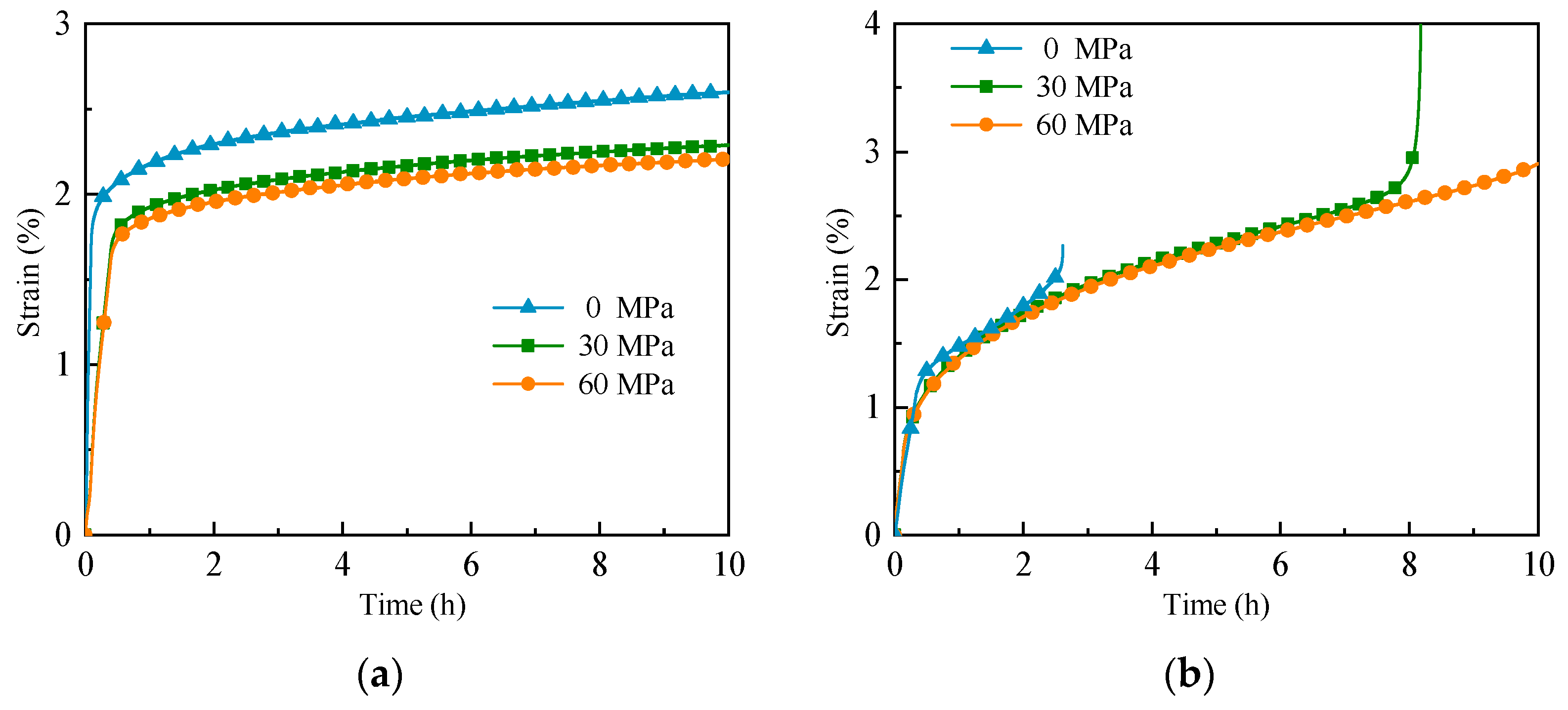
3.3.2. Effect of Confining Pressure
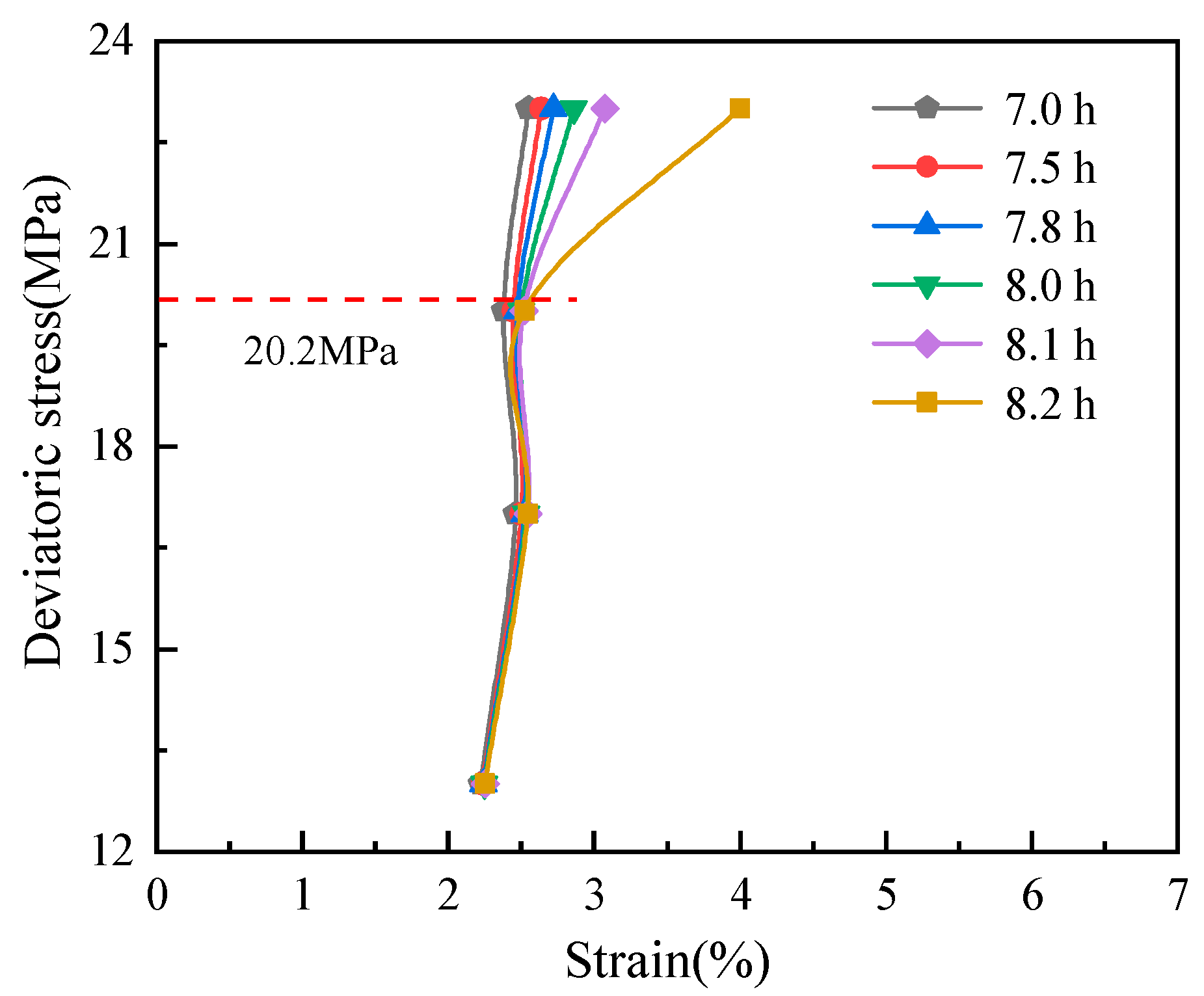
3.3.3. Long-Term Strength
4. Parameter Identification and Model Validation
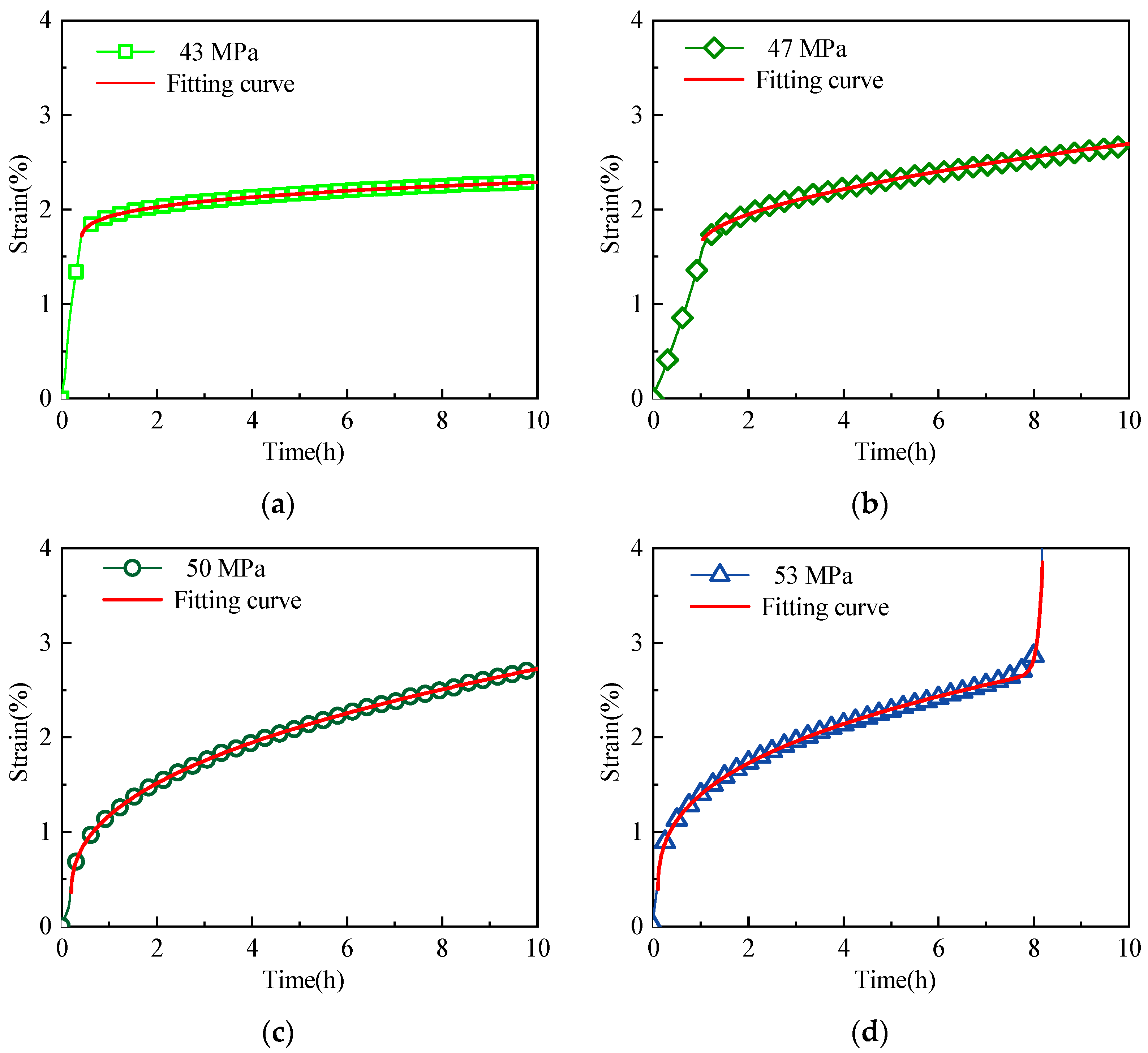
4.1. Parameter Identification
4.2. Model Validation
5. Parametric Sensitivity Analysis
5.1. Parameter η1 Analysis
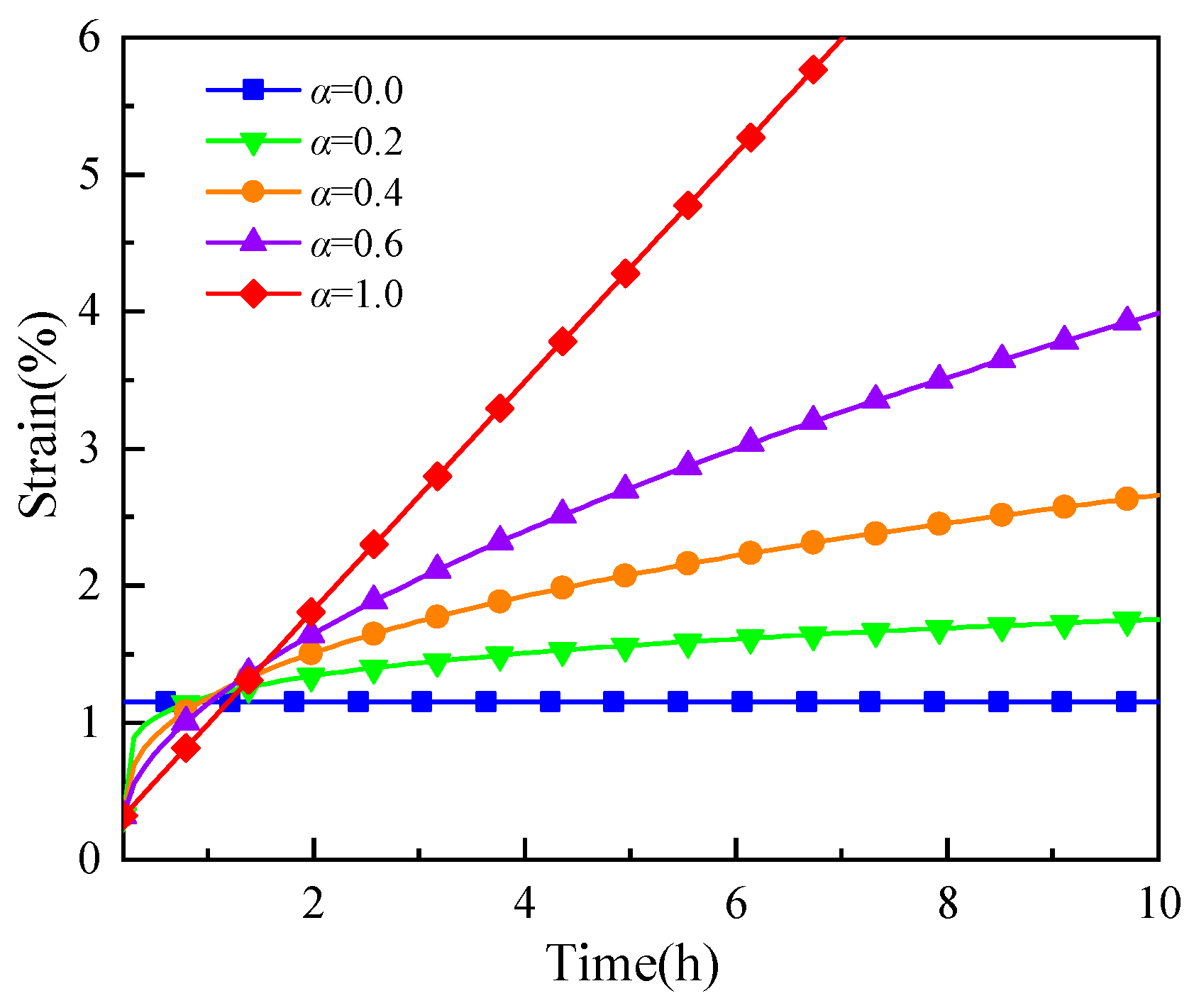
5.2. Parameter α Analysis
5.3. Parameter η2 Analysis
5.4. Parameter λ Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, R.B.; Wu, F.; Chen, J.; Zhu, C.; Ji, C.X. Study on creep characteristics and constitutive model of typical argillaceous salt rock in energy storage caverns in China. J. Energy Storage 2022, 50, 104248. [Google Scholar] [CrossRef]
- Wang, X.K.; Song, L.B.; Xia, C.C.; Han, G.S.; Zhu, Z.M. Nonlinear elasto-visco-plastic creep behavior and new creep damage model of dolomitic limestone subjected to cyclic incremental loading and unloading. Sustainability 2021, 13, 12376. [Google Scholar] [CrossRef]
- Chen, F.; Ye, L.L.; Ma, H.L.; Shi, X.L.; Liu, H.D.; Yang, C.H. Subsidence above gas storage in salt caverns predicted with viscoelastic theory. J. Nat. Gas Sci. Eng. 2022, 103, 104620. [Google Scholar] [CrossRef]
- Li, J.C.; Wan, J.F.; Liu, H.M.; Jurado, M.J.; He, Y.X.; Yuan, J.G.; Xia, Y. Stability Analysis of a Typical Salt Cavern Gas Storage in the Jintan Area of China. Energies 2022, 15, 4167. [Google Scholar] [CrossRef]
- Ma, L.J.; Wang, Y.X.; Wang, M.Y.; Xue, B.; Duan, L.Q. Mechanical properties of rock salt under combined creep and fatigue. Int. J. Rock Mech. Min. Sci. 2021, 141, 104654. [Google Scholar] [CrossRef]
- Wang, J.B.; Zhang, Q.; Liu, X.; Son, Z.P.; Feng, S.J. Creep properties and constitutive model for salt rock subjected to uniaxial trapezoidal cyclic loading. J. Energy Storage 2022, 52, 105023. [Google Scholar] [CrossRef]
- Nawrocki, P.A.; Mroz, Z. A viscoplastic degradation model for rocks. Int. J. Rock Mech. Min. Sci. 1998, 35, 991–1000. [Google Scholar] [CrossRef]
- Ma, J.J. An Elasto-Viscoplastic Model for Soft Porous Rocks Within the Consistent Framework. Rock Mech. Rock Eng. 2017, 50, 3109–3114. [Google Scholar] [CrossRef]
- Ma, J.J.; Guan, J.W.; Gui, Y.L.; Huang, L.C. Anisotropic Bounding Surface Plasticity Model for Porous Media. Int. J. Geomech. 2021, 21, 04021033. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Cormeau, I.C. Visco-plasticity–plasticity and creep in elastic solids–a unified numerical solution approach. Int. J. Numer. Methods Eng. 1974, 8, 821–845. [Google Scholar] [CrossRef]
- Ma, J.J.; Chen, J.J.; Chen, W.X.; Huang, L.C. A coupled thermal-elastic-plastic-damage model for concrete subjected to dynamic loading. Int. J. Plast. 2021, 21, 103279. [Google Scholar] [CrossRef]
- Cristescu, N.D. A general constitutive equation for transient and stationary creep of rock salt. Int. J. Rock Mech. Min. Sci. 1993, 30, 125–140. [Google Scholar] [CrossRef]
- Zhou, H.W.; Wang, C.P.; Han, B.B.; Duan, Z.Q. A creep constitutive model for salt rock based on fractional derivatives. Int. J. Rock Mech. Min. Sci. 2011, 48, 116–121. [Google Scholar] [CrossRef]
- Deng, H.L.; Zhou, H.W.; Wei, Q.; Li, L.F.; Jia, W.H. A creep constitutive model based on Atangana–Baleanu fractional derivative. Mech. Time-Depend. Mater. 2022. [Google Scholar] [CrossRef]
- Chen, J.; Lu, D.; Wu, F.; Fan, J.Y.; Liu, W. A non-linear creep constitutive model for salt rock based on fractional derivatives. Therm. Sci. 2019, 23, S773–S779. [Google Scholar] [CrossRef] [Green Version]
- Lyu, C.; Liu, J.F.; Ren, Y.; Liang, C.; Liao, Y.L. Study on very long-term creep tests and nonlinear creep-damage constitutive model of salt rock. Int. J. Rock Mech. Min. Sci. 2021, 146, 104873. [Google Scholar] [CrossRef]
- Zhou, H.W.; Liu, D.; Lei, G.; Xue, D.J.; Zhao, Y. The creep-damage model of salt rock based on fractional derivative. Energies 2018, 11, 2349. [Google Scholar] [CrossRef] [Green Version]
- Wu, F.; Zhou, X.H.; Ying, P.; Li, C.B.; Zhu, Z.M.; Chen, J. A Study of uniaxial acoustic emission creep of salt rock based on improved fractional-order derivative. Rock Mech. Rock Eng. 2022, 55, 1619–1631. [Google Scholar] [CrossRef]
- Gao, Y.H.; Zhou, Z.; Zhang, H.; Jin, S.; Yang, W.; Meng, Q.H. Viscoelastoplastic displacement solution for deep buried circular tunnel based on a fractional derivative creep model. Adv. Civ. Eng. 2021, 2021, 3664578. [Google Scholar] [CrossRef]
- Kamdem, T.C.; Richard, K.G.; Béda, T. New description of the mechanical creep response of rocks by fractional derivative theory. Appl. Math. Model. 2023, 116, 624–635. [Google Scholar] [CrossRef]
- Shen, M.; Zhou, Z.; Ma, W. Experimental and Theoretical Investigation on the Unloading Creep Behaviors of Frozen Soil. Rock Mech. Rock Eng. 2023. [Google Scholar] [CrossRef]
- Yin, Z.; Zhang, X.; Liu, Y.; Yu, H.; Zhang, Q.S.; Li, X.H. A fractional-order damage creep model for grouting-reinforcement body under dry–wet cycle. Bull. Eng. Geol. Environ. 2023, 82, 172. [Google Scholar] [CrossRef]
- He, Q.C.; Wu, F.; Gao, R.B. Nonlinear creep-damage constitutive model of surrounding rock in salt cavern reservoir. J. Energy Storage 2022, 55, 105520. [Google Scholar] [CrossRef]
- Wu, F.; Liu, J.; Zou, Q.L.; Li, C.B.; Chen, J.; Gao, R.B. A triaxial creep model for salt rocks based on variable-order fractional derivative. Mech. Time-Depend. Mater. 2020, 25, 101–118. [Google Scholar]
- Lyu, C.; Liu, J.; Zhao, C.X.; Ren, Y.; Liang, C. Creep-damage constitutive model based on fractional derivatives and its application in salt cavern gas storage. J. Energy Storage 2021, 44, 103403. [Google Scholar] [CrossRef]
- Yu, M.Y.; Liu, B.G.; Liu, K.Y.; Sun, J.L.; Deng, T.B.; Wang, Q. Creep behavior of carbonaceous mudstone under triaxial hydraulic coupling condition and constitutive modelling. Int. J. Rock Mech. Min. Sci. 2023, 164, 105357. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, H.W.; Wang, X.Y.; Deng, T.F.; Chen, C.F.; Zhang, H.; Nagel, T. Modeling the visco-elastoplastic behavior of deep coal based on conformable derivative. Mech. Time-Depend. Mater. 2023. [Google Scholar] [CrossRef]
- Adolfsson, K.; Enelund, M.; Olsson, P. On the fractional order model of viscoelasticity. Mech. Time-Depend. Mater. 2005, 9, 15–34. [Google Scholar] [CrossRef]
- Sapora, A.; Cornetti, P.; Carpinteri, A.; Baglieri, O.; Santagata, E. The use of fractional calculus to model the experimental creep-recovery behavior of modified bituminous binders. Mater. Struct. 2016, 49, 45–55. [Google Scholar] [CrossRef]
- He, Z.L.; Zhu, Z.D.; Ni, X.H.; Li, Z.J. Shear creep tests and creep constitutive model of marble with structural plane. Eur. J. Environ. Civ. Eng. 2019, 23, 1275–1293. [Google Scholar] [CrossRef]
- Chen, L.; Wang, C.P.; Liu, J.F.; Liu, Y.M.; Liu, J.; Su, R.; Wang, J. A damage-mechanism-based creep model considering temperature effect in granite. Mech. Res. Commun. 2014, 56, 76–82. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, H.; Zou, Q.; Li, C.; Chen, J.; Gao, R. Viscoelastic-plastic damage creep model for salt rock based on fractional derivative theory. Mech. Mater. 2020, 150, 103600. [Google Scholar] [CrossRef]
- Lemaitre, J. A continuous damage mechanics model for ductile fracture. J. Eng. Mater. Tech. 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Q.; Song, Z.; Feng, S.J.; Zhang, Y.W. Nonlinear creep model of salt rock used for displacement prediction of salt cavern gas storage. J. Energy Storage 2022, 48, 103951. [Google Scholar] [CrossRef]
- Liu, J.S.; Jin, H.W.; Meng, B.; Wang, L.G.; Yang, J.J.; You, Y.W.; Zhang, S.J. Fractional-order creep model for soft clay under true triaxial stress conditions. Arab. J. Geosci. 2020, 13, 834. [Google Scholar]
- Zhang, L.; Zhou, H.W.; Wang, X.Y.; Wang, L.; Su, T.; Wei, Q.; Deng, T.F. A triaxial creep model for deep coal considering temperature effect based on fractional derivative. Acta Geotech. 2022, 17, 1739–1751. [Google Scholar] [CrossRef]
- Huang, T.Z.; Li, J.L.; Zhao, B.Y. Nonlinear creep damage model of rock salt considering temperature effect and its implement in FLAC3D. Geomech. Eng. 2021, 26, 581–591. [Google Scholar]
- Jiang, Q.; Qi, Y.; Wang, Z.; Zhou, C.B. An extended Nishihara model for the description of three stages of sandstone creep. Geophys. J. Int. 2013, 193, 841–854. [Google Scholar] [CrossRef]














| Specimen Number | Confining Pressure (MPa) | Axial Pressure (MPa) | Deviatoric Stress (MPa) | Loading Time (h) |
|---|---|---|---|---|
| 1 | 30 | 43 | 13 | 10 |
| 2 | 30 | 47 | 17 | 10 |
| 3 | 30 | 50 | 20 | 10 |
| 4 | 30 | 53 | 23 | 8.2 |
| 5 | 0 | 13 | 13 | 10 |
| 6 | 60 | 73 | 13 | 2.4 |
| 7 | 0 | 23 | 23 | 10 |
| 8 | 60 | 83 | 23 | 10 |
(MPa) | K (MPa) | G1 (MPa) | η1 (MPa·h) | α | η2 (GPa·h) | G2 (GPa·h) | λ | tF (h) | R2 |
|---|---|---|---|---|---|---|---|---|---|
| 13 | 1532.57 | 522.64 | 1202.97 | 0.26 | 0.999 | ||||
| 17 | 1775.62 | 597.61 | 1937.20 | 0.54 | 0.996 | ||||
| 20 | 6204.93 | 5569.87 | 801.26 | 0.41 | 0.998 | ||||
| 23 | 6579.05 | 5623.11 | 773.35 | 0.36 | 4.36 × 1023 | 1.73 × 106 | 10.65 | 6.5 | 0.995 |
| Model | K (GPa) | G1 (GPa) | η1 (GPa·h) | α | η2 (GPa·h) | G2 (GPa·h) | λ | tF (h) | R2 |
|---|---|---|---|---|---|---|---|---|---|
| Classical Nishihara | 3.86 | 0.25 | 1.24 | 1.25 | 0.76 | 0.869 | |||
| Fractional damage | 3.86 | 0.25 | 1.58 | 0.26 | 1.71 | 1.11 | 0.12 | 124 | 0.995 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Chen, H.; Lv, J.; He, X.; Qin, Y.; Sun, K. Triaxial Creep Damage Model for Salt Rock Based on Fractional Derivative. Sustainability 2023, 15, 10369. https://doi.org/10.3390/su151310369
Zhao X, Chen H, Lv J, He X, Qin Y, Sun K. Triaxial Creep Damage Model for Salt Rock Based on Fractional Derivative. Sustainability. 2023; 15(13):10369. https://doi.org/10.3390/su151310369
Chicago/Turabian StyleZhao, Xinbo, Heng Chen, Jian Lv, Xiaohong He, Yiwei Qin, and Keming Sun. 2023. "Triaxial Creep Damage Model for Salt Rock Based on Fractional Derivative" Sustainability 15, no. 13: 10369. https://doi.org/10.3390/su151310369




