Transcending Time and Space: Survey Methods, Uncertainty, and Development in Human Migration Prediction
Abstract
:1. Introduction
2. Research: Related Works and Methodology
2.1. Theoretical Review
2.2. Problem Statement
2.3. Research Methodology
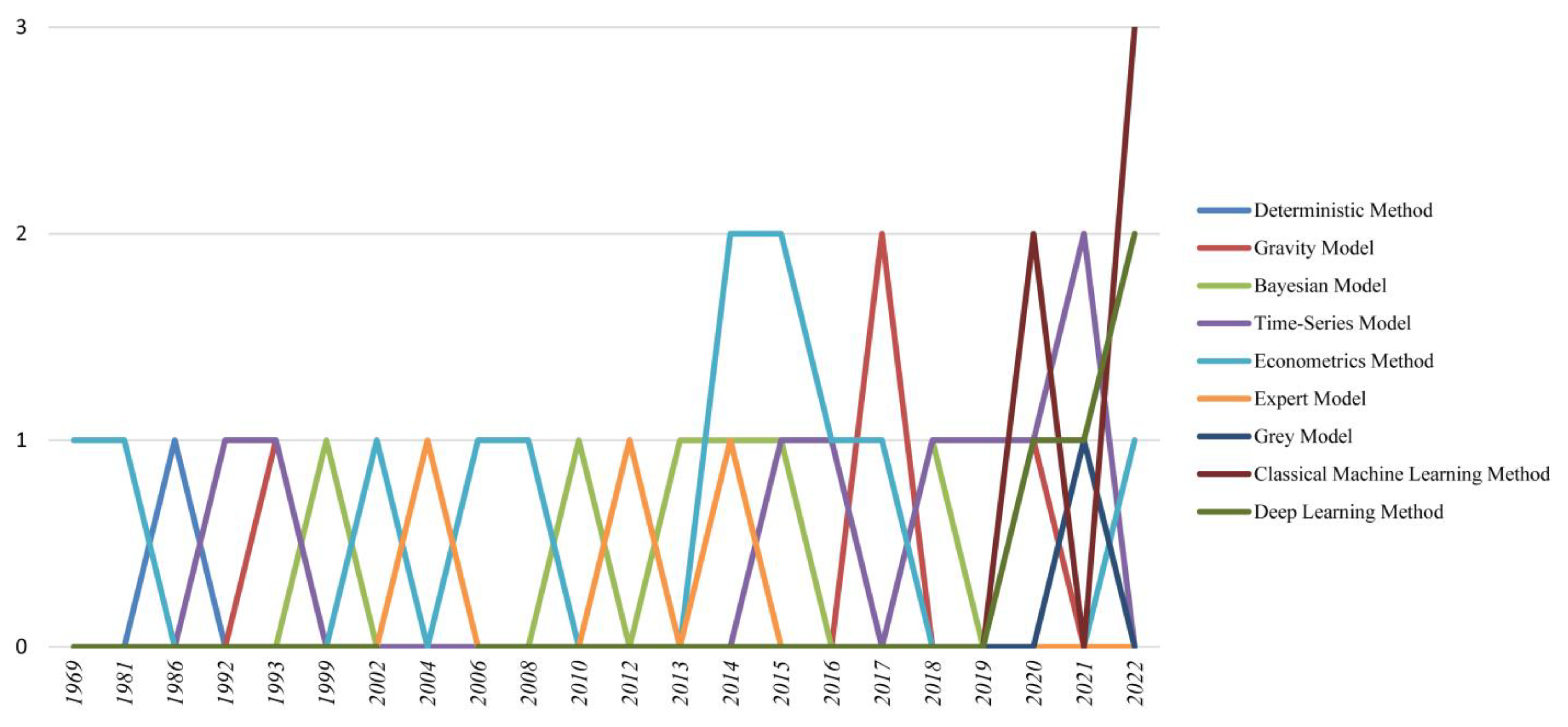
3. Human Migration Forecasting Approaches
3.1. Deterministic Methods
3.2. Stochastic Methods
3.2.1. Econometric Forecasting Models
3.2.2. Gravity Model
3.2.3. Time-Series Models
3.2.4. Bayesian Prediction Model
3.2.5. Expert Prediction Model
3.3. Machine-Learning Prediction Methods
3.3.1. Classical Machine-Learning Prediction Method
- Artificial Neural Network
- 2.
- Random Forest
- 3.
- Support Vector Machine
3.3.2. Deep-Learning Prediction Method
- Recurrent Neural Networks
- 2.
- Graph Neural Networks
4. Uncertainty in Population Migration Projections
5. Conclusions
6. Outlook
Author Contributions
Funding
Conflicts of Interest
References
- China’s State Council. China Population Census Yearbook 2020; China Statistics Press: Beijing, China, 2022; pp. 10–23. [Google Scholar]
- United Nations. International Migrant Stock 2019; (United Nations Database, POP/DB/MIG/Stock/Rev.2019); Department of Economic and Social Affairs, United Nations: Geneva, Switzerland, 2019. [Google Scholar]
- Sharma, D.R.; Kandpal, D.V. COVID 19 pandemic and international migration: An initial view. Sustain. Oper. Comput. 2021, 2, 122–126. [Google Scholar] [CrossRef]
- Willekens, F.; Massey, D.; Raymer, J.; Beauchemin, C. International migration under the microscope. Science 2016, 352, 897–899. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- King, R.; Skeldon, R. “Mind the gap!” integrating approaches to internal and international migration. J. Ethn. Migr. Stud. 2010, 36, 1619–1646. [Google Scholar] [CrossRef]
- Zipf, G.K. The P 1 P 2/D hypothesis: On the intercity movement of persons. Am. Sociol. Rev. 1946, 11, 677–686. [Google Scholar] [CrossRef]
- Bogue, D.J. Internal migration. In The Study of Population; Hauser, P.M., Duncan, O.D., Eds.; University of Chicago Press: Chicago, IL, USA, 1959. [Google Scholar]
- Lee, E.S. A theory of migration. Demography 1966, 3, 47–57. [Google Scholar] [CrossRef]
- Simini, F.; González, M.C.; Maritan, A.; Barabási, A.L. A universal model for mobility and migration patterns. Nature 2012, 484, 96–100. [Google Scholar] [CrossRef] [Green Version]
- Brockmann, D.; Hufnagel, L.; Geisel, T. The scaling laws of human travel. Nature 2006, 439, 462–465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, Y.; Pan, K. Prediction of the intercity migration of Chinese graduates. J. Stat. Mech. Theory Exp. 2014, 12, P12022. [Google Scholar] [CrossRef]
- Geng, Y.; Wang, R.; Wei, Z.; Zhai, Q. Temporal-spatial measurement and prediction between air environment and inbound tourism: Case of China. J. Clean. Prod. 2021, 287, 125486. [Google Scholar] [CrossRef]
- Pu, T.; Huang, M.; Yang, J. Forecasting international migrants using grey model with heat label. In Proceedings of the 5th International Conference on Computer Science and Software Engineering (CSSE), Guilin, China, 21–23 October 2022; pp. 652–656. [Google Scholar] [CrossRef]
- Weber, H. How well can the migration component of regional population change be predicted? A machine learning approach applied to German municipalities. Comp. Popul. Stud. 2020, 45, 143–178. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Azizi, S.; Yektansani, K. Artificial intelligence predicting illegal immigration to the USA. Int. Migr. 2020, 58, 183–193. [Google Scholar] [CrossRef]
- Giang, N.H.; Nguyen, T.-T.; Tay, C.C.; Phuong, L.A.; Dang, T.-T. Towards Predictive Vietnamese Human Resource Migration by Machine Learning: A Case Study in Northeast Asian Countries. Axioms 2022, 11, 151. [Google Scholar] [CrossRef]
- Best, K.; Gilligan, J.; Baroud, H.; Carrico, A.; Donato, K.; Mallick, B. Applying machine learning to social datasets: A study of migration in southwestern Bangladesh using random forests. Reg. Environ. Chang. 2022, 22, 52. [Google Scholar] [CrossRef]
- Disney, G.; Wiśniowski, A.; Forster, J.J.; Smith, P.W.F.; Bijak, J. Evaluation of existing migration forecasting methods and models. In Report for the Migration Advisory Committee; University of Southampton: Southampton, UK, 2015. Available online: https://www.gov.uk/government/publications/evaluationof-existing-migration-forecasting-methods-and-models (accessed on 18 January 2022).
- Sardoschau, S. The Future of Migration to Germany. Assessing Methods in Migration Forecasting. DeZIM Briefing Notes 4, Berlin: Deutsches Zentrum für Integrations- und Migrationsforschung (DeZIM). 2020. Available online: https://policycommons.net/artifacts/1930344/the-future-of-migration-to-germany/2682114/ (accessed on 18 January 2022.).
- Vanella, P.; Deschermeier, P.; Wilke, C.B. An Overview of Population Projections—Methodological Concepts, International Data Availability, and Use Cases. Forecasting 2020, 2, 19. [Google Scholar] [CrossRef]
- Celi, G.; Sica, E. Globalization and internal migration: Evidence from inter-provincial mobility in Vietnam. Reg. Stud. Reg. Sci. 2023, 10, 1–19. [Google Scholar] [CrossRef]
- Van de Walle, E.; Henry, L. Multilingual Demographic Dictionary: English Section; Ordina Editions: Liege, Belgium, 1982. [Google Scholar]
- Möhring, M. Tourism and Migration: Interrelated Forms of Mobility. Comparativ 2014, 24, 116–123. [Google Scholar] [CrossRef]
- Skeldon, R. International Migration, Internal Migration, Mobility and Urbanization: Towards more Integrated Approaches; United Nations: New York, NY, USA, 2018. [Google Scholar]
- Otoiu, A.; Titan, E.; Dumitrescu, R. Internal and international migration: Is a dichotomous approach justified? Procedia-Soc. Behav. Sci. 2014, 109, 1011–1015. [Google Scholar] [CrossRef] [Green Version]
- Cirillo, M.; Cattaneo, A.; Miller, M.; Sadiddin, A. Establishing the link between internal and international migration: Evidence from Sub-Saharan Africa. World Dev. 2022, 157, 105943. [Google Scholar] [CrossRef]
- Bernard, A.; Perales, F. Linking internal and international migration in 13 European countries: Complementarity or substitution? J. Ethn. Migr. Stud. 2022, 48, 655–675. [Google Scholar] [CrossRef]
- Provenzano, D.; Baggio, R. The contribution of human migration to tourism: The VFR travel between the EU 28 member states. Int. J. Tour. Res. 2017, 19, 412–420. [Google Scholar] [CrossRef]
- Marschall, S. Memory, Migration and Travel; Marschall, S., Ed.; Routledge: London, UK, 2018; pp. 1–23. [Google Scholar]
- Ravenstein, E.G. The laws of migration. J. Stat. Soc. Lond. 1885, 48, 167–235. [Google Scholar] [CrossRef] [Green Version]
- O’Reilly, K. Migration theories: A critical overview. In Routledge Handbook of Immigration and Refugee Studies; Routledge: Abingdon, UK, 2015; pp. 25–33. [Google Scholar]
- Arango, J. Theories of international migration. In International Migration in the New Millennium; Ashgate: Aldershot, UK, 2017; pp. 25–45. [Google Scholar]
- Lewis, G.J. Human Migration: A Geographical Perspective; Croom Helm: London, UK, 1982. [Google Scholar]
- Sohst, R.; Tjaden, J.; de Valk, H.; Melde, S. The Future of Migration to Europe: A Systematic Review of the Literature on Migration Scenarios and Forecasts; International Organization for Migration: Geneva, Germany, 2020. [Google Scholar]
- Kupiszewski, M.; Bijak, J.; Kicinger, A. The Use of International Migration Theories in Migration Forecasting—A Practical Approach. In International Migration and the Future of Populations and Labour in Europe; Kupiszewski, M., Ed.; The Springer Series on Demographic Methods and Population Analysis; Springer: Dor-drecht, The Netherlands, 2013; Volume 32. [Google Scholar] [CrossRef]
- Salamo’nska, J. Quantitative methods in migration research. In Introduction to Migration Studies: An In-teractive Guide to the Literatures on Migration and Diversity IMISCOE Research Series; Scholten, P., Ed.; Springer International Publishing: Cham, Switzerland, 2022; pp. 425–438. [Google Scholar]
- Chen, Y.; Rosenthal, S.S. Local amenities and life-cycle migration: Do people move for jobs or fun? J. Urban Econ. 2008, 64, 519–537. [Google Scholar] [CrossRef]
- Demirel, D.F.; Basak, M. A fuzzy bi-level method for modeling age-specific migration. Socio-Econ. Plan. Sci. 2018, 68, 100664. [Google Scholar] [CrossRef]
- Spyratos, S.; Vespe, M.; Natale, F.; Ingmar, W.; Zagheni, E.; Rango, M. Migration Data Using Social Media: A European Perspective; EUR 29273 EN; Publications Office of the European Union: Luxembourg, 2018; ISBN 978-92-79-87989-0. [Google Scholar] [CrossRef]
- Beduschi, A. International migration management in the age of artificial intelligence. Migr. Stud. 2021, 9, 576–596. [Google Scholar] [CrossRef] [Green Version]
- Smith, S.K. Accounting for migration in cohort-component projections of state and local populations. Demography 1986, 23, 127–135. [Google Scholar] [CrossRef] [PubMed]
- Hyndman, R.J.; Booth, H. Stochastic population forecasts using functional data models for mortality, fertility and migration. Int. J. Forecast. 2008, 24, 323–342. [Google Scholar] [CrossRef]
- Fuchs, J.; Söhnlein, D.; Vanella, P. Migration Forecasting—Significance and Approaches. Encyclopedia 2021, 1, 54. [Google Scholar] [CrossRef]
- Gorbey, S.; James, D.; Poot, J. Population forecasting with endogenous migration: An application to trans-Tasman migration. Int. Reg. Sci. Rev. 1999, 22, 69–101. [Google Scholar] [CrossRef]
- Bijak, J.; Wiśniowski, A. Bayesian forecasting of immigration to selected European countries by using expert knowledge. J. R. Stat. Soc. A 2010, 173, 775–796. [Google Scholar] [CrossRef]
- Abel, G.; Bijak, J.; Findlay, A.; McCollum, D.; Wiśniowski, A. Forecasting environmental migration to the United Kingdom: An exploration using Bayesian models. Popul. Environ. 2013, 35, 183–203. [Google Scholar] [CrossRef]
- Wiśniowski, A.; Bijak, J.; Shang, H.L. Forecasting Scottish migration in the context of the 2014 constitutional change debate. Popul. Space Place 2014, 20, 455–464. [Google Scholar] [CrossRef]
- Azose, J.J.; Raftery, A.E. Bayesian probabilistic projection of international migration. Demography 2015, 52, 1627–1650. [Google Scholar] [CrossRef] [Green Version]
- Raymer, J.; Wiśniowski, A. Applying and testing a forecasting model for age and sex patterns of immigration and emigration. Popul. Stud. 2018, 72, 339–355. [Google Scholar] [CrossRef]
- Frees, E.W. Short-Term Forecasting of Internal Migration. Environ. Plan. A Econ. Space 1993, 25, 1593–1606. [Google Scholar] [CrossRef]
- Ramos, R.; Surinach, J. A Gravity Model of Migration between ENC and EU. In IZA Discussion Papers, No. 7700; Institute for the Study of Labor (IZA): Bonn, Germany, 2013. [Google Scholar]
- Campos, R.G. Migratory pressures in the long run: International migration projections to 2050. Banco De Esp. Artic. 2017, 38, 17. [Google Scholar]
- Iancu, N.; Badulescu, A.; Urziceanu, R.M.; Iancu, E.A.; Simut, R. The use of the gravity model in forecasting the flows of emigrants in EU countries. Technol. Econ. Dev. Econ. 2017, 23, 392–409. [Google Scholar] [CrossRef]
- Böhme, M.H.; Gröger, A.; Stöhr, T. Searching for a better life: Predicting international migration with online search keywords. J. Dev. Econ. 2020, 142, 102347. [Google Scholar] [CrossRef]
- Frees, E.W. Forecasting state-to-state migration rates. J. Bus. Econ. Stat. 1992, 10, 153–167. [Google Scholar] [CrossRef]
- Beer, J.D. Forecast intervals of net migration: The case of the Netherlands. J. Forecast. 1993, 12, 585–599. [Google Scholar] [CrossRef]
- García-Guerrero, V.M. A probabilistic method to forecast the international migration of Mexico by age and sex. Pap. De Población 2016, 22, 113–140. [Google Scholar]
- Schoumaker, B.; Beauchemin, C. Reconstructing trends in international migration with three questions in household surveys: Lessons from the MAFE project. Demogr. Res. 2015, 32, 983–1030. [Google Scholar] [CrossRef] [Green Version]
- Vanella, P.; Deschermeier, P. A stochastic Forecasting Model of international Migration in Germany. In Familie—Bildung—Migration. Familienforschung Im Spannungsfeld Zwischen Wissenschaft, Politik Und Praxis. Tagungsband Zum 5. Europäischen Fachkongress Familienforschung; Kapella, O., Schneider, N.F., Rost, H., Eds.; Verlag Barbara Budrich: Opladen/Berlin, Germany; Toronto, ON, Canada, 2018; pp. 261–280. [Google Scholar]
- Bijak, J.; Disney, G.; Findlay, A.M.; Forster, J.J.; Smith, P.W.; Wiśniowski, A. Assessing time series models for forecasting international migration: Lessons from the United Kingdom. J. Forecast. 2019, 38, 470–487. [Google Scholar] [CrossRef] [Green Version]
- Vollset, S.E.; Goren, E.; Yuan, C.W.; Cao, J.; Smith, A.E.; Hsiao, T.; Bisignano, C.; Azhar, G.S.; Castro, E.; Chalek, J.; et al. Fertility, mortality, migration, and population scenarios for 195 countries and territories from 2017 to 2100: A forecasting analysis for the Global Burden of Disease Study. Lancet 2020, 396, 1285–1306. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, S.; Shin, S. Applicability of SARIMA Model in Tokyo Population Migration Forecast. In Proceedings of the 2021 14th International Conference on Human System Interaction (HSI), Gdańsk-Wrzeszcz, Poland, 8–10 July 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Fantazzini, D.; Pushchelenko, J.; Mironenkov, A.; Kurbatskii, A. Forecasting Internal Migration in Russia Using Google Trends: Evidence from Moscow and Saint Petersburg. Forecasting 2021, 3, 48. [Google Scholar] [CrossRef]
- Kupiszewski, M. How trustworthy are forecasts of international migration between Poland and the European Union? J. Ethn. Migr. Stud. 2002, 28, 627–645. [Google Scholar] [CrossRef]
- Cappelen, Å.; Skjerpen, T.; Tønnessen, M. Forecasting Immigration in Official Population Projections Using an Econometric Model. Int. Migr. Rev. 2015, 49, 945–980. [Google Scholar] [CrossRef]
- Azose, J.J.; Sevcikova, H.; Raftery, A.E. Probabilistic population projections with migration uncertainty. Proc. Natl. Acad. Sci. USA 2016, 113, 6460–6465. [Google Scholar] [CrossRef]
- Vasilyeva, A.V. The Forecast of Labour Migration, Reproduction of the Population and Economic Development of Russia. Econ. Reg. 2017, 13, 812–826. [Google Scholar] [CrossRef]
- Shayegh, S.; Emmerling, J.; Tavoni, M. International Migration Projections across Skill Levels in the Shared Socioeconomic Pathways. Sustainability 2022, 14, 4757. [Google Scholar] [CrossRef]
- Brücker, H.; Siliverstovs, B. On the estimation and forecasting of international migration: How relevant is heterogeneity across countries? Empir. Econ. 2006, 31, 735–754. [Google Scholar] [CrossRef] [Green Version]
- Bahna, M. Predictions of Migration from the New Member States after Their Accession into the European Union: Successes and Failures. Int. Migr. Rev. 2008, 42, 844–860. [Google Scholar] [CrossRef]
- Rogers, T.W. Migration Prediction On The Basis Of Prior Migratory Behavior: A Methodological Note. Int. Migr. 1969, 7, 13–19. [Google Scholar] [CrossRef]
- Zagheni, E.; Garimella, V.R.K.; Weber, I.; State, B. Inferring international and internal migration patterns from Twitter data. In Proceedings of the 23rd International Conference on World Wide Web, Seoul, Korea, 7–11 April 2014; pp. 439–444. [Google Scholar]
- Plaut, T.R. An econometric model for forecasting regional population growth. Int. Reg. Sci. Rev. 1981, 6, 53–70. [Google Scholar] [CrossRef] [PubMed]
- Ovchynnikova, O.; Nahornova, O.; Mylko, I.; Begun, S.; Buniak, N.; Kolenda, N. Forecasting Regional Migration Flows. In Proceedings of the 10th International Conference on Advanced Computer Information Technologies (ACIT), Deggendorf, Germany, 16–18 September 2020; pp. 165–169. [Google Scholar]
- Jurdak, R.; Zhao, K.; Liu, J.; AbouJaoude, M.; Cameron, M.; Newth, D. Understanding Human Mobility from Twitter. PLoS ONE 2015, 10, e0131469. [Google Scholar] [CrossRef] [PubMed]
- Carammia, M.; Iacus, S.M.; Wilkin, T. Forecasting asylum-related migration flows with machine learning and data at scale. Sci. Rep. 2022, 12, 1457. [Google Scholar] [CrossRef] [PubMed]
- Terroso-Sáenz, F.; Muñoz, A. Nation-wide human mobility prediction based on graph neural networks. Appl. Intell. 2022, 52, 4144–4160. [Google Scholar] [CrossRef] [PubMed]
- Terroso-Saenz, F.; Flores, R.; Muñoz, A. Human mobility forecasting with region-based flows and geotagged Twitter data. Expert Syst. Appl. 2022, 203, 117477. [Google Scholar] [CrossRef]
- Terroso-Sáenz, F.; Muñoz, A.; Fernández-Pedauye, J.; Cecilia, J.M. Human Mobility Prediction With Region-Based Flows and Water Consumption. IEEE Access 2021, 9, 88651–88663. [Google Scholar] [CrossRef]
- Gaigbe-Togbe, V.; Bassarsky, L.; Gu, D.; Spoorenberg, T.; Zeifman, L. World Population Prospects 2022; United Nations: New York, NY, USA, 2022; ISBN 978-92-1-148373-4. [Google Scholar]
- Fertig, M.; Schmidt, C.M. Aggregate-level migration studies as a tool for forecasting future migration streams. In International Migration: Trends, Policy and Economic Impact; Institute for the Study of Labor: London, UK; New York, NY, USA, 2005; pp. 110–136. [Google Scholar]
- Dustmann, C.; Casanova, M.; Fertig, M.; Preston, I.; Schmidt, C.M. The Impact of EU Enlargement on Migration Flows; Home Office Online Report 25/03; Research Development and Statistics Directorate, Home Office: London, UK, 2003; pp. 1–76. [Google Scholar]
- Alvarez-Plata, P.; Brücker, H.; Siliverstovs, B. Potential Migration from Central and Eastern Europe into the EU-15: An Update; European Commission, Directorate-General for Employment and Social Affairs: Brussels, Belgium, 2003. [Google Scholar]
- Dao, T.H.; Docquier, F.; Maurel, M.; Schaus, P. Global migration in the twentieth and twenty-first centuries: The unstoppable force of demography. Rev. World Econ. 2021, 157, 417–449. [Google Scholar] [CrossRef]
- Burzynski, M.; Deuster, C.; Docquier, F. Geography of skills and global inequality. J. Dev. Econ. 2020, 142, 102333. [Google Scholar] [CrossRef]
- Anderson, J.E. The gravity model. Annu. Rev. Econ. 2011, 3, 133–160. [Google Scholar] [CrossRef] [Green Version]
- Beine, M.; Bertoli, S.; Fernández-Huertas Moraga, J. A practitioners’ guide to gravity models of international migration. World Econ. 2016, 39, 496–512. [Google Scholar] [CrossRef] [Green Version]
- Hanson, G.; McIntosh, C. Is the Mediterranean the new Rio Grande? US and EU immigration pressures in the long run. J. Econ. Perspect. 2016, 30, 57–82. [Google Scholar] [CrossRef] [Green Version]
- Bertoli, S.; Brücker, H.; Moraga, J.F.H. The European crisis and migration to Germany. Reg. Sci. Urban Econ. 2016, 60, 61–72. [Google Scholar] [CrossRef] [Green Version]
- Sjaastad, L.A. The costs and returns of human migration. J. Political Econ. 1962, 70 Pt 2, 80–93. [Google Scholar] [CrossRef]
- Backhaus, A.; Martinez-Zarzoso, I.; Muris, C. Do climate variations explain bilateral migration? A gravity model analysis. IZA J. Migr. 2015, 4, 3. [Google Scholar] [CrossRef] [Green Version]
- Friebel, G.; Manchin, M.; Mendola, M.; Prarolo, G. International Migration Intentions and Illegal Costs: Evidence Using Africa-to-Europe Smuggling Routes. CEPR Discussion Paper No. DP13326. 2018. Available online: https://ssrn.com/abstract=3290517 (accessed on 20 March 2022).
- Rikani, A.; Schewe, J. Global bilateral migration projections accounting for diasporas, transit and return flows, and poverty constraints. Demogr. Res. 2021, 45, 87–140. [Google Scholar] [CrossRef]
- Beyer, R.M.; Schewe, J.; Lotze-Campen, H. Gravity models do not explain, and cannot predict, international migration dynamics. Humanit. Soc. Sci. Commun. 2022, 9, 56. [Google Scholar] [CrossRef]
- Bijak, J. Forecasting International Migration in Europe: A Bayesian View; Springer Science+Business Media: Dordrecht, The Netherlands; Heidelberg, Germany; London, UK.; New York, NY, USA, 2011. [Google Scholar]
- Wiśniowski, A.; Smith, P.W.F.; Bijak, J.; Raymer, J.; Forster, J.J. Bayesian Population Forecasting: Extending the Lee-Carter Method. Demography 2015, 52, 1035–1059. [Google Scholar] [CrossRef] [Green Version]
- Lutz, W.; Goldstein, J.R. Introduction: How to deal with uncertainty in population forecasting? Int. Stat. Rev. 2004, 72, 1–4. [Google Scholar] [CrossRef]
- Billari, F.C.; Graziani, R.; Melilli, E. Stochastic population forecasts based on conditional expert opinions. J. R. Stat. Soc. Ser. A (Stat. Soc.) 2012, 175, 491–511. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Billari, F.C.; Graziani, R.; Melilli, E. Stochastic Population Forecasting Based on Combinations of Expert Evaluations Within the Bayesian Paradigm. Demography 2014, 51, 1933–1954. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mitchell, T. Machine Learning; McGraw Hill: New York, NY, USA, 1997. [Google Scholar]
- Robinson, C.; Dilkina, B. A machine learning approach to modeling human migration. In Proceedings of the 1st ACM SIGCAS Conference on Computing and Sustainable Societies, Menlo Park and San Jose, CA, USA, June 2018; pp. 1–8. [Google Scholar] [CrossRef] [Green Version]
- Tarasyev, A.A.; Agarkov, G.A.; Hosseini, S.I. Machine learning in labor migration prediction. In Proceedings of the AIP Conference, Thessaloniki, Greece, 25–30 September 2017; AIP Publishing LLC: Melville, NY, USA, 2018; Volume 1978, p. 440004. [Google Scholar] [CrossRef]
- Kiossou, H.S.; Schenk, Y.; Docquier, F.; Houndji, V.R.; Nijssen, S.; Schaus, P. Using an interpretable Machine Learning approach to study the drivers of International Migration. arXiv 2020, arXiv:2006.03560. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Biau, G.; Scornet, E. A random forest guided tour. TEST 2015, 25, 197–227. [Google Scholar] [CrossRef] [Green Version]
- Aoga, J.; Bae, J.; Veljanoska, S.; Nijssen, S.; Schaus, P. Impact of weather factors on migration intention using machine learning algorithms. arXiv 2020, arXiv:2012.02794. [Google Scholar]
- Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw. 2004, 17, 113–126. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Luo, L.; Hu, L.; Sun, M. An SVM-based classification model for migration prediction of Beijing. Eng. Lett. 2020, 28, 1023–1030. [Google Scholar]
- Golenvaux, N.; Alvarez, P.G.; Kiossou, H.S.; Schaus, P. An LSTM approach to Forecast Migration using Google Trends. arXiv 2020, arXiv:2005.09902. [Google Scholar]
- Simini, F.; Barlacchi, G.; Luca, M.; Pappalardo, L. A Deep Gravity model for mobility flows generation. Nat. Commun. 2021, 12, 6576. [Google Scholar] [CrossRef]
- Bijak, J. Migration Forecasting: Beyond the Limits of Uncertainty; Global Migration Data Analysis Centre Data Briefing Series: Berlin, Germany, 2016; Issue 6; pp. 1–7. [Google Scholar]
- Sirbu, A.; Andrienko, G.; Andrienko, N.; Boldrini, C.; Sharma, R. Human migration: The big data perspective. Int. J. Data Sci. Anal. 2021, 11, 341–360. [Google Scholar] [CrossRef]


| Method | Model | Data Source | Spatial Attributes | Temporal Attributes | References |
|---|---|---|---|---|---|
| Deterministic method | -- | US Department of Health and Human Services and US Bureau of the Census statistics | internal migration | long-term | [42] |
| Human Mortality Database; Federal Statistical Office of Germany | international migration | long-term | [43,44] | ||
| Stochastic methods | Bayesian Model | Statistics New Zealand online database INFOS and Australian Bureau of Statistics database | international migration | short-term | [45] |
| Eurostat, United Nations Statistics Division statistics and the Council of Europe’s Demographic Yearbooks; Office for National Statistics census data; National Records of Scotland and the Office for National Statistics census data; United Nations Population Division’s biennial World Population Prospects report; Statistics Sweden census data; Korean Statistical Information Service statistics, Australian Bureau of Statistics census data. | international migration | long-term | [46,47,48,49,50] | ||
| Gravity Model | Internal Revenue Service statistics; | internal migration | long-term | [51] | |
| Internal Revenue Service statistics; World Bank’s Global Bilateral Migration database; Eurostat statistics, World DataBank statistical data (2016), Organization for Economic Co-Operation and Development statistics, French Centre d’Etudes Prospectives et d’Informations Internationals statistics; | international migration | long-term | [52,53,54] | ||
| Google Trends data, Organization for Economic Co-Operation and Development statistics. | international migration | short-term | [55] | ||
| Time Series Model | Internal Revenue Service statistics | internal migration | short-term | [56] | |
| Netherlands Central Bureau of Statistics census data | international migration | short-term | [57] | ||
| Mexican demographic surveys of households and American Community Survey data; Household surveys data; Federal Statistical Office of Germany census data | international migration | long-term | [58,59,60] | ||
| Internal Revenue Service statistics; International migration report (2017) | international migration | long and short-term | [61,62] | ||
| Author-collected datasets; Google Trends data | internal migration | short and long-term | [63,64] | ||
| Econometrics Method | Trends in International Migration statistics, Migration Potential in Central and Eastern Europe statistics; Statistics Norway’s “Statbank”; World Population Prospects (2015); Russian Federation and Commonwealth of Independent States countries statistics; World Bank Global Bilateral Migration | international migration | long-term | [65,66,67,68,69] | |
| Organization for Economic Co-Operation and Development statistics, World Bank statistics, Federal Statistical Office census data; the Candidate Country Eurobarometer survey series; Household surveys data; Twitter; Google Trends data; | international migration | short-term | [55,70,71,72,73] | ||
| United States Bureau of the Census da-ta; | internal migration | long-term | [74] | ||
| Site of the Main Department of Statistics in the Khmelnytskyi Region statistics; Twitter; data collected by the author. | internal migration | short-term | [11,75,76] | ||
| Grey Model | China Statistical Yearbook; US Department of Health and Human Services and US Bureau of the Census statistics. | international migration | long-term | [12,13] | |
| Machine-learning method | Classical Machine-Learning Method | Data collected by the author; | internal migration | long-term | [14] |
| Department of Overseas Labor statistics | international migration | long-term | [16] | ||
| Household survey data; | internal migration | -- | [17] | ||
| Mexican Migrant Project statistics; Google Trends Index. | international migration | short-term | [15,18] | ||
| Deep-Learning Method | Nationwide Human Mobility Dataset released by the Spanish Ministry of Transportation; | internal migration | short-term | [77,78,79] | |
| Google Trends Index; Organization for Economic Co-Operation and Development International Migration Database | international migration | long-term | [80] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, T.; Huang, C.; Yang, J.; Huang, M. Transcending Time and Space: Survey Methods, Uncertainty, and Development in Human Migration Prediction. Sustainability 2023, 15, 10584. https://doi.org/10.3390/su151310584
Pu T, Huang C, Yang J, Huang M. Transcending Time and Space: Survey Methods, Uncertainty, and Development in Human Migration Prediction. Sustainability. 2023; 15(13):10584. https://doi.org/10.3390/su151310584
Chicago/Turabian StylePu, Tongzheng, Chongxing Huang, Jingjing Yang, and Ming Huang. 2023. "Transcending Time and Space: Survey Methods, Uncertainty, and Development in Human Migration Prediction" Sustainability 15, no. 13: 10584. https://doi.org/10.3390/su151310584
APA StylePu, T., Huang, C., Yang, J., & Huang, M. (2023). Transcending Time and Space: Survey Methods, Uncertainty, and Development in Human Migration Prediction. Sustainability, 15(13), 10584. https://doi.org/10.3390/su151310584







