Design and Performance Analysis of New Multilevel Inverter for PV System
Abstract
1. Introduction
2. Materials and Methods
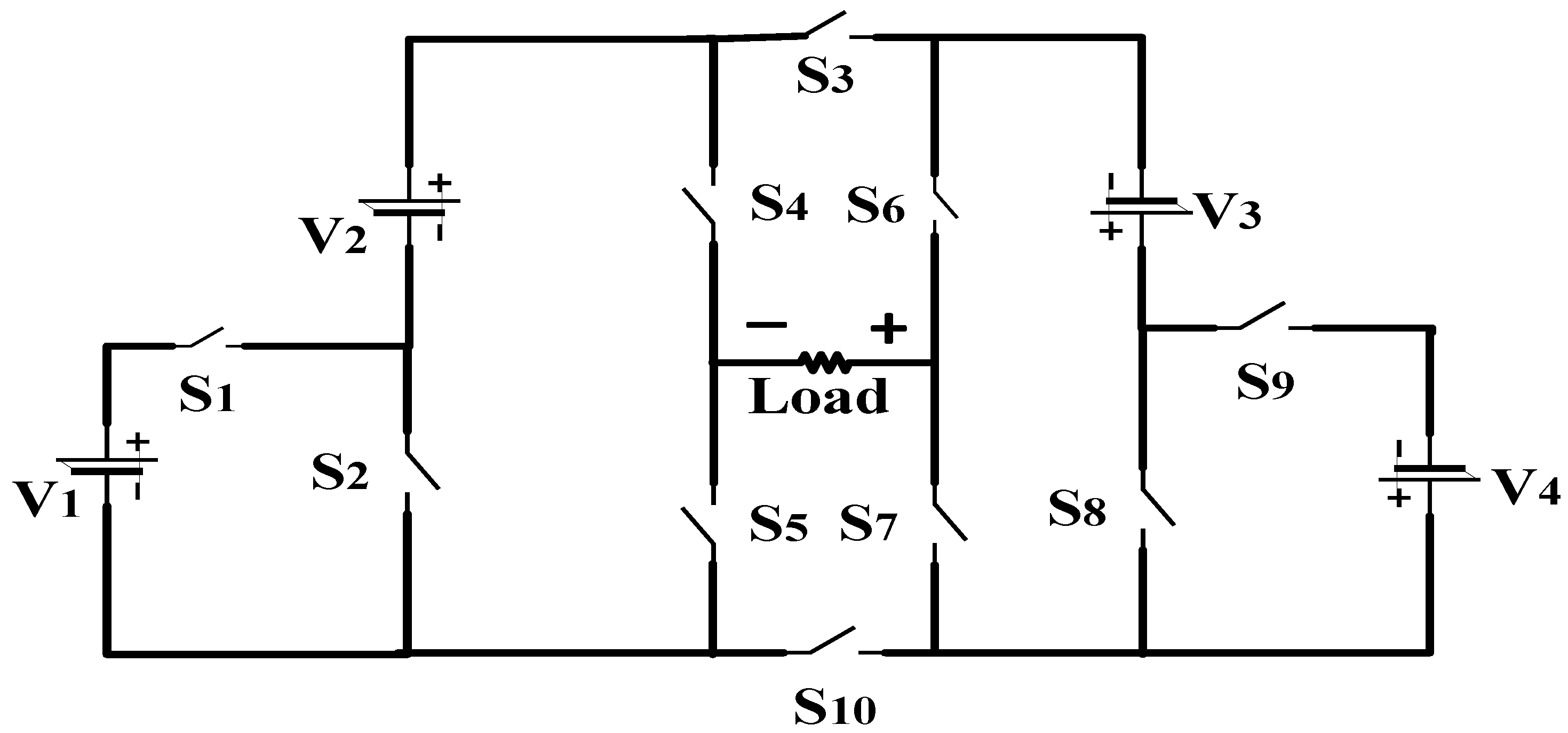
2.1. Proposed New Multilevel Inverter Topology
2.1.1. Switching States of New Multilevel Inverter
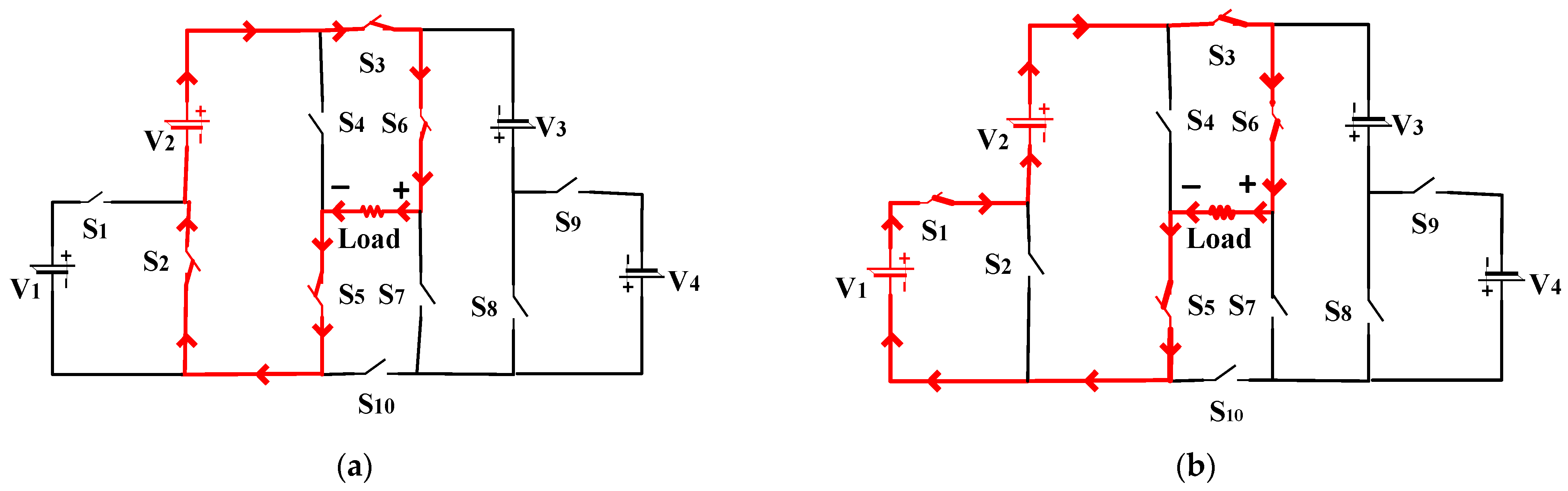
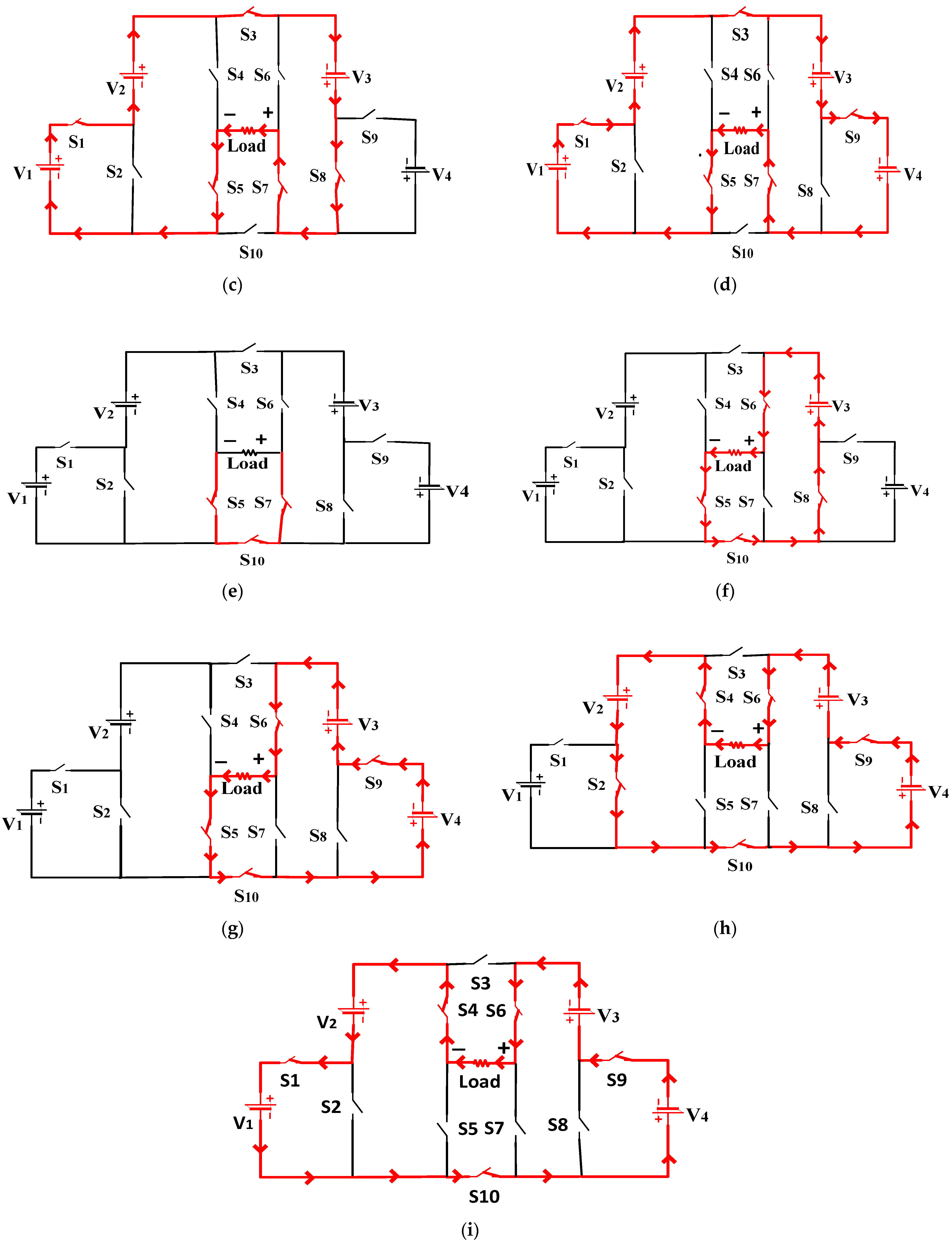
2.1.2. Modes of Operation of Proposed Topology
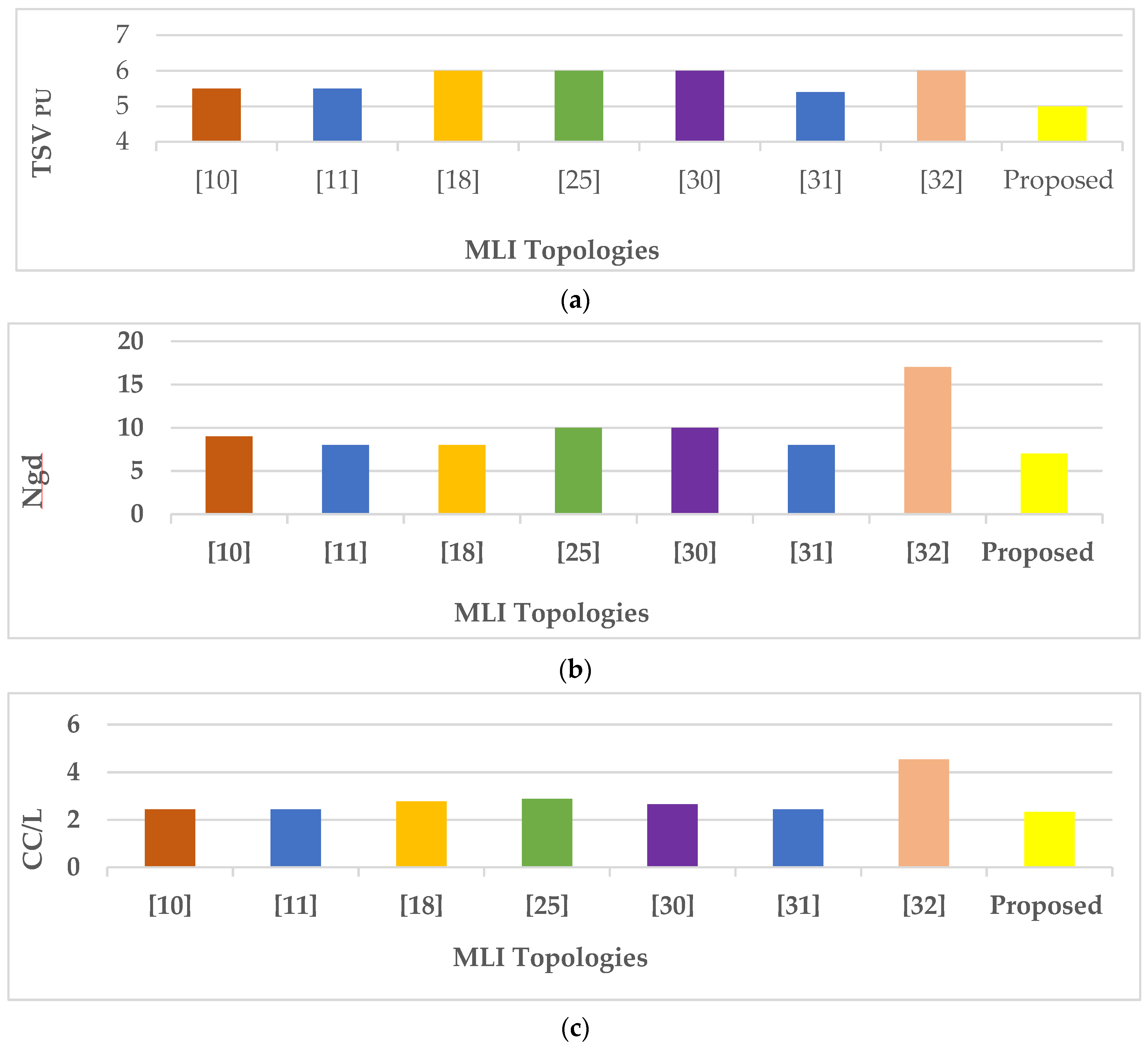
2.2. Total Standing Voltage (TSV)
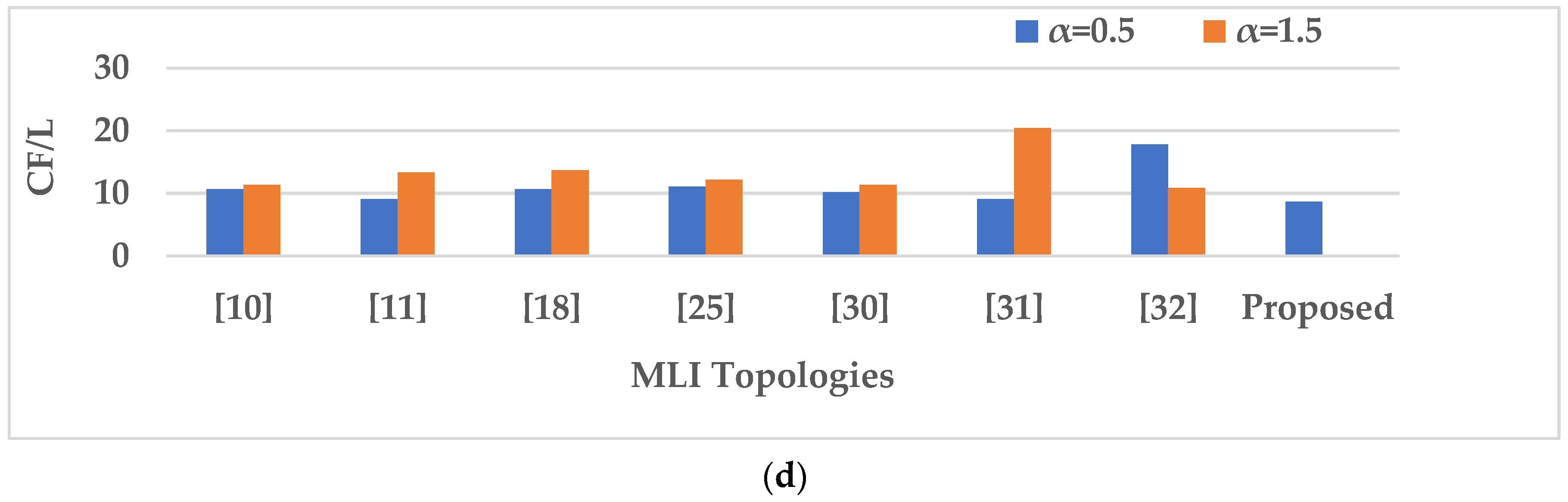
2.3. Cost Function (CF)
2.4. Components Count per Level (CC/L)
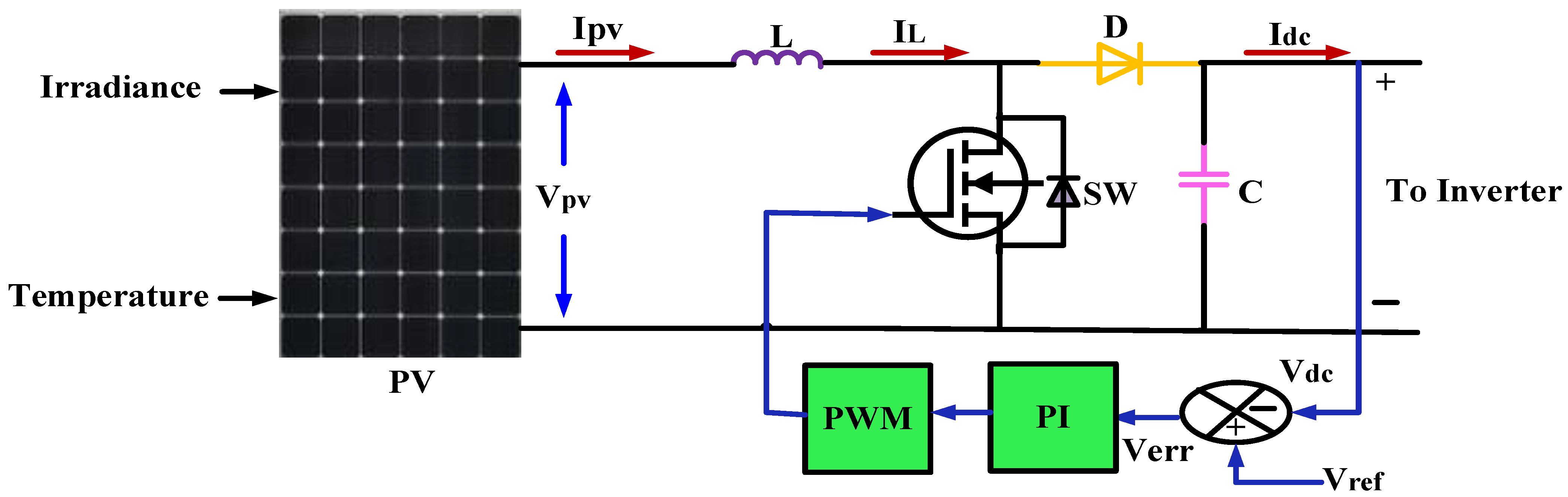
2.5. Boost Converter with PV System with PI Controller
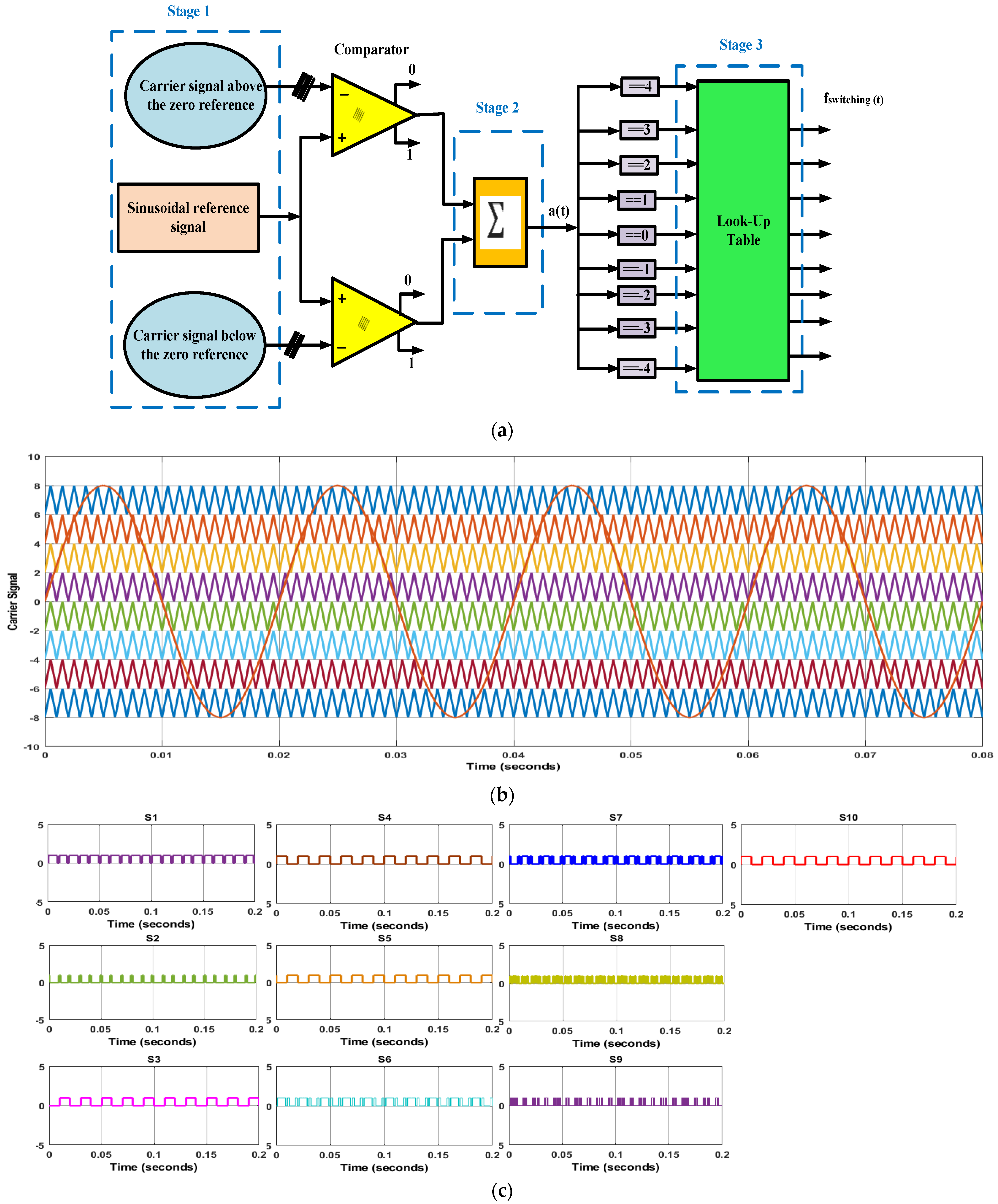
3. Control Circuit of New Topology of MLI
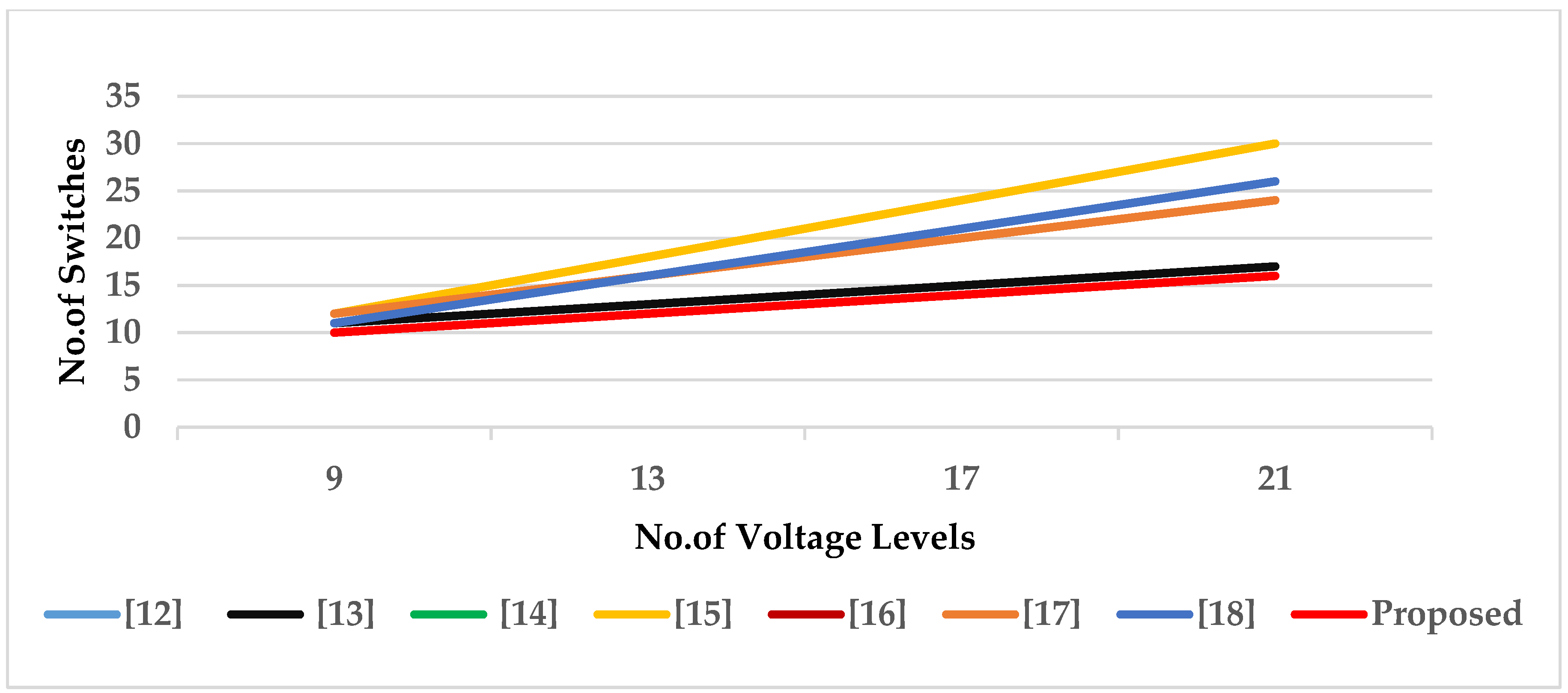
4. Comparative Analysis
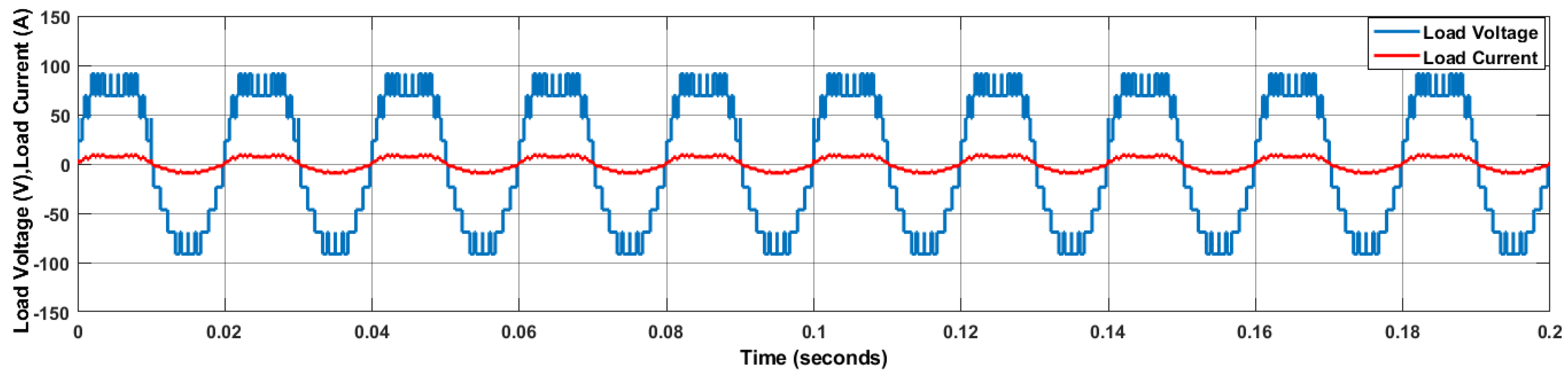
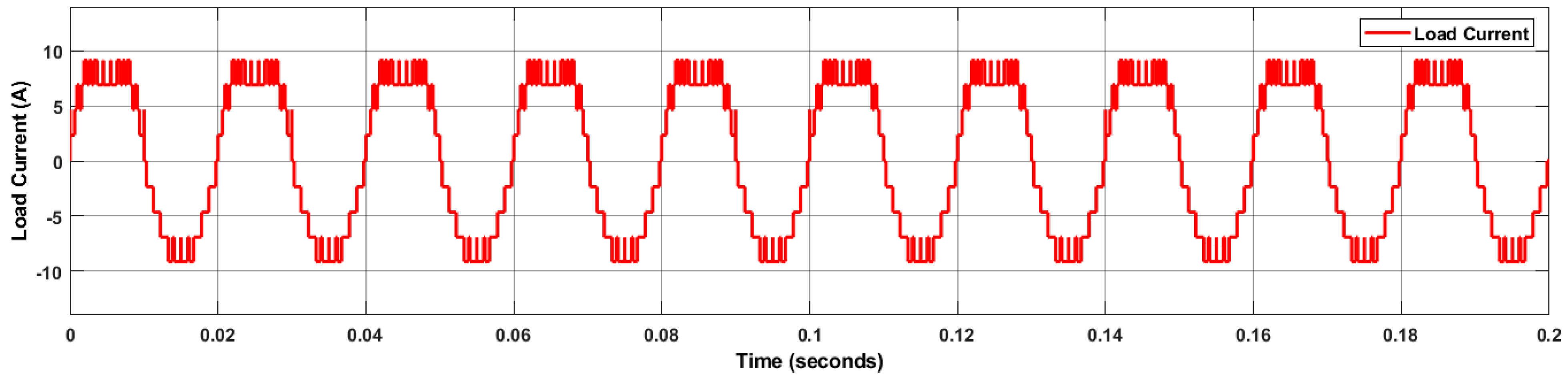
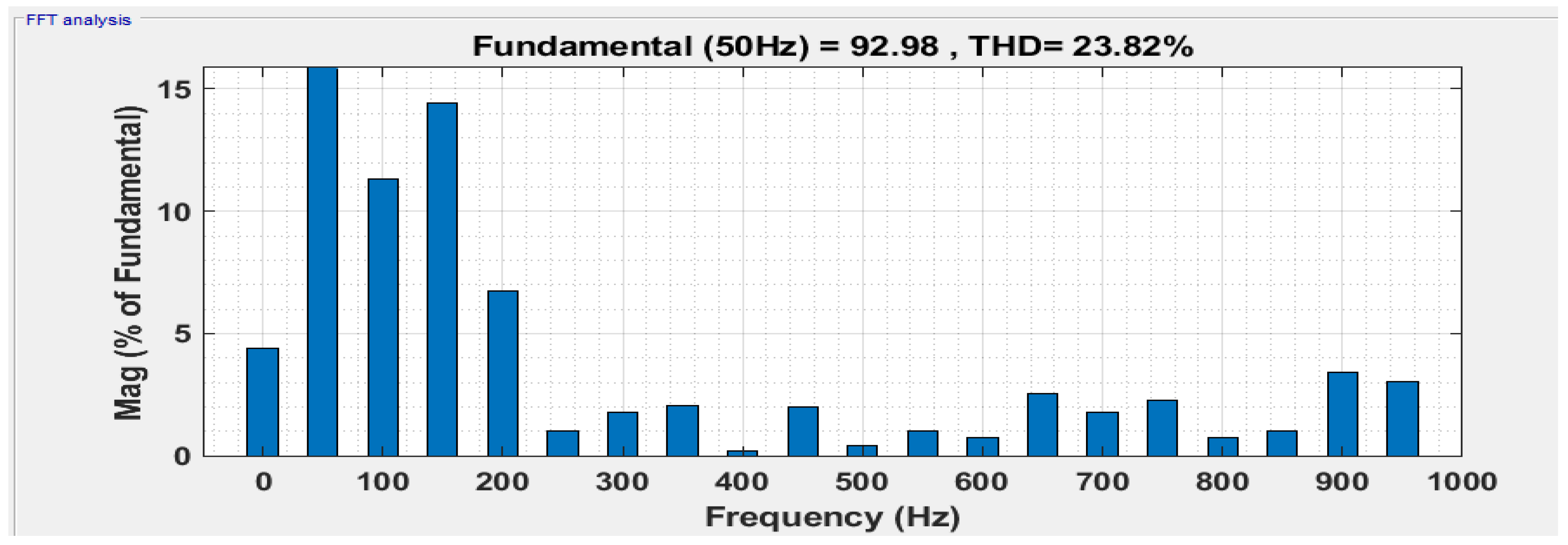
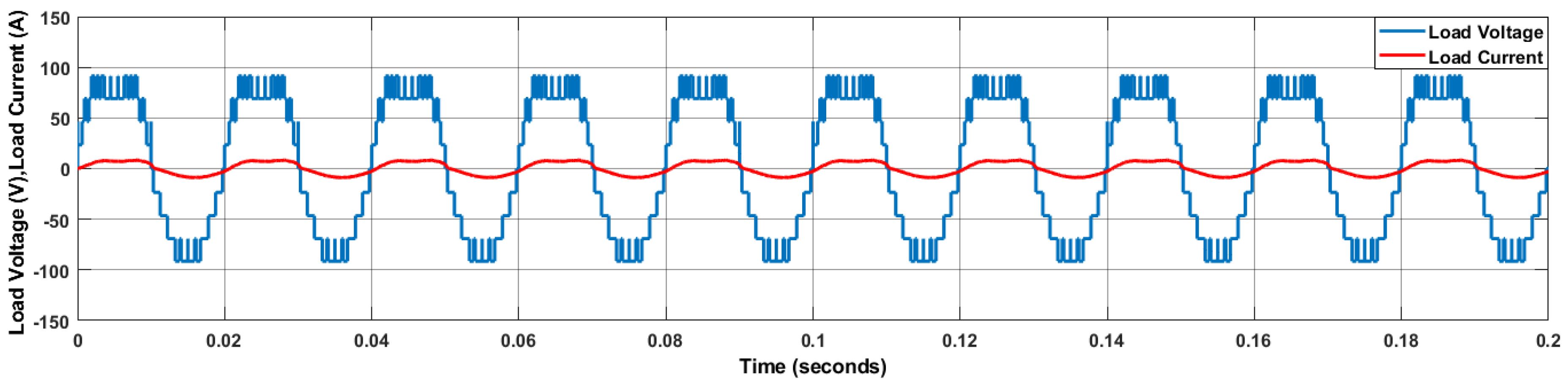
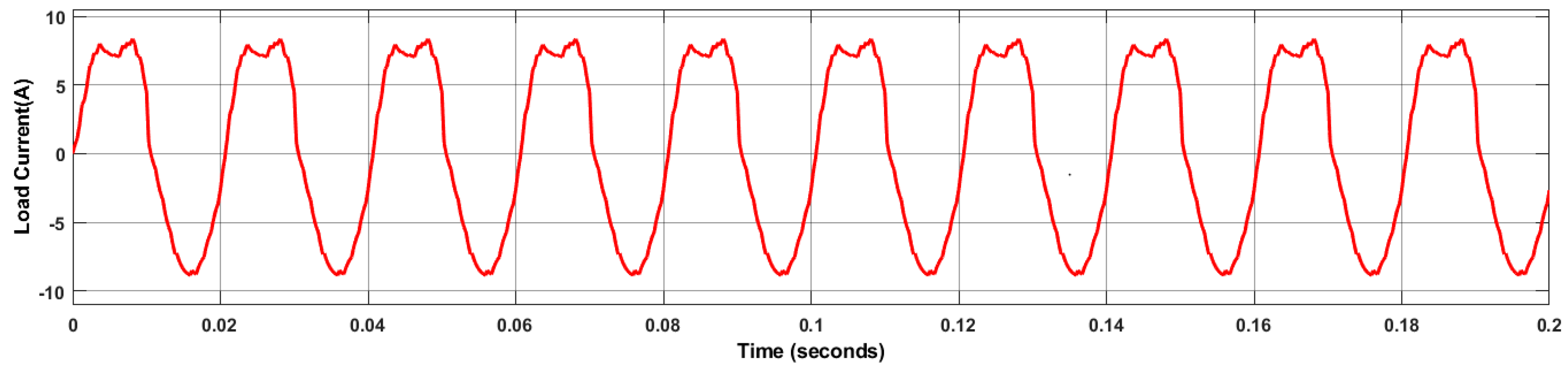
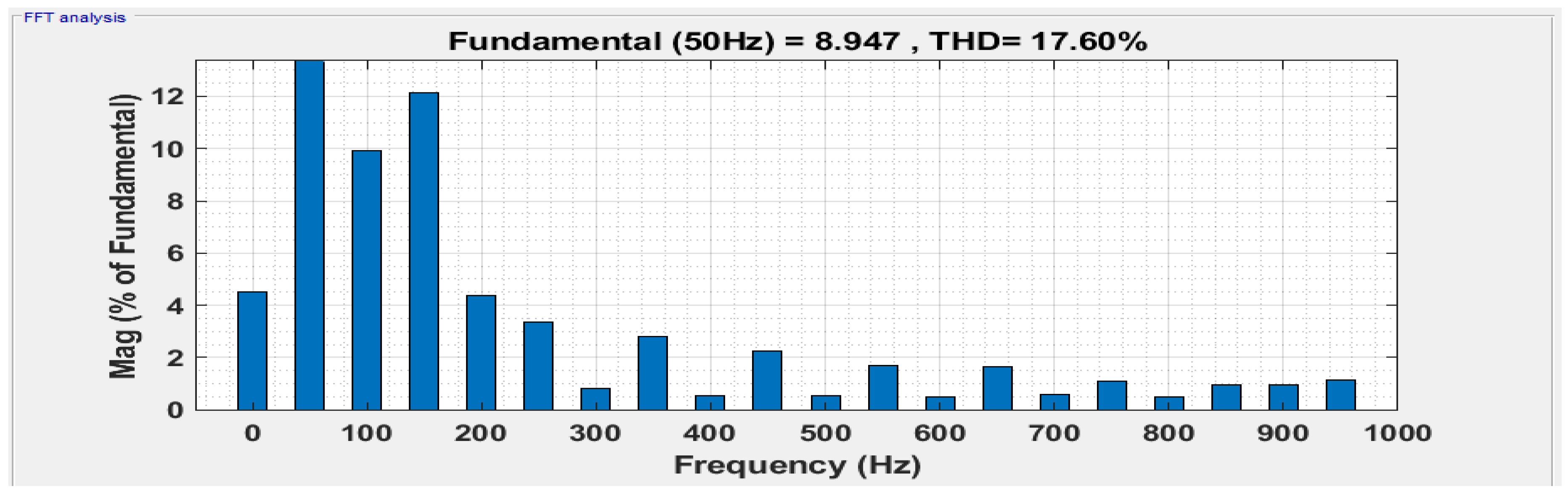
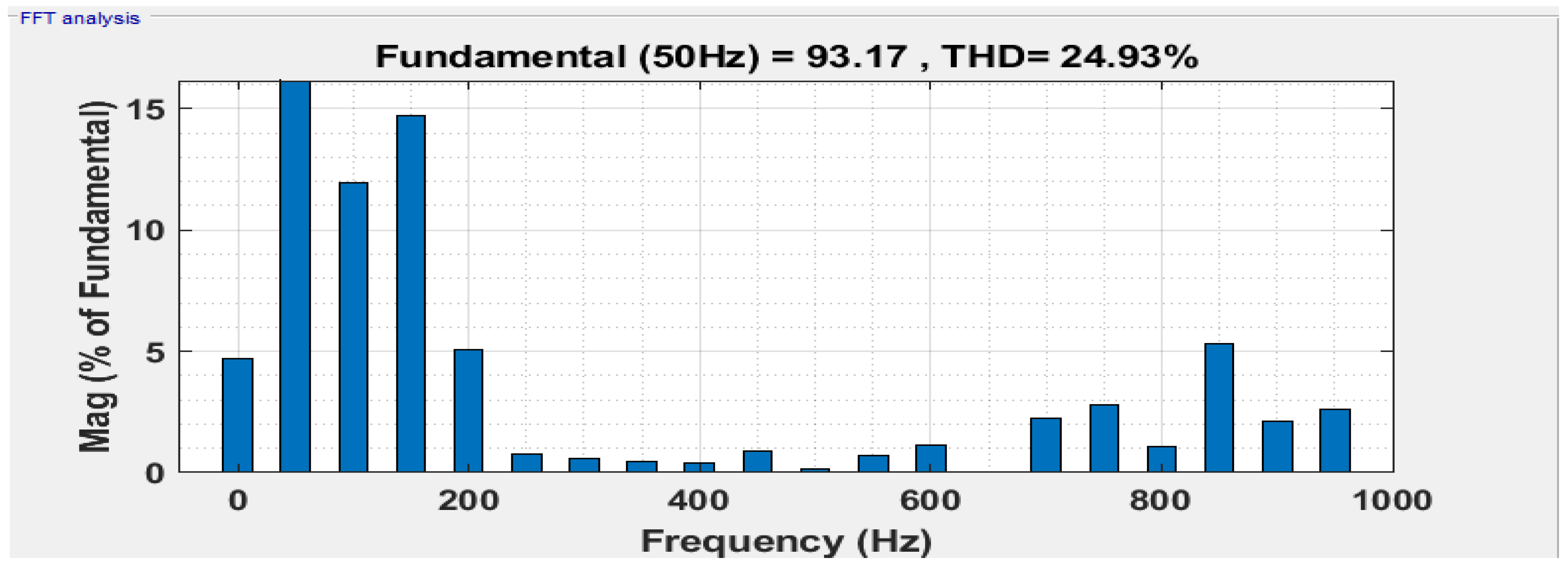
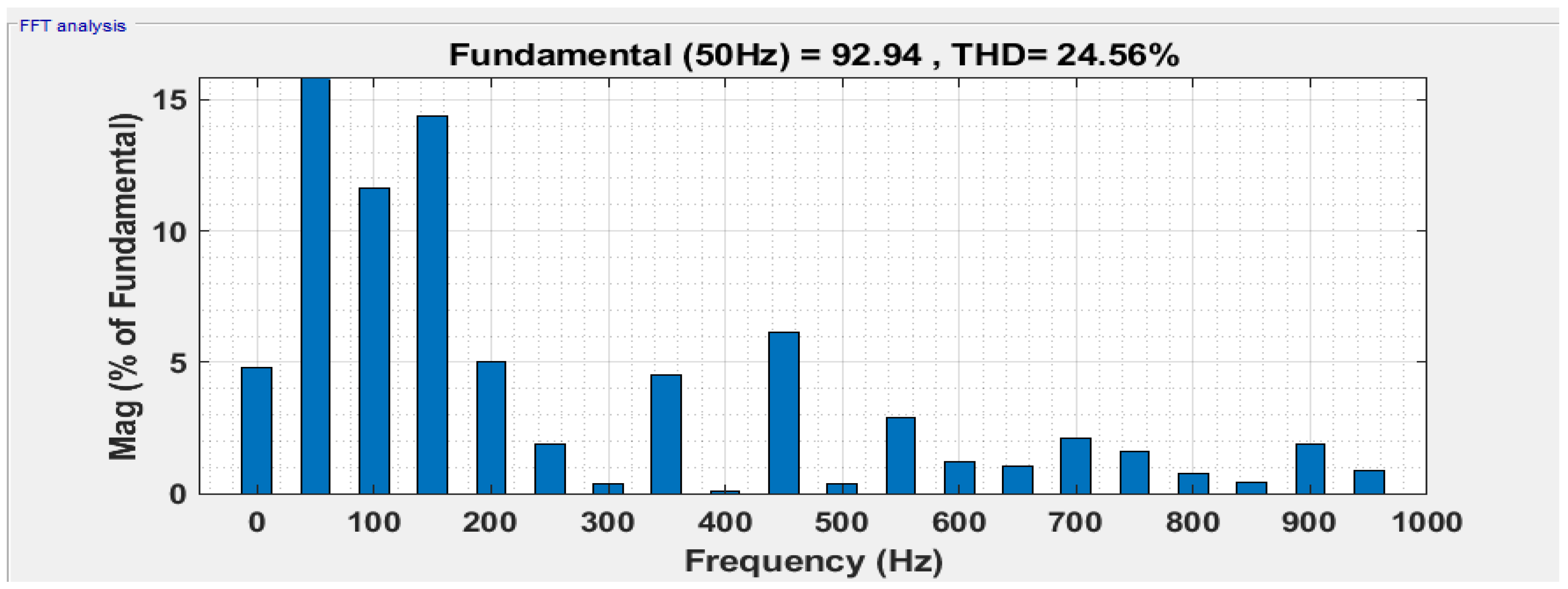
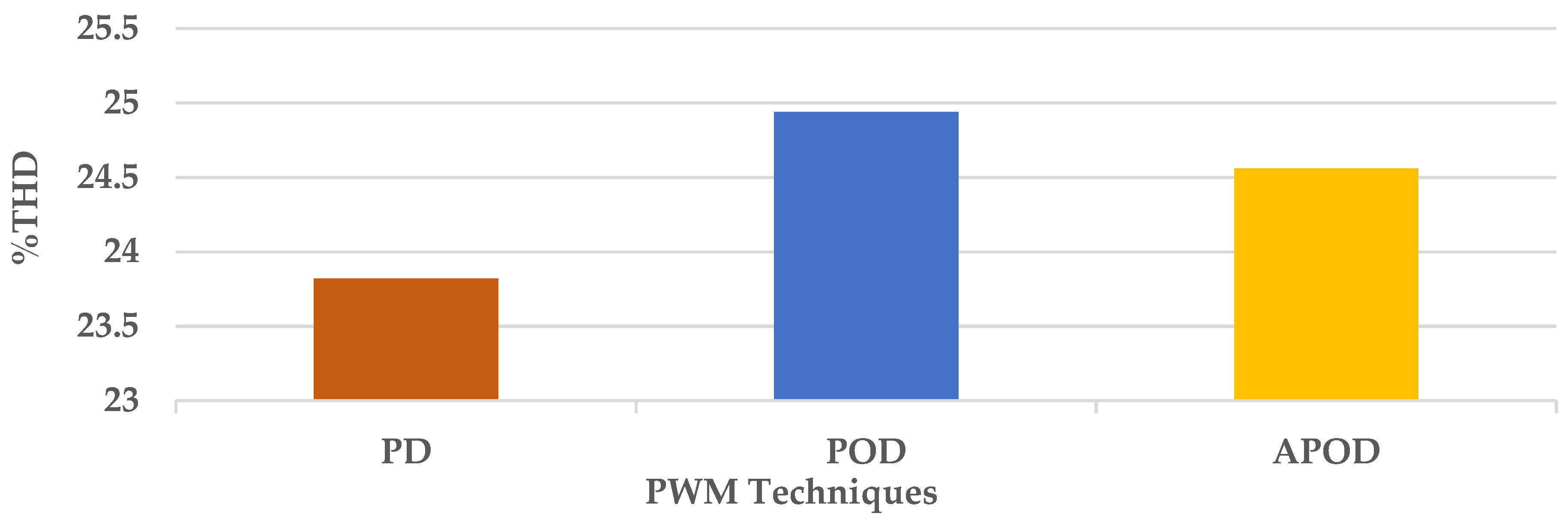
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ellabban, O.; Abu-Rub, H.; Blaabjerg, F. Renewable energy resources: Current status, future prospects and their enabling technology. Renew. Sustain. Energy Rev. 2014, 39, 748–764. [Google Scholar] [CrossRef]
- Das, S.R.; Sahoo, A.K.; Dhiman, G.; Singh, K.K.; Singh, A. Photo voltaic integrated multilevel inverter based hybrid filter using spotted hyena optimizer. Comput. Electr. Eng. 2021, 96, 107510. [Google Scholar] [CrossRef]
- Bana, P.R.; Panda, K.P.; Naayagi, R.; Siano, P.; Panda, G. Recently developed reduced switch multilevel inverter for renewable energy integration and drives application: Topologies, comprehensive analysis and comparative evaluation. IEEE Access 2019, 7, 54888–54909. [Google Scholar] [CrossRef]
- Kumar, P.; Kour, M.; Goyal, S.K.; Singh, B.P. Multilevel inverter topologies in renewable energy applications. In Intelligent Computing Techniques for Smart Energy Systems; Springer: Berlin/Heidelberg, Germany, 2020; pp. 891–902. [Google Scholar]
- Das, S.R.; Ray, P.K.; Sahoo, A.K.; Dhiman, G. Application of optimisation technique in PV integrated multilevel inverter for power quality improvement. Comput. Electr. Eng. 2022, 97, 107606. [Google Scholar] [CrossRef]
- Rajalakshmi, S.; Rangarajan, P. Investigation of modified multilevel inverter topology for PV system. Microprocess. Microsyst. 2019, 71, 102870. [Google Scholar] [CrossRef]
- Bughneda, A.; Salem, M.; Richelli, A.; Ishak, D.; Alatai, S. Review of multilevel inverters for PV energy system applications. Energies 2021, 14, 1585. [Google Scholar] [CrossRef]
- Maheswari, K.; Bharanikumar, R.; Arjun, V.; Amrish, R.; Bhuvanesh, M. A comprehensive review on cascaded H-bridge multilevel inverter for medium voltage high power applications. Mater. Today Proc. 2021, 45, 2666–2670. [Google Scholar] [CrossRef]
- Tarassodi, P.; Siadatan, A.; Keshani, M. Single-Phase Multi-Level Inverter Suitable for Symmetrical and Asymmetrical Photovoltaic (PV) Applications. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; IEEE: New York, NY, USA, 2019; pp. 980–984. [Google Scholar]
- Sun, X.; Wang, B.; Zhou, Y.; Wang, W.; Du, H.; Lu, Z. A single DC source cascaded seven-level inverter integrating switched-capacitor techniques. IEEE Trans. Ind. Electron. 2016, 63, 7184–7194. [Google Scholar] [CrossRef]
- Yousofi-Darmian, S.; Barakati, S.M. A new asymmetric multilevel inverter with reduced number of components. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 4333–4342. [Google Scholar] [CrossRef]
- Ali, A.I.; Sayed, M.A.; Mohamed, E.E.; Azmy, A.M. Advanced single-phase nine-level converter for the integration of multiterminal DC supplies. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 1949–1958. [Google Scholar] [CrossRef]
- Booma, N.; Sridhar, N. Nine level cascaded H-bridge multilevel DC-link inverter. In Proceedings of the 2011 International Conference on Emerging Trends in Electrical and Computer Technology, Nagercoil, India, 23–24 March 2011; IEEE: New York, NY, USA, 2011; pp. 315–320. [Google Scholar]
- Nagarajan, R.; Saravanan, M. Performance analysis of a novel reduced switch cascaded multilevel inverter. J. Power Electron. 2014, 14, 48–60. [Google Scholar] [CrossRef]
- Babaei, E.; Laali, S.; Alilu, S. Cascaded multilevel inverter with series connection of novel H-bridge basic units. IEEE Trans. Ind. Electron. 2014, 61, 6664–6671. [Google Scholar] [CrossRef]
- Mokhberdoran, A.; Ajami, A. Symmetric and asymmetric design and implementation of new cascaded multilevel inverter topology. IEEE Trans. Power Electron. 2014, 29, 6712–6724. [Google Scholar] [CrossRef]
- Venkataramanaiah, J.; Suresh, Y.; Panda, A.K. A review on symmetric, asymmetric, hybrid and single DC sources based multilevel inverter topologies. Renew. Sustain. Energy Rev. 2017, 76, 788–812. [Google Scholar] [CrossRef]
- Venkatraman, T.; Periasamy, S. Multilevel inverter topology with modified pulse width modulation and reduced switch count. Acta Polytech. Hung. 2018, 15, 141–167. [Google Scholar]
- Alishah, R.S.; Hosseini, S.H.; Babaei, E.; Sabahi, M. A new general multilevel converter topology based on cascaded connection of submultilevel units with reduced switching components, DC sources, and blocked voltage by switches. IEEE Trans. Ind. Electron. 2016, 63, 7157–7164. [Google Scholar] [CrossRef]
- Sadanala, C.; Pattnaik, S.; Singh, V.P. A flying capacitor based multilevel inverter architecture with symmetrical and asymmetrical configurations. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 10, 2210–2222. [Google Scholar] [CrossRef]
- Firdous, Z.; Rehman, H.; Tariq, M.; Sarwar, A. Investigation of Fault-Tolerant Capabilities of a Reduced Device Multilevel Inverter. In Proceedings of the 2022 2nd International Conference on Emerging Frontiers in Electrical and Electronic Technologies (ICEFEET), Patna, India, 24–25 June 2022; IEEE: New York, NY, USA, 2022; pp. 1–5. [Google Scholar]
- Ali, M.; Tariq, M.; Sarwar, A.; Alamri, B. A 13-, 11-, and 9-Level Boosted Operation of a Single-Source Asymmetrical Inverter with Hybrid PWM Scheme. IEEE Trans. Ind. Electron. 2022, 69, 12817–12828. [Google Scholar] [CrossRef]
- Upadhyay, D.; Ali, M.; Tariq, M.; Khan, S.A.; Alamri, B.; Alahmadi, A. Thirteen-level UXE-type inverter with 12-band hysteresis current control employing PSO based PI controller. IEEE Access 2022, 10, 29890–29902. [Google Scholar] [CrossRef]
- Asif, M.; Tariq, M.; Sarwar, A.; Hussan, M.R.; Ahmad, S.; Mihet-Popa, L.; Shah Noor Mohamed, A. A Robust Multilevel Inverter Topology for Operation under Fault Conditions. Electronics 2021, 10, 3099. [Google Scholar] [CrossRef]
- Wasiq, M.; Sarwar, A.; Sarwer, Z.; Tariq, M.; Ahmad, S.; Al-Shayea, A.M.; Hossain, J. Design and Validation of a Reduced Switching Components Step-Up Multilevel Inverter (RSCS-MLI). Processes 2021, 9, 1948. [Google Scholar] [CrossRef]
- Ponnusamy, P.; Sivaraman, P.; Almakhles, D.J.; Padmanaban, S.; Leonowicz, Z.; Alagu, M.; Ali, J.S.M. A new multilevel inverter topology with reduced power components for domestic solar PV applications. IEEE Access 2020, 8, 187483–187497. [Google Scholar] [CrossRef]
- Rubeena, A.; Paulose, S.; Thomas, M.; Joy, J. PWM control strategies for Switched-Capacitor inverters. Mater. Today Proc. 2022, 58, 516–522. [Google Scholar]
- Samadaei, E.; Sheikholeslami, A.; Gholamian, S.A.; Adabi, J. A square T-type (ST-Type) module for asymmetrical multilevel inverters. IEEE Trans. Power Electron. 2017, 33, 987–996. [Google Scholar] [CrossRef]
- Khasim, S.R.; Dhanamjayulu, C. Design and Implementation of Asymmetrical Multilevel Inverter with Reduced Components and Low Voltage Stress. IEEE Access 2022, 10, 3495–3511. [Google Scholar] [CrossRef]
- Prabaharan, N.; Palanisamy, K. Analysis of cascaded H-bridge multilevel inverter configuration with double level circuit. IET Power Electron. 2017, 10, 1023–1033. [Google Scholar] [CrossRef]
- Pradhan, A.; Panda, B. A simplified design and modeling of boost converter for photovoltaic sytem. Int. J. Electr. Comput. Eng. 2018, 8, 141. [Google Scholar] [CrossRef]
- Sarker, R. Phase Opposition Disposition PWM (POD-PWM) Strategy to Reduce WTHD Content from an NPC Inverter-Fed Electric Vehicle System. In Proceedings of the 2020 IEEE 17th India Council International Conference (INDICON), New Delhi, India, 10–13 December 2020; IEEE: New York, NY, USA, 2020; pp. 1–6. [Google Scholar]
- Thakre, K.; Mohanty, K.B. Performance improvement of multilevel inverter through trapezoidal triangular carrier based PWM. In Proceedings of the 2015 International Conference on Energy, Power and Environment: Towards Sustainable Growth (ICEPE), Shillong, India, 12–13 June 2015; IEEE: New York, NY, USA, 2015; pp. 1–6. [Google Scholar]
- Jagabar Sathik, M.A.; Abdel Aleem, S.H.E.; Kannan, R.; Zobaa, A.F. A new switched DC-link capacitor-based multi-level converter (SDC2MLC). Electr. Power Compon. Syst. 2017, 45, 1001–1015. [Google Scholar] [CrossRef]
- Alishah, R.S.; Hosseini, S.H.; Babaei, E.; Sabahi, M. Optimal design of new cascaded switch-ladder multilevel inverter structure. IEEE Trans. Ind. Electron. 2016, 64, 2072–2080. [Google Scholar] [CrossRef]
- Alishah, R.S.; Hosseini, S.H.; Babaei, E.; Sabahi, M.; Gharehpetian, G.B. New high step-up multilevel converter topology with self-voltage balancing ability and its optimization analysis. IEEE Trans. Ind. Electron. 2017, 64, 7060–7070. [Google Scholar] [CrossRef]





| 1 0 1 1 0 1 1 0 0 0 0 + |
| 2 1 0 1 0 1 1 0 0 0 0 + |
| 3 1 0 1 0 1 0 1 1 0 0 +3 |
| 4 1 0 1 0 1 0 1 0 1 0 +4 |
| 5 0 0 0 0 1 0 1 0 0 1 0 |
| 6 0 0 0 0 1 1 0 1 0 1 − |
| 7 0 0 0 0 1 1 0 0 1 1 − |
| 8 0 1 0 1 0 1 0 0 1 1 − |
| 9 1 0 0 1 0 1 0 0 1 1 − |
| [11] 9 4 11 0 0 9 2.44 5.5 10.66 12.8 |
| [12] 9 4 10 0 0 8 2.44 5.5 9.1 11.33 |
| [19] 9 4 12 0 1 8 2.77 6 10.66 13.33 |
| [28] 9 4 12 0 0 10 2.88 6 11.1 13.7 |
| [34] 9 4 11 0 0 10 2.66 6 10.22 12.22 |
| [35] 9 4 10 0 0 8 2.44 5.4 9.2 11.6 |
| [36] 9 4 20 0 0 17 4.55 6 17.8 20.44 |
| Proposed 9 4 10 0 0 7 2.33 5 8.66 10.88 |
| Topologies No. of Switches No. of Voltage Levels |
|---|
| [13] m + 3 = 12, 16, 20, 24 2m + 1 = 9, 13, 17, 21 |
| [14] 2m + 1 = 11, 13, 15, 17n + 4 = 9,13,17, 21 |
| [15] 6n = 12, 18, 24, 30 4n + 1 = 9, 13, 17, 21 |
| [16] 6n = 12, 18, 24, 30 4n + 1 = 9, 13, 17, 21 |
| [17] = 9, 13, 17, 21 |
| [18] 4(p + 1) = 12, 16, 20, 24 4p + 1 = 9, 13, 17, 21 |
| [19] 5n + 6 = 11, 16, 21, 26 6n + 3 = 9, 13, 17, 21 |
| Proposed 2n + 6 = 10, 12, 14, 16 4n + 1 = 9, 13, 17, 21 |
| Parameters Values |
|---|
| PV voltage ), PV current ( 17.5 V, 2.86 A |
| Sinusoidal wave frequency 50 Hz |
| Switching frequency () 1 kHz |
| Output voltage levels 9 |
| No. of carrier signals 8 |
| Resistive load 12 Ω |
| No. of DC voltage source ( 4 |
| Voltage magnitude (24 V |
| Inductance(L) 92 mH |
| Capacitance(C) 46 F |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Memon, R.; Mahar, M.A.; Larik, A.S.; Shah, S.A.A. Design and Performance Analysis of New Multilevel Inverter for PV System. Sustainability 2023, 15, 10629. https://doi.org/10.3390/su151310629
Memon R, Mahar MA, Larik AS, Shah SAA. Design and Performance Analysis of New Multilevel Inverter for PV System. Sustainability. 2023; 15(13):10629. https://doi.org/10.3390/su151310629
Chicago/Turabian StyleMemon, Rabail, Mukhtiar Ahmed Mahar, Abdul Sattar Larik, and Syed Asif Ali Shah. 2023. "Design and Performance Analysis of New Multilevel Inverter for PV System" Sustainability 15, no. 13: 10629. https://doi.org/10.3390/su151310629
APA StyleMemon, R., Mahar, M. A., Larik, A. S., & Shah, S. A. A. (2023). Design and Performance Analysis of New Multilevel Inverter for PV System. Sustainability, 15(13), 10629. https://doi.org/10.3390/su151310629





