A Review of Modern Wind Power Generation Forecasting Technologies
Abstract
:1. Introduction
2. Review of Research Status
2.1. Reviews for Technologies and Applications
2.2. Problem
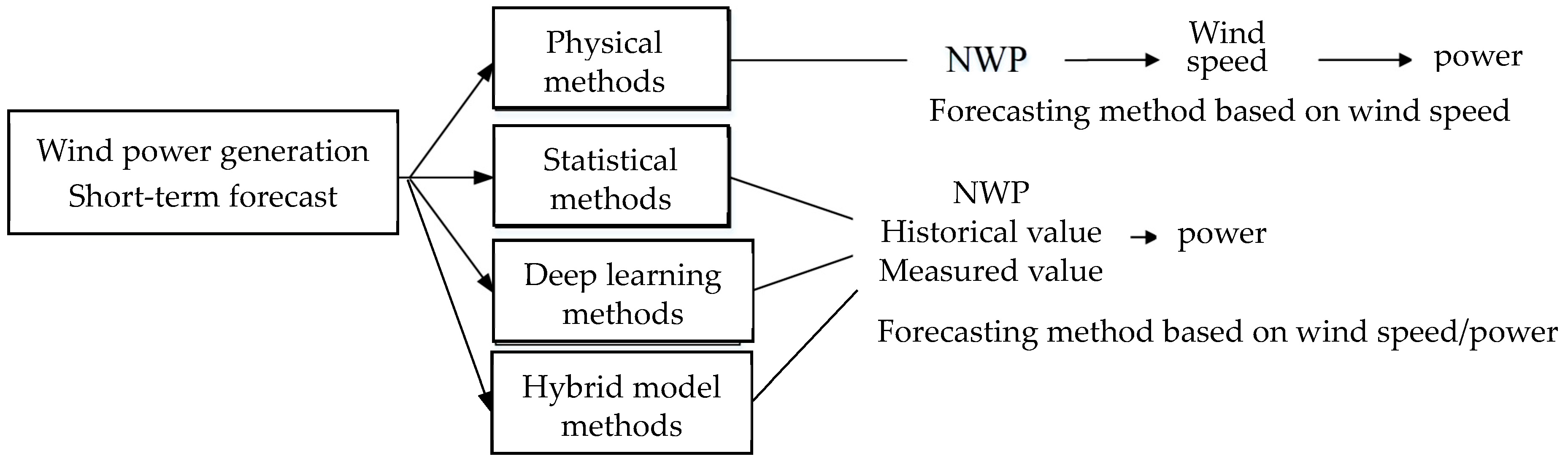
2.3. Comparative Study of the Reviewed WPPF Models and Methodologies
- A.
- Neural Network (NN)-based approaches
- B.
- Machine-learning (ML)-based approaches
- C.
- Deep-learning-based approaches
- D.
- Hybrid predictive model approaches
- E.
- Statistical-analysis-based approaches
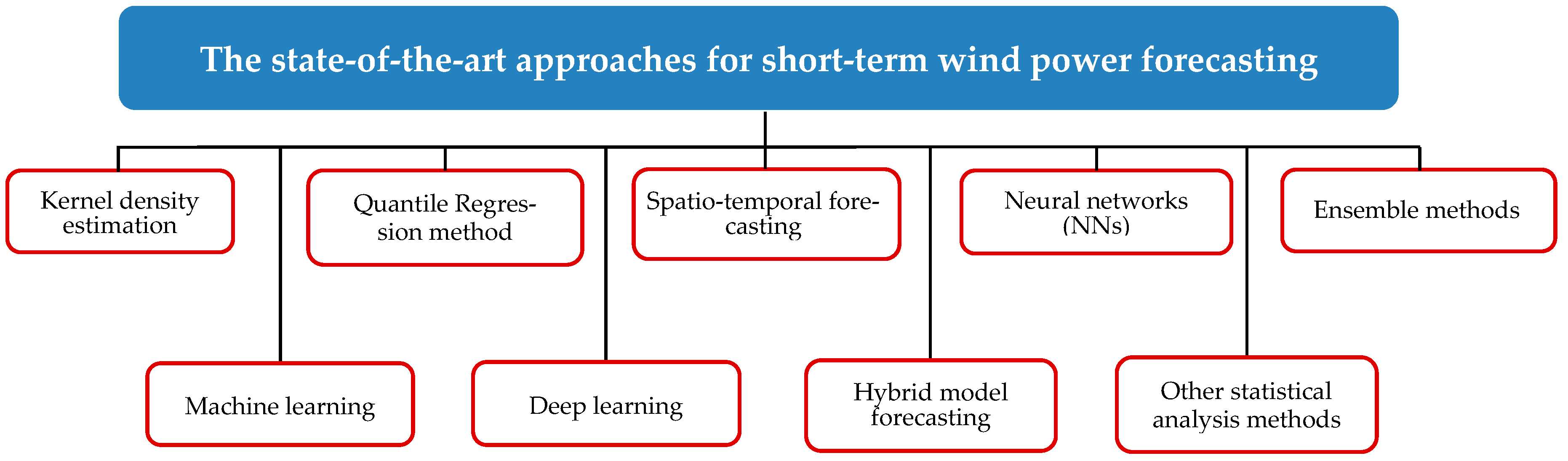
3. State-of-the-Art Approaches for Short-Term Wind Power Forecasting
4. Scientific Contributions, Advantages, and Disadvantages of Reviewed Works
4.1. Neural Network (NN)-Based Approach
4.2. Machine Learning (ML)-Based Approaches
4.3. Deep-Learning-Based Approaches
4.4. Hybrid Predictive Model Approaches
4.5. Statistical-Analysis-Based Approaches
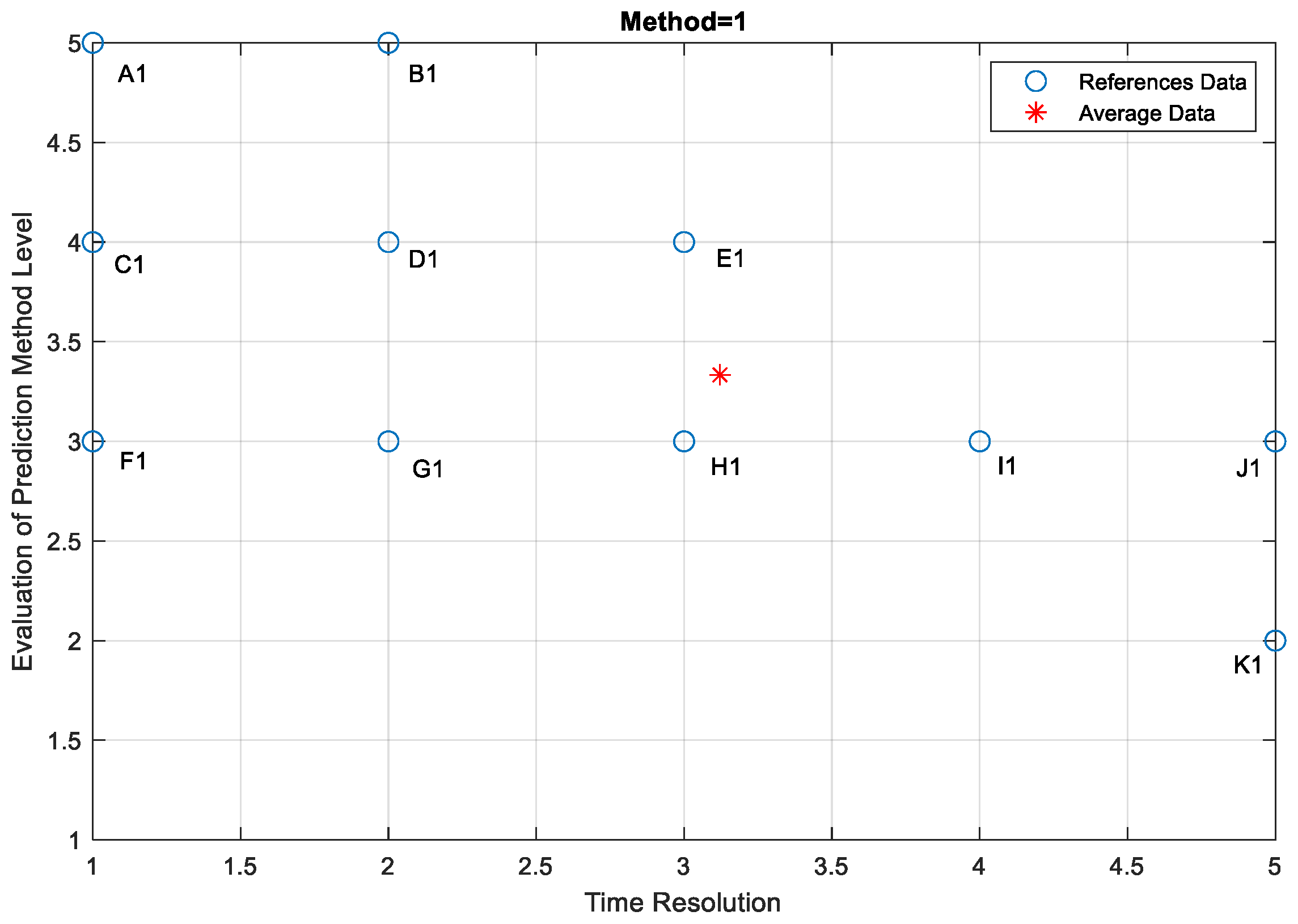
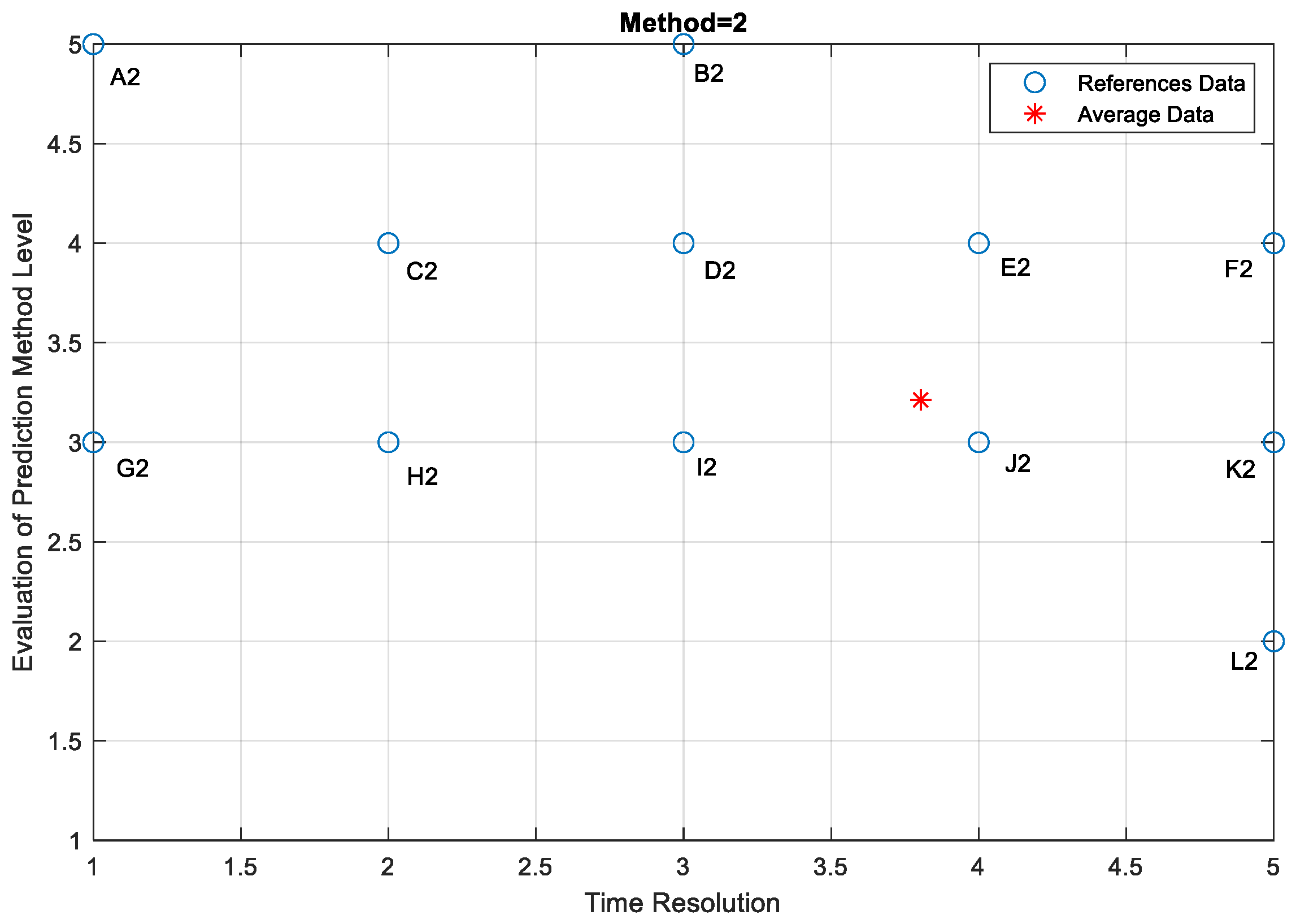
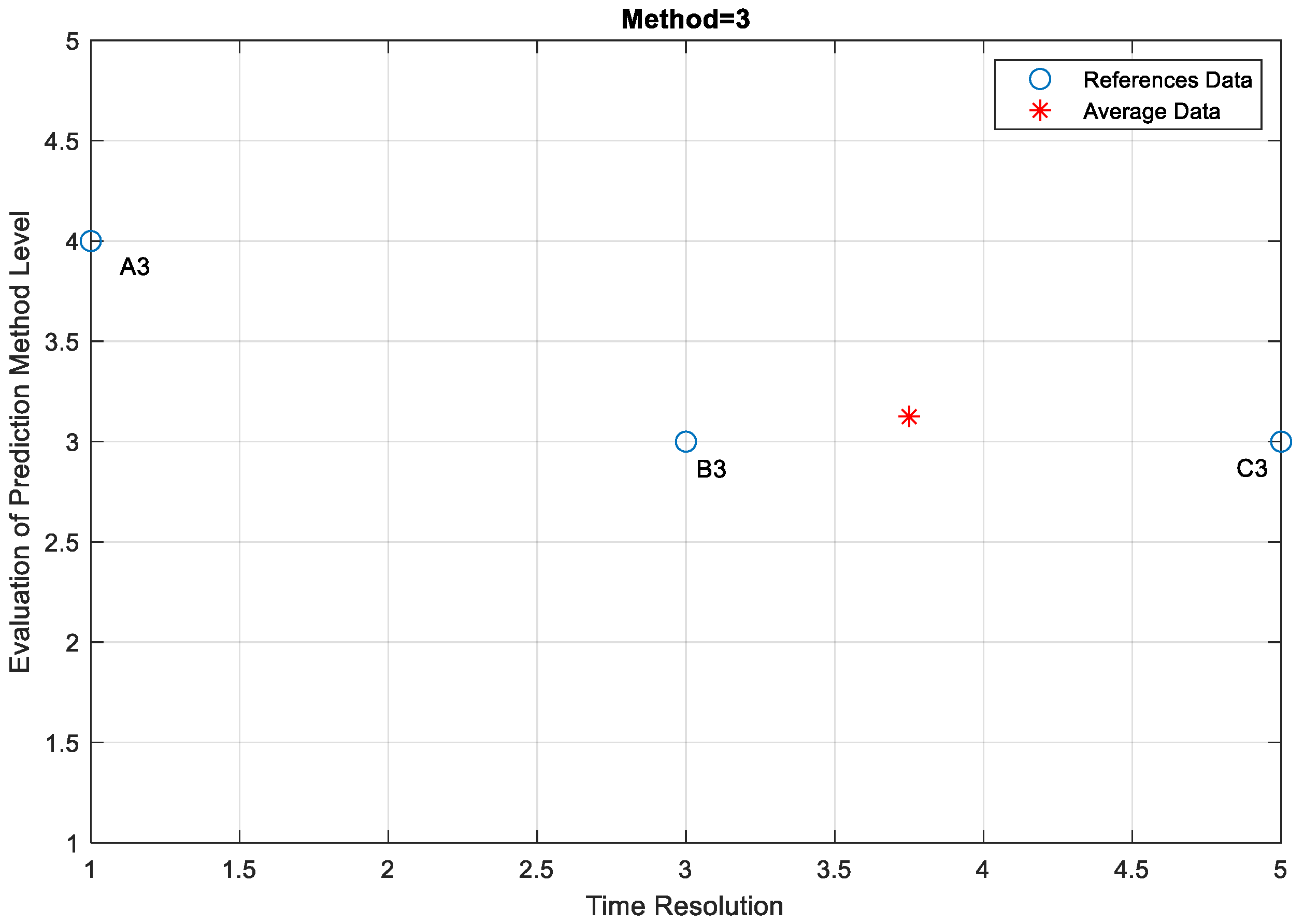
4.6. Evaluation of Prediction Method Levels and Research Limitations
4.7. Evaluation of Excellent Wind Power Prediction Models
5. Future Studies and Development
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| BNN | Backpropagation Neural Network |
| QR | Quantile Regression |
| NWP | Numerical Weather Prediction |
| WPF | Wind Power Forecasting |
| WPPF | Wind Power Probabilistic Forecasting |
| WSF | Wind Speed Forecasting |
| WRF | Weather Research and Forecasting |
| WPG | Wind Power Generation |
| WFP | Wind Farm Parameterization |
| RWPF | Regional Wind Power Forecasting |
| QRNN | Quantile Regression Neural Network |
| CSTWPP | Convolutional Spatial-temporal Wind Power Predictor |
| STCN | Spatio-temporal Convolutional Network |
| CEEMDAN | Complete Ensemble Empirical Mode Decomposition with Adaptive Noise |
| IBA | Improved Backfill Algorithm |
| GPR | Gaussian Process Regression |
| MFF-SAM-GCN | Multi-Feature Fusion/Self-Attention Mechanism/Graph Convolutional Network |
| WMTSM | Weighted Multivariate Time Series Motifs |
| CLP | Conditional Linear Programming |
| ABQs | Adaptive Boundary Quantiles |
| WNN | Wavelet Neural Network |
| EMD | Empirical Mode Decomposition |
| EBSO | Enhanced Bee Swarm Optimization |
| LSTM | Long-Short Term Memory |
| CLSTM | Convolutional-Long Short Term Memory |
| DOCLER | Deep Optimized Convolutional LSTM-Based Ensemble Reinforcement Learning |
| SVM | Support Vector Machine |
| DR-SVM | Distributionally-Robust Support Vector Machines |
| SOM | Self-Organizing Map |
| k-NN | k-Nearest Neighbors |
| KNNR | K-Nearest Neighbour Based Routing Protocol |
| KDE | Kernel Density Estimation |
| ELM | Extreme Learning Machine |
| KELM | Kernel Based Extreme Learning Machine |
| Adaboost | Adaptive Boosting |
| PSO | Particle Swarm Optimization |
| LSSVM | Least Squares Support Vector Machine |
| GMMN | Generative Moment Matching Network |
| WindGMMN | Wind Power Using Generative Moment Matching Networks |
| MSIN | Multi-Step Informer Network |
| WPD | Wavelet Packet Decomposition |
| VMD | Variational Mode Decomposition |
| SSA | Salp Swarm Algorithms/Singular Spectrum Analysis |
| IGWO | Improved Grey Wolf Optimization |
| GRNN | Generalized Regression Neural Network |
| SVR | Support Vector Regression |
| HMMC | Higher-Order Multivariate Markov Chain |
| MSTAN | Multi-Source and Temporal Attention Network |
| ARMA | Auto-Regression Moving Average |
| ARIMA | Autoregressive Integrated Moving Average |
| MRE | Mean Relative Error |
| MAE | Mean Absolute Error |
| MBE | Mean Bias Error |
| RMSE | Root Mean Squared Error |
| MAPE | Mean Absolute Percent Error |
| nMBE | Normalized Mean Bias Error |
| nRMSE | Normalized Root Mean Squared Error |
| R2 | Coefficient of Determination |
| MG | Microgrid |
References
- WindEurope: Wind Energy in Europe–2020 Statistics and the Outlook for 2021–2025. Available online: https://s1.eestatic.com/2021/02/24/actualidad/210224_windeurope_combined_2020_stats.pdf (accessed on 2 October 2021).
- Song, R.; Yang, L.; Chen, L.; Dong, Z. Capacity Estimation Method of Lithium-Ion Batteries Based on Deep Convolution Neural Network. Int. J. Bio-Inspired Comput. 2022, 20, 119–125. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Ma, C.; Kou, L. A Survey on the Development Status and Application Prospects of Knowledge Graph In Smart Grids. IET Gener. Transm. Distrib. 2021, 15, 383–407. [Google Scholar] [CrossRef]
- Kou, L.; Li, Y.; Zhang, F.; Gong, X.; Hu, Y.; Yuan, Q.; Ke, W. Review on Monitoring, Operation and Maintenance of Smart Offshore Wind Farms. Sensors 2022, 22, 2822. [Google Scholar] [CrossRef]
- Yang, Y.; Li, W.; Gulliver, T.A.; Li, S. Bayesian Deep Learning-Based Probabilistic Load Forecasting in Smart Grids. IEEE Trans. Ind. Inform. 2020, 16, 4703–4713. [Google Scholar] [CrossRef]
- Su, Z.; Wang, Y.; Luan, T.H.; Zhang, N.; Li, F.; Chen, T.; Cao, H. Secure and Efficient Federated Learning for Smart Grid with Edge-Cloud Collaboration. IEEE Trans. Ind. Inform. 2022, 18, 1333–1344. [Google Scholar] [CrossRef]
- Kou, L.; Liu, C.; Cai, G.W.; Zhang, Z.; Zhou, J.N.; Wang, X.M. Fault Diagnosis for Three-phase PWM Rectifier Based on Deep Feedforward Network with Transient Synthetic Features. ISA Trans. 2020, 101, 399–407. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Gao, S.; Yu, L.; Zhang, D.; Xie, C.; Chen, K.; Kou, L. Data-driven Lightning-related Failure Risk Prediction of Overhead Contact Lines Based on Bayesian Network with Spatiotemporal Fragility Model. Reliab. Eng. Syst. Saf. 2023, 231, 109016. [Google Scholar] [CrossRef]
- Li, M.; Yang, M.; Yu, Y.; Lee, W. -J. A Wind Speed Correction Method Based on Modified Hidden Markov Model for Enhancing Wind Power Forecast. IEEE Trans. Ind. Appl. 2022, 58, 656–666. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, W.; Liu, C.; Wang, B. Forecasted Scenarios of Regional Wind Farms Based on Regular Vine Copulas. J. Mod. Power Syst. Clean Energy 2020, 8, 77–85. [Google Scholar] [CrossRef]
- Mararakanye, N.; Dalton, A.; Bekker, B. Incorporating Spatial and Temporal Correlations to Improve Aggregation of Decentralized Day-Ahead Wind Power Forecasts. IEEE Access 2022, 10, 116182–116195. [Google Scholar] [CrossRef]
- Krannichfeldt, L.V.; Wang, Y.; Zufferey, T.; Hug, G. Online Ensemble Approach for Probabilistic Wind Power Forecasting. IEEE Trans. Sustain. Energy 2022, 13, 1221–1233. [Google Scholar] [CrossRef]
- Yu, Y.; Han, X.; Yang, M.; Yang, J. Probabilistic Prediction of Regional Wind Power Based on Spatiotemporal Quantile Regression. IEEE Trans. Ind. Appl. 2020, 56, 6117–6127. [Google Scholar] [CrossRef]
- Yu, Y.X.; Yang, M.; Han, X.S.; Zhang, Y.M.; Ye, P.F. A Regional Wind Power Probabilistic Forecast Method Based on Deep Quantile Regression. IEEE Trans. Ind. Appl. 2021, 57, 4420–4427. [Google Scholar] [CrossRef]
- Hu, T.; Wu, W.; Guo, Q.; Sun, H.; Shi, L.; Shen, X. Very Short-Term Spatial and Temporal Wind Power Forecasting: A Deep Learning Approach. CSEE J. Power Energy Syst. 2020, 6, 434–443. [Google Scholar]
- Dong, X.; Sun, Y.; Li, Y.; Wang, X.; Pu, T. Spatio-temporal Convolutional Network Based Power Forecasting of Multiple Wind Farms. J. Mod. Power Syst. Clean Energy 2022, 10, 388–398. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Yan, J.; Han, S.; Li, L.; Long, Q. Improved Deep Mixture Density Network for Regional Wind Power Probabilistic Forecasting. IEEE Trans. Power Syst. 2020, 35, 2549–2560. [Google Scholar] [CrossRef]
- Medina, S.V.; Ajenjo, U.P. Performance Improvement of Artificial Neural Network Model in Short-term Forecasting of Wind Farm Power Output. J. Mod. Power Syst. Clean Energy 2020, 8, 484–490. [Google Scholar] [CrossRef]
- Akhtar, I.; Kirmani, S.; Ahmad, M.; Ahmad, S. Average Monthly Wind Power Forecasting Using Fuzzy Approach. IEEE Access 2021, 9, 30426–30440. [Google Scholar] [CrossRef]
- Akram, U.; Mithulananthan, N.; Raza, M.Q.; Shah, R.; Milano, F. RoCoF Restrictive Planning Framework and Wind Speed Forecast Informed Operation Strategy of Energy Storage System. IEEE Trans. Power Syst. 2021, 36, 224–234. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Z.Y.; Yu, X.N.; Li, B.J.; Yang, M. Research on Ultra-Short-Term Wind Power Prediction Considering Source Relevance. IEEE Access 2020, 8, 147703–147710. [Google Scholar] [CrossRef]
- Hao, J.; Zhu, C.S.; Guo, X.T. Wind Power Short-Term Forecasting Model Based on the Hierarchical Output Power and Poisson Re-Sampling Random Forest Algorithm. IEEE Access 2021, 9, 6478–6487. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J.; Li, J.; Wei, L. Dual-meta pool method for wind farm power forecasting with small sample data. Energy 2023, 267, 126504. [Google Scholar] [CrossRef]
- Meng, A.B.; Chen, S.; Ou, Z.H.; Ding, W.F.; Zhou, H.M.; Fan, J.M.; Yin, H. A hybrid deep learning architecture for wind power prediction based on bi-attention mechanism and crisscross optimization. Energy 2022, 121795. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, Y.; Wang, S.; Mahfoud, R.J.; Alhelou, H.H.; Hatziargyriou, N.; Siano, P. Performance Improvement of Very Short-term Prediction Intervals for Regional Wind Power Based on Composite Conditional Nonlinear Quantile Regression. J. Mod. Power Syst. Clean Energy 2022, 10, 60–70. [Google Scholar] [CrossRef]
- Lee, J.; Wang, W.; Harrou, F.; Sun, Y. Wind Power Prediction Using Ensemble Learning-Based Models. IEEE Access 2020, 8, 61517–61527. [Google Scholar] [CrossRef]
- Abbasipour, M.; Igder, M.A.; Liang, X. A Novel Hybrid Neural Network-Based Day-Ahead Wind Speed Forecasting Technique. IEEE Access 2021, 9, 151142–151154. [Google Scholar] [CrossRef]
- Tu, C.S.; Hong, C.M.; Huang, H.S.; Chen, C.H. Short Term Wind Power Prediction Based on Data Regression and Enhanced Support Vector Machine. Energies 2020, 13, 6319. [Google Scholar] [CrossRef]
- Lagos, A.; Caicedo, J.E.; Coria, G.; Quete, A.R.; Martínez, M.; Suvire, G.; Riquelme, J. State-of-the-Art Using Bibliometric Analysis of Wind-Speed and -Power Forecasting Methods Applied in Power Systems. Energies 2022, 15, 6545. [Google Scholar] [CrossRef]
- An, G.; Jiang, Z.; Cao, X.; Liang, Y.; Zhao, Y.; Li, Z.; Dong, W.; Sun, H. Short-Term Wind Power Prediction Based On Particle Swarm Optimization-Extreme Learning Machine Model Combined With Adaboost Algorithm. IEEE Access 2021, 9, 94040–94052. [Google Scholar] [CrossRef]
- Tan, L.; Han, J.; Zhang, H. Ultra-Short-Term Wind Power Prediction by Salp Swarm Algorithm-Based Optimizing Extreme Learning Machine. IEEE Access 2020, 8, 44470–44484. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, G.P.; Hu, W.S. Priori-guided and data-driven hybrid model for wind power forecasting. ISA Trans. 2023, 134, 380–395. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.L.; Yang, P.; Zhao, S.Y.; Chevallier, J.L.; Xiao, Q.T. A hybrid intelligent framework for forecasting short-term hourly wind speed based on machine learning. Expert Syst. Appl. 2023, 119223. [Google Scholar] [CrossRef]
- Liu, Y.L.; Wang, J.Y. Transfer learning based multi-layer extreme learning machine for probabilistic wind power forecasting. Appl. Energy 2022, 312, 118729. [Google Scholar] [CrossRef]
- Pombo, D.V.; Rincón, M.J.; Bacher, P.; Bindner, H.W.; Spataru, S.V.; Sørensen, P.E. Assessing stacked physics-informed machine learning models for co-located wind–solar power forecasting. Sustain. Energy Grids Netw. 2022, 32, 100943. [Google Scholar] [CrossRef]
- Moayyed, H.; Moradzadeh, A.; Mohammadi-Ivatloo, B.; Aguiar, A.P.; Ghorbani, R. A Cyber-Secure generalized supermodel for wind power forecasting based on deep federated learning and image processing. Energy Convers. Manag. 2022, 267, 115852. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J.J.; Li, J.P.; Wei, L. An online transfer learning model for wind turbine power prediction based on spatial feature construction and system-wide update. Appl. Energy 2023, 340, 121049. [Google Scholar] [CrossRef]
- Nascimento, E.G.S.; de Melo, T.A.; Moreira, D.M. A transformer-based deep neural network with wavelet transform for forecasting wind speed and wind energy. Energy 2023, 278, 127678. [Google Scholar] [CrossRef]
- Dong, W.C.; Sun, H.X.; Tan, J.X.; Li, Z.; Zhang, J.X.; Yang, H.F. Regional wind power probabilistic forecasting based on an improved kernel density estimation, regular vine copulas, and ensemble learning. Energy 2022, 122045. [Google Scholar] [CrossRef]
- Sobolewski, R.A.; Tchakorom, M.; Couturier, R. Gradient boosting-based approach for short- and medium-term wind turbine output power prediction. Renew. Energy 2023, 203, 142–160. [Google Scholar] [CrossRef]
- Yu, L.; Meng, G.; Pau, G.; Wu, Y.; Tang, Y. Research on Hierarchical Control Strategy of ESS in Distribution Based on GA-SVR Wind Power Forecasting. Energies 2023, 16, 2079. [Google Scholar] [CrossRef]
- Park, S.; Jung, S.; Lee, J.; Hur, J. A Short-Term Forecasting of Wind Power Outputs Based on Gradient Boosting Regression Tree Algorithms. Energies 2023, 16, 1132. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Shao, L.; Liu, H.; Ren, L.; Zhu, L. Short-Term Wind Power Prediction by an Extreme Learning Machine Based on an Improved Hunter–Prey Optimization Algorithm. Sustainability 2023, 15, 991. [Google Scholar] [CrossRef]
- Liao, S.; Tian, X.; Liu, B.; Liu, T.; Su, H.; Zhou, B. Short-Term Wind Power Prediction Based on LightGBM and Meteorological Reanalysis. Energies 2022, 15, 6287. [Google Scholar] [CrossRef]
- Jalali, S.M.J.; Osorio, G.J.; Ahmadian, S.; Lotfi, M.; Campos, V.M.A.; Shafie-Khah, M.; Khosravi, A.; Catalao, J.P.S. New Hybrid Deep Neural Architectural Search-Based Ensemble Reinforcement Learning Strategy for Wind Power Forecasting. IEEE Trans. Ind. Appl. 2022, 58, 15–27. [Google Scholar] [CrossRef]
- Sun, Z.; Zhao, M. Short-Term Wind Power Forecasting Based on VMD Decomposition, ConvLSTM Networks and Error Analysis. IEEE Access 2020, 8, 134422–134434. [Google Scholar] [CrossRef]
- Abedinia, O.; Bagheri, M.; Naderi, M.S.; Ghadimi, N. A New Combinatory Approach for Wind Power Forecasting. IEEE Syst. J. 2020, 14, 4614–4625. [Google Scholar] [CrossRef]
- Ye, L.; Dai, B.H.; Pei, M.; Lu, P.; Zhao, J.L.; Chen, M.; Wang, B. Combined Approach for Short-Term Wind Power Forecasting Based on Wave Division and Seq2Seq Model Using Deep Learning. IEEE Trans. Ind. Appl. 2022, 58, 2586–2596. [Google Scholar] [CrossRef]
- Piotrowski, P.; Baczyński, D.; Kopyt, M.; Gulczyński, T. Advanced Ensemble Methods Using Machine Learning and Deep Learning for One-Day-Ahead Forecasts of Electric Energy Production in Wind Farms. Energies 2022, 15, 1252. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, X.; Yang, J. Modified Particle Swarm Optimization with Attention-Based LSTM for Wind Power Prediction. Energies 2022, 15, 4334. [Google Scholar] [CrossRef]
- Blazakis, K.; Katsigiannis, Y.; Stavrakakis, G. One-Day-Ahead Solar Irradiation and Windspeed Forecasting with Advanced Deep Learning Techniques. Energies 2022, 15, 4361. [Google Scholar] [CrossRef]
- Miao, C.; Li, H.; Wang, X.; Li, H. Ultra-Short-Term Prediction of Wind Power Based on Sample Similarity Analysis. IEEE Access 2021, 9, 72730–72742. [Google Scholar] [CrossRef]
- Liao, W.; Yang, Z.; Chen, X.; Li, Y. WindGMMN: Scenario Forecasting for Wind Power Using Generative Moment Matching Networks. IEEE Trans. Artif. Intell. 2022, 3, 843–850. [Google Scholar] [CrossRef]
- Ko, M.S.; Lee, K.G.; Kim, J.K.; Hong, C.W.; Dong, Z.Y.; Hur, K. Deep Concatenated Residual Network With Bidirectional LSTM for One-Hour-Ahead Wind Power Forecasting. IEEE Trans. Sustain. Energy 2021, 12, 1321–1335. [Google Scholar] [CrossRef]
- Huang, X.; Jiang, A. Wind Power Generation Forecast Based on Multi-Step Informer Network. Energies 2022, 15, 6642. [Google Scholar] [CrossRef]
- Wu, X.; Jiang, S.; Lai, C.S.; Zhao, Z.; Lai, L.L. Short-Term Wind Power Prediction Based on Data Decomposition and Combined Deep Neural Network. Energies 2022, 15, 6734. [Google Scholar] [CrossRef]
- Yu, G.; Liu, C.; Tang, B.; Chen, R.; Lu, L.; Cui, C.; Hu, Y.; Shen, L.; Muyeen, S. Short term wind power prediction for regional wind farms based on spatial-temporal characteristic distribution. Renew. Energy 2022, 199, 599–612. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, L.; Wang, J.; Zhou, Y.; Gan, W. A unified multi-step wind speed forecasting framework based on numerical weather prediction grids and wind farm monitoring data. Renew. Energy 2023, 211, 948–963. [Google Scholar] [CrossRef]
- Han, Y.C.; Tong, X.Q.; Shi, S.Y.; Li, F.; Deng, Y.P. Ultra-short-term wind power interval prediction based on hybrid temporal inception convolutional network model. Electr. Power Syst. Res. 2023, 217, 109159. [Google Scholar] [CrossRef]
- Hossain, M.A.; Chakrabortty, R.K.; Elsawah, S.D.; Ryan, M.J. Very short-term forecasting of wind power generation using hybrid deep learning model. J. Clean. Prod. 2021, 296, 126564. [Google Scholar] [CrossRef]
- Shi, J.H.; Wang, B.; Luo, K.Y.; Wu, Y.F.; Zhou, M.; Watada, J.Z. Ultra-short-term wind power interval prediction based on multi-task learning and generative critic networks. Energy 2023, 272, 127116. [Google Scholar] [CrossRef]
- Garg, S.; Krishnamurthi, R. A CNN encoder decoder LSTM model for sustainable wind power predictive analytics. Sustain. Comput. Inform. Syst. 2023, 38, 100869. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, D.; Li, Z.; Han, X.; Liu, H.; Dong, C.; Wang, J.; Liu, C.; Xia, Y. Power prediction of a wind farm cluster based on spatiotemporal correlations. Appl. Energy 2021, 302, 117568. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Zhang, G. Short-term wind power forecasting approach based on Seq2Seq model using NWP data. Energy 2020, 213, 118371. [Google Scholar] [CrossRef]
- LLiao, W.; Bak-Jensen, B.; Pillai, J.R.; Yang, Z.; Liu, K. Short-term power prediction for renewable energy using hybrid graph convolutional network and long short-term memory approach. Electr. Power Syst. Res. 2022, 211, 108614. [Google Scholar] [CrossRef]
- Eikeland, O.F.; Hovem, F.D.; Olsen, T.E.; Chiesa, M.; Bianchi, F.M. Probabilistic forecasts of wind power generation in regions with complex topography using deep learning methods: An Arctic case. Energy Convers. Manag. X 2022, 15, 100239. [Google Scholar] [CrossRef]
- Chandran, V.; Patil, C.K.; Manoharan, A.M.; Ghosh, A.; Sumithra, M.G.; Karthick, A.; Rahim, R.; Arun, K. Wind power forecasting based on time series model using deep machine learning algorithms. Mater. Today Proc. 2021, 115–126. [Google Scholar] [CrossRef]
- Tian, C.N.; Niu, T.; Wei, W. Developing a wind power forecasting system based on deep learning with attention mechanism. Energy 2022, 257, 124750. [Google Scholar] [CrossRef]
- Yildiz, C.; Acikgoz, H.; Korkmaz, D.; Budak, U. An improved residual-based convolutional neural network for very short-term wind power forecasting. Energy Convers. Manag. 2021, 228, 113731. [Google Scholar] [CrossRef]
- Liu, Z.; Li, X.; Zhao, H. Short-Term Wind Power Forecasting Based on Feature Analysis and Error Correction. Energies 2023, 16, 4249. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Y.; Zhang, K.; Liu, Y.; Qiang, W.; Han Wen, Q. Artificial Intelligent Power Forecasting for Wind Farm Based on Multi-Source Data Fusion. Processes 2023, 11, 1429. [Google Scholar] [CrossRef]
- Huang, J.; Niu, G.; Guan, H.; Song, S. Ultra-Short-Term Wind Power Prediction Based on LSTM with Loss Shrinkage Adam. Energies 2023, 16, 3789. [Google Scholar] [CrossRef]
- Xiao, Z.; Tang, F.; Wang, M. Wind Power Short-Term Forecasting Method Based on LSTM and Multiple Error Correction. Sustainability 2023, 15, 3798. [Google Scholar] [CrossRef]
- Sun, S.; Fu, J.; Wei, L.; Li, A. Multi-Objective Optimal Dispatching for a Grid-Connected Micro-Grid Considering Wind Power Forecasting Probability. IEEE Access 2020, 8, 46981–46997. [Google Scholar] [CrossRef]
- Zou, Y.; Feng, W.; Zhang, J.; Li, J. Forecasting of Short-Term Load Using the MFF-SAM-GCN Model. Energies 2022, 15, 3140. [Google Scholar] [CrossRef]
- Zhang, H.; Yan, J.; Liu, Y.; Gao, Y.; Han, S.; Li, L. Multi-Source and Temporal Attention Network for Probabilistic Wind Power Prediction. IEEE Trans. Sustain. Energy 2021, 12, 2205–2218. [Google Scholar] [CrossRef]
- Aisyah, S.; Simaremare, A.A.; Adytia, D.; Aditya, I.A.; Alamsyah, A. Exploratory Weather Data Analysis for Electricity Load Forecasting Using SVM and GRNN, Case Study in Bali, Indonesia. Energies 2022, 15, 3566. [Google Scholar] [CrossRef]
- Han, Y.; Tong, X. Multi-Step Short-Term Wind Power Prediction Based on Three-level Decomposition and Improved Grey Wolf Optimization. IEEE Access 2020, 8, 67124–67136. [Google Scholar] [CrossRef]
- Ye, L.; Li, Y.; Pei, M.; Zhao, Y.; Li, Z.; Lu, P. A novel integrated method for short-term wind power forecasting based on fluctuation clustering and history matching. Appl. Energy 2022, 327, 120131. [Google Scholar] [CrossRef]
- Zhao, Z.; Yun, S.; Jia, L.; Guo, J.; Meng, Y.; He, N.; Li, X.; Shi, J.; Yang, L. Hybrid VMD-CNN-GRU-based model for short-term forecasting of wind power considering spatio-temporal features. Eng. Appl. Artif. Intell. 2023, 121, 105982. [Google Scholar] [CrossRef]
- Che, J.X.; Yuan, F.; Deng, D.; Jiang, Z.Y. Ultra-short-term probabilistic wind power forecasting with spatial-temporal multi-scale features and K-FSDW based weight. Appl. Energy 2023, 331, 120479. [Google Scholar] [CrossRef]
- Hu, S.; Xiang, Y.; Zhang, H.C.; Xie, S.Y.; Li, J.H.; Gu, C.H.; Sun, W.; Liu, J.Y. Hybrid forecasting method for wind power integrating spatial correlation and corrected numerical weather prediction. Appl. Energy 2021, 293, 116951. [Google Scholar] [CrossRef]
- Dong, W.; Sun, H.; Tan, J.; Li, Z.; Zhang, J.; Zhao, Y.Y. Short-term regional wind power forecasting for small datasets with input data correction, hybrid neural network, and error analysis. Energy Rep. 2021, 7, 7675–7692. [Google Scholar] [CrossRef]
- Cui, Y.; Chen, Z.; He, Y.; Xiong, X.; Li, F. An algorithm for forecasting day- ahead wind power via novel long short-term memory and wind power ramp events. Energy 2023, 125888. [Google Scholar] [CrossRef]
- Khazaei, S.R.; Ehsan, M.D.; Soleymani, S.D.B.; Mohammadnezhad-Shourkaei, H.S. A high-accuracy hybrid method for short-term wind power forecasting. Energy 2022, 122020. [Google Scholar] [CrossRef]
- Wen, S.K.; Li, Y.T.; Su, Y. A new hybrid model for power forecasting of a wind farm using spatial–temporal correlations. Renew. Energy 2022, 198, 155–168. [Google Scholar] [CrossRef]
- Hu, S.; Xiang, Y.; Huo, D.; Jawad, S.Q.; Liu, J.Y. An improved deep belief network based hybrid forecasting method for wind power. Energy 2021, 224, 120185. [Google Scholar] [CrossRef]
- Lu, P.; Ye, L.; Zhong, W.Z.; Qu, Y.; Zhai, B.X.; Tang, Y.; Zhao, Y.N. A novel spatio-temporal wind power forecasting framework based on multi-output support vector machine and optimization strategy. J. Clean. Prod. 2020, 254, 119993. [Google Scholar] [CrossRef]
- Gu, B.; Hu, H.; Zhao, J.; Zhang, H.T.; Liu, X.Y. Short-term wind power forecasting and uncertainty analysis based on FCM–WOA–ELM–GMM. Energy Rep. 2023, 9, 807–819. [Google Scholar] [CrossRef]
- Al-Duais, F.S.; Al-Sharpi, R.S. A unique Markov chain Monte Carlo method for forecasting wind power utilizing time series model. Alex. Eng. J. 2023, 74, 51–63. [Google Scholar] [CrossRef]
- Yan, J.; Möhrlen, C.N.; Göçmen, T.F.; Kelly, M.; Wessel, A.; Giebel, G.G. Uncovering wind power forecasting uncertainty sources and their propagation through the whole modelling chain. Renew. Sustain. Energy Rev. 2022, 165, 112519. [Google Scholar] [CrossRef]
- Zheng, J.Q.; Du, J.; Wang, B.H.; Klemeš, J.J.; Liao, Q.; Liang, Y.T. A hybrid framework for forecasting power generation of multiple renewable energy sources. Renew. Sustain. Energy Rev. 2023, 172, 113046. [Google Scholar] [CrossRef]
- Wang, L.; He, Y. M2STAN: Multi-modal multi-task spatiotemporal attention network for multi-location ultra-short-term wind power multi-step predictions. Appl. Energy 2022, 324, 119672. [Google Scholar] [CrossRef]
- Xiong, B.; Lou, L.; Meng, X.Y.; Wang, X.; Ma, H.; Wang, Z.G. Short-term wind power forecasting based on Attention Mechanism and Deep Learning. Electr. Power Syst. Res. 2022, 206, 107776. [Google Scholar] [CrossRef]
- Wang, Q.; Pan, L.; Wang, H.; Wang, X.; Zhu, Y. Short-term wind power probabilistic forecasting using a new neural computing approach: GMC-DeepNN-PF. Appl. Soft Comput. 2022, 126, 109247. [Google Scholar] [CrossRef]
- Xiang, L.; Liu, J.N.; Yang, X.; Hu, A.J.; Su, H. Ultra-short term wind power prediction applying a novel model named SATCN-LSTM. Energy Convers. Manag. 2022, 252, 115036. [Google Scholar] [CrossRef]
- Ma, Z.J.; Mei, G. A hybrid attention-based deep learning approach for wind power prediction. Appl. Energy 2022, 323, 119608. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, R.; Zhao, Y.; Qiu, J.; Bu, S.; Zhu, Y.; Li, G. Deterministic and Probabilistic Prediction of Wind Power Based on a Hybrid Intelligent Model. Energies 2023, 16, 4237. [Google Scholar] [CrossRef]
- Yuan, D.-D.; Li, M.; Li, H.-Y.; Lin, C.-J.; Ji, B.-X. Wind Power Prediction Method: Support Vector Regression Optimized by Improved Jellyfish Search Algorithm. Energies 2022, 15, 6404. [Google Scholar] [CrossRef]
- Sanjari, M.J.; Gooi, H.B.; Nair, N.-K.C. Power Generation Forecast of Hybrid PV–Wind System. IEEE Trans. Sustain. Energy 2020, 11, 703–712. [Google Scholar] [CrossRef] [Green Version]
- Bezerra, E.C.; Pinson, P.; Leao, R.P.S.; Braga, A.P.S. A Self-Adaptive Multikernel Machine Based on Recursive Least-Squares Applied to Very Short-Term Wind Power Forecasting. IEEE Access 2021, 9, 104761–104772. [Google Scholar] [CrossRef]
- Oh, E.S.; Wang, H.H. Reinforcement-Learning-Based Energy Storage System Operation Strategies to Manage Wind Power Forecast Uncertainty. IEEE Access 2020, 8, 20965–20976. [Google Scholar] [CrossRef]
- Zhao, Y.; Xue, Y.; Gao, S.; Wang, J.; Cao, Q.; Sun, T.; Liu, Y. Computation and Analysis of an Offshore Wind Power Forecast: Towards a Better Assessment of Offshore Wind Power Plant Aerodynamics. Energies 2022, 15, 4223. [Google Scholar] [CrossRef]
- Ma, J.; Yang, M.; Lin, Y. Ultra-Short-Term Probabilistic Wind Turbine Power Forecast Based on Empirical Dynamic Modeling. IEEE Trans. Sustain. Energy 2020, 11, 906–915. [Google Scholar] [CrossRef]
- Dong, Y.; Ma, S.; Zhang, H.; Yang, G. Wind Power Prediction Based on Multi-class Autoregressive Moving Average Model with Logistic Function. J. Mod. Power Syst. Clean Energy 2022, 10, 1184–1193. [Google Scholar] [CrossRef]
- Shavolkin, O.; Gerlici, J.; Shvedchykova, I.; Kravchenko, K. Solar–Wind System for the Remote Objects of Railway Transport Infrastructure. Energies 2022, 15, 6546. [Google Scholar] [CrossRef]
- Feroz, R.M.A.; Javed, A.; Syed, A.H.; Kazmi, S.A.A.; Uddin, E. Wind speed and power forecasting of a utility-scale wind farm with inter-farm wake interference and seasonal variation. Sustain. Energy Technol. Assess. 2020, 42, 100882. [Google Scholar] [CrossRef]
- Ghafarian, P.; Penchah, M.M. Wind resource assessment over the Persian Gulf and Oman Sea using a numerical model simulation and satellite data. J. Ocean Eng. Mar. Energy 2023, 1–10. [Google Scholar] [CrossRef]
- Wang, L.; He, Y.G.; Li, L.; Liu, X.Y.; Zhao, Y.Y. A novel approach to ultra-short-term multi-step wind power predictions based on encoder–decoder architecture in natural language processing. J. Clean. Prod. 2022, 354, 131723. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, J.; Qin, J.; Li, H.; Zhang, Z. A novel pure data-selection framework for day-ahead wind power forecasting. Fundam. Res. 2023, 3, 392–402. [Google Scholar] [CrossRef]
- Xue, H.; Jia, Y.; Wen, P.; Farkoush, S.G. Using of improved models of Gaussian Processes in order to Regional wind power forecasting. J. Clean. Prod. 2020, 262, 121391. [Google Scholar] [CrossRef]
- Meng, A.; Chen, S.; Ou, Z.; Xiao, J.; Zhang, J.; Zhang, Z.; Liang, R.; Zhang, Z.; Xian, Z.; Wang, C.; et al. A novel few-shot learning approach for wind power prediction applying secondary evolutionary generative adversarial network. Energy 2022, 125276. [Google Scholar] [CrossRef]
- Zhou, Q.; Ma, Y.; Lv, Q.; Zhang, R.; Wang, W.; Yang, S. Short-Term Interval Prediction of Wind Power Based on KELM and a Universal Tabu Search Algorithm. Sustainability 2022, 14, 10779. [Google Scholar] [CrossRef]
- Gu, X.; Wang, X. A Review on Wind Power Forecast Technologies. Power Syst. Technol. 2007, 31, 335–338. [Google Scholar]
- Wang, L.; Yang, G.; Gao, S. A Review on Modeling and Forecasting of Wind Power. Proc. Control Power Syst. 2009, 37, 118–121. [Google Scholar]
- Hanifi, S.; Liu, X.; Lin, Z.; Lotfian, S. A Critical Review of Wind Power Forecasting Methods—Past, Present and Future. Energies 2020, 13, 3764. [Google Scholar] [CrossRef]
- Dhiman, H.S.; Deb, D. A Review of Wind Speed and Wind Power Forecasting Techniques. arXiv 2020, arXiv:2009.02279. [Google Scholar]
- Lu, P.; Ye, L.; Zhao, Y.; Dai, B.; Pei, M.; Tang, Y. Review of Meta-Heuristic Algorithms for Wind Power Prediction: Methodologies, Applications and Challenges. Appl. Energy 2021, 301, 117446. [Google Scholar] [CrossRef]
- Bazionis, I.K.; Karafotis, P.A.; Georgilakis, P.S. A Review of Short-Term Wind Power Probabilistic Forecasting and a Taxonomy Focused on Input Data. IET Renew. Power Gener. 2022, 16, 77–91. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Miah, S.; Hannan, M.A.; Hussain, A.; Sarker, M.R.; Ayob, A.; Saad, M.H.M.; Mahmud, S. Artificial Intelligence Based Hybrid Forecasting Approaches for Wind Power Generation: Progress, Challenges and Prospects. IEEE Access 2021, 9, 102460–102489. [Google Scholar] [CrossRef]
- Landberg, L. Short-term Prediction of The Power Production from Wind Farms. J. Wind Eng. Ind. Aerodyn. 1999, 80, 207–220. [Google Scholar] [CrossRef]
- Nielsen, T.S.; Madsen, H.; Tofting, J. Experiences with Statistical Methods for Wind Power Prediction. In Proceedings of the European Wind Energy Conference and Exhibition, Nice, France, 1–5 March 1999. [Google Scholar]
- Beyer, H.D.; Mellinghoff, H.; Monnich, K.; Waldl, H.P. Forecast of Regional Power Output of Wind Turbines. In Proceedings of the European Wind Energy Conference, Nice, France, 1–5 March 1999; p. 1073. [Google Scholar]
- Landberg, L. Short-term Prediction of Local Wind Conditions. J. Wind Eng. Ind. Aerodyn. 2001, 89, 235–245. [Google Scholar] [CrossRef] [Green Version]
- Giebel, G.; Landberg, L.; Nielsen, T.S.; Madsen, H. The Zephyr-project. The Next Generation Prediction System (Poster). In Proceedings of the CD-ROM European Wind Energy Association (EWEA) 2002, Paris, France, 2–5 April 2002. [Google Scholar]
- Landberg, L.; Giebel, G.; Nielsen, H.A.; Nielsen, T.; Madsen, H. Shortterm PredictionAn Overview. Wind. Energy 2003, 6, 273280. [Google Scholar] [CrossRef]
- Xu, Q.; He, D.; Zhang, N.; Kang, C.; Xia, Q.; Bai, J.; Huang, J. A Short-Term Wind Power Forecasting Approach with Adjustment of Numerical Weather Prediction Input by Data Mining. IEEE Trans. Sustain. Energy 2015, 6, 1283–1291. [Google Scholar] [CrossRef]
- Lange, B.; Rohrig, K.; Ernst, B.; Schlögl, F.; Cali, Ü.; Jursa, R.; Moradi, J. Wind Power Prediction in Germany-Recent Advances and Future Challenges. In Proceedings of the European Wind Energy Conference, Athens, Greece, 27 February–2 March 2006. [Google Scholar]
- Focken, U.; Lange, M.; Waldl, H.P. Previento–A Wind Power Prediction System with an Innovative Upscaling Algorithm. In Proceedings of the 2001 EuropeanWind Energy Association Conference, EWEC’01, Copenhagen, Danmark, 2 July 2001; pp. 826–829. [Google Scholar]
- Jorgensen, J.; Moehrlen, C.; Gallaghoir, B.O.; Mckeogh, E. HIRPOM: Description of An Operational Numerical Wind Power Prediction Model for Large Scale Integration of On-and Offshore Wind Power in Denmark. In Proceedings of the Poster on the Global Wind Power Conference and Exhibition, London, UK, 1 January–30 September 2002. [Google Scholar]
- Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A Review of Wind Power and Wind Speed Forecasting Methods with Different Time Horizons. In Proceedings of the 2010 North American Power Symposium, Arlington, TX, USA, 26–28 September 2010. [Google Scholar]
- Costa, A.; Crespo, A.; Navarro, J.; Lizcano, G.; Madsen, H.; Feitosa, E. A Review on the Young History of the Wind Power ShortTerm Prediction. Renew. Sustain. Energy Rev. 2008, 12, 17251744. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.Q. Research on Ultra-Short-Term Wind Power Combination Forecasting Model Based on Least Squares Support Vector Machine. Master’s Thesis, Hunan University, Changsha, China, 2017. [Google Scholar]
- Gong, W.; Meyer, F.J.; Liu, S.; Hanssen, R.F. Temporal Filtering of InSAR Data Using Statistical Parameters from NWP Models. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4033–4044. [Google Scholar] [CrossRef]
- Carpinone, A.; Giorgio, M.; Langella, R.; Testa, A. Markov Chain Modeling for Very-Short-Term Wind Power Forecasting. Electr. Power Syst. Res. 2015, 122, 152–158. [Google Scholar] [CrossRef] [Green Version]
- Karadas, M.; Celik, H.M.; Serpen, U.; Toksoy, M. Multiple Regression Analysis of Performance Parameters of a Binary Cycle Geothermal Power Plant. Geothermics 2015, 54, 68–75. [Google Scholar] [CrossRef]
- Babazadeh, H.; Gao, W.; Cheng, L.; Lin, J. An Hour Ahead Wind Speed Prediction by Kalman Filter. In Proceedings of the 2012 IEEE Power Electronics and Machines in Wind Applications, Denver, CO, USA, 16–18 July 2012. [Google Scholar]
- Zhang, J.; Wang, C. Application of ARMA Model in Ultra-Short Term Prediction of Wind Power. In Proceedings of the International Conference on Computer Sciences and Applications, San Francisco, CA, USA, 23–25 October 2013. [Google Scholar]
- Tagliaferri, F.; Viola, I.M.; Flay, R.G.J. Wind Direction Forecasting with Artificial Neural Networks and Support Vector Machines. Ocean Eng. 2015, 97, 65–73. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Zheng, Y.; Li, L.; Zhou, L.; Yao, G.; Huang, T. Short-term Wind Power Prediction Based on Wavelet Decomposition and Extreme Learning Machine. In Proceedings of the Advances in Neural Networks 9th International Symposium on Neural Networks, Shenyang, China, 11–14 July 2012; pp. 645–653. [Google Scholar]
- Zhang, Q.; Lai, K.K.; Niu, D.; Wang, Q.; Zhang, X. A Fuzzy Group Forecasting Model Based on Least Squares Support Vector Machine (LS-SVM) for Short-Term Wind Power. Energies 2012, 5, 3329–3346. [Google Scholar] [CrossRef]
- Tu, C.S.; Tsai, W.C.; Hong, C.M.; Lin, W.M. Short-Term Solar Power Forecasting via General Regression Neural Network with Grey Wolf Optimization. Energies 2022, 15, 6624. [Google Scholar] [CrossRef]
- Shi, C.Q.; Zhang, X.L. Recurrent Neural Network Wind Power Prediction Based on Variational Modal Decomposition Improvement. AIP Adv. 2023, 13, 025027. [Google Scholar] [CrossRef]
- Xiong, J.; Peng, T.; Tao, Z.; Zhang, C.; Song, S.; Nazir, M.S. A Dual-Scale Deep Learning Model Based on Elm-Bilstm and Improved Reptile Search Algorithm for Wind Power Prediction. Energy 2023, 266, 126419. [Google Scholar] [CrossRef]
- Tarek, Z.; Shams, M.Y.; Elshewey, A.M.; El-Kenawy, E.M.; Ibrahim, A.; Abdelhamid, A.A.; El-Dosuky, M.A. Wind Power Prediction Based on Machine Learning and Deep Learning Models. Comput. Mater. Contin. 2023, 74, 715–732. [Google Scholar] [CrossRef]
- Wang, J.N.; Zhu, H.Q.; Zhang, Y.J.; Cheng, F.; Zhou, C. A Novel Prediction Model for Wind Power Based on Improved Long Short-Term Memory Neural Network. Energy 2023, 265, 126283. [Google Scholar] [CrossRef]
- Yu, M.; Niu, D.X.; Gao, T.; Wang, K.K.; Sun, L.J.; Li, M.Y.; Xu, X.M. A Novel Framework for Ultra-Short-Term Interval Wind Power Prediction Based on RF-WOA-VMD and BiGRU Optimized By The Attention Mechanism. Energy 2023, 269, 126738. [Google Scholar] [CrossRef]
- Qin, B.; Huang, X.; Wang, X.; Guo, L.Z. Ultra-Short-Term Wind Power Prediction Based on Double Decomposition and LSSVM. Trans. Inst. Meas. Control 2023. [CrossRef]
- A Novel Approach to Ultra-Short-Term Wind Power Prediction Based on Feature Engineering and Informer. Energy Rep. 2023, 9, 1236–1250. [CrossRef]
- Sheng, Y.W.; Wang, H.; Yan, J.; Liu, Y.Q.; Han, S. Short-Term Wind Power Prediction Method Based on Deep Clustering-Improved Temporal Convolutional Network. Energy Rep. 2023, 9, 2118–2129. [Google Scholar] [CrossRef]
- Hossain, M.A.; Gray, E.; Lu, J.W.; Islam, M.R.; Alam, M.S.; Chakrabortty, R.; Pota, H.R. Optimized Forecasting Model to Improve the Accuracy of Very Short-Term Wind Power Prediction. IEEE Trans. Ind. Inform. 2023, 19, 1–13. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions, and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions, or products referred to in the content. |

| Name of Forecasting System | R&D Institutions | Methods |
|---|---|---|
| Prediktor | Danish National Laboratory | Physical methods |
| SIPREÓLICO | University of Carlos III, Madrid, Spain | Physical methods |
| HIRPOM | University College Cork, Ireland | Physical methods |
| Previnto | University of Oldenburg, Germany | Physical methods |
| WPFS Ver 1.0 system | China Electric Power Research Institute | Physical methods/Meta-heuristic |
| WPPT | Copenhagen University, Denmark | Statistical methods |
| AWPPS | MINES ParisTech | Statistical methods, Fuzzy ANN |
| RAL | Appleton Laboratory, Rutherford, UK | Statistical methods |
| GH Forecaster | Garrad Hassan, UK | Statistical methods |
| WPMS | Germany-ISET | Statistical methods, ANN |
| Zephry | Risø National Laboratory | Statistical/Physical methods |
| LocalPred-RegioPred | Spanish National Energy Center | Statistical/Physical methods |
| ANEMOS | 23 scientific research institutions in 7 EU countries | Statistical/Physical methods |
| eWind | True Wind USA, Inc. | Statistical/Physical methods |
| WEPROG | University College Cork, Ireland | Statistical/Physical methods |
| Time Resolution | Reviewed Works | Forecasting Time Scale |
|---|---|---|
| 1 min | [22,29] | Ultra short term |
| 5 min | [15,16,29,61,101,103] | Ultra short term |
| 10 min | [15,28,30,36,37,43,55,63,64,70,72,81,95,96,97,103,107,112,113] | Ultra short term |
| 15 min | [12,15,20,21,23,30,38,42,52,53,56,57,59,60,71,74,88,93,98,99,100,103,108,110,114] | Ultra short term |
| 30 min | [15,16,26,30,45,47,59,74,83,90,103,104,105,108] | Ultra short term |
| 1 h | [14,16,18,24,27,30,33,35,38,39,40,41,44,46,48,49,50,51,54,59,62,65,66,67,69,74,75,76,77,80,83,86,90,91,94,102,106,108,111] | Short term |
| 2 h | [16,25,30,35,59,80,83,86,90,94] | Short term |
| 3 h | [16,30,35,59,79,80,83,86,90,94] | Short term |
| 4 h | [25,30,35,59,78,79,80,83,86,89,90] | Short term |
| 6 h | [35,86,89,90] | Short term |
| 12 h | [35,86,89] | Short term |
| 24 h | [9,10,11,17,29,35,53,58,79,80,82,84,85,87,89,92] | Short term |
| 48 h | [31,32,46,89] | Short term |
| 72 h–1 week | [13,29,34,89] | Medium term |
| 1 month–years | [19] | Long term |
| Ref | Model Type | Parameters Used | Accuracy | Future Studies |
|---|---|---|---|---|
| [14] | A quantile regression neural network (QRNN) for regional wind power forecasting (RWPF) | Enhancing the abilities of nonlinear mapping and dealing with massive data | NMAE: DQR:9.086; QRNN:9.479 SBL:13.451; IFPA:13.967 NRMSE: DQR:10.917; QRNN:10.227 SBL:14.185; IFPA:14.538 | -To verify the model validation for the four-season test. |
| [17] | Improved deep mixture density network model | Wind speed, wind direction, wind vector, wind power | NRMSE = 0.138 | -To avoid the problem of the curse of dimensionality when the number of wind farms increases -To further consider spatial and temporal information. |
| [18] | New artificial neural network (ANN) models | Wind speed, wind direction, wind power output | (MARE) = 7.5%; Rj = 5.4% (mean value of the Pearson correlation coefficient) | To improve the performance of the new model for the long-term forecasting of wind power |
| [19] | A fuzzy logic approach and ANN | Wind speed, air density | RMSE = 1.04%; MAD = 0.91% MSE = 1.05% | Wind power prediction technique with integration to the grid would be analyzed for considering load scheduling and demand side management. |
| [20] | An ensemble neural forecast (ENFF) with three neural predictors 1.ELM 2. FNN 3.RBF | Wind speed, meteorological | Errors around 0.6 m/s | Planning framework and operation strategy are developed for the storage providing virtual inertia support (VIS) in a low inertia power system. |
| [21] | Day-ahead numerical weather prediction (NWP) with neural network | The persistence method with BP three rolling prediction effect | The model accuracy improved by 7.61% and the RMSE reduced by 8.76% | Generalization and robustness of the BP neural network model will be the focus of future research. |
| [22] | -A classification model with the output wind power. -Use of Poisson re-sampling | The random forest with Poisson re-sampling and setting the parameters by oneself | Mean square error (MSE) GBRT: 0.224; MLP: 0.117 Random forest with Bootstrap sampling: 0.111 Random forest with Poisson re-sampling: 0.096 | To improve the accuracy and speed of prediction for the characteristics of big data in wind power by parallel modeling of the prediction algorithm. |
| [23] | Dual-meta pool method | Wind farm power | MAE = 2.42, RMSE = 2.67 and MAPE = 0.12. | The prediction accuracy can be improved by using multi-source data. |
| [24] | Gated recurrent unit (GRU) network combined with ensemble empirical mode decomposition(EEMD) | Wind speed (m/s) Wind power (kW) Wind direction | RMSE(MW) = 0.2949 | To apply it to the wind power prediction of offshore wind farms. |
| Ref | Model Type | Parameters Used | Accuracy | Future Studies |
|---|---|---|---|---|
| [25] | Weighted multivariate time series motifs (WMTSM) and conditional LP (CLP) combined with the adaptive boundary quantiles (ABQs) | Wind speed, wind power | Both MAE and RMSE of less than 10% | The advanced method of dynamic analysis, which can accurately describe the characteristics of wind power time series. |
| [26] | Ensemble learning models (GRF, RF, XGB) | Wind power, wind speed, gearbox bearing temperatures | R2 = 98.9; RMSE = 50.36; MAE = 23.63 | To consider spatio-temporal dependence, which is not considered in ensemble learning models and machine learning models, for improving prediction quality |
| [27] | -Wavelet neural network (WNN) trained by ISCA, ELM, RBF, MLP, and PSO. -The best performing models are the WNN trained by ICSA and ELM-based NN models. | Selecting parameters by using particle swarm optimization | The average nRMSE for WNN trained by ISCA and ELM are 5.4059% and 6.925%; The average nMAE for WNN trained by ISCA and ELM are 4.2893% and 5.4787%. | To improve for large errors due to time by using five hybrid NN algorithms for short-term prediction of wind power. |
| [28] | Enhanced bee swarm optimization (EBSO) to perform the parameter optimization for least squares support vector machine (LSSVM) | Picking parameters for LSSVM by enhanced bee swarm optimization (EBSO) | DR-SVM VMED(m/s): 6.895 MAE (m/s): 0.723 RMSE(m/s): 0.932 MAPE(%): 11.87 CPU time(s): 148.15 | To calculate errors using nMAE and nRMSE. |
| [29] | The state of the art of wind speed and power forecasting models for wind turbines located in different segments of power systems | Data preprocessing (EMD and ICEEMDAN) and parameter optimization | No description | To investigate whether the correction of the obtained forecast values can significantly reduce the error caused by the forecast models within the postprocessing data techniques in hybrid models. |
| [30] | The Adaboost-PSO-ELM method | Wind speed, wind direction, wind power | MAPE = 0.0372; NBE = 0.4621 RMBE = 0.2950; R2 = 0.9857 | -To consider reconstructing the training samples; -To select specific indicators as training samples for short-term wind power prediction to further improve prediction performance based on numerical weather forecast (NWP) data. |
| [31] | Salp swarm algorithms–extreme learning machine (SSA-ELM) | Wind speed, wind direction, temperature, atmospheric pressure, and other data are sampled every 10 min | MAPE = 1.2677 RMSE = 0.2576 | -To avoid the over-fitting phenomenon of the ELM and improve its generalization ability. |
| [32] | Priori-guided and data-driven hybrid model | Wind speed, wind direction, and wind power | MAE = 0.0861, RMSE = 0.1262, R2 = 0.8333, AR = 87.38% | -The online learning approach; -To apply wind power forecasting to turbine control or economic dispatch to facilitate the better operation of the wind turbines connected to the power grid. |
| [33] | Intelligent hybrid prediction framework | Wind speed | MAPE = 2.62 and RMSE = 0.14 | The more efficient and advanced methods in the prediction sub-models may be beneficial to further improve the performance of the proposed framework. |
| [34] | ELM-based quantile regression model | Historical data on wind power | Reliability and skill score are reduced by 10% to 33%. | - Improving structures of NNs and adjusting network parameters; -The quantiles provided by the proposed method can enclose actual wind power output data more accurately. |
| [35] | Stacked physics-informed machine learning model | Ambient temperature, humidity, wind speed, wind direction, irradiance, and atmospheric pressure | RMSE = 5% and R2 = 0.95 | Future work involves the employment of new and unexplored ML methods striving for deeper learning. |
| [36] | Cyber-secure generalized supermodel | Wind speed, temperature, humidity, radiation | RMSE = 0.02, MAE = 0.007 MAPE = 0.60 R2 = 0.84 | -Sensitivity analysis of the correlation between input and output variables; -Users and operators of power grids can make the best decision in selecting input data to achieve maximum forecasting accuracy. |
| [37] | Online transfer learning model | Active power, wind speed, wind direction, vane position, and temperature | PA = 0.934 MAE = 84.837 RMSE = 134.837 | -Improve the prediction accuracy of the proposed online transfer learning method; -Advanced neural networks can be used to replace the ConvLSTM neural network. |
| [38] | Discrete wavelet transform | Wind speed, wind direction, air temperature, air humidity, and air pressure. | Anemometric height 100 m RMSE [m/s] = 0.383 150 m RMSE [m/s] = 0.368 120 m RMSE [m/s] = 0.375 | -The proposed transformer model, integrated with wavelet transform, can be applied to other multivariate time series forecasting tasks. |
| [39] | Improved kernel density estimation (IKDE) | wind speed, wind direction, and wind power of the wind farm, and numerical weather prediction (NWP) data. | Mean skill score=-0.527 | -The effect of outliers for our forecasting model shall be addressed in future research. |
| [40] | Goddard earth observing system model | Wind speed (m/s) Wind power (kW) Wind direction | RMSE [kW] = 76.18 | To incorporate the uncertainty of GEOS FP weather forecasts against MERRA-2 reanalysis into data set to be used for output power prediction for each hour of the time horizon ahead. |
| [41] | Support vector regression (SVR) | Wind speed (m/s) Wind power (kW) | RMSE/MW = 14.7435 | -To reduce the number of charging and discharging cycles of hybrid energy storage devices; -To prolong the operation life of the system, and improve the overall performance of the system. |
| [42] | Gradient-boosting machine (GBM) | Wind speed (m/s) Wind power (KW) | NMAE = 5.15% | To expand the periods of the test set for various months and seasons of wind-power forecasting. |
| [43] | Improved hunter-prey optimization (IHPO) algorithm-based extreme learning machine (ELM) | Data from the SCADA systems Wind speed (m/s) Wind power (kW) | RMSE(kW) = 50.55 | To improve the prediction accuracy for wind power. |
| [44] | Kernel extreme learning machine (KELM) | Wind data | Reliability performance parameter P (%) = 90.92 | To explore the relevance of the implications for BRICS countries. |
| Ref | Model Type | Parameters Used | Accuracy | Future Studies |
|---|---|---|---|---|
| [15] | A convolution-based spatial–temporal wind power predictor (CSTWPP) | Historical wind power | MASE = 190.02 RMSE = 7.49 | CSTWPP model is essentially a multi-task model, predicting all the wind farms’ future power at the same time. |
| [16] | The spatiotemporal convolutional network (STCN) with a directed graph convolutional structure. | -Historical power data -STCN parameters selected by oneself | MAEs = 3.17% RMSEs = 2.88%, | A wind power forecasting framework will be investigated to ensure data security for multiple wind farms. |
| [45] | A deep optimized convolutional LSTM-based ensemble reinforcement learning strategy (DOCLER) | Wind power | RMSE = 7.1322% MAE = 4.6713% | Optimization of grid integration issues. |
| [46] | A variational mode decomposition (VMD) and convolutional long short-term memory network (Conv LSTM) model | Wind power | MRE(KW) = 0.016 MAE(KW) = 792 MSE(KW) = 1,568,305.38 RMSE(KW) = 1252.32 | Other intelligent algorithms to optimize the proposed model are studied. |
| [47] | A multi-source and temporal attention network (MSTAN) | Wind speed, pressure, temperature, humidity, and wind direction | NRMSE = 0.154 NMAE = 0.110 | -Novel spatial attention or spatial feature extraction modules should be merged into MSTAN; -The applicability of MSTAN at other time resolutions should be verified. |
| [48] | Two-dimensional convolution neural network trained by improved accidental floater PSO | Fine-tuning the weights of TDCNN by proposed AFPSO | MAPE:3.76 NMAE:2.46 NRMSE:3.12 | Using AFPSO algorithms will lead to a longer modeling time. |
| [49] | Deep neural network: LSTM method (best); MLP (second best) while using SVR, KNNR, and physical model with an expert correction | More LSTM parameters and setting these parameters by oneself | GBT, RF, PHYS(v1&v2)→ KNNR, MLP, LSTM with additional expert SS:0.5925; nMAE[%]:11.3055; nRMSE:0.1618; nMBE:0.0146 | The proposed ensemble methods are also applicable to short-term generation forecasting for other renewable energy sources (RES). -Input data requires pre-processing to extract features to solve long running time due to too much input data. |
| [50] | -Optimizing the hyperparameters of the LSTM network by the modified PSO algorithm -A PSO_LSTM model | Selecting parameters by PSO | MPSO_ATT_LSTM MAPE: 4.6%; MAE: 211.5 kW Device capacity > 20,000 kW | It is required to avoid overfitting in optimization algorithms and modeling. Therefore, training data and test data are usually required to be evaluated together. |
| [51] | Advanced deep learning techniques Encoder–Decoder LSTM | Setting parameters by oneself | Annual and monthly errors | Additional meteorological and site determination factors such as the amount of rain, azimuth for solar irradiation, wind direction, etc. for windspeed forecasting could be considered. |
| [52] | The CNN-MLSTMs-T Model | Wind power | RMSE = 0.1998; MAE = 0.1523 | The combination of the sample similarity analysis idea and other hybrid models will be our future research focus. |
| [53] | Generative moment matching network (GMMN) | Historical wind power | PINAW = 8.66 MW; PICP = 84% RMSE = 127.10; MAE = 0.6855 MW | The WindGMMN can be extended to the robust optimization of distribution networks. |
| [54] | Bidirectional long short-term memory (Bi-LSTM) | Manual adjustment layers | Error can be divided into training, test, and validation errors | New optimization algorithms or the integration of multiple optimization algorithms will be investigated to optimize the forecasting model. |
| [55] | Multi-step informer network (MSIN) | Manual selection of parameters | Multi-step informer network (MSIN) improves forecast accuracy by 29% compared with the informer network for RMSE | To consider the non-trivial correlations of meteorological variables without relying on single historical data in forecasting. |
| [56] | Long short-term memory neural network (LSTM) with the improved particle swarm optimization algorithm (IPSO) | Determining the LSTM and DENSE layers, the number of neurons | VMD-CNN-IPSO-LSTM MAE:2.92668; RMSE:3.59604 MAPE:0.20147; adj-R2:0.96639 | To examine a multi-step decomposition model for feature extraction through different neural networks, such as graph convolutional neural networks for implicit mining. |
| [57] | Spatiotemporally multiple clustering and I–CNN-BILSTM deep learning network. | Historical power and meteorological data | MAPE(%) = 4.86, MAE = 18.64, abd RMSE = 28.45. | The uncertain power prediction of multiple wind farms with spatio-temporal coupling in extreme weather. |
| [58] | 1.The model input data organization framework 2.The unified forecast based on STC-DPN 3.The single site error correction of TCN-LSTM. | Wind speed, wind direction | MAE = 2.071, RMSE = 2.431, COR = 0.568 | To apply the strategies and models proposed to more research fields, such as wind power forecast or wind turbine fault early warning. |
| [59] | Temporal inception convolutional network (TICN) wind speed interval prediction model | Wind speed | PICP = 0.994 PINAW = 0.087 | It may have a better effect on some short-term prediction occasions. |
| [60] | Hybrid deep learning model | Wind speed, air temperature, and air pressure | MAE = 1.59, RMSE = 3.73 and MAPE = 8.13. | -To tune the parameters of the model using advanced optimization algorithms. -To reduce computation time and provide more accurate results. |
| [61] | Multi-Task GCN (MTGCN) | Temperature, humidity, weather, historical wind power | PICP = 0.9634, PINAW = 0.0363, CWC = 0.2178 | To utilize advanced ML techniques such as transformer to further improve wind power forecasting performance. |
| [62] | CNN-ED-LSTM model | Air temperature, pressure, wind direction, wind power | MSE = 0.0102 MAPE = 46.24 MAE = 0.0623 RMSE = 0.1012 | -To improve the accuracy of the CNN-ED-LSTM model in WPPA, hyperparametric optimization strategies using intelligent algorithms to efficiently enhance DL models to obtain optimal values of hyperparameters. |
| [63] | Long short-term memory (LSTM) neural network | Actual historical data | RMSE (MW) = 0.94 MAE (MW) = 0.67 MAPE (%) = 49.71 | To extend to the power prediction derived from wind over a large area. |
| [64] | Seq2Seq model | The historical wind speed, wind direction, and total power output of 24 wind turbines with a 10-min resolution | RMSE = 129.3 MAE = 81.1 | To implement an adaptively sized time window on the input variables based on cross-correlation analysis |
| [65] | Long short-term memory (LSTM) | Actual historical data | RMSE(MW) = 1.27 MAE(MW) = 0.90 | A good starting point can range from 1 × 10 without the time of day and numerical weather prediction information -Easily be incorporated in the extension work. |
| [66] | Deep learning | Historical data on measured weather and numerical weather predictions (NWPs) | NRMSE = 0.16 MAPE = 0.15 | Using historical weather measurements as input allows the prediction model to compensate for the errors in weather predictions |
| [67] | Gated reference unit (GRU) | Ambient temperature, direction of the wind flow, speed of the wind, and wind power generated from the wind turbine. | Mean Square Error = 0.130 | The GRU network is better suited to extract extremely non-linear and complex data from an input data set in real time to boost wind speed prediction. |
| [68] | A deep learning model (gated recurrent unit, GRU) | Meteorological wind speed, wind direction, and wind power data | RMSE = 111.9766 | To implement multistep wind power forecasting based on deep learning. |
| [69] | Residual CNN-based deep forecasting method. | Meteorological wind speed, wind direction, and wind power data | 1-h ahead. RMSE = 0.9947 | To examine in detail different decomposition approaches |
| [70] | Bidirectional long short-term memory network (BiLSTM) | Numerical weather prediction (NWP) Wind speed Wind direction Temperature | RMSE/MW = 1.0822 | -To develop probability forecasting based on single point forecasting in order to realize the quantitative description of wind energy uncertainty; -To better serve the multi-aspect optimization decisions of the power system. |
| [71] | The Encoder–Decoder framework is constructed with LSTM as the basic unit | Wind direction Wind speed (m/s) Wind power (kW) | RMSE = 0.1243 | To significantly affect the performance of such data-driven forecasting methods. These remain our further research questions. |
| [72] | Long short-term memory (LSTM) network using an improved Adam optimizer with loss shrinkage (LsAdam) | Data from the SCADA systems Wind speed (m/s) Wind power (kW) | Train set MSE(×10−3) = 3.5961 Test set MSE(×10−3) = 2.1628 | The trained model will have better performance since the learning rate is iteratively tuned with past loss-changing information. |
| [73] | Long short-term memory (LSTM) | Temperature, humidity, pressure, wind power, | RMSE(%) = 10.23 | To improve the prediction accuracy for wind power |
| Ref | Model Type | Parameters Used | Accuracy | Future Studies |
|---|---|---|---|---|
| [20] | An ensemble neural forecast framework (ENFF) with three neural predictors for wind speed forecasting below. Elman neural network (ELM) Feedforward neural network (FNN) Radial basis function (RBF) neural network | Wind speed, meteorological | Errors around 0.6 m/s | Planning framework and operation strategy are developed for the storage providing virtual inertia support (VIS) in a low-inertia power system. |
| [74] | The CEEMDAN-IBA-GPR model | Historical wind power data | Stand deviation = 10.42 | Optimal dispatching of isolated or grid-connected MG considerations of economic cost, net pollutant emission, and operational security objectives will be the focus of future work. |
| [75] | A multi-feature fusion self-attention mechanism graph convolutional network (MFF-SAM-GCN) forecasting model | Hyperparameter optimization of the predictive model by Bayesian optimization (BO) | RMSE of the proposed (MFF-SAM- GCN) model is 0.0284, while the SMAPE is 9.453%, the MBE is 0.025, and R2 is 0.989. | New optimization algorithms or the integration of multiple optimization algorithms will be investigated to optimize the forecasting model. |
| [76] | The WD-IGFCM-LSTMS model for the accuracy of short-term wind power forecasting (WPF) approach | The best parameters determined by the IGWO algorithm | Case A: NMAE 10.32%; NRMSE 14.59% CR: 85.41%; QR: 91.53% Case B: NMAE 10.18%; NRMSE 13.52% CR: 86.48%; QR: 91.53% | -The forecasting accuracy for short-term WPF can be improved by correcting NWP data; -The possibility of extending the wave-oriented approach to NWP data correction will be further done. |
| [77] | Generalized regression neural network (GRNN) and support vector machine (SVM) | Turning GRNN and SVM parameters by oneself | The GRNN model gives the CC value of 0.956, RMSE of 28.82 The SVR model gives a CC value of 0.965 and an RMSE of 44.40. | A new technique for feature selection is needed to design electricity load forecasting for this type of area, which is connected to multiple electricity grid systems. |
| [78] | The WPD-VMD-SSA-IGWO-KELM model | Wind speed | NMAE = 11.2% MAPE = 4.2% | -The suitable length of the train set is variable when wind power significantly changed. -The error sequence can be used to correct the prediction. |
| [79] | Variational mode Decomposition (VMD) and Random forest (RF) | NWP data containing 24 meteorological factors and wind power trend component data. | NRMSE(%) = 11.421 NMAE(%) = 8.152 | The implicit law of wind power sequence in frequency and time domain. |
| [80] | Hybrid VMD-CNN-GRU-based model | Wind power, wind speed, wind direction, temperature, pressure, air density and humidity. | RMSE = 1.5651, MAE = 0.8161, MAPE = 11.62%, and R2 = 0.9964. | The impact assessment and cost-benefit analysis should be performed in future work. |
| [81] | Spatiotemporally multiple clustering and I-CNN-BILSTM deep learning network. | Historical power and meteorological data | MAPE (%) = 4.86, MAE = 18.64, abd RMSE = 28.45. | The subsequent research will focus on the uncertain power prediction of multiple wind farms with spatio-temporal coupling in extreme weather. |
| [82] | The hybrid forecasting method based on the corrected NWP data and the SC. | Temperature, humidity, wind direction, wind speed. | RMSE = 1.238, MAPE = 0.325, MAE = 0.7002 | To introduce advanced artificial intelligence and machine learning methods to assist the automatic scene division of the complex input data. |
| [83] | MMMD-K-means-SDAE-LSTM model | Wind speed, wind direction, wind power data | NMAE = 6.43, NRMSE = 9.59 | -The operating costs of the model for computational time and hardware costs are higher than those of a simple forecasting model. -The time horizon for effective forecasts is short (30 min to 24 h). |
| [84] | LSTM-WPRE model | Wind speed, wind direction, air temperature, relative humidity, and pressure | MAPE = 0.094, rRMSE = 0.112 | -The overall running time should decrease; -The proposed model should be suitable for newly installed wind farms. |
| [85] | Outlier detection, decomposition of time series, effective feature selection, and prediction of each time series decomposed. | Wind direction, wind speed, or wind power | NRMSE = 0.1020 NMAE = 0.0803 | The economic, technical, and environmental benefits achieved from high-accuracy wind power forecasting. |
| [86] | KHC algorithm for clustering, components extraction and selection with SVD, and building SVR forecast model. | Wind power, wind direction, wind speed, temperature, pressure, and density | MAE = 0.273 RMSE = 0.343 | With the increasing number of wind turbines a more efficient and effective measurement of similarity of weather patterns between different wind turbines. |
| [87] | GBRBM-DBN consists of the PCA, NWP, and SC for wind power forecasting. | Wind direction, wind speed, rainfall, temperature, surface sensible heat, air pressure, and air density | RMSE = 2.6018, MAPE = 0.2859, MAE = 2.3857 | The utilization of the adaptive learning step technique further improves system accuracy. |
| [88] | ST-GWO-MSVM model | Wind power | NMAE = 3.3221, NRMSE = 4.64875, FB = 0.0029, DA = 0.8342 | To improve the performance of ST-GWO-MSVM. |
| [89] | FCM-WOA-ELM-GMM Model | Wind speed, wind direction, air pressure, temperature, and humidity | MAE = 3.8%, RMSE = 5.24% | To improve the calculation accuracy of the probability density distribution of wind power forecasting errors. |
| [90] | Seasonal Autoregressive Integrated Moving Average (SARIMA) model | Historical wind velocity | RMSE = 13.09 MAPE = 1.03 | If the time series is non-stationary, the study needs to use differencing or de-trending techniques to make it stationary before applying the AR method. |
| [91] | Historical wind climate model and Physical model | Wind speed and weather data | RMSE = 13% MAE = 20.7% | These span the areas of resource assessment, wind power forecasting, and validation, as well as market instruments. |
| [92] | Hybrid prediction method | Wind power and direction | MAPE = 16.87% MAE = 27.1% CI = 0.968 | The region’s correlations between different renewable energy systems on the performance of the prediction model. |
| [93] | Multi-modal Multi-task Spatiotemporal Attention Network (M2STAN) model | Wind direction, wind speed, temperature, atmospheric pressure, and air density | RMSE = 6.27% MAE = 4.01% | To explore efficient and reliable machine learning hyperparameter optimization methods. |
| [94] | AMC-LSTM hybrid model | Historical wind power, torsion angle, wind speed, impeller speed, temperature, generator speed, wind direction | MSE(e−2) = 0.8951 MAE = 0.0505 RMSE = 0.0946 | -To integrate multi-scale extended features -To improve short-term wind power prediction accuracy. |
| [95] | Gaussian mixed clustering-Deep neural network probabilistic forecasting (GMC-DeepNN-PF) | Wind direction, wind speed, wind power | RMSE(MW) = 56.6893 MAPE(%) = 4.839 MAE(MW) = 42.0201 | -To expand wind direction and time properties for improving the accuracy of WPF. |
| [96] | Self-attention temporal convolutional network Long-short term memory (SATCN-LSTM) | Wind speed, air density, wind direction, temperature, and surface pressure. | RMSE = 0.680 | No description |
| [97] | Multiple stacked bi-directional long and short-term memory (Bi-LSTM) networks | Wind direction Wind speed (m/s) Wind power (kW) | RMSE(×10−2) = 6.47473 | To develop more efficient and accurate prediction methods for wind power prediction by exploiting adaptive denoising. |
| [98] | The Proposed Hybrid Intelligence Model XGBoost, Tree, SVR, and BPNN methods | Converting wind data to wavelet information | RMSE = 1.8313 | The proposed hybrid model will be of great attraction and practical application in power systems. |
| [99] | Long short-term memory (LSTM) | Wind speed (m/s) Wind power (kW) | RMSE = 2.63109 | -To use a multi-step decomposition model; -The sub-sequence obtained from the decomposition is passed through different neural networks for feature extraction. |
| Ref | Model Type | Parameters Used | Accuracy | Future Studies |
|---|---|---|---|---|
| [9] | Modified hidden Markov model | Wind speed, wind direction, wind power | RMSE = 3.093 MAE = 2.451 | The error transfer mechanism from wind speed forecast (WSF) to wind power forecast (WPF) are of great interest for the improvement of WPF. |
| [10] | Distance-weighted kernel density estimation (KDE) and regular vine (R-vine) copula | Wind power output, wind speed | RMSE = 0.1089 MAE = 0.075 | As computing becomes faster and less expensive, the task of achieving enough scenarios will become easier in the future. |
| [11] | The k-NN and conditional KDE models | Historical wind power | MAE = 3.18; RMSE = 4.63; R2 = 0.94 | More work needs to be done in terms of bandwidth selection for high-dimensional datasets in KDE based approaches. |
| [12] | A quantile passive–aggressive regression (QPAR) model for online convex optimization problems | Wind power | Pinball loss (PBL) = 13.3 Average coverage error (ACE) = 4.86%, Winkler score (WKS) = 78.71 and Continuous ranked probability score (CRPS) = 26.21 | Addressing this missing data problem is necessary for the actual implementation of these methods. |
| [13] | Spatiotemporal quantile regression (SQR) | Wind power data | RMSE = 16.62%; MAE = 11.23% | To enhance predictive effects and computational efficiency for wind power prediction. |
| [100] | Higher-order multivariate Markov chain (HMMC) | Wind power; PV power, Heat index | NRMSE = 2.59 | -The HI index was utilized as an additional meteorological variable. -The dynamic update of the model parameters was applied to the wind power forecast. |
| [101] | Five minute-ahead wind power forecasts in terms of point forecast skill scores and calibration | To deduce the value of kernel methods for parameter adjustment | The error value is represented by a picture rather than a simple number. | Future work will focus on extending this approach to other variables, e.g., temperature, wind speed, wind direction; additional forecast horizons; investigation of other kernel machines; and development of other adaptive models. |
| [104] | Empirical dynamic modeling (EDM)-based probabilistic forecast | Historical wind turbine power | CRPS (%) = 5.12 | The real-time WTP measurements are added to the reconstructed state space during the forecast process. |
| [105] | Multi-class autoregressive moving average (ARMA) | Historical wind power | RMSE = 127.10 MAPE = 1.25% | -To improve the interpretability of the combined models for further accuracy enhancement; -To incorporate the spatial correlation features into the classification and prediction. |
| [106] | Renewable energy is directly distributed to power dispatch | Incorporating renewable energy into the power flow | With an increase in power by 1.6 times, there is a decrease in energy of RES by 15-19. | -To generalize the model and evaluate the model accuracy |
| [107] | Weather research and forecasting model. | Wind power, wind speed, atmospheric and density | MAE = 15% (summer) and MAE = 26% (winter) | To improve large variance in winter model output. |
| [108] | WRF forecasting model; CCMP satellite data | Wind power, wind speed, | WRF model: RMSE = 1.68 to 2.85 m/s CCMP satellite data: RMSE = 1.79 to 2.89 m/s | To focus on the effects of the sea breeze across the region studied, the prediction of these conditions, and their impact on wind farm power generation. |
| [109] | Transformer | Wind power and NWP data | 8-step ahead RMSE = 7.51 16-step ahead RMSE = 10.88 | To further explore machine learning strategies for small sample data, such as data augmentation and transfer learning. |
| [110] | SVR with RBF kernel | Number of wind turbines Installed capacity (MW) Manufacturer type Hub height of tower/s (m) Cut-in/Cut-out wind speed (m/s) Rated wind speed (m/s) Swept area of a wind turbine (m2) | RMSE = 8.3404(Spring) RMSE = 6.6873(Summer) | To reduce computation time to enable the use of a smaller subset with 5-day data or even less. |
| [111] | ACE in the dynamic-indirect GP (DYINGP) mode | Wind speed (m/s) Wind power (kW) Wind direction | NRMSE = 3.66 | The coefficients could be controlled with state-of-the-art algorithms due to the covariance functions being very important in the GP results. |
| [112] | Secondary evolutionary generative adversarial networks (SEGAN) and dual-dimension attention mechanism (DDAM) assisted bidirectional gate recurrent unit (BiGRU) | Wind speed (m/s) Wind power (kW) Wind direction | RMSE = 119.645 (kW) MAE = 83.179 (kW) MAPE = 0.354% | -To consider the combination of the proposed SEGAN-DDAM-BiGRU with transfer learning. -To better address the wind power prediction problem without sufficient historical data available. |
| [113] | Support vector regression (SVR) | Wind data | RMSE (kW) = 66.26 | To be used as a reference for grid power generation planning and power system economic dispatch. |
| [114] | Support vector regression (SVR) | Wind power data Meteorological data | RMSE(MW) = 373 | The reanalysis data used in this paper may not fully represent the real data in practical applications, which affects the actual prediction of future wind power. |
| Ref | Methods/Models | Time Resolution | Accuracy | Prediction Method Level | Research Limitations |
|---|---|---|---|---|---|
| [9] | 6 | 24 h | RMSE = 3.093 MAE = 2.451 | 3 | A |
| [10] | 6 | 24 h | RMSE = 0.1089 MAE = 0.075 | 4 | A |
| [11] | 2,3,6 | 24 h | MAE = 3.18; RMSE = 4.63; R2 = 0.94 | 4 | A,C |
| [12] | 4,6 | 15 min | Pinball loss (PBL) = 13.3 Average coverage error (ACE) = 4.86%, Winkler score (WKS) = 78.71 and Continuous ranked probability score (CRPS) = 26.21 | 3 | A,C |
| [13] | 6 | 72 h–1 week | RMSE = 16.62%; MAE = 11.23% | 5 | A,E |
| [14] | 1 | 1 h | NMAE: DQR:9.086; QRNN:9.479 SBL:13.451; IFPA:13.967 NRMSE: DQR:10.917; QRNN:10.227 SBL:14.185; IFPA:14.538 | 3 | B,E |
| [15] | 4 | 15 min | MASE = 190.02 RMSE = 7.49 | 3 | A,E |
| [16] | 4 | 5 min~1 h | MAEs = 3.17% RMSEs = 2.88%, | 3 | B,F |
| [17] | 1 | 24 h | NRMSE = 0.138 | 4 | A,B |
| [18] | 1 | 1 h | Mean absolute relative error (MARE) = 7.5%; Rj = 5.4% (mean value of the Pearson correlation coefficient) | 3 | C,F |
| [19] | 1 | 1 month-years | RMSE = 1.04%; MAD = 0.91% MSE = 1.05% | 5 | C,D,E |
| [20] | 1,2 | 15 min | Errors around 0.6 m/s | 3 | E,F |
| [21] | 1 | 15 min | The model accuracy improved by 7.61% and the RMSE reduced by 8.76% | 3 | B,D,F |
| [22] | 1 | 1 min | Mean square error (MSE) GBRT: 0.224; MLP: 0.117 Random forest with Bootstrap sampling: 0.111 Random forest with Poisson re-sampling: 0.096 | 2 | A,F |
| [74] | 5 | 15 min~1 h | Stand deviation = 10.42 | 3 | A |
| [75] | 5 | 1 h | RMSE of proposed (MFF-SAM- GCN) model is 0.0284, while the SMAPE is 9.453%, the MBE is 0.025, and R2 is 0.989. | 3 | B,E |
| [25] | 5 | 2 h, 4 h | Both MAE and RMSE of less than 10% | 3 | C,D,F |
| [26] | 2,3 | 30 min | R2 = 98.9; RMSE = 50.36; MAE = 23.63 | 3 | C,E |
| [27] | 1,2,3 | 1 h | The average nRMSE for WNN trained by ISCA, ELM, RBF, MLP, WNN trained by PSO are 5.4059%, 6.925%, 10.294%, 12.407%, and 17.038%. The average nMAE for WNN trained by ISCA, ELM, RBF, MLP, and WNN trained by PSO, are 4.2893%, 5.4787%, 8.2527%, 9.5773%, and 13.4847%. | 3 | D,E,F |
| [28] | 2,3 | 10 min | DR-SVM VMED(m/s): 6.895 MAE (m/s): 0.723 RMSE(m/s): 0.932 MAPE(%): 11.87 CPU time(s): 148.15 | 3 | D,F |
| [29] | 2,3 | 1~5 min, 24 h, 72 h–1 week | No description | 4 | A,B |
| [30] | 2,3 | 10~30 min, 1–4 h | MAPE = 0.0372; NBE = 0.4621 RMBE = 0.2950; R2 = 0.9857 | 4 | D |
| [31] | 2,3 | 48 h | MAPE = 1.2677 RMSE = 0.2576 | 5 | A |
| [45] | 4 | 30 min | RMSE = 7.1322% MAE = 4.6713% | 3 | A,B |
| [46] | 4,2 | 1 h,48 h | MRE(KW) = 0.016 MAE(KW) = 792 MSE(KW) = 1,568,305.38 RMSE(KW) = 1252.32 | 5 | C,D |
| [47] | 4,2 | 30 min | NRMSE = 0.154 NMAE = 0.110 | 3 | A,C |
| [48] | 4,3 | 1 h | Average error of four seasons MAPE:3.76 NMAE:2.46 NRMSE:3.12 | 3 | C,D |
| [76] | 4,5 | 1 h | Case A: NMAE 10.32%; NRMSE 14.59% CR: 85.41%; QR: 91.53% Case B: NMAE 10.18%; NRMSE 13.52% CR: 86.48%; QR: 91.53% | 3 | A,B |
| [49] | 4,6 | 1 h | INT_OUT_EXT[GBT, RF, PHYS(v1&v2)→KNNR, MLP, LSTM] with additional expert SS:0.5925; nMAE[%]:11.3055 nRMSE:0.1618; nMBE:0.0146 | 3 | A,C,D |
| [50] | 4,3,2 | 1 h | MPSO_ATT_LSTM MAPE: 4.6%; MAE: 211.5 kW Device capacity > 20,000 kW | 3 | A,B,F |
| [51] | 4,2 | 1 h | Annual and monthly errors | 3 | D,F |
| [52] | 4,1,2 | 15 min | RMSE = 0.1998; MAE = 0.1523 | 3 | C,E |
| [53] | 4,1 | 15 min | PINAW = 8.66 MW; PICP = 84% RMSE = 127.10; MAE = 0.6855 MW | 3 | E,F |
| [54] | 4,2 | 1 h | Error can be divided into training, test, and validation errors | 3 | A,F |
| [55] | 4,2 | 10 min | Multi-step informer network (MSIN) improves forecast accuracy by 29% compared with the informer network for RMSE | 2 | C,D |
| [56] | 4,2,3 | 15 min | VMD-CNN-IPSO-LSTM MAE:2.92668; RMSE:3.59604 MAPE:0.20147; adj-R2:0.96639 | 3 | A,B |
| [77] | 5 | 1 h | The GRNN model gives a CC value of 0.956, an RMSE of 28.82, and the SVR model gives a C value of 0.965 and RMSE value of 44.40. | 3 | C,F |
| [78] | 5 | 4 h | NMAE = 11.2% MAPE = 4.2% | 3 | A,E |
| [100] | 6 | 15 min | NRMSE = 2.59 | 3 | A,C |
| [101] | 6 | 5 min | The error value is represented by a picture rather than a simple number. | 2 | D,F |
| [102] | 6 | 1 h | 1% point analysis gap to the optimal solution, which requires complete information, including future values | 3 | C,D |
| [103] | 6 | 5~15 min | No description | 2 | C,D,F |
| [104] | 2,6 | 30-min | CRPS (%) = 5.12 | 3 | F |
| [105] | 4,6 | 15 min | RMSE = 127.10 MAPE = 1.25% | 2 | C,E |
| [106] | 6 | 1 h | With an increase in power by 1.6 times, there is a decrease in the energy of RES by 15–19. | 3 | E,F |
| [79] | 5 | 3 h~24 h | NRMSE(%) = 11.421 NMAE(%) = 8.152 | 4 | C,E |
| [80] | 5 | 1 h~24 h | RMSE = 1.5651, MAE = 0.8161, MAPE = 11.62%, and R2 = 0.9964. | 4 | E |
| [57] | 1,4 | 15 min | MAPE (%) = 4.86, MAE = 18.64, RMSE = 28.45. | 3 | C,D,F |
| [81] | 1,3 | 10-min | RMSE = 0.0921, MAPE = 0.0081, MAE = 0.0706 PICP = 0.982, PINAW = 0.025, CPIA = 0.973 APL = 0.0267, CRPS = 0.053 | 3 | D,F |
| [82] | 5 | 24 h | RMSE = 1.238, MAPE = 0.325, MAE = 0.7002 | 5 | D |
| [58] | 1,2 | 24 h | MAE = 2.071, RMSE = 2.431, COR = 0.568 | 4 | A,C |
| [23] | 1,4 | 15 min | MAE = 2.42, RMSE = 2.67 and MAPE = 0.12. | 3 | D,E |
| [59] | 4,5 | 0.25 h~4 h | PICP = 0.994 PINAW = 0.087 | 3 | B,C |
| [32] | 2,5 | 48-h | MAE = 0.0861, RMSE = 0.1262, R2 = 0.8333, AR = 87.38% | 5 | C,D |
| [83] | 5,1 | 30 min to 24 h | NMAE = 6.43, NRMSE = 9.59 | 4 | A |
| [84] | 5,4 | 24-h | MAPE = 0.094, rRMSE = 0.112 | 4 | A |
| [60] | 4 | 15 min | MAE = 1.59, RMSE = 3.73 and MAPE = 8.13. | 3 | A,C |
| [85] | 5 | 24 h | NRMSE = 0.1020 NMAE = 0.0803 | 4 | C,D |
| [86] | 5 | 1 h~12 h | MAE = 0.273 RMSE = 0.343 | 4 | E |
| [107] | 6 | 10 min | MAE = 15% (summer) and MAE = 26% (winter) | 3 | D,F |
| [87] | 5,4 | 24 h | RMSE = 2.6018, MAPE = 0.2859, MAE = 2.3857 | 4 | C,E |
| [88] | 5,3 | 15 min | NMAE = 3.3221, NRMSE = 4.64875,FB = 0.0029, DA = 0.8342 | 3 | A,E |
| [61] | 4 | 5 min | PICP = 0.9634, PINAW = 0.0363, CWC = 0.2178 | 2 | A,B |
| [89] | 5 | 4 h~72 h | MAE = 3.8%, RMSE = 5.24% | 5 | E |
| [90] | 5 | 30 min ~ 6 h 1~7 days | RMSE = 13.09 MAPE = 1.03 | 3 | E,F |
| [91] | 5,6 | 1 h | RMSE = 13% MAE = 20.7% | 3 | A,D |
| [92] | 5,4 | 24 h | MAPE = 16.87% MAE = 27.1% CI = 0.968 | 3 | A,B |
| [33] | 5,2 | 1 h | MAPE = 2.62 and RMSE = 0.14 | 3 | C,F |
| [34] | 4,3 | 1 week | reliability and skill score are reduced by 10% to 33%. | 3 | F |
| [35] | 5,2 | 1~24 h | RMSE = 5% and R2 = 0.95 | 4 | A |
| [93] | 5,4 | 15 min | RMSE = 6.27% MAE = 4.01% | 3 | A,C |
| [94] | 5,4 | 1~3 h | MSE(e-2) = 0.8951 MAE = 0.0505 RMSE = 0.0946 | 4 | C,E |
| [36] | 1,4 | 10 min | RMSE = 0.02 MAE = 0.007 MAPE = 0.60 R2 = 0.84 | 3 | C,D |
| [37] | 1,4 | 10 min | PA = 0.934 MAE = 84.837 RMSE = 134.837 | 2 | A,C |
| [95] | 5,4 | 10 min | RMSE(MW) = 56.6893 MAPE(%) = 4.839 MAE(MW) = 42.0201 | 3 | A,B |
| [62] | 4,1 | 1 h | MSE = 0.0102 MAPE = 46.24 MAE = 0.0623 RMSE = 0.1012 | 4 | A,F |
| [63] | 6,1 | 10 min | RMSE (MW) = 0.94 MAE (MW) = 0.67 MAPE (%) = 49.71 | 3 | C,E |
| [38] | 2,4 | Anemometric height | Anemometric height 100 m RMSE [m/s] = 0.383 150 m RMSE [m/s] = 0.368 120 m RMSE [m/s] = 0.375 | 3 | A |
| [108] | 6 | 1 h | WRF: RMSE = 1.68 to 2.85 m/s CCMP: RMSE = 1.79 to 2.89 m/s; | 4 | D |
| [64] | 4,6 | 10 min. | RMSE = 129.3 MAE = 81.1 | 2 | B |
| [65] | 2,1 | 1 h | RMSE(MW) = 1.27 MAE(MW) = 0.90 | 3 | A |
| [66] | 4,2 | 1 h | NRMSE = 0.16 MAPE = 0.15 | 3 | C,E |
| [96] | 5,2 | 10 min | RMSE = 0.680 | 3 | A,B |
| [39] | 3,2 | 1 h | Mean skill score = −0.527 | 3 | A |
| [67] | 2,4,5 | 1 h | MSE = 0.130 | 3 | A,C |
| [68] | 4,3,2 | -No description -Establishing wind power curves for wind turbines | RMSE = 111.9766 | 2 | E,F |
| [69] | 1,4 | 1 h | 1-h ahead. RMSE = 0.9947 | 3 | B,C |
| [97] | 1,2,5 | 10 min | RMSE(×10−2) = 6.47473 | 3 | A |
| [109] | 3,6,2 | -No time unit written | 8-step ahead RMSE = 7.51 16-step ahead RMSE = 10.88 | 2 | E |
| [24] | 1,3 | 1 h | RMSE (MW) = 0.2949 | 4 | A |
| [110] | 6,3 | 15 min | Spring RMSE = 8.3404 Summer RMSE = 6.6873 | 3 | A,D |
| [111] | 4,6 | 1 h | NRMSE = 3.66 | 4 | A |
| [112] | 4,1,6 | 10 min | RMSE = 119.645 (kW) | 3 | A,B |
| [40] | 2,6 | 1 h | RMSE(kW) = 76.18 | 4 | C,D |
| [70] | 2,5 | 10 min | RMSE(MW) = 1.0822 | 3 | A,B |
| [98] | 5,4 | 15-min | RMSE = 1.8313 | 3 | A |
| [71] | 4,1 | 15 min | RMSE = 0.1243 | 3 | C,D |
| [72] | 4,2 | 10 min | -Train set MSE (×10−3) = 3.5961 -Test set MSE (×10−3) = 2.1628 | 3 | B |
| [41] | 3,2 | 1 h | RMSE(MW) = 14.7435 | 3 | F |
| [73] | 2,3 | -No description -Establishment of wind turbine power capacity | RMSE (%) = 10.23 | 2 | A,B |
| [42] | 3,2 | 15 min | NMAE = 5.15% | 3 | C,D |
| [43] | 2,3 | 10 min | RMSE (kW) = 50.55 | 2 | A,B |
| [99] | 5,3 | 15 min | RMSE = 2.63109 | 3 | A,B |
| [113] | 3,6 | 10 min | RMSE (kW) = 66.26 | 2 | B,D |
| [44] | 3,2 | 1 h | Reliability performance parameter P (%) = 90.92 | 4 | E,F |
| [114] | 2,3 | 15 min | RMSE(MW) = 373 | 3 | C,D,F |
| Methods | Distribution Region | Reviewed Works | Distribution Region | Reviewed Works |
|---|---|---|---|---|
| 1 | A1 | [13,19] | G1 | [25,77,90] |
| B1 | [82,89] | H1 | [14,18,75,77,100,106] | |
| C1 | [10,17] | I1 | [45] | |
| D1 | [79,80,85,86] | J1 | [15,16,21,60,74,107] | |
| E1 | [108] | K1 | [22,61,101,103] | |
| F1 | [9] | |||
| 2 | A2 | [31,32] | G2 | [34] |
| B2 | [46] | H2 | [59,92] | |
| C2 | [35,58,84,87,94] | I2 | [33,39,48,49,51,54,65,66,76,91] [41,69] | |
| D2 | [24,40,44,62,111] | J2 | [26,47,104] | |
| E2 | [83] | K2 | [12,20,23,28,36,42,53,57,63,70,71,72,81,88,93,95,96,98,99,110,114] | |
| F2 | [29,30] | L2 | [37,43,55,64,105,113] | |
| 3 | A3 | [11] | References [29,30,46,83] using two methods as shown in Figure 5 are even better than the average value of Method 2, which is worth recommending for future studies of wind power prediction models. References [38,68,73,109] are eliminated due to a lack of time resolution and a non-wind power prediction model. | |
| B3 | [27,50,67] | |||
| C3 | [52,56,97,112] | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, W.-C.; Hong, C.-M.; Tu, C.-S.; Lin, W.-M.; Chen, C.-H. A Review of Modern Wind Power Generation Forecasting Technologies. Sustainability 2023, 15, 10757. https://doi.org/10.3390/su151410757
Tsai W-C, Hong C-M, Tu C-S, Lin W-M, Chen C-H. A Review of Modern Wind Power Generation Forecasting Technologies. Sustainability. 2023; 15(14):10757. https://doi.org/10.3390/su151410757
Chicago/Turabian StyleTsai, Wen-Chang, Chih-Ming Hong, Chia-Sheng Tu, Whei-Min Lin, and Chiung-Hsing Chen. 2023. "A Review of Modern Wind Power Generation Forecasting Technologies" Sustainability 15, no. 14: 10757. https://doi.org/10.3390/su151410757









